Edge Detection and Depth Estimation Using a Tilt Angle Map from Gravity Gradient Data of the Kozaklı-Central Anatolia Region, Turkey

Abstract

In this paper the application of an edge detection technique to gravity data is described. The technique is based on the tilt angle map (TAM) obtained from the first vertical gradient of a gravity anomaly. The zero contours of the tilt angle correspond to the boundaries of geologic discontinuities and are used to detect the linear features in gravity data. I also present that the distance between zero and $\pm {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-\nulldelimiterspace} 4}$ pairs obtained from the TAM corresponds to the depth to the top of the vertical contact model. Alternatively, the half distance between $- {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-\nulldelimiterspace} 4}$ and $+ {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-\nulldelimiterspace} 4}$ radians is equal to the depth to the same model. I illustrate the applicability of the present method by gravity data due to buried vertical prisms, imaging the positions of the edges of the prisms. The results obtained from the theoretical data, with and without random noise, have been discussed. The analysis of the TAM has been demonstrated on a field example from the Kozaklı-Central Anatolian region, Turkey, and the location and depth of the edges of the structural uplifts of the Kozaklı graben are imaged. The results indicated that depth values from these sources have ranged between 0.2 and 0.6 km. I have also compared the Euler deconvolution technique with the TAM images obtained from the first vertical gradient of residual gravity anomaly. Both techniques have agreed closely in detecting the horizontal location and depth of the uplift edges in the subsurface with good precision.

1 Introduction

Gravity anomalies are the result of the interference among geological sources with different shape, densities and depths. Of particular interest to the geologist are the linear anomalies in geophysical maps which may correspond to buried faults, contacts, and other tectonic and geological features.

Most short-wavelength anomalies are caused by near-surface contacts of rocks that have different density contrasts. There are many techniques that have been employed to achieve edge enhancement and detection of such features. The horizontal and vertical gradients are often used to highlight subtle features, as well as accentuate discontinuities and breaks in anomaly trends. The advantages of using the vertical gradient of gravity data were first recognized by Evjen (1936). Cordell and Grauch (1985) developed the horizontal derivative method to locate the horizontal position of the density or magnetization boundaries. Hansen et al. (1987) used the horizontal gradient magnitude and the analytic signal for interpreting edges and dips in gravity anomaly data. Rajagopalan and Milligan (1995) used automatic-gain-control to enhance the amplitude of short-wavelength anomalies without diminishing long-wavelength anomalies. Thurston and Smith (1997) introduced the local wavenumber method as edge detection. Pawlowski (1997) has shown the usefulness of the Radon transform in displaying linear features in magnetic data according to their strike direction. Cooper (2003) has developed a sunshading technique, a directional filter to enhance features in certain directions and suppress the linear features which are perpendicular to the desired direction. The tilt angle technique was first proposed by Miller and Singh (1994) to estimate the location of magnetic causative bodies on profile data. Verduzco et al. (2004) enhanced this method so that it could be applied to grid data and suggested using the total horizontal derivative of the tilt angle as an edge detector. Wijns and Kowalczyk (2005) explained a theta map technique for edge detection in magnetic data. The only difference from the TAM is that they plotted the cosine of the tilt angle. The first application of tilt angle technique in the interpretation of gravity gradient tensor (GGT) data was carried out by Oruç and Keskinsezer (2008). Oruç and Keskinsezer (2008) showed that the tilt angle values from GGT are highly suitable for mapping linear geological structures.

I describe the application of a new edge detection technique based on the first vertical gradient of gravity anomaly from semi-infinite vertical contact model. The practical utility of the technique is demonstrated to improve the gravity resolution and emphasized the effects of the geological boundaries for the structural framework of the Kozaklı-Central Anatolian region, Turkey.

2 Methodology

In this section I have developed a method for mapping the edges of the contact-like structures and depth to source.

2.1 Tilt Angle of Gravity Vertical Gradient from Semi-Infinite Vertical Contact

Verduzco et al. (2004) developed the tilt angle filter. This filter is defined as

$$ {\text{TDR}} = \tan^{ - 1} \left( {{\frac{{{{\partial f} \mathord{\left/ {\vphantom {{\partial f} {\partial z}}} \right. \kern-\nulldelimiterspace} {\partial z}}}}{{\sqrt {\left( {{{\partial f} \mathord{\left/ {\vphantom {{\partial f} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}} \right)^{2} + \left( {{{\partial f} \mathord{\left/ {\vphantom {{\partial f} {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}}} \right)^{2} } }}}} \right) $$

(1)

where f is the magnetic or gravity field and ${{\partial f} \mathord{\left/ {\vphantom {{\partial f} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}$, ${{\partial f} \mathord{\left/ {\vphantom {{\partial f} {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}}$ and ${{\partial f} \mathord{\left/ {\vphantom {{\partial f} {\partial z}}} \right. \kern-\nulldelimiterspace} {\partial z}}$ are the first derivatives of the field f in the x, y and z directions. The tilt amplitudes are restricted to values between $- {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-\nulldelimiterspace} 2}$ and $+ {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-\nulldelimiterspace} 2}$ and respond to a large dynamic range of amplitudes for anomalous sources at the different depths. The tilt angle produces a zero value over the source edges and, therefore, can be used to trace the outline of the edges (Miller and Singh, 1994). The angle also performs an automatic-gain-control filter which tends to equalize the response from both weak and strong potential field anomalies (Verduzco et al., 2004).

Applying tilt angle technique to the first vertical gradient (${{\partial g_{z} } \mathord{\left/ {\vphantom {{\partial g_{z} } {\partial z}}} \right. \kern-\nulldelimiterspace} {\partial z}}$) of the gravity field ($g_{z} = f$) provides a new tilt angle ϕ:

$$ \phi = \tan^{ - 1} \left( {{\frac{{{\frac{{\partial^{2} g_{z} }}{{\partial z^{2} }}}}}{{\sqrt {\left( {{\frac{{\partial^{2} g_{z} }}{\partial x\partial z}}} \right)^{2} + \left( {{\frac{{\partial^{2} g_{z} }}{\partial y\partial z}}} \right)^{2} } }}}} \right) $$

(2)

The denominator term in Eq. (2) is usually defined as the horizontal gradient magnitude (HGM). Figure 1 shows that the tilt angle ϕ is obtained from the second vertical gradient (${{\partial^{2} g_{z} } \mathord{\left/ {\vphantom {{\partial^{2} g_{z} } {\partial z^{2} }}} \right. \kern-\nulldelimiterspace} {\partial z^{2} }}$) and the HGM. A map of ϕ can therefore be considered an image of the tangent of the angle.

Fig. 1

Schematic diagram showing the second gravity gradients (${{\partial^{2} g_{z} } \mathord{\left/ {\vphantom {{\partial^{2} g_{z} } {\partial z^{2} }}} \right. \kern-\nulldelimiterspace} {\partial z^{2} }}$, ${{\partial^{2} g_{z} } \mathord{\left/ {\vphantom {{\partial^{2} g_{z} } {\partial x\partial z}}} \right. \kern-\nulldelimiterspace} {\partial x\partial z}}$ and ${{\partial^{2} g_{z} } \mathord{\left/ {\vphantom {{\partial^{2} g_{z} } {\partial y\partial z}}} \right. \kern-\nulldelimiterspace} {\partial y\partial z}}$) and tilt angle ϕ. HGM and $\left| A \right|$ represent the horizontal gradient magnitude and analytic signal, respectively

The equations for the second vertical and the mixed derivative of gravity field from two-dimensional (${{\partial^{2} g_{z} } \mathord{\left/ {\vphantom {{\partial^{2} g_{z} } {\partial z\partial y}}} \right. \kern-\nulldelimiterspace} {\partial z\partial y}} = 0$) geological contact or fault model (modified from Klingele et al., 1991) are given by, respectively:

$$ {\frac{{\partial^{2} g_{z} }}{{\partial z^{2} }}} = 2G\rho \sin d\left[ {{\frac{{(x - x_{0} )\sin d + (z - z{}_{0})\cos d}}{{(x - x_{0} )^{2} + (z - z_{0} )^{2} }}}} \right] $$

(3)

and

$$ {\frac{{\partial^{2} g_{z} }}{\partial z\partial x}} = 2G\rho \sin d\left[ {{\frac{{(x - x_{0} )\cos d - (z - z_{0} )\sin d}}{{(x - x_{0} )^{2} + (z - z_{0} )^{2} }}}} \right] $$

(4)

where G is the universal gravitational constant, ρ is the density, d is the slope of the contact, x ₀ is the horizontal location, z is the observation plane, and z ₀is the depth to the top of the contact (Fig. 2).

Fig. 2

2D sloping contact model. d is the dip (measured from the x-axis), $z_{0}$ is the depth to the top of the contact, $x_{0}$is the horizontal location, and $\rho$ is the density contrast

By substituting Eqs. (3) and (4) into Eq. (2), I infer that the tilt angle ϕ for vertical contact model (d = 90°) can be easily written as

$$ \phi = \tan^{ - 1} \left( {{\frac{{x - x_{0} }}{{ - (z - z_{0} )}}}} \right) $$

(5)

Considering $z = 0$ as the observation plane, θ is calculated using

$$ \phi = \tan^{ - 1} \left( {{\frac{{x - x_{0} }}{{z_{0} }}}} \right) $$

(6)

Equation (6) is equivalent to the tilt derivative from magnetic data developed by Salem et al. (2007).

The value of the tilt angle is 0 radians at the measuring point ($x = x_{0}$) above the edges of the contact. It is evident that this property identifies the horizontal location of the source. In addition, one can determine the depth estimation since the tilt angle equals ${\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-\nulldelimiterspace} 4}$ when $x - x_{0} = z_{0}$ and $- {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-\nulldelimiterspace} 4}$ when $x - x_{0} = - z_{0}$. Therefore, half the horizontal distance between the $\pm {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-\nulldelimiterspace} 4}$ contours of the tilt angle is the depth to source. In addition, the depth to source can be obtained from the distance between zero and $\pm {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-\nulldelimiterspace} 4}$ radians at the point $x = x_{0}$ over the vertical contact.

3 Theoretical Examples

The profiles in Fig. 3a and b show the relationship between the tilt angle and source depths for vertical contact models. The tilt angles are calculated by sampling interval 0.1 km along profile of 4 km. These models are placed at the horizontal location of 2 km, depth of 0.5 and 1 km, respectively. The profile of the tilt angle passes through zero directly over the contact edge ($x = x_{0}$), and passes through the points marking $\pm {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-\nulldelimiterspace} 4}$ at a distance from the edge. Note that the half distance between these two points corresponds to the depth to source.

Fig. 3

Tilt angle over a vertical contact model at a depth of a 0.5 km and b 1 km. Tilt values are restricted to within $\pm {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-\nulldelimiterspace} 2}$. The contact coincides with the zero crossing and the part of the tilt angle between $\pm {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-\nulldelimiterspace} 4}$ is highlighted

Because the vertical-sided rectangular prism model is designed to test the vertical contact hypothesis and is well approximated by the edge detection and depth estimation procedures, I illustrate the performance of the method by applying it to theoretical gravity anomaly produced by a vertical prism model. Figures 4a and b show the gravity anomalies due to the vertical prism models at two different depths. The depths to the tops of the two prisms are 0.5 and 1 km, respectively. The theoretical gravity anomalies of the vertical prisms are calculated using the formula given by Banerjee and Das Gupta (1977) on a regular grid with a spacing of 1 km. Both models are defined with a density contrast of 1 g/cc.

Fig. 4

Theoretical gravity anomaly maps and the plan and cross sectional view of the vertical prism models used for theoretical examples

The first vertical gradient of gravity data has been calculated by using the fast Fourier transform (FFT) technique (Gunn, 1975). The horizontal derivatives and vertical derivative of g _z , necessary for the calculation of Eq. (2), have also been calculated using the FFT technique. The reason for the calculation of numerical derivatives is that the TAM technique employed in processing and interpretation procedures is checked on the reliability of the numerical derivative. Note that the zero contours of the TAM delineate the spatial location of the edges of the models, responding well to the edge locations. The TAM is useful in imaging the edges, although the models are located at the different depths. The depths obtained from the distance between the zero and either the $- {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-\nulldelimiterspace} 4}$ or the $+ {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-\nulldelimiterspace} 4}$ contour are very close to the actual depths at the horizontal location of the models (Fig. 5).

Fig. 5

First vertical gradient maps (${{\partial g_{z} } \mathord{\left/ {\vphantom {{\partial g_{z} } {\partial z}}} \right. \kern-\nulldelimiterspace} {\partial z}}$) and the TAM (ϕ) over the shallow vertical prism in the left panel and the deeper prism on the right. Dashed lines indicate the 0 radian contour of the TAM. Solid lines are contours of the TAM for ${{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 4}} \right. \kern-\nulldelimiterspace} 4}$and ${{ + \pi } \mathord{\left/ {\vphantom {{ + \pi } 4}} \right. \kern-\nulldelimiterspace} 4}$

To test the noise effect on source location and depth estimation, Gaussian noise, generated from numbers normally distributed with zero mean and variance of 2% was added to the gravity anomaly, caused by vertical prism models in Fig. 4a and b. Figure 6 illustrates the gravity anomalies, the first vertical gradients and TAM images of vertical prisms in case of the presence of noise. Note that the TAM is not susceptible to noise and works well in imaging the edges of the models; that is, the horizontal location of the vertical prisms are at the position where the TAM has the zero contours of ϕ (Fig. 6). The estimated depths at the horizontal location of the models were found in the same range with those from Fig. 5. This means that the horizontal locations and source depths are independent of the noise effect, although the unwanted high frequency components were strongly amplified on the vertical gradient map and the TAM, as expected.

Fig. 6

Gravity anomalies ($g_{z}$) with Gaussian noise, generated from random numbers normally distributed with a variance of 2%, first vertical gradients and the TAM images of the shallow (left side) and the deeper vertical prism (right side). Dashed lines indicate the 0 radian contour of the tilt angle. Solid lines are contours of the TAM for ${{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 4}} \right. \kern-\nulldelimiterspace} 4}$ and ${{ + \pi } \mathord{\left/ {\vphantom {{ + \pi } 4}} \right. \kern-\nulldelimiterspace} 4}$

4 Application to Field Example

To examine the applicability of the proposed method, the following field example is presented.

4.1 Geological Setting

This example illustrates the application of the presented method to the determination of the horizontal location and depth of the edges of structural uplifts of the Kozaklı-Central Anatolia region, Turkey.

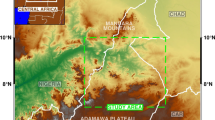
As shown in Fig. 7a, many NW-SE and NE-SW trending faults have been mapped in central Anatolia, but they are associated with neotectonic deformation after the Mio-Pliocene (Bozkurt, 2001). Some of the faults cut both cover and basement and could be reactivated older faults. In particular, those along the contacts between the basement rocks and cover units (Fig. 7a) could represent persistent zones of weakness. Bozkurt (2001) pointed out that isolated pieces of continental lithosphere deformed internally along new structures or reactivated older structures during the neotectonic episode in central Anatolia. The NW-SE and NE-SW trending faults are oblique faults, extending grabens, volcanic ashflow plateaus. Note that stratovolcanoes characterize the region. The geologic conditions look suitable for the development of a local high-heat flow anomaly.

Fig. 7

a Simplified geologic setting of central Anatolia in Turkey (modified after Bingöl 1989) and the location of the Kozaklı area. b Geologic sketch map of the Kozaklı area, compiled from the 1/100,000 geological map (mta, 1997)

Kozaklı area is a geothermal region. In this field, the metamorphic basement is overlain by young sediments (Serpen et al., 2009). As shown in Fig. 7b, in Kozaklı area, the Kızılırmak formation of Upper Miocene-Pliocene age, composed of terrestrial clastic, volcanic, and carbonate rocks lies unconformably over the former units, covered by the Quaternary travertines and alluvial deposits (MTA, 1997). The Deliceırmak formation of Upper Eocene-Miocene age is composed of lacustrine-fluvial conglomerate, sandstone and mudstone (mta, 1997).

The Kozaklı Graben, extending in the NW-SE direction has been formed as a result of the doming uplift and predominantly north–south tensional forces. A typical step faulting system is seen at the graben flanks. The geothermal resources exist at the edge of this graben (Ekingen, 1971).

4.2 Gravity Data

Gravity data provided by the General Directorate of the Mineral Research and Exploration Company of Turkey (MTA) have been compiled from Kozaklı region. The Bouguer anomaly map is shown in Fig. 8a. Note that the Bouguer anomaly map does not reflect the surface geological features, and thus is associated with lateral variations in density at depth. Thus, the Bouguer anomalies reflect all heterogeneities of density beneath the surface and delineate the subsurface geology. The Bouguer anomaly map shows gravity contours with NE-SW trends. The central and SE part of the survey area is characterized by high-gravity values (~20 mGal). The gravity highs are presumably produced by long linear NE-SW trending structural features in the basement complex beneath the sediments of the central and SE portion. The major axis of central uplift lies near the southern boundaries of the Kozaklı graben.

Fig. 8

a Bouguer gravity anomaly map of the Kozaklı area. b Residual gravity anomaly map computed by removing a first-order polynomial surface from the Bouguer gravity anomaly map

To help differentiate various gravity signals, I have implemented a three-stage analysis. First, a residual gravity anomaly was computed by removing a first-order polynomial surface from the complete Bouguer anomaly map and is shown in Fig. 8b. The NE-SW trending lineaments in the study area are also supported by the residual gravity contours. Second, the first vertical gradient of the residual gravity anomaly has been calculated by using the FFT algorithm developed by Gunn (1975) as illustrated in Fig. 9. Figure 9 shows that the structural framework is bordered by NE-SW-directed entities similar to Fig. 8b. Finally, an image of the TAM has been provided to illustrate in recognizing the horizontal location and depth of geologic contacts as shown in Fig. 10.

Fig. 9

First vertical gravity gradient map produced from Fig. 8b

Fig. 10

TAM obtained from Fig. 9. Dashed lines show the 0 radian contour of the tilt angle. Solid lines are contours of the tilt angle for ${{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 4}} \right. \kern-\nulldelimiterspace} 4}$ and $+ {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-\nulldelimiterspace} 4}$ radians

4.3 TAM Images

Figure 10 shows the simple form of the TAM only displaying the contours $- {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-\nulldelimiterspace} 4}$, 0, and $+ {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-\nulldelimiterspace} 4}$ radians. The zero contours estimate the location of abrupt lateral changes in density of basement materials. This map accentuates short wavelength and reveals the presence of main gravity trends, NE–SW, which is coincident with the main regional structural lineaments. One can conclude that there are more local uplifts in the northern edges of central uplift than those of others. It is interesting to note that the TAM tends to convey the edge detection from uplifts at all scales and depths. The half distance between $\pm {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-\nulldelimiterspace} 4}$ contours is used to estimate the depths of the edges of the uplifts. The depth estimates from these distances are determined to be between 0.2 and 0.6 km. It should be noted that the southern edges of the central uplift are more stable than those of the northern edges. In addition, the edges of the SE sector of the area produce only minor changes.

4.4 A Comparison of Euler Deconvolution with TAM images

In order to compare with the depths obtained from the TAM of the study area, I have used the Euler deconvolution (ED) technique. From the Euler theorem of homogenous functions we can write

$$ f(tx,ty,tz) = t^{n} f(x,y,z) $$

(7)

where n is the homogeneity degree of f. Equation (7) can also be expressed through Euler’s homogeneity equation as

$$ x{\frac{\partial f}{\partial x}} + y{\frac{\partial f}{\partial y}} + z{\frac{\partial f}{\partial z}} = nf . $$

(8)

The potential fields of simple sources can be described by means of rational functions. That is,

$$ f = {\frac{K}{{r^{N} }}} $$

(9)

where r is the distance, $r = \sqrt {(x - x_{0} )^{2} + (y - y_{0} )^{2} + (z - z_{0} )^{2} }$, $(x_{0} ,y_{0} ,z_{0} )$ denotes the position of the anomalous sources, K is a constant and N assumes different integer values of 0,1,2….., depending on the source geometry (Thompson, 1982). It has been ascertained that Eq. (9) is homogeneous of order $n = - N$. Thus, Euler’s homogeneous equation corresponding to (8) can be written as

$$ (x - x_{0} ){\frac{\partial f}{\partial x}} + (y - y_{0} ){\frac{\partial f}{\partial y}} + (z - z_{0} ){\frac{\partial f}{\partial z}} = - Nf . $$

(10)

Hsu (2002) gave the general formula for Euler’s equation as

$$ {\frac{\partial }{\partial x}}\left( {{\frac{{\partial^{n} f}}{{\partial z^{n} }}}} \right)\left( {x - x_{0} } \right) + {\frac{\partial }{\partial y}}\left( {{\frac{{\partial^{n} f}}{{\partial z^{n} }}}} \right)\left( {y - y_{0} } \right) + {\frac{\partial }{\partial z}}\left( {{\frac{{\partial^{n} f}}{{\partial z^{n} }}}} \right)\left( {z - z_{0} } \right) = - N\left( {{\frac{{\partial^{n} f}}{{\partial z^{n} }}}} \right) , $$

(11)

where n is the order of the gradient used. Note that the second vertical gravity gradient of the semi-infinite contact model from Eq. (3) is homogeneous in the sense of the Euler theorem. Therefore, the ED can be applied to the second vertical gradient (${{\partial^{2} g_{z} } \mathord{\left/ {\vphantom {{\partial^{2} g_{z} } {\partial z^{2} }}} \right. \kern-\nulldelimiterspace} {\partial z^{2} }}$) of the gravity field ($g_{z} = f$) since the analytical formula in Eq. (3) of the semi-infinite vertical contact model satisfies the Euler theorem. Thus, applying Eq. (11) to the second vertical gradient of the gravity field provides a solution:

$$ (x - x_{0} ){\frac{{\partial^{3} g_{z} }}{{\partial x\partial z^{2} }}} + (y - y_{0} ){\frac{{\partial^{3} g_{z} }}{{\partial y\partial z^{2} }}} + (z - z_{0} ){\frac{{\partial^{3} g_{z} }}{{\partial z^{3} }}} = - N{\frac{{\partial^{2} g_{z} }}{{\partial z^{2} }}} . $$

(12)

As presented in “Appendix A” (Eqs. A1–A4), the value of N obtained from Eq. (3) leads to a value of 1.

The second vertical gradient of residual gravity data (Fig. 7b) was examined with the ED from Eq. (12) to estimate the source locations and depths. In this example, I have adopted the moving window used (5 × 5 with a 0.55 km grid cell size) in the ED to the size of the observed structure to mostly encompass the effects of edges of the causative bodies (Fig. 11). Therefore, this window should be covered to resolve local source depths. The ED computation produced a great number of solutions filtered by adjusting uncertainty tolerances of source locations by a statistical approach (Reid et al., 1990). Accordingly, the horizontal locations and depths after rejecting solutions exceeding a tolerance level of 0.10. Note that clustering of Euler solutions imaged well the edges of uplift in central and SE sector of the study area (Fig. 11). Thus, the source points from the ED are positioned at the estimated boundaries of contrasting density and range from 0.3 to 0.5 km.

Fig. 11

ED solutions obtained from the second vertical gravity gradient. The circles representing the ED results are superimposed on the second vertical gravity gradient map, and each circle with a different diameter is related to one of the estimated depths

In order to compare the TAM images with ED results, I have superimposed the ED and TAM images (Fig. 12). It is evident that the source locations obtained from the ED are compatible with the zero contours of the TAM images. The depths, computed assuming $N = 1$, are also in good agreement with depths obtained from the TAM.

Fig. 12

Comparison of TAM images and ED results. Note that the source locations and depths from TAM and ED methods produce good correlations

5 Conclusions

The TAM, as obtained from the gravity vertical gradient in its simplest form, assumes that the source structures have vertical contacts. The tilt angle of the vertical gravity gradient is a very useful interpretation tool since it provides a simple and clean image. The technique tends to enhance mapping of the subtle gravity anomalies, and maximizes characterizing the geometrical contrast of the anomalous sources. The coherence of results indicates that the method produces satisfactory depth estimates under noise conditions. The main advantage of this technique is that it boosts amplitudes in areas with smooth anomalies, without sacrificing the long-wavelength information. Therefore, the spatial images of the TAM reflect different attributes of linear features, such as faults, contacts, and edges of basins and uplifts.

The TAM and ED can be applied in the process of interactive interpretation of the gravity anomalies. While both methods have been able to delimit the edges of features in sedimentary terrains, it is evident that the TAM images have more clear indications of utility than those of ED solutions. Because the analysis of TAM are only based on the contours of three angles (0, $+ {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-\nulldelimiterspace} 4}$ and $- {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-\nulldelimiterspace} 4}$ radians), the TAM images are easily interpreted by following these contours. The TAM images contain many details for detecting the edges of anomalous sources and some further analysis would improve the gravity interpretation. However, the TAM images should be compared with the ED solutions since the ED provides the depth estimates and especially helps to identify the source geometry. Thus, the ED confirms the results from the TAM under the assumption that the edges of anomalous sources are caused by vertical contacts. This correlation is the easiest way to confirm the horizontal location and depth of the edges, especially when there is a lack of any geophysical data in the corresponding area.

Appendix A: Derivation of structural index from the second vertical gravity gradient of semi-infinite contact

For 2D sources, where ${{\partial^{2} g_{z} } \mathord{\left/ {\vphantom {{\partial^{2} g_{z} } {\partial y\partial z}}} \right. \kern-\nulldelimiterspace} {\partial y\partial z}} = 0$, Eq. (12) is written as

$$ (x - x_{0} ){\frac{{\partial^{3} g_{z} }}{{\partial x\partial z^{2} }}} + (z - z_{0} ){\frac{{\partial^{3} g_{z} }}{{\partial z^{3} }}} = - N{\frac{{\partial^{2} g_{z} }}{{\partial z^{2} }}} . $$

(A1)

The derivatives of Eq. (3) with respect to x and z are defined, respectively;

$$ {\frac{{\partial^{3} g_{z} }}{{\partial x\partial z^{2} }}} = 2G\rho \sin d{\frac{{\sin d[(z - z_{0} )^{2} - (x - x_{0} )^{2} ] - 2(x - x_{0} )(z - z_{0} )\cos d}}{{[(x - x_{0} )^{2} + (z - z_{0} )^{2} ]^{2} }}} $$

(A2)

and

$$ {\frac{{\partial^{3} g_{z} }}{{\partial z^{3} }}} = 2G\rho \sin d{\frac{{\cos d[(x - x_{0} )^{2} - (z - z_{0} )^{2} ] - 2(x - x_{0} )(z - z_{0} )\sin d}}{{[(x - x_{0} )^{2} + (z - z_{0} )^{2} ]^{2} }}} . $$

(A3)

Substitution into the left-hand side of Euler’s Eq. (A1) yields

$$ \left( {x - x_{0} } \right){\frac{{\partial^{3} g_{z} }}{{\partial x\partial z^{2} }}} + (z - z_{0} ){\frac{{\partial^{3} g_{z} }}{{\partial z^{3} }}} = {\frac{1}{{r^{4} }}}\left\{ {(x - x_{0} )\sin d[ - (x - x_{0} )^{2} - (z - z_{0} )^{2} ] + (z - z_{0} )\cos d[ - (x - x_{0} )^{2} - (z - z_{0} )^{2} ]} \right\} = - {\frac{1}{{r^{2} }}}[(x - x_{0} )\sin d + (z - z_{0} )\cos d] $$

(A4)

If Eq. (A4) is compared with the right-hand side of Eq. (A1), the structural index N leads to 1.0.