1 Introduction

The impact of local topography on ground motion is one of the key topics of concern in the field of earthquake engineering. It is indicated by theoretical research and damage experience that the ground motions of canyons or hills are stronger than that of the plane. The ground motion responses of different forms of topography are diverse when an earthquake occurs, so a remarkable amount of work has been done on the scattering of seismic waves from local topography of various shapes.

To reveal the amplification effects due to topography of the canyon, semi-cylindrical canyon was the first form to be considered in terms of analytical solution [16]. The research on the scattering of SH wave by semi-circular canyon provided convenience for the following studies on other shaped canyons. By introducing a Graf’s addition formula and combining with the expression of scattering wave excited by the circular arc boundary, the ground motion of the circular arc canyon topography could be further studied [24]. For the concave topography with more complex geometry, it is difficult to give the scattered wave field excited by the terrain boundary. The introduction of auxiliary boundary is an effective way to solve this kind of problem. Based on the region-matching technique (RMT), Tsaur and Chang [17] adopted the wave function expansion method and the fractional Bessel function to give the analytical solution of the scattering of SH wave by a shallow symmetrical V-shaped canyon. The combination of fractional-order Bessel function and RMT had been proved to be feasible in the ground motion investigation of the canyon topography with complex shapes [3, 4, 6, 7, 19, 27]. In addition to analytical methods, many methods such as semi-analytical method [5], boundary element method [23] and hybrid method [13] can be adopted to analyze the influence of canyon and valley topography on seismic wave propagation.

Compared with the concave topography, there are much fewer analytical methods to study the ground motion of hills. Yuan and Men [26] had proposed an analytical method to solve the scattering problem of SH waves by a semi-cylindrical hill. Although an effective partitioning method is proposed, the results are only applicable to low-frequency incident SH waves due to solving errors. To get high precision numerical results, Lee et al. [10] proposed an improved analytical series solution adopting a cosine half-range expansion to meet the boundary conditions. For convex topography with circular arc cross section, Tsaur and Chang [18] found that series solution of [25] was in error due to unsuitable connection between the domain decomposition and the expression of corresponding wavefield and rederived the wave field expressions based on the RMT by introducing a semi-circular auxiliary boundary. Similarly, by establishing the elliptic coordinate system and introducing the Mathieu function, the ground motion of a semi elliptical hill under incident SH waves was studied [2, 9, 11]. In addition to the hills with circular and elliptical boundaries, ground motions for hills with slopes had also been considered. Hayir and Todorovska [8] attempted to get the series solution for the isosceles triangle topography by wavefunctions expansion method. Unfortunately, their calculated results did not coincide with the numerical results of Sánchez-Sesma et al. [15]. By introducing fractional Bessel function, Qiu and Liu [12] constructed the displacement field expression which satisfies the stress-free condition of triangle boundary rigorously. However, the numerical results [9, Sect. 5] were correct just under very low wave frequency incidence and could only be applied to the case of shallow hill.

In this paper, the analytic solution of SH wave scattering by an isosceles triangular hill is presented. The proposed method is not only applicable to hills of any height, but also can be used to calculate the numerical results of good convergence in the case of high incident wave frequency. Although the ground motions of more geometrically complex hill have been studied analytically [14, 22], it is necessary to give exact analytical results for the triangular hill as a typical convex topography, which can provide references for engineering practice and serve as a benchmark for comparison of numerical methods. In addition, investigating simple local topography under inhomogeneous geological conditions has been a hot topic in recent years [20, 21, 28, 29]. The research methods and solution ideas proposed in this paper provide a theoretical basis for subsequent studies combining complex geology. Furthermore, by changing the medium parameters, the mechanical model can be established to study the rock-soil interaction, and the dynamic response of dam foundation and soil can be studied by changing the form of triangular bottom boundary.

In Sect. 2 of this paper, the isosceles triangle hill is modeled and the partition method of this problem and the related parameters are explained. We rederived the wave field expressions in each subregion and establish the infinite algebraic equations for programming in Sect. 3. Then, in Sect. 4, the convergence and correctness of the results are verified, and the steady-state responses with different parameters are analyzed. Finally, the methods adopted in this paper and some important results are summarized in Sect. 5.

2 Model

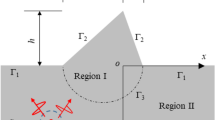
The two-dimensional model studied in this paper is shown in Fig. 1 which represents an elastic, isotropic and homogeneous half space (with shear modulus μ and shear wave velocity c) supporting an isosceles triangle hill of height h and half-width a. The origin of the global coordinate systems \(\left( {x_{1} ,y_{1} } \right)\) and \(\left( {r_{1} ,\theta_{1} } \right)\) is set at the hill top, while that of the local coordinate systems \(\left( {x_{2} ,y_{2} } \right)\) and \(\left( {r_{2} ,\theta_{2} } \right)\) is set at the center of the hill bottom. The angle \(\theta_{1}\) and \(\theta_{2}\) are measured anticlockwise from the vertical \(y_{1}\)-axis and \(y_{2}\)-axis, respectively. The angles between the hillsides and the vertical \(y_{1}\)-axis are \(- \beta\) and \(\beta\), which means the central angle of the hill top is \(2\beta\), ranging from 0 to \({\uppi }\). Based on the region-matching technique, a circular arc auxiliary boundary \(S_{a}\) is introduced to divide the half-space into two subregions. Region I involves an enclosed sector area and region II is a semi-infinite region with a circular arc canyon. Half of the hill span is a, which means the radius of the circular arc auxiliary boundary \(S_{a}\) is \({a \mathord{\left/ {\vphantom {a {\sin \beta }}} \right. \kern-\nulldelimiterspace} {\sin \beta }}\).

Fig. 1
figure 1

Model of the isosceles triangle hill

Full size image

3 Theoretical formulation

All the displacement \(w_{j}\) (j = 1, 2) within region I and region II must satisfy the two-dimensional wave equation

$$ \frac{{\partial^{2} w_{j} }}{{\partial r_{j}^{2} }} + \frac{1}{{r_{j} }}\frac{{\partial w_{j} }}{{\partial r_{j} }} + \frac{1}{{r_{j}^{2} }}\frac{{\partial^{2} w_{j} }}{{\partial \theta_{j}^{2} }} = \frac{1}{{c^{2} }}\frac{{\partial^{2} w_{j} }}{{\partial t^{2} }} $$
(1)

By letting

$$ w\left( {r_{j} ,\theta_{j} ,t} \right) = w\left( {r_{j} ,\theta_{j} } \right)\exp \left( { - {\text{i}}\omega t} \right) $$
(2)

and omitting the term \(\exp \left( { - {\text{i}}\omega t} \right)\), the steady-state anti-plane wave motion equation can be obtained

$$ \nabla^{2} w_{j} + k^{2} w_{j} = 0 ,$$
(3)

where \(\nabla^{2}\) is the Laplacian and \(k = {\omega \mathord{\left/ {\vphantom {\omega c}} \right. \kern-\nulldelimiterspace} c}\) is the shear wave number.

The zero-stress boundary conditions on the horizontal ground surface and the hill surface are

$$ \tau_{{\theta_{1} z_{1} }}^{\left( 1 \right)} = \frac{\mu }{{r_{1} }}\frac{{\partial w_{1} }}{{\partial \theta_{1} }} = 0, \, \theta_{1} = \pm \beta , \, 0 \le r_{1} \le b $$
(4)
$$ \tau_{{\theta_{2} z_{2} }}^{\left( 2 \right)} = \frac{\mu }{{r_{2} }}\frac{{\partial w_{2} }}{{\partial \theta_{2} }} = 0, \, \theta_{2} = \pm \frac{\pi }{2}, \, r_{2} > a $$
(5)

Since the auxiliary boundary is introduced to divide the model into two regions, the continuity conditions of displacement and stress at the auxiliary boundary must also be satisfied. The matching conditions on the auxiliary boundary can be written as

$$ w_{1} \left( {r_{1} ,\theta_{1} } \right) = w_{2} \left( {r_{1} ,\theta_{1} } \right), \, r_{1} = b, \, - \beta \le \theta_{1} \le \beta $$
(6)
$$ \tau_{{r_{1} z}}^{\left( 1 \right)} \left( {r_{1} ,\theta_{1} } \right) = \tau_{{r_{1} z}}^{\left( 2 \right)} \left( {r_{1} ,\theta_{1} } \right), \, r_{1} = b, \, - \beta \le \theta_{1} \le \beta,$$
(7)

where \(\tau_{{r_{1} z}}^{\left( 1 \right)} \left( {r_{1} ,\theta_{1} } \right) = \mu \frac{{\partial w_{1} }}{{\partial r_{1} }}\) and \(\tau_{{r_{1} z}}^{\left( 2 \right)} \left( {r_{1} ,\theta_{1} } \right) = \mu \frac{{\partial w_{2} }}{{\partial r_{1} }}\).

The total wave in region II can be split into the scattered wave \(w^{{\text{s}}}\) by the circular arc auxiliary boundary \(S_{a}\) and the free-field displacement \(w^{{\text{f}}}\), that is

$$ w_{1} = w^{{\text{f}}} + w^{{\text{s}}}, $$
(8)

where the free-field displacement \(w^{{\text{f}}}\) is expressed as

$$ w^{{\text{f}}} \left( {r_{2} ,\theta_{2} } \right) = \exp \left[ { - {\text{i}}kr_{2} \cos \left( {\theta_{2} + \alpha } \right)} \right] + \exp \left[ {{\text{i}}kr_{2} \cos \left( {\theta_{2} - \alpha } \right)} \right] $$
(9)

Note that this expression is written in the coordinate system \(\left( {r_{2} ,\theta_{2} } \right)\), and for later computation, it should be converted to the coordinate system \(\left( {r_{1} ,\theta_{1} } \right)\). According to the transformation relationship between the two coordinate systems, \(x_{1} = x_{2}\) and \(y_{1} = y_{2} + h\), Eq. (9) can be re-expressed in the coordinate systems \(\left( {r_{1} ,\theta_{1} } \right)\) as

$$ \begin{aligned} w^{{\text{f}}} \left( {r_{1} ,\theta_{1} } \right) = & \exp \left( {{\text{i}}kh\cos \alpha } \right)\exp \left[ { - {\text{i}}kr_{1} \cos \left( {\theta_{1} + \alpha } \right)} \right] \\ & + \exp \left( { - {\text{i}}kh\cos \alpha } \right)\exp \left[ {{\text{i}}kr_{1} \cos \left( {\theta_{1} - \alpha } \right)} \right] \\ \end{aligned} $$
(10)

Employing the Jacobi–Anger expansion [1],

$$ \exp ( \pm {\text{i}}kr\cos \theta ) = \sum\limits_{n = 0}^{\infty } {\varepsilon_{n} } ( \pm {\text{i}})^{n} J_{n} (kr)\cos n\theta, $$
(11)

where \(\varepsilon_{n}\) is the Neumann factor (\(\varepsilon_{0} = 1; \, \varepsilon_{n} = 2, \, n > 0\)) and \(J_{n} \left( \cdot \right)\) is the Bessel function with order n. Equation (10) is expressed as

$$ w^{{\text{f}}} (r_{1} ,\theta_{1} ) = \sum\limits_{n = 0}^{\infty } {J_{n} (kr_{1} )\left( {a_{n} \cos n\theta_{1} + b_{n} \sin n\theta_{1} } \right)} , \, - \beta \le \theta_{1} \le \beta $$
(12)

in which

$$ a_{n} = \varepsilon_{n} \left[ {\left( { - {\text{i}}} \right)^{n} \exp \left( {{\text{i}}kh\cos \alpha } \right) + {\text{i}}^{n} \exp \left( { - {\text{i}}kh\cos \alpha } \right)} \right]\cos n\alpha $$
(13)
$$ b_{n} = \varepsilon_{n} \left[ { - \left( { - {\text{i}}} \right)^{n} \exp \left( {{\text{i}}kh\cos \alpha } \right) + {\text{i}}^{n} \exp \left( { - {\text{i}}kh\cos \alpha } \right)} \right]\sin n\alpha $$
(14)

Due to the existence of auxiliary boundary \(S_{a}\), there is scattered wave in region I. It is given as

$$ w^{{\text{s}}} \left( {r_{2} ,\theta_{2} } \right) = \sum\limits_{n = 0}^{\infty } {A_{n} } H_{2n}^{(1)} \left( {kr_{2} } \right)\cos 2n\theta_{2} + \sum\limits_{n = 0}^{\infty } {B_{n} } H_{2n + 1}^{(1)} \left( {kr_{2} } \right)\sin (2n + 1)\theta_{2} ,$$
(15)

where \(A_{n}\) and \(B_{n}\) are unknown complex coefficients, \(H_{n}^{\left( 1 \right)} \left( \cdot \right)\) denotes the Hankel function of the first kind with order n.

It is convenient further on to represent \(w^{{\text{s}}}\) also in the coordinate system \(\left( {r_{1} ,\theta_{1} } \right)\). The application of the Graf addition formula [1] gives

$$ w^{{\text{s}}} \left( {r_{1} ,\theta_{1} } \right) = \sum\limits_{n = 0}^{\infty } {A_{n} } \sum\limits_{m = 0}^{\infty } {I_{m,2n}^{c} H_{m}^{\left( 1 \right)} \left( {kr_{1} } \right)} \cos m\theta_{1} + \sum\limits_{n = 0}^{\infty } {B_{n} } \sum\limits_{m = 0}^{\infty } {I_{m,2n + 1}^{s} H_{m}^{\left( 1 \right)} \left( {kr_{1} } \right)} \sin m\theta_{1}, $$
(16)

where

$$ I_{m,n}^{c} = \left( { - 1} \right)^{n} \frac{{\varepsilon_{m} }}{2}\left[ {\left( { - 1} \right)^{n} J_{m - n} \left( {kd} \right) + J_{m + n} \left( {kd} \right)} \right] $$
(17)
$$ I_{m,n}^{s} = \left( { - 1} \right)^{n + 1} \frac{{\varepsilon_{m} }}{2}\left[ {J_{m + n} \left( {kd} \right) - \left( { - 1} \right)^{n} J_{m - n} \left( {kd} \right)} \right] $$
(18)

In the enclosed region II, the standing wave expression \(w_{2}\) is given by

$$ w_{2} = w^{t} \left( {r_{1} ,\theta_{1} } \right) = \sum\limits_{n = 0}^{\infty } {C_{n} } J_{2np} \left( {kr_{1} } \right)\cos 2np\theta_{1} + \sum\limits_{n = 0}^{\infty } {D_{n} } J_{{\left( {2n + 1} \right)p}} \left( {kr_{1} } \right)\sin (2n + 1)p\theta_{1} $$
(19)

in which \(C_{n}\) and \(D_{n}\) are unknown complex coefficients, \(p = {{\uppi } \mathord{\left/ {\vphantom {{\uppi } {\left( {2\beta } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {2\beta } \right)}}\) is a fractional factor missed to consider in Ref. [8], which is used to make the expression of standing wave automatically satisfy the stress-free condition of hill surface.

Notice that the unknown coefficients \(A_{n}\), \(B_{n}\), \(C_{n}\) and \(D_{n}\) need to be determined according to Eqs. (6) and (7). Multiplying both sides of Eqs. (6) and (7) by cosine/sine functions, and integrating over the range of \(\left[ { - \beta ,\beta } \right]\) gives

$$ - \sum\limits_{n = 0}^{\infty } {A_{n} } \sum\limits_{m = 0}^{\infty } {I_{m,2n}^{c} } H_{m}^{\left( 1 \right)} \left( {kb} \right)U_{m,l} + \sum\limits_{n = 0}^{\infty } {C_{n} } J_{2np} \left( {kb} \right)U_{2np,l} = \sum\limits_{n = 0}^{\infty } {a_{n} } J_{n} \left( {kb} \right)U_{n,l} , \, l = 0,1, \ldots , $$
(20)
$$ - \sum\limits_{n = 0}^{\infty } {A_{n} } \sum\limits_{m = 0}^{\infty } {I_{m,2n}^{c} } H_{m}^{(1)\prime } \left( {kb} \right)U_{m,l} + \sum\limits_{n = 0}^{\infty } {C_{n} } J_{2np}^{\prime } \left( {kb} \right)U_{2np,l} = \sum\limits_{n = 0}^{\infty } {a_{n} } J_{n}^{\prime } \left( {kb} \right)U_{n,l} , \, l = 0,1, \ldots , $$
(21)
$$ - \sum\limits_{n = 0}^{\infty } {B_{n} } \sum\limits_{m = 0}^{\infty } {I_{m,2n + 1}^{s} } H_{m}^{\left( 1 \right)} \left( {kb} \right)V_{m,l} + \sum\limits_{n = 0}^{\infty } {D_{n} } J_{{\left( {2n + 1} \right)p}} \left( {kb} \right)V_{{\left( {2n + 1} \right)p,l}} = \sum\limits_{n = 0}^{\infty } {b_{n} } J_{n} \left( {kb} \right)V_{n,l} , \, l = 0,1, \ldots , $$
(22)
$$ - \sum\limits_{n = 0}^{\infty } {B_{n} } \sum\limits_{m = 0}^{\infty } {I_{m,2n + 1}^{s} } H_{m}^{( 1)\prime } \left( {kb} \right)V_{m,l} + \sum\limits_{n = 0}^{\infty } {D_{n} } J^{\prime}_{{\left( {2n + 1} \right)p}} \left( {kb} \right)V_{{\left( {2n + 1} \right)p,l}} = \sum\limits_{n = 0}^{\infty } {b_{n} } J^{\prime}_{n} \left( {kb} \right)V_{n,l} , \, l = 0,1,\ldots, $$
(23)

where

$$ U_{m,l} = \int_{ - \beta }^{\beta } {\cos m\theta \cos l\theta {\text{d}}\theta } = \left\{ \begin{gathered} 2\beta , \, m = l = 0 \hfill \\ \frac{{\sin \left( {2m\beta } \right)}}{2m} + \beta , \, m = l \ne 0 \hfill \\ \frac{{\sin \left( {m + l} \right)\beta }}{m + l} + \frac{{\sin \left( {m - l} \right)\beta }}{m - l}, \, m \ne l \hfill \\ \end{gathered} \right. $$
(24)
$$ V_{m,l} = \int_{ - \beta }^{\beta } {\sin m\theta \sin l\theta {\text{d}}\theta } = \left\{ \begin{gathered} 0, \, m = l = 0 \hfill \\ - \frac{{\sin \left( {2m\beta } \right)}}{2m} + \beta , \, m = l \ne 0 \hfill \\ - \frac{{\sin \left( {m + l} \right)\beta }}{m + l} + \frac{{\sin \left( {m - l} \right)\beta }}{m - l}, \, m \ne l \hfill \\ \end{gathered} \right. $$
(25)

All necessary formula derivation has been completed. By truncating the infinite term, the matrix is established to solve the unknown coefficients in the wave field expression, so as to carry out the subsequent case analysis.

4 Numerical results

We define the dimensionless frequency of incident waves as

$$ \eta = {{2a} \mathord{\left/ {\vphantom {{2a} \lambda }} \right. \kern-\nulldelimiterspace} \lambda } = {{ka} \mathord{\left/ {\vphantom {{ka} {\uppi }}} \right. \kern-\nulldelimiterspace} {\uppi }} ,$$
(26)

where \(\lambda\) is the wavelength of the incident waves. The dimensionless frequency \(\lambda\) can be used not only to characterize the ratio of the span of the triangle hill to the wavelength, but also to represent the magnitude of the wavenumber. The displacement amplitude which is used to characterize the magnitude of ground motion, is defined as

$$ \left| {w_{j} } \right| = \sqrt {\left( {{\text{Re}} w_{j} } \right)^{2} + \left( {{\text{Im}} w_{j} } \right)^{2} } $$
(27)

4.1 Convergence test

A number of convergence tests are carried out to determine the truncation values of n, m, l. Generally, more terms of n and l are required for higher dimensionless frequency of incident waves. For the number of truncation terms of m, 150 is enough to get the convergence results of the examples in this paper. Successive tests suggest that the horizontally incident cases take more truncation terms than others to reach convergence. In other words, as long as the displacement amplitudes converge in the case of \(\alpha = 90^\circ\), the truncation term is sufficient for other incident angles. Take the case of \({h \mathord{\left/ {\vphantom {h a}} \right. \kern-\nulldelimiterspace} a} = 0.4\) as an example. Figure 2a shows the five test positions where \(S_{1} - S_{5}\) are located at \({x \mathord{\left/ {\vphantom {x a}} \right. \kern-\nulldelimiterspace} a} = - 2.0\), \(- 0.5\), 0, 0.5 and 2.0, respectively. The convergence of the displacement amplitudes of the five test positions at three different dimensionless frequencies is shown in Fig. 2b–d. The abscissa N represents the truncation values of n and l. The displacement amplitudes of five positions need N to reach a certain value before they tend to be stable. Before that, the displacement amplitudes all present irregular and violent oscillations, so the results of non-convergence cannot be adopted. Although the positions of the five observation points are different, their convergence trend of displacement amplitude is similar. When the dimensionless frequency \(\eta\) is 5.0, the amplitude of the displacement is stabilized as N increases to 19. For high-frequency case with \(\eta = 10.0\) and \(\eta = 15.0\), the corresponding N when the displacement amplitudes begin to stabilize are 35 and 50, respectively.

Fig. 2
figure 2

Convergence of displacement amplitudes at five positions with increasing N: a five selected positions; b \(\eta = 5.0\); c \(\eta = 10.0\); d \(\eta = 15.0\)

Full size image

4.2 Correctness verification

Qiu and Liu [12] have derived the correct wave field expressions of the isosceles triangle hill by complex function method. Although the numerical results given in this paper are not satisfactory for the most part, the displacement amplitudes of the shallow hill under low-frequency incidence can still be adopted as a reference under low-frequency incidence. In this paper, the method of model establishment and coefficient solution are different from that adopted by Qiu and Liu [12]. We set the hill height \({h \mathord{\left/ {\vphantom {h a}} \right. \kern-\nulldelimiterspace} a} = 0.25, \, 0.5, \, 0.75\). Figure 3a shows the displacement amplitudes at vertical incidence with the dimensionless frequency \(\eta = 0.5\) and Fig. 3b represents the case of oblique incidence. It can be seen that the results of present work are in good agreement with the results in Ref. [12]. The results obtained by the two different methods are basically coincident with each other, so it can be considered that the research method in this paper is effective.

Fig. 3
figure 3

Comparison between our results for different hill height at \(\eta = 0.5\) and those of Qiu and Liu: a \(\alpha = 0^\circ\); b \(\alpha = 45^\circ\)

Full size image

To verify the accuracy of the numerical results obtained by the proposed model and method under the high-frequency incident SH waves, the finite element method is used for comparison. The height of the triangle hill is set as \({h \mathord{\left/ {\vphantom {h a}} \right. \kern-\nulldelimiterspace} a} = 1.0\). The dimensionless frequency is \(\eta = 5.0\), and seismic wave is incident from two different angles (\(\alpha = 0^\circ\) and \(30^\circ\)). A comparison is performed to validate the solution results with those by the finite element method as shown in Fig. 4. The solid lines are the results obtained by the series solution in this paper, and the scatter points of the triangle are the results obtained by the finite element method. It can be seen that due to the limitation of the mesh division and the size of the solution domain, the results of the finite element method have errors, which cannot be completely consistent with the analytical results in this paper. But the distribution trend of displacement amplitude is consistent, which can prove that the results obtained by this method in the case of high-frequency incident SH wave are effective.

Fig. 4
figure 4

Surface displacement amplitude versus x/a with h/a = 1.0 at \(\eta = 5.0\): a \(\alpha = 0^\circ\); b \(\alpha = 30^\circ\). The solid lines show the results from the series solution and the scatter points show the results from the FEM

Full size image

4.3 Surface motion analysis

Figures 5 and 6 show the displacement amplitudes \(\left| w \right|\) as a function of the distance \({x \mathord{\left/ {\vphantom {x a}} \right. \kern-\nulldelimiterspace} a}\) for \(\eta = 1.0\) at various incident angles (\(\alpha = 0^\circ\), \(30^\circ\), \(60^\circ\), \({9}0^\circ\)). Set the dimensionless frequency equal to the span of the hill, i.e., \(\eta = 1.0\). The effect of the triangle height on displacement amplitudes is considered when the ratio of hill height to span is less than 1.0 (shallow case) and greater than 1.0 (deep case). In Fig. 5, four cases of the height of hill are analyzed, which are \({h \mathord{\left/ {\vphantom {h a}} \right. \kern-\nulldelimiterspace} a} = 0.2\), 0.4, 0.6 and 0.8, respectively. Despite the different angles of incidence, the surface displacement amplitudes show a general rule. That is, a higher hill corresponds to a larger oscillation range of displacement amplitude. In the case of vertical incidence, the maximum displacement amplitude \(\left| w \right|_{\max }\) corresponding to the four heights of the hill appears at the hilltop, and the minimum value \(\left| w \right|_{\min }\) appears at the hillside. As the incident angle increases, the positions of \(\left| w \right|_{\max }\) and \(\left| w \right|_{\min }\) shift from the original position to the right. Generally, extreme values of displacement amplitude occur on the surface of the isosceles triangle hill.

Fig. 5
figure 5

Amplitudes of surface displacement versus \({x \mathord{\left/ {\vphantom {x a}} \right. \kern-\nulldelimiterspace} a}\) at \(\eta = 1.0\) for various incident angles: shallow hill

Full size image
Fig. 6
figure 6

Amplitudes of surface displacement versus \({x \mathord{\left/ {\vphantom {x a}} \right. \kern-\nulldelimiterspace} a}\) at \(\eta = 1.0\) for various incident angles: deep hill

Full size image

For deep hill, the displacement amplitudes at four incident angles are investigated when the height of the hill is set as \({h \mathord{\left/ {\vphantom {h a}} \right. \kern-\nulldelimiterspace} a} = 1.2\), 1.4, 1.6 and 1.8, respectively. When the dimensionless frequency is 1.0, the rule of surface displacement amplitudes corresponding to different hill height are quite different from that of shallow case. For the deep triangle hill, the influence of the height on the displacement amplitudes is not obvious. In the case of vertical incidence, although the maximum displacement amplitude of higher hill is larger, the increment of amplitude is slight. With the increase of incident angle, the influence of hill height on displacement amplitude is weakened, which is especially reflected in the left part of the surface (\({x \mathord{\left/ {\vphantom {x a}} \right. \kern-\nulldelimiterspace} a} < 0\)). It is worth noting that the maximum surface displacement amplitude \(\left| w \right|_{\max }\) occurs on the horizontal surface to the left of the hill when \(\alpha = 60^\circ\) and \(90^\circ\).

After analyzing the surface displacement of the triangle hills with various heights under the low-frequency incident, the ground motion of the triangle hill at high dimensionless frequency is further analyzed in Figs. 7, 8, 9 and 10. The displacement amplitudes of the triangle hill with height of 0.25 and 1.5, respectively, at four incident angles (\(\alpha = 0^\circ\), \(30^\circ\), \(60^\circ\), \(90^\circ\)) are given, and the maximum and minimum values of the amplitudes in each case are marked out.

Fig. 7
figure 7

Displacement amplitudes versus \({x \mathord{\left/ {\vphantom {x a}} \right. \kern-\nulldelimiterspace} a}\) for \({h \mathord{\left/ {\vphantom {h a}} \right. \kern-\nulldelimiterspace} a} = 0.25\) at \(\eta = 5.0\)

Full size image
Fig. 8
figure 8

Displacement amplitudes versus \({x \mathord{\left/ {\vphantom {x a}} \right. \kern-\nulldelimiterspace} a}\) for \({h \mathord{\left/ {\vphantom {h a}} \right. \kern-\nulldelimiterspace} a} = 0.25\) at \(\eta = 10.0\)

Full size image
Fig. 9
figure 9

Displacement amplitudes versus \({x \mathord{\left/ {\vphantom {x a}} \right. \kern-\nulldelimiterspace} a}\) for \({h \mathord{\left/ {\vphantom {h a}} \right. \kern-\nulldelimiterspace} a} = 1.5\) at \(\eta = 5.0\)

Full size image
Fig. 10
figure 10

Displacement amplitudes versus \({x \mathord{\left/ {\vphantom {x a}} \right. \kern-\nulldelimiterspace} a}\) for \({h \mathord{\left/ {\vphantom {h a}} \right. \kern-\nulldelimiterspace} a} = 1.5\) at \(\eta = 10.0\)

Full size image

For vertical incidence (\(\alpha = 0^\circ\)) in Figs. 7a and 8a, the maximum ground motion occurs at the hilltop (\({x \mathord{\left/ {\vphantom {x a}} \right. \kern-\nulldelimiterspace} a} = 0\)) while the minimum one is at two rims of the hill (\({x \mathord{\left/ {\vphantom {x a}} \right. \kern-\nulldelimiterspace} a} = \pm 1.0\)). In this case, the displacement amplitude of the hill surface is generally greater than that of the flat surface on both sides. For oblique incidence (\(\alpha = 30^\circ , \, 60^\circ\)) in Figs. 7b, c and 8b, c, the position of the maximum displacement amplitude is shifted to the right-hand side, but it is still on the surface of the hill. When the seismic wave is incident at \(60^\circ\), the corresponding maximum displacement amplitude reaches 2.77 at \(\eta = 5.0\) and 3.25 at \(\eta = 10.0\). It is noted that with the increase of the incident angle, the oscillation frequency of the ground displacement on the left side of the hill (\({x \mathord{\left/ {\vphantom {x a}} \right. \kern-\nulldelimiterspace} a} < - 1.0\)) increases, but the oscillation amplitude decreases. However, the motion pattern on the right side of the hill (\({x \mathord{\left/ {\vphantom {x a}} \right. \kern-\nulldelimiterspace} a} > 1.0\)) is the opposite of the one on the left. And the displacement amplitude of the left hillside is obviously lower than that of the right hillside. For horizontal incidence (\(\alpha = 90^\circ\)) in Figs. 7d and 8d, the distribution of displacement results shows an obvious characteristic. That is, the amplification effect of triangular hill on seismic waves is mainly reflected on the right-side slope, while the ground motion on the left-side slope is obviously weakened. It is noted that this rule is just opposite to the result of V-shaped canyon in Ref. [17].

In order to analyze the surface displacement amplitudes of deep hill at high-frequency incidence, we set the hill height as \({h \mathord{\left/ {\vphantom {h a}} \right. \kern-\nulldelimiterspace} a} = 1.5\), dimensionless frequency as \(\eta = 5.0\) in Fig. 9 and \(\eta = 10.0\) in Fig. 10. Compared with the cases of low frequency, the amplitude distribution of ground displacement under high-frequency incidence is much more complex. To show the displacement amplitude of the hill surface \(\left( { - 1.0 \le {x \mathord{\left/ {\vphantom {x a}} \right. \kern-\nulldelimiterspace} a} \le 1.0} \right)\) more clearly, we reduce the abscissa interval to \(\left( { - 3.0,3.0} \right)\). For vertical incidence, the maximum and minimum amplitudes still occur near the top of the hill, and the amplification effect of the amplitude is significant. In the two examples, the maximum amplitude reaches 6.03 at the frequency of 5.0. With the increase of incident angle \(\alpha\), the displacement amplitudes of the hill surface decrease. When the incident angle is 60° and 90°, the initial amplification effect (while \(\alpha = 0^\circ , \, 30^\circ\)) of the hill on the seismic wave energy changes to the shielding effect. This shielding effect is reflected in the displacement amplitudes of the hill surface are obviously less than 2.0, and the displacements of the flat surface on the right side of the hill also have a certain reduction. The closer to grazing incidence \(\left( {\alpha = 90^\circ } \right)\), the more obvious the shielding effect is. In addition, large incident angle makes the maximum displacement amplitude occur at the left rim of the hill.

Figure 11 illustrates the displacement amplitudes \(\left| w \right|\) as a function of the dimensionless frequency \(\eta\) at two incident angles (\(\alpha = 60^\circ\), \(90^\circ\)). Five observer points are selected to study the displacement amplitudes of five typical locations as shown in Fig. 11a in a large frequency interval. For point 1, the displacement amplitudes under low-frequency incident corresponding to the two incident angles are basically the same. As the dimensionless frequency increases, the difference in displacement amplitude at two incident angles becomes apparent. The displacement amplitudes fluctuate regularly with the dimensionless frequency and are always less than 2.0. For point 2 and point 3, the displacement amplitudes are less than 2.0 at \(60^\circ\) incidence, and they decrease with the increase of dimensionless frequency \(\eta\). In contrast, the displacements of oblique incidence are significantly larger than that of horizontal incidence. The magnifying effect of the hill on the seismic wave is reflected in the right part of the triangle hill at \(\alpha = 90^\circ\). As shown in Fig. 11e, f, the black curve presents an upward trend and is always greater than 2.0. The displacement of the right rim of the hill at the horizontal incidence of SH wave is significantly larger than that at the oblique incidence.

Fig. 11
figure 11

Five observer points’ seismic responses versus \(\eta\) at \({h \mathord{\left/ {\vphantom {h a}} \right. \kern-\nulldelimiterspace} a} = 0.1\) for two incident angles

Full size image

Figure 12 is presented to show the displacement amplitudes of a deep hill versus dimensionless frequency \(\eta\). We find that the oscillation forms of displacement amplitudes are similar under two incident angles (\(\alpha = 60^\circ\), \(90^\circ\)), which is different from the case of shallow hill. For the observer points on hillside and hilltop, in general, the surface displacements caused by oblique incidence of SH waves are larger than that of grazing incidence. This means that for the deep hill, a larger incident angle corresponds to a more significant earthquake wave energy absorption effect, which is applicable to the whole frequency range \(\left( {0 < \eta \le 15} \right)\). With regard to observer point 1 at the left rim of the deep hill, the oscillation range of displacement amplitudes under oblique incidence (\(\alpha = 60^\circ\)) is larger than that under grazing incidence (\(\alpha = 90^\circ\)). And the displacement amplitude of point 1 is larger than that of other locations, which indicates that this point may be an earthquake risk position that needs attention. Compared with shallow hill, the ground motion response of deep hill is much more complex, and with the increase of dimensionless frequency, the distribution of ground displacement amplitude has no obvious regularity.

Fig. 12
figure 12

Five observer points’ seismic responses versus \(\eta\) at \({h \mathord{\left/ {\vphantom {h a}} \right. \kern-\nulldelimiterspace} a} = 1.5\) for two incident angles

Full size image

For the sake of revealing the influence of dimensionless frequency \(\eta\) and incident angle \(\alpha\) on surface motions, Fig. 13 displays the displacement amplitudes as a function of \({x \mathord{\left/ {\vphantom {x a}} \right. \kern-\nulldelimiterspace} a}\) and \(\eta\) at various angles of incidence (\(\alpha = 90^\circ\), \(60^\circ\), \(30^\circ\), \(0^\circ\)). We set \({h \mathord{\left/ {\vphantom {h a}} \right. \kern-\nulldelimiterspace} a} = 0.25\). Surface motion around the triangle hill under horizontal incidence (\(\alpha = 90^\circ\)) is shown in Fig. 13a. It can be seen intuitively that at any dimensionless frequency, the displacement oscillation of the flat surface on the right side of the hill (\({x \mathord{\left/ {\vphantom {x a}} \right. \kern-\nulldelimiterspace} a} > 1.0\)) is gentle, while that on the left side (\({x \mathord{\left/ {\vphantom {x a}} \right. \kern-\nulldelimiterspace} a} < 1.0\)) is violent. For oblique incidence, the maximum amplitude of surface displacement generally occurs around the right foot of the hill (\({x \mathord{\left/ {\vphantom {x a}} \right. \kern-\nulldelimiterspace} a} = 1.0\)), and the ground motion of the flat surface on the right side (\({x \mathord{\left/ {\vphantom {x a}} \right. \kern-\nulldelimiterspace} a} > 1.0\)) is significantly stronger than that on the left (\({x \mathord{\left/ {\vphantom {x a}} \right. \kern-\nulldelimiterspace} a} < 1.0\)). At vertical incidence, the ground motion on both sides is the same because of the symmetrical shape of the triangle hill. Maximum displacement amplitude occurs on the hill surface (\(- 1.0 \le {x \mathord{\left/ {\vphantom {x a}} \right. \kern-\nulldelimiterspace} a} \le 1.0\)).

Fig. 13.
figure 13

3D plots of surface displacement amplitudes around the isosceles triangle hill for \({h \mathord{\left/ {\vphantom {h a}} \right. \kern-\nulldelimiterspace} a} = 0.25\) at different incident angles

Full size image

5 Conclusion

In this paper, an exact solution using wave-function series expansion method for the scattering of SH waves by an isosceles triangle hill has been presented. By introducing the fractional Bessel function, the expression of standing wave field satisfying the stress-free condition in polar coordinate system is constructed. The research method proposed in this paper is applicable for isosceles triangle hill with arbitrary height. Based on the orthogonality of trigonometric functions, the infinite algebraic equations for solving coefficients are derived. The numerical results are accurate and convergent in spite of high-frequency incidence. According to the foregoing analysis, some findings can be summarized as follows:

  1. 1.

    Steeper hill makes more complex ground motion responses. For small incident angle, the amplification effect of deep hill is more obvious than that of shallow hill.

  2. 2.

    The position of the maximum displacement is affected by the incident angle. In the case of vertical and horizontal incidence, the maximum displacement amplitude \(\left| w \right|_{\max }\) appears at the hill top (\({x \mathord{\left/ {\vphantom {x a}} \right. \kern-\nulldelimiterspace} a} = 0\)) and at the left rim of the hill, respectively.

  3. 3.

    Once the incident angle is greater than \(45^\circ\), the displacement of the hill surface decreases, and the triangle hill has a barrier effect on seismic waves.

  4. 4.

    The method presented in this paper is applicable for the further study of the scattering of SH waves by non-isosceles triangular hill.