1 Introduction

Optical solitons, which can be stably transmitted by virtue of the offset about the group velocity dispersion (GVD) and self-phase modulation (SPM), have induced substantial interests of researchers in mathematics, physics and optics [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]. In particular, the nonlinearity and integrability in the solitons equation are widely concerned [25,26,27,28]. Under ideal conditions, solitons can achieve lossless transmission [29]. However, when two- or multi-solitons are transmitted simultaneously in the optical fiber, these solitons can attract each other [29,30,31]. Due to the existence of solitary interactions, which causes transmission rate of the optical communication system to be seriously degraded, studying how to minimize the interactions becomes one of the meaningful directions [32, 33].

Phase-shift controlling, which contributes to an approach for the question mentioned above, has been investigated widely in theory and experiment [34, 35]. Ref. [34] has researched large phase shift of solitons in lead glass under strong nonlocal space. Furthermore, the phase shifts and trajectories during the overtaking interaction of multi-solitons have been analyzed in Ref. [35]. The propagation of three solitons in the dispersion-decreasing fiber (DDF) can be explained by the nonlinear Schrödinger (NLS) equation as follows [36, 37]:

$$\begin{aligned} \phi _\xi -i\frac{D(\xi )}{2}\phi _{\tau \tau }+i\rho (\xi )|\phi |^2\phi =g(\xi )\phi . \end{aligned}$$
(1)

Here, \(\phi \) is complex function with \(\xi \) and \(\tau \) representing scaled distance and time. \(D(\xi )\) is the GVD parameter, \(\rho (\xi )\) is the Kerr nonlinear parameter, and \(g(\xi )\) is a parameter related to fiber loss or amplification. With regard to Eq. (1), the formation and amplification of solitons have been studied [38]. Interactions between two solitons have been attenuated by phase-shift controlling [36]. Besides, researches have done about how to amplify, reshape, fission and annihilate solitons [39] and investigated the propagation properties of optical solitons in the DDF [40].

Compared with two solitons, the results of three solitons on propagation and interactions are more abundant. In order to better understand the phase-shift characteristics of three solitons in DDF, results of interactions are shown and analyzed under the GVD parameters with different functions in this paper. By setting appropriate dispersion values, phase-shift controlling of solitons in DDF can be better achieved, which is helpful to improve the transmission quality of the signal in optical communication system. In addition, the loss in the medium can be effectively compensated by changing the constraint value produced by \(D(\xi )\), \(\rho (\xi )\) and \(g(\xi )\), so that the propagation distance can be extended.

The structure of the paper is as follows. Section 2 is arranged to get analytic three solitons solutions of Eq. (1) through the Hirota method. Section 3 is reserved for analyzing interactions influences under different value of related parameters and finding suitable value to weaken the interactions among three solitons. Finally, Sect. 4 is used to compose a conclusion for this paper.

2 Bilinear forms and three solitons solutions

Using the Hirota method to introduce the dependent variable transformation:

$$\begin{aligned} \phi (\xi ,\tau )=\frac{h(\xi ,\tau )}{f(\xi ,\tau )}\hbox {e}^{\int g(\xi )\mathrm{d}\xi }, \end{aligned}$$
(2)

where \(h(\xi ,\tau )\) is assumed as a complex differentiable function while \(f(\xi ,\tau )\) is a real one. After calculation, the following bilinear equations of Eq. (1) are obtained:

$$\begin{aligned}&(2iD_\xi +D(\xi )D^2_\tau )h\cdot f=0, \nonumber \\&D(\xi )D^2_\tau f\cdot f+2\rho (\xi )\hbox {e}^{2\int g(\xi )\mathrm{dx}}h\cdot h^*=0, \end{aligned}$$
(3)

where * denotes complex conjugate. There is a constraint relationship among \(D(\xi )\), \(\rho (\xi )\) and \(g(\xi )\):

$$\begin{aligned} \rho (\xi )=P\frac{D(\xi )}{\hbox {e}^{2\int g(\xi )\mathrm{d}\xi }}. \end{aligned}$$
(4)

As Hirota bilinear operators, \(D_\xi \) and \(D_\tau \) have the following form:

$$\begin{aligned}&D^m_\xi D^n_\tau (a\cdot b)=\Big (\frac{\partial }{\partial \xi }- \frac{\partial }{\partial \xi '}\Big )^m\Big (\frac{\partial }{\partial \tau }- \frac{\partial }{\partial \tau '}\Big )^n\nonumber \\&\quad a(\xi ,\tau )b(\xi ',\tau ')|_{\xi '=\xi ,\tau '=\tau }, \end{aligned}$$
(5)

where both of m and n are non-negative integers, a is the function about \(\xi \) and \(\tau \), and b is the function about \(\xi '\) and \(\tau '\). To solve bilinear forms (3), \(h(\xi ,\tau )\) and \(f(\xi ,\tau )\) can be expanded as:

$$\begin{aligned} h(\xi ,\tau )&=\epsilon h_1(\xi ,\tau )+\epsilon ^3 h_3(\xi ,\tau )+\epsilon ^5 h_5(\xi ,\tau ),\nonumber \\ f(\xi ,\tau )&=1+\epsilon ^2 f_2(\xi ,\tau )+\epsilon ^4 f_4(\xi ,\tau )+\epsilon ^6 f_6(\xi ,\tau ). \end{aligned}$$
(6)

Without affecting the generality, we can define the value of \(\epsilon \) as 1, and expand the bilinear forms (3) by using expression (6). Three solitons solutions of Eq. (1) are constructed as follows:

$$\begin{aligned} \phi (\xi ,\tau )=\frac{h_1(\xi ,\tau )+h_3(\xi ,\tau )+h_5(\xi ,\tau )}{1+f_2(\xi ,\tau ) +f_4(\xi ,\tau )+f_6(\xi ,\tau )}\hbox {e}^{\int g(\xi )\mathrm{d}\xi }, \end{aligned}$$
(7)

where

$$\begin{aligned} h_1(\xi ,\tau )= & {} \hbox {e}^{\theta _1}+\hbox {e}^{\theta _2}+\hbox {e}^{\theta _3}, \\ f_2(\xi ,\tau )= & {} A_1(\xi )\hbox {e}^{\theta ^*_1+\theta _1}+A_2(\xi )\hbox {e}^{\theta ^*_2+\theta _1} \\&+\,A_3(\xi )\hbox {e}^{\theta ^*_3+\theta _1}+A_4(\xi )\hbox {e}^{\theta ^*_1+\theta _2} \\&+\,A_5(\xi )\hbox {e}^{\theta ^*_2+\theta _2} +A_6(\xi )\hbox {e}^{\theta ^*_3+\theta _2}\\&+\,A_7(\xi )\hbox {e}^{\theta ^*_1+\theta _3}+A_8(\xi )\hbox {e}^{\theta ^*_2+\theta _3} \\&+\,A_9(\xi )\hbox {e}^{\theta ^*_3+\theta _3}, \\ h_3(\xi ,\tau )= & {} B_1(\xi )\hbox {e}^{\theta ^*_1+\theta _1+\theta _2}+B_2(\xi )\hbox {e}^{\theta ^*_2 +\theta _1+\theta _2} \\&+\,B_3(\xi )\hbox {e}^{\theta ^*_3+\theta _1+\theta _2} +B_4(\xi )\hbox {e}^{\theta ^*_1+\theta _1+\theta _3}\\&+\,B_5(\xi )\hbox {e}^{\theta ^*_2+\theta _1+\theta _3}+B_6(\xi )\hbox {e}^{\theta ^*_3+\theta _1+\theta _3} \\&+\,B_7(\xi )\hbox {e}^{\theta ^*_1+\theta _2+\theta _3}+B_8(\xi )\hbox {e}^{\theta ^*_2+\theta _2+\theta _3}\\&+\,B_9(\xi )\hbox {e}^{\theta ^*_3+\theta _2+\theta _3}, \\ f_4(\xi ,\tau )= & {} M_1(\xi )\hbox {e}^{\theta ^*_1+\theta ^*_2+\theta _1+\theta _2} +M_2(\xi )\hbox {e}^{\theta ^*_1+\theta ^*_3+\theta _1+\theta _2}\\&+\,M_3(\xi )\hbox {e}^{\theta ^*_2 +\theta ^*_3+\theta _1+\theta _2}+M_4(\xi )\hbox {e}^{\theta ^*_1 +\theta ^*_2+\theta _1+\theta _3}\\&+\,M_5(\xi )\hbox {e}^{\theta ^*_1+\theta ^*_3+\theta _1+\theta _3}+M_6(\xi )\hbox {e}^{\theta ^*_2 +\theta ^*_3+\theta _1+\theta _3}\\&+\,M_7(\xi )\hbox {e}^{\theta ^*_1+\theta ^*_2+\theta _2+\theta _3}+M_8(\xi )\hbox {e}^{\theta ^*_1 +\theta ^*_3+\theta _2+\theta _3}\\&+\,M_9(\xi )\hbox {e}^{\theta ^*_2+\theta ^*_3+\theta _2+\theta _3},\\ h_5(\xi ,\tau )= & {} N_1(\xi )\hbox {e}^{\theta ^*_1+\theta ^*_2+\theta _1+\theta _2+\theta _3} +N_2(\xi )\hbox {e}^{\theta ^*_1+\theta ^*_3+\theta _1+\theta _2+\theta _3}\\&+\,N_3(\xi )\hbox {e}^{\theta ^*_2+\theta ^*_3+\theta _1+\theta _2+\theta _3},\\ f_6(\xi ,\tau )= & {} n(\xi )\hbox {e}^{\theta ^*_1+\theta ^*_2+\theta ^*_3+\theta _1+\theta _2 +\theta _3}, \end{aligned}$$
Fig. 1
figure 1

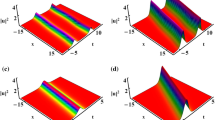
Interactions among three solitons affected with different profiles of \(D(\xi )\). Parameters chosen as: \(r_{11}=2.4,r_{12}=-3.1,r_{21}=-3,r_{22}=1.8,r_{31}=3.2,r_{32}=5,k_{11}=-1,k_{12}=-2,k_{21}=4,k_{22}=8,k_{31}=4,k_{32}=-2,P=-10,g(\xi )=0.02\) with a\(D(\xi )=-0.085\); b\(D(\xi )=-0.07\xi \); c\(D(\xi )=-0.15cos(\xi )\); d\(D(\xi )=-0.07\hbox {e}^{-\xi }\); e\(D(\xi )=-0.07\hbox {e}^{-\xi ^2}\)

Full size image
Fig. 2
figure 2

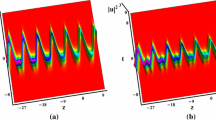
Phase shift affected with the different values before \({\xi }^2\). Parameters chosen as: \(r_{11}=2.4,r_{12}=-3.1,r_{21}=-3,r_{22}=1.8,r_{31}=3.2,r_{32}=5,k_{11}=-1,k_{12}=-2,k_{21}=4,k_{22}=8,k_{31}=4,k_{32}=-2,P=-10,g(\xi )=0.02\) with a\(D(\xi )=-0.057\hbox {e}^{-0.0054\xi ^2}\); b\(D(\xi )=-0.057\hbox {e}^{-0.076\xi ^2}\); c\(D(\xi )=-0.057\hbox {e}^{-0.9\xi ^2}\)

Full size image
Fig. 3
figure 3

Phase shift affected with the different values before \(\hbox {e}^{-0.076\xi ^2}\). Parameters chosen as: \(r_{11}=2.4,r_{12}=-3.1,r_{21}=-3,r_{22}=1.8,r_{31}=3.2,r_{32}=5,k_{11}=-1,k_{12}=-2,k_{21}=4,k_{22}=8,k_{31}=4,k_{32}=-2,P=-10,g(\xi )=0.02\) with a\(D(\xi )=-\,0.21\hbox {e}^{-0.076\xi ^2}\); b\(D(\xi )=-0.048\hbox {e}^{-0.076\xi ^2}\); c\(D(\xi )=-\,0.0034\hbox {e}^{-0.076\xi ^2}\)

Full size image
Fig. 4
figure 4

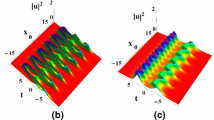
Interactions among three solitons affected with the different values of  P. Parameters chosen as: \(D(\xi )=-0.05\hbox {e}^{-\xi ^2},r_{11}=2.4,r_{12}=-3.1,r_{21}=-3,r_{22}=1.8,r_{31}=3.2,r_{32}=5,k_{11}=-1,k_{12}=-2,k_{21}=4,k_{22}=8,k_{31}=4,k_{32}=-2,g(\xi )=0.02\) with a\(P=-14\); b\(P=-11\); c\(P=-8\)

Full size image

with

$$\begin{aligned} \theta _i= & {} a_{i1}(\xi )+ia_{i2}(\xi )+(r_{i1}+ir_{i2})\tau +k_{i1}+ik_{i2}, \\ a_{i1}(\xi )= & {} -\int r_{i1}r_{i2}D(\xi )\hbox {d}\xi , \\ a_{i2}(\xi )= & {} \frac{1}{2}\int (r_{i1}^2-r_{i2}^2)D(\xi )\hbox {d}\xi (i=1,2,3), \\ A_1(\xi )= & {} -\frac{P}{4r_{11}^2}, A_2(\xi )=-\frac{P}{w_{31}^2}, A_3(\xi )= -\frac{P}{w_{32}^2}, \\ A_4(\xi )= & {} -\frac{P}{w_{21}^2}, A_5(\xi )=-\frac{P}{4r_{21}^2}, A_6(\xi )= -\frac{P}{w_{33}^2}, \\ A_7(\xi )= & {} -\frac{P}{w_{22}^2}, A_8(\xi )=-\frac{P}{w_{23}^2}, A_9(\xi )= -\frac{P}{4r_{31}^2}, \\ B_1(\xi )= & {} -\frac{w_{11}^2P}{4r_{11}^2w_{21}^2}, B_2(\xi )= -\frac{w_{11}^2P}{4r_{21}^2w_{31}^2}, \\ B_3(\xi )= & {} -\frac{w_{11}^2P}{w_{32}^2w_{33}^2}, \\ B_4(\xi )= & {} -\frac{w_{12}^2P}{4r_{11}^2w_{22}^2}, B_5(\xi )= -\frac{w_{12}^2P}{w_{31}^2w_{23}^2}, \\ B_6(\xi )= & {} -\frac{w_{12}^2P}{4r_{31}^2w_{32}^2}, \\ B_7(\xi )= & {} -\frac{w_{13}^2P}{w_{21}^2w_{22}^2}, B_8(\xi )=-\frac{w_{13}^2P}{4r_{21}^2w_{23}^2}, \\ \end{aligned}$$
$$\begin{aligned} B_9(\xi )= & {} -\frac{w_{13}^2P}{4r_{31}^2w_{33}^2}, \\ M_1(\xi )= & {} \frac{J_{11}^2P^2}{16r_{11}^2r_{21}^2J_{12}^2}, M_2(\xi )= \frac{w_{11}^2w_{42}^2P^2}{4r_{11}^2w_{21}^2w_{32}^2w_{33}^2}, \\ M_3(\xi )= & {} \frac{w_{11}^2w_{43}^2P^2}{4r_{21}^2w_{21}^2w_{32}^2w_{33}^2}, \\ M_4(\xi )= & {} \frac{w_{41}^2w_{32}^2P^2}{4r_{11}^2w_{21}^2w_{22}^2w_{23}^2}, M_5(\xi )=\frac{J_{21}^2P^2}{16r_{11}^2r_{31}^2J_{22}^2}, \\ M_6(\xi )= & {} \frac{w_{12}^2w_{43}^2P^2}{4r_{31}^2w_{31}^2w_{32}^2w_{23}^2}, \\ M_7(\xi )= & {} \frac{w_{41}^2w_{13}^2P^2}{4r_{21}^2w_{21}^2w_{22}^2w_{23}^2}, M_8(\xi ) =\frac{w_{13}^2w_{23}^2P^2}{4r_{31}^2w_{21}^2w_{33}^2w_{22}^2}, \\ M_9(\xi )= & {} \frac{J_{31}^2P^2}{16r_{21}^2r_{31}^2J_{32}^2}, \\ \end{aligned}$$
$$\begin{aligned} N_1(\xi )= & {} \frac{J_{11}^2w_{12}^2w_{13}^2P^2}{16r_{11}^2r_{21}^2w_{31}^2 w_{21}^2w_{22}^2w_{23}^2},\\ N_2(\xi )= & {} \frac{J_{21}^2w_{11}^2w_{13}^2P^2}{16r_{11}^2 r_{31}^2w_{21}^2w_{32}^2w_{33}^2w_{22}^2}, \\ N_3(\xi )= & {} \frac{J_{31}^2w_{11}^2w_{12}^2P^2}{16r_{21}^2r_{31}^2w_{31}^2w_{32}^2 w_{33}^2w_{23}^2}, \\ n(\xi )= & {} -\frac{J_{11}^2J_{21}^2J_{31}^2P^3}{64r_{11}^2r_{21}^2 r_{31}^2w_{31}^2w_{21}^2w_{32}^2w_{33}^2w_{22}^2w_{23}^2}, \\ w_{11}= & {} r_{11}+ir_{12}-r_{21}-ir_{22}, \\ w_{12}= & {} r_{11}+ir_{12}-r_{31}-ir_{32}, \\ w_{13}= & {} r_{21}+ir_{22}-r_{31}-ir_{32}, \\ w_{21}= & {} r_{11}-ir_{12}+r_{21}+ir_{22}, \\ w_{22}= & {} r_{11}-ir_{12}+r_{31}+ir_{32}, \\ \end{aligned}$$
$$\begin{aligned} w_{23}= & {} r_{21}-ir_{22}+r_{31}+ir_{32}, \\ w_{31}= & {} r_{11}+ir_{12}+r_{21}-ir_{22}, \\ w_{32}= & {} r_{11}+ir_{12}+r_{31}-ir_{32}, \\ w_{33}= & {} r_{21}+ir_{22}+r_{31}-ir_{32}, \\ w_{41}= & {} r_{11}-ir_{12}-r_{21}+ir_{22}, \\ w_{42}= & {} r_{11}-ir_{12}-r_{31}+ir_{32}, \\ w_{43}= & {} r_{21}-ir_{22}-r_{31}+ir_{32}, \\ J_{11}= & {} (r_{11}-r_{21})^2+(r_{12}-r_{22})^2, \\ J_{12}= & {} (r_{11}+r_{21})^2+(r_{12}-r_{22})^2, \\ J_{21}= & {} (r_{11}-r_{31})^2+(r_{12}-r_{32})^2, \\ J_{22}= & {} (r_{11}+r_{31})^2+(r_{12}-r_{32})^2, \\ J_{31}= & {} (r_{21}-r_{31})^2+(r_{22}-r_{32})^2, \\ J_{32}= & {} (r_{21}+r_{31})^2+(r_{22}-r_{32})^2. \end{aligned}$$

3 Discussions

For solutions (7) obtained by the above process, we choose different correlative coefficients to observe the interactions among three solitons. Subsequently, the degrees of interactions in different situations are analyzed. Figure 1 indicates interactions among three solitons affected with different profiles of \(D(\xi )\) such as the constant one, the linear one, the cosine one, the exponential one and the Gaussian one [41]. In Fig. 1a, we set \(D(\xi )=-\,0.085\). When there is narrow distance between solitons, although influence on the direction of propagation is little, sharp peaks are produced due to the interactions. As shown in Fig. 1b and c, when \(D(\xi )=-\,0.07\xi \) and \(D(\xi )=-\,0.15cos(\xi )\), the direction of the soliton propagation is obviously changed and the amplitude of solitons is reduced at the place of interaction especially in Fig. 1b. The attraction between solitons which leads to the appearance of peak can be seen clearly in Fig. 1d. Compared with above profiles, when \(D(\xi )=-\,0.07\hbox {e}^{-\xi ^2}\), interactions among three solitons are weakened distinctly because of the phase shift of solitons in Fig. 1e. Results suggest that phase-shift controlling of solitons in DDF can be achieved when the dispersion profile is Gaussian.

In order to present the effect of Gaussian profile on phase shift of solitons, we sequentially change correlative coefficient in Gaussian profile by ten times nearly as shown in Figs. 2 and 3. With decreasing the value before \({\xi }^2\), the result of the interactions between solitons shows a process from the generation of peaks to the generation of new solitons and then to the independent propagation in Fig. 2. Compared with Fig. 2, Fig.3 illustrates the same process by increasing the value before \(\hbox {e}^{-0.076\xi ^2}\). It is found that interactions of solitons can be avoided when the value before \({\xi }^2\) is 10 times or larger than before \(\hbox {e}^{-\xi ^2}\) in Figs. 2 and 3. That means phase-shift controlling can also be realized better by changing the value before \({\xi }^2\) or the value before \(\hbox {e}^{-\xi ^2}\).

Besides, we adjust the value of P in expression (4) as shown in Fig. 4. The attenuation of amplitude becomes alleviative as P increasing, which means the loss in optical fibers can be compensated and the propagation distance of solitons can be improved and extended.

4 Conclusion

Phase-shift controlling of three solitons in DDF has been mainly studied in this paper. Hirota method has been used to obtain the analytic three solitons solutions (7) for Eq. (1). By comparing and analyzing different values of the GVD, the phase-shift controlling has been achieved so that the interactions among three solitons can be weakened effectively by choosing a Gaussian profile. Moreover, we have found that the enhancement of phase-shift controlling can be prompted via decreasing the value before \({\xi }^2\) or increasing the value before \(\hbox {e}^{-\xi ^2}\). In addition, the outcome has been given that the propagation distance of solitons can be prolonged by adjusting the value of P in expression (4). Results maybe can apply in ultra-short pulse lasers and fiber compensation systems.