A PSO-based timing-driven Octilinear Steiner tree algorithm for VLSI routing considering bend reduction

Abstract

Constructing a timing-driven Steiner tree is very important in VLSI performance-driven routing stage. Meanwhile, non-Manhattan architecture is supported by several manufacturing technologies and now well appreciated in the chip manufacturing circle. However, limited progress has been reported on the non-Manhattan performance-driven routing problem. In this paper, an efficient algorithm, namely, TOST_BR_MOPSO, is presented to construct the minimum-cost spanning tree with a minimum radius for performance-driven routing in Octilinear architecture (one type of the non-Manhattan architecture) based on multi-objective particle swarm optimization (MOPSO) and Elmore delay model. Edge transformation is employed in our algorithm to make the particles have the ability to achieve the optimal solution while Union-Find partition is used to prevent the generation of invalid solution. For the purpose of reducing the number of bends which is one of the key factors of chip manufacturability, we also present an edge-vertex encoding strategy combined with edge transformation. To our best knowledge, no approach has been proposed to optimize the number of bends in the process of constructing the non-Manhattan timing-driven Steiner tree. Moreover, the theorem of Markov chain is used to prove the global convergence of our proposed algorithm. Experimental results indicate that the proposed MOPSO is worthy of being studied in the field of multi-objective optimization problems, and our algorithm has a better tradeoff between the wire length and radius of the routing tree and has achieved a better delay value. Meanwhile, combining edge transformation with the encoding strategy, the proposed algorithm can significantly reduce nearly 20 % in the number of bends.

1 Introduction

Global routing is one of the most important steps in very large scale integration (VLSI) physical design. The construction of Steiner minimum tree (SMT), which seeks to connect the given points in the plane with additional points (called Steiner points) in the minimum cost, is essential for each signal net of the chip in the global routing stage. In recent years, the optimization goals of global routing include the length of interconnect wires, interconnect delay, congestion, vias and others (Ho et al. 2007; Hu and Sapatnekar 2001).

The early construction methods for SMT focused on achieving a minimal total length of interconnect wires. Warme et al. (1998) presented an exact algorithm called GeoSteiner, which is currently the fastest method for constructing the optimal Rectilinear Steiner minimal tree (RSMT) in plane Steiner tree problem. However, GeoSteiner has a high time complexity and is impractical with the increasing scale of the problem. Recently, researchers have started getting interested in more efficient heuristic algorithms. A well-known near-optimal algorithm was presented (Borah et al. 1994). A very fast and accurate RSMT algorithm called fast lookup table estimation (FLUTE) was presented by Chu and Wong (2008). FLUTE is optimal for the net with degrees below 9 and very fast with high accuracy. An RSMT algorithm based on discrete particle swarm optimization (DPSO) and genetic operators was presented to minimizing the wire length (Liu et al. 2011).

In recent years, as the chip feature size sharply shrinks, timing delay has become a critical issue in the nanometer VLSI routing. As a consequence, some performance-driven routing algorithms have been studied. A provably good timing-driven Steiner tree algorithm was presented to optimize the interconnect delay (Cong et al. 1992). The model for the minimum-cost spanning tree with a minimum radius (MRMCST) was adopted to construct the routing trees for performance optimization (Seo and Lee 1999). Hou et al. (1999) developed a performance-driven routing formulation whose objective is to meet a specified delay constraint at each sink and introduced the flexibility of a Steiner point to reduce wire delay. Yan (2006) proposed an efficient assignment approach by reassigning the feasible locations of the Steiner points in a routing tree to reconstruct a timing-constrained flexibility-driven routing tree.

Generally, congestion and vias are the important metrics of chip quality and impact the routability. A single-layer global router was proposed to control the congestion and reduce the number of bends (Sarrafzadeh et al. 1994). Since a bend in the layer assignment or detailed routing phase usually implies a switching of layers and causes the use of more vias, reducing the number of bends is helpful for reducing the number of vias. Thus, Liang et al. (2007) presented an RSMT algorithm based on gravitation direction to reduce the number of bends through using the gravitation that a point received from other points to judge its moving direction. Bozorgzadeh et al. (2003) presented the concept of flexibility and an algorithm which input a Steiner tree and output a more flexible Steiner tree to increase its routability. Yan (2006) also exploited the flexibility improvement of the edges in a routing tree to release the routing congestion.

However, the above algorithms focus on the construction of the Manhattan Steiner tree. With advances in VLSI fabrication technology, the interconnect effects become the major challenge of chip performance. Manhattan architecture which restricts the routing to be only horizontal and vertical directions has limited the ability to optimize wire length and timing delay. Consequently, there are more and more interest in non-Manhattan routing which allows more routing directions and could further improve the routability (Koh and Madden 2000; Teig 2002).

In order to study non-Manhattan routing, the first work is to construct the SMT in non-Manhattan architecture. Non-Manhattan Steiner tree includes Octilinear Steiner tree (OST) and Hexagonal Steiner tree. An exact algorithm and a variety of pruning techniques were introduced to construct the Octilinear Steiner minimal tree (OSMT) (Coulston 2003). An ${O(|V|+|E|)}$ algorithm was proposed to build an OST which must be isomorphic to the given Rectilinear Steiner tree (Chiang and Chiang 2002). $|V|$ and $|E|$ are the number of vertices and that of the edges of the given tree, respectively. The spanning graph-based Octilinear Steiner tree algorithms were presented by Zhu et al. (2005). Samanta et al. (2006) proposed a heuristic method to constructing Hexagonal Steiner minimal tree. Since the SMT problem is an NP-hard problem (Garey and Johnson 1997), some evolutionary algorithms, which have been shown to have good application prospects in solving NP-hard problems, were presented for solving RSMT problem (Arora and Mose 2009; Liu et al. 2011) and OSMT problem (Arora and Mose 2009; Liu et al. 2012).

For the non-Manhattan routing problem, constructing the timing-driven Steiner minimum tree is very important in dominating the performance of a chip, although related research is fairly inadequate. Yan (2008) proposed an efficient transformation-based approach to construct a timing-driven Octilinear Steiner tree (TOST) based on Octilinear architecture. Furthermore, Samanta et al. (2011) constructed a near-optimal timing-driven Hexagonal Steiner tree based on the two-pole and Elmore delay estimate model in Hexagonal architecture. However, the quality of TOST constructed by the former work was deeply dependent on the optimization order of the Steiner points and the quality of the initial solution. Consequently, it was easy to be converged to the local optimum. The latter proposed by Samanta et al. (2011) focused on the delay estimation model and Hexagonal architecture. Furthermore, via minimization can reduce circuit delay and enhance the manufacturability of the circuit. Reducing the number of bends is helpful for reducing the number of vias and reducing the number of bends is easier than via minimization in the later phases. As a result, it is necessary to study the Steiner tree construction algorithm considering bend reduction. However, to the best of our knowledge, no approach is proposed to reduce the number of bends for the non-Manhattan timing-driven Steiner tree construction. Aiming at the aspects concerned above, this paper employs an effective algorithm based on multi-objective particle swarm optimization (MOPSO) to construct a TOST for VLSI routing considering bend reduction, namely, TOST_BR_MOPSO. Our main contributions are as follows:

• 1. In contrast to previous work (Liu et al. 2012) which only takes into account the transformation of Steiner point, we introduce the edge-transformation strategy to improve the evolutionary process of the particles. And the novel strategy could simultaneously transform the Steiner points and edges of the routing tree. Consequently, compared with OST (Liu et al. 2012), the routing tree can decrease a certain amount of wire length on one hand. It is very necessary that the initial particles have the ability to transform to MRMCST by the introduction of edge-transformation strategy on the other hand.

• 2. On the basis of the definition of the pseudo-Steiner point and the flexibility of the pseudo-Steiner point, an efficient encoding strategy is proposed to optimize the number of bends by reassigning the exact location of each pseudo-Steiner point in four different ways. Simultaneously, the edge transformation is well combined with our proposed edge-vertex encoding scheme for bend reduction which is one of the highlights of our work. As a result, the method with the encoding strategy can reduce nearly 20 % in the number of bends. However, the work (Liu et al. 2012) did not consider the bend reduction without using the edge transformation.

• 3. We make use of the MRMCST model based on the computation of the Octilinear distance to find a timing-driven routing tree in an Octilinear architecture. In order to simultaneously optimize the two objectives of wire length and radius which are often competing objectives, we design a multi-objective algorithm based on discrete particle swarm optimization (PSO) for constructing the timing-driven Octilinear routing tree. The experimental results show that the final trees achieve a major decrease in maximum source-to-sink delay and total source-to-sink delay than the RSMTs and OSMTs which focus on the optimization of wire length and are respectively constructed in one literature (Liu et al. 2011) and the other literature (Liu et al. 2012). Moreover, based on the 0.18 $\upmu$m technology (namely, tost IC technology), the final tree constructed by our algorithm could obtain 2.08 % smaller than the TOST constructed by Yan (2008) in wire length, 5.22 % smaller in radius, 4.93 % smaller in the maximum source-to-sink delay, 10.07 % smaller in the total source-to-sink delay and nearly 20 % smaller in the number of bends. All that work is also different to previous work (Liu et al. 2012).

• 4. Different from the work by Liu et al. (2012), we provide the detail process of convergence analysis for our proposed algorithm, expressed in Sect. 3.3. To study the performance of the proposed algorithm, three groups of experiments including performance analysis of MOPSO, comparison with the two Steiner minimal tree algorithms, and comparison with the timing-driven Octilinear Steiner tree construction method, are carried out in Sect. 4.

The remainder of the paper is organized as follows. We formulate the problem and introduce some basic definitions in Sect. 2. We describe the basic particle swarm optimization algorithm and the PSO-based timing-driven Octilinear Steiner tree algorithm considering bend reduction in Sect. 3, while the detailed process of algorithm convergence analysis is also provided. To prove the good performance of our proposed algorithm, we present several comparisons with other approaches and give the experimental results in Sect. 4. Finally, the conclusions and possible future work are left for Sect. 5.

2 Problem description

2.1 OSMT problem

Octilinear Steiner minimal tree problem is to connect all pins in the plane through Steiner points to achieve a minimal total length in VLSI routing. It allows $45^{\circ }$ and $135^{\circ }$ routing directions in addition to traditional horizontal and vertical orientations (Zhu et al. 2005).

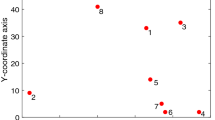
OSMT problem can be stated as follows. Let $P = \{P_{1}, P_{2}, P_{3}, \ldots , P_{m}\}$ be the set for the net N of m pins, where each $P_{i}$ is assigned with its coordinate ($x_{i}, y_{i}$). We show an example net in Fig. 1. The input information for pins is listed in Table 1. The layout is a case of Yan (2008). Each pin has the corresponding coordinate ($x_{i} , y_{i}$), e.g., the pin 1 is located at (1, 6).

Fig. 1

An example net. The layout coordinates of the pins is listed in Table 1

Table 1 Input information for seven pins

2.2 Elmore delay model

In our work, the Elmore delay model (Boese et al. Boese93; Yehea et al. 1999) is used to calculate the delay and this delay model is described as follows. Given the net $N$ and one of the corresponding routing trees $T(N)$, let $e_{i}$, whose resistance and capacitance are respectively denoted by $r_{{e_j}}$ and $c_{{e_j}}$, denote the edge from node $i$ to its parent point in $T(N)$. Let $T(N)_{i}$ denote the subtree of $T(N)$ rooted at $i$ and $C_{i}$, which is the sum of capacitances of all sinks and edges in $T(N)_{i}$, be the lumped capacitance. Let $n_{0}$ be the source node, whose resistance and capacitance are denoted by $R_{0}$ and $C_{0}$, and then the Elmore delay of sink point $i$ can be calculated as follows.

$$\begin{aligned} {t_i} = {R_0} \times {C_0} + \sum \limits _{{e_j} \in \hbox {path}(s,i)} {{r_{{e_j}}} \times ({c_{{e_j}}}} /2 + {C_j})\ \end{aligned}$$

(1)

where path($s,i$) is the set of all edges in the path from source to $i$.

The Elmore delay model has the following advantages. Firstly, the time complexity for evaluating the delay values of all sink points in the routing tree to source point is $O(n)$. Thus, the computation of Elmore delay model is small. Secondly, the computational accuracy of the Elmore delay model is higher than linear delay model. Finally, the near-optimal or optimal routing trees calculated by Elmore delay model have the equal prepotency with those calculated by other high order delay model. Consequently, we evaluate the delay from each sink point in the routing tree to source point according to Eq. 1.

2.3 Definitions

Definition 1

In the $\lambda$-geometry, the routing direction is $i\pi /\lambda$, where $i$ is an arbitrary integer and $\lambda$ is an integer. Different routing directions are obtained with different values of $i$ and $\lambda$.

• 1. Manhattan architecture (or rectilinear architecture): The value of $\lambda$ is set to be 2, i.e., the routing direction is $i\pi /2$, which includes $0^{\circ }$ and $90^{\circ }$, namely, horizontal and vertical orientation.

• 2. Hexagonal architecture: The value of $\lambda$ is set to be 3, i.e., the routing direction is $i\pi /3$, which includes $0^{\circ }$, $60^{\circ }$ and $120^{\circ }$.

• 3. Octilinear architecture: The value of $\lambda$ is set to be 4, i.e., the routing direction is $i\pi /4$, which includes $0^{\circ }$, $45^{\circ }$, $90^{\circ }$ and $135^{\circ }$. Both (2) and (3) belong to non-Manhattan architecture.

Definition 2

(Pseudo-Steiner) For convenience, we assume that the endpoints except for the pins collectively referred to as pseudo-Steiner points.

Definition 3

(0 Choice) In Fig. 2a, let $A = ({x_1}, {y_1})$ and $B = ({x_2}, {y_2})$ be the two endpoints of a line segment $L, {x_1 < x_2}$. The 0 Choice of pseudo-Steiner point corresponding to edge $L$ is given in Fig. 2b, which first from A leads Rectilinear side to pseudo-Steiner point and then leads Octilinear side to B.

Fig. 2

Four options of Steiner point for the given line segment. a Line segment L, b 0 choice, c 1 choice, d 2 choice, e 3 choice

Definition 4

(1 Choice) The 1 Choice of pseudo-Steiner point corresponding to edge L, as shown in Fig. 2c, which first from A leads Octilinear side to pseudo-Steiner point and then leads Rectilinear side to B.

Definition 5

(2 Choice) The 2 Choice of pseudo-Steiner point corresponding to edge L is given in Fig. 2d, which first from A leads vertical side to pseudo-Steiner point and then leads horizontal side to B.

Definition 6

(3 Choice) The 3 Choice of pseudo-Steiner point corresponding to edge L, as shown in Fig. 2e, which first from A leads horizontal side to pseudo-Steiner point and then leads vertical side to B.

2.4 MRMCST model

Given the set of pins shown in Fig. 3a, the special distribution of those pins, which the source, namely, S, is in the center of circle surrounded by other pins, could help us compare images to distinguish the three different types of trees. The minimum spanning tree (MST), as shown in Fig. 3b, has the minimum wire length which is an important metric for placement and routing. However, MST for routing may result in longer critical paths which bring larger time delay and worsen the performance of chip. In Fig. 3c, it shows the shortest path tree (SPT) which rather has the minimum critical path, but the wire length may be larger than MSTs. The radius of tree means the maximum timing delay in chip design. Meanwhile, minimizing the wire length minimizes a drivers output resistance and the total wire capacitance in layout design. Thus, these two metrics should be optimized for improving the overall chip performance (Ho et al. 2007).

Fig. 3

Different topologies for the given pin set. a The set of pins, b minimum spanning tree, c shortest path tree, d MRMCST (Ho et al. 2007)

Furthermore, MRMCST model with smooth trade-off between the radius and the wire length, as shown in Fig. 3d, could be used to construct a timing-driven routing tree (Ho et al. 2007). Since the MRMCST problem is NP-hard (Seo and Lee 1999), we resort to multi-objective particle swarm optimization, which is discussed in Sect. 3, to both optimize the radius and the wire length for better chip performance.

3 Algorithm

3.1 Basic PSO

Particle swarm optimization is a swarm intelligence method, which considers a swarm containing p particles in a D-dimensional continuous solution space. Each ith particle has its own position and velocity. Assuming that the search space is D-dimensional, the position of the ith particle is denoted as a D-dimensional vector: $X_{i} = (X_{i1}, X_{i2}, \ldots , X_{iD})$ and the best particle in the swarm is denoted as $P_g$. The best previous position of the ith particle is recorded and represented as $P_i = (P_{i1}, P_{i2}, \ldots , P_{iD})$, while the velocity for the ith particle can be defined by another D-dimensional vector: $V_i = (V_{i1}, V_{i2}, \ldots , V_{iD})$. According to these definitions, the particle position and velocity can be manipulated according to the following equations:

$$\begin{aligned} V_i^{t + 1}&= w \times V_i^t + {c_1}{r_1}(P_{i}^t - X_i^t) + {c_2}{r_2}(P_{g}^t - X_i^t)\end{aligned}$$

(2)

$$\begin{aligned} X_i^{t + 1}&= X_i^t + V_i^{t+1} \end{aligned}$$

(3)

where w is the inertia weight; $c_1$ and $c_2$ are acceleration coefficients; $r_1$ and $r_2$ are both random numbers on the interval [0, 1).

As a swarm-based evolutionary method, PSO which was introduced by Eberhar and Kennedy (1995) has been proved to be a powerful optimization tool. The advantages of PSO over many other optimization algorithms are its implementation simplicity and ability to converge to a reasonably good solution quickly. In the past several years, PSO has been successfully applied in many researches and application areas (Carlos et al. 2004; Liu et al. 2010; Guo et al. 2011; Shen et al. 2011; Costas et al. 2012; Guo et al. 2012; Agrawal and Silakari 2013; Rada-Vilela et al. 2013). It has been demonstrated that PSO can get better results in a faster and cheaper way compared with other methods.

3.2 PSO-based timing-driven Octilinear Steiner tree considering bend reduction

As given in Eqs. 2 and 3 mentioned in the previous section, it is obvious that the basic PSO cannot obtain a discrete solution for our proposed tree as a result of its continuous nature, thus some additional steps must be taken into the basic PSO. It has led to many discrete PSO algorithms for solving discrete problems. Three typical discrete PSO algorithms have been proposed, including the discrete PSO algorithm of Kennedy and Eberhart (1997), the discrete PSO algorithm for the traveling salesman problem (TSP) by Clerc (2004), and the discrete PSO algorithm for the permutation flowshop sequencing problem with makespan criteria by Pan et al. (2006).

The importance of VLSI physical design and the advantages of PSO has led to many research results in partitioning, floorplanning and routing. We proposed a multi-objective discrete PSO algorithm for the problem of VLSI partitioning, while optimizing the minimum cut and timing delay (Peng et al. 2010). We also proposed a novel intelligent decision algorithm based on the PSO technique to obtain a feasible floorplanning in VLSI circuit physical placement (Chen et al. 2010). For the problem of routing, an improved PSO was proposed for solving the obstacle-avoiding Rectilinear Steiner minimum tree problem (Shen et al. 2011) and an efficient RSMT algorithm based on PSO was presented by Liu et al. (2011). However, those works for SMT are based on Manhattan architecture. We have constructed an OST for non-Manhattan routing based on PSO, but it only optimized the wire length and did not involve timing performance and other important metrics (Liu et al. 2012). Besides, we have successfully constructed the preliminary framework of multi-objective PSO (Guo et al. 2011, 2012) and presented the corresponding update operators and fitness function.

Inspired by the Pan et al. (2006) and our previous work, an efficient MOPSO is designed in this paper to deal with the problem TOST considering bend reduction. In the proposed algorithm, the phenotype sharing function of the objective space is applied in the definition of fitness function to simultaneously optimize the two objectives of wire length and radius. Moreover, an efficient encoding scheme which can be well combined with edge transformation is adapted to reduce the number of bends in the process of TOST construction.

3.2.1 Two important metrics for performance-driven routing

The two metrics of wire length and radius are very important for performance-driven routing, since the cost (i.e., the length of the tree) and radius of the routing tree constructing for each net have an immediate impact on the timing delay. Therefore, we can bring the MRMCST model to construct the timing-driven Octilinear Steiner tree which is essential for performance-driven routing. Different from the work presented by Ho et al. (2007) which is constructed in Euclidean distance and does not show the experimental result, we try to construct the Octilinear MRMCST model in which the length between source and each sink is calculated in Octilinear distance and show the experimental results in Sect. 4. The Octilinear distance between point i and j, namely, $O_\mathrm{dis}(i,j)$, is defined as follows

$$\begin{aligned} {O_\mathrm{dis}}(i,j) = \left\{ \begin{array}{l} \Delta x + \Delta y, \hbox { if pspc } = 2 \hbox { or } 3\\ (\sqrt{2} - 1){\min _{\Delta x\Delta y}} + {\max _{\Delta x\Delta y}}, \hbox { else } \end{array} \right. \end{aligned}$$

(4)

where $\Delta x = |{x_i} - {x_j}|$ and $\Delta y = |{y_i} - {y_j}|$. $x_i$ ($x_j$) and $y_i$ ($y_j$) represent the horizontal and vertical coordinates of point i (j), respectively. Clearly, $|x_i - x_j|$ ($|y_i - y_j|$) denotes the absolute value, and the $\min _{\Delta x\Delta y}$ ($\max _{\Delta x\Delta y}$) denotes the minimum (maximum) between ${\Delta x}$ and ${\Delta y}$.

Definition 7

The length of the Octilinear Steiner tree is the sum of each segment’s length which is formulated as:

$$\begin{aligned} L({T_X}) = \sum \limits _{{e_i} \in {T_x}} {l({e_i}} ) \end{aligned}$$

(5)

where l($e_i$) represents the length of each segment $e_i$ in the tree $T_x$.

Definition 8

The radius of the Octilinear Steiner tree is the maximum length from the source to each sink in Octilinear distance.

When calculating the sum of each segment’s length in OST, we divide all segments into four categories: horizontal side, vertical side, hypotenuse with 45$^\circ$, and hypotenuse with 135$^\circ$. Then we clockwise rotate hypotenuse with 45$^\circ$ into a horizontal side and hypotenuse with 135$^\circ$ into a vertical side. We sort the horizontal sides from bottom to up and from left to right by their left vertex, while sorting the vertical sides from left to right and from bottom to up by their bottom vertex, and then the length of OST is the sum of those segments.

The performance-driven routing mainly optimizes the target of timing delay. Since Elmore delay is a good measure of timing delay for an interconnect design, we calculate the delay between the source of the tree and each sink based on the Elmore delay model using Eq. 1. Let $m_j$ and $n_j$ be the two endpoints of $e_j$, and $r_0$ ($c_0$) denote the resistance (capacitance) per unit length, then the more specific equation for calculating delay is as follows:

$$\begin{aligned} {t_i} = {R_0} \times {C_0} + \sum \limits _{{e_j} \in \hbox {path}(s,i)} {{O_{ij}}} \times {r_0} \times ({O_{ij}} \times {c_0}/2 + {C_j}) \end{aligned}$$

(6)

where ${O_{ij}} = O_\mathrm{dis}({m_j},{n_j})$.

Both wire length and radius minimizations are comparably important for delay minimization (Ho et al. 2007). However, the two metrics are often competing. While trying to minimize wire length, the radius maybe large, or vice versa. Therefore, we design MOPSO, which as discussed later, aims to simultaneously optimize the two metrics.

3.2.2 The multi-objective approach

VLSI routing, in both Manhattan and non-Manhattan architectures, is a complex multi-objective optimization problem. Some metrics of electrical performance and geometrical constraints, which are conflicting and cannot be optimized simultaneously, must be taken into account in the process of nano-level VLSI routing. This undoubtedly increases the complexity of the nano-level VLSI routing. Therefore, how to construct an efficient and stable multi-objective optimization algorithm for VLSI routing is a significant issue.

Traditional algorithms for multi-objective optimization problem polymerized several sub-objectives to form a single-objective function with a positive coefficient, which is defined by the decision-makers according to the actual situation, and then used the mature single-objective optimization algorithms to tackle the problem. Those approaches including weighted summation method, constraint method, and objective programming method, and so on, were presented to seek better solutions with relatively small computational cost. However, they still have some disadvantages. Firstly, since the decision-makers cannot obtain the prior knowledge related to that issue, it is difficult to select the coefficients, which would lead to be unable to construct the appropriate algorithm. Secondly, using the methods mentioned above to solve the issues is highly vulnerable to the impact of non-inferior front distribution and is powerless to tackle the recess of non-inferior front. In addition, each optimization process which obtains the set of Pareto optimal solution using those methods is independent and consequently it is extremely difficult for the decision-makers to make decisions. Above all, the traditional algorithms can only obtain a single optimal solution while Pareto method might get multiple Pareto approximate solutions for choosing by decision-makers.

In this paper, we apply the multi-objective PSO on the construction of timing-driven Octilinear Steiner tree for the non-Manhattan performance-driven routing to optimize both targets of wire length and radius, and at the same time reduce the number of bends. Some basic preliminaries for MOPSO are described as follows.

Definition 9

(Target Distance $fd_{ij}$) $fd_{ij}$ is the distance between two particles i and j. Supposed that the distance has m dimensions which are noted as respectively, and

$$\begin{aligned} f{d_{ij}}&= {f_1}d_{ij} + {f_2}d_{ij} + \dots + {f_m}d_{ij}\nonumber \\&= \left| {{f_1}({\mathbf{{x}}^i}) - {f_1}({\mathbf{{x}}^j})} \right| + \left| {{f_2}({\mathbf{{x}}^i}) - {f_2}({\mathbf{{x}}^j})} \right| \nonumber \\&\quad + \dots + \left| {{f_m}({\mathbf{{x}}^i}) - {f_m}({\mathbf{{x}}^j})} \right| ,\quad i \ne j. \end{aligned}$$

(7)

There are two dimensions in our proposed algorithm, noted as $f_1$ and $f_2$, respectively. $f_1$ represents the function of the wire length, and $f_2$ represents the function of the radius of the tree.

Definition 10

(Dominance Measure D(i)) D(i) expresses the number of particles that dominate the ith particle in the current population, and

$$\begin{aligned} D(i) = \sum \limits _{j = 1}^p {nd(i,j)} \end{aligned}$$

(8)

where $p$ represents the population size. nd(i, j) is one if particle j dominates particle i, and zero otherwise.

Definition 11

(Sharing Function)

$$\begin{aligned} sh(f{d_{ij}}) = \left\{ \begin{array}{l@{\quad }l} 1, &{} \hbox {if } f{d_{ij}} \le {\sigma _s}\\ 0, &{} \hbox {otherwise} \end{array} \right. \end{aligned}$$

(9)

where $\sigma _s$ is a sharing parameter.

Definition 12

(Neighbor Density Measure N(i)) N(i) associated with particle i is defined as

$$\begin{aligned} N(i) = \sum \limits _{j = 1}^p {sh(f{d_{ij}})} \end{aligned}$$

(10)

Definition 13

(Fitness Function) The fitness of a given particle F(i) can be defined as follows:

$$\begin{aligned} F(i) = {(1 + D(i))^\alpha } \times {(1 + N(i))^\beta } \end{aligned}$$

(11)

where $\alpha$ and $\beta$ are nonlinear parameters.

Compared with the single-objective PSO, during the search process of MOPSO, particles often have more than one personal best and global best value. We save these information into two external archives in a same way as Balling (2003), namely, A1 and A2, respectively. The archive A1 stores the present Pareto fronts of the population as a candidate set to guide the particles, while the archive A2 stores the generational Pareto fronts of the population. In the process of updating the position of particles, some better particle is randomly selected to guide the flight of other particles. When each update has finished, the candidate set A1 is renewed. A proper mechanism of choosing a leader particle can help to find more Pareto solutions in a shorter time. So it is very important to decide how to choose the proper leader particle to direct the movement of particle. In order to avoid the external archive from growing too big, we adopt $\varepsilon$-dominance (Laumanns et al. 2002) to reduce the external archive.

3.2.3 Encoding scheme

Our algorithm represents a candidate OST as lists of spanning tree edges, each augmented with a pseudo-Steiner point choice so that it specifies the conversion from the spanning tree edge to the Octilinear edge. Each pseudo-Steiner point choice, namely, pspc, includes four types shown in Definition 3–6 and the value of pspc is 0, 1, 2 or 3 which denote 0 Choice, 1 Choice, 2 Choice or 3 Choice, respectively. If a net has n pins, a spanning tree would have $n-1$ edges, $n-1$ pseudo-Steiner points and three extra digits which are the particles fitness, the value of wire length and the value of radius, respectively. Besides, two digits represent the two vertices of each edge and $n-1$ digits represent $n-1$ pseudo-Steiner points, so the length of a particle is $3 \times (n-1) +3$. For example, one OST tree ($n = 7$) can be expressed as one particle whose code can be expressed as the following numeric string:

$$\begin{aligned} 5 \ 7 \ \mathbf 2 \ 5 \ 4 \ \mathbf 0 \ 2 \ 4 \ \mathbf 1 \ 5 \ 3 \ \mathbf 1 \ 2 \ 1 \ \mathbf 1 \ 5 \ 6 \ \mathbf 0 \ 72 \ 18.7279 \ 11.0711 \end{aligned}$$

where the number ‘72’ is the fitness of the particle, which is the value of phenotype sharing function of the objective space. The last two digits ‘18.7279’ and ‘11.0711’ are the value of wire length and the value of radius, respectively. Each digit in bold font is the pseudo-Steiner point choice of the corresponding edge. For example, the first substring (5, 7, 2) represents one edge of the spanning tree which is composed of Vertex 5, Vertex 7 and the pseudo-Steiner point choice 2 in bold font.

Definition 14

(Bend Point) The point in the tree whose degree is greater than 1 is defined as bend point, which may be Steiner point, corner point or pin point.

In recent years, while VLSI feature size continues to shrink in the very deep-submicron technology, the number of vias becomes a critical issue in the global routing phase. Via minimization can reduce circuit delay and enhance the manufacturability of the circuit. Reducing the number of bends is helpful for reducing the number of vias, since a bend in the layer assignment or detailed routing phase usually implies a switching of layers, causing the use of more vias. Reducing the number of bends is easier than via minimization in the later phases, and hence it is necessary to study the Steiner tree construction algorithm considering bend reduction.

Yan (2008) adopted the representation of tree edge like the encoding scheme with two pseudo-Steiner point choices, i.e., including 0 Choice and 1 Choice shown in Fig. 2b, c. In contrast, the encoding scheme with four pseudo-Steiner point choices is applied in our proposed algorithm which has the potential ability to reduce the number of bends. The reason is that the existence of the last two pseudo-Steiner point choices maybe overlaps with the first two choices in the location of bend. For example, as shown in Fig. 4b, the edge (4, 2) and the edge (2, 5) have the overlapping location of bend where the point 4 is defined as the source point of the net by Yan (2008). Generally, this situation could frequently exist among the net with more pins. Therefore, for the most part, using the second encoding scheme combined with edge transformation, as shown in Fig. 4b can be more helpful to reduce the number of bends than the former, as shown in Fig. 4a. And this situation has been experimentally verified in latter section.

Fig. 4

Two kinds of encoding schemes for the potential impact on the bend reduction. a The encoding scheme with two pseudo-Steiner point choices (Yan 2008), b the encoding scheme with four pseudo-Steiner point choices

3.2.4 Update formula of the particle

Since the Steiner tree construction problem is a discrete problem, we employ the novel discrete position updating method based on genetic operations and propose the TOST_BR_MOPSO algorithm for timing-driven Octilinear Steiner tree construction with considering bend reduction.

The update formula of the particle is represented as:

$$\begin{aligned} X_i^t = {N_3}\left( {N_2}\left( {N_1}(X_i^{t - 1},w),{c_1}\right) ,{c_2}\right) \end{aligned}$$

(12)

where w is an inertia weight, $c_1$ and $c_2$ are acceleration constants. $N_1$ denotes the mutation operation and $N_2$, $N_3$ denote the crossover operations. We assume that $r_1$, $r_2$, $r_3$ are random numbers on the interval [0, 1).

In the process of constructing OSMT (Liu et al. 2012), the update operations only take into account the transformation of Steiner point. However, the edges of MRMCST are changing in the evolutionary process. For example, two Octilinear trees as shown in Fig. 5, the edge of tree is changing between them, which the edge (4, 2) exists in the tree shown in Fig. 5b but not in the other tree shown in Fig. 5a. Therefore, in addition to the transformation of Steiner point, we need to introduce the edge transformation into our proposed update operations for constructing MRMCST. Moreover, the introduction of the edge transformation increases the capacity to optimize the wire length, which is discussed in Sect. 4.1. Simultaneously, when edge transformation is adopted by the update operations, it ensures that the optimization space of the algorithm presented by Liu et al. (2011) contains the optimal solution.

Fig. 5

The edge transformation in the evolutionary process of constructing MRMCST. a One Octilinear tree, b the other Octilinear tree

However, the introduction of edge transformation might lead to the appearance of loop and generate the invalid solution in the iterative process, which destroys the soundness of the particle encoding. How to overcome the shortcoming caused by edge transformation in the evolutionary process of constructing MRMCST? The Union-Find partition (Alfred et al. 1983) which keeps track of the components connected so far is integrated into the three update operations described in the following sections.

The velocity of particles can be written as

$$\begin{aligned} W_i^t = {N_1}\left( X_i^{t - 1},w\right) = \left\{ \begin{array}{l@{\quad }l} M(X_i^{t - 1}), &{} {r_1} < w\\ X_i^{t - 1}, &{} \hbox {others} \end{array} \right. \end{aligned}$$

(13)

where w denotes the mutation probability. In the process of the particle mutation, we randomly select one edge of the particle to be mutated and the tree is divided into two sub-trees corresponding to two sets of pins. We can use the Union-Find partition to get those two sets of pins and randomly generate the two endpoints of the new mutated edge from the two sets of pins, respectively. The principle is shown in Fig. 6, where the edge $M_1$ represents the edge to be removed and the edge $M_2$ represents the new edge. The pseudo code of mutation operator is shown in Algorithm 1.

Fig. 6

Mutation operation with union-find partition

The cognitive personal experience of particles can be written as:

$$\begin{aligned} S_i^t = {N_2}\left( W_i^t,{c_1}\right) = \left\{ \begin{array}{l@{\quad }l} {C_p}(W_i^t), &{} {r_2} < {c_1}\\ W_i^t, &{} \hbox {others} \end{array} \right. \end{aligned}$$

(14)

where $c_1$ denotes the crossover probability of the particle with the personal optimal solution. In the process of the particle crossover with the personal optimal particle, we will generate the new particle which composes of the common portion between the two particles and random portion from the two particles. We store the other edges into the set of edges, namely, remaining edges, and we randomly select the edge from the remaining edges until the complete spanning tree is generated while using the Union-Find partition to avoid the appearance of loop in the process of random selection. The principle is shown in Fig. 7, where $C_1, C_2, C_3, C_4, C_5, C_6$ represents the different edges between the two spanning tree, and the set $C_1, C_3, C_5$ represents the new edges of the new spanning tree. The pseudo code of crossover operator is shown in Algorithm 2.

Fig. 7

Crossover operation with union-find partition

The cooperative global experience of particles can be written as

$$\begin{aligned} X_i^t = {N_3}(S_i^t,{c_2}) = \left\{ \begin{array}{l@{\quad }l} {C_g}(S_i^t), &{} {r_3} < {c_2}\\ S_i^t, &{} \hbox {others} \end{array} \right. \end{aligned}$$

(15)

where $c_2$ denotes the crossover probability of the particle with the global optimal solution. The process of the particle crossover with the global optimal particle is same to the process of the particle crossover with the personal optimal particle, and we no longer repeat description.

3.2.5 Parameter setting

Property 1

The setting of inertia weight affects the balance between local search ability and global search ability of particle.

As we can see from the velocity update formula, the first part provides the flight impetus of particle in search space, and represents the effect of previous velocity on the flight trajectory. Thus inertia weight is a numerical value which indicates the extent of such influence.

Property 2

Larger inertia weight will make the algorithm has strong global search ability.

Property 1 and Eq. 2 show that inertia weight decides how much previous velocity will be preserved. Thus a lager inertia weight can strengthen the capability of searching the unreached area. It is conducive to enhance the global search ability of the algorithm and jump out of the local minima. A smaller inertia weight suggests that the algorithm mainly search near the current solution. It is conducive to enhance the local search ability and accelerate convergence.

In the work by Shi and Eberhart (1998), the researchers presented a PSO algorithm based on liner decreasing inertia weight. In order to ensure a stronger global search, they employed a lager inertia weight early in the program, and a smaller one in the later stages to guarantee the local search. Simulation on four kinds of different benchmark functions showed that such strategy of parameters actually improved the performance of PSO.

Property 3

Larger acceleration coefficients $c_1$ may cause wandering in local scope. Larger acceleration coefficients $c_2$ will make the algorithm prematurely converge on local optimal solution.

Acceleration coefficients $c_1$ and $c_2$ are used in communicating between particles. Ratnaweera et al. (2004) proposed a kind of strategy which employs a lager $c_1$ and a smaller $c_2$ in the early phases and the opposite in the later. In this way, the algorithm will guarantee detailed search in local scope, not have to directly move to the position of global optimal in early phases, and speed up convergence in the later stages. Similarly, the experiment achieved great results.

Based on the above analysis, we have tested 567 kinds of the acceleration coefficients in Oliver30 TSP which is a minimization problem (Chen et al. 2010). Each experimental setting is conducted five runs and each average is calculated. Consequently, $c_1$ = 0.82–0.5 and $c_2$ = 0.4–0.83 are considered as the optimal combination of parameter settings. We adopt the idea of linear decline proposed by Shi and Eberhart (1998) and the optimal combination of parameter settings of $c_1$ and $c_2$ to update the acceleration coefficients according to Eqs. 16 and 17. Besides, the other parameters in the proposed algorithm are given as follows: population size is 200, $w$ decreases linearly from 0.95 to 0.4 according to Eq. 18 which is similar to the acceleration coefficients.

$$\begin{aligned}&c_1 = c_1 \_\mathrm{start} - \frac{{c_1 \_\mathrm{start} - c_1 \_\mathrm{end}}}{\mathrm{evaluations}} \times \mathrm{eval} \end{aligned}$$

(16)

$$\begin{aligned}&c_2 = c_2 \_\mathrm{start} - \frac{{c_2 \_\mathrm{start} - c_2 \_\mathrm{end}}}{\mathrm{evaluations}} \times \mathrm{eval}\end{aligned}$$

(17)

$$\begin{aligned}&w = w\_\mathrm{start} - \frac{{w\_\mathrm{start} - w\_\mathrm{end}}}{\mathrm{evaluations}} \times \mathrm{eval} \end{aligned}$$

(18)

where eval represents the current iteration number and evaluations represents the maximum number of iterations.

3.2.6 Processes of TOST_BR_MOPSO

The detail procedure of TOST_BR_MOPSO can be summarized as follows:

• Step 1: Load the circuit netlist data, initialize various parameters, and randomly generate the initial population.

• Step 2: Calculate the fitness value of each particle according to Eq. 11.

• Step 3: Update the personal optimal solution of each particle and set A1 and then randomly select a guide particle from A1.

• Step 4: Adjust the position and velocity of each particle according to Eqs. 12–15.

• Step 5: Recalculate the wire length, radius and fitness value of each particle.

• Step 6: Update the set of global optimal solution of the population, namely, A2.

• Step 7: Check the termination condition (a good enough position or the maximum number of iterations is reached). If fulfilled, the run is terminated and output the set of global optimal solution A2, i.e., the final solution. Otherwise, go to Step 3.

3.2.7 Complexity analysis

Lemma 1

Assume the population size is $p$, the number of iterations is iters and the number of pins is $n$. The time complexity of the proposed algorithm is $O(\hbox {iter} \times p \times {n^2})$.

Proof

In the inner loop of the proposed algorithm, from Step 3 to Step 6, it includes mutation, crossover and fitness calculation. In the mutation and crossover operations, the sorting steps determine those operations’ time complexity: $O(n\log n)$, because the time of Union-Find partition is just more than linear (Julstrom 2001). Besides, in the fitness calculation, the time complexity of calculating the radius is $O(n^2)$ while the sorting steps also determine calculating the wire length of the routing tree. Therefore, the complexity of the inner loop is $O(n\log n + {n^2} + n\log n) = O({n^2})$. The outer loop is related to the number of particles p and the number of iterations iters, consequently, the time complexity of the proposed algorithm is $O(\hbox {iter} \times p \times {n^2})$.

3.3 Convergence analysis of TOST_BR_MOPSO

Definition 15

(Finite Markov Chain) Let $X(X = {X_k}, k = 1,2, \ldots )$ be the stochastic process of discrete parameters defined in probability space $(\Omega ,F,P)$ over a finite state space $S$. If $X$ has Markov properties, i.e., for any nonnegative integer $k$ and state ${i_0},{i_1}, \ldots ,{i_{k - 1}} \in S$, then $X$ is a finite Markov chain when

$$\begin{aligned}&P({X_{k + 1}} = {i_{k + 1}}|{X_0} = {i_0},{X_1} = {i_1}, \ldots ,{X_k} = {i_k}) \nonumber \\&\qquad \ \ \quad \quad = P({X_{k + 1}} = {i_{k + 1}}|{X_k} = {i_k}) \\&P({X_0} = {i_0},{X_1} = {i_1}, \ldots ,{X_k} = {i_k}) > 0\nonumber \end{aligned}$$

(19)

where $P({X_{k + m}} = j|{X_k} = i)$ is called $m$-step transition probability of $X$, which is the conditional probability of process from state $i$ at time $k$, after the $m$th step, to state $j$ at time $k +m$, denoted as ${P_{ij}}(k,k + m)$. For $i,j \in S$, if ${P_{ij}}(k,k + 1)$, ${P_{ij}}$ for short, does not depend on the time $k$, the Markov chain is said to be homogeneous. $P = [{P_{ij}}]$ is called transition matrix with ${P_{ij}}$ as the element of $i$th row and $j$th column. The long-term behavior of homogeneous finite Markov chain was completely determined by its initial distribution and first step transition probability.

Theorem 1

The Markov chain of TOST_BR_MOPSO is finite and homogeneous.

Proof

In its global search, TOST_BR_MOPSO obtains the global and individual optimum through updating the positions of particles by stochastic mutation and crossover operator. Judging from the process of global searching, the generation of a new population depends on the current population. Thus, the conditional probability of search process, from a state to a certain specific state, satisfies Eq. 19. That means it satisfies the property of Markov. Therefore, the Markov chain of TOST_BR_MOPSO is finite and homogeneous. In this algorithm, the set constituted of all the populations $\{ {\alpha _1},{\alpha _2}, \ldots ,{\alpha _m}\}$ is finite. That is, events occurring at time $k = 0,1, \ldots$ all belong to a finite countable event aggregate, thus its Markov chain is finite as well. Hence, in the above analysis theories and methods of Markov chain can be directly applied to the analysis of this algorithm.

Theorem 2

Transition probability matrix of the Markov chain made up of TOST_BR_MOPSO is positive definite.

Proof

While searching, the population transits from state ${i_i} \in S$ to state ${i_j} \in S$, through mutation operator and crossover operators with the global optimum and the individual optimum. The transition probabilities of these three operators are ${m_{ij}}, {g_{ij}}, {p_{ij}}$, respectively. And the stochastic matrixes what they consist of are $M = \{ {m_{ij}}\}$, $G = \{ {g_{ij}}\}$, $D = \{ {d_{ij}}\}$, respectively, let $P = MGD$, then ${m_{ij}} > 0,\sum \nolimits _{{i_j} \in E} {{m_{ij}}} = 1;{g_{ij}} \ge 0,\sum \nolimits _{{i_j} \in E} {{g_{ij}}} = 1;{d_{ij}} \ge 0,\sum \nolimits _{{i_j} \in E} {{d_{ij}}} = 1$.

Therefore, $M, G, D$ are all stochastic and $M$ is positive definite. Then we can prove $P$ is positive definite. Let $B = GD$. For $\forall \mathrm{{ }}{i_i} \in S,{i_j} \in S$, we have

$$\begin{aligned} {b_{ij}} = \sum \limits _{{\lambda _k} \in E} {{g_{ik}}{d_{kj}}} \ge 0, \end{aligned}$$

then $\sum \nolimits _{{\lambda _j} \in E} {{b_{ij}}} = \sum \nolimits _{{\lambda _j} \in E} {\sum \nolimits _{{\lambda _k} \in E} {{g_{ik}}{d_{kj}}} } = \sum \nolimits _{{\lambda _k} \in E} {{g_{ik}}} \sum \nolimits _{{\lambda _j} \in E} {{d_{kj}}} = \sum \nolimits _{{\lambda _k} \in E} {{g_{ik}}} = 1$.

Hence, $B$ is a stochastic matrix, similarly, we get ${d_{ij}} = \sum \nolimits _{{\lambda _k} \in E} {{b_{ik}}{m_{kj}}} > 0$.

Theorem 3

(Limit theorem for Markov chain) Assume that $P$ is a positive stochastic transition matrix of definite homogeneous Markov chain, then:

• (1) There exists a unique probability vector ${\overline{P} ^T} > 0$ which satisfies ${\overline{P} ^T}P = {\overline{P} ^T}$.

• (2) For any initial state $i$ ($e_i^T$ as its corresponding initial probability), we get $\lim \nolimits _{k \rightarrow \infty } e_i^T{P^k} = {\overline{P} ^T}$.

• (3) Limit probability matrix $\lim \nolimits _{k \rightarrow \infty } {P^k} = {\overline{P} ^{}}$, where $\overline{P}$ is a $n \times n$ stochastic matrix, and all its rows equal to ${\overline{P} ^T}$.

The limit theorem explains that the long-term probability of Markov chain does not depend on its initial states. This theorem is the basis for the convergence of an algorithm.

Lemma 2

If mutation probability $m \succ 0$, the algorithm is an ergodic irreducible Markov chain which has only one limited distribution and nothing to do with the initial distribution; moreover, the probability at a random time and random state is greater than zero.

Proof

At the $t$th time, the $j$th state probability distribution of population $X(t)$ is:

$$\begin{aligned} {P_j}(t) = \sum \limits _{j \in S} {{P_i}(1)P_{ij}^{(t)}},\quad t = 1,2, \ldots \end{aligned}$$

(20)

According to Theorem 3, we can get the formulation as following:

$$\begin{aligned}&{P_j}(\infty ) = \mathop {\lim }\limits _{t \rightarrow \infty } \left( \sum \limits _{i \in S} {{P_i}(1)} P_{ij}^{(t)}\right) = \sum \limits _{i \in S} {{P_i}(1)P_{ij}^{(\infty )}} > 0,\nonumber \\&\qquad \forall j \in S\nonumber \\ \end{aligned}$$

(21)

Definition 16

Suppose a stochastic variant ${Z_t} = \max \{ f(x_k^{(t)}(i))|k = 1,2, \ldots ,N\}$ which represents individual best fitness at the $t$th step and $i$th state of the population. Then the algorithm converges to the global optimum, if and only if

$$\begin{aligned} \mathop {\lim }\limits _{t \rightarrow \infty } P\{ {Z_t} = {Z^*}\} = 1, \end{aligned}$$

(22)

where ${Z^*} = \max \{ f(x)|x \in S\}$ represents the global optimum.

Theorem 4

For any $i$ and $j$, the time transiting of an ergodic Markov chain from the $i$th state to the $j$th state is limited.

Theorem 5

TOST_BR_MOPSO algorithm can converge to the global optimum.

Proof

Suppose that $i \in S$, ${Z_t} < {Z^*}$ and ${P_i}(t)$ is the probability of TOST_BR_MOPSO algorithm at $i$th state and the $t$th step. Obviously $P\{ {Z_t} \ne {\mathrm{Z}^ * }\} \ge {P_i}(t)$, hence we can know that $P\{ {Z_t} = {Z^*}\} \le 1 - {P_i}(t)$.

According to Lemma 2, the $i$th state probability of the operator in TOST_BR_MOPSO algorithm is ${P_i}(\infty ) > 0$, then

$$\begin{aligned} \mathop {\lim }\limits _{t \rightarrow \infty } P\{ {Z_t} = {Z^*}\} \le 1 - {P_i}(\infty ) < 1 \end{aligned}$$

(23)

Observe a new population such as $X_t^ + = \{ {Z_t},{X_t}\} ,t \ge 1,{x_{ti}} \in S$ denoting the search space (which is a finite set or a countable set), where ${Z_t}$, the same to that in Definition 16, represents individual best fitness in current population, ${X_t}$ denotes the population during the search. As it is easy to prove that the group shift process $\{ X_t^ + ,t \ge 1\}$ is still a homogeneous and ergodic Markov chain, we can know that

$$\begin{aligned}&P_j^ + (t) = \sum \limits _{i \in S} {P_i^ + (1)P_{ij}^ + (t)} \nonumber \\&P_{ij}^ + > 0 (\forall i \in S,\forall j \in {S_0}) \\&P_{ij}^ + = 0 (\forall i \in S,\forall j \notin {S_0})\nonumber \end{aligned}$$

(24)

So

$$\begin{aligned}&{(P_{ij}^ + )^t} \rightarrow 0\mathrm{{ }}(t \rightarrow \infty ) \nonumber \\&P_j^ + (\infty ) \rightarrow 0\mathrm{{ }}(j \notin {S_0}) \\&\mathop {\lim }\limits _{t \rightarrow \infty } P\{ {Z_t} = {Z^*}\} = 1\nonumber \end{aligned}$$

(25)

4 Experimental results

All the algorithms have been implemented and executed in MATLAB R2009a on a PC with 2.00 GHz CPU and 2.00 GB RAM (Windows XP environment). One set of the test problems in OR-Library (Beasley 1990) is used to study the performance of the proposed algorithm. To study the performance of the proposed algorithm, four experiments are carried out from Sects. 4.1 to 4.4.

4.1 Experimental validation of edge transformation

In order to verify the effectiveness of the proposed edge transformation strategy, we compare our algorithm with the OSMT construction algorithm without edge transformation on the wire length. As shown in Table 2, the introduction of edge transformation (the algorithm is named EOSMT) increases the ability to optimize the wire length which is 1.57 % smaller than the wire length of OSMT (Liu et al. 2012).

Table 2 Comparison on the wire length between EOSMT and OSMT

4.2 Performance analysis of the proposed MOPSO

To study the performance of PSO under our multi-objective strategy, the solution sets generated by the MOPSO are compared with the NSGA II (Deb et al. 2002) and SPEA 2 (Zitzler et al. 2001) which are two classic multi-objective evolutionary algorithms in ZDT1, ZDT2 and ZDT6 benchmarks (Zitzler 1999). Those three benchmarks were proposed by Zitzler (1999) and represented some typical function types of non-inferior front in multi-objective optimization problem, respectively. ZDT1 is a convex function, ZDT2 is a non-convex function, and ZDT6 is a noncontiguous function. In this paper, we use three quantitative indicators (unary additive EPS indicator $I_{\varepsilon + }^1$, HYP indicator $I_H^ -$ and unary $R2$ indicator $I_{R2}^1$), which proposed by Zitzler et al. (2003), to verify the validity of our proposed multi-objective strategy.

For the three test functions ZDT1, ZDT2 and ZDT6, in most cases, the proposed algorithm (MOPSO) can converge to the Pareto front within 100 iterations and consume less computing cost. The Kruskal–Wallis test statistical method (Conover 1999) is used to compare the experimental results of those algorithms. The Kruskal–Wallis test results of three quantitative indicators are shown in Table 3. This table shows each pair of the value of $P$ which is composed of algorithm $Q_R$ (row) and algorithm $Q_C$ (column), and the corresponding alternative hypothesis is that algorithm $Q_R$ is superior to algorithm $Q_C$ in indicator. The value of significance level is 0.05. For the convenience of said, EPS represents $I_{\varepsilon + }^1$, HYP represents $I_H^ -$ and $R2$ represents $I_{R2}^1$ in our work. From Table 3, as to the ZDT2, the proposed MOPSO algorithm is better than the other multi-objective evolutionary algorithms in the three indicators and it shows that the proposed algorithm is especially suitable for solving the Pareto front of the non-convex function. For the ZDT6, MOPSO is better than the NSGA II and SPEA 2 in both $R2$ and HYP indicators and just a bit poor in the EPS indicator. Based on Zitzler et al. (2003), it also shows that if the results from multiple Pareto compliant indicators are different, it is hard to know which algorithm is better. Therefore, MOPSO algorithm can achieve good results in the ZDT6 function of non-uniform front. For ZDT1 problem, although MOPSO is inferior to the NSGA II and SPEA 2 in the three indicators, the overall difference value is small. Given that the obvious differences with other evolutionary algorithms cannot be found in the dominance ranking distribution of the solution and the proposed algorithm can converge to Pareto front under less number of iterations, it can be seen that the proposed algorithm can obtain satisfactory solutions in the optimization function of convex Pareto front. From the comprehensive results of three test functions, it can be seen that the proposed MOPSO algorithm has stronger global searching ability and can converge to Pareto front under less computational cost, and has a better distribution of solutions. Thus it can be seen that MOPSO is worthy of being studied in the field of multi-objective optimization problems.

Table 3 The Kruskal–Wallis test results of EPS, HYP and $R2$ indicator

4.3 Comparison with the two SMT algorithms

In order to validate the proposed algorithm on the ability of optimizing the wire length and radius of routing tree, we compare it with the already existing SMT algorithms (Liu et al. 2011, 2012), namely, RA and OA, which are in Rectilinear and Octilinear architectures, respectively, and both only consider the single objective of the wire length. Tables 4 and 5 show our experiment results as compared with the results of RA and OA methods. Note that the instance ’S0’, shown as the first instance in Tables 4, 5, 6, 7, comes from a case study (Yan 2008). Columns 5 and 10 of Table 4 show that the routing trees constructed by our proposed algorithm outperform the RSMTs (RA) by 24.07 % in the radius and 6.59 % in the wire length. Columns 6 and 11 of Table 4 indicate that the radius of TOST_BR_MOPSO is 19.30 % smaller than the radius of OSMTs (OA), only with the 2.07 % additional cost in wire length.

Table 4 Comparison on the wire length and radius with the two SMT algorithms (RA and OA)

Table 5 Comparison on the max s-t delay and sum s-t delay with the two SMT algorithms (RA and OA)

Table 6 Comparison on the wire length and radius with the TOST algorithm (TOA)

Table 7 Comparison on the max s-t delay, sum s-t delay and number of bends with the TOST algorithm (TOA)

As can be observed from Table 5, the proposed algorithm can get 32.97 and 36.13 % smaller than RSMTs (RA) in the maximum delay value between source and each sink (namely, max s-t delay) and the sum of each delay value between source and each sink (namely, sum s-t delay), respectively. Compared to OSMTs (OA), the proposed algorithm achieves 24.39 and 23.95 % far better results in the two performance metrics. The experimental results show that the non-Manhattan architecture is better in the ability of optimizing the wire length and timing delay than Manhattan architecture, and at the same time our algorithm can significantly optimize the timing delay, but only at the cost of a small amount of wire length increasing under the same routing architecture.

4.4 Comparison with the timing-driven Octilinear Steiner tree construction method

Tables 6 and 7 show the comparison of the proposed TOST_BR_MOPSO algorithm with timing-driven Octilinear Steiner tree construction (Yan 2008), namely, TOA, under the five metrics which includes the wire length, radius, max s-t delay, sum s-t delay and the number of bends. In order to effectively compare with TOA, each experimental data in OR-Library is multiplied by 15 and rounded (in Sect. 4.3, each experimental data in OR-Library is also processed in this way). From Table 6, we can find that the two former metrics of our algorithm outperform TOA by 2.08 and 5.22 %, respectively. Moreover, the three latter metrics of our algorithm are 4.93, 10.07 and 19.67 % smaller than TOA on the average as shown in Table 7. Because our algorithm tries a global search and optimizes the wire length and radius which both have an immediate impact in the timing delay, we can get a better timing delay than TOA which is based on greedy strategy and easy to be convergent to the local optimum. Furthermore, the significant reduction in the number of bends shows that our proposed encoding strategy combined with edge transformation is effective for bend reduction.

As shown in Table 8, the parameter values of five IC technologies are specified in the four previous columns and the last five columns represent the comparison results on the wire length, radius, max s-t delay, sum s-t delay and number of bends with the TOA under different IC technologies. Since standard deviation can reflect the discrete degree of a data set, from Fig. 8, we can find that the standard deviation for each metric is very small and less than 0.014 (especially the standard deviation for the bend metric is zero) and it shows that our proposed algorithm is very stable and effective under different IC technologies.

Fig. 8

The standard deviation for each metric in Table 8

Table 8 Comparison on the wire length, radius, max s-t delay, sum s-t delay and number of bends with the TOST algorithm (TOA) under different IC technologies

5 Conclusions

Constructing the timing-driven Steiner tree is very important in VLSI performance-driven routing stage. In this paper, we presented an efficient algorithm to construct the MRMCST for performance-driven routing in Octilinear architecture based on MOPSO and Elmore delay model. We adopted edge transformation and Union-Find partition to make the evolutionary process more effective. Furthermore, optimizing the number of bends which is one of the key factors of chip manufacturability is meaningful for VLSI routing. To the best of our knowledge, this is the first time to optimize the number of bends in non-Manhattan performance-driven routing. Experimental results on OR-Library indicate that our algorithm demonstrates a great performance compared to others and is very stable and effective under different IC technologies. Further work will focus on non-Manhattan obstacle-avoiding performance-driven routing problem.