Obtaining more appropriate temperature sensor locations for thermal error modeling: reduction, classification, and selection

Abstract

Obtaining appropriate temperature sensor locations is crucial for data-driven thermal error modeling. The pseudo-correlation and variable ranking will cause inappropriate sensor selection results. In this paper, a three-step sensor selection strategy based on the detrended cross-correlation coefficient is proposed to obtain a stable and robust set of thermal key points. Combined with sensor reduction and classification, 15 sensors are reduced to 9 and classified into 3 groups. Finally, three sensors are selected as thermal key points. The sensor selection results are applied to a support vector machine model for a CNC grinding machine. The modeling results of 49 predictions based on 7 speed spectrums show that the root mean square error and maximum error are less than 2.32 μm and 3.73 μm, respectively. Compared with two traditional methods, the proposed method has higher accuracy and stronger robustness, which is effective for sensor selection of thermal error modeling.

1 Introduction

Thermal error is one of the major errors in machine tools, which occurs due to the heat generated at the moving elements [1]. The effects of temperature can induce up to 75% of overall geometrical errors of machined workpieces [2]. Thermal error compensation is a convenient and cost-efficient way to minimize the influence of thermal error [3]. There are two kinds of models for thermal error compensation: the data-driven model and the physically-based model [4]. Many data-driven models have been used in thermal error modeling, such as multiple linear regression, BP neural network, support vector machine, principal component regression [5], and ridge regression algorithm [6]. A robust data-driven model can be established by selecting only a few temperature sensors with appropriate locations [7]. The optimal temperature sensors (known as thermal key points (TKP) or temperature-sensitive points) have two basic requirements [3]: Firstly, the temperature of TKP have close relationships with thermal error. Secondly, the number of TKP is limited. Too many sensors will increase the workload and expense, even reduce the accuracy of the model.

Initially, researchers directly use the sensors with large correlation coefficients with the thermal error as optimal sensors. However, the correlation among temperatures of different sensors can impact the correctness of selection [3]. Multicollinearity among temperature data will affect modeling accuracy. Therefore, many researchers follow two steps to select TKP: (1) classifying temperature sensors into several groups and (2) choosing one optimal sensor for each group based on some sorting criteria. There are two main classification strategies: (1) the grouping approach (GA) method [8] and (2) the unsupervised classification method. The GA method is based on such principle that the correlation coefficients between different temperature sensors are calculated to form a correlation matrix. By setting a threshold, the sensors with a coefficient greater than the threshold are classified into the same group. Pearson correlation coefficient (PCC) [9] and gray correlation coefficient [10] are the commonly used correlation coefficients in the GA method. The unsupervised classification methods, such as fuzzy c-means clustering (FCM) [11] and K-means clustering [12], are also widely used in sensor classification. Due to the unsupervised characteristics, they are sensitive to the input variables. After sensor classification, the correlation coefficients between the data of temperature sensors and thermal error are calculated. The sensor with the largest coefficient in each group is selected as TKP. The PCC [13] and gray correlation coefficient [10] are the commonly used criteria for calculating the correlation coefficient.

However, there are still some problems with the traditional sensor selection methods. In this paper, we summarize it as follows.

• 1. The classification without preselection. Generally, when there is no prior knowledge about the locations of TKP, as many sensors as possible will be placed on the surface of the spindle system. This arrangement is reasonable because no potential optimal position will be missed. However, the following problem is that some sensors with low correlation with thermal error will be classified in the same group, and then one of them will be selected as TKP. Thus, a preselection is important for maintaining the correlation between the selected sensors and thermal error data.

• 2. The selection based on pseudo-correlation. Many statistical methods for calculating the correlation between two time series have strict application conditions. For example, the PCC is unsuitable for non-Gaussian [14] and nonstationary [15] time series, especially when there is an obvious trend in the time series. However, the temperature and thermal error data have been proved to follow the exponential trend [16]. Thus, a new method is necessary to overcome the weakness of traditional correlation calculation methods.

• 3. The processing based on a single speed spectrum. Ideally, the TKP selected by a single speed spectrum are also applicable to other speed spectrums. In the error compensation stage, a set of fixed TKP are more acceptable, because it will reduce the complexity and implementation difficulty of the model. But in fact, the TKP selected by different speed spectrums are variable [5, 6, 17]. It is not only the classification and ranking that will cause the instability of TKP, but also the speed spectrums with different correlation calculation methods. Therefore, it should be checked whether the speed spectrum is suitable for the correlation calculation methods, and the selection results should be determined by the results of more than one speed spectrum.

This paper proposes a three-step sensor selection strategy for thermal error modeling: reduction, classification, and selection. The theoretical reasons for inappropriate sensor selection are analyzed. The detrended cross-correlation coefficient (DCCC) is used as a robust and accurate criterion to calculate the correlation between time series. In the sensor reduction stage, the number of sensors was reduced from 15 to 9 based on the change of DCCC value. After sensor reduction, the GA method was used for sensor classification. The nine sensors were classified into three groups. Finally, the TKP were selected based on the ranking order calculated by the mean DCCC value between temperature and thermal error data.

The rest of this paper is as follows. In Sect. 2, the theoretical reasons for inappropriate sensor selection are analyzed, and the DCCC is introduced. Section 3 shows the thermal error experiment on a CNC grinding machine. Section 4 shows the detailed process of the three-step sensor selection strategy. In Sect. 5, the accuracy and robustness of the proposed method are verified with the comparison with two traditional methods. Conclusions are provided in Sect. 6.

2 The theoretical reasons for inappropriate sensor selection and detrended cross-correlation coefficient

2.1 Pseudo-correlation caused by the trend-driven time series

The PCC between two time series (x and y) is expressed as:

$$r_{{{\varvec{x}}, \, {\varvec{y}}}} = \frac{{\sum\limits_{i = 1}^{n} {\left( {x_{i} - \overline{x}} \right)\left( {y_{i} - \overline{y}} \right)} }}{{\sqrt {\sum\limits_{i = 1}^{n} {\left( {x_{i} - \overline{x}} \right)^{2} } } \sqrt {\sum\limits_{i = 1}^{n} {\left( {y_{j} - \overline{y}} \right)^{2} } } }}$$

(1)

where $\overline{x }$ and $\overline{y }$ are the average value of x and y, respectively, n is the length of each variable.

As a widely used correlation calculation method, PCC has been successfully applied to many fields. But the PCC is unsuitable for nonstationary time series. If two time series are nonstationary (they have similar trends), a large PCC value could not guarantee the real correlation.

According to the exponential thermal error model, the temperature and thermal error data of the spindle system follow the exponential trend [16], as shown in Eq. (2).

$$\Delta Z = Z_{0} + (Z_{SS} - Z_{0} )*(1 - e^{ - t/\tau } )$$

(2)

where ΔZ is the change in spindle growth over time t, Z₀ is the spindle deformation at time 0, Z_SS is the steady state spindle deformation, and τ is the time constant.

Thus, the pseudo-correlation is inevitable when PCC is used as the evaluation index of correlation.

Figure 1 shows three nonstationary time series. The expressions are as follows:

$$\begin{cases} y1 = 10\sin x + 200(1 - 2^{ - x/30} ) + 20 \hfill \\ y2 = 5\sin (x + (3/8)\pi ) + 150(1 - 2^{ - x/30} ) + 10 \\ y3 = 100(1 - 2^{ - x/30} ) + 5 \end{cases}$$

(3)

Fig. 1

Three nonstationary time series and the division of subseries

where x = 0.1, 0.2, 0.3, …, 30.

There are three basic terms in Eq. (3). y1 is taken as an example. The fluctuation term is 10sinx, the trend term is 200(1–2^−x/30), and the base term is 20.

By taking y1, y2, and y3 into Eq. (1), the PCC value r_{y1, y2} is 0.973, and the r_{y1, y3} is 0.970. The values of r_{y1, y2} and r_{y1, y3} show a strong correlation. But the PCC values between subseries are variable. Six subseries are formed when the length of the subseries is 5, as shown in Fig. 1. Each subseries pair is calculated by Eq. (1). Table 1 tabulates the calculation results.

Table 1 The PCC values of six subseries

Similarly, when the length of subseries is 3, each time series is divided into ten subseries. The PCC values between subseries pairs are tabulated in Table 2.

Table 2 The PCC values of ten subseries

Tables 1 and 2 show that the PCC is not effective for nonstationary time series. The strong correlation calculated by PCC for the whole time series cannot reflect the real correlation relationship between subseries. For example, r_{y1, y2} in Table 1 can be as high as 0.877 and as low as 0.027 and even show a negative correlation as -0.200.

Figure 1 shows that there are two possible cases of pseudo-correlation. The first case corresponds to the relationship between y1 and y2. The fluctuation terms of y1 and y2 are different. But with the existence of the trend term, the PCC value can be as high as 0.973. The second case corresponds to the relationship between y1 and y3. Note that y3 has only trend term and base term. It indicates that the time series affected only by the trend term will also have a large correlation coefficient.

Thus, a conclusion can be made that the pseudo-correlation sensors have two characteristics: (1) they are affected by the trend and have small temperature change in the whole measurement process; (2) they have significant variation in correlation value with the change of subseries size. To obtain these two characteristics and ensure an effective correlation relationship, a new correlation calculation method is introduced in Sect. 2.3.

2.2 Variable ranking from the geometric properties

Besides the pseudo-correlation, another noteworthy phenomenon is the variable ranking based on the correlation coefficient between different speed spectrums.

If we regard $\left( {x_{i} - \overline{x}} \right)$ and $\left( {y_{i} - \overline{y}} \right)$ in Eq. (1) as new vectors:

$$\begin{cases} {\varvec{X}} = x_{i} - \overline{x} = (x_{1} - \overline{x}), \, (x_{2} - \overline{x}), \, ..., \, (x_{n} - \overline{x}) \\ {\varvec{Y}} = y_{i} - \overline{y} = (y_{1} - \overline{y}), \, (y_{2} - \overline{y}), \, ..., \, (y_{n} - \overline{y}) \end{cases}$$

(4)

Thus, Eq. (1) is rewritten as:

$$r_{{{\varvec{x}}, \, {\varvec{y}}}} = \cos \theta_{{{\varvec{X}}, \, {\varvec{Y}}}} = \frac{{{\varvec{X}} \cdot {\varvec{Y}}}}{{\left\| {\varvec{X}} \right\| \times \left\| {\varvec{Y}} \right\|}}$$

(5)

Eq. (5) shows that the value of PCC is equal to the cosine of the angle between X and Y.

Considering a simplified situation that n is 3, as shown in Fig. 2, P (a, b, c) is a reference vector. If an angle θ is fixed, then all the vectors have the same angle with P will form a conical surface. For example, P₁ (a₁, b₁, c₁), P₃ (a₁, b₁, c₃), and P₄ (a₄, b₄, c₄) are three vectors on the conical surface, and the correlation coefficients for the original time series r_{p, p1}, r_{p, p2}, and r_{p, p4} are the same. From P₁ to P₃, there is a P₂. The angle between P₂ and P is 0, and the corresponding correlation coefficient is 1. Thus, with a change in Z axis from c₁ to c₃, the correlation coefficient increases first and then decreases. For vectors having small angle with P₂, a small change in any axis will cause a large change in the correlation coefficient. When temperature sensors are densely arranged on the headstock surface, the temperature data of many sensors have strong correlation with thermal error. Thus, the vectors of these sensors also have small angles with the vector of thermal error data. It is unrealistic to achieve a complete stable ranking for different speed spectrums based on the correlation coefficient. Besides, for vectors with large modules such as P₄, in order to achieve the same change in correlation coefficient (Δθ) as P₁, a larger change in Z axis (ΔL) is necessary. Thus, it is inappropriate to directly sort the vectors with different module lengths based on the correlation coefficient. Besides, the variable characteristic is independent of the trend in Sect. 2.1. Thus, after removing the influence of the trend, the variable phenomenon still exists in the correlation calculation results.

Fig. 2

Diagram of the geometric properties of the correlation coefficient calculation

In order to achieve a relatively stable ranking, some strategies need to be implemented. Firstly, the speed spectrums have to be preselected. Since the temperature and thermal error data are non-Gaussian and nonstationary, some testing has to be carried out to ensure the data of the selected speed spectrums are suitable for the determined correlation calculation method. Secondly, classification is essential before ranking. After sensor classification, the vectors in the same group have similar module length and variation, which makes the correlation coefficients comparable. Thirdly, after speed spectrums selection and classification, the ranking of sensors in the same group needs to be determined by the results of more than one speed spectrum.

2.3 Detrended cross-correlation based method

2.3.1 Detrended cross-correlation coefficient

The DCCC [18] method is a detrended strategy to calculate the correlation between two nonstationary time series. It combines the detrended fluctuation analysis [19] and the detrended cross-correlation analysis [20]. The DCCC is approximately equal to PCC after detrending [21], but it is more suitable for nonstationary time series [15] and can obtain the correlation between different subseries.

The main content of DCCC includes the following two parts: (1) removing the trend of raw data by detrended fluctuation analysis and (2) forming an evaluation index similar to PCC after detrended cross-correlation analysis.

Firstly, the original variables x (x₁, x₂, …, x_n) and y (y₁, y₂, …, y_n) with the same length n are calculated by (4). The new time series are x* (x₁*, x₂*, …, x_n*) and y* (y₁*, y₂*, …, y_n*).

Secondly, divide the time series into 2 N subseries. The length of each subseries is S, as shown in Fig. 3. The division starts from both the positive and the negative directions.

Fig. 3

Diagram of subseries division

Thirdly, the polynomial fitting is performed for each subseries, and the covariance is calculated by following.

$$F_{{{\varvec{x}}, \, {\varvec{y}}}}^{2} \left( {s,\tau } \right) = \begin{cases} \frac{1}{s}\sum\limits_{j = 1}^{s} {(x_{(\tau - 1)s + j}^{*} - \hat{x}_{(\tau - 1)s + j}^{*} )(y_{(\tau - 1)s + j}^{*} - \hat{y}_{(\tau - 1)s + j}^{*} ), \, \tau { = 1, 2, }...{, }N} \\ \frac{1}{s}\sum\limits_{j = 1}^{s} {(x_{n - (\tau - N)s + j}^{*} - \hat{x}_{n - (\tau - N)s + j}^{*} )(y_{n - (\tau - N)s + j}^{*} - \hat{y}_{n - (\tau - N)s + j}^{*} ), \, \tau { = }N{ + 1, }N{ + 2, }...{, 2}N} \end{cases}$$

(6)

where ${\widehat{x}}^{*}$ and ${\widehat{y}}^{*}$ are fitted values of the polynomial fitting.

Fourthly, calculate the fluctuation function.

$$F_{x,y} \left( s \right) = \frac{1}{2N}\sum\limits_{\tau = 1}^{2N} {F_{x,y}^{2} \left( {s,\tau } \right)}$$

(7)

Finally, take either of the two vectors as the reference vector; the DCCC value is expressed as:

$$\rho_{x,y} \left( s \right) = \rho_{y,x} \left( s \right) = \frac{{F_{x,y} \left( s \right)}}{{\sqrt {F_{x,x} \left( s \right)} \sqrt {F_{y,y} \left( s \right)} }}$$

(8)

Thus, the DCCC is a function of the length of subseries (S). It reflects the detrended correlation of two time series with different time scales and can obtain a robust correlation coefficient.

In this section, two evaluation indexes are proposed based on the DCCC, as expressed in Eq (9).

$$\begin{cases} V - DCCC_{x,y} = \max (\rho_{x,y} \left( S \right)) - \min (\rho_{x,y} \left( S \right)) \\ M - DCCC_{x,y} = \frac{1}{m}\sum\limits_{S = 1}^{m} {(\rho_{x,y} \left( S \right))} \end{cases}$$

(9)

The first index is the variation of the DCCC curve (V-DCCC), which reflects the change of correlation between different subseries. The smaller the V-DCCC, the stronger the stability of the correlation. The second index is the mean value of the DCCC curve (M-DCCC), which indicates the degree of correlation. The larger the M-DCCC, the stronger the correlation.

2.3.2 Detrended cross-correlation coefficient with sliding window

The DCCC reflects the correlation of two time series with different subseries length. In dealing with the selection of time series, such as the selection of speed spectrum, it is equally important to consider the correlation of two time series with different subseries location. Based on the sliding window method in multiple detrended cross-correlation coefficient [22], a detrended cross-correlation coefficient with sliding window (SW-DCCC) is proposed in this paper. The division starts from the first value of the time series until the last sliding window reaches the last value, and the length of the sliding window is w, as presented in Fig. 4. In each sliding window, the M-DCCC is calculated. For m sliding windows, the SW-DCCC value is a curve with m values. Similar to DCCC, if the SW-DCCC curve has small fluctuation and large value, it shows that the speed arrangement of the speed spectrum is reasonable, and every location can ensure consistent and high correlation.

Fig. 4

Diagram of the sliding window division

3 Thermal error experiment

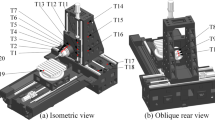
The thermal error experiment was carried out on a peripheral CNC grinding machine. As shown in Fig. 5, temperature sensors (DOCOROM PT100) were fixed on one side of the headstock after removing the grinding wheel joined to the front flange. The 15 sensors were arranged along 3 lines. The first line is from the end cap of the front bearing (sensor 09) to the connecting flange between spindle and motor (sensors 14 and 15). The second line is along the four grooves of the headstock. The third line is close to four bolted joints. Besides, another temperature sensor was placed outside the spindle to monitor the temperature variation in different seasons. The laser displacement sensor (Micro-Epsilon optoNCDT2300) was used for the axial thermal error measurement of the spindle. The sampling frequency of laser displacement sensor was 5000 Hz. To reduce the influence of spindle rotation, the average value of displacement sensor per minute was taken as the measured value. The sampling frequency of temperature sensors was 1/60 Hz. The relative value based on the value of the first minute of the measured temperature and thermal error data is used to form the dataset in thermal error modeling.

Fig. 5

Experimental setup of spindle system

Two sets of experiments were conducted in different seasons to obtain thermal error and temperature data in different environments, as shown in Fig. 6. The speed spectrums A1 and A2 are designed based on ISO 230–3: 2020 [23]. Speed spectrums A2 and B2 are transformations based on A1 and B1. Speed spectrums A3, B3, and B4 are constant speed spectrums.

Fig. 6

Variable speed spectrums

The experimental parameters of all speed spectrums are shown in Table 3. Figures 7, 8 and 9 show the axial thermal error and temperature data of three typical speed spectrums, where (a) corresponds to thermal error and (b) ~ (d) correspond to the temperature change of 15 sensors.

Table 3 Experimental parameters

Fig. 7

Thermal error and temperature data of A1

Fig. 8

Thermal error and temperature data of B2

Fig. 9

Thermal error and temperature data of B3

4 Sensor selection process

4.1 Spontaneous sensors and flow chart of sensor selection process

All the detrended cross-correlation-based methods are calculations between two time series. When using SW-DCCC and V-DCCC, a reference time series from one sensor needs to be defined. The main purpose of sensor reduction is to remove the sensors that their temperature data are affected by the trend. Thus, 15 temperature sensors can be divided into 2 types: the spontaneous sensors and the trend-driven sensors. For the spontaneous sensors, the temperature changes are related to the heat transfer process of the spindle. For the trend-driven sensors, they are affected by the trend of the headstock surface temperature. Instead of finding the trend-driven sensors, the most spontaneous sensor is determined, and other spontaneous sensors can be obtained based on the correlation coefficient.

Figure 10 shows the temperature data of 15 sensors in A1 after calculating by Eq. (4). Obviously, sensor 04 has the largest temperature change. And this phenomenon is consistent in all seven speed spectrums. The sensor with the largest temperature change will not be affected by the trend. And the correlation between the temperature data of this sensor and the thermal error data should be strong and stable. In other words, sensor 04 can be regarded as the most spontaneous sensor.

Fig. 10

Temperature data of 15 sensors in A1 after subtracting the mean value

Figure 11 shows the flowchart of the sensor selection process. The temperature and thermal error data of different speed spectrums are used to form different datasets. After determining the most spontaneous sensor (sensor 04), the SW-DCCC between the data of sensor 04 and thermal errors is used to select the appropriate speed spectrums. Meanwhile, the V-DCCC between the data of sensor 04 and other sensors is used to reduce the trend-based sensors. Then, the M-DCCC between the data of different sensors is calculated in sensor classification process. Finally, the TKP are selected based on M-DCCC between thermal error data and the data of sensors in the same group.

Fig. 11

Flowchart of sensor selection process

4.2 Selection of speed spectrums based on SW-DCCC

The SW-DCCC between temperature data of sensor 04 and thermal error data is calculated for seven speed spectrums, as shown in Fig. 12. The length of the sliding windows is set to 100. In each sliding window, the M-DCCC is calculated. Speed spectrums A1, A2, and B1 are selected for the sensor selection process because the most spontaneous sensor (sensor 04) shows a strong and stable correlation with the change of sliding windows.

Fig. 12

The SW-DCCC curve of seven speed spectrums

To prove the correctness of the selection results, the histograms and distribution curves of sensor 04 for seven speed spectrums are calculated, as shown in Fig. 13. Although all the curves are not strictly conformed to Gaussian distribution, it is clear that the data of variable speed spectrums (A1, A2, B1, and B2) are more approximate to Gaussian distribution than that of constant speed spectrums (A3, B3, and B4). Combining the results of Figs. 12 and 13, the data of speed spectrums A1, A2, and B1 are used in the sensor selection process. Although the data of speed spectrums A3, B2, B3, and B4 are also real and effective, they are not suitable for the DCCC-based method.

Fig. 13

Histograms and distribution curves of thermal error data for seven speed spectrums

4.3 Sensor reduction based on V-DCCC

The temperature data of sensor 04 are used as the reference; then each sensor is calculated with sensor 04. Figure 14 shows the DCCC value of 14 sensors in A1. The length of subseries (S) varies from 10 to 270 (n). When S is too small, the curve changes drastically, indicating the subseries are not large enough. In this paper, the DCCC value between 45 (n/6) and 270 (n) is used for the following calculation.

Fig. 14

The DCCC value of 14 sensors in A1 (Temperature data of Sensor 04 is the reference)

It is worth noting that the V-DCCC is used in sensor reduction instead of the DCCC value itself. For example, the DCCC values of sensor 01 and sensor 13 are similar when S is greater than 135, but the V-DCCC of the whole range shows a significant difference, as shown in Fig. 15. Compared with sensor 13, sensor 01 is more suitable to be classified as a spontaneous temperature sensor.

Fig. 15

The change of DCCC value of sensor 01 and sensor 13 in A1 (Temperature data of sensor 04 is the reference)

For each DCCC value curve between 45 ~ 270, the V-DCCC is calculated, as shown in Table 4. The threshold is set to 0.5. The sensors with V-DCCC value greater than 0.5 are reduced. For each sensor, if the reduction results of two speed spectrums are consistent, it can be considered as the final result. Thus, the original 15 sensors are reduced to 9 (sensors 01, 03, 04, 05, 07, 08, 09, 14, and 15).

Table 4 The change of DCCC value of 14 sensors for 4 variable speed spectrums (Temperature data of sensor 04 is the reference)

4.4 Sensor classification based on M-DCCC and GA

There are two common classification strategies: (1) the unsupervised classification method; (2) the GA method. The GA method is based on a correlation matrix calculated by a correlation criterion. In this paper, the M-DCCC between different sensors is used to form the correlation matrix.

After sensor reduction, the correlation matrix is expressed as:

$$\left[ \begin{array}{cccc} \overline{\rho }_{1,1} & \overline{\rho }_{1,3} & \cdots & \overline{\rho }_{1,14} \\ \overline{\rho }_{3,1} & \overline{\rho }_{3,3} & \cdots & \overline{\rho }_{3,14} \\ \vdots & \vdots & \ddots & \vdots \\ \overline{\rho }_{14,1} & \overline{\rho }_{14,3} & \cdots & \overline{\rho }_{14,14} \end{array} \right]$$

(10)

where ${\overline{\rho }}_{i,j}$ is the M-DCCC between sensor i and sensor j.

Table 5 shows the symmetric correlation matrix of A1. By setting different thresholds, sensors greater than the threshold are classified into the same group. For example, when the threshold is set to 0.85, the 15 sensors are classified into 3 groups, as tabulated in Table 6.

Table 5 Correlation matrix calculated by DCCC (A1)

Table 6 Classification results of 15 sensors of A1 (threshold = 0.85)

The stable classification results for different speed spectrums are necessary to keep a constant set of TKP. Besides, the number of groups is the same as the number of TKP. Considering that only 9 sensors are kept after sensor reduction, the number of TKP is set to 3 and 4, respectively.

The same sensor classification process is applied to the other three variable speed spectrums. The classification results are tabulated in Table 7. Obviously, the classification results tend to be stable only when there are three groups: (sensor 09), (sensor 01 and 05), and (sensor 03, 04, 07, 08, 14, and 15).

Table 7 Classification results of 4 variable speed spectrums

4.5 Sensor selection based on M-DCCC

A stable set of TKP depends on constant classification and ranking. The effective ranking is very important to evaluate the correlation between temperature data and thermal error data. After sensor reduction and classification, we use the M-DCCC between temperature data and thermal error data as the ranking criterion. For each sensor group, the sensor with the highest ranking is selected as TKP. Figure 16 shows the DCCC value curve of nine sensors in A1, where the thermal error data is used as the reference.

Fig. 16

The DCCC value of eight sensors in A1 (Thermal error data is the reference)

The M-DCCC of the second and third groups is tabulated in Table 8. For each group, the sensor with the largest M-DCCC is selected as TKP. In group 2, the M-DCCC of sensor 01 is larger than sensor 05 for all speed spectrums. In group 3, the M-DCCC of sensor 14 is also larger than other sensors for all speed spectrums. Thus, a stable set of TKP is achieved by the proposed sensor selection method, and the TKP are sensors 09, 01, and 14.

Table 8 The M-DCCC of the second and third group (Thermal error data is the reference)

5 Results and discussion

5.1 Modeling method and evaluation index

Figure 17 shows the relationship between thermal error data and temperature data of A1. There is a nonlinear relationship between the temperature data of each sensor and thermal error data. Thus, a nonlinear support vector machine (SVM) regression model is used in thermal error modeling.

Fig. 17

The relationship between thermal error data and temperature data of A1

SVM has been proved to be an effective model for thermal error modeling of the spindle system. The regression model of SVM is defined as:

$$\begin{cases} f({\varvec{X}}) = \sum\limits_{i = 1}^{l} {(\alpha_{i} - \alpha_{i}^{*} )} K\left( {{\varvec{X}}_{i} ,{\varvec{X}}} \right) + b \hfill \\ \sum\limits_{i = 1}^{l} {\left( {\alpha_{i} - \alpha_{i}^{*} } \right) = 0} \\ 0 \le \alpha_{i} , \, \alpha_{i}^{*} \le C \end{cases}$$

(11)

where f(X) is the prediction function of SVM; X is the temperature vector of TKP; X_i means support vector; l is the number of support vectors; $\alpha_{i}$ and $\alpha_{i}^{*}$ are Lagrange multipliers; k (X_i, X) represents kernel function; C is penalty parameter.

In this paper, the radial basis kernel function is selected as kernel function, which is defined as:

$$K({\varvec{X}}_{i} , \, {\varvec{X}}) = \exp \left( { - \left\| {{\varvec{X}} - {\varvec{X}}_{i} } \right\|^{2} /\sigma^{2} } \right)$$

(12)

where σ is width parameter of radial basis kernel function, mark 1/σ² as parameter g.

There are two crucial parameters in the SVM model: C and g (1/σ²). In this paper, the grid search method is used to find the correct parameters. The search range is set to 2^–4 ~ 2⁴ after several preliminary tests. After determining the parameters g and C, parameters ($\alpha_{i} - \alpha_{i}^{*}$) can be obtained by:

$$\begin{cases} \max \left\{ { - \frac{1}{2}\sum\limits_{\begin{subarray}{l} i = 1 \\ j = 1 \end{subarray} }^{l} {\left( {\alpha_{i} - \alpha_{i}^{*} } \right)\left( {\alpha_{j} - \alpha_{j}^{*} } \right)\left( {{\varvec{X}}_{i} \cdot {\varvec{X}}_{j} } \right) - } } \right. \\ \left. {\varepsilon \sum\limits_{i = 1}^{l} {\left( {\alpha_{i} + \alpha_{i}^{*} } \right) + \sum\limits_{i = 1}^{l} {y_{i} \left( {\alpha_{i} - \alpha_{i}^{*} } \right)} } } \right\} \\ 0 \le \alpha_{i} , \, \alpha_{i}^{*} \le C \\ \sum\limits_{i = 1}^{l} {\left( {\alpha_{i} - \alpha_{i}^{*} } \right) = 0} \end{cases}$$

(13)

LIBSVM toolbox [24] and MATLAB R2018a software are used to obtain the four parameters of SVM: C, g, (α_i-α* i), and b. The training function “svmtrain” and predictive function “svmpredict” are used to accomplish the training and prediction process.

Two evaluation indexes are used to display the modeling accuracy of the selection method: the root mean square error (RMSE) and the maximum error (MAX).

$$RMSE = \sqrt {\frac{1}{n}\sum\limits_{j = 1}^{n} {\left( {y_{j} - y_{j}^{*} } \right)^{2} } }$$

(14)

$$MAX = \mathop {\max }\limits_{j = 1}^{n} \left| {y_{j} - y_{j}^{*} } \right|$$

(15)

where y_j is the measured value at j minute, y*_j means the corresponding prediction value, n represents the total minutes of the experiment.

5.2 Modeling results for the proposed method

The temperature and thermal error data are obtained from seven speed spectrums of two different seasons. When the TKP are determined, the data of each speed spectrum can be used as both training set and test set. Thus, there are 49 (7 × 7) predictions for each set of TKP. The numbering rules of 49 predictions are tabulated in Table 9.

Table 9 Numbering rules of 49 predictions

The data of TKP are taken into the SVM model. Figure 18 shows the modeling results (RMSE and MAX). The root mean square error and maximum error are less than 2.32 μm and 3.73 μm, respectively. The modeling results of the proposed method show a high accuracy and strong robustness.

Fig. 18

Modeling results of 49 predictions

5.3 Traditional sensor selection method and sensor selection results

The traditional sensor selection method is a combination of classification and sorting. The correlation coefficient between temperature data of 15 sensors and thermal error data is calculated by PCC, and the ranking results are tabulated in Table 10. The direct use of PCC causes the sensor selection results to be variable. For example, sensors 02 and 06 have a high ranking in A1 but low ranking in other speed spectrums; sensors 14 and 15 have a high ranking in B2, B3, and B4 but low ranking in other speed spectrums. The variable ranking will cause variable sensor selection results, no matter whether the classification is stable or not.

Table 10 The ranking order of 7 speed spectrums based on PCC

This paper considers two traditional classification methods: (1) the FCM method and (2) the GA method. For the FCM method, the weighting exponent is set as 2. The temperature data of 15 sensors are normalized between 0 and 1 before being taken into the calculation. For the GA method, the PCC values between different sensors are used to form the correlation matrix. Tables 11 and 12 show the classification results of FCM and GA, respectively.

Table 11 Classification results of seven speed spectrums based on FCM

Table 12 Classification results of seven speed spectrums based on GA

The variable sensor selection results of the two traditional strategies are tabulated in Table 13. The seven sets of TKP selected by FCM and PCC are marked as FP1 ~ FP7, and the other seven sets of TKP selected by GA and PCC are marked as GP1 ~ GP7.

Table 13 Sensor selection results of the two traditional strategies (FCM + PCC and GA + PCC)

5.4 Modeling results and discussion

The sensor selection result of the proposed method is marked as Model1 (sensors 01, 09, and 14). For each set of TKP, the 49 predictions are carried out. The RMSE and MAX are recorded as the evaluation index of modeling accuracy.

For example, when the prediction number is 2 (see Table 9), the training set is A1, and the test set is A2. The prediction value and residual of Model1, FP1, and GP1 are shown in Fig. 19.

Fig. 19

Prediction value and residual of Model1, FP1, and GP1

The modeling accuracy of Model1 is compared with FP and GP, as shown in Figs. 20 and 21, respectively. Compared with FP or GP, Model1 shows high accuracy and strong robustness. The RMSE and MAX of 49 predictions of Model1 are less than 2.32 μm and 3.73 μm, respectively. Besides, the sensor selection process achieves a relatively stable TKP. With the same sensor selection results from three speed spectrums, the selected TKP are suitable for all seven speed spectrums.

Fig. 20

Modeling accuracy comparison between Model1 and FP

Fig. 21

Modeling accuracy comparison between Model1 and GP

Besides, after the sensor reduction and classification based on the proposed method, there are three groups: (sensor 09), (sensor 01 and 05), and (sensor 03, 04, 07, 08, 14, and 15). The PCC can also be used to sort sensors. The selection results based on PCC are tabulated in Table 14. Thus, sensors 01, 09, and 03 are selected as TKP. This selection result is marked as Model 2, and the modeling results are compared with the proposed model (Model 1), as shown in Fig. 22. With the same reduction and classification, the DCCC-based method still has higher accuracy and stronger robustness than the PCC-based method.

Table 14 The sensor selection results based on PCC

Fig. 22

The modeling results of Model 1 and Model 2

6 Conclusion

This paper proposes a three-step sensor selection strategy for thermal error modeling: reduction, classification, and selection. The thermal error experiments with seven speed spectrums were carried out on a grinding machine in two seasons. The theoretical reasons for inappropriate sensor selection are discussed. The proposed method based on DCCC achieves a stable set of TKP and shows high accuracy and strong robustness. Some conclusions can be obtained as follows:

• 1. The preselection of speed spectrums and reduction of sensors before classification are necessary. A stable set of TKP relies on stable classification and ranking. The variable speed spectrums are more suitable for the DCCC method than the constant speed spectrums due to the characteristic of data distribution.

• 2. The temperature time series affected by trend can be calculated with a large correlation coefficient. The DCCC method can capture this pseudo-correlation phenomenon by removing the trends and dividing the time series into different subseries. The V-DCCC, M-DCCC, and SW-DCCC are effective evaluation indexes in sensor selection process.

• 3. Sensor selection for the data-driven thermal error modeling is a complex and interactive process. Different combinations of TKP have significant differences in modeling accuracy. It is achievable to ensure high accuracy and strong robustness of the thermal error model with a stable and appropriate set of TKP.