Over the past few decades, there has been a considerable research interest in the area of numerical cognition, with a proliferation of studies aimed at clarifying the neurocognitive mechanisms subserving number processing (Nieder, 2016). Although this field has progressed rapidly over the years, many central questions remain unanswered, with a fervent debate surrounding the possible link between nonsymbolic and symbolic number processing (Leibovich & Ansari, 2015). Previous research has indeed provided conflicting evidence about such a relationship and has consequently generated competing theoretical perspectives. That is, whereas some theories have maintained that both the representation of symbolic and nonsymbolic numbers can be traced back to the same preverbal approximate number system (ANS; Cantlon et al., 2009; Dehaene, 1997; Feigenson et al., 2004; Gallistel & Gelman, 1992; Rinaldi & Marelli, 2020a), other competing theoretical perspectives have rather proposed the existence of two independent systems (e.g., Krajcsi, 2017; Krajcsi et al., 2018; Sasanguie et al., 2017).

One of the main hallmarks of the ANS is that the ability to discriminate between two nonsymbolic numerosities depends on their ratio, a phenomenon that has been interpreted as Weber’s law compliance (Cantlon et al., 2009; Leibovich et al., 2013). Weber’s law states that the difference in intensity necessary to discriminate between two stimuli (also known as “just noticeable difference”) is proportional to their objective intensities. Accordingly, the ability to discriminate between two visual arrays of dots in number comparison tasks has been repeatedly shown to depend on their ratio (i.e., smaller set divided by larger set). In these tasks, participants are typically presented with two arrays of dots and are asked to indicate the numerically smaller/larger set: Participant’s performance tends to be more difficult (e.g., higher error rates and reaction times) when comparing larger as compared with smaller numerical ratios. Interestingly, such a ratio-dependent behaviour has been observed as well in human infants and other species, thus indicating that the ANS should have a long phylogenetic history (Cantlon et al., 2009).

Whether numerical symbols would rely on this early preverbal system has been the subject of an intense debate. The perhaps most widely accepted theoretical account maintains that numerical symbols are mapped onto the ANS. Rather surprisingly, indeed, a ratio dependency has been as well observed in symbolic number comparison tasks (i.e., either with number words or Arabic digits; Gallistel & Gelman, 1992; Moyer & Landauer, 1967). Yet this theoretical account has been challenged in the more recent years by an increasing body of evidence supporting two separate systems for the representation of symbolic and nonsymbolic numbers (Krajcsi, 2017; Krajcsi et al., 2016; Lyons et al., 2015; Marinova et al., 2020; Sasanguie et al., 2017). Some studies have shown, indeed, that the performance in number comparison tasks is fully ratio dependent only with nonsymbolic numbers (e.g., Marinova et al., 2020).

Here, differently from these previous theoretical proposals, we trace back the similarities between nonsymbolic and symbolic number processing to the mathematical framework known as information theory (Shannon, 1948) and to the principle of efficient coding, which has a long history in the study of perceptual systems and according to which neural responses should be optimized with respect to the frequency of stimuli in the natural environment—that is, perception would be more precise for those stimuli occurring relatively more frequently (Atick & Redlich, 1992; Attneave, 1954). Under this theoretical scenario, learning is conceived as a process that has evolved to facilitate the individual in understanding the predictive value of a given event (i.e., an outcome to be predicted) as a function of the available discrepancies between what is expected and what is actually observed in experience (Ramscar et al., 2010). Hence, this error-driving learning would be based on the probabilistic relationships between important regularities in the environment (i.e., events) and the cues that allow those events to be predicted. Put differently, learning would be influenced both by positive evidence (i.e., co-occurrences between cues and predicted events) and negative evidence (i.e., nonoccurrences of predicted events). Notably, it has been recently proposed that the ratio-sensitivity of behavior—which Weber’s law embodies—is an adaptive strategy to extract information from the environment and could therefore be a product of computational principles such as efficient coding (Wei & Stocker, 2017; see also Brus et al., 2019).

Insofar, the idea that both encoding and decoding are optimized for the specific statistical structure of the environment has been mostly documented within the sensory domain. Yet, the linguistic system is ideally suited to be a learning environment that is guided by the very same principles. Language use is indeed fundamentally contextual and probabilistic, with linguistic context exerting a pervasive influence on the form and content of human communication (Ramscar, 2019). As such, because (language) learning is a probabilistic process, words having learning histories that vary only slightly from one another will be less discriminated and therefore more similar in terms of their usage. Interestingly, recent progress in distributional semantics provide us with a convenient way to approximate such learning histories, allowing for a quantification of a word distribution in language experience (Günther et al., 2019). In particular, word-embeddings are based on a neural network architecture predicting word co-occurrences (Mikolov et al., 2013). These models are trained on large collections of texts that document natural language use. Nodes in the input and output layers represent words and the system learns to predict a target word on the basis of the lexical contexts in which it appears (i.e., the words it co-occurs with in the text), incrementally updating a set of weights by minimizing the difference between model predictions and observed data at each learning event (i.e., every word occurrence). The estimated set of weights will eventually capture linguistic behaviour associated with a specific word in distributed terms. These distributed representations, or vectors, can be quantitatively compared by measuring their proximity in a multidimensional space: similar words will occur in similar contexts, ending up being associated with vectors that are geometrically close. By analyzing this system output, Rinaldi and Marelli (2020a) demonstrated that vectors representing the usage of number words in different languages show a typical ratio-signature, with number word pairs associated with higher numerical ratios being less discriminable in natural language (e.g., seven/eight would be less discriminable than three/eight, as captured from the corresponding word-embeddings).

Based on this, and to directly probe whether efficient coding can explain the (dis)similarities between nonsymbolic and symbolic number processing, in the present study we employed data extracted from word-embeddings to account for human performance in number comparison tasks. In particular, we tried to predict the performance in nonsymbolic and symbolic comparison tasks not only from numerical ratio (i.e., the typical predictor used in previous research), but also through estimates from purely linguistic data (i.e., measures obtained through the analysis of natural language usage, as extracted from word-embeddings).

We first expect both linguistic data and numerical ratio to account for human performance in the symbolic as well as in the nonsymbolic task, since these two predictors are positively correlated, thus further corroborating word-embeddings as a valid model in capturing the mental organization of number words (Rinaldi & Marelli, 2020a). Critically, if efficient coding is the explanatory principle for the similar behaviour across the two tasks, we should also expect the specific environment from which numerical information is learned to impact on the performance. This should be reflected in a dissociation of the variance explained in each task by the specific predictor, with the linguistic-model data better explaining participants’ performance in the symbolic task, whereas the numerical ratio should better predict the performance in the nonsymbolic task. This would demonstrate that the ratio-dependency in number comparisons can be explained by efficient coding of context-sensitive environmental regularities.

Methods

Participants

Forty-one university students, Italian native speakers, participated in the study for academic credits (16 males; Mage = 22.3 years, SD = 1.78 years; we had overall recruited 43 participants, but two of them were excluded from the analyses because of their high reaction times in the nonsymbolic task, indicative of a counting strategy). The protocol of the study was approved by the Local Ethical Committee (CRIP, University of Milano-Bicocca, RM-2018-154).

Stimuli

In the symbolic task, the stimuli were the Italian number words from 4 to 16. We opted for the range four–sixteen for two reasons. First, this range is characterized by a relatively low correlation between the numbers of letters of the Italian number words and the corresponding quantities, avoiding confounding effects related to word length. The correlation of the actual range was indeed equal to r = .4653, which was lower than the correlation between the numbers of letters and the numerical quantity for the four–twenty range r = .5375. Second, we decided to use a relatively small range (i.e., four–sixteen) because the higher the numbers, the lower the frequency in language, leading in turn to the extraction of low-quality vectors from word-embeddings (Dehaene & Mehler, 1992).

In the nonsymbolic task, the stimuli were arrays of dots depicting quantities from 4 to 16. The arrangements of dots were created with MATLAB (The MathWorks, USA), using the script available from Gebuis and Reynvoet (2011). The program controls for five variables that typically correlate with numerosity: area extended by the stimulus (or convex hull), total surface (the aggregate value of the different dot surfaces within one display), item size (the average diameter of the different dots within one display), density (area extended divided by total surface) and total circumference. This was made in order to avoid any effect of continuous visual properties on the number comparison process (Gebuis & Reynvoet, 2012a, 2012b; Leibovich & Henik, 2013, 2014; Szűcs et al., 2013). Hence, the program generates nonsymbolic number stimuli with a set of associated visual cues that can only explain a very small portion of variance in numerical distance (Gebuis & Reynvoet, 2011). The script generated by Gebuis and Reynvoet (2011) was adapted to our experiment to select the arrays of dots in which the five visual cues correlated less with numerical distance/ratio (for further information, see the Supplemental Materials).

Procedure

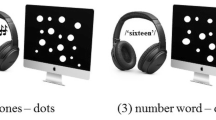
In both the symbolic and the nonsymbolic tasks, stimuli were randomly presented in pairs, one on the left and one on the right at the same distance (350 pixels) from the centre of the screen. All possible pairwise combinations were considered, for a total of 156 pairs. Each pair was presented twice, and with their spatial arrangement counterbalanced (e.g., five vs. seven and seven vs. five). The numerical ratio between the two numbers presented ranged from 0.25 to 0.94.

The two experimental tasks (i.e., the symbolic and nonsymbolic number comparison tasks) were presented to all participants (i.e., hence being a within-subject variable), with their order of presentation counterbalanced between subjects. The response assignment (i.e., whether participants had to indicate the numerically smaller or larger stimulus) was pseudorandomly attributed across participants: half of the participants were asked to decide, as quickly as possible, which number word was larger in numerosity (number comparison task with symbolic stimuli) or which array contained more dots (number comparison task with nonsymbolic stimuli). The second half of participants were asked to indicate which number word was smaller or which array contained fewer dots. All the participants were presented with the very same numerical set (e.g., 4–16, whether in the symbolic or nonsymbolic format). The two tasks were presented in two different experimental sessions with a 10-minute break between them. Both tasks followed the same procedure (see Fig. 1).

Fig. 1
figure 1

The experimental design of the nonsymbolic (a) and symbolic (b) number comparison tasks

Full size image

In each task participants judged 312 pairs of number words/arrays of dots divided in two blocks by a break of 5 minutes. A block of nine practice trials was presented before each task. In both tasks, a fixation cross was presented for 300 ms, followed by a blank screen for 500 ms. Then, the two stimuli (e.g., number words or arrays of dots) appeared on the left and right sides of the screen, until the participant’s response. A blank screen lasting 500 ms preceded the presentation of the next trial. All the subjects performed the tasks individually under similar controlled laboratory conditions

The stimuli were presented with OpenSesame software (Mathôt et al., 2012) on a black background, in gray font. The number words were presented in Bahnschrift font (size 58).

Word-embeddings

We used the same word-embeddings model described in the work of Rinaldi and Marelli (2020a), in which the vector space was trained using the Continuous Bag of Words (CBOW) method, an approach originally proposed by Mikolov et al. (2013). The model, released by Marelli (2017), was trained on itWaC, a free Italian text corpus based on web-collected data and consisting of about 1.9 billion tokens. The model is set on the parameters also applied by Rinaldi and Marelli (2020a) on the Italian semantic space: 9-word co-occurrence window, 400-dimension vectors, negative sampling with k = 10, subsampling with t = 1e-5 (for more detailed results see the Supplemental Materials). From this vector space, we extracted vector representations for number words ranging from four to sixteen and, in turn, measures for Vector-Distance (VD) for each pair of words and Vector Variance (VV) for each word. VD values are expression of the dissimilarity between number-word vectors, and this measure is thus conceived as a proxy for the distance effect. VV values are indicators for the specificity with which the target word can be predicted by the linguistic context in which it typically appears, thus representing a proxy for the size effect. Using these variables, we obtained language-based predictions (hence, linguistic estimates) from a linear-regression model including the effects of VD of the number-word pair and VV of each number word on the numerical ratio for the tested range (Rinaldi & Marelli, 2020a). Therefore, linguistic estimates express the prediction of the numerical ratio from usage metrics of the two corresponding words, as indexed by the employed computational model (for further details see the Supplemental Materials).

Statistical analysis

Behavioural data were analyzed using linear mixed models (Baayen et al., 2008). Reaction times (RTs) were entered as the dependent variable, while numerical ratio and linguistic estimates were entered as predictors in separate analyses. Random intercepts for subjects were also included. The same analyses were run for both symbolic and nonsymbolic tasks independently. Only RTs with accurate responses were considered (11.28% and 6.04% of nonaccurate responses were removed from the analyses of the nonsymbolic and symbolic tasks, respectively). Moreover, RTs higher than 2500 ms were excluded from the analysis by visually inspecting data distribution (additional 1.98% and .47% of trials were removed from the nonsymbolic and symbolic tasks, respectively). RTs included in the analysis were then transformed in logarithmic values. To exclude the impact of overly influential outliers, after having fitted the model, data points were removed on the basis of a threshold of 2.5 SD standardized residual errors (model criticism; Baayen, 2008). Results based on the refitted models are reported. Mixed models were run using the R package lme4 (Bates et al., 2014). The Satterthwaite’s approximation for degrees of freedom was employed to estimate p values (Kuznetsova et al., 2017).

The models were compared using the Akaike information criterion (AIC), which returns an estimation of the quality of the model (e.g., see Akaike, 1973). AIC allows to select the model that gives the most accurate description of the data. Models with smaller AIC values are to be preferred (Wagenmakers & Farrell, 2004). Such an adjudication approach, based on an estimate of model-fit like AIC, was adopted in order to avoid collinearity issues, since numerical ratio and linguistic estimates were positively correlated, r(76) = .702; p < .001 (see the Supplemental Materials; see also Rinaldi & Marelli, 2020a). Considering the AIC index allows us to ideally dissociate the predictive value of these measures, without incurring in multicollinearity-related statistical aberrations. To get further insight on the possible differences between models fit, we employed a bootstrapping process, running 1,000 simulations for each model and extracting the relative AIC values through the bootMer function. We then compared the simulated AIC values with an independent t test.

Finally, we also analyzed accuracy. In particular, we performed a generalized linear mixed models (GLMMs) with accuracy as dependent variable, while numerical ratio and linguistic estimates were entered as predictors in separated analyses. Random intercepts for subjects were also included. Consistently with RTs data, accurate trials slower than 2,500 ms were excluded from the analyses. The same analyses were run for both symbolic and nonsymbolic tasks independently and the obtained models were compared using the AIC criterion.

Results

Reaction times

Participants’ mean reaction time in the nonsymbolic task was 796ms (SD=379 ms), while in the symbolic task was 951 ms (SD=277 ms).

Nonsymbolic task

In the analysis with numerical ratio as predictor we found a significant positive effect of this variable on RTs, β = .0585, 95% CI [.0561, .0608], b = .3103, 95% CI [.2977, .3228], t(10906.17) = 48.41, p<.001 (see Fig. 2, left panel). Crucially, in a second model, we also observed a significant positive effect of linguistic estimates on RTs, β = .0426, 95% CI [.0401, .0451], b = .3321, 95% CI [.3129, .3512], t(10879.07) = 33.97, p < .001 (see Fig. 2, right panel).

Fig. 2
figure 2

RTs (log-transformed) for the nonsymbolic task as a function of numerical ratio (left panel) or linguistic estimates (right panel). The histograms at the top of each graph show the marginal distribution of the respective predictor on the x-axis (Note that to exclude the impact of overly influential outliers, after having fitted the model, data points were removed on the basis of a threshold of 2.5 SD standardized residual errors. Despite this, from a visual inspection, a few outliers seem to still be included in the distribution of linguistic estimates (i.e., one of the predictors employed). However, and critically, removing these datapoints did not affect our results neither in the nonsymbolic nor in the symbolic task), and the histograms on the right show the marginal distribution of RTS (log-transformed)

Full size image

Symbolic task

In the model with numerical ratio, we found a significant positive effect of this variable on RTs, β = .0175, 95% CI [.0158, .0191], b = .091, 95% CI [.0825, .0996], t(11684.09) = 20.9, p < .001 (see Fig. 3, left panel). Crucially, in a second model, we also observed a significant positive effect of linguistic estimates on RTs, β = .0218, 95% CI [.0202, .0234], b = .1695, 95% CI [.1569, .1821], t(11680.28) = 26.37, p < .001 (see Fig. 3, right panel).

Fig. 3
figure 3

RTs (log-transformed) for the symbolic task as a function of numerical ratio (left panel) or linguistic estimates (right panel). The histograms at the top of each graph show the marginal distribution of the respective predictor on the x-axis, and the histograms on the right show the marginal distribution of RTS (log-transformed)

Full size image

Analysis of model fit

For the nonsymbolic task, both models (the one with numerical ratio and the one with linguistic estimates as predictors) showed significant effects. We therefore explored the corresponding AIC values to identify the best fitting model (in this case, we compared the models without applying model criticism). The resulting AICs were AICNumerical = −12774.92 and AICLinguistic = −11692.26. Hence, the model with numerical ratio largely outperforms the one with linguistic estimates in predicting performance in the nonsymbolic task with a ΔAIC = 1082.66. Based on Akaike weights (Wagenmakers & Farrell, 2004), a ΔAIC = 1083 between the two models would indicate that the model with numerical ratio as predictor is overwhelmingly more likely to be a better model (in terms of Kullback–Leibler distance from the “real” distribution) than the one with linguistic estimates. This was also supported by the bootstrapping process (e.g., 1,000 simulated data), with a significantly lower AICNumerical as compared to the AICLinguistic value, t(1998) = 163.44, p < .001, Cohen’s d = 7.31 (for a graphical representation. see Fig. 4, left panel).

Fig. 4
figure 4

Simulated bootstrap AIC values (e.g., bootstrap resampling with 1,000 replicates) for each model tested in the nonsymbolic and symbolic tasks for the RTs data. Error bars represent the 95% confidence interval

Full size image

We ran the same analyses on the results of the symbolic task and found an AICNumerical = −21147.04 and an AICLinguistic = −21368.4. In this case, the model with linguistic estimates outperforms the one with numerical ratio with a ΔAIC = 221.36. Based on Akaike weights, a ΔAIC = 221 between two models would indicate that the model with linguistic estimates as predictor is overwhelmingly more likely to be a better model (in terms of Kullback–Leibler distance from the “real” distribution) than the one with numerical ratio. This was again supported by the bootstrapping process, with a significantly lower AICLinguistic as compared with the AICNumerical value, t(1998) = 31.42, p < .001, Cohen’s d = 1.4 (for a graphical representation, see Fig. 4, right panel).

Accuracy

Participants overall made 11.28% of errors in the nonsymbolic task (11,349 accurate trials out of a total of 12,792 trials), while they overall made 6.04% of errors in the symbolic task (12,020 accurate trials out of a total of 12,792 trials).Footnote 1

Nonsymbolic task

In a first model, we found a significant negative effect of numerical ratio on accuracy, standardized logit = −1.5569, 95% CI [−1.6519, −1.4646], logit = −8.0707, 95% CI [−8.5633, 7.5922], z = −32.67, p < .001. This means that accuracy is predicted by the numerical ratio of the to-be-compared numbers. Crucially, in a second model, we found a significant negative effect of linguistic estimates, standardized logit = −.6112, 95% CI [−.6611, −.5615], logit = −4.5313, 95% CI [−4.9015, −4.1633], z = −24.07, p < .001. This means that accuracy in the nonsymbolic task is also predicted by linguistic estimates.

Symbolic task

In a first model, we found a significant negative effect of numerical ratio on accuracy, standardized logit = −.6257, 95% CI [−.7116, −.5414], logit = −3.2388, 95% CI [−3.6837, −2.8026], z = −14.54, p < .001. This means that accuracy is predicted by the numerical ratio of the to-be-compared numbers. Crucially, in a second model, we found a significant negative effect of linguistic estimates, standardized logit = −.6067, 95% CI [−.6678, −.5462], logit = −4.4757, 95% CI [−4.9262, −4.0252], z = −19.62, p < .001. This means that accuracy in the symbolic task is also predicted by linguistic estimates.

Model comparison

For the nonsymbolic task, both models (the one with numerical ratio and the one with linguistic estimates as predictors) showed significant effects. We therefore explored the corresponding AIC values to identify the best fitting model. The resulting AICs were AICRatio = 6880.18 and AICLinguistic = 8009.63. Hence, the model with numerical ratio outperforms the one with linguistic estimates in predicting accuracy performance in the nonsymbolic task with a ΔAIC = 1129.45. This was also supported by the bootstrapping process, with a significantly lower AICNumerical as compared with the AICLinguistic value, t(1998) = 82.04, p < .001, Cohen’s d = 3.67 (for a graphical representation, see Fig. 5, left panel).

Fig. 5
figure 5

Simulated bootstrap AIC values (e.g., bootstrap resampling with 1000 replicates) for each model tested in the nonsymbolic and symbolic tasks for the accuracy data. Error bars represent the 95% confidence interval

Full size image

For the symbolic task, we found an AICRatio = 5267.01 and an AICLinguistic = 5150.01. In this case, the model with linguistic estimates outperforms the one with numerical ratio with a ΔAIC = 117. Hence, the results on accuracy fully replicate the patterns observed for RTs. This was again supported by the bootstrapping process, with a significantly lower AICLinguistic as compared with the AICNumerical value, t(1998) = 4.95, p < .001, Cohen’s d = . 221 (for a graphical representation, see Fig. 5, right panel).

Discussion

The present study was aimed at shedding light on the controversial debate around the commonalities between the representation of nonsymbolic and symbolic numerical information. We reasoned that these similarities, including the well-described ratio-dependency of human responses, could be the result of an adaptive strategy in extracting information from the statistical regularities of the specific learning environment (i.e., perceptual or linguistic), adhering consequently to computational principles such as efficient coding. To this aim, we employed a new methodological approach, based on the integration of data from behavioural tasks (i.e., number comparison tasks) and computational linguistics (i.e., predictions from word-embeddings models, informative about the way humans use number words in natural language). We thus tried to predict the performance of adult humans in number comparison tasks with both symbolic and nonsymbolic numbers using not only numerical ratio, but also language-based estimates. As expected, numerical ratio significantly accounted for human performance in number comparison tasks with symbolic (i.e., number words) and nonsymbolic (i.e., arrays of dots) numbers. More critically, our findings showed that also linguistic estimates predicted behavioural data in both tasks. The fact that data-driven metrics obtained from purely linguistic data can account for participants’ performance in the processing of nonsymbolic numbers provides direct support to the alleged commonalities between the ANS and the symbolic faculty for number. A possible explanation for such a pattern is that not only the perceptual system but also the linguistic domain would be constrained by general-purpose efficient coding principles and this would determine the commonalities between nonsymbolic and symbolic representations of number. This means that similar encoding and decoding strategies operate in domains other than low-level perceptual systems.

However, if efficient coding is the explanatory principle of the observed commonalities, we should also expect a dissociation as a function of the specific regularities in a learning environment—that is, the distributional pattern of number words in language should better predict performance in the symbolic task, while numerical ratio should better account for performance in the nonsymbolic task. In line with this hypothesis, we observed a dissociation in terms of AIC, which is an estimator of the relative quality of the explanatory models (Wagenmakers & Farrell, 2004). In fact, we found that linguistic data better predicted the performance in the symbolic task, whereas numerical ratio better predicted the performance in the nonsymbolic task, with these results being informative about a simple rather than a double dissociation between the two types of numerical processes. To account for such a dissociation, we propose that the environmental regularities in the specific learning environment (i.e., perceptual or linguistic) differently affect how the brain interprets and ultimately represents sensory or linguistic information.

The view that the (scalar) variability of number words in natural language does not necessarily presuppose anything like Weber’s law, but may rather rely on more general and independent principles (Piantadosi, 2014, 2016), is in line with the mathematical framework known as information theory, which provides a formal account for describing the efficiency of communicative systems (Shannon, 1948). According to this framework, the structure of the functional distributions of languages (as also captured by vector-space models) would be consistent with predictions from information theory (Ramscar, 2020). Accordingly, this approach may well account for the acquisition of number words (Ramscar et al., 2011) and for the distributional pattern of number words in natural language, in which events (i.e., number words) can be predicted by environmental regularities (i.e., the linguistic context in which they typically appear; Rinaldi & Marelli, 2020b).

In the vector-space model that we used only number words were treated as tokens. Future studies may therefore investigate whether the current findings can be replicated for Arabic digits to help clarify whether numerical encoding is dependent on a single notation-independent abstract representation (Dehaene, 1992) or it is rather mediated by modality-specific processes. Indeed, there is evidence that Arabic digits and number words are processed in a notation-dependent manner, with the distance effect being smaller for the verbal notation than for the Arabic notation (Cohen Kadosh et al., 2008; see also Cohen Kadosh et al., 2007). Accordingly, future studies should ideally aim at employing linguistic estimates of Arabic digits extracted from vector-space models and probe whether a similar notation-dependent pattern may also emerge from natural language. Moreover, the use of data from vector-space models may be informative about whether linguistic experience contributes in shaping the developmental trend of numerical representations. In fact, despite numerical processing in infancy and early childhood is qualitatively similar to that of adults, the distance effect has been shown to increase significantly over developmental time (Holloway & Ansari, 2008; Sekuler & Mierkiewicz, 1977). Whether such a developmental trend is influenced by language experience is a possibility that deserves targeted investigation, ideally combining behavioral data from comparison tasks with those from vector-space models.

Taken together, these findings indicate that both nonsymbolic and symbolic number processing may rely on domain-general cognitive processes based on the statistical learning of regularities in the environment and on associative-learning mechanisms. More generally, our study adds to the potentiality of vector-space models in predicting human behaviour (Günther et al., 2019; Rinaldi & Marelli, 2020b). In fact, one of the criticisms against vector-space models is that they would be limited to linguistic knowledge, as they are based on linguistic input only. As a consequence, these models have been usually tested to predict the performance in purely linguistic tasks. Our findings rather point to a wider potentiality of vector-space models: since they are a reliable tool to predict performance in perceptual tasks such as when comparing visual sets of dots, this supports the view that perceptual information is partially encoded into linguistic data (Louwerse, 2011).