Abstract
In numerical cognition research, it has traditionally been argued that the processing of symbolic numerals (e.g., digits) is identical to the processing of the non-symbolic numerosities (e.g., dot arrays), because both number formats are represented in one common magnitude system—the Approximate Number System (ANS). In this study, we abandon this deeply rooted assumption and investigate whether the processing of numerals and numerosities can be dissociated, using an audio-visual paradigm in combination with various experimental manipulations. In Experiment 1, participants performed four comparison tasks with large symbolic and non-symbolic numbers: (1) number word–digit (2) tones–dots, (3) number word–dots, (4) tones–digit. In Experiment 2, we manipulated the number range (small vs. large) and the presentation modality (visual–auditory vs. auditory–visual). Results demonstrated ratio effects (i.e., the signature of ANS being addressed) in all tasks containing numerosities, but not in the task containing numerals only. Additionally, a cognitive cost was observed when participants had to integrate symbolic and non-symbolic numbers. Therefore, these results provide robust (i.e., independent of presentation modality or number range) evidence for distinct processing of numerals and numerosities, and argue for the existence of two independent number processing systems.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
During the past decade of research in the domain of numerical cognition, the relation between symbolic numbers (e.g., Arabic numerals, number words) and non-symbolic numerosities (e.g., dot arrays) has been the subject of debate. According to the most popular view, “[…] numerical symbols and nonnumerical numerosities converge onto shared neural representations” (Piazza, Pinel, Le Bihan, & Dehaene, 2007, p. 302), and are thus represented by one and the same evolutionary-determined brain system (Nieder, 2016), referred to as the ‘Approximate Number System’, or shortly ANS (e.g., Dehaene, 2007; Nieder & Dehaene, 2009). Consequently, it has been extensively argued that the processing (and the acquisition) of numerical symbols requires these symbols to be mapped on their corresponding pre-existing non-symbolic numerosities (for explicit statements, see Cantlon, et al., 2009, p. 2218; Dehaene & Cohen, 1995, p. 85–86; Feigenson, Dehaene, & Spelke, 2004, p. 309; see also Kutter, Bostroem, Elger, Mormann, & Nieder, 2018, p. 7; Nieder, 2016, p. 379; Piazza, 2010, p. 4; Piazza et al., 2007, p. 302). One of the main arguments in favor of the mapping of numerical symbols onto the ANS is the presence of a ratio and or/distance effects in both symbolic and non-symbolic numerical tasks. The distance effect and the ratio effect are two strongly related observations, showing that, respectively, the absolute distance (|n1–n2|) or the relative distance (n1/n2) between two numbers have an impact on the behavioral performance. Typically, the distance effect is reported in studies using symbolic numbers (Defever, Sasanguie, Gebuis, & Reynvoet, 2011; Sasanguie, De Smedt, Defever, & Reynvoet, 2012), while the ratio effect is the most common metric in studies involving numerosities only (Barth, Kanwisher, & Spelke, 2003; Halberda & Feigenson, 2008), and in studies where the symbolic and non-symbolic numbers are combined, (e.g., Marinova, Sasanguie, & Reynvoet, 2018; Sasanguie, De Smedt, & Reynvoet, 2017; Van Hoogmoed & Kroesbergen, 2018). More specifically, when participants have to compare two numbers with a small absolute difference between them, their performance is worse than when comparing numbers with a large absolute difference (e.g., comparing 4 and 6 is harder than comparing 4 and 8, hence a distance effect) irrespective of whether both numbers were presented in the same notation (i.e., two digits) or not (i.e., word number and a digit, Dehaene & Akhavein, 1995). Similarly, participants’ performance is also worse when the relative distance (i.e., the ratio) of the numbers to be compared is closer to 1 (e.g., comparing 6 and 8 (ratio = 1.33) is harder than comparing 2 and 4 (ratio = 2)). Both the distance and the ratio effects are typically explained by the ‘mental number line’ (Dehaene, 2001). Thus, it is argued that the smaller the absolute distance and/or the relative distance between two numbers on this number line is, the greater the representational overlap of their magnitude distributions, making it harder to discriminate between them (Gallistel & Gelman, 1992; Moyer & Landauer, 1967). It is proposed that the relative metric (i.e., ratio) accounts for the compressive nature of the mental number line.
Alternatively, other researchers proposed the existence of two independent numerical systems: one for exact symbolic numbers and another for approximate quantities (e.g., Krajcsi, Lengyel, & Kojouharova, 2016; Núñez, 2017; Reynvoet & Sasanguie, 2016). They did so in part on the basis of two behavioral observations. First, several studies observed a different impact of the ratio on the performance in different conditions, in which the numerical notation was manipulated (i.e., symbolic, non-symbolic, or mixed). More specifically, Sasanguie, De Smedt, and Reynvoet (2017), and Marinova, Sasanguie, and Reynvoet (2018) used an audio-visual paradigm in which participants were instructed to numerically match (i.e., to decide whether two numbers are numerically the same or not, Sasanguie et al., 2017) or to compare (Ex.3 in Marinova et al., 2018) pairs of symbolic numbers (i.e., visually presented digits or auditory presented number words) and/or non-symbolic quantities (i.e., visually presented dot arrays or auditory presented sequences of beeps). In both studies, no ratio effect was present when participants had to match/compare purely symbolic pairs (i.e., a digit and a number word). By contrast, the ratio effect was observed when at least one of the numbers to be matched/compared was a non-symbolic numerosity. The authors interpreted these findings as evidence for two distinct systems underlying the performances in these tasks: a symbolic system, in which symbolic numbers are processed exactly, and an approximate system processing the non-symbolic numerosities. A second behavioral observation supporting the distinct numerical systems view is the presence of cognitive switch cost when participants have to integrate symbolic and non-symbolic numbers in a specific task. For instance, Lyons, Ansari, and Beilock (2012) instructed participants to compare pairs of visually presented pure symbolic numbers (i.e., number words and digits), pure non-symbolic quantities (i.e., pairs of dot arrays) and mixed pairs (i.e., dots and digits). The authors reasoned that if only one common system is activated for all notations, similar performances could be expected in pure and mixed pairs. Alternatively, if different numerical representations would be used to perform the task depending on the presentation format, it is more plausible to assume slower reaction times in mixed pairs than in pure pairs, due to a cognitive cost needed to switch between the two different numerical representation systems. Confirming the latter hypothesis, slower RTs for mixed pairs compared to pure pairs were indeed observed. Later on, Marinova et al. (2018) demonstrated similar findings using an audio-visual paradigm. In this study, again slower responses were observed for mixed compared to pure number pairs. Altogether, these studies support the idea of two independent number processing systems.
The absence of the ratio effect in the symbolic tasks could, however, also be explained by specific stimulus set characteristics which were shared in all previously mentioned studies. For example, the above studies only have used small numbers and small sets of numerosities (Experiments 1 and 3 in Marinova et al., 2018; Sasanguie et al., 2017). Small numbers are frequently encountered in daily life (Dehaene & Mehler, 1992; Gielen, Brysbaert, & Dhondt, 1991) and, therefore, distinct symbolic representations may have been formed for these small numbers only (see Verguts, Fias, & Stevens, 2005). In Lyons et al. (2012) and in Ex. 2 of Marinova et al. (2018), in fact, also large numbers were used—more specifically, the tens (i.e., 10, 20, 30, 40). However, many studies have shown that two-digit numbers can be decomposed under specific task settings (e.g., Moeller, Huber, Nuerk, & Willmes, 2011; Nuerk & Willmes, 2005; Reynvoet, Notebaert, & Van den Bussche, 2011), something we believe is very likely to occur in a stimulus set containing only tens. In these studies, participants most probably based their decisions on the decades of the numbers only, which is equivalent to comparing 1, 2, 3, and 4 (i.e., small numbers). Therefore, the question remains whether a dissociation between symbolic and non-symbolic numbers, reflected by the different impact of the ratio effect on the behavior across pure symbolic, pure non-symbolic, and mixed tasks, can be replicated when using larger numbers.
We investigated exactly this by conducting two audio-visual experiments in adults. In Experiment 1, participants were presented with four audio-visual comparison tasks with large numbers (> 5), falling outside of the subitizing range (Kaufman, Lord, Reese, & Volkmann, 1949): (1) a number word–digit task, (2) a tones–dots task, (3) a number word–dots task and (4) a tones–digit task. Each task contained number/quantity pairs ranging between 10 and 40, with ratios of various difficulties (from 1.11 to 2.00). Using this paradigm, we first avoid the possibility that participants base their judgements on the physical properties of the stimuli (see also Barth et al., 2003; Marinova et al., 2018; Sasanguie et al., 2017). Second, we also avoid the possibility that numbers are decomposed (e.g., Nuerk & Willmes, 2005). A decomposition strategy is very efficient in unimodal presentations, because participants can base their comparison decisions on the decade only. However, with audio-visual presentation, a decomposition strategy would be inefficient because, in languages like Dutch where a unit–decade inversion exists, the place of units and decades differs between the two consecutive stimuli (e.g., auditory: “one-and-twenty”; visual: “21”). In Experiment 2, we wanted to replicate and extend the findings of Experiment 1 by additionally manipulating the number range and the order of the stimulus presentation (i.e., visual stimulus first or auditory stimulus first). This way, we could directly address potential differences between small and large numbers, and we could examine whether the order of the stimulus modality presentation matters. In line with the distinct system account, we expected that the ratio effect would differ across the four audio-visual tasks, depending on whether the tasks contained only symbolic, only non-symbolic, or mixed number pairs. Consequently, this should result in an interaction between the task and the ratio. More precisely, in all tasks containing non-symbolic numbers (i.e., tones–dots, number word–dots, and tones–digits), where we expected the ANS to be activated, a ratio effect should be observed. In contrast, in the purely symbolic condition (i.e., number word–digit), where numbers will be processed exactly without activating the ANS, a smaller ratio effect is to be expected, if present at all (Marinova et al., 2018; Sasanguie et al., 2017). Furthermore, we expect the participants to show slower responses for mixed number pairs—where they presumably have to switch between different systems, in contrast to pure number pairs—where such a switch is not required. Alternately, if all tasks are performed via ANS mapping mechanisms, we expect to observe only main effect of ratio, and no difference between the pure and mixed trails.
Experiment 1
Method
Participants
Participants were recruited via a university online subscription system.Footnote 1 Twenty-four university students and university employees participated in exchange of a non-monetary reward. The experimental protocol was approved by the university’s ethical committee (file number G-20160679). All participants gave written informed consent. All of them had normal or corrected to normal vision and hearing. Three participants were removed because they were too slow (> 3SD from the group mean, per audio-visual task) or because they did not perform above chance level in one of the tasks. Consequently, the final sample consisted of 21 adults aged between 18 and 28 (Mage = 21.05 years, SD = 3.37, 9 males). We performed power analysis to determine the sample size, using the G*Power software version 3.1 (Faul, Erdfelder, Lang, & Buchner, 2007). To obtain the effect size, \(\eta_{\text{p}}^{2}\) = 0.19 (the lowest size of ratio effect reported in Appendix in Marinova et al., 2018), with α = 0.05 and power set at 80%, the required sample was 16 participants. As a consequence, power is guaranteed with our current sample size of 21 participants (data available upon request to the corresponding author).
Procedure, tasks, and stimuli
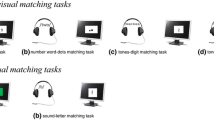
All participants performed four audio-visual comparison tasks (1) a number word–digit task, (2) a number word–dots task, (3) a tones–digit task and (4) tones–dots task (see Fig. 1). The stimuli consisted of numbers between 10 and 40, presented in the auditory modality as spoken number words or tones (i.e., beep sequences) and in the visual modality as digits or dot arrays. There were six ratios: 1.11, 1.14, 1.20, 1.25, 1.50, and 2.00.Footnote 2 The complete stimulus list is shown in Table 1.
The number words were digitally recorded (sampling rate 44.1 kHz, 16-bit quantization) by a female native Dutch speaker. The recordings were band-pass filtered (180–10,000 Hz), resampled at 22.05 kHz and matched for loudness. The beep sequences were generated with a custom Python 2.7 script in a way that each individual beep lasted a fixed 40 ms. Its pitch randomly varied (300–1200 Hz) and also the duration of silence between the beeps (i.e., the inter-tone interval) was randomly varied (the minimal silence duration allowed by the parameters of the program was 10 ms).Footnote 3 This way, we ensured that the presentation rate of the beeps in each sequence was fast enough to encourage participants to use approximations, instead of engaging in counting strategies as demonstrated in previous studies (see Barth et al., 2003; Philippi, van Erp, & Werkhoven, 2008; Tokita, Ashitani, & Ishiguchi, 2013; Tokita & Ischiguchi, 2012, 2016). The dot stimuli were generated with the MATLAB script of Gebuis and Reynvoet (2011), controlling for non-numerical cues (i.e., total surface, convex hull, density, dot size and circumference). The digits were written in font Arial, size 40. The number words and beeps were presented binaurally through headphones at about 65 dB SPL. Participants were tested simultaneously in small groups of six people, in a quiet room equipped with 15-in. LG LCD displays and individual active noise control headphone sets. E-prime 2.0 software (Psychology Software Tools, http://pstnet.com) was used for controlling the stimulus presentation and recording of the data.
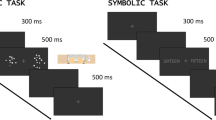
Each trial began with a 600-ms white fixation cross in the center of a black screen. Then the auditory stimulus was presented for 2500 ms in the case of number words, or 3500 ms in the case of beep sequences, immediately followed by the visual stimulus presented for 2500 ms. Afterwards, a blank screen was presented. Participants were instructed to judge which quantity (the auditory or the visual) was larger by pressing the “a” or “p” buttons on an AZERTY keyboard. Participants could respond either during the presentation of the visual stimulus, or during the blank screen, presented immediately after the second stimulus. The next trial began after a 1500-ms intertrial interval. Prior to each audio-visual task, each subject received five practice trials, during which feedback was provided. The practice trials were followed by 72 randomly presented trials of the same type (without feedback). In half of the trials, the small number of the number pair was presented first, followed by the larger number (e.g., 19–21); in the other, half the larger number was presented first, followed by the smaller number (e.g., 21–19). Each audio-visual task was presented in a separate block. Consequently, the order of the tasks was fully counterbalanced across participants in a Latin square design.
Results
Ratio effect
First, the median reaction times on correct responses (18% errors, leaving 4943 trials) and the mean accuracies (6048 trials) were submitted to a repeated measures ANOVA with task (four levels) and ratio (six levels) as within-subject factors. Whenever the assumption of sphericity was violated, the Greenhouse–Geisser correction was applied. Mean accuracies and median reaction times are depicted in Table 2. To make our data as informative as possible, next to the classical statistics, we also report the Bayes factors (BF)—or log(BF) in case the BF values are too large to interpret (Jarosz & Wiley, 2014; Wagenmakers, Marsman, et al., 2018; Wagenmakers, Love, et al., 2018). To obtain both classical and Bayesian results, the JASP statistical package version 0.9.0.1 (https://jasp-stats.org/) was used. The default Cauchy prior was used for calculating the BFs.Footnote 4
The ANOVA on the reaction times showed a main effect of task, F(3, 60) = 28.19, p < 0.001, \(\eta_{\text{p}}^{2}\) = 0.59, 90% CI [0.43, 0.66],Footnote 5 log(BFInclusion) = 36.33, a main effect of ratio, F(2.58, 51.54) = 17.80, pGG < 0.001, \(\eta_{\text{p}}^{2}\) = 0.47, 90% CI [0.28, 0.57], log(BFInclusion) = 16.04, and moderate evidence for a task × ratio interaction, F(6.74, 134.87) = 3.74, pGG = 0.001, \(\eta_{\text{p}}^{2}\) = 0.16, 90% CI [0.04, 0.21], BFInclusion = 3.97 (see Fig. 2). The presence of a ratio effect in each task was further investigated via separate post hoc one-way ANOVAs.
In the number word–digit task, there was no main effect of ratio, F(2.82, 56.30) = 1.78, pGG = 0.12, \(\eta_{\text{p}}^{2}\) = 0.08, 90% CI [0.00, 0.18], BFInclusion = 0.36. In the tones–dots task, there was strong evidence for the presence of a ratio effect, F(3.42,68.48) = 8.74, pGG < 0.001, \(\eta_{\text{p}}^{2}\) = 0.304, 90% CI [0.13, 0.41], BFInclusion = 23.68. In the number word–dots task there was extreme evidence for the presence of a ratio effect, F(2.66, 53.26) = 10.01, pGG < 0.001, \(\eta_{\text{p}}^{2}\) = 0.33, 90% CI [0.143, 0.451], BFInclusion = 152.51. Finally, in the tones–digits task, the evidence for the presence of ratio effect was moderate, F(4.06, 81.17) = 3.74, pGG = 0.007, \(\eta_{\text{p}}^{2}\) = 0.33, 90% CI [0.03, 0.24], BFInclusion = 8.75.
The ANOVA on the accuracies showed a main effect of task, F(3, 60) = 65.66, p < 0.001, \(\eta_{\text{p}}^{2}\) = 0.77, 90% CI [0.66, 0.81], BFInclusion = ∞,Footnote 6 a main effect of ratio, F(3.13, 62.54) = 64.98, pGG < 0.001, \(\eta_{\text{p}}^{2}\) = 0.77, 90% CI [0.66, 0.81], BFInclusion = ∞, and a task × ratio interaction, F(15, 300) = 9.63, p < 0.001, \(\eta_{\text{p}}^{2}\) = 0.33, 90% CI [0.22, 0.36], BFInclusion = 34.49 (see Fig. 2). In the number word–digit task, there was no ratio effect, F(5, 100) = 0.36, p = 0.88, \(\eta_{\text{p}}^{2}\) = 0.02, 90% CI [0.00, 0.02], BFInclusion = 0.04. In the tones–dots task, there was extreme evidence for the presence of ratio effect, F(5, 100) = 31.56, p < 0.001, \(\eta_{\text{p}}^{2}\) = 0.61, 90% CI [0.49, 0.67], BFInclusion = ∞. In the number word–dots task, there was again extreme evidence for a ratio effect, F(5, 100) = 29.41, p < 0.001, \(\eta_{\text{p}}^{2}\) = 0.60, 90% CI [0.47, 0.65], log(BFInclusion) = 36.04. In the tones–digit task, there was extreme evidence for a ratio effect, F(5, 100) = 19.95, p < 0.001, \(\eta_{\text{p}}^{2}\) = 0.50, 90% CI [0.36, 0.57], log(BFInclusion) = 26.65 (Fig. 3).
Switch cost
To examine whether a cost for switching between two magnitude systems is present in tasks where integrating two independent number representations was required (i.e., number word–dots and tones–digits), we analyzed these tasks together as mixed pair tasks, and compared them to the pure number pairs, where no integration was required (number word–digit and tones–dots). Presence of a switch cost should be indicated by significantly slower RTs for the mixed number pairs.
For the analysis, we only included the ratios where the accuracies in all audio-visual tasks were above 70%, i.e., the ratios 1.25, 1.5 and 2.00 (see Table 2). This was done because we wanted to compare the current switch cost results for large numbers with the results for small numbers from our previous study (Experiment 3 in Marinova et al., 2018), while keeping the ratios as similar as possible (i.e., in Ex. 3 Marinova et al., 2018 the easy ratios were 1.8 and 2.00, and hard ratios were 1.28 and 1.33). Moreover, in the other three more difficult ratio conditions, participants made a lot of mistakes which made a reaction time analysis of the switch cost unreliable.
The one-tailed paired t tests showed that in all ratios, responses were significantly slower for mixed number pairs than for pure number pairs, ratio 1.25, t(20) = 5.72, p < 0.001, d = 1.25, 95% CI [0.66, 1.18], BF+0 = 3348.41; ratio 1.5, t(20) = 3.62, p < 0.001, d = 0.79, 95% CI [0.29, 1.28], BF+0 = 45.54; and ratio 2.00, t(20) = 2.60, p = 0.009, d = 0.57, 95% CI [0.10, 1.02], BF+0 = 6.42 (see Fig. 4). The size of the switch cost between the ratios was not significantly different: 1.50 vs 1.25, t(20) = 1.57, p = 0.13, d = 0.34, 95% CI [− 0.10, 0.78], BF10 = 0.65, 2.00 vs 1.25, t(20) = 1.76, p = 0.09, d = 0.39, 95% CI [− 0.06, 0.82], BF10 = 0.85, and 2.00 vs. 1.50, t(20) = 0.459, p = 0.65, d = 0.10, 95% CI [− 0.33,0.53], BF10 = 0.25.
Discussion
In line with previous studies (Marinova et al., 2018; Sasanguie et al., 2017), the current data showed ratio effect in all tasks containing a non-symbolic numerosity (i.e., tones–dots, number words–dots, tones–digits), but not in the tasks with symbolic numbers only (i.e., number word–digits), suggesting distinct representations for non-symbolic and symbolic numbers. Also with regard to the switch cost, the results confirmed our (and those of others) previous findings: responses to the mixed number pairs were significantly slower than those to the pure number pairs (Lyons et al., 2012; Marinova et al., 2018), indicating that, when symbolic and non-symbolic numbers have to be integrated for the task requirements, participants have to link two distinct representations.
Before drawing any strong conclusions, however, we additionally wanted to verify whether the absence of a ratio effect in the number word–digit task was not due to other factors. First, we wanted to verify that the presence of ratio effect was not masked by a floor effect in the RTs in most of the ratio conditions. Therefore, to increase the strength of the potentially masked ratio effect, we averaged the RT performance in the two easiest ratio conditions (1.50 and 2.00) and compared it with the averaged RT in the two hardest ratio conditions (1.11 and 1.14). If a ratio effect is present in the number word–digit task, the easy ratios should be significantly faster than the hard ratios. One-tailed paired t test showed no support for this claim, t(20) = − 1.63, p = 0.06, d = − 0.356, 95% CI [− 0.00, 0.02], BF10 = 1.32.
Second, although we try to avoid the decomposition of double-digit numbers with the current cross-modal presentation technique, it remains possible that participants adopt such a strategy, especially given the long presentation of the number words. Second, although the ratio between numbers did not affect the performance in the pure symbolic condition, the absolute distance between the numbers could still be relevant. To exclude both alternatives, we conducted multiple linear regressions on the accuracy, and on the reaction time data, with: (a) absolute distance (the absolute distance between the auditory and the visual numbers), (b) ratio, (c) unit distance (the distance between the units of the auditory and the visual stimulus), and (d) decade distance (the distance between decades of the auditory and the visual stimulus). If participants would decompose the numbers, the data should be best predicted by the decade distance (and/or the unit distance). In addition, if participants based their decisions on the absolute distance between numbers and not on the ratio between them, absolute distance should also be a significant predictor. In the accuracy data, the effect of decade distance approached significance (p = 0.053), however, this finding was not supported by the Bayesian linear regression (BF10 = 0.34). In the RT data, none of the predictors were significant (all ts < 1.5, all ps > 0.05 all BFs10 < 1). Therefore, we did not find evidence for decomposition, neither with the classical nor with the Bayesian analyses.
The lack of ratio effect in the number word–digit condition could also be caused by the order in which the stimuli were presented (auditory first, then visual) in the current and in all of our previous studies (Sasanguie et al. 2017; Marinova et al., 2018; and the current Exp. 1). In an EEG study measuring the mismatch negativity (MMN) by Finke et al. (2018), no ratio-dependent MMN in the symbolic auditory–visual condition was observed, whereas a significant ratio-dependent MMN amplitude in the visual–auditory condition was present. Although it is not clear what caused this asymmetry in Finke et al. (2018), it is in any case not consistent with the current interpretation of the results of Experiment 1. More specifically, if the findings in Experiment 1 are due to two distinct representations for symbolic and non-symbolic numbers, the order of presentation (auditory–visual vs. visual–auditory) should not matter. Therefore, in Experiment 2, we manipulated the order of modality presentation. In addition, we included both small (i.e., single digit) and large (i.e., two-digit) numbers with exactly the same ratios, making it possible to test directly whether the same effects occur for frequent small numbers and less frequent large numbers. Finally, we averaged data across items (i.e., across number pairs; see also Brysbaert, 2007), to test whether our current and also previous findings can be generalized across item as well. Because this results in a lot of repetitions (see also Brysbaert & Stevens, 2018), participants could not complete the experiment in one single session. Participants completed three 1-h sessions, spread over three consecutive days, during different times of the day. Participants performed the same four audio-visual tasks as in Experiment 1, either in a “visual–auditory” or in “auditory–visual” presentation order. A ratio effect was expected for both small (i.e., frequent) numbers and large (less frequent) numbers in the tones–dots, tones–digit, and numbers word–dots tasks, but not in the number word–digit task. Furthermore, we expected similar findings for the two presentation order conditions.
Experiment 2
Method
Participants
Participants were recruited similarly as in Experiment 1. Eight adults aged between 24 and 30 (Mage = 26.25 years, SD = 1.92, all females) participated in exchange for a monetary reward of 15 euros. All participants gave written informed consent. All of them had normal or corrected to normal vision and hearing. No participants were removed as outliers because no one performed too slow (> 3SD from the group mean per task) or performed at chance level (≈ 50%, per task). Because in this experiment we focused on the item-based analysis with many observations (more than 1600 per condition; see Brysbaert & Stevens, 2018), our sample size was not determined by an a priori power analysis.
Procedure, tasks, and stimuli
Half of the participants conducted the four audio-visual tasks in the visual–auditory order, i.e., (1) digits–number word, (2) dots–tones, (3) dots–number word, (4) digits–tones. The other half performed the tasks in the auditory–visual order, i.e., (1) number word–digit, (2) number word–dot, (3) tones–digit, and (4) tones–dots. Two sets of numbers were used as stimuli for the tasks: set 1 consisted of small numbers (4–9), and set 2 of large numbers (13–28). Both the small and the large number sets contained pairs with nine different ratios, which were grouped into “easy”, “medium”, and “hard” ratios (see Table 3). Only numbers with a compound structure were used in the large numbers condition, i.e., all of the tens, as well as the numbers 11 and 12, were not included in the stimulus set.
Participants were tested in groups of two. The stimuli, instructions and trial procedure were identical to Experiment 1, except for two small modifications. First, because smaller numerosities were now included in the experiment, all auditory stimuli (also beep sequences) were presented for only 2500 ms, followed by the visual stimulus that was presented for 1000 ms. This reduction in presentation time was made to maintain a presentation rate that prevents counting. Second, participants were instructed to respond during the presentation of a centrally positioned questioned mark (‘?’) following immediately after the second stimulus without any delay. We modified the design in this way to avoid preliminary responses on the auditory stimulus. Concretely, in the visual–auditory condition, we wanted to make sure that participants would process the stimulus in its full length, and not press the response button, for instance, before the end of the beep sequence. Prior to each task, participants received five practice trials with feedback. After that, participants were presented with 144 experimental trials per task. All tasks were administered once during a session. The order of the tasks was counterbalanced across participants and across sessions.
Results
We focused on the ‘by item’ analysis. In addition, because participants were required to retain their response until the question mark appeared, their RTs could no longer be considered genuine choice RTs and, therefore, only the accuracies were analyzed. Hereto, and given that the focus of this second experiment was to examine whether a ratio effect was present, we no longer report findings considering the switch cost. The interpretations and conclusions of the results reported below are based predominantly on the obtained BFs. However, for the readers’ convenience, we do report also the classical statistical results.
We conducted a repeated measures ANOVA on the accuracy data, aggregated by item (i.e., by number pair; 13,824 trials in total), with presentation order (two levels), and task (four levels) as within-item factors, and ratio (three levels) and number range (two levels) as between-item factors. There was no main effect of presentation order, F(1, 12) = 0.93, p = 0.354, \(\eta_{\text{p}}^{2}\) = 0.072, 90% CI [0.00, 0.33], BFInclusion = 0.06. There was a main effect of task, F(1.96, 23.52) = 99.95, pGG < 0.001, \(\eta_{\text{p}}^{2}\) = 0.89, 90% CI [0.80, 0.92], BFInclusion = ∞, with highest accuracies for the number word–digit task, and lowest accuracies for the tones–dots task (see Table 4). There was also main effect of ratio, F(2, 12) = 26.68, p < 0.001, \(\eta_{\text{p}}^{2}\) = 0.82, 90% CI [0.54, 0.87], log(BFInclusion) = 32.05, and main effect of number range, F(1, 12) = 11.18, p = 0.006, \(\eta_{\text{p}}^{2}\) = 0.48, 90% CI [0.11, 0.67], BFInclusion = 7999.46. More importantly, there was no presentation order × task × ratio interaction, F(6, 36) = 0.66, p = 0.62, \(\eta_{\text{p}}^{2}\) = 0.10, 90% CI [0.00, 0.13], BFInclusion = 0.006, indicating that the presence/absence of a ratio effect was not influenced by the presentation order. Presentation order was also further not included in any of the other significant interactions, (all Fs < 1.5, all ps > 0.05, all \(\eta_{\text{p}}^{2}\)s < 0.14, all BFs Inclusion < 1), except for the presentation order × task × range, F(3, 36) = 5.37, p = 0.004, \(\eta_{\text{p}}^{2}\) = 0.31, 90% CI [0.07, 0.44]. This interaction, however, was not supported by the Bayesian analyses, BFInclusion = 0.16. Furthermore, there was a significant task × ratio interaction, F(3.92, 23.52) = 11.76, pGG < 0.001, \(\eta_{\text{p}}^{2}\) = 0.66, 90% CI [0.37, 0.73], BFInclusion = 7999.46 (see Fig. 5a), and a significant task × range interaction, F(1.96, 23.52) = 6.49, pGG = 0.006, \(\eta_{\text{p}}^{2}\) = 0.35, 90% CI [0.07, 0.51], BFInclusion = 3807.90 (Fig. 5b). Bayesian analysis showed moderate evidence for the task × ratio × range interaction, F(3.92, 23.52) = 2.00, pGG = 0.13, \(\eta_{\text{p}}^{2}\) = 0.25, 90% CI [0.00, 0.38], BFInclusion = 15.33, and anecdotal evidence for the ratio × range interaction, F(2, 12) = 0.39, p = 0.69, \(\eta_{\text{p}}^{2}\) = 0.06, 90% CI [0.00, 0.23], BFInclusion = 3.29.
To address the ratio and range effects in the audio-visual tasks, separate ANOVAs per task were conducted with either ratio or range as between-item factor. In the number word and digit task, there was no main effect of ratio, F(2, 15) = 0.98, p = 0.69, \(\eta_{\text{p}}^{2}\) = 0.12, 90% CI [0.000, 0.307], BF10 = 0.49. There was also no main effect of range, F(1, 16) = 0.95 p = 0.35, \(\eta_{\text{p}}^{2}\) = 0.06, 90% CI [0.00, 0.29], BF10 = 0.57. In the tones and dots task, there was a main effect of ratio, F(2, 15) = 19.15, p < 0.001, \(\eta_{\text{p}}^{2}\) = 0.72, 90% CI [0.41, 0.80], BF10 = 279.90. There was no main effect of range, F(1, 16) = 1.46, p = 0.25, \(\eta_{\text{p}}^{2}\) = 0.08, 90% CI [0.00, 0.31], BF10 = 0.674. In the number words and dots task, there was a main effect of ratio, F(2, 15) = 5.23, p = 0.02, \(\eta_{\text{p}}^{2}\) = 0.72, 90% CI [0.05, 0.58], BF10 = 3.64, and there was anecdotal evidence for a main effect of range, F(1, 16) = 6.83, p = 0.02, \(\eta_{\text{p}}^{2}\) = 0.30, 90% CI [0.03, 0.52], BF10 = 3.32. Finally, in the tones and digit task, there was a main effect of ratio, F(2, 15) = 24.09, p < 0.001, \(\eta_{\text{p}}^{2}\) = 0.76, 90% CI [0.45, 0.83], BF10 = 831.80, but no main effect of range, F(1, 16) = 0.99, p = 0.34, \(\eta_{\text{p}}^{2}\) = 0.06, 90% [0.00, 0.28], BF10 = 0.58.
Discussion
In contrast to the study by Finke et al. (2018), presentation order (visual first vs. auditory first) did not influence the presence/absence of the ratio effect in any way. There was no main effect of presentation order nor was there evidence for an interaction between the presentation order and any of the remaining factors (i.e., task, ratio and number range). The findings from Experiment 2 are fully in line with our previous studies: again, a similar ratio effect was present whenever the task contained a non-symbolic numerosity (tones and dots, number word and dots, tones and digit). In contrast, the ratio effect was absent in the pure symbolic task (i.e., number word and digit), suggesting distinct systems for symbolic and non-symbolic number.
Similar to Experiment 1, we verified whether the absence of a ratio effect in the number word–digit task was not due to a decompositional strategy in the large (i.e., double-digit) trails. That is why we performed a multiple linear regression analysis on the accuracy data for the large numbers, using as predictors: (a) presentation order (visual vs auditory first), (b) absolute distance, (c) ratio, (d) unit distance, and (e) decade distance. In line with the results of Experiment 1, there was no support for any of these predictors (all ts < 1.8, all ps > 0.05 all BFs10 < 1). Another argument against a possible decomposition strategy for double-digit numbers is that the same results were obtained in double- and single-digit numbers, as we described in the results above.
Alternatively, it could be argued that the absence of a ratio effect in the number word–digit task in the second experiment is due to ceiling effects in accuracies (see Table 4). As participants had to refrain from responding until the question mark appeared on the screen (see Method and Results section for Experiment 2), reaction times were not analyzed in Experiment 2. However, it should be emphasized that the results are fully in line with the findings obtained in our previous studies measuring RT, in which no ratio effect was observed (see Ex. 1 in the current study; Marinova et al., 2018; Sasanguie et al., 2017).
Finally, we do not believe that the lack of a ratio effect is due to low statistical power. As we described in our Method section of Experiment 2, we had more than 1600 observations per condition, and thus sufficient power to detect the effect of interest (Brysbaert & Stevens, 2018). Therefore, the dissociation between symbolic and non-symbolic numbers seems as the most straightforward explanation for the different patterns of the ratio effect obtained in our second experiment.
General discussion
The relation between symbolic numerals and non-symbolic numerosities has been a subject of debate for the past few years. Whereas it has been traditionally assumed that both of these numerical notations are processed by the same system, i.e., the ANS (Dehaene, 2007; Piazza et al., 2007; Nieder, 2016), recent studies argue in favor of separate symbolic and non-symbolic number systems. To gather more robust evidence for the hypothesis about dissociated number systems, we conducted two experiments with adults. Hereby, we used an audio-visual comparison task, in which we manipulated three factors: the number range (small and large), the ratio difficulty (easy, medium and hard), and the order or presentation modality (visual first vs auditory first). Results of Experiment 1 showed evidence for a dissociation between large numerals and numerosities. On the one hand, there was no ratio effect in the symbolic comparison task, and on the other, a cost for switching between symbolic and non-symbolic number pairs was observed. Also the results of Experiment 2 completely supported our hypotheses: no ratio effects were observed in the pure symbolic task, neither with small or large numbers, nor in the visual–auditory or in the auditory–visual presentation order.
Overall, our findings thus add robust evidence to the currently still increasing number of studies showing support for the separate systems approach. For instance, using a priming paradigm, Koechlin, Naccache, Block, and Dehaene (1999) observed a cross-notational semantic priming effect between digits and number words only (Ex. 1A), but not between digits and dots (Ex. 2B). Stated differently, the digits and the number words were automatically associated, whereas the digits and the dot patterns were not. In another study (Sasanguie et al., 2017, Ex. 2), a go/no-go numerical matching paradigm was used, in which participants were instructed to respond when both numbers were larger than 5, and to withhold their response when the numbers were smaller than 5 (and vice versa in another condition). The go/no-go instructions were introduced to force the participants to process the magnitude of the numbers. Here again, a ratio effect in the number word–digit task was absent, in contrast to the presence of a ratio effect in the tones–dots task. Recently, Van Hoogmoed and Kroesbergen (2018) examined the presence of a ratio effect for symbolic numbers by means of event-related potentials (ERPs). In this study, participants were presented with four matching tasks (dots–dots, dots–digits, digits–dots, and digits–digits). As in our current study, the authors hypothesized that, if the ANS mapping hypothesis holds true, two observations can be reasonably expected. First, “[…]one would expect similar distance effects in symbolic and mapping tasks as in the non-symbolic task if symbolic numbers are indeed mapped onto the ANS” (Van Hoogmoed & Kroesbergen, 2018, p. 4). Second, the neurological signatures of symbolic and non-symbolic number processing, in terms of ERPs, should remain similar, regardless of whether they need to be compared within (i.e., dot–dot and digits–digits task) or across notations (i.e., dots–digits, digits–dots). Contrary to these expectations, different ERPs were obtained across the tasks, suggesting that the performance in them is not driven by one and the same mechanism, but that there are different cognitive processes involved in the processing of symbolic and non-symbolic numbers. Moreover, the behavioral data of this study were fully in line with the data from the studies of Marinova et al. (2018) and Experiment 1 of Sasanguie et al. (2017). This is so because a ratio effect was observed in all tasks containing a numerosity, but not in the purely symbolic task. Finally, in a neuroimaging study using multivoxel pattern analysis (MVPA), Bulthé, De Smedt, and Op de Beeck (2014) showed that a neural distance effect was present only for non-symbolic numbers, but not for symbolic numbers (see also Bulthé, De Smedt, & Op de Beeck 2015). All of these results lead us to suggest that there are separate systems for numerical processing: one for exact symbolic numbers and another for approximate quantities (see also Reynvoet & Sasanguie, 2016).
A lot of research has been devoted to the specific characteristics of the ANS (e.g., Dehaene, 2007; Nieder, 2016; Piazza et al., 2007). It is less clear, however, how an exact numerical system for symbols would be organized. One suggestion was provided by Krajcsi et al. (2016, 2018), who assumed, in their so-called ‘Discrete Semantic System’ that numbers are represented as nodes, similar to a mental lexicon. The connections between these nodes reflect the semantic relations between two symbolic numbers, and may be formed by overlapping semantic features (e.g., “both smaller than 5”, “both are odd numbers”, etc.) and co-occurrences (i.e., associations, see also Vos, Sasanguie, Gevers, & Reynvoet, 2017). The main difference between such a system and the typical ANS organization is that close numbers (e.g., 7 and 8) do not have overlapping representations, as is claimed by the ANS, but are instead non-overlapping precise representations with strong connections between them (Krajcsi et al., 2016, 2018).
However, the model of Krajcsi et al. (2016, 2018) also predicts a ratio effect when symbolic numbers have to be compared, as a combination of association-based mechanisms and frequency effects (see Krajcsi et al., 2016, 2018 for a full elaboration). Consequently, this model could also not account for the absence of the ratio effect in symbolic comparison. One possibility is that the present pattern of results is caused by the sequential presentation technique adopted in this study. More specifically, the long SOA between the auditory and the visually presented numbers may have weakened the automatic association-based and/or frequency-based mechanisms that are normally involved in symbolic number comparison, resulting in the absence of a ratio effect. In line with this possibility, Lin and Göbel (2019) have recently observed a decreasing distance effect when the SOA between both numbers increased. However, this possibility needs to be explored in further studies, and is yet unclear how such an observation could be accounted for by the current models of symbolic number processing (Krajcsi et al., 2016; 2018; see also Verguts et al., 2005).
In conclusion, the aim of the current study was to add robust evidence for the hypothesis about dissociated symbolic and non-symbolic number processing systems in both small and large numbers. We succeeded in doing so using an audio-visual paradigm. First, we demonstrated that when participants evaluate symbolic numbers (i.e., digit–number word) independent of both the number range and the modality of presentation, a ratio effect is absent. In contrast, a ratio effect is always present when the task involves non-symbolic numbers (e.g., tones–dots, number word–dot, tones–digit). Second, an additional processing cost was observed when mixed number pairs (i.e., a symbolic and non-symbolic) had to be evaluated, as compared to evaluating pure number pairs (i.e., symbolic and symbolic, or non-symbolic and non-symbolic). Clearly, more research is needed to unravel how exactly the symbolic numbers are represented and what is the organization of the symbolic number system. We hope to have clarified that when pursuing this goal one should take into account not only the similarities in the processing of symbolic and non-symbolic numbers, but also the dissimilarities between them, as highlighted in the current study.
Notes
With respect to the credibility and the scientific integrity of our research, we report how we determined our sample size, all data exclusions (if any), all manipulations, and all measures in the study (Simmons, Nelson, & Simonsohn, 2012).
Because our study focused on comparing both symbolic and non-symbolic number pairs, we manipulated the relative difference (i.e., ratio) between the numbers, but not the absolute distance between them. As we mentioned in “Introduction”, the ratio and the distance are two very strongly related metrics.
Because the duration of the silence is dependent on the amount of tones that have to be presented within the stimulus timeframe, for these experiments, the shortest and the longest inter-tone intervals registered by the program were 20 ms and 1373 ms, respectively.
The BF10 is the ratio of the likelihood of the alternative hypothesis and the likelihood of the null hypothesis (while BF01 is simply the inverse ratio of these two likelihoods). For the more complicated models involving a larger numbers of factors (e.g., repeated measures ANOVA), we reported the BFInclusion (see Wagenmakers et al., 2018 for the rationale). According to the interpretation of Jeffreys (1961), BF values between 1 and 3 are considered as anecdotal evidence (“not worth more than a bare mention”, Jeffreys, 1961) for the alternative hypothesis, BF values between 3 and 10 are considered as moderate evidence, BF values between 10 and 30 are considered as strong evidence, BF values between 30 and 100 are considered very strong evidence, and BF values above 100 are considered as extreme evidence.
The confidence intervals (CI) around the effect sizes were computed with an SPSS plug in calculator by Karl Wuensch, freely available from http://core.ecu.edu/psyc/wuenschk/SPSS/SPSS-Programs.htm. Following the author`s recommendations (see Wuensch, 2009), and Steigner (2004), we report the 90% CI for partial eta squared (\(\eta_{\text{p}}^{2}\)), and the 95% CI for Cohen’s d.
References
Barth, H., Kanwisher, N., & Spelke, E. (2003). The construction of large number representations in adults. Cognition, 86(3), 201–221. https://doi.org/10.1016/S0010-0277(02)00178-6.
Brysbaert, M. (2007). The language-as-fixed-effect-fallacy: Some simple SPSS solutions to a complex problem (Version 2.0). London: Royal Holloway, University of London.
Brysbaert, M., & Stevens, M. (2018). Power analysis and effect size in mixed effects models: A tutorial. Journal of Cognition, 1(1), 1–20. https://doi.org/10.5334/joc.10.
Bulthé, J., De Smedt, B., & de Beeck, H. O. (2014). Format-dependent representations of symbolic and non-symbolic numbers in the human cortex as revealed by multi-voxel pattern analyses. Neuroimage, 87, 311–322. https://doi.org/10.1016/j.neuroimage.2013.10.049.
Bulthé, J., De Smedt, B., & Op de Beeck, H. P. (2015). Visual number beats abstract numerical magnitude: Format-dependent representation of Arabic digits and dot patterns in human parietal cortex. Journal of Cognitive Neuroscience, 27(7), 1376–1387. https://doi.org/10.1162/jocn_a_00787.
Cantlon, J. F., Libertus, M. E., Pinel, P., Dehaene, S., Brannon, E. M., & Pelphrey, K. A. (2009). The neural development of an abstract concept of number. Journal of Cognitive Neuroscience, 21(11), 2217–2229. https://doi.org/10.1162/jocn.2008.21159.
Defever, E., Sasanguie, D., Gebuis, T., & Reynvoet, B. (2011). Children’s representation of symbolic and nonsymbolic magnitude examined with the priming paradigm. Journal of Experimental Child Psychology, 109(2), 174–186. https://doi.org/10.1016/j.jecp.2011.01.002.
Dehaene, S. (2001). Précis of the number sense. Mind & Language, 16(1), 16–36. https://doi.org/10.1111/1468-0017.00154.
Dehaene, S. (2007). Symbols and quantities in parietal cortex: Elements of a mathematical theory of number representation and manipulation. In P. Haggard & Y. Rossetti (Eds.), Attention and performance XXII. Sensori-motor foundations of higher cognition (pp. 527–574). Cambridge: Harvard University Press.
Dehaene, S., & Akhavein, R. (1995). Attention, automaticity, and levels of representation in number processing. Journal of Experimental Psychology. Learning, Memory, and Cognition, 21(2), 314.
Dehaene, S., & Cohen, L. (1995). Towards an anatomical and functional model of number processing. Mathematical Cognition, 1(1), 83–120.
Dehaene, S., & Mehler, J. (1992). Cross-linguistic regularities in the frequency of number words. Cognition, 43(1), 1–29.
Faul, F., Erdfelder, E., Lang, A. G., & Buchner, A. (2007). G* Power 3: A flexible statistical power analysis program for the social, behavioral, and biomedical sciences. Behavior Research Methods, 39(2), 175–191. https://doi.org/10.3758/BF03193146.
Feigenson, L., Dehaene, S., & Spelke, E. (2004). Core systems of number. Trends in Cognitive Sciences, 8(7), 307–314. https://doi.org/10.1016/j.tics.2004.05.002.
Finke, S., Kemény, F., Perchtold, C., Göbel., S., & Landerl, K. (2018). Same or different? The ERP signatures of uni- and cross-modal integration of number words and Arabic digits. Poster presented at the First Mathematical Cognition and Learning Society Conference, Oxford, UK.
Gallistel, C. R., & Gelman, R. (1992). Preverbal and verbal counting and computation. Cognition, 44(1–2), 43–74.
Gebuis, T., & Reynvoet, B. (2011). Generating nonsymbolic number stimuli. Behavior Research Methods, 43(4), 981–986. https://doi.org/10.3758/s13428-011-0097-5.
Gielen, I., Brysbaert, M., & Dhondt, A. (1991). The syllable-length effect in number processing is task-dependent. Perception & Psychophysics, 50(5), 449–458.
Halberda, J., & Feigenson, L. (2008). Developmental change in the acuity of the “Number Sense”: The approximate number system in 3-, 4-, 5-, and 6-year-olds and adults. Developmental Psychology, 44(5), 1457. https://doi.org/10.1037/a0012682.
Jarosz, A. F., & Wiley, J. (2014). What are the odds? A practical guide to computing and reporting Bayes factors. The Journal of Problem Solving, 7(1), 2. https://doi.org/10.7771/1932-6246.1167.
Jeffreys, H. (1961). Theory of probability (3rd ed.). Oxford: Oxford University Press.
Kaufman, E. L., Lord, M. W., Reese, T. W., & Volkmann, J. (1949). The discrimination of visual number. The American journal of psychology, 62(4), 498–525.
Koechlin, E., Naccache, L., Block, E., & Dehaene, S. (1999). Primed numbers: Exploring the modularity of numerical representations with masked and unmasked semantic priming. Journal of Experimental Psychology: Human Perception and Performance, 25(6), 1882–1905.
Krajcsi, A., Lengyel, G., & Kojouharova, P. (2016). The source of the symbolic numerical distance and size effects. Frontiers in Psychology, 7, 1795. https://doi.org/10.3389/fpsyg.2016.01795.
Krajcsi, A., Lengyel, G., & Kojouharova, P. (2018). Symbolic number comparison is not processed by the analog number system: Different symbolic and non-symbolic numerical distance and size effects. Frontiers in Psychology, 9, 124. https://doi.org/10.3389/fpsyg.2018.00124.
Kutter, E. F., Bostroem, J., Elger, C. E., Mormann, F., & Nieder, A. (2018). Single neurons in the human brain encode numbers. Neuron, 100(3), 753–761. https://doi.org/10.1016/j.neuron.2018.08.036.
Love, J. (2015). Infinite number for BFInclusion [Online discussion forum]. https://github.com/jasp-stats/jasp-desktop/issues/1039. Accessed 1 Feb 2019.
Lyons, I. M., Ansari, D., & Beilock, S. L. (2012). Symbolic estrangement: Evidence against a strong association between numerical symbols and the quantities they represent. Journal of Experimental Psychology: General, 141(4), 635. https://doi.org/10.1037/a0027248.
Marinova, M., Sasanguie, D., & Reynvoet, B. (2018). Symbolic estrangement or symbolic integration of numerals with quantities: Methodological pitfalls and a possible solution. PLoS One. https://doi.org/10.1371/journal.pone.0200808.
Moeller, K., Huber, S., Nuerk, H. C., & Willmes, K. (2011). Two-digit number processing: Holistic, decomposed or hybrid? A computational modelling approach. Psychological Research, 75(4), 290–306. https://doi.org/10.1007/s00426-010-0307-2.
Moyer, R. S., & Landauer, T. K. (1967). Time required for judgements of numerical inequality. Nature, 215, 1519–1520. https://doi.org/10.1038/2151519a0.
Nieder, A. (2016). The neuronal code for number. Nature Reviews Neuroscience, 17(6), 366. https://doi.org/10.1038/nrn.2016.40.
Nieder, A., & Dehaene, S. (2009). Representation of number in the brain. Annual Review of Neuroscience, 32, 185–208. https://doi.org/10.04122/annurev.neuro.051508.135550.
Nuerk, H. C., & Willmes, K. (2005). On the magnitude representations of two-digit numbers. Psychology Science, 47(1), 52–72.
Núñez, R. E. (2017). Is there really an evolved capacity for number? Trends in Cognitive Sciences, 21(6), 409–424. https://doi.org/10.1016/j.tics.2017.03.005.
Philippi, T. G., van Erp, J. B. F., & Werkhoven, P. J. (2008). Multisensory temporal numerosity judgment. Brain Research, 1242, 116–125. https://doi.org/10.1016/j.brainres.2008.05.056.
Piazza, M. (2010). Neurocognitive start-up tools for symbolic number representations. Trends in Cognitive Sciences, 14, 542–551. https://doi.org/10.1016/j.tics.2010.09.008.
Piazza, M., Pinel, P., Le Bihan, D., & Dehaene, S. (2007). A magnitude code common to numerosities and number symbols in human intraparietal cortex. Neuron, 53, 293–305. https://doi.org/10.1016/j.neuron.2006.11.022.
Reynvoet, B., Notebaert, K., & Van den Bussche, E. (2011). The processing of two-digit numbers depends on task instructions. Zeitschrift für Psychologie/Journal of Psychology, 219(1), 37–41. https://doi.org/10.1027/2151-2604/a000044.
Reynvoet, B., & Sasanguie, D. (2016). The symbol grounding problem revisited: A thorough evaluation of the ANS mapping account and the proposal of an alternative account based on symbol–symbol associations. Frontiers in Psychology, 7, 1581. https://doi.org/10.3389/fpsyg.2016.01581.
Sasanguie, D., De Smedt, B., Defever, E., & Reynvoet, B. (2012). Association between basic numerical abilities and mathematics achievement. British Journal of Developmental Psychology, 30(2), 344–357. https://doi.org/10.1111/j.2044-835X.2011.02048.x.
Sasanguie, D., De Smedt, B., & Reynvoet, B. (2017). Evidence for distinct magnitude systems for symbolic and non-symbolic number. Psychological Research, 81(1), 231–242. https://doi.org/10.1007/s00426-015-0734-1.
Simmons, J. P., Nelson, L. D., & Simonsohn, U. (2012). A 21 Word solution. SSRN Electronic Journal, 1–4. https://doi.org/10.2139/ssrn.2160588.
Steiger, J. H. (2004). Beyond the F test: Effect size confidence intervals and tests of close fit in the analysis of variance and contrast analysis. Psychological Methods, 9(2), 164–182. https://doi.org/10.1037/1082-989X.9.2.164.
Tokita, M., & Ishiguchi, A. (2012). Behavioral evidence for format-dependent processes in approximate numerosity representation. Psychonomic Bulletin and Review, 19(2), 285–293. https://doi.org/10.3758/s13423-011-0206-6.
Tokita, M., & Ishiguchi, A. (2016). Precision and bias in approximate numerical judgment in auditory, tactile, and cross-modal presentation. Perception, 45(1–2), 56–70. https://doi.org/10.1177/030100661559688.
Tokita, M., Ashitani, Y., & Ishiguchi, A. (2013). Is approximate numerical judgment truly modality-independent? Visual, auditory, and cross-modal comparisons. Attention, Perception, and Psychophysics, 75(8), 1852–1861. https://doi.org/10.3758/s13414-013-0526-x.
Van Hoogmoed, A. H., & Kroesbergen, E. H. (2018). On the difference between numerosity processing and number processing. Frontiers in Psychology, 9, 1650. https://doi.org/10.3389/fpsyg.2018.01650.
Verguts, T., Fias, W., & Stevens, M. (2005). A model of exact small-number representation. Psychonomic Bulletin & Review, 12(1), 66–80. https://doi.org/10.3758/BF03196349.
Vos, H., Sasanguie, D., Gevers, W., & Reynvoet, B. (2017). The role of general and number-specific order processing in adults’ arithmetic performance. Journal of Cognitive Psychology, 29(4), 469–482. https://doi.org/10.1080/20445911.2017.1282490.
Wagenmakers, E. J. (2015). Zero-inclusion Probabilities When Multiple Bf10s Are Infinite [Online discussion forum]. https://github.com/jasp-stats/jasp-desktop/issues/771. Accessed 1 Feb 2019.
Wagenmakers, E. J., Love, J., Marsman, M., Jamil, T., Ly, A., Verhagen, A. J., & Morey, R. D. (2018a). Bayesian statistical inference for psychological science. Part II: Example applications with JASP. Psychonomic Bulletin & Review, 25(1), 58–76. https://doi.org/10.3758/s13423-017-1323-7.
Wagenmakers, E. J., Marsman, M., Jamil, T., Ly, A., Verhagen, J., Love, J., & Matzke, D. (2018b). Bayesian inference for psychology. Part I: Theoretical advantages and practical ramifications. Psychonomic Bulletin & Review, 25(1), 35–57. https://doi.org/10.3758/s13423-017-1343-3.
Wuensch, K. (2009). Confidence intervals for Eta-squared and RMSSE. http://core.ecu.edu/psyc/wuenschk/StatsLessons.htm. Accessed 1 Feb 2019.
Funding
This research was supported by KU Leuven research funds (Grant number C14/16/029). Delphine Sasanguie is a postdoctoral research fellow of the Research Fund Flanders (www.fwo.be).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
Mila Marinova declares that she has no conflict of interest. Delphine Sasanguie declares that she has no conflict of interest. Bert Reynvoet declares that he has no conflict of interest.
Ethical approval
All procedures performed in the studies involving human participants were in accordance with the ethical standards of the institutional research committee at KU Leuven (file number G-20160679), and with the 1964 Helsinki declaration, and its later amendments or comparable ethical standards.
Informed consent
Informed consent was obtained from all individual participants included in the study.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Marinova, M., Sasanguie, D. & Reynvoet, B. Numerals do not need numerosities: robust evidence for distinct numerical representations for symbolic and non-symbolic numbers. Psychological Research 85, 764–776 (2021). https://doi.org/10.1007/s00426-019-01286-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00426-019-01286-z