INTRODUCTION

Information about the dependence or independence of random variables is a necessary condition for the synthesis of effective algorithms for information processing and decision-making. In [1–3], the properties of a nonparametric Rosenblatt–Parzen-type probability density estimation of independent random variables are investigated. It is found that the presence of a priori information about the independence of random variables allows us to improve the approximation properties of the nonparametric estimation of their probability density in comparison with the kernel statistics for dependent random variables. This advantage increases with the increase in the dimension of random variables. The obtained results are confirmed by studying the asymptotic properties of the nonparametric estimation of the separating surface equation in the two-alternative problem of pattern recognition [4].

The traditional method of testing the hypothesis of the independence of random variables is based on the use of the universal \(\chi^{2}\)-Pearson criterion. However, its formation contains a difficult-to-formalize stage of dividing the range of values of random variables into multidimensional intervals [5]. Therefore, the problem arises of developing a new method of testing the hypothesis providing a bypass for the problem of decomposing the domain of values of random variables. A similar problem is solved when testing the hypothesis of the identity of the distribution laws of random variables based on the use of a nonparametric pattern recognition algorithm [6–8]. It is shown that it can be replaced by the task of testing the hypothesis that the image recognition error is equal to a certain threshold value. The training sample in the synthesis of a nonparametric pattern recognition algorithm is formed based on statistical data that characterize the distribution laws of the compared random variables.

The purpose of this paper is to develop the proposed approach to the problem of testing the hypothesis of the independence of random variables using a nonparametric pattern recognition algorithm.

METHOD FOR TESTING THE HYPOTHESIS OF THE INDEPENDENCE OF RANDOM VARIABLES

Let there be a sample \(V=(x^{i}\), \(i=\overline{1,n})\) of volume \(n\) made up of independent observations of a two-dimensional random variable \(x=(x_{1},x_{2})\). The sample \(V\) is extracted from general populations characterized by probability densities \(p(x_{1})p(x_{2})\) or \(p(x_{1},x_{2})\). It is necessary to check the hypothesis

$$H_{0}{:}\quad p(x_{1},x_{2})\equiv p(x_{1})p(x_{2})$$
(1)

about the independence of random variables \(x_{1}\), \(x_{2}\) using the statistical data \(V\).

To test the hypothesis \(H_{0}\) (1), we will solve a two-alternative pattern recognition problem. The classes \(\Omega_{1}\), \(\Omega_{2}\) are defined as the areas for determining probability densities \(p(x_{1})p(x_{2})\), \(p(x_{1},x_{2})\). Under these conditions, the Bayesian decision rule corresponding to the maximum likelihood criterion has the form

$$m(x){:}\begin{cases}x\in\Omega_{1},\quad\text{of}\quad p(x_{1},x_{2})<p(x_{1})p(x_{2});\\ x\in\Omega_{2},\quad\text{of}\quad p(x_{1},x_{2})>p(x_{1})p(x_{2}).\end{cases}$$
(2)

In contrast to the traditional formulation of the pattern recognition problem, the synthesis of the decision rule (2) a priori lacks a training sample containing information about the membership of elements of the sample \(V\) to a particular class. This information should be detected during the implementation of the \(H_{0}\) hypothesis testing technique, which is based on performing the following actions.

From the sample \(V\), we reconstruct the probability densities \(p(x_{1},x_{2})\), \(p(x_{1})p(x_{2})\) using their nonparametric Rosenblatt–Parzen-type estimates [9, 10]:

$$\bar{p}(x_{1},x_{2})=\frac{1}{nc_{1}c_{2}}\sum\limits_{i=1}^{n}\Phi\Big{(}\frac{x_{1}-x_{1}^{i}}{c_{1}}\Big{)}\Phi\Big{(}\frac{x_{2}-x_{2}^{i}}{c_{2}}\Big{)},$$
(3)
$$\bar{p}(x_{1})\bar{p}(x_{2})=\frac{1}{n^{2}c_{1}c_{2}}\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}\Phi\Big{(}\frac{x_{1}-x_{1}^{i}}{c_{1}}\Big{)}\Phi\Big{(}\frac{x_{2}-x_{2}^{j}}{c_{2}}\Big{)}.$$
(4)

In statistics (3) and (4), the kernel functions \(\Phi(u_{v})\) satisfy the following conditions:

$$\Phi(u_{v})=\Phi(-u_{v}),\quad 0\leqslant\Phi(u_{v})<\infty,\quad\int\limits_{-\infty}^{+\infty}\Phi(u_{v})du_{v}=1,$$
$$\int\limits_{-\infty}^{+\infty}u^{m}\Phi(u_{v})du_{v}<\infty,\quad 0\leqslant m<\infty,\quad v=1,2.$$

The values of the blur coefficients \(c_{v}\) of the kernel functions decrease with the growth of the volume \(n\) of the statistical data sample \(V\). Taking into account expressions (2)–(4), we can write the nonparametric decision rule for the classification of random variables \(x=(x_{1},x_{2})\) as

$$\bar{m}(x){:}\begin{cases}x\in\Omega_{1},\quad\text{of}\quad\bar{p}(x_{1},x_{2})<\bar{p}(x_{1})\bar{p}(x_{2});\\ x\in\Omega_{2},\quad\text{of}\quad\bar{p}(x_{1},x_{2})>\bar{p}(x_{1})\bar{p}(x_{2}).\end{cases}$$
(5)

Under conditions of such uncertainty, we will choose the optimal blur coefficients of the kermel functions of the decision rule (5) based on the approximation properties for the nonparametric estimates \(\bar{p}(x_{1},x_{2})\), \(\bar{p}(x_{1})\bar{p}(x_{2})\) of probability densities \(p(x_{1},x_{2})\), \(p(x_{1})p(x_{2})\). To select the optimal blur coefficients of the nonparametric estimate of the probability density \(p(x_{1},x_{2})\), as a criterion, for example, the maximum of the likelihood function is used [11, 12]

$$L(c_{1},c_{2})=\prod\limits_{j=1}^{n}\bar{p}(x_{1}^{j},x_{2}^{j}),\quad\bar{p}(x_{1}^{j},x_{2}^{j})=\frac{1}{(n-1)c_{1}c_{2}}\sum\limits_{i=1,\ i\neq j}^{n}\Phi\Big{(}\frac{x_{1}^{j}-x_{1}^{i}}{c_{1}}\Big{)}\Phi\Big{(}\frac{x_{2}^{j}-x_{2}^{i}}{c_{2}}\Big{)}.$$
(6)

By analogy with expression (6), it is easy to determine the criterion for choosing the optimal blur coefficients for the statistics \(\bar{p}(x_{1})\bar{p}(x_{2})\) (4).

Note that the choice of the optimal blur coefficients of nonparametric estimates of the probability densities \(\bar{p}(x_{1},x_{2})\), \(\bar{p}(x_{1})\bar{p}(x_{2})\) can be carried out from the condition of the minimum statistical estimates of the standard deviations \(\bar{p}(x_{1},x_{2})\), \(\bar{p}(x_{1})\bar{p}(x_{2})\) from \(p(x_{1},x_{2})\), \(p(x_{1})p(x_{2})\), respectively [13–19].

Optimization of the nonparametric decision rule (5) with respect to the diffusion coefficients of the kernel functions \(c_{1}\), \(c_{2}\) can be simplified by setting in statistics (3) and (4) the values \(c_{v}=c\bar{\sigma}_{v}\), \(v=1,2\). Here, \(\bar{\sigma}_{v}\) is the estimate of the standard deviation of the random variable \(x_{v}\) in the sample \(V\). This statement is obvious, since a larger length of the interval of values \(x_{v}\) corresponds to a greater blur coefficient \(c_{v}\) of the kernel function \(\Phi(u_{v})\), \(v=1,2\). A similar approach was used in the construction of fast procedures for the optimization of nonparametric estimates of the kernel-type probability density [20–23].

The values of the estimates of the standard deviations \(\bar{\sigma}_{v}\) are determined from the statistical data of the sample \(V\):

$$\bar{\sigma}_{v}=\Big{(}\frac{1}{n-1}\sum\limits_{i=1}^{n}(x_{v}^{i}-\bar{x}_{v})^{2}\Big{)}^{1/2},\quad v=1,2.$$

Here, \(\bar{x}_{v}\) is the average value of the random variable \(x_{v}\), which is calculated from the sample \(V\).

Therefore, it becomes possible to optimize the nonparametric pattern recognition algorithm (5) using only one parameter \(c\) of the blur coefficients of the kernel functions.

Let us determine the estimates of the probabilities of pattern recognition errors \(\bar{\rho}_{1}(\bar{c}_{1},\bar{c}_{2})\), \(\bar{\rho}_{2}(\bar{c}_{1},\bar{c}_{2})\) by the decision rule (5) based on the initial statistical data \(V\) for the optimal blur coefficients \(\bar{c}(1)=(\bar{c}_{1}(1),\bar{c}_{2}(1))\), \(\bar{c}(2)=(\bar{c}_{1}(2),\bar{c}_{2}(2))\) of the kernel functions of statistics \(\bar{p}(x_{1})\bar{p}(x_{2})\), \(\bar{p}(x_{1},x_{2})\), respectively.

The values \(\bar{\rho}_{t}(\bar{c}(1),\bar{c}(2))\) are calculated in the sliding exam mode for the sample \(V\), assuming that its elements belong to the class \(\Omega_{t}\):

$$\bar{\rho}_{t}(\bar{c}(1),\bar{c}(2))=\frac{1}{n}\sum\limits_{j=1}^{n}1(\delta(j),\bar{\delta}(j)),\quad t=1,2,$$

where \(\delta(j)=t\) are indications of type \(x^{j}=(x_{1}^{j},x_{2}^{j})\in\Omega_{t}\);

$$\bar{\delta}(j)=\begin{cases}t\quad\text{if}\quad x^{j}\in\Omega_{t};\\ 0\quad\text{if}\quad x^{j}\notin\Omega_{t},\end{cases}$$

is the decision of algorithm (5) about the situation \(x^{j}\) belonging to one of the classes \(\Omega_{t}\), \(t=1,2\).

When calculating \(\bar{\rho}_{t}(\bar{c}(1),\bar{c}(2))\) according to the method of the sliding exam method, the situation \(x^{j}=(x_{1}^{j},x_{2}^{j})\) from the sample \(V\), which is submitted for control to algorithm (5), is excluded from the process of generating statistics (3) and (4).

The indicator function is determined by the expression

$$1(\delta(j),\bar{\delta}(j))=\begin{cases}0\quad\text{if}\quad\delta(j)=\bar{\delta}(j);\\ 1\quad\text{if}\quad\delta(j)\neq\bar{\delta}(j).\end{cases}$$

Let us denote by \(\bar{\bar{\rho}}_{t}\) the minimum value of the estimate of the probability of a pattern recognition error under the assumption that the elements of the sample \(V\) belong to the class \(\Omega_{t}\), \(t=1,2\). Compare the values \(\bar{\bar{\rho}}_{1}\), \(\bar{\bar{\rho}}_{2}\).

The hypothesis \(H_{0}\) is valid if \(\bar{\bar{\rho}}_{1}<\bar{\bar{\rho}}_{2}\). Otherwise, for \(\bar{\bar{\rho}}_{2}<\bar{\bar{\rho}}_{1}\) the random variables \(x_{1}\) and \(x_{2}\) are dependent.

It is natural that with limited volumes \(n\) of the \(V\) sample, the problem of confidence estimation of the probabilities of image recognition errors arises. To solve it, we can use the traditional method of confidence estimation of probabilities [5] or the Kolmogorov–Smirnov criterion [24].

For example, when using the Kolmogorov–Smirnov criterion, the deviation \(\bar{D}_{12}=|\bar{\bar{\rho}}_{1}-\bar{\bar{\rho}}_{2}|\) is compared with the threshold value

$$D_{\beta}=\sqrt{-\ln(\beta/2)/n}.$$

Here, \(\beta\) is the probability (risk) to reject the hypothesis \(\bar{H}_{0}\): \(\rho_{1}(c_{1},c_{2})=\rho_{2}(c_{1},c_{2})\). If the relation \(\bar{D}_{12}<D_{\beta}\) is satisfied, then the hypothesis \(\bar{H}_{0}\) is valid and the risk of rejecting it does not exceed the value \(\beta\). If \(\bar{D}_{12}>D_{\beta}\), the hypothesis \(\bar{H}_{0}\) is rejected.

ANALYSIS OF THE RESULTS OF A COMPUTATIONAL EXPERIMENT

Let us investigate the dependence of the effectiveness of the proposed method for testing the hypothesis of the independence of two-dimensional random variables on the volume of the initial statistical data. We will assume that the random variables \(x_{1}\) and \(x_{2}\) have Gaussian distribution laws. When generating the values \(x_{1}\), \(x_{2}\) in the \(V\) sample, we use the random variable generators

$$x_{1}^{i}=M(x_{1})+\sigma_{1}\Big{(}\sum\limits_{j=1}^{12}\varepsilon_{1}^{j}-6\Big{)},\quad x_{2}^{i}=x_{1}^{i}+\sigma_{2}\Big{(}\sum\limits_{j=1}^{12}\varepsilon_{2}^{j}-6\Big{)},\quad i=\overline{1,n},$$

where \(M(x_{1})\) is the mathematical expectation of the random variable \(x_{1}\), \(\sigma_{1}\), and \(\sigma_{2}\) are standard deviations of \(x_{1}\) and \(x_{2}\), and \(\varepsilon_{1}\) and \(\varepsilon_{2}\) are random variables with uniform distribution laws over the interval \([0;1]\).

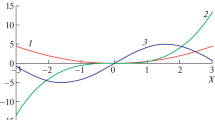
When selecting the values \(\sigma_{1}\), \(\sigma_{2}\), the dependence index (correlation coefficient) between the random variables \(x_{1}\), \(x_{2}\) changes, which is calculated from the obtained statistical data \(V\). The values of \(\bar{\bar{\rho}}_{1}^{t}\), \(\bar{\bar{\rho}}_{2}^{t}\) for a specific volume \(n(t)=n\) of the sample \(V\) are determined 50 times. The obtained data \(\bar{\bar{\rho}}_{1}^{t}\), \(\bar{\bar{\rho}}_{2}^{t}\), \(t=\overline{1,50}\) are averaged, and their results are denoted by \(\tilde{\rho}_{1}\), \(\tilde{\rho}_{2}\) and shown in Fig. 1.

Fig. 1
figure 1

Dependence of the averaged estimates of the probabilities of errors in belonging of elements of \(V\) to independent random variables \(x_{1}\), \(x_{2}\) on the sample size \(n\) (curves 1–5 correspond to the values of the correlation coefficients \(r=\) 0.9, 0.7, 0.45, 0.33, and 0).

Full size image

The results of computational experiments confirm the effectiveness of the proposed method. With the correlation coefficient \(r\geqslant 0.35\), the application of the method under consideration makes it possible to exclude errors in assigning the initial statistical data \(V\) to independent random variables in 50 computational experiments. Let us denote this estimate of the probability of confirming the hypothesis \(H_{0}\) by \(\bar{P}_{1}=0\). If \(r=0\), the values are \(\bar{P}_{1}=\) 0.6, 0.62, and 0.8 with the volume of statistical data \(n=\) 100, 200, and 500 respectively.

Let us analyze the values \(\tilde{\rho}_{1}\), \(\tilde{\rho}_{2}\), which determine the criterion for testing the hypothesis \(H_{0}\) in computational experiments. With an increase in the correlation coefficient \(r\), a decrease in the average estimate of the error probability \(\tilde{\rho}_{2}\) of belonging of elements of the sample \(V\) to the class \(\Omega_{2}\) of values of dependent random variables is observed. For example, when increasing \(r\) in the interval \([0.45;0.9]\) the estimate of the probability of a pattern recognition error \(\tilde{\rho}_{2}\) decreases from 0.37 to 0.055. This fact is explained by a decrease in the area of intersection of the classes \(\Omega_{1}\), \(\Omega_{2}\) and, as a consequence, an increase in the values of the kernel estimate of the probability density \(\bar{p}(x_{1},x_{2})\) in comparison with \(\bar{p}(x_{1})\bar{p}(x_{2})\) in the nonparametric decision rule (5), which leads to a decrease in \(\tilde{\rho}_{2}\). With a decrease in \(r\) in the range \([0.33;0]\), estimates of the probabilities of the pattern recognition error \(\tilde{\rho}_{2}\) increase from 0.45 to 0.53. Under these conditions, there is a tendency for the region of intersection of the classes \(\Omega_{1}\), \(\Omega_{2}\) and the values \(\tilde{\rho}_{2}\), \(\tilde{\rho}_{1}\) to converge as a criterion for the identity of the distribution laws \(p(x_{1},x_{2})\), \(p(x_{1})p(x_{2})\) of the compared random variables.

The stability of the proposed method to the volume of initial statistical data was found at specific values of the correlation coefficient, which manifests itself in close values of \(\tilde{\rho}_{2}\) at \(n\in[100;500]\). For example, for \(r=0.9\), the values are \(\tilde{\rho}_{2}\in[0.044;0.06]\), and under the conditions \(r=0.45\) the values are \(\tilde{\rho}_{2}\in[0.35;0.39]\) (see Fig. 1). The noted pattern weakens with decreasing values of \(r\). This conclusion is confirmed by the values of \(\tilde{\rho}_{2}\) in the interval \([0.423;0.496]\) for \(r=0.33\).

The above statements are reliable, which is verified using the Kolmogorov–Smirnov criterion with the risk \(\beta=0.05\) to reject the hypothesis being tested. Doubtful decisions appear at values of \(r\) close to zero. Under these conditions, the proposed method provides a reliable solution for \(n\geqslant 300\). For example, for \(n=300\), 400, 500 the values are \(\bar{D}_{12}=\) 0.23, 0.141, and 0.189, that exceed the thresholds \(D_{\beta}=\) 0.111, 0.096, and 0.086. The results confirm the hypothesis of the independence of random variables.

The results of computational experiments were compared with the confidence limits of the correlation coefficient

$$\textrm{tanh}\Big{(}\frac{1}{2}\ln\frac{1+\bar{r}}{1-\bar{r}}-\frac{\varepsilon_{\alpha}}{\sqrt{n-3}}\Big{)}<r<\textrm{tanh}\Big{(}\frac{1}{2}\ln\frac{1+\bar{r}}{1-\bar{r}}+\frac{\varepsilon_{\alpha}}{\sqrt{n-3}}\Big{)},$$

where \(\varepsilon_{\alpha}\) is defined by the relation \(2F(\varepsilon_{\alpha})=\alpha\) and \(\bar{r}\) is the estimate of the correlation coefficient. Here, \(F(\varepsilon_{\alpha})\) is the Laplace function, \(\alpha\) is confidence factor, and \(\textrm{tanh}(\cdot)\) is the hyperbolic tangent. For these conditions at \(\bar{r}=0\), \(\alpha=0.95\), and \(\varepsilon_{\alpha}=1.96\), the confidence limits for the correlation coefficient are determined by the intervals \(r\in({\pm}0.196)\), \(({\pm}0.139)\), \(({\pm}0.113)\), \(({\pm}0.098)\), \(({\pm}0.088)\), which correspond to the volumes of statistical data \(n=100\), 200, 300, 400, 500.

Let us compare the effectiveness of the proposed method with the approach that uses the correlation coefficient as a criterion for the linear dependence between random variables. To do this, we determine the estimates of the probabilities of decisions with respect to the hypothesis \(H_{0}\), taken in accordance with the proposed method, under the conditions of the value of the correlation coefficient \(r=0.196\). Note that this value of \(r\) corresponds to its confidence boundary at \(n=100\) and \(\alpha=0.95\). Under these conditions, the estimate of the probability of confirming the hypothesis \(H_{0}\) corresponds to the value of \(\bar{P}_{1}=0.4\), and its refutation is \(\bar{P}_{2}=0.6\) in 50 computational experiments. By the values of \(\bar{P}_{1}\), \(\bar{P}_{2}\), the proposed method is more sensitive to changes in the indicator \(r\) of the linear dependence between the random variables \(x_{1}\), \(x_{2}\). The results are consistent with the traditional approach of testing the hypothesis of linear dependence of random variables. However, the presented method applies to the conditions of nonlinear dependence between random variables.

CONCLUSIONS

The method proposed in this paper for testing the hypothesis of the independence of random variables bypasses the problem of decomposing the range of values of random variables into multidimensional intervals, which is characteristic of the Pearson criterion. To solve this problem, we use a nonparametric pattern recognition algorithm that meets the maximum likelihood criterion. Optimization of the kernel probability density estimations of the blur coefficients is carried out from the condition of the maximum likelihood function. Under the assumption of independence or dependence of random variables in the initial statistical data, estimates of the probabilities of pattern recognition errors are determined. Based on their minimum value, a decision is made about the independence or dependence of random variables.

The effectiveness of the proposed method is confirmed by the results of computational experiments when testing the hypothesis of the independence of a two-dimensional random variable the components of which are characterized by normal distribution laws. It was found that with a correlation coefficient \(r\geqslant\) 0.35 between random variables, the proposed method accurately rejects the initial hypothesis with the volume of initial statistical data from 100 to 500. With independent random variables in conditions when the correlation coefficient is zero, the initial hypothesis is confirmed by probability estimates of 0.6, 0.62, and 0.8 with the volume of statistical data \(n=\) 100, 200, and 500, respectively. The stability of the values of the used criterion for testing the hypothesis under consideration to changes in the volume of statistical data under specific experimental conditions is observed.

Promising research in this direction is the application of the proposed technique to test the hypothesis of a nonlinear relationship between random variables and the formation of a set of independent random variables, which will simplify the task of synthesizing effective information processing algorithms.