A new method is proposed for probabilistic analysis of the results of cyclic fatigue-strength tests. This method is based on the possibility of plotting and statistically describing fatigue curves, which express the number of cycles to failure as a function of the stress amplitude. If the initial test results in Cartesian coordinates are converted to double logarithmic coordinates, they may be described by simple linear formulas. Their parameters are calculated by the least-squares method.

Statistically, the number of cycles to failure may be described by a three-parameter Weibull distribution in terms of the lowest guaranteed values. With fixed values of the number of cycles to failure, the resulting family of fatigue curves corresponding to different probabilities may be used to determine the scattering of the fatigue limits and the conditional fatigue limits.

The results obtained permit prediction of the life of structures with previously unattainable reliability.

In the first approximation, the characteristics of the fatigue strength are determined for a few (6–7) small ground metal samples in failure tests with harmonic stress of different amplitude \(\sigma = {{\sigma }_{1}},\;{{\sigma }_{2}},\;{{\sigma }_{3}},...\) (Fig. 1a). For each stress, we determine the number of cycles to failure \({{N}_{1}}\left( {{{\sigma }_{1}}} \right),\)\({{N}_{2}}\left( {{{\sigma }_{2}}} \right),...,{{N}_{n}}\left( {{{\sigma }_{n}}} \right)\) and plot curves of N against σ (Fig. 1b). The points in Fig. 1b correspond to the test results, which may be compared with the expected fatigue curve \(N = N\left( \sigma \right)\). In the tests, the greatest amplitude of the stress \({{\sigma }_{1}}\) is 80–90% of the yield point σy, at which the expected number of cycles to failure is (3–5) × 104. The least amplitude of the stress \({{\sigma }_{n}}\) in the tests is such that the expected number of cycles to failure \({{N}_{n}}\) = (2–10) × 106.

Fig. 1.
figure 1

Plotting the fatigue curve.

Full size image

To establish the analytical dependence N = N(σ) and plot the corresponding fatigue curve, the test results are plotted in double logarithmic coordinates log σ–log N and a linear dependence of the following form is obtained by the least-squares method (Fig. 2)

$$m{\text{log}}\sigma + {\text{log}}N = {\text{log}}C.$$
((1))
Fig. 2.
figure 2

Fatigue curve in double logarithmic coordinates.

Full size image

The constants m and C are then determined [1].

We find C from the formula

$$C = \sigma _{{ - 1}}^{m}{{N}_{0}},$$
((2))

where N0 is the limiting number of loading cycles in the tests. (As a rule, N0 = 2 × 106 cycles.)

In Eq. (2), \({{\sigma }_{{ - 1}}}\) is the fatigue limit with symmetric loading cycles, when the asymmetry coefficient \(R = {{{{\sigma }_{{\min }}}} \mathord{\left/ {\vphantom {{{{\sigma }_{{\min }}}} {{{\sigma }_{{\max }}}}}} \right. \kern-0em} {{{\sigma }_{{\max }}}}} = - 1.\) According to Eqs. (1) and (2), the equation of the fatigue curve takes the form [2]

$$N = \left\{ \begin{gathered} {{N}_{0}}{{\left( {\frac{{{{\sigma }_{{ - 1}}}}}{\sigma }} \right)}^{m}}\,\,\,\,{\text{when}}\,\,\,\,\sigma \geqslant {{\sigma }_{{ - 1}}}; \hfill \\ \infty \,\,\,\,{\text{when}}\,\,\,\,\sigma < {{\sigma }_{{ - 1}}}. \hfill \\ \end{gathered} \right.$$
((3))

The fatigue curve given by Eq. (3) is shown in Fig. 3 in Cartesian (a) and double logarithmic (b) coordinates.

Fig. 3.
figure 3

Fatigue curve for low-carbon steel.

Full size image

On the basis of Fig. 3b and Eqs. (1) and (2), we may determine m from the formula [3]

$$m = \cot \alpha = \frac{{{\text{log}}{{N}_{0}} - {\text{log}}N}}{{{\text{log}}\sigma - {\text{log}}{{\sigma }_{{ - 1}}}}}.$$

We may only use Eq. (3) when σ ≤ σy. When σu ≥ σ ≥ σy, the fatigue equation may be written in the approximate form [3]

In repeated experiments with the same stress amplitudes \({{\sigma }_{1}},{{\sigma }_{2}},{{\sigma }_{3}},...,\) we may establish the statistical spread of the results for the number of cycles to failure (Fig. 4a). Each value of \(\sigma \) corresponds to a particular threshold (guaranteed) number \({{N}_{0}} = {{N}_{0}}\left( \sigma \right)\) of cycles, below which failure does not occur.

Fig. 4.
figure 4

Scattering of the results in plotting the fatigue curve.

Full size image

We determine the function \({{N}_{0}} = {{N}_{0}}\left( \sigma \right)\) as for N in Eq. (3): the test results for the guaranteed number of cycles to failure are expressed in double logarithmic coordinates and described by a linear formula of the form in Eq. (1). The form of the function is determined by the least-squares method

$${{N}_{0}}\left( \sigma \right) = \left\{ \begin{gathered} {{N}_{0}}{{\left( {\frac{{{{\sigma }_{{ - 1}}}}}{\sigma }} \right)}^{m}}\,\,\,\,{\text{when}}\,\,\,\,\sigma \geqslant {{\sigma }_{{ - 1}}}; \hfill \\ \infty \,\,\,\,{\text{when}}\,\,\,\,\sigma < {{\sigma }_{{ - 1}}}, \hfill \\ \end{gathered} \right.$$
((4))

where \({{\sigma }_{{ - 1}}}\) is the fatigue limit corresponding to the selected \({{N}_{0}}\) value for the tests.

The expected distribution density of the probabilities for the number of cycles to failure is shown in Fig. 4b.

Information regarding the scattering of \(N\left( \sigma \right)\) may be expressed as a frequency polygon (Fig. 5).

Fig. 5.
figure 5

Scattering of the number of cycles to failure.

Full size image

The mean number N − N0 of cycles to failure is determined from the formula

$$\left\langle {N - {{N}_{0}}} \right\rangle = \sum\limits_{i = 1}^n {{{p}_{i}}\left( {{{N}_{i}} - {{N}_{0}}} \right)} ,$$
((5))

where pi is the frequency at which the number Ni appears; \(\sum\nolimits_{i = 1}^n {{{p}_{i}}} = 1;\)n is the number of tests at stress \({{\sigma }_{i}}.\)

The mean square value is determined from the formula

$$\left\langle {{{{\left( {N - {{N}_{0}}} \right)}}^{2}}} \right\rangle = \sum\limits_{i = 1}^n {{{p}_{i}}{{{\left( {{{N}_{i}} - {{N}_{0}}} \right)}}^{2}}} ,$$

while its dispersion is determined from the formula [4]

$$S_{{N - {{N}_{0}}}}^{2} = \left\langle {{{{\left( {N - {{N}_{0}}} \right)}}^{2}}} \right\rangle - {{\left( {\left\langle {N - {{N}_{0}}} \right\rangle } \right)}^{2}}.$$

The corresponding variation coefficient is determined from the formula

$${{\delta }_{{N - {{N}_{0}}}}} = \frac{{{{S}_{{N - {{N}_{0}}}}}}}{{\left\langle {N - {{N}_{0}}} \right\rangle }}.$$
((6))

The distribution functions of the probabilities for N at fixed \(\sigma \) may be expressed by the Weibull law [5, 6]

$$F\left( {{N \mathord{\left/ {\vphantom {N \sigma }} \right. \kern-0em} \sigma }} \right) = \left\{ \begin{gathered} 1 - \exp \left( { - \beta \left( \sigma \right){{{\left( {N - {{N}_{0}}\left( \sigma \right)} \right)}}^{{\alpha \left( \sigma \right)}}}} \right) \hfill \\ {\text{when}}\,\,N \geqslant {{N}_{0}}; \hfill \\ 0\,\,\,\,{\text{when}}\,\,\,\,N < {{N}_{0}}, \hfill \\ \end{gathered} \right.$$
((7))

where α and β are parameters.

The variation coefficient of N − N0 is determined from the formula [7]

$${{\delta }_{{N - {{N}_{0}}}}} = \frac{{\sqrt {\Gamma \left( {1 + \frac{2}{\alpha }} \right) - {{\Gamma }^{2}}\left( {1 + \frac{1}{\alpha }} \right)} }}{{\Gamma \left( {1 + \frac{1}{\alpha }} \right)}},$$
((8))

where \(\Gamma \left( x \right) = \int_0^\infty {{{e}^{{ - t}}}{{t}^{{x - 1}}}{\text{d}}t} \) is a gamma function.

Substituting the statistical estimate of the variation coefficient from Eq. (8) into Eq. (6), we obtain an algebraic equation for α. We now consider the case where δ and α do not depend on the stress σ.

According to Eq. (7), the mean value of N − N0 is calculated from the formula

$$\left\langle {N - {{N}_{0}}} \right\rangle = {{\beta }^{{ - {1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-0em} \alpha }}}}\Gamma \left( {1 + \frac{1}{\alpha }} \right).$$
((9))

Substituting \(\left\langle {N - {{N}_{0}}} \right\rangle \) from Eq. (5) and α from Eq. (8) into Eq. (9), we calculate \(\beta \) from the formula

$$\beta = {{\left( {\frac{{\Gamma \left( {1 + \frac{1}{\alpha }} \right)}}{{\left\langle {N - {{N}_{0}}} \right\rangle }}} \right)}^{\alpha }}.$$

The parameter \(\beta \) depends on the stress amplitudes σ1, σ2, …, σn. The expected form of the function \(\beta = \beta \left( \sigma \right)\) is shown in Fig. 6a. The results given by Eq. (4) are plotted in double logarithmic coordinates (log β, log σ). By the least-squares method, we obtain a linear dependence (Fig. 6b) and determine the constants k and γ

$${\text{log}}\beta = {\text{log}}k + \gamma {\text{log}}\sigma .$$
((10))
Fig. 6.
figure 6

Determining the parameters of the Weibull distribution.

Full size image

This relation may be obtained by substituting Eq. (9) into Eq. (1).

From Eq. (10), we obtain

$$\beta = k{{\sigma }^{\gamma }}.$$
((11))

Substituting β from Eq. (11) into Eq. (7), we find that

$$F\left( {{N \mathord{\left/ {\vphantom {N \sigma }} \right. \kern-0em} \sigma }} \right) = 1 - \exp \left( { - k{{\sigma }^{\gamma }}{{{\left[ {N - {{N}_{0}}\left( \sigma \right)} \right]}}^{\alpha }}} \right),$$

and hence we obtain the fatigue curve corresponding to fixed probability \(p = F\left( {{N \mathord{\left/ {\vphantom {N \sigma }} \right. \kern-0em} \sigma }} \right)\)

$$\begin{gathered} {{\sigma }^{m}}\left( {N - {{N}_{0}}\left( \sigma \right)} \right) = {{\sigma }^{m}}N - \sigma _{{ - 1}}^{m}{{N}_{0}} \\ = C = {{\left( { - \frac{1}{k}\ln \left( {1 - p} \right)} \right)}^{{\frac{1}{\alpha }}}}, \\ \end{gathered} $$
((12))

where \(m = \frac{\gamma }{\alpha },\,\,\,\,p = F\left( {{N \mathord{\left/ {\vphantom {N \sigma }} \right. \kern-0em} \sigma }} \right).\)

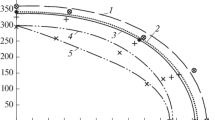
Equation (12) describes the family of fatigue curves corresponding to different p (Fig. 7a). When \(p = 0,\) we have the guaranteed number \(N = {{N}_{0}}\left( \sigma \right)\) of cycles to failure.

Fig. 7.
figure 7

Scattering of the conditional fatigue limits.

Full size image

The points of intersection of this family of curves with the curves N = const determine the scattering of the stresses \({{\sigma }_{{ - 1,N}}},\) known as the conditional fatigue limits. We find the probability distribution for these stresses at different N. To that end, Eq. (12) with \(\sigma = {{\sigma }_{{ - 1,p}}},\) which describes the conditional fatigue limit for the fatigue curve with probability p, may be written in the following form, taking account of Eq. (4)

$$\begin{gathered} \sigma _{{ - 1,p}}^{m} = \frac{{{{N}_{0}}}}{N}\sigma _{{ - 1}}^{m} + \frac{C}{N} \\ = \frac{{{{N}_{0}}}}{N}\sigma _{{ - 1}}^{m} + \frac{1}{N}{{\left( { - \frac{1}{k}\ln \left( {1 - p} \right)} \right)}^{{\frac{1}{\alpha }}}}. \\ \end{gathered} $$

On that basis, we obtain the integral probability distribution for the conditional fatigue limits in the form

$$\begin{gathered} p \equiv F\left( {{{\sigma }_{{ - 1,N}}}} \right) \\ = 1 - \exp \left[ { - k{{N}^{\alpha }}{{{\left( {\sigma _{{ - 1,N}}^{m} - \frac{{{{N}_{0}}}}{N}\sigma _{{ - 1}}^{m}} \right)}}^{\alpha }}} \right]. \\ \end{gathered} $$
((13))

We now obtain the Weibull probability distribution with the lowest guaranteed values of the fatigue limit in the form

$$\min \left( {{{\sigma }_{{ - 1,N}}}} \right) = {{\sigma }_{{ - 1}}}{{\left( {\frac{{{{N}_{0}}}}{N}} \right)}^{{\frac{1}{m}}}}.$$

The distribution of the fatigue limit from Eq. (13) is obtained when \(N = {{N}_{0}}.\) The fatigue distribution density for \({{\sigma }_{{ - 1,N}}}\) is shown in Fig. 7b when \(N = {{N}_{0}},{{N}_{1}},{{N}_{2}}.\)

The fatigue characteristics here derived correspond to metal samples. For transition to the actual structural elements, taking account of the scale factor, the surface quality, and the effective stress concentration, we use empirical formulas based on experimental data, as a rule.

We now consider the possibility of taking the number n of identical structural elements or identical stress concentrators into account. This is known as the WFD (widespread fatigue damage) problem.

The probability distribution function for the fatigue limit of a sample with a single stress concentrator (for example, a hole) is denoted by \(F\left( {{{\sigma }_{{ - 1}}},1} \right).\) Then the probability that the fatigue limit for a structure with n identical stress concentrators (or n identical elements) will be larger than some value \({{\sigma }_{{ - 1}}}\) will depend on how the failure of a single element affects the stability of the whole structure.

If the failure of any single element leads to failure of the whole structure, the corresponding integral probability distribution function takes the form

$$F\left( {{{\sigma }_{{ - 1}}},n} \right) = 1 - {{\left( {1 - F\left( {{{\sigma }_{{ - 1}}},1} \right)} \right)}^{n}}.$$

If failure of the whole structure is only observed after the failure of all the elements, the corresponding integral probability distribution function takes the form

$$F\left( {{{\sigma }_{{ - 1}}},n} \right) = F{{\left( {{{\sigma }_{{ - 1}}},1} \right)}^{n}}.$$

If failure of the whole structure is observed after the failure of m or more elements (out of the n elements present), the corresponding integral probability distribution function takes the form

$$\begin{gathered} F\left( {{{\sigma }_{{ - 1}}},n,m} \right) \\ = \sum\limits_{k = m}^n {C_{n}^{k}F{{{\left( {{{\sigma }_{{ - 1}}},1} \right)}}^{k}}{{{\left[ {1 - F\left( {{{\sigma }_{{ - 1}}},1} \right)} \right]}}^{{n - k}}}} , \\ \end{gathered} $$

where \(C_{n}^{k} = \frac{{n!}}{{k!\left( {n - k} \right)!}}.\)

In the first case, taking account of Eq. (13), the corresponding integral probability distribution function takes the form

$$\begin{gathered} F\left( {{{\sigma }_{{ - 1}}},n} \right) = 1 - {{\left( {1 - F\left( {{{\sigma }_{{ - 1}}},1} \right)} \right)}^{n}} \\ = 1 - \exp \left[ { - nk{{N}^{\alpha }}{{{\left( {\sigma _{{ - 1,N}}^{m} - \frac{{{{N}_{0}}}}{N}\sigma _{{ - 1}}^{m}} \right)}}^{\alpha }}} \right]. \\ \end{gathered} $$

In terms of statistical variables (the mean and dispersion), the fatigue limit of a real structure is less than that of a single element. The statistical information obtained by the methods here outlined regarding the fatigue strength of metals may effectively be used to improve the precision in predicting the life of machine tools and structural elements at the design stage.