1 INTRODUCTION

In biopolymers, various processes in biological systems often result in or are accompanied by a helix-coil transition. Despite the successes achieved, the problem of the helix-coil transition is still one of the most popular problems in structural biology, and at present interest in the problem is unabated [1–5]. In this publication, we base ourselves on the microscopic theory of the helix-coil transition [6–11]. This became possible thanks to the approaches and methods of modern theoretical physics, which make it possible to use in the statistical physics of polymers a large number of theoretical models that describe the subject of study more adequately than is accepted today and do not require the introduction of an additional phenomenological parameter to take into account the cooperativity of the system. The theory of the helix-coil transition in polypeptides was developed based on the Potts-like model [12–18]. It has also been shown that neglecting large-scale loops, the characteristic equation for the DNA model is the same as that for the Generalized Polypeptide Chain Model (GMPC) [15]. The difference from the polypeptide model is that the number of repeated units fixed to a single hydrogen bond enters the GMPC as a parameter. As a result the description of Helixl-coil transition in polypeptides, as well as in polynucleotides, and also for the study of the influence of factors of different natures can be done by the same model GMPC with different parameters. Taking into account that further research should be carried out based on the Generalised Model of Polypeptide Chain, let us bring its fundamentals.

2 GMPC MODEL

Suppose one has a biopolymer containing N repeating units. It is assumed that each repeating unit can be in Q discrete states corresponding to different discrete values of conformations (the rotational isomer approximation), the energies of these states are assumed to be the same and do not depend on the states of neighboring units. Let us describe the state of the i-th unit using the spin variable γi, so γi = 1, …Q. A hydrogen bond, resulting in the formation of a helical structure, is formed when the Δ adjacent repeating units are in the same defined conformation. Let this be called the number one conformation. The Hamiltonian of such GMPC model has the form

$$ - \beta H = J\sum\limits_{i = 1}^N {\prod\limits_{k = \Delta - 1}^0 {\delta ({{\gamma }_{{i - k}}},1) = J\sum\limits_{i = 1}^N {\delta _{i}^{{(\Delta )}}} } } ,$$
(1)

where \(\delta _{i}^{{(\Delta )}} = \prod\nolimits_{k = \Delta - 1}^0 {\delta ({{\gamma }_{{i - k}}},1)} \) is the product of Kronecker symbols, which provides energy release J only in the case when ∆ consecutively adjacent repeating units are in a helical conformation, designated by us as number 1. The transfer matrix GMPC (\({{\Delta }} \times {{\Delta }}\)) can be constructed for specific values of ∆ and Q based on the Hamiltonian (1). It has the following properties [15–21]:

— the element (1, 1) is equal to \(W = {{e}^{J}}\);

— all elements of the last line are equal to 1;

— the elements of the first upper pseudo-diagonal are equal to 1;

— elements (∆ − 1, ∆) and (∆, ∆) are equal to Q−1;

— all other elements are zero.

Generalizing to the case of arbitrary finite Δ and Q, we obtain the transfer matrix of the model

$$G = \left( {\begin{array}{*{20}{c}} {{{e}^{J}}}&1&0&{...}&0&0&0 \\ 0&0&1&{...}&0&0&0 \\ {...}&{...}&{...}&{...}&{...}&{...}&{...} \\ 0&0&0&{...}&0&1&0 \\ 0&0&0&{...}&0&0&{Q - 1} \\ 1&1&1&{...}&1&1&{Q - 1} \end{array}} \right).$$
(2)

For the homopolymer of sufficiently large length, the partition function and the characteristic equation for the transfer matrix of the model have the form:

$$Z = Tr{{G}^{N}},$$
(3)
$${{\lambda }^{{(\Delta - 1)}}}(\lambda - {{e}^{J}})(\lambda - Q) = ({{e}^{J}} - 1)(Q - 1).$$
(4)

As mentioned above [5]: J is the energy of the hydrogen bond, reduced to temperature; Q is the number of conformations of repeating units, the conformation number 1 corresponds to the helical state; ∆ is the number of repeating units fixed by one hydrogen bond; W = eJ is the temperature parameter that determines the energy properties of repeating units. The latter parameters define various properties of the system. This Hamiltonian corresponds to the transfer matrix (2) and the secular equation W = eJ (4).

For the basic model defined above, the temperature parameter W has the form \(W = {{e}^{{ - {U \mathord{\left/ {\vphantom {U {\left( {KT} \right)}}} \right. \kern-0em} {\left( {KT} \right)}}}}}\), where U is the hydrogen bond energy, and the entropy parameter Q is a constant. However, when the interaction with the solvent and lianas is taken into account, W becomes a complex function of temperature, and Q also becomes temperature-dependent [11].

3 FREE ENERGY OF A BIMODAL HETEROPOLYMER

Consider the bimodal heteropolymer consisting of repeating units of two classes “A” and “B”. In this case, the GMPC Hamiltonian will have the form

$$ - \beta H = \sum\limits_{i = 1}^N {{{J}_{i}}\delta _{i}^{\Delta }} ,$$
(5)

where \({{J}_{i}} = \left\{ {\begin{array}{*{20}{c}} {{{J}_{A}}} \\ {{{J}_{B}}} \end{array}} \right.\), and \({{Q}_{i}} = \left\{ {\begin{array}{*{20}{c}} {{{Q}_{A}}} \\ {{{Q}_{B}}} \end{array}} \right.\).

Because we will investigate the dependence of the free energy on N, the partition function of such a system will have the form [18], although, for large N, one can use the expression (3)

$$Z = J{\text{*}} \times \prod\limits_{i = 1}^N {{{G}_{i}}} \times J,$$
(6)

where Gi is the transfer matrix GMPC (2) corresponding to the given model, \(J^* = \left( {\begin{array}{*{20}{c}} 0&0&{...}&1 \end{array}} \right)\), ∆ is the component row vector, and \(J = {{\left( {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 0&0 \end{array}}&{...}&0&1 \end{array}} \right)}^{{\text{T}}}}\) is the column vector.

Because the product of matrices is not commutative, then, generally speaking, the partition function depends on the sequence of matrices, which corresponds to the primary sequence of repeating units. However, it was shown earlier that for a random sequence at sufficiently large N the value \({{\ln Z} \mathord{\left/ {\vphantom {{\ln Z} N}} \right. \kern-0em} N}\) tends to a finite limit [22], as well as the reduced free energy, then we need to determine the order of magnitude of N when the system can be considered as a thermodynamic with a given degree of accuracy.

4 HELICITY DEGREE

From the definition of the degree of helicity θ as the average fraction of repeating units in a helix state

$${{\theta }_{N}} = {{{{N}_{h}}} \mathord{\left/ {\vphantom {{{{N}_{h}}} N}} \right. \kern-0em} N},$$
(7)

where Nh is the number of repeating units in a Helixl state. For bimodal case, we suppose \({{J}_{A}} = {{J}_{0}} + \Delta J\), \({{J}_{B}} = {{J}_{0}} - \Delta J\), \({{J}_{0}} = {{({{J}_{A}} + {{J}_{B}})} \mathord{\left/ {\vphantom {{({{J}_{A}} + {{J}_{B}})} 2}} \right. \kern-0em} 2}\), \(\Delta J = {{({{J}_{A}} - {{J}_{B}})} \mathord{\left/ {\vphantom {{({{J}_{A}} - {{J}_{B}})} 2}} \right. \kern-0em} 2}\). Then the magnitude of the statistical sum will be determined by the following expression:

$$Z = \sum\limits_{\{ {{\gamma }_{i}}\} } {{{e}^{{\sum {{{J}_{i}}\delta _{i}^{\Delta }} }}}} ,$$
(8)

\({{J}_{i}} = {{J}_{0}} + \Delta J\varepsilon \) where ε takes the values ±1. Hence, from (6), \({{N}_{h}} = \frac{1}{Z}\sum\nolimits_{\{ {{\gamma }_{i}}\} } {\sum\nolimits_{i = 1}^N {\delta _{i}^{\Delta }} } {{e}^{{\sum\nolimits_i {{{J}_{i}}\delta _{i}^{\Delta }} }}} = \frac{1}{Z}\frac{{\partial Z}}{{\partial {{J}_{0}}}}\). The degree of helicity will have the form:

$${{\theta }_{N}} = \frac{1}{{NZ}}\tilde {J}(G_{1}^{'}{{G}_{2}}{{G}_{3}}...{{G}_{N}} + {{G}_{1}}G_{2}^{'}{{G}_{3}}...{{G}_{N}} + ... + {{G}_{1}}{{G}_{2}}G_{3}^{'}{{G}_{4}}...{{G}_{N}} + ... + {{G}_{1}}{{G}_{2}}{{G}_{3}}{{G}_{4}}...G_{N}^{'})J,$$
(9)

where \(G_{i}^{'}\) is the matrix Gi, where all elements except the first are zero. Following [9, 10], the expression in parenthesis can be written as \(\left( {\begin{array}{*{20}{c}} E&O \end{array}} \right)\prod\nolimits_{i = 1} {{{M}_{i}}} \left( {\begin{array}{*{20}{c}} E \\ O \end{array}} \right)\), where Mi is a supermatrix of the form \(\left( {\begin{array}{*{20}{c}} {{{G}_{i}}}&{G_{i}^{'}} \\ O&{{{G}_{i}}} \end{array}} \right)\), E is the identity matrix of size Δ, and O is the null matrix of the same size. Finally, we obtain

$${{\theta }_{N}} = \frac{1}{{N{{Z}_{N}}}}J{\text{*}}\left( {\begin{array}{*{20}{c}} E&O \end{array}} \right)\prod\limits_{i = 1}^N {{{M}_{i}}} \left( {\begin{array}{*{20}{c}} E \\ O \end{array}} \right)J = \frac{1}{N}\frac{{J_{\theta }^{*}\prod\limits_{i = 1}^N {{{M}_{i}}} {{J}_{\theta }}}}{{J{\text{*}}\prod\limits_{i = 1}^N {{{G}_{i}}} {{J}_{{}}}}},$$
(10)

Here \(J_{\theta }^{*} = \left( {\begin{array}{*{20}{c}} 0&0&{...}&0&0&1&{...}&1 \end{array}} \right)\), \(J = {{\left( {\begin{array}{*{20}{c}} 0&0&{...}&{\begin{array}{*{20}{c}} 1&1 \end{array}} \end{array}} \right)}^{{\text{T}}}}\) vector row and vector column with size 2Δ.

5 THE AVERAGE PORTION OF JUNCTIONS BETWEEN HELIX AND COILED SECTIONS

The average portion of junctions ηN is defined as the fraction of pairs of the helical state and any other state

$$\left\langle {{{\eta }_{N}}} \right\rangle = p({{\gamma }_{i}} = 1,{{\gamma }_{{i + 1}}} = k),\quad k \ne 1.$$
(11)

Hence, \({{\eta }_{N}} = \theta - p(hh).\) Similarly to (8), we obtain

$$p(hh) = \frac{1}{{NZ}}J{\text{*}}(G_{1}^{'}G_{2}^{'}{{G}_{3}}{{G}_{4}}...{{G}_{N}} + {{G}_{1}}G_{2}^{'}G_{3}^{'}...{{G}_{N}} + ... + {{G}_{1}}G_{2}^{'}...G_{{N - 1}}^{'}G_{N}^{'})J.$$
(12)

Similarly to how the expression for θ was obtained, we introduce the supermatrix Li

$${{L}_{i}} = \left( {\begin{array}{*{20}{c}} {{{G}_{i}}}&{G_{i}^{'}}&O \\ O&O&{G_{i}^{'}} \\ O&O&{{{G}_{i}}} \end{array}} \right).$$
(13)

The expression in parentheses in (12) is obtained in terms of Li as

$$\left( {\begin{array}{*{20}{c}} E&O&O \end{array}} \right)\prod\limits_{i = 1}^{N - 1} {{{L}_{i}}} {{\left( {\begin{array}{*{20}{c}} O&O&E \end{array}} \right)}^{{\text{T}}}}.$$
(14)

from which \({{{{\eta }}}_{N}} = \frac{1}{{ZN}}J_{L}^{*}\prod\nolimits_{i = 1}^{N - 1} {{{L}_{i}}{{J}_{L}}} \), where \(J_{L}^{*}\) is the row vector of size 3Δ \(\left( {\begin{array}{*{20}{c}} 0&0&{...}&0&0&1&{...}&1 \end{array}} \right)\), and JL is the column vector of the same size \({{\left( {\begin{array}{*{20}{c}} 0&0&{...}&{\begin{array}{*{20}{c}} 1&1 \end{array}} \end{array}} \right)}^{{\text{T}}}}\). Thus, the average part of joints

$${{\eta }_{N}} = \frac{1}{{ZN}}J_{\theta }^{*}\prod\limits_{i = 1}^N {{{M}_{i}}} {{J}_{\theta }} - \frac{1}{{ZN}}J_{\eta }^{*}\prod\limits_{i = 1}^{N - 1} {{{L}_{i}}} {{J}_{\eta }},$$
(15)

where Z is defined from (6). From here, one can go to the expression for the average length of the helix section. Because the average length of the helix region is \({{\nu }_{N}} = {{{{\theta }_{N}}} \mathord{\left/ {\vphantom {{{{\theta }_{N}}} {{{\eta }_{N}}}}} \right. \kern-0em} {{{\eta }_{N}}}}\), we obtain

$${{\nu }_{N}} = {{\left( {1 - \frac{{J_{\eta }^{*}\prod {{{L}_{i}}} {{J}_{\eta }}}}{{J_{\theta }^{*}\prod {{{M}_{i}}} {{J}_{\theta }}}}} \right)}^{{ - 1}}}.$$
(16)

6 RESULTS AND DISCUSSION

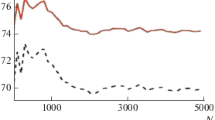
Let us enter the value x as the probability of repeating units “A” in a random sequence, and 1–x –“B”, respectively. So, one can generate a random sequence of repeating units “A” and “B” of a given length N. Accordingly, \({{C}_{A}} = {{{{N}_{A}}} \mathord{\left/ {\vphantom {{{{N}_{A}}} N}} \right. \kern-0em} N}\), \({{C}_{B}} = {{{{N}_{B}}} \mathord{\left/ {\vphantom {{{{N}_{B}}} N}} \right. \kern-0em} N}\), where NA and NB are the numbers of repeating units of a given type in a given sequence. Figure 1 shows the dependence of the quantity \({{\ln Z} \mathord{\left/ {\vphantom {{\ln Z} N}} \right. \kern-0em} N}\) on N. It can be seen that for a sufficiently long chain N > 3000, the reduced free energy tends to a finite limit. For short chains, the reduced free energy strongly depends on the implementation of the sequence (primary structure). Figure 1 shows the behavior of the reduced free energy for different x and two temperatures for the same realization. It should be noted that for all graphs the temperature is indicated in the given values \(t = J_{A}^{{ - 1}}\), this method of introducing the temperature makes it possible to qualitatively compare the graphs of the dependence of the averaged parameters.

Fig. 1.
figure 1

Dependence of the reduced free energy on the number of repeating units for different x and temperatures. x1 = 0.4, x2 = 0.5, Δ = 4, t1 = 0.213, t2 = 0.219, UA = 1, UA = 0.8, QA = 71, QB = 51.

Full size image

With a good degree of accuracy, the number N* ≈ 3000 is confirmed for a wide set of realizations, as evidenced by Fig. 2. For sufficiently large lengths, the free energy does not depend on the realization. Thus, in terms of the reduced free energy, it can be argued at N > 3000 that the heteropolymer behaves like a homopolymer.

Fig. 2.
figure 2

Dependence of the reduced free energy on the number of repeating units for different sequences x1 = 0.4, t = 0.219, UA = 1, UA = 0.8, QA = 71, QB = 51.

Full size image

Figure 2 shows the behavior of the reduced free energy at the same value of x and reduced temperature. However, it can be seen that the situation changes upon passing to the degree of helicity.

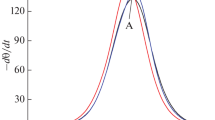
Figure 3 shows denaturation curves for different N. It can be seen that the position of the curves depends on N, however, even at N = 5000, when the reduced free energy no longer depends on the primary structure (realization), the denaturation curve depends.

Fig. 3.
figure 3

Temperature dependence of 1 – θ for sequences with different N. x1 = 0.4, Δ = 4, UA = 1, UA = 0.8, QA = 71, QB = 51. (The temperature is reduced to the value \(t = J_{A}^{{ - 1}}\).)

Full size image

Figure 4 shows that the general properties of denaturation curves do not depend on the realization, but the details of the profile of the curves vary with the realization.

Fig. 4.
figure 4

Temperature dependence of 1 – θ for different implementations at x1 = 0.4, Δ = 4, UA = 1, UA = 0.8, QA = 71, QB = 51, N = 5000. (The temperature is reduced to the value \(t = J_{A}^{{ - 1}}\).)

Full size image

Figure 5 shows the curves of denaturation at different x. The result of our computations is \({{t}_{m}}(x) = x{{t}_{{mA}}} + (1 - x){{t}_{{mB}}}\), where tm is the transition point.

Fig. 5.
figure 5

Temperature dependence of 1 – θ for sequences with different x in the thermodynamic limit Δ = 4, UA = 1, UA = 0.8, QA = 71, QB = 51, N = 5000. (The temperature is reduced to the value \(t = J_{{\text{A}}}^{{ - 1}}\).)

Full size image

Let us consider the details of the melting of the Helixl structure. When melting, the macromolecule breaks down into Helixl fragments separated by coil-like sections. The proportion of such fragments is determined by the proportion of joints \(\left( {h,\bar {h}} \right)\), that is, in the GMPC language \(p\left( {{{{{\gamma }}}_{i}} = 1,{{{{\gamma }}}_{{i + 1}}} = k} \right),~k \ne 1\), which is expressed by formula (15).

Figure 6 shows the dependence of the fraction of joints η on the degree of helicity at different x, including the homopolymer ‘A’ and ‘B’. This dependence was chosen to compare the behavior at different x because η(t) for different x will be in different temperature regions. So, we chose the dependence η(θ).

Fig. 6.
figure 6

Dependence η(θ) for different x, Δ = 4, UA = 1, UA = 0.8, QA = 71, QB = 51, N = 5000.

Full size image

As it was clear and as seen in Fig. 6, the curves η(θ) are the curves with the maximum in the region of θ = 0.5. The curve at x = 0 (less stable homopolymer polyB) is located above the curve at x = 1 (the more stable polyA). However, the heteropolymer is located above both homopolymers. This is clear because the heteropolymers have more joint variants. It can be seen from the figure that a higher maximum is obtained at x = 0.5, that is, at the highest heterogeneity. Nevertheless, the case with x = 0.5 also exhibits a large scatter for different realizations of Fig. 7. The scatter at x = 0.4 is lesser (Fig. 8), and at x = 0.1 and x = 0.9, the scatter is no longer visible and is not shown in the figures. As for the maximum value, it varies from 2.2 × 10–3 (x = 0.5) to 6 × 10–4 (x = 1), which corresponds to 11 to 3 joints.

Fig. 7.
figure 7

Dependence η(θ) for three realizations η(θ), x = 0.5, Δ = 4, UA = 1, UA = 0.8, QA = 71, QB = 51, N = 5000.

Full size image
Fig. 8.
figure 8

Dependence η(θ) for four realizations, x = 0.5, Δ = 4, UA = 1, UA = 0.8, QA = 71, QB = 51, N = 5000.

Full size image

Thus, even with such a superficial consideration, the picture of the transition turns out to be quite paradoxical. With a length of 5000 repeating units, we observe 11 joints for the heteropolymer and on the order of single joints for homopolymers. So, analyzing the behavior of the fraction of joints, we conclude that the length of 5000 repeating units, although it is enough for the free energy of the heteropolymer (and even more so for homopolymer) would go to saturation, and division into sections does not lead to such results. In the recently published work of A. Badasyan [25], using the Zimm-Bragg model as an example, it was shown that even in the homopolymer case, there is an intermediate in length regime associated with the correlation length. In this regard, our next studies will be related to the study of the correlations of conformations in heteropolymers.