Helix-Coil Transition in Heterogeneous Biopolymers: Influence of Fixing Bond Scale

Abstract

Within the framework of the GMPC model, a two-component heteropolymer is considered. The Differential Melting Curves (DMC) of this model are computed with the number of repeating units of 5000 when the reduced free energy of a repeating unit reaches its saturation. The DMC curves were obtained for different sequences. Models with different degrees of closure Δ (from 2 to 12) are considered. It is shown that the DMC depends on the sequence and has a fine structure at intermediate values Δ (4–7).

1 INTRODUCTION

One of the most important tasks of the science of biopolymers is to elucidate the physical principles of the structure and biological activity of macromolecules of proteins and nucleic acids. It has long been established that the biological activity of these biopolymers very strongly depends on their spatial structure. In this regard, an important task is to identify significant factors and patterns that affect the conformation and the course of conformational rearrangements. Various processes in biological systems often result or are accompanied by a helix-coil transition in biopolymers. This phenomenon has been studied and discussed from the 1960s to the present [1–5]. Despite the progress made in the theoretical study of this phenomenon, some issues related to heteropolymers remain open. That is why the further theoretical study of conformational transitions in one-dimensional cooperative systems based on simple models that enable an adequate interpretation of the input parameters is of interest for biophysicists. Such a model is the Generalized Polypeptide Chain Model (GMPC) used to describe the helix-coil transition in both polypeptides and DNA. It has been successfully used to describe the transition in homopolymers [5–11]. Recently, we have used this model for heteropolymers. However, several types of interactions playing an important role in all processes associated with the transition are not fully taken into account within the framework of this model. From this point of view, the relevance of this work is determined by the development of approaches with the introduction of the GMPC Hamiltonian with different multiparticity.

2 GMPC MODEL

In our previous works devoted to the helix-coil transition in macromolecules, the validity of this model was described within the framework of the GMPC in detail [6, 7]. Here, we only present the Hamiltonian and the transfer matrix of the model.

The Hamiltonian of the homopolymer GMPC (basic model) has the form

$$ - \beta H = J\sum\limits_{i = 1}^N {\delta _{i}^{\Delta }} .$$

(1)

In frames of GMPC, the Hamiltonian of a heteropolymer system is as follows:

$$ - \beta H = \sum\limits_{i = 1}^N {{{J}_{i}}\prod\limits_{k = \Delta - 1}^0 {\delta ({{\gamma }_{{i - k}}},1) = \sum\limits_{i = 1}^N {{{J}_{i}}\delta _{i}^{{(\Delta )}}} } } .$$

(2)

Here, $\delta _{i}^{{(\Delta )}}$ is the product of the Kronecker symbols $\Delta$ for the i-th repeating unit, depending on the previous repeating units, the reduced energy ${{J}_{i}}$ depends on the number of the repeating unit. The transfer matrix of the heteropolymer model has the form of a matrix $\Delta \times \Delta$, where the element 11 is equal to ${{W}_{i}}$, the first upper pseudo-diagonal, and the last row consist of units, and the elements $\Delta - 1,\;\Delta$ and $\Delta \Delta$, and equal to ${{Q}_{i}} - 1$.

$$\mathop {{{G}_{i}}}\limits^ \wedge = \left( {\begin{array}{*{20}{c}} {{{W}_{i}}}&1&0& \cdots &0&0&0 \\ 0&0&1& \cdots &0&0&0 \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0&0&0& \cdots &0&1&0 \\ 0&0&0& \cdots &0&0&{{{Q}_{i}} - 1} \\ 1&1&1& \cdots &1&1&{{{Q}_{i}} - 1} \end{array}} \right),$$

(3)

where ${{W}_{i}} = \exp ({{J}_{i}})$ and ${{Q}_{i}}$ is the number of conformations, and in our case (of bimodal heteropolymer) can take the values ${{J}_{{\text{A}}}}$ and ${{J}_{{\text{B}}}}$.

In the framework of the transfer-matrix representation, the partition function has the form

$$Z = \operatorname{Tr} \prod\limits_{k = 1}^N {\mathop {{{G}_{k}}}\limits^ \wedge } ,$$

(4)

For the degree of helicity, we obtain the following expression

$${{\theta }_{N}} = \frac{1}{{NZ}}\sum\limits_i {Tr} \prod\limits_{k = 1}^{i - 1} {\mathop {{{G}_{k}}}\limits^ \wedge \mathop {G_{i}^{'}}\limits^ \wedge } \prod\limits_{k = i + 1}^N {\mathop {{{G}_{k}}}\limits^ \wedge } ,$$

(5)

or

$${{\theta }_{N}} = \frac{{\operatorname{Tr} \left[ {\mathop E\limits^ \wedge ,\mathop 0\limits^ \wedge } \right]\prod\limits_{i = 1}^N {\mathop {{{M}_{i}}}\limits^ \wedge \left| \begin{gathered} \mathop 0\limits^ \wedge \hfill \\ \mathop E\limits^ \wedge \hfill \\ \end{gathered} \right|} }}{{N\operatorname{Tr} \left[ {\mathop E\limits^ \wedge ,\mathop 0\limits^ \wedge } \right]\prod\limits_{i = 1}^N {\mathop {{{M}_{i}}}\limits^ \wedge \left| \begin{gathered} \mathop E\limits^ \wedge \hfill \\ \mathop 0\limits^ \wedge \hfill \\ \end{gathered} \right|} }}.$$

(6)

$\hat {M}$ is the supermatrix

$$\mathop M\limits^ \wedge = \left( {\begin{array}{*{20}{c}} {\mathop {{{G}_{i}}}\limits^ \wedge }&{\mathop {{{G}^{'}}_{i}}\limits^ \wedge } \\ {\mathop 0\limits^ \wedge }&{\mathop {{{G}_{i}}}\limits^ \wedge } \end{array}} \right),$$

(7)

and $\hat {G}{\kern 1pt} '$ is $\hat {G}$, where there is only one non-null element $\hat {G}_{{i,11}}^{'} = \exp ({{J}_{i}})$, $\hat {E}$ and $\hat {0}$ identity and zero matrices, respectively.

Differential Melting Curve (DMC) $\theta {\kern 1pt} ' = {{\partial \theta } \mathord{\left/ {\vphantom {{\partial \theta } {\partial t}}} \right. \kern-0em} {\partial t}}$ is obtained by numerically differentiating the degree of helicity relative to temperature.

3 RESULTS AND DISCUSSION

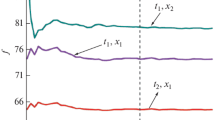
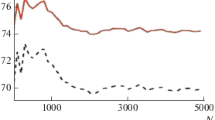
Heteropolymers with different primary structures have been investigated to study random heteropolymers; the sequences were generated as follows: randomly, a sequence was generated from “–1” and “1”, where “1” appeared in sequence “x”, and “–1”: with probability “1 – x”. Thus, a given primary structure for a binary heteropolymer is determined by a sequence of plus and minus units. Earlier [11], we showed that the reduced free energy tends to the limit at N > 3000. For our computations, we chose the sequence length N = 5000. It has long been known that the reduced free energy is a self-averaging quantity [12], which cannot be said about the degree of helicity. We consider the DMC of three different primary sequences for a binary heteropolymer for different values $\Delta$ from 2 to 12. The choice of such a wide scatter $\Delta$ is determined by the fact that $\Delta$ = 2 corresponds to the Zimm-Bragg model, $\Delta$ = 3 is determined by the closure of hydrogen bonds in polypeptides, $\Delta$from 6 to 9 corresponds to the GMPC model of DNA [1, 2]. The transfer matrix is given by expression (3), and the degree of helicity (6). Initially, we investigated the role of the primary structure at various values $\Delta$. The DMCs of three different sequences were considered for different $\Delta$. Figures 1–3 show the graphs of dependences $\theta {\kern 1pt} '(t)$ on the reduced temperature t. The value of the reduced temperature is determined by the expression ${{J}_{A}} = {{{{U}_{A}}} \mathord{\left/ {\vphantom {{{{U}_{A}}} T}} \right. \kern-0em} T} = {1 \mathord{\left/ {\vphantom {1 t}} \right. \kern-0em} t}$, then ${{J}_{B}} = {\alpha \mathord{\left/ {\vphantom {\alpha t}} \right. \kern-0em} t}$ where $\alpha = {{{{U}_{B}}} \mathord{\left/ {\vphantom {{{{U}_{B}}} {{{U}_{A}}}}} \right. \kern-0em} {{{U}_{A}}}}$. The values ${{Q}_{A}}$, ${{Q}_{B}}$were chosen so that the results corresponded to the previous given in [11]. It follows from the computations that for each sequence DMC at small $\Delta$ (2,3) (Fig. 1) are quite smooth and at large widths differ slightly from each other for different primary sequences. At large $\Delta$ (Figs. 2,3), a clear dependence of DMC on the sequence is seen, which indicates that the degree of helicity is not a self-averaging quantity, in contrast to the reduced free energy. The interval of change narrows, and the maxima increase. It should be noted that for better clarity the plots are shown on different scales both in temperature and in the derivative of the degree of helicity. The narrowing of the curves and the growth of the maxima are related to the fact that the total area under the DMC curve is equal to 1 ($\int_{{{t}_{1}}}^{{{t}_{2}}} {\left( {{{\partial \theta } \mathord{\left/ {\vphantom {{\partial \theta } {\partial t}}} \right. \kern-0em} {\partial t}}} \right)} dt = {{\theta }_{2}} - {{\theta }_{1}} = 1$). In other words, increasing the scale of bond closure results in a sharper denaturation curve. As regards the dependence of the curves on the primary sequence, for small $\Delta$ (2.3) the curves weakly depend on the sequence because of the small dependence of the conformations. For small $\Delta$ (2,3), we do not observe the fine structure of DMC (Fig. 1). At intermediate $\Delta$ (5.7), a rich fine structure takes place (Fig. 2), part of which disappears at large values $\Delta$ (Fig. 3). This behavior of DMC is explained as follows: at the transition, melting occurs in blocks of the order of the correlation length of the mutual dependence of conformations, which is greater than $\Delta$, and increases with growth $\Delta$ (for a homopolymer $\sim {{Q}^{{{{(\Delta - 1)} \mathord{\left/ {\vphantom {{(\Delta - 1)} 2}} \right. \kern-0em} 2}}}}$). For small $\Delta$, the number of combinations of different types of repeating units is also small. At the same time, the curves themselves are quite wide and some of them overlap each other (Fig. 1). At large $\Delta$ (Fig. 3), the number of combinations increases and some self-averaging of various combinations takes place, and some peaks merge. That is, the richest fine structure is observed at intermediate $\Delta$(Fig. 2); as for the dependence on the sequence, it is observed for all studied $\Delta$. For small $\Delta$, because of the width of the interval, the curves are superimposed on each other. For large $\Delta$, the dependencies on the sequence are more noticeable. This again indicates that the degree of helicity (as well as DMC) is not a self-averaging quantity, like the reduced free energy, which, as our calculations show, saturates at all studied by us $\Delta$ at N ~ 3000, so in the language of free energy at N = 5000 we are at the thermodynamic limit. Naturally, our research is qualitative. To develop our results, we need the same results but with different parameters ${{J}_{A}},{{J}_{B}},{{Q}_{A}},{{Q}_{B}}$. Further research is needed for different “x”, and also taking into account the influence of the solvent, which will be the topic of our further research.

Fig. 1.

DMC curves for different sequences of repeating units (A, B, C) N = 5000, Δ = 3.

Fig. 2.

DMC curves for different sequences of repeating units (A, B, C) N = 5000, Δ = 5.

Fig. 3.

DMC curves for different sequences of repeating units (A, B, C) N = 5000, Δ = 10.