Generalized Finite-Time Stability and Stabilization for Fractional-Order Memristive Neural Networks

Abstract

This paper is concerned with the generalized finite-time stability, boundedness and stabilization for fractional-order memristive neural networks (FMNNs) with the fractional-order 0 < α < 1. Under the fractional-order Filippov differential inclusion frame, FMNNs are modelled as a fractional-order differential equation with discontinuous right-hand. Based on the topological degree property, the existence of equilibrium point of FMNNs is proved. By means of the generalized Gronwall inequality, the Laplace transform and the Lyapunov functional candidate, some conditions to guarantee the generalized finite-time stability and boundedness for FMNNs are derived in terms of linear matrix inequalities (LMIs). In addition, by using appropriate feedback controller, the generalized finite-time stabilization condition is also addressed in forms of LMIs. Finally, two examples are given to demonstrate the validity of the theoretical results.

1 INTRODUCTION

In recent years, neural networks (NNs) have been applied in different fields widely, such as secure quantum communication, optimization, signal and image processing and automatic control, etc. [1–4]. Many results with respect to dynamics of integer-order NNs have been done (see [5–8], and references therein).

As we all know, compared with integer-order calculus, fractional-order calculus has better advantage for the description of memory and hereditary properties of various processes. It has found that, fractional calculus can be applied to precisely describe physical systems, biological system, colored noise, finance and so on [9–11]. Taking the above facts into account, it is significant for scholars to analyze the dynamical behavior of NNs by applying the fractional-order calculus. In [12], Arena et al., firstly proposed a fractional-order cellular neural network model. In [13], the authors presented a fractional-order three-network, which put forward limit cycles and stable orbits for different parameter values. It is worth noting that some excellent results on dynamical behaviors, such as the stability, stabilization and synchronization, have been developed for fractional-order neural networks (see [14–20]).

Memristor, as the fourth basic passive circuit element along with resistor, inductor and capacitor (see Fig. 1) was firstly proposed by Chua [21], and is realized by the research team from the Hewlett-Packard Lab in 2008 [22]. As a two-terminal passive device, the value of Memristor which is called as memristance, relays on magnitude and polarity of the voltage, and shares many properties of resistor and the same unit of measurement (Ohm). According to the characteristics of current–voltage (see Fig. 2), it is easy to find that memristor exhibits the feature of pinched hysteresis and is same as the neurons in the human brain. Therefore, the memristor possesses a great potential in application.

Fig. 1.

The relation between four fundamental elements.

Fig. 2.

Theoretical i–u characteristics of a memristor with applied voltage.

Recently, some researchers begin to construct the memristive neural dynamic networks through replacing the resistor with the memristor [23, 24]. The hybrid complementary metal-oxide-semiconductor is an important component of the memristor-based neural networks, so that memristive neural networks could have a much wider application in bioinspired engineering [25–28].

Meanwhile, more and more scholars have paid attention to the dynamic behavior of the memristor-based neural networks and achieved many significative results (see [29–40]). In [29], Bao and Zeng discussed global Mittag–Leffler multistability for periodic delayed recurrent neural network with memristors, and the global exponential stability for switched memristive neural networks with time-varying delays was considered in [30]. In [31], authors studied the global exponential stability of memristive neural networks with impulse time window and time-varying delays, some stability conditions were proposed. Zhang and Shen proposed some new algebraic criteria for synchronization stability of chaotic memristive neural networks with time-varying delays in [32]. In [33], weak, modified and function projective synchronization of chaotic memristive neural networks with time delays was given by Wu and Li et al. Besides, Wu and Zhang et al. also investigated the adaptive anti-synchronization and ${{H}_{\infty }}$ anti-synchronization for memristive neural networks with mixed time delays and reaction-diffusion terms in [34]. In [35], authors derived some sufficient conditions and explored the global anti-synchronization of a class of chaotic memristive neural networks with time-varying delays. For the memristive neural networks with mixed time-varying delays, Wu and Han et al. considered its exponential passivity in [36]. In [37] and [38], Chen et al. discussed the global Mittag–Leffler stability and synchronization of memristor-based fractional-order neural networks with or without delays. In [39], authors investigated the global finite-time synchronization for fractional-order memristor-based neural networks with time delays. In [40], Bao and Cao considered the global projective synchronization for fractional-order memristor-based neural networks. The reliable stabilization condition was proposed for memristor-based recurrent neural networks with time-varying delays by Mathiyalagan etc. in [41].

It should be mentioned that, in practical applications, the main attention is paid to the dynamics of systems over a finite time interval (see [16, 18–20, 39]). In [16], authors studied the global synchronization in finite time for fractional-order neural networks with discontinuous activations and time delays. Subsequently, in [18] and [19] Peng and Wu considered the global non-fragile synchronization and the global projective synchronization in finite time for fractional-order discontinuous neural networks with nonlinear growth activations based on sliding mode control strategy. In [20], the non-fragile robust finite-time stabilization and ${{H}_{\infty }}$ performance analysis was proposed for fractional-order delayed neural networks with discontinuous activations under the asynchronous switching. In [42], Song etc. discussed the global robust stability in finite time for fractional-order neural networks. And finite-time stability analysis of fractional-order time-delay systems with Gronwall’s approach was performed in [43]. It should be pointed out that, very little attention has been paid on the generalized finite-time stability and stabilization of FMNNs.

Motivated by the preceding description, our aim is to explore the issue of generalized finite-time stability, boundedness and stabilization for FMNNs. The main novelty of our contribution lies in three aspects:

(1) The existence of equilibrium point is proved by applying the topological degree theory;

(2) The conditions to guarantee the generalized finite-time stability and boundedness are given in terms of LMIs;

(3) A new feedback controller is designed;

(4) The generalized finite-time stabilization condition is presented in forms of LMIs.

The rest of this paper is organized as follows. In Section 2, some preliminaries and the model formulation are introduced. Sufficient criteria about generalized finite-time stability, boundedness, and stabilization of FMNNs are derived in Section 3. Two numerical simulations are given in Section 4. Finally conclusion is drawn in Section 5.

2 PRELIMINARIES AND MODEL DESCRIPTION

2.1 Preliminaries

In this section, we first recall some definitions and Lemmas, which will be useful to derive the main results.

Definition 2.1 [9]. The fractional integral of order ${{\alpha }}$ for a function $g\left( t \right)$ is defined as

$$\begin{array}{*{20}{r}} {{{}_{t}}I_{0}^{\alpha }g\left( t \right) = \frac{1}{{\Gamma \left( \alpha \right)}}\mathop \smallint \limits_0^t \frac{{g\left( s \right)}}{{{{{(t - s)}}^{{1 - \alpha }}}}}ds,} \end{array}$$

where $t \geqslant 0$ and ${{\alpha }} > 0$, ${{\Gamma }}\left( \cdot \right)$ is the gamma function, which is ${{\Gamma }}\left( {{\alpha }} \right) = \int_0^\infty {{{t}^{{\alpha - 1}}}} {{e}^{{ - t}}}dt$.

Definition 2.2 [9]. Caputo’s derivative with fractional-order ${{\alpha }}$ for a function $g\left( t \right) \in {{C}^{n}}\left( {\left[ {0, + \infty } \right],R} \right)$ is defined as

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {{{}_{t}}D_{0}^{\alpha }g\left( t \right) = \frac{1}{{\Gamma \left( {n - \alpha } \right)}}\mathop \smallint \limits_0^t {{g}^{{\left( n \right)}}}\left( s \right){{{(t - s)}}^{{n - \alpha - 1}}}ds,} \end{array}} \end{array}$$

where $t \geqslant 0$ and n is a positive integer such that $n - 1 < \alpha < n$. Moreover, when 0 < α < 1,

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {_{t}D_{0}^{\alpha }g\left( t \right) = \frac{1}{{\Gamma \left( {1 - \alpha } \right)}}\mathop \smallint \limits_0^t \frac{{g{\kern 1pt} '\left( s \right)}}{{{{{(t - s)}}^{\alpha }}}}ds.} \end{array}} \end{array}$$

A function frequently used in the solutions of fractional-order systems is the Mittag–Leffler function

$$\begin{array}{*{20}{r}} {{{E}_{\alpha }}\left( z \right) = \mathop \sum \limits_{i = 0}^\infty \frac{{{{z}^{i}}}}{{\Gamma \left( {i\alpha + 1} \right)}},} \end{array}$$

where ${{\alpha }} > 0$. The Mittag–Leffler function with two parameters appears most frequently and has the form as follows:

$${{E}_{{\alpha ,\beta }}}\left( z \right) = \mathop \sum \limits_{i = 0}^\infty \frac{{{{z}^{i}}}}{{\Gamma \left( {i\alpha + \beta } \right)}},$$

where ${{\;}{\alpha }} > 0,\beta > 0$, and z is complex number. Obviously, for ${{\beta }} = 1$, we have ${{E}_{\alpha }}\left( z \right) = {{E}_{{\alpha ,1}}}\left( z \right)$, ${{E}_{{0,1}}}\left( z \right) = \frac{1}{{1 - z}}$, also ${{E}_{{1,1}}}\left( z \right) = {{e}^{z}}$.

The Laplace transform $\mathfrak{L}\left\{ \cdot \right\}$ of ${{E}_{{\alpha ,\beta }}}\left\{ \cdot \right\}$ is defined by

$$\begin{array}{*{20}{r}} {\mathfrak{L}\left\{ {{{t}^{{\beta - 1}}}{{E}_{{\alpha ,\beta }}}\left( {\nu {{t}^{\alpha }}} \right)} \right\} = \frac{{{{s}^{{\alpha - \beta }}}}}{{{{s}^{\alpha }} - \nu }},\,\,\,\,t > 0,} \end{array}$$

where t and s denote the variables in the time domain and Laplace domain, respectively, ν is the real number, the real part $\operatorname{Re} \left( s \right)$ of s is $\operatorname{Re} \left( s \right) > {{\left| \nu \right|}^{{\frac{1}{\alpha }}}}$.

Consider the fractional-order differential equation with discontinuous right-hand

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {_{t}D_{0}^{\alpha }x\left( t \right) = f\left( {x\left( t \right)} \right),} \end{array}} \end{array}$$

(1)

where f(x) is a discontinuous function. Define the set-valued map of f(x) as

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {F\left( x \right) = \bigcap\limits_{\delta > 0} {\bigcap\limits_{\mu \left( N \right) = 0} {\overline {co} \left[ {f\left( {B\left( {x,\delta } \right)\backslash N} \right)} \right]} } ,} \end{array}} \end{array}$$

where $B\left( {x,\delta } \right) = \left\{ {y{\kern 1pt} :\,\left| {\left| {y - x} \right|} \right| \leqslant \delta } \right\}$ is the ball of center x and radius ${{\delta }}$, intersection is taken over all sets N of measure zero and over all ${{\delta }} > 0$, and $\mu \left( N \right)$ is Lebesgue measure of set N.

Definition 2.3 [44]. A Filippov solution x(t) of the system (1) with initial condition x(0) = x₀ is an absolutely continuous function on any compact subinterval [t₁, t₂] of [0, T], which satisfies x(0) = x₀ and the differential inclusion:

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {_{t}D_{0}^{\alpha }x\left( t \right) \in F\left( {x\left( t \right)} \right),\,\,\,\,a.a.\,\,\,t \in \left[ {0,T} \right].} \end{array}} \end{array}$$

Let $x{\text{*}} \in {{R}^{n}}$ be a constant vector, if $0 \in F\left( {x{\text{*}}} \right)$, then $x{\text{*}}$ is said to be the equilibrium point of the fractional-order system (1).

Definition 2.4. The equilibrium point $x{\text{*}}$ of the system (1) is said to be generalized finite-time stable with respect to (b₁, b₂, T, R) with positive scalars b₁, b₂, T, b₂ > b₁ and matrix $R > 0$, if

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {{{{(x\left( 0 \right) - x{\text{*}})}}^{T}}R\left( {x\left( 0 \right) - x{\text{*}}} \right) \leqslant {{b}_{1}},} \end{array}} \end{array}$$

then

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {{{{(x\left( t \right) - x{\text{*}})}}^{T}}R\left( {x\left( t \right) - x{\text{*}}} \right) < {{b}_{2}},\,\,\,\,t \in \left[ {0,T} \right].} \end{array}} \end{array}$$

Moreover, consider the fractional-order differential equation system

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {_{t}D_{0}^{\alpha }x\left( t \right) = f\left( {x\left( t \right)} \right) + Dw\left( t \right),\,\,\,\,t \in \left[ {0,T} \right],} \end{array}} \end{array}$$

where $w \in {{R}^{m}}$ is the disturbance input, and satisfies ${{w}^{T}}\left( t \right)w\left( t \right) \leqslant S$, $S \geqslant 0$ is a constant, $D \in {{R}^{{n \times m}}}$.

Definition 2.5. The equilibrium point $x{\text{*}}$ of the system (1) is said to be generalized finite-time bounded with respect to (b₁, b₂, T, R, S) with positive scalars b₁, b₂, T, b₂ > b₁ and matrix R > 0, if

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {{{{(x\left( 0 \right) - x{\text{*}})}}^{T}}R\left( {x\left( 0 \right) - x{\text{*}}} \right) \leqslant {{b}_{1}},} \end{array}} \end{array}$$

then

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {{{{(x\left( t \right) - x{\text{*}})}}^{T}}R\left( {x\left( t \right) - x{\text{*}}} \right) < {{b}_{2}},\,\,\,\,t \in \left[ {0,T} \right].} \end{array}} \end{array}$$

Lemma 2.1 [42]. Let $x\left( t \right) \in {{R}^{n}}$ be a continuous and differential function and $P$ be a positive definite matrix. For ${{\alpha }} \in \left( {0,1} \right)$, then the following inequality holds

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {_{t}D_{0}^{\alpha }\left\{ {{{x}^{T}}\left( t \right)Px\left( t \right)} \right\} \leqslant 2{{x}^{T}}\left( t \right){{P}_{t}}D_{0}^{\alpha }x\left( t \right).} \end{array}} \end{array}$$

Lemma 2.2 [43]. Consider that $x\left( t \right)$ and $a\left( t \right)$ are nonnegative and local integrable on [0, T], $T \leqslant + \infty$, $f(t)$ is a nonnegative, nondecreasing, and continuous function defined on $t \in \left[ {0,T} \right]$, $f\left( t \right) \leqslant M$(constant), ${{\alpha }} > 0$, satisfying

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {x\left( t \right) \leqslant a\left( t \right) + f\left( t \right)\mathop \smallint \limits_0^t {{{(t - \tau )}}^{{\alpha - 1}}}x\left( \tau \right)d\tau ,\,\,\,t \in \left[ {0,T} \right].} \end{array}} \end{array}$$

If $a\left( t \right)$ is a nondecreasing function on [0, T], then

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {x\left( t \right) \leqslant a\left( t \right){{E}_{\alpha }}\left( {f\left( t \right)\Gamma \left( \alpha \right){{t}^{\alpha }}} \right),\,\,\,\,t \in \left[ {0,T} \right],} \end{array}} \end{array}$$

where ${{E}_{\alpha }}$ is Mittag–Leffler function.

Lemma 2.3. Let ${{\varepsilon }} > 0$, given any $x,y \in {{R}^{n}}$, and matrix A, such taht

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {{{x}^{T}}Ay \leqslant \frac{1}{{2\varepsilon }}{{x}^{T}}A{{A}^{T}}x + \frac{\varepsilon }{2}{{y}^{T}}y.} \end{array}} \end{array}$$

Supposing ${{\Omega }}$ is a nonempty, bounded and open subset of ${{R}^{n}}$. The closure of ${{\Omega }}$ is denoted by $\bar {\Omega }$ , and the boundary of ${{\Omega }}$ is denoted by $\partial {{\Omega }}$. The following two Lemmas give two properties of the topological degree.

Lemma 2.4 [42]. Let $H\left( {\mu ,x} \right):\left[ {0,1} \right] \times \bar {\Omega } \to {{R}^{n}}$ be a continuous homotopy mapping. If $H\left( {\mu ,x} \right) = z$ has no solutions in $\partial {{\Omega }}$ for ${{\mu }} \in \left[ {0,1} \right]$ and $z \in {{R}^{n}}\backslash H\left( {\mu ,\partial \Omega } \right)$, then the topological degree $\deg \left( {H\left( {\mu ,x} \right),\Omega ,z} \right)$ of $H\left( {\mu ,x} \right)$ is a constant which is independent of ${{\mu }}.$ In this case, $\deg \left( {H\left( {0,x} \right),\Omega ,z} \right) = \deg \left( {H\left( {1,x} \right),\Omega ,z} \right)$.

Lemma 2.5 [42]. Let $H\left( {\mu x} \right):\bar {\Omega } \to {{R}^{n}}$be a continuous mapping. If $\deg \left( {H\left( x \right),\Omega ,z} \right) \ne 0$, then there exists at least one solution of H(x) = z in Ω.

2.2 Model Description

In this paper, we consider FMNNs described by

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {_{t}D_{0}^{\alpha }{{x}_{i}}\left( t \right) = - {{c}_{i}}{{x}_{i}}\left( t \right) + \mathop \sum \limits_{j = 1}^n {{a}_{{ij}}}\left( {{{x}_{j}}\left( t \right)} \right){{f}_{j}}\left( {{{x}_{j}}\left( t \right)} \right) + {{I}_{i}},} \end{array}} \end{array}$$

(2)

where 0 < α < 1, $i = 1,2, \ldots ,n$, $n$ is the number of units in a neural network, ${{x}_{i}}\left( t \right)$ denotes the state variable associated with the ith neuron; c_i > 0 is a constant; ${{I}_{i}}$ represents the external input; ${{f}_{i}}\left( \cdot \right)$ stands for the neural activation function; ${{a}_{{ij}}}\left( \cdot \right)$ is connection memristive weight, which is defined as

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {{{a}_{{ij}}}\left( {{{x}_{j}}\left( t \right)} \right) = \left\{ {\begin{array}{*{20}{l}} {\acute{a} _{{ij}}^{{}},\,\,\,\left| {{{x}_{j}}\left( t \right)} \right| \leqslant {{\chi }_{j}},} \\ {\grave{a} _{{ij}}^{{}},\,\,\,\left| {{{x}_{j}}\left( t \right)} \right| > {{\chi }_{j}},} \end{array}} \right.} \end{array}} \end{array}$$

where switching jump ${{\chi }_{j}} > 0$, and weights ${{\acute{a} }_{{ij}}}$ and ${{\grave{a} }_{{ij}}}$ are constants, and $\widetilde {{{a}_{{ij}}}} = \max \left\{ {\left| {\acute{a} _{{ij}}^{{}}} \right|,\left| {\acute{a} _{{ij}}^{{}}} \right|} \right\}$.

Set, x(t) = ${{\left( {{{x}_{1}}\left( t \right),{{x}_{2}}\left( t \right), \ldots ,{{x}_{n}}\left( t \right)} \right)}^{T}},$ $\left| {x\left( t \right)} \right| = {{\left( {\left| {{{x}_{1}}\left( t \right)} \right|,\left| {{{x}_{2}}\left( t \right)} \right|, \ldots ,\left| {{{x}_{n}}\left( t \right)} \right|} \right)}^{T}},$ $\acute{A} = {{({{\acute{a} }_{{ij}}})}_{{n \times n}}}$, $\grave{A}\,\, = {{({{\grave{a} }_{{ij}}})}_{{n \times n}}}$, $\chi = {{({{\chi }_{1}},{{\chi }_{2}}, \ldots ,{{\chi }_{n}})}^{T}}$. The system (2) can be rewritten as the following vector form:

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {_{t}D_{0}^{\alpha }{{x}_{i}}\left( t \right) = - Cx\left( t \right) + A\left( {x\left( t \right)} \right)f\left( {x\left( t \right)} \right) + I,} \end{array}} \end{array}$$

(3)

where C = diag(c₁, c₂, …, c_n), $A\left( {x\left( t \right)} \right) = {{\left( {{{a}_{{ij}}}\left( {{{x}_{j}}\left( t \right)} \right)} \right)}_{{n \times n}}}$, $f\left( {x\left( t \right)} \right) = {{\left( {{{f}_{1}}\left( {{{x}_{1}}\left( t \right)} \right),{{f}_{2}}\left( {{{x}_{2}}\left( t \right)} \right), \ldots ,{{f}_{n}}\left( {{{x}_{n}}\left( t \right)} \right)} \right)}^{T}}$, I = ${{\left( {{{I}_{1}},{{I}_{2}}, \ldots ,{{I}_{n}}} \right)}^{T}}$ , and

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {A\left( {x\left( t \right)} \right) = \left\{ {\begin{array}{*{20}{l}} {\acute{A},\,\,\,\,\left| {x\left( t \right)} \right| \leqslant \chi ,} \\ {\grave{A},\,\,\,\,\left| {x\left( t \right)} \right| > \chi .} \end{array}} \right.} \end{array}} \end{array}$$

Noting that system (3) is a fractional-order differential equation with discontinuous right-hand, the solution of the system (3) is usually considered in Filippov’s sense. Based on Definition 2.3, $x\left( t \right)$ is the solution of FMNNs (3) if $x\left( t \right)$ is an absolutely continuous function on any compact subinterval [t₁, t₂] of $\left[ {0,T} \right]$, and satisfies x(0) = x₀ and the differential inclusion:

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {_{t}D_{0}^{\alpha }x\left( t \right) \in - cx\left( t \right) + \mathop \sum \limits_{j = 1}^n \overline {co} \left[ {A\left( {x\left( t \right)} \right)} \right]f\left( {x\left( t \right)} \right) + I,\,\,\,a.a.\,\,\,t \in \left[ {0,T} \right]} \end{array}.} \end{array}$$

In order to ensure the existence and uniqueness of the solutions of FMNNs (3), the following assumption is made for the activation function $f\left( x \right)$ : $\left( {{{H}_{1}}} \right)$ : $\left( i \right)f\left( x \right)$ is Lipschitz continuous, i.e. for any given $u,{v} \in R$, there exists L = diag(l₁, l₂, …, l_n), such that $\left| {\left| {f\left( u \right) - f\left( {v} \right)} \right|} \right| \leqslant \left| {\left| {L\left( {u - {v}} \right)} \right|} \right|$; $\left( {ii} \right){{f}_{j}}\left( { \pm {{\chi }_{j}}} \right) = 0,j = 1,2, \ldots ,n$.

Lemma 2.6. Under the assumption $\left( {{{H}_{1}}} \right)$, the following inequality holds

$$\left| {\left| {\overline {co} \left[ {{{a}_{{ij}}}\left( {{{x}_{j}}\left( t \right)} \right)} \right]{{f}_{j}}\left( {{{x}_{j}}\left( t \right)} \right) - \overline {co} \left[ {{{a}_{{ij}}}\left( {{{y}_{j}}\left( t \right)} \right)} \right]{{f}_{j}}\left( {{{y}_{j}}\left( t \right)} \right)} \right|} \right| \leqslant \widetilde {{{a}_{{ij}}}}\left| {\left| {{{l}_{j}}\left( {{{x}_{j}}\left( t \right) - {{y}_{j}}\left( t \right)} \right)} \right|} \right|,\,\,\,i,j = 1,2, \ldots ,n.$$

Proof. For any $i,j = 1,2, \ldots ,n$, we separate four cases to illustrate the inequality in the above Lemma. Case 1: Let $\left| {{{x}_{i}}\left( t \right)} \right| < {{\chi }_{i}},\left| {{{y}_{i}}\left( t \right)} \right| > {{\chi }_{i}}$ one has

$$\left| {\left| {\overline {co} \left[ {{{a}_{{ij}}}\left( {{{x}_{j}}\left( t \right)} \right)} \right]{{f}_{j}}\left( {{{x}_{j}}\left( t \right)} \right) - \overline {co} \left[ {{{a}_{{ij}}}\left( {{{y}_{j}}\left( t \right)} \right)} \right]{{f}_{j}}\left( {{{y}_{j}}\left( t \right)} \right)} \right|} \right| = \left| {\left| {\acute{a} _{{ij}}^{{}}{{f}_{j}}\left( {{{x}_{j}}\left( t \right)} \right)\, - \, \acute{a} _{{ij}}^{{}}{{f}_{j}}\left( {{{y}_{j}}\left( t \right)} \right)} \right|} \right| \leqslant \widetilde {{{a}_{{ij}}}}\left| {\left| {{{l}_{j}}\left( {{{x}_{j}}\left( t \right) - {{y}_{j}}\left( t \right)} \right)} \right|} \right|.$$

Case 2: If $\left| {{{x}_{i}}\left( t \right)} \right| > {{\chi }_{i}},\left| {{{y}_{i}}\left( t \right)} \right| > {{\chi }_{i}}$ then

$$\left| {\left| {\overline {co} \left[ {{{a}_{{ij}}}\left( {{{x}_{j}}\left( t \right)} \right)} \right]{{f}_{j}}\left( {{{x}_{j}}\left( t \right)} \right) - \overline {co} \left[ {{{a}_{{ij}}}\left( {{{y}_{j}}\left( t \right)} \right)} \right]{{f}_{j}}\left( {{{y}_{j}}\left( t \right)} \right)} \right|} \right| = \left| {\left| {\grave{a} _{{ij}}^{{}}{{f}_{j}}\left( {{{x}_{j}}\left( t \right)} \right)\, - \, \grave{a} _{{ij}}^{{}}{{f}_{j}}\left( {{{y}_{j}}\left( t \right)} \right)} \right|} \right| \leqslant \widetilde {{{a}_{{ij}}}}\left| {\left| {{{l}_{j}}\left( {{{x}_{j}}\left( t \right) - {{y}_{j}}\left( t \right)} \right)} \right|} \right|.$$

Case 3: Let $\left| {{{x}_{i}}\left( t \right)} \right| \leqslant {{\chi }_{i}}$, $\left| {{{y}_{i}}\left( t \right)} \right| \geqslant {{\chi }_{i}}$, in this case, we have ${{y}_{i}}\left( t \right) \leqslant - {{\chi }_{i}}$ or ${{y}_{i}}\left( t \right) \geqslant {{\chi }_{i}}$. If ${{y}_{i}}\left( t \right) \leqslant - {{\chi }_{i}}$, then

$$\begin{gathered} \left| {\left| {\overline {co} \left[ {{{a}_{{ij}}}\left( {{{x}_{j}}\left( t \right)} \right)} \right]{{f}_{j}}\left( {{{x}_{j}}\left( t \right)} \right) - \overline {co} \left[ {{{a}_{{ij}}}\left( {{{y}_{j}}\left( t \right)} \right)} \right]{{f}_{j}}\left( {{{y}_{j}}\left( t \right)} \right)} \right|} \right| = \left| {\left| {\acute{a} _{{ij}}^{{}}{{f}_{j}}\left( {{{x}_{j}}\left( t \right)} \right) - \grave{a} _{{ij}}^{{}}{{f}_{j}}\left( {{{y}_{j}}\left( t \right)} \right)} \right|} \right| \\ \leqslant \left| {\left| {\acute{a} _{{ij}}^{{}}{{f}_{j}}\left( {{{x}_{j}}\left( t \right)} \right) - \acute{a} _{{ij}}^{{}}{{f}_{j}}\left( {{{\chi }_{j}}} \right)} \right|} \right| + \left| {\left| {\grave{a} _{{ij}}^{{}}{{f}_{j}}\left( { - {{\chi }_{j}}} \right) - \grave{a} _{{ij}}^{{}}{{f}_{j}}\left( {{{y}_{j}}\left( t \right)} \right)} \right|} \right| \leqslant \widetilde {{{a}_{{ij}}}}\left| {\left| {{{l}_{j}}\left( {{{x}_{j}}\left( t \right) - {{y}_{j}}\left( t \right)} \right)} \right|} \right|. \\ \end{gathered} $$

And another case, if ${{y}_{i}}\left( t \right) \geqslant {{\chi }_{i}}$, then

$$\begin{gathered} \left| {\left| {\overline {co} \left[ {{{a}_{{ij}}}\left( {{{x}_{j}}\left( t \right)} \right)} \right]{{f}_{j}}\left( {{{x}_{j}}\left( t \right)} \right) - \overline {co} \left[ {{{a}_{{ij}}}\left( {{{y}_{j}}\left( t \right)} \right)} \right]{{f}_{j}}\left( {{{y}_{j}}\left( t \right)} \right)} \right|} \right| = \left| {\left| {\acute{a} _{{ij}}^{{}}{{f}_{j}}\left( {{{x}_{j}}\left( t \right)} \right) - \grave{a} _{{ij}}^{{}}{{f}_{j}}\left( {{{y}_{j}}\left( t \right)} \right)} \right|} \right| \\ \leqslant \left| {\left| {\acute{a} _{{ij}}^{{}}{{f}_{j}}\left( {{{x}_{j}}\left( t \right)} \right) - \acute{a} _{{ij}}^{{}}{{f}_{j}}\left( {{{\chi }_{j}}} \right)} \right| + \left| {\grave{a} _{{ij}}^{{}}{{f}_{j}}\left( {{{x}_{j}}} \right) - \grave{a} _{{ij}}^{{}}{{f}_{j}}\left( {{{y}_{j}}\left( t \right)} \right)} \right|} \right| \leqslant \widetilde {{{a}_{{ij}}}}\left| {\left| {{{l}_{j}}\left( {{{x}_{j}}\left( t \right) - {{y}_{j}}\left( t \right)} \right)} \right|} \right|. \\ \end{gathered} $$

Case 4: This case $\left| {{{y}_{i}}\left( t \right)} \right| \leqslant {{\chi }_{i}} \leqslant \left| {{{x}_{i}}\left( t \right)} \right|$ is similar to Case 3, so we can also get

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {\left| {\left| {\overline {co} \left[ {{{a}_{{ij}}}\left( {{{x}_{j}}\left( t \right)} \right)} \right]{{f}_{j}}\left( {{{x}_{j}}\left( t \right)} \right) - \overline {co} \left[ {{{a}_{{ij}}}\left( {{{y}_{j}}\left( t \right)} \right)} \right]{{f}_{j}}\left( {{{y}_{j}}\left( t \right)} \right)} \right|} \right| \leqslant \widetilde {{{a}_{{ij}}}}\left| {\left| {{{l}_{j}}\left( {{{x}_{j}}\left( t \right) - {{y}_{j}}\left( t \right)} \right)} \right|} \right|,\,\,\,i,j = 1,2, \ldots ,n.} \end{array}} \end{array}$$

3 MAIN RESULTS

In this section, we address some sufficient conditions of the existence of equilibrium point, the generalized finite-time stability, boundedness and stabilization for FMNNs (3).

Theorem 3.1. Under the assumption $\left( {{{H}_{1}}} \right)$, if there exists a scalar ${{\varepsilon }} > 0$, and a positive definite matrix P, such that

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {\psi = }&{ - PC - {{C}^{T}}P + {{\varepsilon }^{{ - 1}}}P\widetilde {\left( A \right)}{{{\widetilde {\left( A \right)}}}^{T}}P + \varepsilon {{L}^{T}}L < 0,} \end{array}} \end{array}$$

(4)

then FMNNs (3) has at least an equilibrium point.

Proof. Set

$$\begin{array}{*{20}{r}} \begin{aligned} U\left( x \right)\, = - Cx + A\left( x \right)f\left( x \right) + I \\ = - Cx + A\left( x \right)\left[ {f\left( x \right) - f\left( 0 \right)} \right] + A\left( x \right)f\left( 0 \right) + I \\ = - Cx + A\left( x \right)\left[ {f\left( x \right) - f\left( 0 \right)} \right] + \tilde {U}, \\ \end{aligned} \end{array}$$

where $\tilde {U} = A\left( x \right)f\left( 0 \right) + I$. It’s obvious that $x{\text{*}} \in {{R}^{n}}$ is an equilibrium point of the FMNNs (3), if and only if $U\left( {x{\text{*}}} \right) = 0$.

Let $H\left( {x,\mu } \right) = - Cx + \mu A\left( x \right)h\left( x \right) + \mu \tilde {U}$, ${{\mu }} \in \left[ {0,1} \right]$, where $h\left( x \right) = f\left( x \right) - f\left( 0 \right)$. It’s easy to find that $H\left( {x,\mu } \right)$ is a continuous homo-topy mapping.

Now, we construct a convex region ${{\Omega }}$, such that

(i) $0 \in {\text{int}{\Omega }}$,

(ii) $H\left( {x,\mu } \right) \ne 0,\,\,x \in \partial \Omega ,\,\,\mu \in \left[ {0,1} \right]$.

By Lemma 2.3, we have

$$\begin{gathered} {{x}^{T}}PH(x,\mu ) = - {{x}^{T}}PCx + \mu {{x}^{T}}PA(x)h(x) + \mu {{x}^{T}}P\tilde {U} \hfill \\ \leqslant - {{x}^{T}}PCx + \mu \frac{1}{{2\varepsilon }}{{x}^{T}}\left( {P\tilde {A}} \right){{\left( {P\tilde {A}} \right)}^{T}}x + \mu \frac{\varepsilon }{2}{{h}^{T}}\left( x \right)h\left( x \right) + \mu {{x}^{T}}P\tilde {U} \hfill \\ \leqslant - {{x}^{T}}PCx + \mu \frac{1}{{2\varepsilon }}{{x}^{T}}\left( {P\tilde {A}} \right){{\left( {P\tilde {A}} \right)}^{T}}x + \mu \frac{\varepsilon }{2}{{x}^{T}}{{L}^{T}}Lx + \mu {{x}^{T}}P\tilde {U} \hfill \\ \leqslant \frac{1}{2}{{x}^{T}}\left[ { - PC - {{C}^{T}}P + \frac{1}{\varepsilon }\left( {P\tilde {A}} \right){{{\left( {P\tilde {A}} \right)}}^{T}} + \varepsilon {{L}^{T}}L} \right]x + {{x}^{T}}P\tilde {U} \hfill \\ = \frac{1}{2}{{x}^{T}}\psi x + {{x}^{T}}P\tilde {U} \hfill \\ \leqslant - \frac{1}{2}{{\lambda }_{{\min }}}\left( { - \psi } \right){{x}^{T}}x + {{x}^{T}}P\tilde {U} \hfill \\ = - \frac{1}{2}{{\lambda }_{{\min }}}\left( { - \psi } \right)\sum\limits_{i = 1}^n {\left| {{{x}_{i}}} \right|\left[ {\left| {{{x}_{i}}} \right| - 2\lambda _{{\min }}^{{ - 1}}\left( { - \psi } \right){{{\left( {P\tilde {U}} \right)}}_{i}}} \right].} \hfill \\ \end{gathered} $$

(5)

Let ${{\pi }_{i}} = 2\lambda _{{\min }}^{{ - 1}}\left( { - \psi } \right)\left| {{{{(P\tilde {U})}}_{i}}} \right|$, $\Omega = \{ x \in {{R}^{n}}:\left| {{{x}_{i}}} \right| < {{\pi }_{i}} + 1,i = 1,2, \ldots ,n\}$. Obviously, ${{\Omega }}$ is an open convex bounded set independent of parameter ${{\mu }}$. If $x \in \partial \Omega$, then combining with (5), it follows that ${{x}^{T}}PH\left( {x,\mu } \right) < 0$, which implies that $H\left( {x,\mu } \right) \ne 0$ for any $x \in \partial \Omega$, ${{\mu }} \in \left[ {0,1} \right]$. According to Lemma 2.4, it follows that $\deg \left( {H\left( {1,x} \right),\Omega ,0} \right) = \deg \left( {H\left( {0,x} \right),\Omega ,0} \right)$, i.e., $\deg \left( {U\left( x \right),\Omega ,0} \right) = \deg \left( { - Dx,\Omega ,0} \right) = \operatorname{sgn} \left| { - D} \right| \ne 0,$ where $\left| { - D} \right|$ is the determinant of $- D$. By Lemma 2.5, U(x) = 0 has at least a solution in ${{\Omega }}$. This indicates that FMNNs (3) has at least an equilibrium point in ${{\Omega }}$.

Theorem 3.2. Suppose that the condition of Theorem 3.1 holds, and there exists a scalar ${{\delta }}$, a matrix $Q > 0$, $Q \in {{R}^{{n \times n}}}$, such that

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {{{E}_{\alpha }}\left( {\delta {{T}^{\alpha }}} \right){\text{cond}}\left( Q \right) < \frac{{{{b}_{2}}}}{{{{b}_{1}}}},} \end{array}} \end{array}$$

(6)

where P = ${{R}^{{\frac{1}{2}}}}Q{{R}^{{\frac{1}{2}}}},{\text{cond}}\left( Q \right) = \frac{{{{\lambda }_{{\max }}}\left( Q \right)}}{{{{\lambda }_{{\min }}}\left( Q \right)}}$ denotes the condition number of Q, ${{\lambda }_{{\max }}}\left( Q \right)$ and ${{\lambda }_{{\min }}}\left( Q \right)$ indicate the maximum and minimum eigenvalue of the matrix, respectively, then, FMNNs (3) is generalized finite-time stable with respect to (b₁, b₂, T, R).

Proof. Let $x{\text{*}}$ be the equilibrium point of system (3), and shift it to the origin by using $y\left( t \right) = x\left( t \right) - x{\text{*}}$. We have

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {{{}_{t}}D_{0}^{\alpha }y\left( t \right) \in }&{ - C\left( {y\left( t \right) + x{\text{*}}} \right) + \overline {co} \left[ {A\left( {y\left( t \right) + x{\text{*}}} \right)} \right]f\left( {y\left( t \right) + x{\text{*}}} \right) - \overline {co} \left[ {A\left( {x{\text{*}}} \right)} \right]f\left( {x{\text{*}}} \right).} \end{array}} \end{array}$$

(7)

It is easy to check that $F\left( x \right) = - cx\left( t \right) + \sum\nolimits_{j = 1}^n {\overline {co} } \left[ {A\left( {x\left( t \right)} \right)} \right]f\left( {x\left( t \right)} \right) + I$ is an upper semicontinuous set-valued map with nonempty, compact and convex values. Hence, $F\left( x \right)$ is measurable. By the measurable selection theorem, there exists a measurable function $\gamma \left( {y\left( t \right)} \right) \in \overline {co} \left[ {A\left( {y\left( t \right) + x{\text{*}}} \right)} \right]f\left( {y\left( t \right) + x{\text{*}}} \right) - \overline {co} \left[ {A\left( {x{\text{*}}} \right)} \right]f\left( {x{\text{*}}} \right)$, such that

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {_{t}D_{0}^{\alpha }y\left( t \right) = - Cy\left( t \right) + \gamma \left( {y\left( t \right)} \right).} \end{array}} \end{array}$$

(8)

From Lemma 2.6, it follows that

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {\left| {\left| {\gamma \left( {y\left( t \right)} \right)} \right|} \right| \leqslant \tilde {A}\left| {\left| {Ly\left( t \right)} \right|} \right|.} \end{array}} \end{array}$$

Consider the Lyapunov functional candidate

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {V\left( {y\left( t \right)} \right) = {{y}^{T}}\left( t \right)Py\left( t \right).} \end{array}} \end{array}$$

Calculating Caputo’s derivative with order ${{\alpha }}$ for $V\left( {y\left( t \right)} \right)$ along the trajectory of (8), by using Lemma 2.1 we have

$$\begin{array}{*{20}{r}} \begin{gathered} \begin{array}{*{20}{r}} \begin{gathered} _{t}D_{0}^{\alpha }V\left( {y\left( t \right)} \right) \leqslant 2{{y}^{T}}\left( t \right){{P}_{t}}D_{0}^{\alpha }y\left( t \right) \hfill \\ = 2{{y}^{T}}\left( t \right)P\left\{ { - Cy\left( t \right) + \gamma \left( {y\left( t \right)} \right)} \right\} \hfill \\ \leqslant - 2{{y}^{T}}\left( t \right)PCy\left( t \right) + {{\varepsilon }^{{ - 1}}}{{y}^{T}}\left( t \right)P\left( {\tilde {A}} \right){{\left( {\tilde {A}} \right)}^{T}}P + \varepsilon {{y}^{T}}\left( t \right){{L}^{T}}Ly\left( t \right) \hfill \\ = {{y}^{T}}\left( t \right)\left\{ { - PC - {{C}^{T}}P + {{\varepsilon }^{{ - 1}}}P\left( {\tilde {A}} \right){{{\left( {\tilde {A}} \right)}}^{T}}P + \varepsilon {{L}^{T}}L} \right\}y\left( t \right) \hfill \\ \end{gathered} \end{array} \hfill \\ = {{y}^{T}}\left( t \right)\psi y\left( t \right) \hfill \\ = {{y}^{T}}\left( t \right){{P}^{{\frac{1}{2}}}}\left( {{{P}^{{ - \frac{1}{2}}}}\psi {{P}^{{ - \frac{1}{2}}}}} \right){{P}^{{\frac{1}{2}}}}y\left( t \right). \hfill \\ \end{gathered} \end{array}$$

Let $\delta = {{\lambda }_{{\max }}}\left( {{{P}^{{ - \frac{1}{2}}}}\psi {{P}^{{ - \frac{1}{2}}}}} \right)$, we can get $\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {_{t}D_{0}^{\alpha }V\left( {y\left( t \right)} \right) \leqslant \delta V\left( {y\left( t \right)} \right).} \end{array}} \end{array}$ Correspondingly, there exists a nonnegative function $M\left( t \right)$, such that

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {V\left( {y\left( t \right)} \right) + M\left( t \right) = \delta V\left( {y\left( t \right)} \right).} \end{array}} \end{array}$$

(9)

Applying Laplace transform to (9), it results that

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {{{s}^{\alpha }}V\left( {y\left( s \right)} \right) - V\left( {y\left( 0 \right)} \right){{s}^{{\alpha - 1}}} + M\left( s \right) = \delta V\left( {y\left( s \right)} \right).} \end{array}} \end{array}$$

The above equality is equivalent to

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {V\left( {y\left( s \right)} \right) = \frac{{V\left( {y\left( 0 \right)} \right){{s}^{{\alpha - 1}}} - M\left( s \right)}}{{{{s}^{\alpha }} - \delta }}.} \end{array}} \end{array}$$

(10)

Taking the inverse Laplace transform of (10) gives

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {V\left( {y\left( t \right)} \right)}&{ = V\left( {y\left( 0 \right)} \right){{E}_{\alpha }}\left( {\delta {{t}^{\alpha }}} \right) - \mathop \smallint \limits_0^t M\left( \tau \right)[{{{(t - \tau )}}^{{\alpha - 1}}}{{E}_{{\alpha ,\alpha }}}\left( {\delta \left( {t - \tau {{)}^{\alpha }}} \right)} \right]d\tau .} \end{array}} \end{array}$$

Since both ${{(t - \tau )}^{{\alpha - 1}}}$ and ${{E}_{{\alpha ,\alpha }}}(\delta \left( {t - \tau {{)}^{\alpha }}} \right)$ are nonnegative functions, the above equation can be converted into

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {V\left( {y\left( t \right)} \right) \leqslant {{E}_{\alpha }}\left( {\delta {{t}^{\alpha }}} \right)V\left( {y\left( 0 \right)} \right).} \end{array}} \end{array}$$

From the definition of Lyapunov function $V\left( {y\left( t \right)} \right)$, the aforementioned inequality can be written as

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {{{y}^{T}}\left( t \right)Py\left( t \right) \leqslant {{E}_{\alpha }}\left( {\delta {{t}^{\alpha }}} \right){{y}^{T}}\left( 0 \right)Py\left( 0 \right).} \end{array}} \end{array}$$

Noting that $P = {{R}^{{\frac{1}{2}}}}Q{{R}^{{\frac{1}{2}}}}$, we can obtain that

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {{{y}^{T}}\left( t \right){{R}^{{\frac{1}{2}}}}Q{{R}^{{\frac{1}{2}}}}y\left( t \right) \leqslant {{E}_{\alpha }}\left( {\delta {{t}^{\alpha }}} \right){{y}^{T}}\left( 0 \right){{R}^{{\frac{1}{2}}}}Q{{R}^{{\frac{1}{2}}}}y\left( 0 \right).} \end{array}} \end{array}$$

It implies that

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {{{\lambda }_{{\min }}}\left( Q \right){{y}^{T}}\left( t \right)Ry\left( t \right) < {{\lambda }_{{\max }}}\left( Q \right){{E}_{\alpha }}\left( {\delta {{t}^{\alpha }}} \right){{y}^{T}}\left( 0 \right)Ry\left( 0 \right).} \end{array}} \end{array}$$

Combining ${{y}^{T}}\left( 0 \right)Ry\left( 0 \right) \leqslant {{b}_{1}}$ with (6) yields

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {{{y}^{T}}\left( t \right)Ry\left( t \right) < {{b}_{2}},\,\,\,\forall t \in \left[ {0,T} \right].} \end{array}} \end{array}$$

This shows that FMNNs (3) is generalized finite-time stable.

Consider the following FMNNs

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {{{}_{t}}D_{0}^{\alpha }y\left( t \right) = }&{ - Cy\left( t \right) + \gamma \left( {y\left( t \right)} \right) + Dw\left( t \right),t \in \left[ {0,T} \right].} \end{array}} \end{array}$$

(11)

The following theorem introduces the generalized finite-time boundedness of FMNNs (11).

Theorem 3.3. Under the assumption $\left( {{{H}_{1}}} \right)$, if there exists a scalar ${{\beta }} > 0$, a matrix Q₁ > 0, ${{Q}_{1}} \in {{R}^{{n \times n}}}$, and a nonsingular matrix ${{Q}_{2}} \in {{R}^{{m \times m}}}$, such that

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {}&{\left( {\begin{array}{*{20}{c}} { - PC - {{C}^{T}}P + \frac{1}{\varepsilon }\tilde {A}{{{\tilde {A}}}^{T}} + \varepsilon P{{L}^{T}}LP - \beta P}&{D{{Q}_{2}}} \\ {{{Q}_{2}}{{D}^{T}}}&{ - \beta {{Q}_{2}}} \end{array}} \right) < 0,} \end{array}} \end{array}$$

(12)

$${{E}_{\alpha }}\left( {\beta {{T}^{\alpha }}} \right)\left[ {\frac{{\beta S{{T}^{\alpha }}}}{{{{\lambda }_{{{\text{min}}}}}\left( {{{Q}_{2}}} \right)\Gamma \left( {\alpha + 1} \right)}} + \frac{{{{b}_{1}}}}{{{{\lambda }_{{{\text{min}}}}}\left( {{{Q}_{1}}} \right)}}} \right] < \frac{{{{b}_{2}}}}{{{{\lambda }_{{{\text{max}}}}}\left( {{{Q}_{1}}} \right)}},$$

(13)

where $P = {{R}^{{ - \frac{1}{2}}}}{{Q}_{1}}{{R}^{{ - \frac{1}{2}}}}$, then, FMNNs (11) is generalized finite-time bounded with respect to (b₁, b₂, T, R, S).

Proof. Consider the Lyapunov function:

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {V\left( {y\left( t \right)} \right) \leqslant {{y}^{T}}\left( t \right){{P}^{{ - 1}}}y(t).} \end{array}} \end{array}$$

In the light of Lemma 2.1, computing the Caputo’s derivative along the trajectory of (11), we have

$$\begin{array}{*{20}{r}} \begin{gathered} \begin{array}{*{20}{r}} \begin{gathered} _{t}D_{0}^{\alpha }V\left( {y\left( t \right)} \right) \leqslant 2{{y}^{T}}\left( t \right){{\left( {{{P}^{{ - 1}}}} \right)}_{t}}D_{0}^{\alpha }y\left( t \right) \hfill \\ = 2{{y}^{T}}\left( t \right){{P}^{{ - 1}}}\left\{ { - Cy\left( t \right) + \gamma \left( {y\left( t \right)} \right) + Dw\left( t \right)} \right\} \hfill \\ \leqslant 2{{y}^{T}}\left( t \right){{P}^{{ - 1}}}\left( { - Cy\left( t \right) + Dw\left( t \right)} \right) + {{\varepsilon }^{{ - 1}}}{{y}^{T}}\left( t \right)\left( {{{P}^{{ - 1}}}\tilde {A}} \right){{\left( {{{P}^{{ - 1}}}\tilde {A}} \right)}^{T}} + \varepsilon {{y}^{T}}\left( t \right){{L}^{T}}Ly\left( t \right) \hfill \\ \end{gathered} \end{array} \hfill \\ = \left( {{{y}^{T}}\left( t \right){{w}^{T}}\left( t \right)} \right)\left( {\begin{array}{*{20}{c}} \Delta &{{{P}^{{ - 1}}}D} \\ {{{D}^{T}}{{P}^{{ - 1}}}}&0 \end{array}} \right)\left( \begin{gathered} y\left( t \right) \hfill \\ w\left( t \right) \hfill \\ \end{gathered} \right), \hfill \\ \end{gathered} \end{array}$$

(14)

where $\Delta = - {{P}^{{ - 1}}}C - {{C}^{T}}{{P}^{{ - 1}}} + {{\varepsilon }^{{ - 1}}}\left( {{{P}^{{ - 1}}}\tilde {A}} \right){{({{P}^{{ - 1}}}\tilde {A})}^{T}} + \varepsilon {{L}^{T}}L$. Under condition (12), pre- and post-multiplying (12) by the symmetric positive definite matrix $\left( {\begin{array}{*{20}{c}} {{{P}^{{ - 1}}}}&0 \\ 0&{Q_{2}^{{ - 1}}} \end{array}} \right)$, it derives that:

$$\left( {\begin{array}{*{20}{c}} \Theta &{{{P}^{{ - 1}}}D} \\ {{{D}^{T}}{{P}^{{ - 1}}}}&{ - \beta Q_{2}^{{ - 1}}} \end{array}} \right) < 0,$$

(15)

where $\Theta = - {{P}^{{ - 1}}}C - {{C}^{T}}{{P}^{{ - 1}}} + \frac{1}{\varepsilon }\left( {{{P}^{{ - 1}}}\tilde {A}} \right){{({{P}^{{ - 1}}}\tilde {A})}^{T}} + \varepsilon {{L}^{T}}L - \beta {{P}^{{ - 1}}}.$ By (14) and (15), we can obtain that

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} \begin{gathered} _{t}D_{0}^{\alpha }V\left( {y\left( t \right)} \right) < \left( {{{y}^{T}}\left( t \right){{w}^{T}}\left( t \right)} \right)\left( {\begin{array}{*{20}{c}} {\beta {{P}^{{ - 1}}}}&0 \\ 0&{\beta Q_{2}^{{ - 1}}} \end{array}} \right)\left( \begin{gathered} y\left( t \right) \hfill \\ w\left( t \right) \hfill \\ \end{gathered} \right) \\ = \beta V\left( {y\left( t \right)} \right) + \beta {{w}^{T}}\left( t \right))Q_{2}^{{ - 1}}w\left( t \right). \\ \end{gathered} \end{array}} \end{array}$$

(16)

Applying

${{w}^{T}}\left( t \right)Q_{2}^{{ - 1}}w\left( t \right) \leqslant {{\lambda }_{{\max }}}\left( {Q_{2}^{{ - 1}}} \right){{w}^{T}}\left( t \right)w\left( t \right) \leqslant \frac{S}{{{{\lambda }_{{\min }}}\left( {{{Q}_{2}}} \right)}}$, (16) can be changed as

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {_{t}D_{0}^{\alpha }V\left( {y\left( t \right)} \right) < \beta V\left( {y\left( t \right)} \right) + \frac{{\beta S}}{{{{\lambda }_{{\min }}}\left( {{{Q}_{2}}} \right)}},\,\,\,t \in \left[ {0,T} \right].} \end{array}} \end{array}$$

(17)

Integrating with order ${{\alpha }}$ on both sides of (17) from 0 to t, where $t \leqslant T$, we can obtain that

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {V\left( {y\left( t \right)} \right)}&{ < V\left( {y\left( 0 \right)} \right) + \frac{{\beta S{{t}^{\alpha }}}}{{{{\lambda }_{{{\text{min}}}}}\left( {{{Q}_{2}}} \right)\Gamma \left( {\alpha + 1} \right)}} + \frac{\beta }{{\Gamma \left( \alpha \right)}}\mathop \smallint \limits_0^t {{{(t - \tau )}}^{{\alpha - 1}}}V\left( {y\left( \tau \right)} \right)d\tau .} \end{array}} \end{array}$$

By means of Lemma 2.2, it follows that

$$\begin{array}{*{20}{r}} \begin{gathered} V\left( {y\left( t \right)} \right) < \left( {V\left( {y\left( 0 \right)} \right) + \frac{{\beta S{{t}^{\alpha }}}}{{{{\lambda }_{{{\text{min}}}}}\left( {{{Q}_{2}}} \right)\Gamma \left( {\alpha + 1} \right)}}} \right){{E}_{\alpha }}\left( {\frac{\beta }{{\Gamma \left( \alpha \right)}}\Gamma \left( \alpha \right){{t}^{\alpha }}} \right) \\ \leqslant \left( {V\left( {y\left( 0 \right)} \right) + \frac{{\beta S{{t}^{\alpha }}}}{{{{\lambda }_{{{\text{min}}}}}\left( {{{Q}_{2}}} \right)\Gamma \left( {\alpha + 1} \right)}}} \right){{E}_{\alpha }}\left( {\beta {{T}^{\alpha }}} \right). \\ \end{gathered} \end{array}$$

(18)

Noting $P = {{R}^{{ - \frac{1}{2}}}}{{Q}_{1}}{{R}^{{ - \frac{1}{2}}}}$, we have

$$\begin{gathered} \begin{array}{*{20}{r}} \begin{gathered} V\left( {y\left( t \right)} \right) < {{y}^{T}}\left( t \right){{P}^{{ - 1}}}y\left( t \right) = {{y}^{T}}\left( t \right){{R}^{{\frac{1}{2}}}}Q_{1}^{{ - 1}}{{R}^{{\frac{1}{2}}}}y\left( t \right) \\ \geqslant {{\lambda }_{{{\text{min}}}}}\left( {Q_{1}^{{ - 1}}} \right){{y}^{T}}\left( t \right)Ry\left( t \right) = \frac{{{{y}^{T}}\left( t \right)Ry\left( t \right)}}{{{{\lambda }_{{\max }}}\left( {{{Q}_{1}}} \right)}}, \\ \end{gathered} \end{array} \hfill \\ \begin{array}{*{20}{r}} \begin{gathered} V\left( {y\left( 0 \right)} \right) = {{y}^{T}}\left( 0 \right){{P}^{{ - 1}}}y\left( 0 \right) = {{y}^{T}}\left( 0 \right){{R}^{{\frac{1}{2}}}}Q_{1}^{{ - 1}}{{R}^{{\frac{1}{2}}}}y\left( 0 \right) \\ \leqslant {{\lambda }_{{{\text{max}}}}}\left( {Q_{1}^{{ - 1}}} \right){{y}^{T}}\left( 0 \right)Ry\left( 0 \right) \leqslant \frac{{{{b}_{1}}}}{{{{\lambda }_{{\min }}}\left( {{{Q}_{1}}} \right)}}, \\ \end{gathered} \end{array} \hfill \\ \end{gathered} $$

Taking above two inequalities into (18), it forms that

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {\frac{{{{y}^{T}}\left( t \right)Ry\left( t \right)}}{{{{\lambda }_{{{\text{max}}}}}\left( {{{Q}_{1}}} \right)}} < }&{{{E}_{\alpha }}\left( {\beta {{T}^{\alpha }}} \right)\left[ {\frac{{\beta S{{t}^{\alpha }}}}{{{{\lambda }_{{{\text{min}}}}}\left( {{{Q}_{2}}} \right)\Gamma \left( {\alpha + 1} \right)}} + \frac{{{{b}_{1}}}}{{{{\lambda }_{{{\text{min}}}}}\left( {{{Q}_{1}}} \right)}}} \right].} \end{array}} \end{array}$$

(19)

Comparing (19) with (13), it follows that ${{y}^{T}}\left( t \right)Ry\left( t \right) < {{b}_{2}},\,\,\,\forall t \in \left[ {0,T} \right]$. This proof is completed.

In the subsection, we pay attention to designing the feedback controller u(t) = Ky(t) for solving the finite-time boundedness problem of the following fractional-order system

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {{{}_{t}}D_{0}^{\alpha }y\left( t \right) = }&{ - Cy\left( t \right) + \gamma \left( {y\left( t \right)} \right) + Bu\left( t \right) + Dw\left( t \right),\,\,\,t \in \left[ {0,T} \right].} \end{array}} \end{array}$$

(20)

Theorem 3.4. Suppose that $\left( {{{H}_{1}}} \right)$ holds. If there exist a scalar ${{\beta }} > 0$, a matrix Q₁ > 0, ${{Q}_{1}} \in {{R}^{{n \times n}}}$, a nonsingular matrix ${{Q}_{2}} \in {{R}^{{m \times m}}}$, and a matrix $N \in {{R}^{{l \times n}}}$, such that (13) and

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {\left( {\begin{array}{*{20}{c}} \Phi &{D{{Q}_{2}}} \\ {{{Q}_{2}}{{D}^{T}}}&{ - \beta {{Q}_{2}}} \end{array}} \right) < 0} \end{array}} \end{array}$$

(21)

hold, where $\Phi = - PC - {{C}^{T}}P + BN + {{N}^{T}}{{B}^{T}} + {{\varepsilon }^{{ - 1}}}\tilde {A}{{\tilde {A}}^{T}} + \varepsilon P{{L}^{T}}LP - \beta P$, and $P = {{R}^{{ - \frac{1}{2}}}}{{Q}_{1}}{{R}^{{ - \frac{1}{2}}}}$, then, FMNNs (20) is generalized finite-time stabilized with respect to (b₁, b₂, T, R, S) under the feedback controller $u\left( t \right) = Ky\left( t \right) = N{{P}^{{ - 1}}}y\left( t \right)$.

The proof is similar as Theorem 3, so omitted.

4 NUMERICAL EXAMPLES

In this section, we apply two examples to illustrate the validity and effectiveness of the proposed theoretical results in this paper.

Example 1. Consider the following FMNNs:

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {{{}_{t}}D_{0}^{\alpha }x\left( t \right) = }&{ - Cx\left( t \right) + A\left( {x\left( t \right)} \right)f\left( {x\left( t \right)} \right) + I,\,\,\,t \in \left[ {0,T} \right],} \end{array}} \end{array}$$

(22)

where $\alpha = 0.5,f\left( x \right) = \tanh \left( x \right),L = {\text{diag}}\left( {1,1} \right),C = {\text{diag}}\left( {1,1} \right)$, and $I = {{(0,0)}^{T}}$,

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {{{a}_{{11}}}\left( {{{x}_{1}}\left( t \right)} \right) = \left\{ {\begin{array}{*{20}{l}} {0.8,\,\,\,\left| {{{x}_{1}}\left( t \right)} \right| \leqslant 1,} \\ { - 0.8,\,\,\,\left| {{{x}_{1}}\left( t \right)} \right| > 1;} \end{array}} \right.} \end{array}} \end{array}\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {\,\,\,\,{{a}_{{12}}}\left( {{{x}_{2}}\left( t \right)} \right) = \left\{ {\begin{array}{*{20}{l}} {0.4,\,\,\,\left| {{{x}_{2}}\left( t \right)} \right| \leqslant 1,} \\ { - 0.4,\,\,\,\left| {{{x}_{2}}\left( t \right)} \right| > 1;} \end{array}} \right.} \end{array}} \end{array}$$

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {{{a}_{{21}}}\left( {{{x}_{1}}\left( t \right)} \right) = \left\{ {\begin{array}{*{20}{l}} {0.3,\,\,\left| {{{x}_{1}}\left( t \right)} \right| \leqslant 1,} \\ { - 0.3,\,\,\,\left| {{{x}_{1}}\left( t \right)} \right| > 1;} \end{array}} \right.} \end{array}} \end{array}\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {\,\,\,{{a}_{{22}}}\left( {{{x}_{2}}\left( t \right)} \right) = \left\{ {\begin{array}{*{20}{l}} {0.3,\,\,\left| {{{x}_{2}}\left( t \right)} \right| \leqslant 1,} \\ { - 0.3,\,\,\left| {{{x}_{2}}\left( t \right)} \right| > 1.} \end{array}} \right.} \end{array}} \end{array}$$

The initial conditions of (22) are determined as $x\left( 0 \right) = {{(1,0)}^{T}}$. Choose parameters b₁ = 1, b₂ = 2, ${{\varepsilon }} = 1$, $T = 6$, $R = E$, where E is taken as the identity matrix. By using Matlab’s LMI control toolbox to calculate (4), we can get the feasible solution

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {P = \left( {\begin{array}{*{20}{c}} {1.2951}&{ - 0.2882} \\ { - 0.2882}&{1.7915} \end{array}} \right).} \end{array}} \end{array}$$

Accordingly, we can know ${{\delta }} = - 0.024$, which satisfies the condition (6). By Theorem 3.2, FMNNs (22) is generalized finite-time stable with respect to $\left( {1,2,6,E} \right)$.

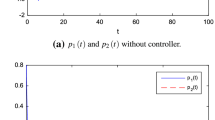
The state trajectory in $0 \sim 6\,\,{\text{s}}$ with the initial value $x\left( 0 \right)$ is shown in Figs. 3 and 4. Figure 4 denotes the trajectory of ${{x}^{T}}\left( t \right)Rx\left( t \right)$ of system (22).

Fig. 3.

The trajectory of state $x(t)$ of system (22) versus time.

Fig. 4.

The trajectory of ${{x}^{T}}\left( t \right)Rx\left( t \right)$ of system (22) versus time.

Example 2. Consider the finite-time boundedness problem about the following FMNNs:

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {{{}_{t}}D_{0}^{\alpha }x\left( t \right) = }&{ - Cx\left( t \right) + A\left( {x\left( t \right)} \right)f\left( {x\left( t \right)} \right) + Dw\left( t \right) + I,\,\,\,\,t \in \left[ {0,T} \right],} \end{array}} \end{array}$$

(23)

where $\alpha = 0.5,f\left( x \right) = \tanh \left( x \right),L = {\text{diag}}\left( {1,1} \right)$, and $I = {{(0,0)}^{T}}$, $C = \left( {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right),\,\,D = \left( {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right)$.

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {{{a}_{{11}}}\left( {{{x}_{1}}\left( t \right)} \right) = \left\{ {\begin{array}{*{20}{l}} {2,\,\,\,\left| {{{x}_{1}}\left( t \right)} \right| \leqslant 1,} \\ { - 2,\,\,\,\left| {{{x}_{1}}\left( t \right)} \right| > 1;} \end{array}} \right.} \end{array}} \end{array}\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {\,\,\,{{a}_{{12}}}\left( {{{x}_{2}}\left( t \right)} \right) = \left\{ {\begin{array}{*{20}{l}} {2,\,\,\left| {{{x}_{2}}\left( t \right)} \right| \leqslant 1,} \\ { - 2,\,\,\left| {{{x}_{2}}\left( t \right)} \right| > 1;} \end{array}} \right.} \end{array}} \end{array}$$

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {{{a}_{{21}}}\left( {{{x}_{1}}\left( t \right)} \right) = \left\{ {\begin{array}{*{20}{l}} {1,\,\,\,\left| {{{x}_{1}}\left( t \right)} \right| \leqslant 1,} \\ { - 1,\,\,\,\left| {{{x}_{1}}\left( t \right)} \right| > 1;} \end{array}} \right.} \end{array}} \end{array}\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {\,\,\,\,{{a}_{{22}}}\left( {{{x}_{2}}\left( t \right)} \right) = \left\{ {\begin{array}{*{20}{l}} {1,\,\,\,\left| {{{x}_{2}}\left( t \right)} \right| \leqslant 1,} \\ { - 1,\,\,\,\left| {{{x}_{2}}\left( t \right)} \right| > 1.} \end{array}} \right.} \end{array}} \end{array}$$

The corresponding parameters are chosen as:$w\left( t \right) = {{(\sin t,\cos t)}^{T}}$, ${{b}_{1}} = 0.05$, ${{b}_{2}} = 3.8$, $S = 1$, $T = 10$, $R = E$. Numerical simulation has been operated for system (23) with the initial value $~x\left( 0 \right) = {{(0.2,0.1)}^{T}}$, which satisfies the condition ${{x}^{T}}\left( 0 \right)Rx\left( 0 \right) \leqslant {{b}_{1}}$. Let ${{\beta }} = 1,$ we attain the reasonable solution:

$$\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {P = \left( {\begin{array}{*{20}{c}} {3.6176}&{0.0823} \\ {0.0823}&{3.4941} \end{array}} \right),} \end{array}} \end{array}\,\,\,\begin{array}{*{20}{r}} {\begin{array}{*{20}{r}} {{{Q}_{2}} = \left( {\begin{array}{*{20}{c}} { - 0.5623}&{ - 2.1075} \\ { - 2.1075}&{2.5989} \end{array}} \right).} \end{array}} \end{array}$$

By Theorem 3.3, FMNNs (23) is finite-time bounded. The state trajectory in $0 \sim 10\,\,{\text{s}}$ is shown in Figs. 5 and 6. From Fig. 6, we conclude that FMNNs (23) is generalized finite-time bounded with respect to $\left( {0.05,3.8,10,E,1} \right)$.

Fig. 5.

The trajectory of state $x(t)$ of system (23) versus time.

Fig. 6.

The trajectory of state ${{x}^{T}}\left( t \right)Rx\left( t \right)$ of system (23) versus time.

5 CONCLUSIONS

In this paper, we have investigated the generalized finite-time stability, boundedness and stabilization for a class of FMNNs. The existence of equilibrium point for the considered FMNNs has been proved. The conditions with respect to the generalized finite-time stability and boundedness have been derived in terms of LMIs. Under designed feedback controller, the generalized finite-time stabilization condition has been also achieved in the forms of LMIs.

It would be interesting to extend the results of this paper to FMNNs with delays, in addition, how solve the equilibrium and uniform charge distribution and of FMNNs, these will be the challenging issues for future research.