The safety analysis of structural and machine parts with crack-like defects can be based on both the probabilistic approach and the deterministic approach. In the latter case, safety factors of crack resistance are added to the criterial equations [1–6]. However, acceptable (safe) dimensions of crack-like defects are determined using models and criteria of fracture mechanics, which includes the addition of safety factors to criterial equations.

In the probabilistic strength calculation, a structure is considered safe when the probability of its failure is below the acceptable level. There is no doubt that probabilistic analysis is more complex and expensive than deterministic analysis and not very convenient for use in daily engineering practice. Moreover, probabilistic fracture mechanics is relatively new in the field of structural integrity, and there are often not enough statistics for using probabilistic approaches and being sufficiently convinced in the validity of calculation results when making decisions about operating critical facilities with crack-like defects. At the same time, even when a purely deterministic approach is used, probabilistic analysis is especially significant because it allows quantitatively estimating the actual safety factors. Probabilistic estimates are helpful in making decisions on fracture and safety analysis and in developing technical maintenance, inspection, and repair strategies [7]. As soon as the statistical uncertainties of the original calculation data are identified, it will be possible to estimate the probability of structural failure or structural safety. Thus, the prediction of the safety factors for ensuring structural integrity can be made using objective estimates based on analyzing original statistical design data instead of empirically determined or generally assigned safety factors [8]. The main principles of the probabilistic approach to estimating the structural integrity are exposed in detail in works [7–15].

This article proposes the main principles of the probabilistic approach to estimating the safety (crack resistance safety) factors with the help of the simplified approach based on criterial approaches from the fracture mechanics through the use of fracture viscosity and the generalized diagram of crack resistance. It is proposed to calculate the probabilistic safety factors by means of the the probabilistic safety factors of the yield stress, taking their interrelation into account.

Principles for Estimating the Probabilistic Safety Factors by the Limit Characteristics

Let us denote the fracture strength as R, whatever the kind of limit state or failure, and the applied external load (or stress) as L. In this case, the safety factor for any kind of limit state is

$$n = \frac{R}{L}.$$
(1)

Parameters L and R should be considered as random due to the uncertainty in the original variables by applied loads and properties of material. The probability of failure is estimated using reliability methods by adding to the consideration the reliability index βf, determined as

$${{{{\beta }}}_{f}} = \frac{{{{{{\mu }}}_{R}} - {{{{\mu }}}_{L}}}}{{\sqrt {s_{R}^{2} + s_{L}^{2}} }}.$$
(2)

In this equation it is assumed that L and R are described using random independent normal distributions with the respective average values µL and µR and the standard deviations sL and sR, respectively.

Relation (2) can be rewritten considering safety factor n for the material’s fracture strength, load variation coefficients \({{{v}}_{L}} = {{s}_{L}}{\text{/}}{{{{\mu }}}_{L}}\), and the material’s fracture strength coefficient \({{{v}}_{R}} = {{s}_{R}}{\text{/}}{{{{\mu }}}_{R}}\):

$${{{{\beta }}}_{f}} = \frac{{n - 1}}{{\sqrt {{{n}^{2}}{v}_{R}^{2} + {v}_{L}^{2}} }}.$$
(3)

In this case, the limit state (failure) probability is determined as

$${{P}_{f}} = 1 - {{\Phi}}\left( {{{{{\beta }}}_{f}}} \right),$$
(4)

where Φ is the function of the normalized normal distribution. The tabulated values of Φ as the functions of reliability index \({{{{\beta }}}_{f}}\) are provided in monograph [10]. If all of the variables have abnormal distributions, they are converted to equivalent normal distributions using the corresponding algorithm from [13].

If a structural element has no crack-like defects, the applied stresses are compared with the limit stresses, that is, yield stress or ultimate stress. When the limit stresses exceed the applied ones, the structural element is considered safe. The region of safe (acceptable) structural states can be determined on the basis of the acceptable stress precalculated by the strength calculation according, for example, to a certain theory of strength. Assume that the acceptable stresses according to [3] must not exceed stresses \({{\sigma }_{Y}}{\text{/}}{{n}_{Y}}\), where \({{\sigma }_{Y}}\) is the material yield stress and \({{n}_{Y}}\) is the safety factor of the yield stress.

To estimate the probability of reaching the limit state on the basis of the distribution of the yield stress reliability index βf becomes

$${{{{\beta }}}_{f}} = \frac{{{{n}_{Y}} - 1}}{{\sqrt {n_{Y}^{2}{v}_{Y}^{2} + {v}_{L}^{2}} }}.$$
(5)

Here the yield stress variation coefficient is indicated as \({{{v}}_{Y}}\).

If a structural element has crack-like defects, the safety analysis must be made by the approaches of fracture mechanics. In this case, the applied parameters of fracture mechanics must be compared with the fracture viscosity in terms of the stress intensity factor, J-integral, crack tip opening displacement, crack resistance diagram, and other such properties.

Correlation Dependences between the Safety Factors of the Yield Stress and the Safety Factors of Crack Resistance

The acceptable (safe) parameters of crack-like defects in a damaged structure are predicted by adding safety factors to criterial fracture mechanics equations to decrease the criterial characteristics of fracture mechanics (crack resistance) and, therefore, reduce the critical defect size \({{a}_{c}}\) to safe size \(\left[ a \right]\) at a fixed design stress (load) \({{{{\sigma }}}_{d}}\), found as

$${{{{\sigma }}}_{d}} \leqslant \left[ {{\sigma }} \right] = \frac{{{{{{\sigma }}}_{Y}}}}{{{{n}_{Y}}}}.$$
(6)

Here \({{n}_{Y}}\) is the safety factor of the yield stress and \(\left[ {{\sigma }} \right]\) is the acceptable applied stress.

In the case of the crack resistance diagram, for example, the acceptable or design stress is related to the safe defect size by an equation from [3, 4, 16]. The equation is recorded as

$${{K}_{I}} \leqslant \frac{{{{K}_{{{\text{mat}}}}}}}{{{{m}_{{{\text{FAD}}}}}}}\sqrt {1 - {{{\left( {\frac{{{{{{\sigma }}}_{d}}}}{{{{{{\sigma }}}_{0}}}}} \right)}}^{2}}} ,$$
(7)

and allows identifying the region of safe structural states in the crack resistance diagram. Here \({{m}_{{{\text{FAD}}}}}\) is the safety (yield stress safety) factor, \({{K}_{{{\text{mat}}}}}\) is the fracture viscosity, and \({{K}_{I}}\) is the coefficient of the intensity of the applied stress. According to formula (7) and considering the safety factor of the yield stress, the local strength of material in the vicinity of the crack tip is recorded as

$$\frac{{{{{{\sigma }}}_{0}}}}{{{{{{\sigma }}}_{Y}}}} = - \frac{{{\beta }}}{{2{{n}_{Y}}}} + \sqrt {\frac{1}{4}{{{\left( {\frac{{{\beta }}}{{{{n}_{Y}}}}} \right)}}^{2}} - \frac{{\left( {1 + {{{{\nu }}}^{2}} - {{\nu }}} \right)~{{{\left( {{{\beta /}}{{n}_{Y}}} \right)}}^{2}} - 1}}{{{{{\left( {1 - 2{{\nu }}} \right)}}^{2}}}}} ,$$
(8)

under plane strain and as

$$\frac{{{{{{\sigma }}}_{0}}}}{{{{{{\sigma }}}_{Y}}}} = - \frac{{{\beta }}}{{2{{n}_{Y}}}} + \sqrt {1 - \frac{3}{4}{{{\left( {\frac{{{\beta }}}{{{{n}_{Y}}}}} \right)}}^{2}}} ,$$
(9)

in the plane stress state. Here, \(\nu \) is the Poisson ratio. In dimensionless equation (7) of the generalized crack resistance diagram, the degree of constraint in the vicinity of the crack tip is represented by local stress biaxiality \(\beta = T{\text{/}}{{\sigma }_{d}}\), based on taking account of the nonsingular component (T stress) in the distribution of stresses in the vicinity of the crack tip. This component is added to the formula for local strength. Biaxiality β is the function of the relative crack length, body geometry, and loading pattern. This parameter is tabulated and also represented as plots for bodies with different configurations and loading patterns [3].

The safety factor for a structure with a crack-like defect is determined, as in [1, 3], by requiring that, in case there is a safe-size defect, the breaking stress be at least equal to the yield stress σY, which corresponds to nonbrittle structural damage. The safety factor value obtained provides a justified reference for choosing the safety factor in the framework of the considered concept of fracture mechanics. In the failure assessment diagram concept, the safety factor \({{m}_{{{\text{FAD}}}}}\) is determined as in [3, 4, 16] as

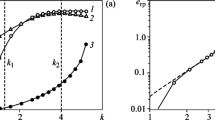
$${{m}_{{{\text{FAD}}}}} = {{n}_{Y}}\frac{{\sqrt {1 - {{{\left( {\frac{{{{\sigma }_{Y}}{\text{/}}{{n}_{Y}}}}{{{{\sigma }_{0}}}}} \right)}}^{2}}} }}{{\sqrt {1 - {{{\left( {\frac{{{{\sigma }_{Y}}}}{{{{\sigma }_{0}}}}} \right)}}^{2}}} }}.$$
(10)

The calculation of \({{m}_{{{\text{FAD}}}}}\) by formula (10), considering expressions (8) and (9), permits deriving the functional dependence of \({{m}_{{{\text{FAD}}}}}\) on the safety factor of the yield stress \({{n}_{Y}}\). This dependence for the plane stress state and the plane strain is presented in Fig. 1.

Fig. 1.
figure 1

Dependence of safety factor \({{m}_{{{\text{FAD}}}}}~\) on the safety factor of the yield stress \({{n}_{Y}}\) for a crack: 1 is the plane stress state and 2 is plane strain.

Full size image

The formulas derived by approximating the results are

$${{m}_{{{\text{FAD}}}}} = 1.44n_{Y}^{{1.34}}$$
(11)

for the planar stress state and

$${{m}_{{{\text{FAD}}}}} = - 0.064 + 1.1{{n}_{Y}}$$
(12)

for the plane strain. It can therefore be accepted in the first approximation for the plane strain that

$${{m}_{{{\text{FAD}}}}} \approx {{n}_{Y}},$$
(13)

which corresponds to the recommendations from [6].

The design formulas of safety factors depend largely on the accepted model of solid fracture and the criterion of fracture mechanics.

The safety factors for the most popular concepts of fracture mechanics are taken from [3, 4] and include the following:

• the concept of the stress intensity factor \({{K}_{I}}\)

$${{m}_{K}} = {{n}_{Y}},$$
(14)

• the concept of the J-integral

$${{m}_{J}} = {{\left( {{{n}_{Y}}} \right)}^{{1 + n}}},$$
(15)

• the concept of displacement of the crack-tip opening

$${{m}_{\delta }} = \frac{{\ln \sec \frac{\pi }{2}\frac{{{{\sigma }_{Y}}}}{{{{\sigma }_{0}}}}}}{{\ln \sec \frac{\pi }{2}\frac{{{{\sigma }_{Y}}}}{{\left( {{{n}_{Y}}} \right){{\sigma }_{0}}}}}}.$$
(16)

In these cases, n is the work hardening index in the Ramberg–Osgood relationship.

Estimation of the Probabilistic Safety Factors

To estimate the probabilistic fracture by fracture mechanics criteria, it is necessary to possess full knowledge of the respective ways of reaching the limit state and the distributions of the initial variables according to loading conditions, as well as to know the statistical crack resistance of the material. In fact, these requirements are impossible to meet in full. In this case, various simplifying assumptions and approximations can be used so as to make the probabilistic analysis feasible [7]. The first reason why this is possible in the approaches of probabilistic fracture mechanics is that the estimation of the probability of failure is based on the distribution of fracture viscosity but implies that the fixed yield stress is the same as the average yield stress. Secondly, the estimation of the probability of failure is based on the yield stress distribution but implies that the fixed fracture viscosity is equal to the average fracture viscosity. In this case, it is assumed that the probability of failure can be estimated as the sum of these two probabilities.

Despite its simplicity, this simplified approach is sufficiently accurate and the error in the probability of failure will unlikely exceed an order of magnitude when compared with the full probabilistic method. These errors are considered relatively insignificant when the original requirement is only to estimate the order of the probability of failure [7].

Let us use fracture mechanics to consider an alternative simplified method of estimating the safety factors which correspond to a preset probability of failure. It can be assumed on a sufficiently reasonable basis that variation coefficients \({{{v}}_{R}} = {{s}_{R}}{\text{/}}{{\mu }_{R}}\) of static mechanical behavior do not depend on the type of limit state. Let us also assume that the applied load is described through a certain random distribution, whatever the limit state of the structure. This means that the safety factor of the yield stress determined by probabilistic approaches can be used to estimate, in terms of fracture mechanics, the safety factors, which correspond to the same preset probability of failure, considering the correlation of the safety factor of the yield stress and the safety (crack resistance safety) factors in the deterministic formulation [4, 16].

The safety factor of the yield stress is calculated with the help of a preset probability of failure (4) and reliability \({{{{\beta }}}_{f}}\) (5), considering known variation coefficients \({{{v}}_{Y}}\) and \({{{v}}_{L}}\). In this case, the safety factors of crack resistance, calculated by the proposed simplified method, can be considered as the probabilistic safety factors corresponding to the probability of failure accepted in calculating the safety factor of the yield stress. This approach allows avoiding a more complex and expensive probabilistic analysis of failure on the basis of distribution of the fracture mechanics characteristics.

Probabilistic Safety Factors in Fracture Mechanics

According to the simplified method of estimating the probabilistic safety factors, it can be assumed that variation of the coefficients \({{{v}}_{R}} = {{s}_{R}}{\text{/}}{{\mu }_{R}}\) does not depend on the type of limit state. The safety factor of the yield stress nY is calculated using preset probability \({{P}_{{f~}}}\) (4) of reaching the limit state and reliability index \({{{{\beta }}}_{f}}\) (5) by representative combinations of variation coefficients of the yield stress and applied stresses. In considering the relation between safety factors mFAD in terms of crack resistance diagrams and the safety factors of the yield stress nY in the form of Eqs. (11) and (13), it is possible to determine safety factors mFAD for a preset probability of failure.

This approach allows drawing the dependence of the probabilistic fracture safety factor mFAD as the function of failure probability, considering the relation between the safety factors of the yield stress and the safety factors of crack resistance.

The safety factor mFAD and the safety factor against plastic collapse nY for plane strain are equal. The influence of the probability of failure \({{P}_{{f~}}}\) on mFAD in terms of the crack resistance diagram is shown in Fig. 2 for representative combinations of the variation coefficients and plane strain conditions.

Fig. 2.
figure 2

Influence of the probability of fracture \({{P}_{{f~}}}\) on safety factor mFAD for a representative combination of variation coefficients (plane strain) (1, \({{{v}}_{L}}\) = 0.1; 2, \({{{v}}_{L}}\) = 0.2; 3, \({{{v}}_{L}}\) = 0.3): (a) \({{{v}}_{R}}\) = 0.1; (b) \({{{v}}_{R}}\) = 0.2; (c) \({{{v}}_{R}}\) = 0.3.

Full size image

According to expectations, safety factor mFAD depended on the probability of failure determined by the original data in use, that is, material homogeneity and quality \(({{{v}}_{R}})\), and also by the stability of the loading condition (\({{{v}}_{L}}\)). In addition, a lower probability of failure means increased safety factor mFAD. It also follows from Fig. 2 that the increased uncertainty upon loading (increase in \({{{v}}_{L}}\)) and degraded material quality (increase in \({{{v}}_{R}}\)) increases mFAD for preset probabilities of failure.

It should be noted that there is an equality of safety factors in terms of fracture viscosity mK (14) and crack resistance diagrams mFAD in the case of plane strain (13).

Let us juxtapose the values of the probabilistic safety factors mK calculated by the proposed simplified method with the values of mK, recommended in API 579 [17]. It is seen from Table 1 that the calculated safety factors of fracture viscosity correlate with the values of mK recommended in API 579, especially with variation coefficients \({{{v}}_{L}}\) < 0.3.

Table 1. Comparison of the calculation safety factors by the fracture viscosity with safety factors mK recommended under API 579 for various values of the probability of failure, and representative variation coefficients \({{{v}}_{L}}\) \(({{{v}}_{R}} = 0.1)\)
Full size table

Unlike in plane strain, probabilistic safety factor mFAD for plane stress is calculated by means of formula (11) against the probabilistic safety factor of the yield stress. The results of calculating the probabilistic safety factors for plane stress with the help of the simplified method described above are presented in Table 2. Probabilistic safety factors mFAD also increase with a reduction in the probability of failure and due to the rise in uncertainty upon loading (increase in variation coefficients \({{{v}}_{L}}\)).

The optimal safety factors are estimated proceeding from the target reliability levels corresponding to the recommended probability of failure [18, 19]. For example, if there is no risk of human demise, the recommended probability of failure is \({{P}_{f}} = {{10}^{{ - 4}}}\); otherwise, this probability is \({{10}^{{ - 6}}}\).

Table 2. Design values of safety factor mFAD for various values of the probability of failure and representative variation coefficients \({{{v}}_{L}}\) \(({{{v}}_{R}} = 0.1)\) : plane stress state
Full size table

CONCLUSIONS

A simplified method of estimating the probabilistic safety factors in fracture mechanics is proposed. This method is based on the correlation dependences between the safety factors of the yield stress and the safety factors of crack resistance. Thus, it is proposed to calculate the safety factors, which correspond to a preset probability of failure, by means of the probabilistic safety factors of the yield stress, taking into account their interrelation and the independence of the variation coefficients of the static mechanical performance from the type of limit state. The calculation of the probabilistic safety factors is shown by the example of the safety factor of the fracture viscosity and the diagram of crack resistance. The calculated safety factors of fracture viscosity correlate with the safety factors recommended under standard API 579. Thus, the structural integrity can be ensured without crack resistance testing but with the help of objective estimates based on the probabilistic analysis of original statistics on the creep limits instead of using the generally assigned safety factors.