Probabilistic Distribution of Crack Length in the Case of Multiple Fracture

A model describing crack length distribution is proposed on the basis of experimental laws governing the formation and growth of fatigue cracks in a flat specimen with multiple stress raisers. The density of this distribution corresponds to that of Pareto and can be used to describe the accumulation of scattered defects in a wide range of cracking scale. The critical values of Pareto distribution exponent, which correspond to the limit states of the multiple fracture of solid bodies, have been substantiated.

Introduction. The ratio between the number and size of continuity defects is a fundamental characteristic of the damage of solid bodies in the case of multiple fracture. This ratio in the form of statistical crack size distribution is widely used to construct fracture models of solid bodies and to solve many problems of predicting the load-carrying ability of real structures.

In studies [1, 2], the similarity of empirical dependences of the number of defects, n, on their size a in the widest damage scale range: from micrometer dimensional level to the scale of crustal destruction had been established. For example, the stagewise nature of the damage of the plastic deformation zone ahead of the growing crack tip is characterized by a change in the size distribution of scattered microdefects from exponential [n ∝ exp(−a)] to power-series one (nxa^−γ) [3]. Based on the hypothesis of similarity of multiple fracture, the exponent γ of the power-series (hyperbolic) distribution of microdefects is related to the exponent b of the generalized Gutenberg–Richter function, which describes the dependence of the number of seismic events on their energy [3, 4]. The parameter b is a diagnostic parameter of tectonic events: its value decreases before earthquake.

The same phenomenon is typical of the fracture of metallic materials with scattered cracks [3].

Using statistical defect size distribution, many problems associated with the life prediction of structures and probabilistic assessment of their strength and reliability are solved. For example, if the limit state of a cracked structure occurs when one of the cracks reaches the maximum permissible length a_*, then the distribution function of the life T of this structure is defined by the relation F (T)=1 − P(a_*, T), where P(a, t) is the probability of the fact that at the instant of time t, there is no crack of length greater than a in the structure (crack length distribution function) [5].

The information on defect size distribution allows one to solve problems of assessing the reliability of defect detection in the nondestructive testing of structures [6] and is basic information in the prediction of the coalescence of cracks scattered on the surface under multiple fracture conditions [7, 8].

A particular case of multiple fracture is the multiple site damage (MSD) of riveted joints of aircraft structures. Taking into account the large number of fracture nuclei (rivet holes) and the random nature of defect formation and growth, it is proposed to use statistical fatigue crack length distribution as a characteristic of the damaged state [9]. The corresponding distribution can be obtained on the basis of the results of control of the technical state of structures, the amount of which is, however, very limited.

It should be noted that the theoretical substantiation of defect size distribution in the case of multiple fracture is a problematic task. The present paper proposes a model describing fatigue crack size stochasticity with allowance for the laws governing random crack formation and growth.

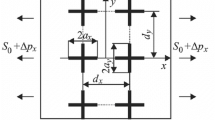
Results of Experimental Investigations. To construct the model, let us make use of the data of an experimental investigation of the fatigue fracture of specimens with multiple stress raisers in the form of holes [10].

Flat specimens of D16AT aluminum sheet alloy 1.5 mm in thickness were tested, in which there were three rows of 14 holes with a diameter of 4 mm. The distance between the centers of the holes was 20 mm. The specimens were loaded with a cyclic tension (R = 0) with a frequency of 11 Hz at three values of the maximum nominal cycle stress: 80, 100, and 120 MPa. The procedure for recording and measuring the size of cracks developed from holes is described elsewhere, e.g., in [10].

Crack Growth. The maximum length of cracks under investigation was limited by the size of the bridge between the edges of the holes, which was 16 mm. In this size range, the plots of the crack length a versus the number of loading cycles N in semi-logarithmic coordinates (Fig. 1) can be described by a linear function of the form

$$ \mathrm{In}\kern0.5em a=p+ hN, $$

(1)

Fig. 1.

Typical plots of crack length versus the number of loading cycles at different values of the maximum stress in the cycle: σ_max = 80 (a) and 100 MPa (b).

where p and h are regression coefficients.

The behavior of 55 cracks was studied on three specimens for each cyclic loading regime. Relation (1) gave a good fit to the growth of each crack. The coefficient of determination averaged over all cracks was: R² = 0.9947 for 13 cracks at σ_max = 80 MPa, R² = 0.9914 for 23 cracks at σ_max = 100 MPa, and R² = 0.9926 for 19 cracks at σ_max = 120 MPa.

For the initial crack length a₀ = 1 mm, it follows from (1) that

$$ p=-{hN}_0, $$

(2)

where N₀ is the number of cycles till the formation of an initial crack. Substituting relation (2) into Eq. (1) yields:

$$ a=\exp \left[h\left(N-{N}_0\right)\right]. $$

(3)

The coefficient h determines the crack velocity depending on crack length (da/dN = ha) and is a function of working stress. Note that exponential fatigue crack growth at the initial propagation stage is typical of many materials [11], including aluminum alloys of aircraft structures [12, 13].

At a fixed working stress level, the coefficient h defines a random crack growth path and hence is a random quantity. For the statistical samples of cracks under investigation at each working stress level, the distribution of values of this coefficient is satisfactorily described by a uniform law with the density of distribution

$$ f(h)=\frac{1}{h_{\mathrm{max}}-{h}_{\mathrm{min}}}, $$

(4)

where h_min and h_max are the limits of the range of possible values of the coefficient h(h ∈ [h_min, h_max]). If follows from experimental data that when the maximum stress in the cycle increases, the h_max value does not change, and the parameter h_min increases (Fig. 2), indicating that the proportion of “slow” cracks decreases on increasing the load. Owing to this, the mean value of the coefficient h increases (Fig. 2).

Fig. 2.

Variation of the maximum (h_max), minimum (h_min), and mean (h _m ) values of the coefficient h as a function of the maximum stress in the cycle σ_max.

Crack Formation. Let us limit the size of initial cracks by the value a₀ = mm. This means that the cracks of length a < 1 mm are not taken into account in the subsequent analysis. From relation (2) it follows that

$$ {N}_0=-\frac{p}{h}. $$

(5)

The rate of crack formation (density of the points on the N axis corresponding to N₀) can be determined from the plots of the number of accumulated cracks n versus the number of loading cycles (Fig. 3).

Fig. 3.

Plots of the number of cracks in specimens versus the number of loading cycles at different values of the maximum stress in the cycle: σ_max = 80 (1), 100 (2), and 120 MPa (3). The abscissas of the points correspond to N₀ values for each crack.

In the case of linear approximation of the obtained data (Fig. 3), it can be assumed that the rate of crack λ formation λ is constant for each stress level and is determined from the following equation:

$$ n=\uplambda N=c, $$

(6)

where c is a regression coefficent. The values of the parameter λ and the limits of the ranges of its applicability are listed in Table 1.

Table 1. Values of the Rate of Crack Formation and the Limits of Ranges at Different Maximum Stresses in the Cycle

Crack Size Stochasticity Model. The statistical spread of crack length values at a constant cyclic stress level is caused by two random factors: growth and formation of defects in time.

Fatigue cracks grow along random paths [14], which may be due, at constant loading parameter, only to the random nature of the material structure [15].

If it is assumed that all crack grow at the same (determinate) rate, but each crack is formed at a random instant of operating time, then the spread of their size values will be due exclusively to growth time: the cracks that formed earlier will have a greater length. The defect size distribution in this case is determined by the distribution of operating time to crack formation [16].

Based on the above experimentally established laws governing the behavior of cracks, let us see how the crack length distribution is described with allowance for random crack formation and growth. In this case, we shall use the approach presented in [17].

Let us introduce a size parameter y, which is unambiguously related to crack length by the relation y = ln a. We assume that the length of cracks a is measured in millimeters, and that their initial length a₀ = 1mm. According to Eq. (1), we get

$$ y=p+ hN. $$

(7)

Let us define the distribution function of the parameter y at a fixed instant of the operating time N′. In this case, N′ > N_min, where N_min is the threshold value of the number of cycles to crack formation.

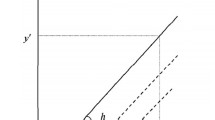
This function is determined by the probability of the event y < y′, where y′ is any fixed value of the parameter y at N′ (Fig. 4).

Fig. 4.

Crack growth diagram.

Suppose all cracks grow with the same value of the velocity parameter h. For some crack, whose velocity is defined by the parameter h, and the length at the operating time N′ is y′, the number of cycles to crack formation will correspond to the ${N}_0^{\prime }$ value (Fig. 4). It is quite obvious that in this particular case, the event y < y′ will be satisfied for all cracks that are formed in the operating time range $\left({N}_0^{\prime },{N}^{\prime}\right]$. The conditional function of the parameter y is determined from the relation:

$$ F\left(y;N\left|h\right.\right)=P\left\{\widehat{y}<{y}^{\prime };{N}^{\prime}\left|h\right.\right\}=P\left\{{N}_0\in \left({N}_0^{\prime },{N}^{\prime}\right]\left|h\right.\right\}, $$

(8)

where the sign ^ denotes a random quantity, while P{∙} is the probability of an event.

We assume that crack formation corresponds to the Poisson stream of events having the properties of ordinariness and absence of aftereffect. According to the experimentally established relation (6), the rate of crack formation λ in the corresponding operating time ranges is a constant. Then the probability of crack formation in the operating time range $\left({N}_0^{\prime },{N}^{\prime}\right]$ will be defined as

$$ P\left\{{N}_0\in \left({N}_0^{\prime },{N}^{\prime}\right]\left|h\right.\right\}=1-\exp \left[-\uplambda \left({N}^{\prime },{N}_0^{\prime}\right)\right]. $$

(9)

According to the adopted crack growth diagram (Fig. 4), the obvious relation

$$ {N}^{\prime }-{N}_0^{\prime }=\frac{y^{\prime }}{h} $$

(10)

is satisfied.

In view of expressions (9) and (10), formula (8) for any values of N ′ and y′ will take the form

$$ F\left(y\left|h\right.\right)=1-\exp \left(-\frac{\uplambda y}{h}\right). $$

(11)

From (11), it follows that the conditional distribution function of the parameter y at the given h value is independent of the cyclic operating time N.

Formula (11) defines the distribution of the size parameter y with allowance for only one factor: random defect formation. The effect of random crack growth on crack length distribution can be described by the random value of the velocity parameter h. Using the total probability formula for the conditional distribution function (11), we obtain the unconditional distribution function of the defect size parameter y:

$$ G(y)=\underset{H(h)}{\int }f(h)F\left(y\left|h\right.\right) dh=1-\underset{H(h)}{\int }f(h)\exp \left(-\frac{\uplambda y}{h}\right) dh, $$

(12)

where f (h) is the distribution density of the parameter h, and H(h) is its domain of definition.

When deriving formula (12), the property of normalization, $\underset{H(h)}{\int }f(h) dh=1$, was taken into account.

Allowing for the obtained empirical distribution of the velocity parameter h (4), expression (12) is rearranged in the form

$$ G(y)=1-\frac{1}{h_{\mathrm{max}}-{h}_{\mathrm{min}}}\underset{h_{\mathrm{min}}}{\overset{h_{\mathrm{max}}}{\int }}\exp \left(-\frac{\uplambda y}{h}\right) dh. $$

(13)

The integral on the right-hand side of Eq. (13) is expressed by the replacement of the variable u = λy/h in terms of the integral exponential function ${E}_1(z)=\underset{z}{\overset{\infty }{\int }}{u}^{-1}\exp \left(-u\right) du$ [18]. After transformations of (13) we have

$$ G(y)=1-\frac{1}{h_{\mathrm{max}}-{h}_{\mathrm{min}}}\left\{{h}_{\mathrm{max}}\exp \left(-\frac{\uplambda y}{h_{\mathrm{max}}}\right)-{h}_{\mathrm{min}}\exp \left(-\frac{\uplambda y}{h_{\mathrm{min}}}\right)+\uplambda y\left[{E}_1\left(\frac{\uplambda y}{h_{\mathrm{min}}}\right)-{E}_1\left(\frac{\uplambda y}{h_{\mathrm{max}}}\right)\right]\right\}. $$

(14)

We obtain the formula for the distribution density of the parameter y by differentiating the distribution function (14) with respect to this parameter:

$$ g(y)=\frac{\uplambda}{h_{\mathrm{max}}-{h}_{\mathrm{min}}}\left[{E}_1\left(\frac{\uplambda y}{h_{\mathrm{max}}}\right)-{E}_1\left(\frac{\uplambda y}{h_{\mathrm{min}}}\right)\right]. $$

(15)

We make transition from the distribution of the parameter y (15) to the distribution of the crack length a on the basis of the rule of transformation of random variables. Allowing for the functional relation y(a) = ln a and expression (15) adopted in the study, we obtain a formula for crack length density:

$$ f(a)=\left|\frac{dy}{da}\right|g\left[y(a)\right]=\frac{\uplambda}{a\left({h}_{\mathrm{max}}-{h}_{\mathrm{min}}\right)}\left[{E}_1\left(\frac{\lambda \kern0.5em \mathrm{In}\kern0.5em a}{h_{\mathrm{max}}}\right)-{E}_1\left(\frac{\lambda \kern0.5em \mathrm{In}\kern0.5em a}{h_{\mathrm{min}}}\right)\right]. $$

(16)

Note that the function (16) is positive and satisfies the normalization condition $\underset{1}{\overset{\infty }{\int }}f(a) da=1$, which meets the requirements to random variable distribution density.

The calculations from formula (16) with allowance for the experimental values of the parameters , h_min , and h_max show that the function for the distribution density of the crack length a is of hyperbolic type (Fig. 5). When the working stresses in the cycle increase, the hyperbola becomes steeper, indicating that small cracks predominate in the sample.

Fig. 5.

Crack length distribution density at different values of the maximum stress in the cycle: calculated curves (lines) – (1) σ_max = 80 MPa, (2) σ_max = 100 MPa, (3) σ_max = 120 MPa, and experimental (points) at σ_max = 80 MPa.

The experimental data for σ_max = 80 MPa do not contradict the calculated values of crack length distribution density (Fig. 5).

Discussion of the Obtained Results. The calculated plots in Fig. 5 are well described by functions of the form

$$ \varphi (a)\cong \frac{A}{a^{\gamma }}, $$

(17)

where A and γ are constants, whose values for the maximum working stresses in the cycle are listed in Table 2. Note that the function (17) is only an approximation of the distribution density (16).

Table 2. Values of the Coefficients in Formula (17) for Different Stresses in the Cycle

The regression relationship between the coefficients A and γ for different maximum stresses in the cycle (Table 2) is of the form A = 1.0036γ−1.0992 (Fig. 6) (correlation coefficient = 0.9937). With allowance for natural approximation errors, it may be assumed that

$$ A=\gamma -1. $$

(18)

Fig. 6.

Dependence between the coefficients A and γ.

Then, formula (7) can be reduced to

$$ \upvarphi (a)=\frac{\upgamma -1}{a^{\gamma }}. $$

(19)

The distribution (19) belongs to power-series distributions, the best known of which are Pareto (or Zipf) distribution for continuous quantities and Yule distribution for discrete quantities [19]. For example, using the agreed notations, the crack length distribution density according to the Pareto law is given by

$$ \upvarphi (a)=\frac{\upgamma \hbox{-} 1}{a_{\mathrm{min}}}{\left(\frac{a_{\mathrm{min}}}{a}\right)}^{\upgamma}, $$

(20)

where a_min is the minimum crack length in the sample (in the case in question, a_min = 1 mm).

Note that power-series distributions describe a fairly wide range of events in nature and in the social sphere [19]. They belong to distributions with “heavy tails,” which reflect the presence in samples of random variables which are close to extremely large values. Therefore, this class of distributions is applicable to the description of the statistics of catastrophic fractures and their consequences as well [20].

Let us show that formula (19), which was obtained for a particular case of exponential crack growth, is able to describe general laws governing the multiple fracture of solid bodies. In this case, the exponent γ in (19) can be interpreted as a dimensional stochasticity parameter of scattered cracks regardless of their scale and orientation.

The numerical characteristics of the Pareto distribution (19) have peculiarities at certain values of the exponent γ. For example, the mathematical expectation of crack length m _a is determined on the basis of (19) at γ > 2:

$$ {m}_a=\frac{\upgamma -1}{\upgamma -2}, $$

(21)

and the variance D _a at γ >3:

$$ {D}_a=\frac{\upgamma -1}{{\left(\upgamma -2\right)}^2\left(\upgamma -3\right)}. $$

(22)

The experimental values of the exponent γ for the multiple fraction of various materials under different types of loading show that γ >3 [2]: γ = 6.2 (polycrystalline copper in fatigue), γ = 7.1 (brass in tension), γ = 77. (iron in creep), γ = 37 . (347 steel in creep), γ = 37. (304 steel in creep), and γ = 3.13 (rock masses).

It was found that as the multiple fracture of metallic materials develops the exponent γ decreases to some threshold value. For example, in the case of tension of 20 steel, the value γ ≈ 2 corresponds to final fracture [3]. As was already pointed out, a similar law holds in tectonic events, when before earthquake, the exponent b of the generalized Gutenberg–Richter function decreases to the critical value b ≈ 1. The hypothesis of the similarity of these manifestations of multiple fracture, which differ in scale (by several orders of magnitude) [3, 4], allows one to estimate the threshold values of the exponent γ, which follow from formulas (21) and (22).

It should be noted that the phenomenon of similarity of the empirical curves of defect size distribution in a wide damage scale range (self-similarity of multiple fracture) follows directly from the property of power-series distributions. This is the only type of distributions which look identically regardless of the scale they are considered (scale-invariant distributions) [19]. Therefore, there is a possibility to simulate multiple fracture processes in a wide size range: from microscopic to macroscopic one.

Within the framework of a self-similar approach based on the similarity of the multiple cracking of solid bodies, a formula for the length distribution probability density of equally oriented cracks is proposed [4, 21]:

$$ p(L)=\frac{c_0}{L^{\gamma \prime +1}},\kern0.5em L>{L}_0, $$

(23)

where L is crack length, γ′ and c₀ are coefficients, and L₀ is some threshold defect size.

The parameter γ′ is expressed, with allowance for the relation between earthquake magnitude and acoustic emission signals, in terms of the exponent b of the generalized Gutenberg–Richter function as [4, 21]

$$ {\gamma}^{\prime }=2b. $$

(24)

From the comparison of formulas (19) and (23) and, in view of (24), it follows that

$$ \upgamma ={\upgamma}^{\prime }+1=2b+1. $$

((25)

The threshold values of the exponent b are estimated with allowance for the fractal dimension of cracked bodies and their size. It is stated that at early fracture stages, b ≥ 1.5 (γ ≥ 3), and before final fracture, b = 1 (γ = 3) [4, 21]. Because, in this case, a leading crack of the length comparable with the size of the body is formed, the variance D _a increases sharply, which is described by formula (22).

For small-sized bodies, however, the case of 0.5 < b < 1 is possible [21], which is confirmed by the results of experimental investigations of defect size distribution. Similar b values are found for tectonic break-ups, e.g., 0.67 < b < 2.07 [3], which is referred to as post-critical regime [21]. For this case on the basis of (25), we have: 2 < γ < 3. The threshold value γ = 2 is the limiting value for the determination of the mean defect size from formula (21).

Thus, the obtained crack length distribution (19) indirectly substantiates, in the presence of multiple defects in the body, the existence of two critical values of the exponent γ, which can be taken as a multiple fracture criterion. At γ = 3, the stability of the accumulation process of scattered cracks is disturbed owing to the coalescence of some of the defects and the formation of a “leading” crack of much greater length, as compared with the existing cracks (D _a →∞). This limit state, in the case of multiple fracture, is treated as “brittle.”

If the “leading” crack does not cause the complete fracture of the body, the accumulation of damages is accompanied by an increase in their size (ma increases), and the limit state occurs at γ → 2, when the avalanche-like growth of defects takes place by their multiple coalescence. This limit state is treated as “viscous.” Its occurrence in metallic materials is accompanied by a change in the scale of multiple fracture, by its becoming stagewise [3]. In this particular case, the singularity of the variance D _a at γ = 3 implies the formation of a stable defect of higher dimensional level.

Conclusions. The probabilistic distribution of fatigue crack length, obtained on the basis of a theoretical model of random crack formation and growth, is described by a power function of hyperbolic type. With allowance for the experimentally determined values of the parameters of random crack formation and growth, this function is transformed to the crack length distribution density, which corresponds to the Pareto distribution. Allowing for data available in publications, it may be assumed that this type of defect size distribution is characteristic of the multiple fracture of solid bodies. In this case, the exponent γ of the Pareto distribution is the main parameter controlling the limit state in the case of multiple fracture. At γ = 3, fracture occurs through the coalescence of some of the defects and the formation of a single large crack, which is comparable with the characteristic size of the body (criterion of “brittle” multiple fracture). At γ → 2, multiple coalescence of scattered defects, their enlargement and transition of damage to a higher dimensional level (via the “viscous” multiple fracture criterion) take place.