INTRODUCTION

A large number of articles have been devoted to theoretical development of methods for the analysis and synthesis of multilayer periodic structures due to the relevance of these issues for solving a number of problems of both applied and fundamental physics [1–6]. The results relating to periodic structures consisting of quarter-wave, half-wave, or layers close to them in optical thicknesses have been sufficiently well developed and generalized with sufficient completeness. However, the development of modern physics and technology, the intensive development of such regions of the electromagnetic spectrum as the mid- and far-infrared ranges, and the need to solve the problems of diagnosis and synthesis of layered heterogeneous media with a given Nyquist plot and with different periods of heterogeneity all require the development of a new approach to both analytical and numerical analysis of the properties and features of layered structures in a more general formulation of the problem and, as a result, the development of a method that makes it possible to find an algorithm analytically for synthesizing layered structures with structural and amplitude-phase properties which differ from the classical ones.

The analytical solution of such a problem is extremely important because the analytical form makes it possible not only to synthesize a multilayer structure with the given Nyquist plot on the whole continuous set of their possible values without resorting to special numerical methods and applied programs [7–11] but also to carry out a generalized analysis of its structural and wave properties depending on different kinds of physical factors (the influence on its Nyquist plot of the variation of layer thicknesses, refractive indices, the presence of losses in the layers of the structure, the order of alternation, etc.). In addition, the analytical form of the algorithm for synthesizing multilayer structures makes it possible to establish general patterns of its Nyquist plot from different structural solutions and find optimal solutions for different criteria (the number of layers, their thicknesses, period contrast, spectral characteristics, etc.).

1 THE METHOD OF COUPLED WAVE THICKNESSES

In order to solve this problem, the normal incidence of a plane monochromatic wave on a system consisting of a multilayer structure with the refractive indices of the layers in the two-layer (most common in practice) period \(n_{1}\) and \(n_{2}\) (the layer adjacent to a medium with the refractive index \(n_{S}\)) which, being located between two media with real refractive indices \(n_{L}\) (the medium from which the wave propagates) and \(n_{S}\) (the antireflection medium), provides a zero reflection factor for a given wavelength \(\lambda\), i.e., the simultaneous fulfillment of the amplitude \(|r_{C}|=|r_{S}|\) and phase \(\varphi_{C}=\varphi_{S}+\pi(2k+1)\), \((k=0,1,2,\dots)\) matching conditions (where \(|r_{C}|,\varphi_{C}\) are the modulus and phase of the reflection coefficient of the wave from the structure when the wave comes from the layer with the refractive index \(n_{2}\) in the absence of the matched medium, \(|r_{S}|\), and \(\varphi_{S}\) is modulus and phase of the reflection coefficient of the wave from the matched medium in the absence of the matching structure).

Consideration of the problem in this formulation corresponds to the main goal of the research, because finding structural solutions of the considered system that satisfies the condition of zero reflection at different values of the refractive index of the matched medium \(n_{s}\) on the entire continuous set of its possible values means that the desired algorithm for synthesizing a new class of multilayer structures with structural-wave properties, which make it possible to implement the solution of the problem.

When solving the initial equations, the wave thicknesses of the layers in the period of the structure were considered not fixed but being in the entire continuous region of physically admissible values. The exact solution of the considered problem in the form of three coupled equations is as follows [12]:

$$n_{s}=\bigg{|}\frac{n_{1}T_{1}+n_{2}T_{2}}{n_{1}T_{2}+n_{2}T_{1}}\bigg{|}\frac{n_{1}n_{2}}{n_{L}},$$
(1)
$$N=2K:$$
$$1-\frac{P}{A}T_{1}T_{2}=\frac{U_{K-2}(x)}{U_{K-1}(x)}\sqrt{(1+T_{1}^{2})(1+T_{2}^{2})},$$
(2)
$$N=2K+1:$$
$$1-\frac{B}{A}T_{1}T_{2}=\frac{U_{K-2}(x)}{U_{K-1}(x)}\sqrt{(1+T_{1}^{2})(1+T_{2}^{2})},$$
(3)

where \(N\) is the number of layers in the structure, and \(K\) is the number of periods,

$$P=\frac{(n_{2}^{2}-n_{L}n_{s})(n_{L}n_{1}^{2}-n_{s}n_{2}^{2})}{n_{2}^{2}(n_{L}-n_{s})(n_{L}n_{s}-n_{1}^{2})},$$
(4)
$$B=\frac{n_{2}^{4}-n_{L}n_{s}n_{1}^{2}}{n_{2}^{2}(n_{L}n_{s}-n_{1}^{2})},$$
(5)
$$A=\frac{n_{1}(n_{2}^{2}-n_{L}n_{s})}{n_{2}(n_{L}n_{s}-n_{1}^{2})},$$
(6)

\(U_{K-1}(x)\), \(U_{K-2}(x)\) are the Chebyshev polynomials of the second kind, where

$$U_{K}(x)=2^{K}\Bigg{[}x^{K}-\frac{K-1}{1!2^{2}}x^{K-2}$$
$${}+\frac{(K-2)(K-3)}{2!2^{4}}x^{K-4}$$
$${}-\frac{(K-3)(K-4)(K-5)}{3!2^{6}}x^{K-6}+\dots\Bigg{]},$$
$$x=(1-pT_{1}T_{2})/\sqrt{(1+T_{1}^{2})(1+T_{2}^{2})},$$
$$p=\frac{n_{1}^{2}+n_{2}^{2}}{2n_{1}n_{2}},$$
$$T_{i}\equiv\tan({2\pi n_{i}d_{i}/\lambda})\quad(i=1,2),$$

\(d_{1,2}\) is the thickness of the physical layer.

1.1 The Coupling Condition of Wave Thicknesses

In order to obtain the coupling conditions of wave thicknesses, let us rewrite Eq. (1) in the following form:

$$T_{1}=AT_{2},$$
(7)

then from relation (7) we obtain

$$D_{1}=\frac{\lambda}{2\pi}\bigg{(}\text{arctg}~A~\text{tg}\frac{2\pi}{\lambda}D_{2}+\pi k\bigg{)},$$
$$(k=0,1,2,\dots)$$
(8)

where \(D_{2}=\frac{\lambda}{2\pi}(\text{arctg}~T_{2}+\pi k)\) \((k=0,1,2,\dots)\), \(D_{1}=n_{1}d_{1}\), \(D_{2}=n_{2}d_{2}\) are wave (optical) thicknesses of the layers in a multilayer structure period.

Therefore, Eq. (1) is the coupling condition for the wave thicknesses of the layers in the period of the structure, and, as can be seen from (6), the coupling coefficient \(A\) is invariant with respect to the number of layers in the structure. Since coupling condition (8) was obtained under the condition of the zero reflection coefficient from the considered system, the independence of the coupling coefficient \(A\) from the number of layers in the structure makes it possible to conclude that such a class of multilayer structures with a two-layer period has a fundamental property which can be formulated as follows: for all multilayer structures of such a class with a two-layer period, which implement the mode of complete matching of two media with real refractive indices \(n_{L}\) and \(n_{S}\), the wave thicknesses of the layers in the period of the structure are always coupled according to relation (8). That is, the fulfillment of coupling condition (8) and its invariance on the number of layers means that for any structures in which the wave thicknesses of the layers in the period are associated with relation (8), the phase matching condition is satisfied. Moreover, it follows from relation (6) that for any real values of \(n_{S}\geq n_{L}\) and arbitrary values of the refractive indices of the layers of the structure and their order of alternation, there always exists a value \(A\) for which the phase matching condition holds, regardless of the number of layers in the structure and the fulfillment of the amplitude matching condition.

1.2 Basic Equations with Coupled Wave Thicknesses

Finally, given coupling condition (7), the system of initial equations (2), (3) can be rewritten as follows [12]

$$N=2K:$$
$$1-PT_{2}^{2}=\frac{U_{K-2}(x)}{U_{K-1}(x)}\sqrt{(1+T_{2}^{2})(1+A^{2}T_{2}^{2})},$$
(9)
$$N=2K+1:$$
$$1-BT_{2}^{2}=\frac{U_{K-2}(x)}{U_{K-1}(x)}\sqrt{(1+T_{2}^{2})(1+A^{2}T_{2}^{2})},$$
(10)

Therefore, considering initially given values \(n_{1}\), \(n_{2}\), and \(n_{L}\), the problem can be solved by finding the numerical values of physical thicknesses \(d_{2}\) for a given value of \(n_{S}\) depending on the number of structure periods \(K\). The numerical values of \(d_{1}\) are determined from relation condition of optical thicknesses (8).

Equations (9), (10) with respect to \(T_{2}\) are the following sum of terms of a convergent alternate power series:

$$\sum_{K=1}^{\infty}(-1)^{K}a_{K}T_{2}^{2K}=-1,$$
(11)

where \(a_{K}\) are the coefficients depending on \(n_{1}\), \(n_{2}\), \(n_{L}\), \(n_{S}\), and \(K\), and, in Eq. (11), the coefficient \(a_{1}=K(\Psi+Q(K-1))\), where \(\Psi=P\) for \(N=2K\) and \(\Psi=B\) for \(N=2K+1\).

2 THIN-LAYER INTERFERENCE STRUCTURES (TIS)

In [12], the problem was set and solved to find such solutions from the entire set of solutions of the system of equations (9), (10) for which there are minimum possible thicknesses of the layers in the period of the multilayer structure. Since in this case the arguments of the functions \(T_{i}\) are small, then, while neglecting the terms with power exponents higher than the second in the functions \(T_{i}\) from Eqs. (9), (10), the following was obtained

$$N=2K,$$
$$d_{2}=\frac{\lambda}{2\pi n_{2}}\text{arctg}~\Big{(}K\big{(}P+Q(K-1)\big{)}\Big{)}^{-1/2},$$
(12)
$$N=2K+1,$$
$$d_{2}=\frac{\lambda}{2\pi n_{2}}\text{arctg}~\Big{(}K\big{(}B+Q(K-1)\big{)}\Big{)}^{-1/2},$$
(13)

where

$$Q=\frac{n_{L}n_{S}(n_{2}^{2}-n_{1}^{2})^{2}}{2n_{2}^{2}(n_{L}n_{S}-n_{1}^{2})^{2}},$$
(14)

In this case, for \(K=1\), relations (12), (13) are exact, and for \(K>1\), the performed approximation is quite justified, because due to the inversely proportional dependence of thickness of layers on their number, their thickness can be tens times less than a quarter-wave; moreover, the total wave thickness of the multilayer structure appears to be less than a quarter-wave one [12].

A sufficiently detailed analytical, numerical, and experimental analysis of the fundamental structural and spectral properties of such thin-layer structures has been performed [12–21]. It showed that they are preserved for this class of structures with two-, three-, and multilayer periods as well as for aperiodic thin-layer structures; in the case of small losses in the layers of the structure and the matched medium; in the case of oblique wave incidence; in small variations of optical and geometric parameters of layers; and if the wavefront of the incident wave is not a flat one.

As an example, the presence of such properties of thin-layer structures as the matching invariance (refractive index of the antireflection medium \(n_{S}\)) on the number of periods of the structure and, at the same time, the inverse relationship of the layer thickness on it, makes it possible to vary the thickness of layers of the structure in a wide range (without changing the total optical thickness of the entire structure), thus meeting different kinds of physical and technological requirements for the thickness of the layers in practical implementation.

The analysis and generalization of the results of studies of the characteristics of such structures showed that they have a number of unique structural and wave properties inherent only to them, which made it possible to allocate such structures to a separate class, that is, thin-layer interference structures (TLIS).

However, in [12] it was shown that according to the proposed algorithm all thin-layer solutions (the thicknesses of both layers in the period of the structure are less than quarter-wave) are implemented for the coupling coefficient \(A\geq 0\), i.e., for the values of the refractive indices of the antireflection media \(n_{S}\) in the following interval:

$$n_{l}^{2}\leq n_{S}n_{L}\leq n_{h}^{2},$$
(15)

where \(n_{l},n_{h}\) are the low and high refractive indices of the layers in the period of the structure, respectively. This circumstance limited the use of the proposed method for matching media with refractive indices outside this interval of values.

3 \(\pi\)-STRUCTURES

In this article, we considered the possibility of synthesizing antireflective structures using the proposed method and algorithm (9), (10) outside interval (15). In this case, the considered intervals of values \(n_{S}\) outside interval (15) are as follows:

$$n_{L}\leq n_{S}<{n_{l}^{2}/n_{L}}\quad\text{and}\quad n_{S}>{n_{h}^{2}/n_{L}}.$$

From expression (6) it can be seen that at any of these intervals the coupling coefficient is \(A<0\) and, as follows from (7), the condition is fulfilled: either \(T_{1}<0\) and \(T_{2}>0\), or vice versa. A negative value of the function \(T_{1}\), e.g., means that the optical thicknesses of layers of such a structure are in the intervals of values \({\lambda/4}<n_{1}d_{1}<\lambda/2\) and \(0<n_{2}d_{2}<\lambda/4\) (\(T_{1}<0\), \(T_{2}>0\)), and the wave thicknesses of the layers can be changed when changing the sign of the function T (\(T_{1}>0\); \(T_{2}<0\)) by simply subtracting the corresponding arguments from \(\pi-2\pi n_{i}d_{i}/\lambda\) and \(\pi-2\pi n_{2}d_{2}/\lambda\), or in expressions for thicknesses:

$$d^{\prime}_{1}={\lambda/2n_{1}-d_{1}}\quad\text{and}\quad d^{\prime}_{2}={\lambda/2n_{2}-d_{2}}.$$

This structural feature is due to the proposed method and the algorithm obtained on its basis in the form of a special condition of coupled wave thicknesses and, therefore, forms a separate class of antireflection structures, which hereafter we will call ‘‘\(\pi\)-structures.’’

3.1 Analytical Solutions of Equations with Coupled Wave Thicknesses

Since it is impossible to obtain the exact analytical solution of Eqs. (9), (10) in a form that is general and convenient for analysis (for any \(K\)), let us consider the exact solutions of Eqs. (9), (10) for different values of the number of the layers of the structure \(N\). From the analysis of the obtained solutions, let us determine the range of values of the refractive indices of the matched media \(n_{S}\), in which for the given number of layers the mode of complete matching is implemented. Considering \(n_{1},n_{2}\), and \(n_{L}\) are a priori set and known values, the main required parameters of such an antireflection \(N\)-layer coating in this case are the thicknesses of layers in the structure period at different values of the refractive indices of the matched media \(n_{S}\).

Solutions of equations (9), (10) are real values of the function \(T_{2}\), knowing which from relation (8) the thicknesses of layers in the period of structure \(d_{1}\) and \(d_{2}\) corresponding to these solutions are found.

3.1.1. Consider the case where \(N=2\).

The solution of Eq. (9) for \(N=2\), \((K=1)\) given that \(U_{0}(x)=0\) has the following form:

$$T_{2}=\pm 1/\sqrt{P}.$$
(16)

The negative sign of the function \(T_{2}\) means that its argument in this case is \(\arg(-T_{2})=\pi-\arg(T_{2}).\)

In the interval of low values of the refractive indices of antireflection media \(n_{L}\leq n_{S}{<n_{l}^{2}/n_{L}}\), given that the real values of the thicknesses of the layers of the structure are at \(P\rangle 0\), we obtain from the analysis of relation (4) that the real thicknesses of the layers are at \(n_{2}<n_{1}\) (\(n_{1}=n_{h};n_{2}=n_{l}\)) and when the following condition is satisfied:

$$n_{h}>{n_{l}^{2}/n_{L}}.$$
(17)

In cases where the antireflection media has high refractive indices such that \(n_{S}>{n_{h}^{2}/n_{L}}\), it follows from the analysis of relation (4) that Eq. (16) has no valid solutions for any values and order of alternation of the refractive indices of the layers \(n_{1}\) and \(n_{2}\).

In particular, if it is possible to select the materials with the refractive index \(n\) that satisfy the condition \(n^{2}=n_{l}^{2}=n_{S}n_{L}\) or \(n^{2}=n_{h}^{2}=n_{S}n_{L}\); the solution of Eq. (16) in these cases is a classical quarter-wave layer and for the values of the refractive indices of the matching structure that satisfy the condition \(({n_{h}/n_{l}})^{2}n_{L}=n_{S}\) the structure becomes two-layer with quarter-wave wave thicknesses of layers.

Therefore, if condition (17) is fulfilled, the two-layer structure can provide a mode of full matching with media whose refractive indices are in the following range:

$$n_{L}\leq n_{S}\leq n_{h}^{2}/n_{L},$$

3.1.2. If \(N=3\), \((K=1)\), the solution of Eq. (10) is as follows:

$$T_{2}=\pm 1/\sqrt{B}.$$
(18)

In the interval \(n_{L}\leq n_{S}<{n_{l}^{2}/n_{L}}\) for any real values of \(n_{1},n_{2}\) provided that \(n_{2}<n_{1}\) (\(n_{2}=n_{l};n_{1}=n_{h}\)), \(B\rangle 0\) and Eq. (18) has two valid solutions.

In the interval \(n_{S}>{n_{h}^{2}/n_{L}}\), there are two valid solutions to Eq. (18) if \(n_{1}<n_{2}\) and \(n_{S}<{n_{h}^{4}/n_{l}^{2}n_{L}}\).

In particular, if the refractive indices of the layers of the structure are such that the condition \(n_{S}={n_{h}^{4}/n_{l}^{2}n_{L}}\) is satisfied, then the matching structure becomes a three-layer structure with quarter-wave wave thicknesses of the layers.

Therefore, the three-layer structure provides a complete matching mode with media whose refractive indices are in the following range:

$$n_{L}\leq n_{S}\leq n_{h}^{4}/n_{l}^{2}n_{L},$$

and the wave thicknesses of the layers, in this case, take values from zero (\(n_{S}=n_{L}\)) to quarter-wave (\(n_{S}={n_{h}^{4}/n_{l}^{2}n_{L}}\)).

3.1.3. If \(N=4\), \((K=2)\) from Eq. (9) for \(N=4\) (\(U_{0}(x)=1,\) \(U_{1}(x)=2x\)), we obtain:

$$a_{2}T_{2}^{4}-a_{1}T_{2}^{2}+1=0,$$
(19)

where: \(a_{2}=A(2Pp-A)\), \(a_{1}=2(P+Q)\) and the solution of Eq. (19) has the following form:

$$T_{2}=\pm\Bigg{(}\frac{a_{1}\pm\sqrt{a_{1}^{2}-4a_{2}}}{2a_{2}}\Bigg{)}^{1/2}.$$
(20)

In the interval of values of the refractive indices \(n_{S}\) of antireflection media \(n_{L}\leq n_{S}<n_{h}^{4}/n_{l}^{2}n_{L}\), Eq. (19) has four solutions for arbitrary values of \(n_{1}\) and \(n_{2}\), and for values of \(({n_{h}/n_{l}})^{4}n_{L}<n_{S}\leq\frac{n_{h}^{3}}{n_{l}n_{L}}\) for any valid values of the refractive indices of the layers in the structure period and their optimal alternation order (\(n_{1}<n_{2}\)), Eq. (19) has two valid solutions.

If the refractive indices of the layers of the structure satisfy the condition \(({n_{h}/n_{l}})^{4}n_{L}=n_{S}\), the wave thicknesses of the layers become quarter-wave.

Therefore, a four-layer structure can form a complete matching mode with media whose refractive indices are in the following range:

$$n_{L}\leq n_{S}\leq n_{h}^{3}/n_{l}n_{L}.$$

3.1.4. We consider a five-layer structure: \(N=5\), \((K=2)\).

In this case, from Eq. (10) we obtain:

$$b_{2}T_{2}^{4}-b_{1}T_{2}^{2}+1=0,$$
(21)

where \(b_{2}=A(2Bp-A),\) \(b_{1}=2(B+Q)\) and the solution of Eq. (21) is as follows

$$T_{2}=\pm\Bigg{(}\frac{b_{1}\pm\sqrt{b_{1}^{2}-4b_{2}}}{2b_{2}}\Bigg{)}^{1/2}.$$
(22)

The analysis of relation (22) for the presence of valid values of the function \(T_{2}\) shows that Eq. (21) has four valid solutions for \(n_{2}>n_{1}\) and \(n_{L}\leq n_{S}<n_{h}^{4}/n_{l}^{2}n_{L}\) and only two solutions for \(n_{h}^{4}/n_{l}^{2}n_{L}\leq n_{S}<n_{h}^{6}/n_{l}^{4}n_{L}\).

When selecting the materials of the layers of the matching structure with refractive indices satisfying the condition \(n_{S}=n_{h}^{6}/n_{l}^{4}n_{L}\), all wave thicknesses of the layers become quarter-wave.

The interval of possible values of the refractive indices of the matched media, in the case of a five-layer structure is as follows:

$$n_{L}\leq n_{S}\leq n_{h}^{6}/n_{l}^{4}n_{L}.$$

It is possible to find exact solutions of Eqs. (9), (10) for \(N>5\), but from the point of view of solving practical problems this problem is redundant because for the entire range of materials used for synthesis of multilayer interference structures, both in optical and microwave ranges, the structures synthesized based on the proposed algorithm with the number of layers of \(N\leq 5\) can ensure that there is no reflected signal from almost any material used in practice with real refractive indices. As an example, for the materials BaF\({}_{2}\) (\(n_{l}=1.45\)) and ZnSe (\(n_{h}=2.55\)), which are often used in the synthesis of multilayer interference coatings, in the middle infrared range the structures created on their basis have the following intervals of the refractive indices of the matched media during wave propagation in free space (\(n_{L}=1\)): (\(N=2\)) \(1\leq n_{S}\leq 6.50\); \((N=3)\) \(1\leq n_{S}\leq 20.11\); \((N=4)\) \(1\leq n_{S}\leq 11.43\); \((N=5)\) \(1\leq n_{S}\leq 62.20\).

3.1.5. Matching capability of \(\pi\)-structures. Taking the results presented in subsections 3.1.1–3.1.4 and the additional numerical analysis of the dependence of the matching capacity of \(\pi\)-structures on the number of layers into account showed that the maximum refractive index value of the matched medium \(n_{S\max}\) on the number of layers of the \(\pi\)-structure in the case of the optimal order of their alternation can be determined from the following relations:

$$N=2K:\quad n_{S\max}=\bigg{(}\frac{n_{h}}{n_{l}}\bigg{)}^{K}\frac{n_{h}n_{l}}{n_{L}},$$
(23)
$$N=2K+1:\quad n_{S\max}=\bigg{(}\frac{n_{h}}{n_{l}}\bigg{)}^{2K}\frac{n_{h}^{2}}{n_{L}},$$
(24)

and the discrete set of values \(n_{S\max}(K)\) has the quarter-wave optical thicknesses of the layers as a structural solution.

From relations (23) and (24), it is possible to determine the minimum number of the layers of the \(\pi\)-structure required to obtain zero reflection from media with refractive indices in the range \(n_{L}\leq n_{S}\leq n_{S\max}\):

$$N=2K:$$
$$K_{\textrm{min}}=\Bigg{[}\bigg{|}{\ln\bigg{(}\frac{n_{S}n_{L}}{n_{h}n_{l}}\bigg{)}\bigg{/}\ln\bigg{(}\frac{n_{h}}{n_{l}}\bigg{)}}\bigg{|}\Bigg{]}+1,$$
(25)
$$N=2K+1:$$
$$K_{\textrm{min}}=\Bigg{[}\bigg{|}{\ln\bigg{(}\frac{n_{S}n_{L}}{n_{h}^{2}}\bigg{)}\bigg{/}2\ln\bigg{(}\frac{n_{h}}{n_{l}}\bigg{)}}\bigg{|}\Bigg{]}+1,$$
(26)

and, as can be seen from the comparison of relations (25) and (26), \(\pi\)-structures with odd number of layers implement the matching mode for the same value of \(n_{S}\) with fewer layers and are more efficient in terms of this optimization criterion.

When only the phase matching condition is satisfied, e.g., when \(K<K_{\textrm{min}}\), a local extremum of the dependence of the reflection coefficient on the wavelength from the considered system is observed at a given wavelength, which can be used as a way to synthesize \(\pi\)-structures that provide a given reflection coefficient \(0\leq|r|<1\) from the medium with the refractive index \(n_{S}\).

3.1.6. Structural properties. Increasing the number of layers of the structure \(K>K_{\textrm{min}}\), if coupling condition (8) is satisfied and \(n_{S}\) is fixed, does not violate the complete matching mode but only increases the number of solutions and changes the thickness of the layers in the structure period so that the optical thickness of one of the layers of the \(\pi\)-structure (depending on the selected sign of the function \(T_{2}\)) for \(K\to\infty\) tends to zero and the other to (\(T_{2}>0\)) \(n_{2}d_{2}\to 0\), and \(n_{1}d_{1}\to{\lambda/2}\). In addition, increasing the number of layers of the structure in the case under consideration leads to the removal of the requirement of a certain alternation order of layers in the period of the structure. As an example, in order to obtain the real values of the thicknesses of the layers in the period of the \(\pi\)- structure in the interval of values of the refractive indices of the matched media \(n_{L}\leq n_{S}<{n_{h}^{2}/n_{L}}\) for nonoptimal alternation order of the layers in the period, it is necessary to synthesize a structure with the number of layers \(K>K_{\textrm{min}}\) determined from the following relations:

$$N=2K(n_{1}<n_{2}):\quad K>\big{[}{|P|/Q}\big{]}+1,$$
$$N=2K+1(n_{1}<n_{2}):\quad K>\big{[}{|B|/Q}\big{]}+1.$$

In analytical and numerical analysis of Eqs. (9), (10) on asymptotic values of \(n_{S}\), it was found that for limiting values of the refractive index of the matched medium \(n_{S}\to n_{L}\) or \(n_{S}\to\infty\), in the first case \(T_{2}\to+0,T_{1}\to-0\) and the optical thicknesses of the layers are either zero or \({\lambda/2}\), which is natural, because in this case no matching is required. In the second case, it follows from the analysis of the solutions of Eqs. (9), (10) that \(T_{2}\to+\infty\), and \(T_{1}\to-\infty\), i.e., the optical thicknesses of the layers of the structure tend to quarter-wave values, which is also obvious.

Therefore, from the results given in subsections 3.1.1–3.1.6, the general conclusion can be drawn that for any arbitrary real values of \(n_{L},n_{1},n_{2}\), and \(n{}_{S}\) in the considered medium–matching structure–matched medium system, if the condition of coupling of the wave thicknesses of the layers of the structure according to relation (8) is satisfied, there always exists such a minimum number of layers \(N\) of the matching periodic structure starting from which the reflection coefficient of the wave from the system becomes zero.

Furthermore, the universal nature of the proposed method and the algorithm for the synthesis of antireflection periodic structures with two-layer period found on its basis should be noted, because the system of Eqs. (9), (10) contains the complete set of all structural solutions for the considered problem (half-wave, quarter-wave, thin-layer, and \(\pi\)-structures).

From the practical point of view, the proposed method and the algorithm obtained on its basis make it possible to solve two main problems: first, to abandon the necessity of searching for the values of the refractive indices of the layers of the matching structure depending on the value of the refractive index of the matched medium and, secondly, to implement a complete matching mode for any valid values of the refractive indices of the matched media on the entire continuous set of their values for any initially selected materials of the layers of the structure.

4 NUMERICAL EXPERIMENT

Multilayer interference structures are widely used to solve various kinds of problems, both applied problems and in basic research (from the ultraviolet to the microwave range). Since the results are valid for any of these ranges of the electromagnetic spectrum, the choice of a particular range for the numerical experiment determines only the requirements for the materials of the layers of the matching structure that meet the technological and physical requirements in the chosen spectral range (strength, hygroscopicity, adhesion properties, low absorption, spatial uniformity, temperature stability parameters, etc.).

The following algorithm was used in the numerical experiment and synthesis of the matching structures: for the selected values of the refractive indices of the layers of the matching structure \(n_{h}\) and \(n_{l}\), the known refractive index of the medium from which the wave propagates \(n_{L}\), and the given refractive index of the matched medium \(n_{S}\), from relations (25), (26) the minimum number of the layers of the structure \(N_{\textrm{min}}\) is determined, then, having calculated the value of the coupling parameter \(A\) from relation (6) all possible values of \(d_{2}\) are determined from the exact analytical relation for the obtained value \(N_{\textrm{min}}\) and their corresponding values \(d_{1}\) from relation (8).

The main goal of the numerical experiment was to illustrate that the proposed algorithm can be used for synthesizing antireflection coatings with a two-layer period for fixed values of \(n_{h}\), \(n_{l}\) for a wide range of the values of the refractive indices \(n_{S}\) of antireflection media.

In this regard, by analogy with [12], wave propagation in free space \((n_{L}=1)\) was considered, with \(\lambda=10\) \(\mu\)m as a working wavelength and BaF\({}_{2}\) (\(n_{l}=1.45\)) and ZnSe (\(n_{h}\) = 2.55) as materials of the layers of the structure materials frequently used in this spectral range. The exact solutions of Eqs. (9), (10) given in subsections 3.1.1–3.1.4 provided the minimum number of the layers of the structure that ensure zero reflection from matched media with given refractive indices \(n_{S}\) were used in the calculation of layer thicknesses.

In all the cases considered below, the reflection coefficient calculated numerically using exact formulas was zero (‘‘machine zero’’).

The refractive indices of the matching media ranged from \(n_{S}=1.1\) to \(n_{S}=60\) with a variable step of \(\Delta n_{S}\):

$$n_{S}\in 1.1-2.1,\quad\Delta n_{S}=0.1;$$
$$n_{S}\in 2.2-6.5,\quad\Delta n_{S}=0.5;$$
$$n_{S}\in 7.0-20,\quad\Delta n_{S}=1.5;$$
$$n_{S}=21-60,\quad\Delta n_{S}=5.$$

In the interval of values \(1.1\leq n_{S}\leq 2.1\), the matching structure consisted of two layers (\(n_{1}=2.55;n_{2}=1.45\)); in the interval \(2.2\leq n_{S}\leq 6.5\), also \(N=2\) (\(n_{1}=1.45;n_{2}=2.55\)); in the interval \(7.0\leq n_{S}\leq 20\), \(N=3\) (\(n_{1}=1.45;n_{2}=2.55\)); and in the interval \(21\leq n_{S}\leq 60\), \(N=5\) (\(n_{1}=1.45;n_{2}=2.55\)).

For brevity, we give the numerical values of the thicknesses of the layers of the matching structure (rounded to the third decimal place) for one arbitrary value of \(n_{S}\) for each of the intervals considered above:

$$n_{S}=1.5\quad(N=2),\quad d_{11}=1.755\text{$\mu$m},$$
$$d_{21}=1.115\text{$\mu$m};d_{12}=0.257\text{ $\mu$m},d_{22}=2.333\text{$\mu$m};$$
$$n_{S}=4.0\quad(N=2),\quad d_{11}=0.585\text{ $\mu$m},$$
$$d_{21}=0.416\text{ $\mu$m};d_{12}=2.863\text{ $\mu$m},d_{22}=1.545\text{ $\mu$m};$$
$$n_{S}=20\quad(N=3),\quad d_{11}=1.838\text{ $\mu$m},$$
$$d_{21}=0.952\text{ $\mu$m};d_{12}=1.610\text{ $\mu$m},d_{22}=1.008\text{ $\mu$m};$$
$$n_{S}=60\quad(N=5),\quad d_{11}=1.909\text{ $\mu$m},$$
$$d_{21}=0.925\text{ $\mu$m};d_{12}=1.539\text{ $\mu$m},d_{22}=1.036\text{ $\mu$m}.$$

In all cases considered above, Eqs. (16), (18), and (21) each have two solutions with respect to the thicknesses of layers in a period: \(\{d_{11},d_{21}\}\) and \(\{d_{12},d_{22}\}\), where the first index is the number of the layer, and the second index is the number of the solution.

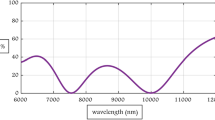
If the refractive index of the matched medium \(n_{S}=4.0\), there is a TLIS class structure (\(d_{11}\), \(d_{21}\)).

Figure 1illustrates the dependence of the energy reflection coefficient \(R=|r|^{2}\) on the wavelength \(\lambda\) for the case considered above for layer thicknesses corresponding to \(\{d_{11},d_{21}\}\).

Fig. 1
figure 1

The dependence of the reflection coefficient \(R\) on the wavelength \(\lambda\) on the matching structure–matched medium system.

Full size image

We consider a problem similar to the previous one as an example illustrating that it is possible to select the optimal thickness of the layers of the structure by synthesizing a structure with the number of layers \(N>N_{\textrm{min}}\) and, accordingly, a larger number of solutions, but in order to match the medium with the refractive index \(n_{S}=4\) (\(N_{\textrm{min}}=2\)), we synthesize a five-layer structure, which according to Section 3.1.4 has in this case four solutions on layer thicknesses:

and since the function \(T_{i}\) is periodic each of all the thicknesses calculated above can be increased by \(({\lambda/2n_{i})}k\), where \(k=0,1,2,\dots\).

CONCLUSIONS

In conclusion, another possible application of the proposed method can be noted. When numerically solving the problems of synthesizing antireflection structures with special spectral characteristics, the proposed algorithm can be used as an initial approximation, because the solutions found on its basis correspond to the global minimum of the reflection coefficient at a given wavelength.