The Problem Solution on the Propagation of a Griffith Crack Based on the Equations of a Nonlinear Model

Abstract

On the basis of a nonlinear model of deformation of a crystalline medium with a complex lattice, the problem of the stationary propagation of a Griffith crack under the action of homogeneous expanding stresses is posed and solved. It is shown that the stressed and deformed states of the medium are determined both by external influences on the medium and by the gradients of the optical mode (mutual displacement of atoms). The contributions from these factors are separated. Finding the components of the stress tensor and macro-displacement vector is reduced to solving Riemann–Hilbert boundary value problems. Their exact analytical solutions are obtained.

1 INTRODUCTION

In [1, 2], a nonlinear model of deformation of crystalline media with a complex lattice is proposed. It describes many physical and mechanical processes that are realized in experiments (the formation of a superlattice, the appearance of defects, martensitic-type phase transitions, etc.), but which are not described by the classical linear model. Based on the general solutions of the dynamic equations of plane deformation of the nonlinear model [3], many dynamic problems (propagation of concentrated forces, stamps of different profiles, etc.) can be solved. In the classical formulation, these problems have been solved and studied by many authors [4–6]. Nevertheless, their solution based on a nonlinear model is of particular interest. It is due to the fact that the results of the study of plane dynamic problems are used in solving many fundamental problems, for example, in constructing the theory of fracture and long-term strength of solids. Local criteria for the destruction of solids determine the local stress and strain fields, and the nonlinear model describes them more adequately. Below, on the basis of a nonlinear model, the problem on the propagation of a Griffith crack in a field of uniform tensile stresses is solved.

2 GENERAL SOLUTION OF DYNAMIC EQUATIONS OF PLANE DEFORMATION OF A NONLINEAR MODEL

In the nonlinear model, the deformation of the medium is described by the vector of macro-displacements ${\mathbf{U}}(t,x,y,z)$ (acoustic mode) and the vector of micro-displacements ${\mathbf{u}}(t,x,y,z)$ (optical mode). The deformation is considered to be plane, parallel to the OZ axis if

$${{U}_{x}} = {{U}_{x}}(t,x,y),\quad {{U}_{y}} = {{U}_{y}}(t,x,y),\quad {{U}_{z}} = 0,$$

(2.1)

$${{u}_{x}} = {{u}_{x}}(t,x,y),\quad {{u}_{y}} = {{u}_{y}}(t,x,y),\quad {{u}_{z}} = 0.$$

(2.2)

For plane deformation, the equations of motion of the nonlinear model take the form [7, 8]

$$\rho \frac{{{{\partial }^{2}}{{U}_{i}}}}{{\partial {{t}^{2}}}} = {{\sigma }_{{ij,j}}},$$

(2.3)

$${{\mu }_{0}}\frac{{{{\partial }^{2}}{{u}_{i}}}}{{\partial {{t}^{2}}}} = {{\chi }_{{ij,j}}} - R\frac{{\partial \Phi ({{u}_{s}})}}{{\partial {{u}_{i}}}}.$$

(2.4)

Here, ${{\sigma }_{{ik}}},\;{{\chi }_{{ik}}}$ are the macro- and micro-stress tensors, $\rho ,\;{{\mu }_{0}}$ are the average and reduced atomic mass densities, respectively, $i,j = 1,2$ and summation is implied by repeated indices. The function $\Phi ({{u}_{s}})$ describes the interaction energy of sublattices. In the fundamental study [9] and most of subsequent ones [10], it is assumed that

$$\Phi ({{u}_{s}}) = 1 - \cos {{u}_{s}},\quad {{u}_{s}} = {\mathbf{Bu}}$$

(2.5)

where B is the reciprocal lattice vector. Factor

$$R = p - {{s}_{{ij}}}{{e}_{{ij}}},\quad {{e}_{{ij}}} = \frac{{{{U}_{{i,j}}} + {{U}_{{j,i}}}}}{2}$$

(2.6)

is the activation energy of bonds. The term p is the half of the activation energy of the hard shear of the sublattices, and ${{s}_{{ij}}}$ is the nonlinear striction tensor.

We confine ourselves to consideration of crystalline media of cubic symmetry, consisting of two sublattices. For them, the material relations of the nonlinear model are written as follows [7, 8]

$${{\sigma }_{{ij}}} = {{\lambda }_{{ijmn}}}{{e}_{{mn}}} - {{s}_{{ij}}}\Phi ({{u}_{s}}),$$

(2.7)

$${{\chi }_{{ij}}} = {{k}_{{ijmn}}}{{\varepsilon }_{{mn}}},\quad {{\varepsilon }_{{mn}}} = \frac{{{{u}_{{m,n}}} + {{u}_{{n,m}}}}}{2}.$$

(2.8)

Tensors ${{\lambda }_{{ijmn}}}$, ${{k}_{{ijmn}}}$ are the coefficients of elasticity and microelasticity, respectively. These tensors are symmetrical to the permutation of pairs of indices and indices of the pair among themselves. In the case of crystalline media of cubic symmetry, the nonzero components are only

$${{\lambda }_{{1111}}} = {{\lambda }_{{2222}}} = {{\lambda }_{{3333}}},\quad {{\lambda }_{{1122}}} = {{\lambda }_{{1133}}},\quad {{\lambda }_{{1212}}} = {{\lambda }_{{1313}}},$$

(2.9)

$${{k}_{{1111}}} = {{k}_{{2222}}} = {{k}_{{3333}}},\quad {{k}_{{1122}}} = {{k}_{{1133}}},\quad {{k}_{{1212}}} = {{k}_{{1313}}}.$$

(2.10)

For independent components, we use the matrix notation introduced by Voigt [11]

$${{\lambda }_{{1111}}} = {{\lambda }_{{11}}},\quad {{\lambda }_{{1122}}} = {{\lambda }_{{12}}} = \lambda ,\quad {{\lambda }_{{1212}}} = {{\lambda }_{{44}}} = \mu ,$$

(2.11)

$${{k}_{{1111}}} = {{k}_{{11}}},\quad {{k}_{{1122}}} = {{k}_{{12}}},\quad {{k}_{{1212}}} = {{k}_{{44}}}.$$

(2.12)

In the general case, ${{\lambda }_{{ijmn}}}$ and ${{k}_{{ijmn}}}$ have the form of the Huang tensor [12]

$$\left( {\begin{array}{*{20}{c}} {{{\lambda }_{{ijmn}}}} \\ {{{k}_{{ijmn}}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} \lambda \\ {{{k}_{{12}}}} \end{array}} \right){{\delta }_{{ij}}}{{\delta }_{{mn}}} + \left( {\begin{array}{*{20}{c}} \mu \\ {{{k}_{{44}}}} \end{array}} \right)\left( {{{\delta }_{{jn}}}{{\delta }_{{im}}} + {{\delta }_{{in}}}{{\delta }_{{jm}}}} \right) + \left( {\begin{array}{*{20}{c}} {{{\lambda }_{{11}}} - {{\lambda }_{{12}}} - 2{{\lambda }_{{44}}}} \\ {{{k}_{{11}}} - {{k}_{{12}}} - 2{{k}_{{44}}}} \end{array}} \right){{\delta }_{{ijmn}}}.$$

(2.13)

Here, ${{\delta }_{{ij}}}$ is the unit tensor, and ${{\delta }_{{ijmn}}} = 1$ if all indices are the same (it is equal to zero in other cases). The last term in (2.13) describes the anisotropy of the medium. In solid state physics [13], the medium anisotropy factor $({{a}_{1}},{{a}_{2}})$ is introduced

$${{\lambda }_{{11}}} - {{\lambda }_{{12}}} - 2{{\lambda }_{{44}}} = ({{\lambda }_{{11}}} - {{\lambda }_{{12}}})(1 - {{a}_{1}}),\quad {{k}_{{11}}} - {{k}_{{12}}} - 2{{k}_{{44}}} = ({{k}_{{11}}} - {{k}_{{12}}})(1 - {{a}_{2}})$$

(2.14)

For media with weak anisotropy ${{a}_{1}} \approx 1$, ${{a}_{2}} \approx 1$ and cubic symmetry ${{s}_{{ij}}} = s{{\delta }_{{ij}}}$, material relations (2.7), (2.8) take the form

$${{\sigma }_{{xx}}} = 2\mu {{U}_{{x,x}}} + \lambda ({{U}_{{x,x}}} + {{U}_{{y,y}}}) - s\Phi ({{u}_{s}}),$$

$${{\sigma }_{{yy}}} = 2\mu {{U}_{{y,y}}} + \lambda ({{U}_{{x,x}}} + {{U}_{{y,y}}}) - s\Phi ({{u}_{s}}),$$

(2.15)

$${{\sigma }_{{xy}}} = \mu ({{U}_{{x,y}}} + {{U}_{{y,x}}}),$$

$${{\chi }_{{xx}}} = 2{{k}_{{44}}}{{u}_{{x,x}}} + {{k}_{{12}}}({{u}_{{x,x}}} + {{u}_{{y,y}}}),$$

$${{\chi }_{{yy}}} = 2{{k}_{{44}}}{{u}_{{y,y}}} + {{k}_{{12}}}({{u}_{{x,x}}} + {{u}_{{y,y}}}),$$

(2.16)

$${{\chi }_{{xy}}} = {{k}_{{44}}}({{u}_{{x,y}}} + {{u}_{{y,x}}}).$$

The components of the stress tensor ${{\sigma }_{{xx}}},\;{{\sigma }_{{yy}}},\;{{\sigma }_{{xy}}}$ must satisfy the Beltrami-Michell conditions [14] For a plane deformation of a nonlinear model, this is one equation

$$\left( {\Delta - \frac{1}{{V_{1}^{2}}}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}} \right)({{\sigma }_{{xx}}} + {{\sigma }_{{yy}}}) + \frac{{2s\mu }}{{\lambda + 2\mu }}\left( {\Delta - \frac{1}{{V_{2}^{2}}}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}} \right)\Phi ({{u}_{s}}) = 0,$$

(2.17)

$$\Delta = \frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}},\quad {{V}_{1}} = \sqrt {\frac{{\lambda + 2\mu }}{\rho }} ,\quad {{V}_{2}} = \sqrt {\frac{\mu }{\rho }} .$$

(2.18)

Here, ${{V}_{1}}$ is the velocity of the longitudinal wave, and ${{V}_{2}}$ is the shear velocity. The tensor ${{\sigma }_{{ij}}}$ and vector ${{U}_{i}}$ are expressed in terms of an arbitrary function $Q(t,x,y)$ [3]:

$$\begin{gathered} {{\sigma }_{{xx}}} = {{L}_{{11}}}(Q) = \left( {\frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}} - \frac{1}{{2V_{2}^{2}}}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}} \right)Q,\quad {{\sigma }_{{yy}}} = {{L}_{{22}}}(Q) = \left( {\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} - \frac{1}{{2V_{2}^{2}}}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}} \right)Q, \\ {{\sigma }_{{xx}}} + {{\sigma }_{{yy}}} = \theta = \left( {\Delta - \frac{1}{{V_{2}^{2}}}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}} \right)Q,\quad \left( {\Delta - \frac{1}{{2V_{2}^{2}}}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}} \right)\left( {{{\sigma }_{{xy}}} + \frac{{{{\partial }^{2}}Q}}{{\partial x\partial y}}} \right) = 0, \\ \end{gathered} $$

(2.19)

$$\begin{gathered} 2\mu {{U}_{{x,x}}} = {{\sigma }_{{xx}}} - \frac{\lambda }{{2(\lambda + \mu )}}\theta + \frac{\mu }{{\lambda + \mu }}s\Phi ({{u}_{s}}), \\ 2\mu {{U}_{{y,y}}} = {{\sigma }_{{yy}}} - \frac{\lambda }{{2(\lambda + \mu )}}\theta + \frac{\mu }{{\lambda + \mu }}s\Phi ({{u}_{s}}). \\ \end{gathered} $$

(2.20)

If we substitute (2.19) into (2.17), then we obtain an equation for finding the function $Q(t,x,y)$

$$\left( {\Delta - \frac{1}{{V_{1}^{2}}}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}} \right)\left[ {\left( {\Delta - \frac{1}{{V_{2}^{2}}}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}} \right)Q + 2s\frac{{V_{2}^{2}}}{{V_{1}^{2}}}\Phi ({{u}_{s}})} \right] = 0.$$

(2.21)

It can be seen from (2.21) that it is a dynamic analogue of the Airy function, which is introduced to solve static problems of classical plane deformation. The function $Q(t,x,y)$, unlike the Airy function, satisfies the inhomogeneous dynamic biharmonic equation. The function $\Phi ({{u}_{s}})$ plays the role of bulk sources of macro-stresses and macro-strains. The general solution of Eq. (2.21) can be written as the sum of two terms

$$Q(t,x,y) = F(t,x,y) + {{Q}_{0}}(t,x,y).$$

(2.22)

The function $F(t,x,y)$ satisfies the homogeneous biharmonic equation

$$\left( {\Delta - \frac{1}{{V_{1}^{2}}}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}} \right)\left( {\Delta - \frac{1}{{V_{2}^{2}}}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}} \right)F(t,x,y) = 0$$

(2.23)

and ${{Q}_{0}}(t,x,y)$ is a solution of the inhomogeneous equation

$$\left( {\Delta - \frac{1}{{V_{1}^{2}}}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}} \right){{Q}_{0}}(t,x,y) + 2s\frac{{V_{2}^{2}}}{{V_{1}^{2}}}\Phi ({{u}_{s}}) = 0.$$

(2.24)

The resulting general solution of the macrofield equations (2.3), (2.4) makes it possible to formulate and find exact analytical solutions of various dynamic problems based on a nonlinear model. Among them, the most simple, but of great interest, are stationary problems (the movement of concentrated forces, stamps and cracks of various profiles, etc.). As an example, we consider the solution of the problem of propagation of a finite cut (y = 0, ${\text{|}}x{\text{|}} \leqslant a$) in a plane under the action of constant tensile stresses.

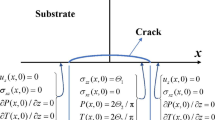
3 SOLUTION OF THE PROBLEM ON GRIFFITH CRACK PROPAGATION

Let the final cut be located on the $OX$ axis (y = 0, ${\text{|}}x{\text{|}} \leqslant a$), and the plane (X, Y) be in the field of uniform tensile stresses. Then the tensor ${{\sigma }_{{ij}}}$ must satisfy the boundary conditions

$${{\left. {{{\sigma }_{{yy}}}} \right|}_{{{\kern 1pt} y = 0,{\kern 1pt} |x| \leqslant a}}} = 0,\quad {{\left. {{{\sigma }_{{xy}}}} \right|}_{{{\kern 1pt} y = 0,{\kern 1pt} |x| \leqslant a}}} = 0,$$

(3.1)

$${{\left. {{{\sigma }_{{yy}}}} \right|}_{{r \to \infty }}} = \sigma _{{yy}}^{\infty },\quad {{\left. {{{\sigma }_{{xx}}}} \right|}_{{r \to \infty }}} \to 0,\quad {{\left. {{{\sigma }_{{xy}}}} \right|}_{{r \to \infty }}} \to 0,\quad r = \sqrt {{{x}^{2}} + {{y}^{2}}} .$$

(3.2)

We assume that the crack propagates along the $OX$ axis with velocity C. Then it is expedient to switch to a moving coordinate system ($\xi = x + Ct$, $y = \eta$). In $(\xi ,\eta )$ coordinates, Eqs. (2.23), (2.24) take the form

$$\left[ {(1 - M_{1}^{2})\frac{{{{\partial }^{2}}}}{{\partial {{\xi }^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{\eta }^{2}}}}} \right]\left[ {(1 - M_{2}^{2})\frac{{{{\partial }^{2}}}}{{\partial {{\xi }^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{\eta }^{2}}}}} \right]F(\xi ,\eta ) = 0,$$

(3.3)

$$(1 - M_{1}^{2})\frac{{{{\partial }^{2}}{{Q}_{0}}}}{{\partial {{\xi }^{2}}}} + \frac{{{{\partial }^{2}}{{Q}_{0}}}}{{\partial {{\eta }^{2}}}} + 2s\frac{{V_{2}^{2}}}{{V_{1}^{2}}}\Phi ({{u}_{s}}) = 0,$$

(3.4)

$${{M}_{1}} = \frac{C}{{{{V}_{1}}}},\quad {{M}_{2}} = \frac{C}{{{{V}_{2}}}}.$$

(3.5)

We set that

$${{M}_{1}} < 1,\quad {{M}_{2}} < 1.$$

(3.6)

Then the solution of (3.3) is

$$\begin{gathered} F(\xi ,\eta ) = {{F}_{1}}({{z}_{1}}) + {{\overline F }_{1}}({{{\bar {z}}}_{1}}) + {{F}_{2}}({{z}_{2}}) + {{\overline F }_{2}}({{{\bar {z}}}_{2}}) = 2[{\kern 1pt} {\text{Re}}{\kern 1pt} {{F}_{1}}({{z}_{1}}) + {\text{Re}}{\kern 1pt} {{F}_{2}}({{z}_{2}})], \\ {{z}_{1}} = \xi + {{\mu }_{1}}\eta ,\quad {{\mu }_{1}} = i\sqrt {1 - M_{1}^{2}} ,\quad {{z}_{2}} = \xi + {{\mu }_{2}}\eta ,\quad {{\mu }_{2}} = i\sqrt {1 - M_{2}^{2}} . \\ \end{gathered} $$

(3.7)

Here, ${{F}_{1}}({{z}_{1}})$ and ${{F}_{2}}({{z}_{2}})$ are arbitrary analytic functions of the corresponding complex variables (${{z}_{1}},{{z}_{2}}$). The overline denotes complex conjugation. The tensor ${{\sigma }_{{ij}}}$ and the vector U_i can be expressed in terms of the functions ${{Q}_{0}}(\xi ,\eta )$, ${{F}_{1}}({{z}_{1}})$ and ${{F}_{2}}({{z}_{2}})$, if (2.22) and (3.7) are taken into account in (2.19), (2.20). Finally we get

$${{\sigma }_{{xx}}} = - (M_{2}^{2} - 2M_{1}^{2} + 2){\kern 1pt} {\text{Re}}{\kern 1pt} {{F}_{{1{\kern 1pt} '{\kern 1pt} '}}} + (M_{2}^{2} - 2){\kern 1pt} {\text{Re}}{\kern 1pt} {{F}_{{2{\kern 1pt} '{\kern 1pt} '}}} + {{L}_{{11}}}({{Q}_{0}}),$$

$${{\sigma }_{{yy}}} = - (M_{2}^{2} - 2)({\kern 1pt} {\text{Re}}{\kern 1pt} {{F}_{{1{\kern 1pt} '{\kern 1pt} '}}} + {\text{Re}}{\kern 1pt} {{F}_{{2{\kern 1pt} '{\kern 1pt} '}}}) + {{L}_{{22}}}({{Q}_{0}}),$$

(3.8)

$${{\sigma }_{{xy}}} = 2\sqrt {1 - M_{1}^{2}} {\kern 1pt} {\text{Im}}{\kern 1pt} {{F}_{{1{\kern 1pt} '{\kern 1pt} '}}} + \frac{{{{{(M_{2}^{2} - 2)}}^{2}}}}{{2\sqrt {1 - M_{2}^{2}} }}{\kern 1pt} {\text{Im}}{\kern 1pt} {{F}_{{2{\kern 1pt} '{\kern 1pt} '}}} - \frac{{{{\partial }^{2}}{{Q}_{0}}}}{{\partial \xi \partial \eta }},$$

$$\mu {{U}_{x}} = - {\kern 1pt} {\text{Re}}{\kern 1pt} {{F}_{{1{\kern 1pt} '}}} + \frac{1}{2}(M_{2}^{2} - 2){\kern 1pt} {\text{Re}}{\kern 1pt} {{F}_{{2{\kern 1pt} '}}} - \frac{1}{2}\frac{{\partial {{Q}_{0}}}}{{\partial \xi }},$$

$$\mu {{U}_{y}} = \sqrt {1 - M_{1}^{2}} {\kern 1pt} {\text{Im}}{\kern 1pt} {{F}_{{1{\kern 1pt} '}}} - \frac{{M_{2}^{2} - 2}}{{2\sqrt {1 - M_{2}^{2}} }}{\kern 1pt} {\text{Im}}{\kern 1pt} {{F}_{{2{\kern 1pt} '}}} - \frac{1}{2}\frac{{\partial {{Q}_{0}}}}{{\partial \eta }}.$$

(3.9)

Hereinafter, the prime denotes the derivative with respect to the argument. In deriving formulas (3.8) and (3.9), we use the partial derivatives

$$\frac{\partial }{{\partial x}}{\kern 1pt} {\text{Re}}{\kern 1pt} {{F}_{1}} = {\text{Re}}{\kern 1pt} {{F}_{{1{\kern 1pt} '}}},\quad \frac{\partial }{{\partial y}}{\kern 1pt} {\text{Re}}{\kern 1pt} {{F}_{1}} = - \sqrt {1 - M_{1}^{2}} {\kern 1pt} {\text{Im}}{\kern 1pt} {{F}_{{1{\kern 1pt} '}}},$$

$$\frac{\partial }{{\partial x}}{\kern 1pt} {\text{Re}}{\kern 1pt} {{F}_{2}} = {\text{Re}}{\kern 1pt} {{F}_{{2{\kern 1pt} '}}},\quad \frac{\partial }{{\partial y}}{\kern 1pt} {\text{Re}}{\kern 1pt} {{F}_{2}} = - \sqrt {1 - M_{2}^{2}} {\kern 1pt} {\text{Im}}{\kern 1pt} {{F}_{{2{\kern 1pt} '}}},$$

$$\frac{\partial }{{\partial x}}{\kern 1pt} {\text{Im}}{\kern 1pt} {{F}_{1}} = {\text{Im}}{\kern 1pt} {{F}_{{1{\kern 1pt} '}}},\;\;\;\frac{\partial }{{\partial y}}{\kern 1pt} {\text{Im}}{\kern 1pt} {{F}_{1}} = \sqrt {1 - M_{1}^{2}} {\kern 1pt} {\text{Re}}{\kern 1pt} {{F}_{{1{\kern 1pt} '}}},$$

$$\frac{\partial }{{\partial x}}{\kern 1pt} {\text{Im}}{\kern 1pt} {{F}_{2}} = {\text{Im}}{\kern 1pt} {{F}_{{2{\kern 1pt} '}}},\quad \frac{\partial }{{\partial y}}{\kern 1pt} {\text{Im}}{\kern 1pt} {{F}_{2}} = \sqrt {1 - M_{2}^{2}} {\kern 1pt} {\text{Re}}{\kern 1pt} {{F}_{{2{\kern 1pt} '}}}.$$

(3.10)

According to (3.1), the functions ${{F}_{1}}({{z}_{1}})$ and ${{F}_{2}}({{z}_{2}})$must satisfy the boundary conditions

$$(M_{2}^{2} - 2){{[{\kern 1pt} {\text{Re}}{\kern 1pt} F_{1}^{'} + {\text{Re}}{\kern 1pt} F_{2}^{{''}}]}_{{{\kern 1pt} \eta = 0,|\xi | \leqslant a}}} = {{\left[ {{{L}_{{22}}}({{Q}_{0}}) - {{\sigma }_{{yy}}}} \right]}_{{{\kern 1pt} \eta = 0,|\xi | \leqslant a}}},$$

(3.11)

$${{\left. {\left( {2\sqrt {1 - M_{1}^{2}} {\kern 1pt} {\text{Im}}{\kern 1pt} F_{1}^{{''}} + \frac{{{{{(M_{2}^{2} - 2)}}^{2}}}}{{2\sqrt {1 - M_{2}^{2}} }}{\kern 1pt} {\text{Im}}{\kern 1pt} F_{2}^{{''}}} \right)} \right|}_{{{\kern 1pt} \eta = 0,{\kern 1pt} |\xi | \leqslant a}}} = {{\left[ {\frac{{{{\partial }^{2}}{{Q}_{0}}}}{{\partial \xi \partial \eta }} + {{\sigma }_{{xy}}}} \right]}_{{{\kern 1pt} \eta = 0,{\kern 1pt} |\xi | \leqslant a}}}.$$

(3.12)

Taking into account

$${\kern 1pt} {\text{Im}}{\kern 1pt} F_{1}^{{''}}({{z}_{1}}) = - {\kern 1pt} {\text{Re}}{\kern 1pt} (iF_{1}^{{''}}),\quad {\text{Im}}{\kern 1pt} F_{2}^{{''}}({{z}_{2}}) = - {\kern 1pt} {\text{Re}}{\kern 1pt} (iF_{2}^{{''}}),$$

(3.13)

boundary condition (3.12) can be written as follows

$${{\left[ {2\sqrt {1 - M_{1}^{2}} {\kern 1pt} {\text{Re}}{\kern 1pt} F_{1}^{{''}} + \frac{{{{{(M_{2}^{2} - 2)}}^{2}}}}{{2\sqrt {1 - M_{2}^{2}} }}{\kern 1pt} {\text{Re}}{\kern 1pt} F_{2}^{{''}}} \right]}_{{{\kern 1pt} \eta = 0,{\kern 1pt} |\xi | \leqslant a}}} = i{{\left[ {\frac{{{{\partial }^{2}}{{Q}_{0}}}}{{\partial \xi \partial \eta }} + {{\sigma }_{{xy}}}} \right]}_{{{\kern 1pt} \eta = 0,{\kern 1pt} |\xi | \leqslant a}}}.$$

(3.14)

It can be seen from the boundary conditions (3.12) and (3.14) that in the nonlinear model the stressed and deformed states of the medium are determined by both external influences (${{\sigma }_{{xy}}},{{\sigma }_{{yy}}}$) and optical mode gradients $\left( {{{L}_{{22}}}({{Q}_{0}}),\frac{{{{\partial }^{2}}{{Q}_{0}}}}{{\partial \xi \partial \eta }}} \right)$. It seems appropriate to consider these contributions separately. For this purpose, we represent the functions ${{F}_{1}}({{z}_{1}})$ and ${{F}_{2}}({{z}_{2}})$ as the sum of two terms

$$F_{1}^{{''}}({{z}_{1}}) = F_{{11}}^{'}({{z}_{1}}) + F_{{12}}^{'}({{z}_{1}}),\quad F_{2}^{{''}}({{z}_{2}}) = F_{{21}}^{'}({{z}_{2}}) + F_{{22}}^{'}({{z}_{2}})$$

(3.15)

and require that the functions ($F_{{11}}^{'}$, $F_{{12}}^{'}$, $F_{{21}}^{'}$, $F_{{22}}^{'}$) satisfy the boundary conditions

$$\begin{gathered} {{[{\kern 1pt} {\text{Re}}{\kern 1pt} F_{{11}}^{'} + {\text{Re}}{\kern 1pt} F_{{21}}^{'}]}_{{{\kern 1pt} \eta = 0,{\kern 1pt} |\xi | \leqslant a}}} = - {{\left. {\frac{{{{\sigma }_{{yy}}}}}{{M_{2}^{2} - 2}}} \right|}_{{{\kern 1pt} \eta = 0,{\kern 1pt} |\xi | \leqslant a}}}, \\ {{\left[ {{\kern 1pt} {\text{Re}}{\kern 1pt} F_{{11}}^{'} + \frac{{{{{(M_{2}^{2} - 2)}}^{2}}}}{{2\sqrt {1 - M_{2}^{2}} }}{\kern 1pt} {\text{Re}}{\kern 1pt} F_{{21}}^{'}} \right]}_{{{\kern 1pt} \eta = 0,{\kern 1pt} |\xi | \leqslant a}}} = i{{\left. {\frac{{{{\sigma }_{{xy}}}}}{{2\sqrt {1 - M_{2}^{2}} }}} \right|}_{{{\kern 1pt} \eta = 0,{\kern 1pt} |\xi | \leqslant a}}}, \\ \end{gathered} $$

(3.16)

$$\begin{gathered} {{[{\kern 1pt} {\text{Re}}{\kern 1pt} F_{{12}}^{'} + {\text{Re}}{\kern 1pt} F_{{22}}^{'}]}_{{{\kern 1pt} \eta = 0,{\kern 1pt} |\xi | \leqslant a}}} = {{\left. {\frac{1}{{M_{2}^{2} - 2}}{{L}_{{22}}}({{Q}_{0}})} \right|}_{{{\kern 1pt} \eta = 0,{\kern 1pt} |\xi | \leqslant a}}}, \\ {{\left[ {{\kern 1pt} {\text{Re}}{\kern 1pt} F_{{12}}^{'} + \frac{{{{{(M_{2}^{2} - 2)}}^{2}}}}{{4\sqrt {(1 - M_{2}^{2})(1 - M_{2}^{2})} }}{\kern 1pt} {\text{Re}}{\kern 1pt} F_{{22}}^{'}} \right]}_{{{\kern 1pt} \eta = 0,{\kern 1pt} |\xi | \leqslant a}}} = {{\left. {\frac{i}{{2\sqrt {1 - M_{2}^{2}} }}\frac{{{{\partial }^{2}}{{Q}_{0}}}}{{\partial \xi \partial \eta }}} \right|}_{{{\kern 1pt} \eta = 0,{\kern 1pt} |\xi | \leqslant a}}}. \\ \end{gathered} $$

(3.17)

Taking into account (3.15), the components of the stress tensor (3.8) and macro-displacement vector (3.9) are written as the sum of two terms

$${{\sigma }_{{ik}}} = \sigma _{{ik}}^{{{\kern 1pt} + }} + \sigma _{{ik}}^{{{\kern 1pt} - }},\quad {{U}_{i}} = U_{i}^{ + } + U_{i}^{ - },\quad (i,k) = (1,2),$$

(3.18)

$$\left( {\begin{array}{*{20}{c}} {\sigma _{{xx}}^{{{\kern 1pt} - }}} \\ {\sigma _{{xx}}^{{{\kern 1pt} + }}} \end{array}} \right) = - (M_{2}^{2} - 2M_{1}^{2} + 2)\left( {\begin{array}{*{20}{c}} {{\kern 1pt} {\text{Re}}{\kern 1pt} F_{{11}}^{'}} \\ {{\kern 1pt} {\text{Re}}{\kern 1pt} F_{{12}}^{'}} \end{array}} \right) + (M_{2}^{2} - 2)\left( {\begin{array}{*{20}{c}} {{\kern 1pt} {\text{Re}}{\kern 1pt} F_{{21}}^{'}} \\ {{\kern 1pt} {\text{Re}}{\kern 1pt} F_{{22}}^{'}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 0 \\ {{{L}_{{11}}}({{Q}_{0}})} \end{array}} \right),$$

$$\left( {\begin{array}{*{20}{c}} {\sigma _{{yy}}^{{{\kern 1pt} - }}} \\ {\sigma _{{yy}}^{{{\kern 1pt} + }}} \end{array}} \right) = - (M_{2}^{2} - 2)\left( {\begin{array}{*{20}{c}} {{\kern 1pt} {\text{Re}}{\kern 1pt} F_{{11}}^{'} + {\text{Re}}{\kern 1pt} F_{{21}}^{'}} \\ {{\kern 1pt} {\text{Re}}{\kern 1pt} F_{{12}}^{'} + {\text{Re}}{\kern 1pt} F_{{22}}^{'}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 0 \\ {{{L}_{{22}}}({{Q}_{0}})} \end{array}} \right),$$

(3.19)

$$\left( {\begin{array}{*{20}{c}} {\sigma _{{xy}}^{{{\kern 1pt} - }}} \\ {\sigma _{{xy}}^{{{\kern 1pt} + }}} \end{array}} \right) = 2\sqrt {1 - M_{1}^{2}} \left( {\begin{array}{*{20}{c}} {{\kern 1pt} {\text{Im}}{\kern 1pt} F_{{11}}^{'}} \\ {{\kern 1pt} {\text{Im}}{\kern 1pt} F_{{12}}^{'}} \end{array}} \right) + \frac{{{{{(M_{2}^{2} - 2)}}^{2}}}}{{2\sqrt {1 - M_{2}^{2}} }}\left( {\begin{array}{*{20}{c}} {{\kern 1pt} {\text{Im}}{\kern 1pt} F_{{21}}^{'}} \\ {{\kern 1pt} {\text{Im}}{\kern 1pt} F_{{22}}^{'}} \end{array}} \right) - \left( {\begin{array}{*{20}{c}} 0 \\ {\frac{{{{\partial }^{2}}{{Q}_{0}}}}{{\partial \xi \partial \eta }}} \end{array}} \right),$$

$$\mu \left( {\begin{array}{*{20}{c}} {U_{x}^{ - }} \\ {U_{x}^{ + }} \end{array}} \right) = - \left( {\begin{array}{*{20}{c}} {{\kern 1pt} {\text{Re}}{\kern 1pt} F_{{11}}^{'}} \\ {{\kern 1pt} {\text{Re}}{\kern 1pt} F_{{12}}^{'}} \end{array}} \right) + \frac{1}{2}(M_{2}^{2} - 2)\left( {\begin{array}{*{20}{c}} {{\kern 1pt} {\text{Re}}{\kern 1pt} F_{{21}}^{'}} \\ {{\kern 1pt} {\text{Re}}{\kern 1pt} F_{{22}}^{'}} \end{array}} \right) - \left( {\begin{array}{*{20}{c}} 0 \\ {\frac{1}{2}\frac{{\partial {{Q}_{0}}}}{{\partial \xi }}} \end{array}} \right),$$

$$\mu \left( {\begin{array}{*{20}{c}} {U_{y}^{ - }} \\ {U_{y}^{ + }} \end{array}} \right) = \sqrt {1 - M_{1}^{2}} \left( {\begin{array}{*{20}{c}} {{\kern 1pt} {\text{Im}}{\kern 1pt} F_{{11}}^{'}} \\ {{\kern 1pt} {\text{Im}}{\kern 1pt} F_{{12}}^{'}} \end{array}} \right) - \frac{{M_{2}^{2} - 2}}{{2\sqrt {1 - M_{2}^{2}} }}\left( {\begin{array}{*{20}{c}} {{\kern 1pt} {\text{Im}}{\kern 1pt} F_{{21}}^{'}} \\ {{\kern 1pt} {\text{Im}}{\kern 1pt} F_{{22}}^{'}} \end{array}} \right) - \left( {\begin{array}{*{20}{c}} 0 \\ {\frac{1}{2}\frac{{\partial {{Q}_{0}}}}{{\partial \eta }}} \end{array}} \right).$$

(3.20)

To satisfy the conditions at infinity (3.2), from the functions $F_{{11}}^{'}({{z}_{1}})$ and $F_{{21}}^{'}({{z}_{2}})$ we select the linear terms

$$\begin{gathered} {{F}_{{11}}}({{z}_{1}}) = A{{z}_{1}} + {{F}_{{10}}}({{z}_{1}}),\quad {{F}_{{21}}}({{z}_{2}}) = B{{z}_{2}} + {{F}_{{20}}}({{z}_{2}}), \\ A = - \frac{1}{{2(M_{2}^{2} - M_{1}^{2})}}\sigma _{{yy}}^{\infty },\quad B = \frac{{M_{2}^{2} - 2M_{1}^{2} + 2}}{{2(2 - M_{2}^{2})(M_{2}^{2} - M_{1}^{2})}}\sigma _{{yy}}^{\infty }, \\ A + B = \frac{1}{{2 - M_{2}^{2}}}\sigma _{{yy}}^{\infty }. \\ \end{gathered} $$

(3.21)

Then the boundary conditions (3.16) take the form

$$\begin{gathered} {{F}_{{11}}}({{z}_{1}}) = A{{z}_{1}} + {{F}_{{10}}}({{z}_{1}}),\quad {{F}_{{21}}}({{z}_{2}}) = B{{z}_{2}} + {{F}_{{20}}}({{z}_{2}}), \\ A = - \frac{1}{{2(M_{2}^{2} - M_{1}^{2})}}\sigma _{{yy}}^{\infty },\quad B = \frac{{M_{2}^{2} - 2M_{1}^{2} + 2}}{{2(2 - M_{2}^{2})(M_{2}^{2} - M_{1}^{2})}}\sigma _{{yy}}^{\infty }, \\ A + B = \frac{1}{{2 - M_{2}^{2}}}\sigma _{{yy}}^{\infty }. \\ \end{gathered} $$

(3.21)

From (3.22), we find the boundary conditions for $F_{{10}}^{'}$ and $F_{{20}}^{'}$:

$${\kern 1pt} {\text{Re}}{\kern 1pt} F_{{10}}^{'}{{]}_{{{\kern 1pt} \eta = 0,{\kern 1pt} |\xi | \leqslant a}}} = (1 - {{G}_{1}})\frac{{\sigma _{{yy}}^{\infty }}}{{M_{2}^{2} - 2}},$$

$${\kern 1pt} {\text{Re}}{\kern 1pt} F_{{20}}^{'}{{]}_{{{\kern 1pt} \eta = 0,{\kern 1pt} |\xi | \leqslant a}}} = \frac{{{{G}_{1}}}}{{M_{2}^{2} - 2}}\sigma _{{yy}}^{\infty },$$

(3.23)

$${{G}_{1}} = \frac{{4\sqrt {(1 - M_{1}^{2})(1 - M_{2}^{2})} }}{{4\sqrt {(1 - M_{1}^{2})(1 - M_{2}^{2})} - {{{(2 - M_{2}^{2})}}^{2}}}}.$$

and from (3.12), we obtain the boundary conditions for $F_{{12}}^{'}$, $F_{{22}}^{'}$:

$$\begin{gathered} {\kern 1pt} {\text{Re}}{\kern 1pt} F_{{12}}^{'}{{]}_{{{\kern 1pt} \eta = 0,{\kern 1pt} |\xi | \leqslant a}}} = {{T}_{{12}}}(\xi ),\quad {{T}_{{12}}}(\xi ) = \frac{1}{{M_{2}^{2} - 2}}{{\left. {{{L}_{{22}}}({{Q}_{0}})} \right|}_{{{\kern 1pt} \eta = 0,{\kern 1pt} |\xi | \leqslant a}}} - {{T}_{{22}}}(\xi ), \\ {\kern 1pt} {\text{Re}}{\kern 1pt} F_{{22}}^{'}{{]}_{{{\kern 1pt} \eta = 0,{\kern 1pt} |\xi | \leqslant a}}} = {{T}_{{22}}}(\xi ),\quad {{T}_{{22}}}(\xi ) = {{G}_{1}}{{\left[ {\frac{{{{L}_{{22}}}({{Q}_{0}})}}{{M_{2}^{2} - 2}} - \frac{i}{{2\sqrt {1 - M_{1}^{2}} }}\frac{{{{\partial }^{2}}{{Q}_{0}}}}{{\partial \xi \partial \eta }}} \right]}_{{{\kern 1pt} \eta = 0,{\kern 1pt} |\xi | \leqslant a}}}. \\ \end{gathered} $$

(3.24)

It can be seen from (3.23) and (3.24) that finding $F_{{10}}^{'}$, $F_{{20}}^{'}$, $F_{{12}}^{'}$, $F_{{22}}^{'}$ is reduced to constructing a function Z(z), which is regular outside the interval ${\kern 1pt} \eta = 0,$ ${\text{|}}\xi {\text{|}} \leqslant a$, at infinity ($r \to \infty$) $Z \to 0$, and on the interval it satisfies the boundary condition of the form

$${{\left. {{\kern 1pt} {\text{Re}}{\kern 1pt} Z} \right|}_{{{\kern 1pt} \eta = 0,{\kern 1pt} |\xi | \leqslant a}}} = - g(\xi ).$$

(3.25)

The stated problem is a particular case of the Riemann–Hilbert problem [14]. Its solution has the form

$$Z(z) = \frac{1}{{\pi \sqrt {{{z}^{2}} - {{a}^{2}}} }}\int\limits_{ - a}^a \frac{{g(\xi )\sqrt {{{a}^{2}} - {{\xi }^{2}}} }}{{z - \xi }}d\xi .$$

(3.26)

Based on (3.23) and (3.26), we find

$$\begin{gathered} {{F}_{{10}}}({{z}_{1}}) = (1 - {{G}_{1}})\frac{{\sigma _{{yy}}^{\infty }}}{{M_{2}^{2} - 2}}[{{z}_{1}} - \sqrt {z_{1}^{2} - {{a}^{2}}} ], \\ {{F}_{{20}}}({{z}_{2}}) = {{G}_{1}}\frac{{\sigma _{{yy}}^{\infty }}}{{M_{2}^{2} - 2}}[{{z}_{2}} - \sqrt {z_{2}^{2} - {{a}^{2}}} ]. \\ \end{gathered} $$

(3.27)

The stated problem can also be solved using the Keldysh-Sedov formula [15].

The functions ${{F}_{{10}}}$ and ${{F}_{{20}}}$ allow one to find the components of the tensor $\sigma _{{ik}}^{ - }$ and macro-displacement vector $U_{i}^{ - }$. To do this, we need to substitute (3.21) and (3.27) into (3.19) and (3.20). Thus, for the components of the stress tensor we get

$$\sigma _{{xx}}^{ - } = \sigma _{{yy}}^{\infty }{\kern 1pt} {\text{Re}}{\kern 1pt} \left[ {(1 - {{G}_{1}})\frac{{M_{2}^{2} - 2M_{1}^{2} + 2}}{{2 - M_{2}^{2}}}\left( {1 - \frac{{{{z}_{1}}}}{{\sqrt {z_{1}^{2} - {{a}^{2}}} }}} \right) + {{G}_{1}}\left( {1 - \frac{{{{z}_{2}}}}{{\sqrt {z_{2}^{2} - {{a}^{2}}} }}} \right)} \right],$$

$$\sigma _{{yy}}^{ - } = \sigma _{{yy}}^{\infty }{\kern 1pt} {\text{Re}}{\kern 1pt} \left[ {(1 - {{G}_{1}})\frac{{{{z}_{1}}}}{{\sqrt {z_{1}^{2} - {{a}^{2}}} }} + {{G}_{1}}\frac{{{{z}_{2}}}}{{\sqrt {z_{2}^{2} - {{a}^{2}}} }}} \right],$$

(3.28)

$$\sigma _{{xy}}^{ - } = \sigma _{{yy}}^{\infty }\frac{{2 - M_{2}^{2}}}{{2\sqrt {1 - M_{2}^{2}} }}{\kern 1pt} {\text{Re}}{\kern 1pt} \left[ {{{G}_{1}}i\left( {\frac{{{{z}_{1}}}}{{\sqrt {z_{1}^{2} - {{a}^{2}}} }} - \frac{{{{z}_{2}}}}{{\sqrt {z_{2}^{2} - {{a}^{2}}} }}} \right)} \right].$$

Relations (3.28) correspond to the solution of the Griffith crack propagation problem based on the classical linear model. This problem was solved by Ioffe [16]. If we accept that the crack propagation velocity C = 0, then, assuming ${{z}_{1}} = {{z}_{2}}$ in (3.28) and passing to the limit ${{M}_{1}},{{M}_{2}} \to 0$, we obtain the stress field in the plane with a cut y = 0 ${\text{|}}x{\text{|}} \leqslant a$ in the static case

$$\sigma _{{xx}}^{ - } = \left\{ {\begin{array}{*{20}{l}} { - \sigma _{{yy}}^{\infty },\quad {\text{|}}x{\text{|}} < a} \\ { - \sigma _{{yy}}^{\infty }\left( {1 - \frac{x}{{\sqrt {{{x}^{2}} - {{a}^{2}}} }}} \right),\quad {\text{|}}x{\text{|}} > a,} \end{array}} \right.$$

$$\sigma _{{yy}}^{ - } = \left\{ {\begin{array}{*{20}{l}} {0,\quad {\text{|}}x{\text{|}} < a} \\ {\sigma _{{yy}}^{\infty }\frac{x}{{\sqrt {{{x}^{2}} - {{a}^{2}}} }},\quad {\text{|}}x{\text{|}} > a,} \end{array}} \right.$$

(3.29)

$$\sigma _{{xy}}^{ - } = 0,\;\;\; - \infty < x < \infty .$$

Expressions (3.29) coincide with the results obtained by S. Inglis [17].

The tensor $\sigma _{{ik}}^{ + }$ and macro-displacement vector $U_{i}^{ + }$ components can be found if the optical mode u_s is known. It is found from the micro-field equations (2.4).

3.1 Solution of Micro-Field Equations

The micro-field equations (2.4) can be written in component form if the micro-stress tensor ${{\chi }_{{ij}}}$ (2.8) is substituted into equation (2.4) and the form of the tensor ${{k}_{{ijmn}}}$ is taken into account:

$${{\mu }_{0}}\frac{{{{\partial }^{2}}{{u}_{x}}}}{{\partial {{t}^{2}}}} = {{k}_{{44}}}\Delta {{u}_{x}} + ({{k}_{{12}}} + {{k}_{{44}}})({{u}_{{x,xx}}} + {{u}_{{y,xy}}}) + ({{k}_{{11}}} - {{k}_{{12}}} - 2{{k}_{{44}}}){{u}_{{x,xx}}} - \frac{R}{b}\sin {{u}_{s}},$$

$${{\mu }_{0}}\frac{{{{\partial }^{2}}{{u}_{y}}}}{{\partial {{t}^{2}}}} = {{k}_{{44}}}\Delta {{u}_{y}} + ({{k}_{{12}}} + {{k}_{{44}}})({{u}_{{x,xy}}} + {{u}_{{y,yy}}}) + ({{k}_{{11}}} - {{k}_{{12}}} - 2{{k}_{{44}}}){{u}_{{y,yy}}} - \frac{R}{b}\sin {{u}_{s}}$$

(3.30)

Instead of components (${{u}_{x}},{{u}_{y}}$), we introduce ${{u}_{s}}$ and ${{u}_{m}} = ({{u}_{x}} - {{u}_{y}}){\text{/}}b$. Then the sum and difference of Eqs. (3.30) are written as follows

$$\begin{gathered} 2{{\mu }_{0}}\frac{{{{\partial }^{2}}{{u}_{s}}}}{{\partial {{t}^{2}}}} = ({{k}_{{11}}} + {{k}_{{44}}})\Delta {{u}_{s}} + 2({{k}_{{12}}} + {{k}_{{44}}}){{u}_{{s,xy}}} + ({{k}_{{11}}} - {{k}_{{44}}})({{u}_{{m,xx}}} - {{u}_{{m,yy}}}) - \frac{{4R}}{{{{b}^{2}}}}\sin {{u}_{s}}, \\ 2{{\mu }_{0}}\frac{{{{\partial }^{2}}{{u}_{m}}}}{{\partial {{t}^{2}}}} = ({{k}_{{11}}} + {{k}_{{44}}})\Delta {{u}_{m}} - 2({{k}_{{12}}} + {{k}_{{44}}}){{u}_{{m,xy}}} + ({{k}_{{11}}} - {{k}_{{44}}})({{u}_{{s,xx}}} - {{u}_{{s,yy}}}). \\ \end{gathered} $$

(3.31)

In the moving coordinate system ($\xi ,\eta$), Eqs. (3.31) take the form

$$({{k}_{{11}}} + {{k}_{{44}}})\left[ {(1 - m_{1}^{2})\frac{{{{\partial }^{2}}{{u}_{s}}}}{{\partial {{\xi }^{2}}}} + \frac{{{{\partial }^{2}}{{u}_{s}}}}{{\partial {{\eta }^{2}}}} + 2{{k}_{0}}\frac{{{{\partial }^{2}}{{u}_{s}}}}{{\partial \xi \partial \eta }}} \right]$$

$$\begin{gathered} \, + ({{k}_{{11}}} - {{k}_{{44}}})({{u}_{{m,\xi \xi }}} - {{u}_{{m,\eta \eta }}}) - \frac{{4R}}{{{{b}^{2}}}}\sin {{u}_{s}} = 0, \\ ({{k}_{{11}}} + {{k}_{{44}}})\left[ {(1 - m_{1}^{2})\frac{{{{\partial }^{2}}{{u}_{m}}}}{{\partial {{\xi }^{2}}}} + \frac{{{{\partial }^{2}}{{u}_{m}}}}{{\partial {{\eta }^{2}}}} - 2{{k}_{0}}\frac{{{{\partial }^{2}}{{u}_{m}}}}{{\partial \xi \partial \eta }}} \right] + ({{k}_{{11}}} - {{k}_{{44}}})({{u}_{{s,\xi \xi }}} - {{u}_{{s,\eta \eta }}}) = 0. \\ \end{gathered} $$

(3.32)

$${{m}_{1}} = \frac{C}{{{{{v}}_{1}}}},\quad {v}_{1}^{2} = \frac{{{{k}_{{12}}} + {{k}_{{44}}}}}{{2{{\mu }_{0}}}},\quad {{k}_{0}} = \frac{{{{k}_{{12}}} + {{k}_{{44}}}}}{{{{k}_{{11}}} + {{k}_{{44}}}}}$$

It can be seen that equations (3.32) are related. They are separated if ${{k}_{{11}}} = {{k}_{{44}}}$. We accept this condition and instead of the variables (ξ, η) we introduce

$$\begin{gathered} {{q}_{1}} = {{L}_{1}}(\xi + \alpha \eta ),\quad {{q}_{2}} = {{L}_{2}}(\xi - \alpha \eta ),\quad \alpha = \sqrt {1 - m_{1}^{2}} \\ {{L}_{1}} = \frac{1}{b}\sqrt {\frac{{2p}}{{({{k}_{{11}}} + {{k}_{{44}}})\alpha (\alpha + {{k}_{0}})}}} ,\quad {{L}_{2}} = \frac{1}{b}\sqrt {\frac{{2p}}{{({{k}_{{11}}} + {{k}_{{44}}})\alpha (\alpha - {{k}_{0}})}}} \\ \end{gathered} $$

(3.33)

Via variables (${{q}_{1}},{{q}_{2}}$), Eqs. (3.32) take the form

$$\frac{{{{\partial }^{2}}{{u}_{s}}}}{{\partial q_{1}^{2}}} + \frac{{{{\partial }^{2}}{{u}_{s}}}}{{\partial q_{2}^{2}}} = \frac{R}{p}\sin {{u}_{s}},$$

(3.34)

$${{\omega }^{2}}\frac{{{{\partial }^{2}}{{u}_{m}}}}{{\partial q_{1}^{2}}} + \frac{{{{\partial }^{2}}{{u}_{m}}}}{{\partial q_{2}^{2}}} = 0,\quad \omega = \sqrt {\frac{{\alpha - {{k}_{0}}}}{{\alpha + {{k}_{0}}}}} .$$

(3.35)

From relations (2.6), (2.15) we find

$$\frac{R}{p} = {{p}_{1}} + 2{{p}_{2}}\cos {{u}_{s}},$$

$${{p}_{1}} = 1 - 2{{p}_{2}} - \frac{{{{p}_{2}}}}{s}({{\sigma }_{{xx}}} + {{\sigma }_{{yy}}}),$$

(3.36)

$${{p}_{2}} = \frac{{{{s}^{2}}}}{{2p(\lambda + \mu )}}.$$

Taking into account (3.36), Eq. (3.34) takes the form

$$\frac{{{{\partial }^{2}}{{u}_{s}}}}{{\partial q_{1}^{2}}} + \frac{{{{\partial }^{2}}{{u}_{s}}}}{{\partial q_{2}^{2}}} = {{p}_{1}}\sin {{u}_{s}} + {{p}_{2}}\sin 2{{u}_{s}}.$$

(3.37)

Equation (3.37) differs from the classical double sine-Gordon equation in that the amplitude ${{p}_{1}}$ is not a constant value, but a function $(t,x,y,{{u}_{s}})$. There are no analytical methods for solving such an equation in the literature. For this reason, the assumptions that transform (3.37) to equations with exact analytical solutions are justified. For media for which ${{s}^{2}} \ll 2p(\lambda + \mu )$ it is possible to accept ${{p}_{2}} = 0$ and ${{p}_{1}} = 1$. Then equation (3.37) becomes the classical sine-Gordon equation

$$\frac{{{{\partial }^{2}}{{u}_{s}}}}{{\partial q_{1}^{2}}} + \frac{{{{\partial }^{2}}{{u}_{s}}}}{{\partial q_{2}^{2}}} = \sin {{u}_{s}}.$$

(3.38)

If ${{s}^{2}} \ll 2p(\lambda + \mu )$, but $s({{\sigma }_{{xx}}} + {{\sigma }_{{yy}}}){\text{/}}2p(\lambda + \mu )$ is not a negligible quantity, then (3.37) takes the form of a sine-Gordon equation with a variable amplitude

$$\begin{gathered} \frac{{{{\partial }^{2}}{{u}_{s}}}}{{\partial q_{1}^{2}}} + \frac{{{{\partial }^{2}}{{u}_{s}}}}{{\partial q_{2}^{2}}} = p({{q}_{1}},{{q}_{2}})\sin {{u}_{s}}, \\ p({{q}_{1}},{{q}_{2}}) = 1 - s({{\sigma }_{{xx}}} + {{\sigma }_{{yy}}}){\text{/}}2p(\lambda + \mu ). \\ \end{gathered} $$

(3.39)

The sine-Gordon equation (3.38) has been studied in detail in the literature. For the sine-Gordon equation with variable amplitude, analytical solutions are constructed only for a particular form of functions $p({{q}_{1}},{{q}_{2}})$ [18]–[20]. Since finding the optical mode involves overcoming significant difficulties, to illustrate the method of finding ($\sigma _{{ik}}^{ + },U_{i}^{ + }$) we chose the simplest solution of ${{u}_{s}}$. If we accept that equation (3.38) is valid, and ${{u}_{s}} = {{u}_{s}}({{q}_{1}})$, then the solution of the equation (3.38) is as follows

$${{u}_{s}} = 4\arctan {{e}^{{{{q}_{1}}}}}$$

(3.40)

We find ($\sigma _{{ik}}^{ + },U_{i}^{ + }$) for the optical mode (3.40).

3.2 Finding Stresses and Displacements due to the Optical Mode

For optical mode (3.40)

$$\Phi ({{u}_{s}}) = 1 - \cos {{u}_{s}} = 8g({{q}_{1}}),\quad g({{q}_{1}}) = \frac{{{{e}^{{2{{q}_{1}}}}}}}{{{{{(1 + {{e}^{{2{{q}_{1}}}}})}}^{2}}}}$$

(3.41)

and the function Q₀ is found from equations (2.24), (3.4)

$${{Q}_{0}} = - \frac{D}{{2L_{1}^{2}}}\ln (1 + {{e}^{{2{{q}_{1}}}}}),\quad D = \frac{{8sV_{2}^{2}}}{{V_{1}^{2}(2 - m_{1}^{2} - M_{1}^{2})}}.$$

(3.42)

Taking into account (2.19), (3.24), (3.42), we find

$${{L}_{{11}}}({{Q}_{0}}) = - D(2 - 2m_{1}^{2} - M_{2}^{2})g({{q}_{1}}),\quad {{L}_{{22}}}({{Q}_{0}}) = - D(2 - M_{2}^{2})g({{q}_{1}}),$$

(3.43)

$$\frac{{{{\partial }^{2}}{{Q}_{0}}}}{{\partial \xi \partial \eta }} = - 2D\sqrt {1 - m_{1}^{2}} {\kern 1pt} g({{q}_{1}}),$$

$${{T}_{{12}}}(\xi ) = (D - {{G}_{2}})g({{q}_{1}}),\quad {{G}_{2}} = {{G}_{1}}D\left( {1 + i\sqrt {\frac{{1 - m_{1}^{2}}}{{1 - M_{1}^{2}}}} } \right),\quad {{T}_{{22}}}(\xi ) = {{G}_{2}}g({{q}_{1}}).$$

(3.44)

The functions ${{F}_{{12}}}({{z}_{1}})$ and ${{F}_{{22}}}({{z}_{2}})$ are solutions of the corresponding Riemann–Hilbert problems with boundary conditions (3.44) and are found by formula (3.26)

$${{F}_{{12}}}({{z}_{1}}) = ({{G}_{2}} - D)\Psi ({{z}_{1}}),$$

(3.45)

$${{F}_{{22}}}({{z}_{2}}) = - {{G}_{2}}\Psi ({{z}_{2}}),$$

(3.46)

$$\Psi (z) = \frac{1}{{\pi \sqrt {{{z}^{2}} - {{a}^{2}}} }}\int\limits_{ - a}^a \frac{{{{e}^{{2{{L}_{1}}\xi }}}}}{{{{{(1 + {{e}^{{2{{L}_{1}}\xi }}})}}^{2}}}}\frac{{\sqrt {{{a}^{2}} - {{\xi }^{2}}} }}{{z - \xi }}{\kern 1pt} d\xi .$$

(3.47)

After substituting the functions ${{F}_{{12}}}({{z}_{1}})$ and ${{F}_{{22}}}({{z}_{2}})$ into the corresponding expressions of formulas (3.19) and (3.20), the components of the tensor $\sigma _{{ij}}^{ + }$ and the macro-displacement vector $U_{i}^{ + }$ can be found.

4 CONCLUSIONS

The stated general method for solving nonlinear equations of plane deformation is an effective method for solving dynamic problems. It reduces finding exact analytical solutions of dynamic problems to the problems of the theory of boundary value problems of analytic functions (Riemann, Riemann-Hilbert, Keldysh-Sedov). The stressed and deformed states of the medium are obtained as the sum of two terms. The first one describes the action of external forces, and the second one describes the optical mode. These factors are taken into account separately; which makes it possible to investigate the influence of the optical mode on the deformation of the crystalline medium and to refine such important quantities as stress intensity, local stress criteria, etc.