1 INTRODUCTION

Among the problems solved by means of solids mechanics, there are those in which some threshold events are studied. Such events are often catastrophic and cause destruction in man-made and natural structures. Examples of such events are the phenomenon of bifurcation of equilibrium states, loss of stability in structural elements (flipping of shells) [1, 2], in rocks [3]; formation of brittle fracture cracks [4], avalanches [5], etc. Here we consider the boundary value problem of the theory of large elastic-viscoplastic deformations about an instantaneous change in the slow process of viscometric deformation, which is caused by the shear and slippage of the material. The elastic-viscoplastic deformation of a material in a viscometer is, therefore, a subcritical process, and the dynamic unloading following the moment of separation is a supercritical process. In this case, at both stages, the deformed state is an azimuthal shear. Considering that reversible and irreversible deformations acquired during loading are interconnected and cannot be specified arbitrarily, the problem of dynamic unloading also requires the solution of the problem of active loading [6–8]. The azimuthal shear problems for various models of media under quasi-static and shock-wave deformation have a long history and various applications, including in biomechanics [9–17].

2 MODEL RELATIONSHIPS OF AN ELASTIC-VISCOPLASTIC MATERIAL

To describe the motion of the medium, we will accept the model of large elastoplastic deformations [18, 19], in which the reversible and irreversible components of the total deformations are set by the differential equations of their change (transfer). Then, in Euler’s variables, the main kinematic relations have the form:

$${\frac{{D{\mathbf{e}}}}{{Dt}} = {\boldsymbol{\varepsilon }} - {{{\boldsymbol{\varepsilon }}}^{{\mathbf{p}}}} - \frac{{\text{1}}}{{\text{2}}}(({\boldsymbol{\varepsilon }} - {{{\boldsymbol{\varepsilon }}}^{{\mathbf{p}}}} + {\mathbf{z}}) \cdot {\mathbf{e}} + {\mathbf{e}} \cdot ({\boldsymbol{\varepsilon }} - {{{\boldsymbol{\varepsilon }}}^{{\mathbf{p}}}} - {\mathbf{z}})){\text{,}}}\quad \frac{{D{\mathbf{p}}}}{{Dt}} = {{{\boldsymbol{\varepsilon }}}^{{\mathbf{p}}}} - {\mathbf{p}} \cdot {{{\boldsymbol{\varepsilon }}}^{{\mathbf{p}}}} - {{{\boldsymbol{\varepsilon }}}^{{\mathbf{p}}}} \cdot {\mathbf{p}},$$
$$\begin{gathered} {\frac{{D{\mathbf{n}}}}{{Dt}} = \frac{{d{\mathbf{n}}}}{{dt}} - {\mathbf{r}} \cdot {\mathbf{n}} - {\mathbf{n}} \cdot {{{\mathbf{r}}}^{T}}{\text{,}}\quad {\boldsymbol{\varepsilon }} = \frac{{\text{1}}}{{\text{2}}}(\nabla {\mathbf{v}} + {{\nabla }^{T}}{\mathbf{v}}){\text{,}}\quad {\boldsymbol{\omega }} = \frac{{\text{1}}}{{\text{2}}}(\nabla {\mathbf{v}} - {{\nabla }^{T}}{\mathbf{v}}){\text{,}}} \\ {\mathbf{v}} = \frac{{d{\mathbf{u}}}}{{dt}} = \frac{{\partial {\mathbf{u}}}}{{\partial t}} + {\mathbf{v}}\nabla {\mathbf{u}}{\text{,}}\quad {\mathbf{r}} = {\boldsymbol{\omega }} + {\mathbf{z}}, \\ \end{gathered} $$
$${{\mathbf{z}} = {{A}^{{ - {\text{1}}}}}\{ {{B}^{{\text{2}}}}\left( {{\boldsymbol{\varepsilon }} \cdot {\mathbf{e}} - {\mathbf{e}} \cdot {\boldsymbol{\varepsilon }}} \right) + B({\boldsymbol{\varepsilon }} \cdot {{{\mathbf{e}}}^{{\text{2}}}} - {{{\mathbf{e}}}^{{\text{2}}}} \cdot {\boldsymbol{\varepsilon }}) + {\mathbf{e}} \cdot {\boldsymbol{\varepsilon }} \cdot {{{\mathbf{e}}}^{{\text{2}}}} - {{{\mathbf{e}}}^{{\text{2}}}} \cdot {\boldsymbol{\varepsilon }} \cdot {\mathbf{e}}\} },$$
(2.1)
$$\begin{gathered} {A = {\text{8}} - {\text{8}}{{E}_{{\text{1}}}} + {\text{3}}E_{{\text{1}}}^{{\text{2}}} - {{E}_{{\text{2}}}} - \frac{{E_{{\text{1}}}^{{\text{3}}}}}{{\text{3}}} + \frac{{{{E}_{{\text{3}}}}}}{{\text{3}}}{\text{,}}\quad B = {\text{2}} - {{E}_{{\text{1}}}}{\text{,}}}\quad {{E}_{{\text{1}}}} = {\text{tr}}\left( {\mathbf{e}} \right){\text{,}} \\ {{E}_{{\text{2}}}} = {\mathbf{e}} \cdot \cdot \,{\mathbf{e}}{\text{,}}\quad {{E}_{{\text{3}}}} = {{{\mathbf{e}}}^{{\text{2}}}} \cdot \cdot \,{\mathbf{e}}, \\ \end{gathered} $$
$${{\mathbf{d}} = \frac{1}{2}(\nabla {\mathbf{u}} + {{\nabla }^{T}}{\mathbf{u}} - {{\nabla }^{T}}{\mathbf{u}} \cdot \nabla {\mathbf{u}}) = {\mathbf{e}} + {\mathbf{p}} - \frac{{\text{1}}}{{\text{2}}}{\mathbf{e}} \cdot {\mathbf{e}} - {\mathbf{e}} \cdot {\mathbf{p}} - {\mathbf{p}} \cdot {\mathbf{e}} + {\mathbf{e}} \cdot {\mathbf{p}} \cdot {\mathbf{e}}}.$$

Here, u and v are the vectors of displacement and velocity; d is the Almansi total strain tensor; \({\mathbf{e}}\), \({\mathbf{p}}\) are the tensors of reversible and irreversible deformations, respectively; \({\boldsymbol{\varepsilon }}\), \({{{\boldsymbol{\varepsilon }}}^{{\mathbf{p}}}}\) are strain rate and irreversible strain rate tensors; \({\boldsymbol{\omega }}\) is the vorticity tensor; \(D{\text{/}}Dt\) is the objective time derivative, written for an arbitrary tensor \({\mathbf{n}}\), which transforms into the Jaumann derivative [19], when the nonlinear part \({\mathbf{z}}\) of the rotation tensor \({\mathbf{r}}\) vanishes. According to (2.1), during unloading (\({{{\boldsymbol{\varepsilon }}}^{{\mathbf{p}}}} = 0\)), the components of the tensor of irreversible deformations change in the same way as at rigid body motion. Everywhere below, the condition of incompressibility is adopted in order to focus on the processes in which significant shear deformations are achieved with relatively small changes in volume. In this case, an analogue of Murnaghan’s formula, which determines the stress – elastic strain relationships, takes the form [19]:

$$\begin{gathered} {{\boldsymbol{\sigma }} = - {{p}_{{\text{1}}}}{\mathbf{I}} + \frac{{\partial W}}{{\partial {\mathbf{d}}}}\left( {{\mathbf{I}} - {\text{2}}{\mathbf{d}}} \right){\text{,}}\quad {\mathbf{p}} \equiv {\text{0}}}, \\ {\boldsymbol{\sigma }} = - {{p}_{{\text{2}}}}{\mathbf{I}} + \frac{{\partial W}}{{\partial {\mathbf{e}}}}\left( {{\mathbf{I}} - {\mathbf{e}}} \right),\quad {\mathbf{p}} \ne {\text{0}}{\text{.}} \\ \end{gathered} $$
(2.2)

In (2.2), \({\boldsymbol{\sigma }}\) is the Cauchy stress tensor; \({{{p}_{{\text{1}}}}}\) and \({{{p}_{{\text{2}}}}}\) are functions of the additional hydrostatic pressure, I is the unit tensor of the second rank, W = W(J1, J2) is the elastic potential, which for an incompressible medium can be represented in the form [19, 20]:

$${W = - {\text{2}}\mu {{J}_{{\text{1}}}} - \mu {{J}_{{\text{2}}}} + bJ_{{\text{1}}}^{{\text{2}}} + \left( {b - \mu } \right){{J}_{{\text{1}}}}{{J}_{{\text{2}}}} - \chi J_{{\text{1}}}^{{\text{3}}} + \cdots },$$
(2.3)
$${{J}_{k}} = \left\{ {\begin{array}{*{20}{c}} {{{L}_{k}},\quad {\mathbf{p}} \equiv {\text{0}}} \\ {{{I}_{k}},\quad {\mathbf{p}} \ne {\text{0}}} \end{array},\quad k = {\text{1}}{\text{.2}}} \right.,$$
$${{{L}_{{\text{1}}}} = \operatorname{tr} \left( {\mathbf{d}} \right),\quad {{L}_{{\text{2}}}} = {\mathbf{d}} \cdot \cdot \,{\mathbf{d}},\quad {{I}_{{\text{1}}}} = \operatorname{tr} \left( {\mathbf{e}} \right) - \frac{{\text{1}}}{{\text{2}}}{\mathbf{e}} \cdot \cdot \,{\mathbf{e}},\quad {{I}_{{\text{2}}}} = {\mathbf{e}} \cdot \cdot \,{\mathbf{e}} - {{{\mathbf{e}}}^{{\text{2}}}} \cdot \cdot \,{\mathbf{e}} + \frac{{\text{1}}}{{\text{4}}}{{{\mathbf{e}}}^{{\text{2}}}} \cdot \cdot \,{{{\mathbf{e}}}^{{\text{2}}}}}.$$

Here, \(\mu \), \(b\) and \(\chi \) are the elastic moduli of the material. The invariants \({{{I}_{{\text{1}}}}}\) and \({{{I}_{{\text{2}}}}}\) of the elastic strain tensor are chosen so that the passage to the limit in (2.3) occurs from the second dependence to the first as the plastic deformations tend to zero. We will assume that irreversible deformations begin to accumulate in the material when stresses reach the loading (yield) surface \({f({\boldsymbol{\sigma }}{\text{,}}{{{\boldsymbol{\varepsilon }}}^{{\mathbf{p}}}},k) = {\text{0}}}\). As the loading surface, we take the Tresca yield condition taking into account the viscous resistance to plastic flow [21]:

$${f({{\sigma }_{i}}{\text{,}}\varepsilon _{k}^{p}{\text{,}}k) = \max \left| {{{\sigma }_{i}} - {{\sigma }_{j}}} \right| - {\text{2}}k - {\text{2}}\eta \max \left| {\varepsilon _{k}^{p}} \right|}.$$
(2.4)

In (2.4), \({{{\sigma }_{i}}}\) and \({\varepsilon _{k}^{p}}\) are the eigenvalues of the stress tensor and plastic strain rate tensor, \(k\) is the shear yield strength, \(\eta \) represents the strain rate dependence of the yield stress. We utilize the associated flow rule for plastic strain rate tensor

$${{{{\boldsymbol{\varepsilon }}}^{{\mathbf{p}}}} = {{\lambda }}\frac{{\partial f}}{{\partial {\boldsymbol{\sigma }}}}{\text{,}}\quad {{\lambda }} > {\text{0}}}.$$
(2.5)

In order to obtain a closed system of equations both in the region of elastic deformation and in the region of plastic flow, it is sufficient to supplement the previous relations with the equation of motion or the equilibrium equation

$${\nabla \cdot {\boldsymbol{\sigma }} = {{\rho }}\frac{{d{\mathbf{v}}}}{{dt}}},$$
(2.6)
$${\nabla \cdot {\boldsymbol{\sigma }} = {\mathbf{0}}}.$$
(2.7)

It is not always possible to neglect the inertial forces in (2.6) so as to have (2.7). If this turns out to be possible, then one speaks of a quasi-static approximation in solving the problem.

3 FORMULATION OF THE PROBLEM. QUASI-STATIC DEFORMATION

Let the material, the properties of which are described above, fill the annular gap between rigid cylindrical surfaces with unlimited generatrices. We denote the radius of the inner cylinder by \({{{r}_{{\text{0}}}}}\), and the outer one by \(R\). The outer cylinder rotates around its axis with a preset shear stress, while the inner one remains fixed. We assume that at shear stress values not exceeding a certain specified threshold value \({\left| {{{\sigma }_{{r\varphi }}}} \right| \leqslant {{\sigma }_{{\text{0}}}}}\) (\({{\sigma }_{{\text{0}}}} = {\text{const}}\)), the adhesion conditions are satisfied on the cylinder walls:

$${{\mathbf{u}}\left( {{{r}_{0}},t} \right) = {\mathbf{v}}\left( {{{r}_{0}}{\text{,}}t} \right) = {\text{0,}}\quad {{\sigma }_{{r\varphi }}}\left( {R{\text{,}}t} \right) = \alpha t,\quad \alpha = {\text{const}}}.$$
(3.1)

We assume that \({{\sigma }_{{\text{0}}}} > k\). There are no preliminary deformations. The trajectories of the points of the medium are concentric circles, and all the required functions in the cylindrical coordinate system \({\left( {r{\text{,}}\varphi {\text{,}}z} \right)}\) depend on two variables: the distance from the of the cylinders \(r\) and the time t. According to (2.1), the kinematics of the medium in this case is determined by the dependences

$${{{u}_{r}} = r\left( {{\text{1}} - \cos \psi } \right){\text{,}}\quad {{u}_{\varphi }} = r\sin \psi },$$
$${{{d}_{{rr}}} = - \frac{{{{r}^{{\text{2}}}}}}{{\text{2}}}{{{\left( {\frac{{\partial \psi }}{{\partial r}}} \right)}}^{2}}{\text{,}}\quad {{d}_{{r\varphi }}} = \frac{r}{{\text{2}}}\frac{{\partial \psi }}{{\partial r}}{\text{,}}\quad {{{v}}_{\varphi }} = r\omega = r\frac{{\partial \psi }}{{\partial t}}},$$
(3.2)
$${{{\varepsilon }_{{r\varphi }}} = \frac{r}{{\text{2}}}\frac{{{{\partial }^{{\text{2}}}}\psi }}{{\partial r\partial t}}{\text{,}}\quad {{\omega }_{{r\varphi }}} = - \frac{{\partial \psi }}{{\partial t}} - \frac{r}{{\text{2}}}\frac{{{{\partial }^{{\text{2}}}}\psi }}{{\partial r\partial t}}{\text{,}}\quad {{r}_{{r\varphi }}} = - \frac{{\partial \psi }}{{\partial t}} + \frac{{{\text{2}}{{\varepsilon }_{{r\varphi }}}\left( {{\text{1}} - {{e}_{{\varphi \varphi }}}} \right)}}{{{{e}_{{rr}}} + {{e}_{{\varphi \varphi }}} - {\text{2}}}}},$$

where \({\psi = \psi \left( {r{\text{,}}t} \right)}\) is the central twist angle of the points of the medium, \({\omega = {{{v}}_{\varphi }}{\text{/}}r}\) is the angular velocity.

Before the stress reaches the loading surface, the deformation is reversible. According to (2.2), the components of the stress tensor in this case are determined by the dependences:

$$\begin{gathered} {{{\sigma }_{{rr}}} = {{\sigma }_{{zz}}} = - \left( {p + {\text{2}}\mu } \right) - \frac{{\left( {b + \mu } \right){{r}^{2}}}}{{\text{2}}}{{{\left( {\frac{{\partial \psi }}{{\partial r}}} \right)}}^{2}} = - s\left( {r{\text{,}}t} \right){\text{,}}} \\ {{\sigma }_{{\varphi \varphi }}} = - s\left( {r{\text{,}}t} \right) + \mu {{\left( {r\frac{{\partial \psi }}{{\partial r}}} \right)}^{{\text{2}}}}{\text{,}}\quad {{\sigma }_{{r\varphi }}} = \mu r\frac{{\partial \psi }}{{\partial r}} \\ \end{gathered} $$
(3.3)

We assume that elastic strain is small; therefore, only the leading nonlinear terms of deformations are written out in (3.3). In areas where irreversible deformations are present, stresses are determined according to the second dependence in (2.2):

$$\begin{gathered} {{{\sigma }_{{rr}}} = - p - {\text{2}}\mu + {\text{2}}\left( {b + \mu } \right){{e}_{{rr}}} + {\text{2}}b{{e}_{{\varphi \varphi }}} + \mu e_{{r\varphi }}^{{\text{2}}}{\text{,}}} \\ {{\sigma }_{{\varphi \varphi }}} = - p - {\text{2}}\mu + {\text{2}}\left( {b + \mu } \right){{e}_{{\varphi \varphi }}} + {\text{2}}b{{e}_{{rr}}} + \mu e_{{r\varphi }}^{{\text{2}}}, \\ {{{\sigma }_{{zz}}} = - p - {\text{2}}\mu + {\text{2}}b\left( {{{e}_{{rr}}} + {{e}_{{\varphi \varphi }}}} \right) - {\text{2}}\mu e_{{r\varphi }}^{{\text{2}}}{\text{,}}}\quad {{\sigma }_{{r\varphi }}} = {\text{2}}\mu {{e}_{{r\varphi }}}{\text{,}}\quad \frac{{{{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}}}}{{{{\sigma }_{{r\varphi }}}}} = \frac{{{{e}_{{rr}}} - {{e}_{{\varphi \varphi }}}}}{{{{e}_{{r\varphi }}}}}. \\ \end{gathered} $$
(3.4)

The tensor components not written out in (3.2)–(3.4) are equal to zero. If deformation is sufficiently slow, it is possible to adopt the quasi-static approximation. In this case, integrating the equilibrium equations following from (2.7) and (3.3),

$${\frac{{\partial {{\sigma }_{{rr}}}}}{{\partial r}} + \frac{{{{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}}}}{r} = {\text{0,}}\quad \frac{{\partial {{\sigma }_{{r\varphi }}}}}{{\partial r}} + {\text{2}}\frac{{{{\sigma }_{{r\varphi }}}}}{r} = {\text{0}}}$$
(3.5)

taking into account the boundary conditions (3.1), we write down the solution that is valid in the time interval when the material undergoes only elastic deformation

$${\psi = \frac{{c\left( t \right)}}{{{\text{2}}\mu }}\left( {\frac{{\text{1}}}{{r_{0}^{2}}} - \frac{{\text{1}}}{{{{r}^{{\text{2}}}}}}} \right){\text{,}}\quad \omega = \frac{{\alpha {{R}^{2}}}}{{{\text{2}}\mu }}\left( {\frac{{\text{1}}}{{r_{0}^{2}}} - \frac{{\text{1}}}{{{{r}^{{\text{2}}}}}}} \right){\text{,}}\quad c\left( t \right) = \alpha {{R}^{2}}t},$$
$$\begin{gathered} {{{\sigma }_{{r\varphi }}} = \frac{{c\left( t \right)}}{{{{r}^{{\text{2}}}}}}{\text{,}}\quad {{\sigma }_{{rr}}} = {{\sigma }_{{zz}}} = \frac{{c{{{\left( t \right)}}^{2}}}}{{{\text{4}}\mu }}\left( {\frac{{\text{1}}}{{r_{{\text{0}}}^{{\text{4}}}}} - \frac{{\text{1}}}{{{{r}^{{\text{4}}}}}}} \right) + \sigma _{{rr}}^{{\text{0}}}{\text{,}}} \\ {{{\sigma }_{{\varphi \varphi }}} = \frac{{c{{{\left( t \right)}}^{{\text{2}}}}}}{{{\text{4}}\mu }}\left( {\frac{{\text{1}}}{{r_{{\text{0}}}^{{\text{4}}}}} + \frac{{\text{3}}}{{{{r}^{{\text{4}}}}}}} \right) + \sigma _{{rr}}^{{\text{0}}}{\text{,}}\quad \sigma _{{rr}}^{{\text{0}}} = {{\sigma }_{{rr}}}\left( {{{r}_{0}},t} \right),} \\ \end{gathered} $$
(3.6)
$${{{e}_{{r\varphi }}} = {{d}_{{r\varphi }}} = \frac{{c\left( t \right)}}{{{\text{2}}\mu {{r}^{{\text{2}}}}}}{\text{,}}\quad {{e}_{{rr}}} = - \frac{{\text{3}}}{{\text{2}}}e_{{r\varphi }}^{{\text{2}}}{\text{,}}\quad {{e}_{{\varphi \varphi }}} = \frac{{e_{{r\varphi }}^{{\text{2}}}}}{{\text{2}}}}.$$

Solution (3.6) is valid until moment of time \(t = {{t}_{0}}\), when the plasticity condition \({{{\sigma }_{{r\varphi }}}\left( {{{r}_{{\text{0}}}},{{t}_{{\text{0}}}}} \right) = k}\), \({{t}_{0}} = kr_{0}^{2}{\text{/}}\alpha {{R}^{2}}\) is satisfied on the surface \(r = {{r}_{0}}\). From this moment on, the considered layer \({V{\text{:}}\;{{r}_{{\text{0}}}} \leqslant r \leqslant R}\) contains two regions: the region of viscoplastic flow \({{{V}^{{\left( P \right)}}}{\text{:}}\;{{r}_{{\text{0}}}} \leqslant r \leqslant m\left( t \right)}\) and the region of reversible (elastic) deformation \({{{V}^{{\left( E \right)}}}{\text{:}}\;m\left( t \right) \leqslant r \leqslant R}\); \(r = m\left( t \right)\) is the equation of a moving elastoplastic boundary. Hereinafter, the superscripts “E” and “\(P\)” in parentheses denote the values in the regions \({{V}^{{\left( E \right)}}}\) and \({{V}^{{\left( P \right)}}}\), respectively. We will assume that the stress state is close enough to the state of pure azimuthal shear, neglecting second-order effects. Then, based on (2.4), the plastic flow condition is written in the form:

$${f({{\sigma }_{{r\varphi }}}{\text{,}}\varepsilon _{{r\varphi }}^{p}) = \sigma _{{r\varphi }}^{{\text{2}}} - {{{(k + \eta \left| {\varepsilon _{{r\varphi }}^{p}} \right|)}}^{{\text{2}}}} = {\text{0}}}$$
(3.7)

and by virtue of the associated plastic flow law (2.5), condition (3.7) implies

$${{{\sigma }_{{r\varphi }}} = k + \eta \varepsilon _{{r\varphi }}^{p}{\text{,}}\quad \lambda = \frac{{\varepsilon _{{r\varphi }}^{p}}}{{k + \eta \varepsilon _{{r\varphi }}^{p}}}}.$$
(3.8)

The parameters of the stress-strain state are found by integrating the equilibrium equations in the regions \({{V}^{{\left( E \right)}}}\) and \({{V}^{{\left( P \right)}}}\), and the unknown integration functions are determined from (3.1) and the conditions for the continuity of displacement, velocity and stress at the elastoplastic boundary \(r = m\left( t \right)\). Thus, in the region of viscoplastic flow \({{V}^{{\left( P \right)}}}\), we obtain

$${{{\psi }^{{\left( P \right)}}} = \frac{{c\left( t \right)}}{{{\text{2}}\mu }}\left( {\frac{{\text{1}}}{{r_{0}^{2}}} - \frac{{\text{1}}}{{{{r}^{{\text{2}}}}}}} \right) + \frac{1}{{2\eta }}\left\{ {\alpha {{R}^{2}}{{t}^{2}}\left( {\frac{{\text{1}}}{{r_{0}^{2}}} - \frac{{\text{1}}}{{{{r}^{{\text{2}}}}}}} \right) + 4kt{\kern 1pt} {\text{ln}}\frac{{{{r}_{0}}}}{r} + \frac{{{{k}^{2}}({{r}^{2}} - r_{0}^{2})}}{{\alpha {{R}^{2}}}}} \right\}},$$
$${{{\omega }^{{\left( P \right)}}} = \frac{{\alpha {{R}^{2}}}}{{{\text{2}}\mu }}\left( {\frac{{\text{1}}}{{r_{0}^{2}}} - \frac{{\text{1}}}{{{{r}^{{\text{2}}}}}}} \right) + \frac{1}{\eta }\left\{ {\alpha {{R}^{2}}t\left( {\frac{{\text{1}}}{{r_{0}^{2}}} - \frac{{\text{1}}}{{{{r}^{{\text{2}}}}}}} \right) + 2k{\kern 1pt} {\text{ln}}\frac{{{{r}_{0}}}}{r}} \right\}},$$
(3.9)
$${{{p}_{{r\varphi }}} = \frac{1}{\eta }\left( {\frac{{\alpha {{R}^{{\text{2}}}}{{t}^{2}}}}{{2{{r}^{2}}}} - kt + \frac{{{{k}^{2}}{{r}^{2}}}}{{2\alpha {{R}^{2}}}}} \right){\text{,}}\quad }{{e}_{{r\varphi }}} = \frac{{\alpha {{R}^{{\text{2}}}}t}}{{2\mu {{r}^{2}}}}$$

and in the region of elastic deformation \({{V}^{{\left( E \right)}}}\)

$$\begin{gathered} {{{\psi }^{{\left( E \right)}}} = \frac{{c\left( t \right)}}{{{\text{2}}\mu }}\left( {\frac{{\text{1}}}{{r_{0}^{2}}} - \frac{{\text{1}}}{{{{r}^{{\text{2}}}}}}} \right) + \frac{1}{{2\eta }}\left\{ {\alpha {{R}^{2}}{{t}^{2}}\left( {\frac{{\text{1}}}{{r_{0}^{2}}} - \frac{{\text{1}}}{{m{{{\left( t \right)}}^{{\text{2}}}}}}} \right) + 4kt{\kern 1pt} {\text{ln}}\frac{{{{r}_{0}}}}{{m\left( t \right)}} + \frac{{{{k}^{2}}(m{{{\left( t \right)}}^{2}} - r_{0}^{2})}}{{\alpha {{R}^{2}}}}} \right\}}, \\ {{{\omega }^{{\left( E \right)}}} = \frac{{\alpha {{R}^{2}}}}{{{\text{2}}\mu }}\left( {\frac{{\text{1}}}{{r_{0}^{2}}} - \frac{{\text{1}}}{{{{r}^{{\text{2}}}}}}} \right) + \frac{1}{\eta }\left\{ {\alpha {{R}^{2}}t\left( {\frac{{\text{1}}}{{r_{0}^{2}}} - \frac{{\text{1}}}{{m{{{\left( t \right)}}^{{\text{2}}}}}}} \right) + 2k{\kern 1pt} {\text{ln}}\frac{{{{r}_{0}}}}{{m\left( t \right)}}} \right\}}. \\ \end{gathered} $$
(3.10)

The stresses in the layer, as before, are determined according to (3.5). The position of the elastoplastic boundary is found from the condition that the plastic strain rate \(\varepsilon _{{r\varphi }}^{p}\) is equal to zero on it

$${m\left( t \right) = R\sqrt {\frac{{\alpha t}}{k}} {\text{,}}\quad \varepsilon _{{r\varphi }}^{p} = \frac{{\alpha {{R}^{2}}t}}{{\eta {{r}^{2}}}}}\, - \frac{k}{\eta }.$$
(3.11)

According to (1.1), (3.7), and (3.8), the diagonal components of the reversible \({{{e}_{{rr}}}}\), \({{{e}_{{\varphi \varphi }}}}\) and irreversible \({{{p}_{{rr}}}}\), \({{{p}_{{\varphi \varphi }}}}\) deformations, which are quantities of a higher order of smallness compared with the non-diagonal ones, are found numerically from the following system of equations:

$$\begin{gathered} {\frac{{\partial {{p}_{{r\varphi }}}}}{{\partial t}} = \varepsilon _{{r\varphi }}^{p}{\text{,}}\quad \frac{{\partial {{p}_{{\varphi \varphi }}}}}{{\partial t}} = - \varepsilon _{{r\varphi }}^{p}\frac{{{{p}_{{\varphi \varphi }}} - e_{{r\varphi }}^{{\text{2}}}}}{{{{e}_{{r\varphi }}}}} + \frac{{{\text{4}}{{\varepsilon }_{{r\varphi }}}{{p}_{{r\varphi }}}}}{{{\text{2}} + e_{{r\varphi }}^{{\text{2}}}}}\left( {{\text{1}} + {{p}_{{\varphi \varphi }}} - \frac{{\text{1}}}{{\text{2}}}e_{{r\varphi }}^{{\text{2}}} - {\text{2}}{{e}_{{r\varphi }}}{{p}_{{r\varphi }}}} \right)}, \\ {{{e}_{{rr}}} = {{p}_{{\varphi \varphi }}} - \frac{{{\text{3}}e_{{r\varphi }}^{{\text{2}}}}}{{\text{2}}} - {\text{2}}{{e}_{{r\varphi }}}{{p}_{{r\varphi }}}{\text{,}}\quad {{p}_{{rr}}} + {{p}_{{\varphi \varphi }}} = - {\text{2}}p_{{r\varphi }}^{{\text{2}}}{\text{,}}\quad {{e}_{{rr}}} + {{e}_{{\varphi \varphi }}} = - e_{{r\varphi }}^{{\text{2}}}}. \\ \end{gathered} $$
(3.12)

Then, based on (3.4) and (3.6), the function of the additional hydrostatic pressure is determined.

4 UNLOADING DYNAMICS

At the time moment t = ts = \({{{\sigma }_{{\text{0}}}}r_{0}^{2}{\text{/}}\alpha }{{R}^{2}}\), the static friction stress \({\left| {{{\sigma }_{{r\varphi }}}} \right|}\) on the surface \({r = {{r}_{{\text{0}}}}}\) reaches the threshold value σ0, and the material in the vicinity of this surface begins to slip. From this moment on, the no-slip condition on \({r = {{r}_{{\text{0}}}}}\) must be replaced by some contact friction condition. We take as such the condition of constancy of the shear stress on \({{{r}_{{\text{0}}}}}\), assuming that the latter at the moment \({{t}_{s}}\) changes abruptly, so that

$${\left| {{{\sigma }_{{r\varphi }}}\left( {{{r}_{{\text{0}}}}{\text{,}}t} \right)} \right| = {{\sigma }_{s}}\quad {\text{at}}\quad t \geqslant {{t}_{s}};\quad {{\sigma }_{s}} = \operatorname{const} {\text{,}}\quad {{\sigma }_{s}} < k}.$$
(4.1)

An instantaneous stress drop below the yield point leads to the formation of an unloading wave Σ1, the position of which in space is described by the equation \({r = {{r}_{{\text{1}}}}\left( t \right) = {{r}_{{\text{0}}}} + \int\limits_{{{t}_{s}}}^t {G\left( \xi \right)d\xi } }\). By a shock wave we mean a surface with a strong discontinuity, that is, a surface on which displacements are continuous, and the displacement velocities and stresses experience a finite discontinuity. The surface of a strong discontinuity [22] can be interpreted as a limiting layer of thickness \(\Delta h\) (\({\Delta h \to {\text{0}}}\)), in which the velocities and stresses change from values \({{v}_{i}^{ + }}\), \({\sigma _{{ij}}^{ + }}\) to values \({{v}_{i}^{ - }}\), \({\sigma _{{ij}}^{ - }}\), remaining monotonic and continuous inside the layer. On surfaces of weak discontinuity, which also occur below, stresses and displacement velocities remain continuous, but some of their partial derivatives undergo a discontinuity.

It was shown in [22] that in an elastoviscoplastic medium there are two types of waves: longitudinal and transverse, the velocities of which coincide with the velocities of waves of the same name in an elastic medium. Plastic deformations in an elastoviscoplastic medium remain continuous even when passing through the discontinuity surface [22]. By virtue of the previously accepted small elastic strain approximation, in our case, the velocity of the unloading wave Σ1 is constant \({G = \sqrt {\mu {\text{/}}\rho } }\) (\(\rho \) is the density of the medium). Since the unloading process under consideration is essentially nonstationary, the right-hand side in (2.6) cannot be neglected. The dynamic behavior of the material behind the unloading shock wave obeys the equations of motion:

$${\frac{{\partial {{\sigma }_{{r\varphi }}}}}{{\partial r}} + {\text{2}}\frac{{{{\sigma }_{{r\varphi }}}}}{r} = \rho r\ddot {\psi }{\text{,}}\quad \frac{{\partial {{\sigma }_{{rr}}}}}{{\partial r}} + \frac{{{{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}}}}{r} = - \rho r\dot {\psi },\quad }\dot {\psi } = \frac{{\partial \psi }}{{\partial t}},\quad \ddot {\psi } = \frac{{{{\partial }^{2}}\psi }}{{\partial {{t}^{2}}}}.$$
(4.2)

Thus, from the moment t = ts there are three distinct regions, in which stresses and strains are determined differently. In the unloading region \({{{V}^{{\left( 1 \right)}}}{\text{:}}\;{{r}_{{\text{0}}}} \leqslant r \leqslant {{r}_{{\text{1}}}}\left( t \right)}\) we integrate the equations of motion (4.2), while, in the region of the continuing viscoplastic flow \({{{V}^{{\left( P \right)}}}{\text{:}}\;{{r}_{{\text{1}}}}\left( t \right) \leqslant r \leqslant m\left( t \right)}\) and the region of reversible deformation \({{{V}^{{\left( E \right)}}}{\text{:}}\;m\left( t \right) \leqslant r \leqslant R}\), we consider the solution of the quasi-static problem to be valid.

The first equation in (4.2) is the main one and can be solved independently of the second, and then the additional hydrostatic pressure \({p(r{\text{,}}t)}\) is found from the second equation using the solution obtained. According to the transfer equation for the tensor of irreversible deformations (2.1) in the process of unloading (\(\varepsilon _{{ij}}^{p} = 0\)) its components pij change as at rigid body motion. From (3.9) and (3.12) it follows that the component of the plastic strain tensor \({{{p}_{{r\varphi }}}}\) ceases to change with time at those points of the region \({{V}^{{\left( P \right)}}}\) through which the wave front passed and in the region \({{V}^{{\left( {\text{1}} \right)}}}\) it is only a function of the coordinate \({{{p}_{{r\varphi }}}\left( r \right)}\). Taking this circumstance into account, the equation of motion in the unloading region takes the form:

$${{{\psi }_{{,rr}}} + \frac{{\text{3}}}{r}{{\psi }_{{,r}}} - \frac{{\ddot {\psi }}}{{{{G}^{{\text{2}}}}}} = \frac{{\text{2}}}{\eta }\left( {\frac{{\alpha {{R}^{2}}{{\tau }_{{\text{1}}}}\left( r \right)}}{{G{{r}^{{\text{3}}}}}} - \frac{k}{{Gr}} - \frac{{{\text{2}}k{{\tau }_{{\text{1}}}}\left( r \right)}}{{{{r}^{{\text{2}}}}}} + \frac{{2{{k}^{{\text{2}}}}}}{{\alpha {{R}^{2}}}}} \right)},$$
(4.3)

where \({{\psi }_{{,r}}} = \partial \psi {\text{/}}\partial r\), \({{\psi }_{{,rr}}} = {{\partial }^{2}}\psi {\text{/}}\partial {{r}^{2}}\), \({{{\tau }_{{\text{1}}}}\left( r \right) = {{t}_{s}} + \left( {r - {{r}_{0}}} \right)}{\text{/}}G\) is the arrival time of wave \({{{\Sigma }_{{\text{1}}}}}\) at the point with coordinate r. The boundary conditions for (4.3) are the friction condition (4.1) on the boundary surface \({r = {{r}_{{\text{0}}}}}\) and the condition of continuity of displacements at the front of the unloading wave \(r = {{r}_{{\text{1}}}}\left( t \right)\)

$${{{{\left. {\left[ \psi \right]} \right|}}_{{{{\Sigma }_{1}}}}}}\,{{\left. { = ({{\psi }^{ + }} - {{\psi }^{ - }})} \right|}_{{r = {{r}_{1}}(t)}}} = 0.$$
(4.4)

Square brackets in (4.4) and below denote the jump of a function on the discontinuity surface, ψ+ = ψ+(r1(t), t) is the value of the function ψ(r, t) immediately in front of the discontinuity surface, and ψ– = ψ–(r1(t), t) is immediately behind the discontinuity surface.

Unloading waves were also considered in [23, 24], where the exact solutions of the boundary value problems of the theory of large deformations about dynamic unloading in a flat heavy layer located on an inclined plane and subjected to loading on a free surface were obtained, followed by instantaneous removal of the load [23] or material stripping from an inclined plane [24].

In our case, equation (4.3) cannot be integrated exactly, we construct its approximate solution by the ray method, which consists in representing the solution in the vicinity of the wavefront in the form of a Taylor series. The practice of using ray expansions in solving wave problems is quite extensive [25]. Here we use a version of the method proposed in [26], where the approximate solution was constructed in the form of a power series in time in the vicinity of the moment of arrival of the wave at a given point in space. So for the angular velocity \(\omega \left( {r,t} \right)\) in the area \({{V}^{{\left( {\text{1}} \right)}}}\) we write:

$$\begin{gathered} \omega \left( {r,t} \right) = {{\left. {{{\omega }^{ - }}} \right|}_{{t = {{\tau }_{1}}}}} + {{\left. {{{{\dot {\omega }}}^{ - }}} \right|}_{{t = {{\tau }_{1}}}}}\left( {t - {{\tau }_{1}}} \right) + \frac{1}{2}{{\left. {{{{\ddot {\omega }}}^{ - }}} \right|}_{{t = {{\tau }_{1}}}}}{{\left( {t - {{\tau }_{1}}} \right)}^{2}} + \cdots = \\ \, = {{\left. {({{\omega }^{ + }} - \left[ \omega \right])} \right|}_{{t = {{\tau }_{1}}}}} + {{\left. {({{{\dot {\omega }}}^{ + }} - \left[ {\dot {\omega }} \right])} \right|}_{{t = {{\tau }_{1}}}}}\left( {t - {{\tau }_{1}}} \right) + \frac{1}{2} {{\left. {({{{\ddot {\omega }}}^{ + }} - \left[ {\ddot {\omega }} \right])} \right|}_{{t = {{\tau }_{1}}}}}{{\left( {t - {{\tau }_{1}}} \right)}^{2}} + \cdots . \\ \end{gathered} $$
(4.5)

Similarly, it is possible to write down the ray series for the stress and twist angle functions, and these quantities are also expressed in terms of jumps in the angular velocity and its derivatives \({[{{\partial }^{{n - 1}}}\omega {\text{/}}\partial {{t}^{{n - 1}}}]}\) \({( n = {\text{1,2,}} \ldots )}\). In what follows, we will omit the “+” subscript for the quantities in front of the discontinuity surface. Usually asymptotic series of the type (4.5) are limited by the first few terms. In this work, we will keep the terms linear in time for stresses and velocities and quadratic terms for displacements.

In order to calculate the discontinuity of the function on the shock wave and the discontinuities of its n-th order derivatives, it is necessary to differentiate the first equation in (4.2) n – 1 times with respect to time, write the result on each side of the wave surface and calculate their difference using geometric and kinematic compatibility conditions [21, 27, 28]. Thus, we recursively obtain a system of linear inhomogeneous differential equations of the first order:

$$\begin{gathered} {\frac{{\delta {{\chi }_{1}}}}{{\delta t}} + \frac{{{\text{3}}G}}{{{\text{2}}{{r}_{{\text{1}}}}}}{{\chi }_{1}} = \frac{{2G}}{\eta }\left( {\frac{{\alpha {{R}^{2}}t}}{{r_{1}^{2}}} - k} \right)}, \\ \frac{{\delta {{\zeta }_{1}}}}{{\delta t}} + \frac{{{\text{3}}G}}{{{\text{2}}{{r}_{{\text{1}}}}}}{{\zeta }_{1}} = \frac{{2k{{G}^{2}}}}{{\eta r_{1}^{2}}} - \frac{{\alpha G{{R}^{2}}}}{{\eta r_{1}^{3}}} - \frac{{3{{A}_{1}}{{G}^{2}}}}{{8r_{1}^{{7{\text{/}}2}}}}. \\ \end{gathered} $$
(4.6)

in which \({{\chi }_{1}} = {{\left. {\left[ \omega \right]} \right|}_{{{{\Sigma }_{1}}}}}\), \({{\zeta }_{1}} = {{\left. {\left[ {\dot {\omega }} \right]} \right|}_{{{{\Sigma }_{1}}}}}\); \({\delta {\text{/}}\delta t}\) s the delta time derivative of a function given on a moving surface [27]. After integrating (4.6) in the region V(1), we obtain:

$${{{\chi }_{{\text{1}}}}\left( t \right) = \frac{{{{A}_{1}}}}{{r_{{\text{1}}}^{{{\text{3/2}}}}}} - \frac{{{\text{2}}k}}{{{\text{3}}\eta }} + \frac{{{\text{4}}\alpha {{R}^{2}}}}{{\eta G{{r}_{1}}}}\left( {1 - \frac{{Gt}}{{2{{r}_{1}}}}} \right){\text{,}}\quad {{\zeta }_{{\text{1}}}}\left( t \right) = \frac{{{{B}_{1}}}}{{r_{{\text{1}}}^{{{\text{3/2}}}}}} + \frac{{{\text{3}}{{A}_{1}}G}}{{{\text{8}}r_{{\text{1}}}^{{{\text{5/2}}}}}} + \frac{{{\text{4}}kG}}{{\eta {{r}_{{\text{1}}}}}} + \frac{{{\text{2}}\alpha {{R}^{2}}}}{{\eta r_{{\text{1}}}^{{\text{2}}}}}},$$
$${{{\psi }^{{\left( {\text{1}} \right)}}}\left( {r{\text{,}}t} \right) = {{\psi }^{{\left( P \right)}}}\left( {r,{{\tau }_{{\text{1}}}}} \right) + {{{\left. {({{\omega }^{{\left( P \right)}}} - {{\chi }_{{\text{1}}}})} \right|}}_{{t = {{\tau }_{1}}}}}\left( {t - {{\tau }_{{\text{1}}}}} \right) + \frac{{\text{1}}}{{\text{2}}}{{{\left. {({{{\dot {\omega }}}^{{\left( P \right)}}} - {{\zeta }_{{\text{1}}}})} \right|}}_{{t = {{\tau }_{1}}}}}{{{\left( {t - {{\tau }_{{\text{1}}}}} \right)}}^{{\text{2}}}} + \cdots },$$
$${\begin{array}{*{20}{l}} \begin{gathered} \sigma _{{r\varphi }}^{{\left( {\text{1}} \right)}}\left( {r{\text{,}}t} \right) = \frac{{\alpha {{R}^{2}}{{\tau }_{{\text{1}}}}}}{{{{r}^{{\text{2}}}}}} + \frac{{\mu r{{\chi }_{1}}\left( {{{\tau }_{{\text{1}}}}} \right)}}{G} \\ \, + \left\{ {\frac{{\alpha {{R}^{2}}}}{{{{r}^{{\text{2}}}}}} + \frac{{\mu r}}{G}\left( {\frac{{{\text{3}}G}}{{{\text{2}}r}}{{\chi }_{1}}\left( {{{\tau }_{{\text{1}}}}} \right) + {{\zeta }_{1}}\left( {{{\tau }_{{\text{1}}}}} \right) - \frac{G}{{\eta r}}\left( {k - \frac{{\alpha {{R}^{2}}{{\tau }_{{\text{1}}}}}}{{{{r}^{{\text{2}}}}}}} \right)} \right)} \right\}\left( {t - {{\tau }_{{\text{1}}}}} \right) + \cdots , \\ \end{gathered} \end{array}}$$
(4.7)
$${{{A}_{1}} = \frac{{\sqrt {{{r}_{{\text{0}}}}} G\left( {{{\sigma }_{s}} - {{\sigma }_{{\text{0}}}}} \right)}}{\mu } + \frac{{{\text{2}}r_{{\text{0}}}^{{{\text{3/2}}}}}}{\eta }\left( {\frac{k}{{\text{3}}} + {{\sigma }_{{\text{0}}}} - \frac{{{\text{2}}\alpha {{R}^{2}}}}{{G{{r}_{{\text{0}}}}}}} \right)},$$
$${{B}_{1}} = \frac{{15{{G}^{2}}({{\sigma }_{0}} - {{\sigma }_{s}})}}{{8\mu \sqrt {{{r}_{0}}} }} - \frac{{\sqrt {{{r}_{0}}} G(13k + 7{{\sigma }_{0}})}}{{4\eta }} - \frac{{\alpha G{{R}^{2}}}}{{\mu r_{0}^{{3/2}}}} - \frac{{\alpha {{R}^{2}}}}{{2\eta \sqrt {{{r}_{0}}} }}.$$

The superscript (1) means that the calculated values refer to the region V(1). If necessary, the following terms of the ray series can be calculated in a similar way. There are no fundamental difficulties in this, only the volume of calculations increases.

At the moment of time t = t1, the unloading wave reaches the elastoplastic boundary:

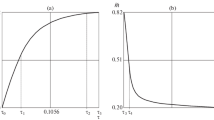
$${{{t}_{1}} = {{t}_{s}} + \frac{{\text{1}}}{{{\text{2}}{{G}^{{\text{2}}}}}}\left( {\frac{{\alpha {{R}^{2}}}}{k} - {\text{2}}{{r}_{{\text{0}}}}G + \sqrt {\frac{{{\text{4}}\alpha {{R}^{2}}G}}{k}\left( {G{{t}_{s}} - {{r}_{{\text{0}}}}} \right) + \frac{{{{\alpha }^{{\text{2}}}}{{R}^{4}}}}{{{{k}^{{\text{2}}}}}}} } \right)}.$$
(4.8)

The distribution over the layer of the shear stress \({{{\sigma }_{{r\varphi }}}\left( {r{\text{,}}t} \right)}\) and the twist angle \({\psi \left( {r{\text{,}}t} \right)}\) are shown in Fig. 1–2 at the moment of collision with the elastoplastic boundary. The calculation was carried out for the following constants: ρ0 = 2.7 × 103 kg/m3, μ = 24.5 GPa, k = 56.3 MPa, η = 1.25 GPa ⋅ s, σ0 = 67.56 MPa, σs = 42.225 MPa, \(R{\text{/}}{{r}_{0}} = 1.5\), α 5213 Pa/s.

Fig. 1.
figure 1

Shear stress distribution at moment of time \(t = {{t}_{{\text{1}}}}\).

Full size image
Fig. 2.
figure 2

Rotation angle distribution at moment of time \(t = {{t}_{{\text{1}}}}\).

Full size image

Starting from the moment \(t = {{t}_{{\text{1}}}}\), the region with accumulated irreversible deformations no longer increases and is bounded by the surfaces \({r = {{r}_{{\text{0}}}}}\) and \({r = m_{*}^{{}} = R\sqrt {\alpha {{t}_{1}}{\text{/}}k} }\). As a result of reflection \({{{\Sigma }_{{\text{1}}}}}\) from elastoplastic boundary \(r = m_{*}^{{}}\) the discontinuity surfaces Σ2: \({r = {{r}_{{\text{2}}}}\left( t \right) = m_{*}^{{}} - G\left( {t - {{t}_{1}}} \right)}\) and Σ3: \({r = {{r}_{{\text{3}}}}(t) = m_{*}^{{}} + G(t - {{t}_{1}})}\) with oppositely directed velocities begin to move to the boundary surfaces \({r = {{r}_{{\text{0}}}}}\) and \({r = R}\), respectively. In the region \({{{V}^{{\left( {\text{2}} \right)}}}{\text{:}}\;{{r}_{{\text{2}}}}\left( t \right) \leqslant r \leqslant m_{*}^{{}}}\) the motion of the medium obeys equation (4.3), and in the region \({{{V}^{{{\text{(3)}}}}}{\text{:}}\;{{m}_{*}} \leqslant r \leqslant {{r}_{{\text{3}}}}(t)}\), the equation of motion takes the form:

$${{{\psi }_{{,rr}}} + \frac{{\text{3}}}{r}{{\psi }_{{,r}}} - \frac{{\ddot {\psi }}}{{{{G}^{{\text{2}}}}}} = {\text{0}}}.$$
(4.9)

The boundary conditions for equations (4.3) and (4.9) are the condition for the continuity of displacements on surfaces r = r2(t) and r = r3(t), as well as the condition for the coincidence of displacements and stresses on the elastoplastic boundary r = \({{m}_{*}}\). The latter provides us with the smoothness of the solution in the region \({{r}_{{\text{2}}}}(t) \leqslant r \leqslant {{r}_{{\text{3}}}}(t)\) at each time moment following

$${{{{\left. {\left[ \psi \right]} \right|}}_{{{{\Sigma }_{2}}}}} = {\text{0,}}\quad {{{\left. {\left[ \psi \right]} \right|}}_{{{{\Sigma }_{3}}}}} = {\text{0,}}\quad {{{\left. {{{\psi }^{{\left( {\text{2}} \right)}}}} \right|}}_{{{{m}_{*}}}}} = {{{\left. {{{\psi }^{{\left( {\text{3}} \right)}}}} \right|}}_{{{{m}_{*}}}}}{\text{,}}\quad }{{\left. {\sigma _{{r\varphi }}^{{\left( {\text{2}} \right)}}} \right|}_{{{{m}_{*}}}}} = {{\left. {\sigma _{{r\varphi }}^{{\left( {\text{3}} \right)}}} \right|}_{{{{m}_{*}}}}}.$$
(4.10)

As before, the index in parentheses takes the value of the number of the wave to the zone of influence of which this value belongs. We represent the solution for the sought function ω(r, t) behind waves \({{\Sigma }_{{\text{2}}}}\) and \({{\Sigma }_{{\text{3}}}}\) by ray series similar to (4.5)

$${{{\omega }^{{\left( {\text{2}} \right)}}} = {{{\left. {({{\omega }^{{\left( {\text{1}} \right)}}} - {{\chi }_{{\text{2}}}})} \right|}}_{{{{\tau }_{{\text{2}}}}}}} + {{{\left. {({{{\dot {\omega }}}^{{\left( {\text{1}} \right)}}} - {{\zeta }_{{\text{2}}}})} \right|}}_{{{{\tau }_{{\text{2}}}}}}}\left( {t - {{\tau }_{{\text{2}}}}} \right) + \cdots },$$
(4.11)
$${{{\omega }^{{\left( {\text{3}} \right)}}} = {{{\left. {({{\omega }^{{\left( E \right)}}} - {{\chi }_{{\text{3}}}})} \right|}}_{{{{\tau }_{{\text{3}}}}}}} + {{{\left. {({{{\dot {\omega }}}^{{\left( E \right)}}} - {{\zeta }_{{\text{3}}}})} \right|}}_{{{{\tau }_{{\text{3}}}}}}}\left( {t - {{\tau }_{{\text{3}}}}} \right) + \cdots },$$
(4.12)
$$\begin{gathered} {{{\chi }_{i}} = {{{\left. {\left[ \omega \right]} \right|}}_{{{{\Sigma }_{i}}}}},\quad {{\zeta }_{i}} = {{{\left. {\left[ {\dot {\omega }} \right]} \right|}}_{{{{\Sigma }_{i}}}}},\quad i = 1,2,\quad {{\tau }_{{\text{2}}}} = {{t}_{1}} + (m_{*}^{{}} - r){\text{/}}G{\text{,}}} \\ {{\tau }_{{\text{3}}}} = {{t}_{1}} + (r - m_{*}^{{}}){\text{/}}G. \\ \end{gathered} $$

Differential equations for the coefficients of the ray series are obtained by applying the algorithm described above to the equation of motion. After integration, substitution of the result in the ray series and comparison with the boundary conditions, it turned out that on the wave \({{\Sigma }_{{\text{2}}}}\) the velocity and acceleration remain continuous, i.e., \({{\chi }_{{\text{2}}}} = {{\zeta }_{{\text{2}}}} = {\text{0}}\), and \({{\Sigma }_{{\text{3}}}}\) is a shock wave. The discontinuities of the derivatives of a higher order in the region \({{V}^{{\left( {\text{2}} \right)}}}\) can be traced if we continue the ray series (4.11) with the required degree of accuracy. Thus, within the framework of the accepted linear in time approximation for the velocity and stress, the solution in the region \({{r}_{{\text{0}}}} \leqslant r \leqslant m_{*}^{{}}\) is still determined by relations (4.7), and in the region \({{V}^{{\left( {\text{3}} \right)}}}\) we have:

$${{{\psi }^{{\left( {\text{3}} \right)}}}\left( {r,t} \right) = {{\psi }^{{\left( E \right)}}}\left( {r,{{\tau }_{{\text{3}}}}} \right) + {{{\left. {({{\omega }^{{\left( E \right)}}} - {{\chi }_{{\text{3}}}})} \right|}}_{{{{\tau }_{{\text{3}}}}}}}\left( {t - {{\tau }_{{\text{3}}}}} \right) + \frac{{\text{1}}}{{\text{2}}}{{{\left. {({{{\dot {\omega }}}^{{\left( E \right)}}} - {{\zeta }_{{\text{3}}}})} \right|}}_{{{{\tau }_{{\text{3}}}}}}}{{{\left( {t - {{\tau }_{{\text{3}}}}} \right)}}^{{\text{2}}}} + \cdots },$$
$$\begin{gathered} {\sigma _{{r\varphi }}^{{\left( {\text{3}} \right)}}\left( {r{\text{,}}t} \right) = \frac{{\alpha {{R}^{2}}{{\tau }_{3}}}}{{{{r}^{2}}}} + \frac{{\mu {{A}_{3}}}}{{G\sqrt r }} + \left( {\frac{{\alpha {{R}^{2}}}}{{{{r}^{2}}}} + \frac{{15\mu {{A}_{3}}}}{{8{{r}^{{3{\text{/}}2}}}}} + \frac{{\mu {{B}_{3}}}}{{G\sqrt r }}} \right)\left( {t - {{\tau }_{{\text{3}}}}} \right) + \cdots ,} \\ {{{\chi }_{{\text{3}}}} = \frac{{{{A}_{3}}}}{{r_{{\text{3}}}^{{{\text{3/2}}}}}}{\text{,}}\quad {{\zeta }_{{\text{3}}}} = \frac{{{{B}_{3}}}}{{r_{{\text{3}}}^{{{\text{3/2}}}}}} + \frac{{{\text{3}}G{{A}_{3}}}}{{{\text{8}}r_{{\text{3}}}^{{{\text{5/2}}}}}}{\text{,}}} \\ \end{gathered} $$
(4.13)
$${{A}_{3}} = {{A}_{1}} - \frac{{8km_{*}^{{3{\text{/}}2}}}}{{3\eta }} + \frac{{4\alpha {{R}^{2}}\sqrt {m_{*}^{{}}} }}{{\eta G}},\quad {{{B}_{3}} = }{{B}_{1}} + \frac{{5kG\sqrt {m_{*}^{{}}} }}{\eta } + \frac{{\alpha {{R}^{2}}}}{{2\eta \sqrt {m_{*}^{{}}} }}.$$

The next change in the wave pattern will occur at moment of time \({{t}_{2}} = {{t}_{{\text{1}}}} + (R - m_{*}^{{}}){\text{/}}G\), when wave \({{\Sigma }_{{\text{3}}}}\) is reflected from the outer cylinder \({r = R}\), giving rise to a new discontinuity surface Σ4: r = r4(t) = \({R - G(t - {{t}_{2}})}\). The motion of the medium in the region \({{{V}^{{\left( {\text{4}} \right)}}}{\text{:}}\;{{r}_{{\text{4}}}}\left( t \right) \leqslant r \leqslant R}\) obeys the equation of motion (4.9), the boundary conditions for which are the adhesion condition on \({r = R}\) (3.1) and the condition of continuity of displacements at the wave front \({{\Sigma }_{{\text{4}}}}\). Thus, in the region \({{V}^{{\left( {\text{4}} \right)}}}\) we have:

$${{{\psi }^{{\left( {\text{4}} \right)}}}\left( {r{\text{,}}t} \right) = {{\psi }^{{\left( 3 \right)}}}\left( {r,{{\tau }_{{\text{4}}}}} \right) + {{{\left. {({{\omega }^{{\left( 3 \right)}}} - {{\chi }_{{\text{4}}}})} \right|}}_{{{{\tau }_{{\text{4}}}}}}}\left( {t - {{\tau }_{{\text{4}}}}} \right) + \frac{{\text{1}}}{{\text{2}}}{{{\left. {({{{\dot {\omega }}}^{{\left( 3 \right)}}} - {{\zeta }_{{\text{4}}}})} \right|}}_{{{{\tau }_{4}}}}}{{{\left( {t - {{\tau }_{{\text{4}}}}} \right)}}^{{\text{2}}}} + \cdots },$$
$${\sigma _{{r\varphi }}^{{\left( {\text{4}} \right)}}\left( {r{\text{,}}t} \right) = \sigma _{{r\varphi }}^{{\left( {\text{3}} \right)}}\left( {r{\text{,}}{{\tau }_{{\text{4}}}}} \right) - \frac{{\mu {{A}_{4}}}}{{G\sqrt r }} + \left( {\dot {\sigma }_{{r\varphi }}^{{\left( {\text{3}} \right)}}\left( {r{\text{,}}{{\tau }_{{\text{4}}}}} \right) + \frac{{15\mu {{A}_{4}}}}{{8{{r}^{{3/2}}}}} - \frac{{\mu {{B}_{4}}}}{{G\sqrt r }}} \right)\left( {t - {{\tau }_{{\text{4}}}}} \right) + \cdots },$$
(4.14)
$$\begin{gathered} {{{\chi }_{{\text{4}}}} = \frac{{{{A}_{4}}}}{{r_{{\text{4}}}^{{{\text{3/2}}}}}}{\text{,}}\quad {{\zeta }_{{\text{4}}}} = \frac{{{{B}_{4}}}}{{r_{{\text{4}}}^{{{\text{3/2}}}}}} - \frac{{{\text{3}}G{{A}_{4}}}}{{{\text{8}}r_{{\text{4}}}^{{{\text{5/2}}}}}}{\text{,}}}\quad {{A}_{4}} = {{A}_{3}},\quad {{{B}_{4}}}\, = {{B}_{3}} + \frac{{15G{{A}_{3}}}}{{4R}}, \\ {{\tau }_{4}} = {{t}_{2}} + \left( {R - r} \right){\text{/}}G. \\ \end{gathered} $$

Surface \(r = {{r}_{{\text{4}}}}\left( t \right)\) is a converging shock wave. It should be noted that as it moves to the inner boundary, a new plastic region may appear due to the increasing intensity of the discontinuity due to an increase in the curvature of the wave front. At this stage, the analytical study is considered complete, it is advisable to carry out the calculation of further deformation numerically, if necessary, using the analytical solution to approximate the solution at the nodes of the frontal region.

5 CONCLUSIONS

The problem considered is characterized by a change in the rate modes of deformation: from low-rate (quasi-static) at the stage of accumulation of irreversible deformations to dynamic at the stage of unloading, propagating in the form of a weak shock wave. If at the first stage it is possible to obtain an exact solution to the boundary value problem, then at the second stage, the method of ray series is used to construct an approximate analytical solution behind the front of the unloading wave. The same method was used to calculate the reflection of the initial unloading wave from the elastic-plastic boundary and the boundary surface. A significant simplification in the solution of the problem is introduced by the small elastic strain approximation and the one-dimensional nature of the deformation. In this case, the wave velocities are constant, and the rays (orthogonal trajectories of points on the wave surface) are straight lines. In the case of finite deformations, the velocity and position of the wavefront will depend on the state ahead of the wave and the intensity of the discontinuities on the wave. In addition, the wave pattern becomes more complicated, since in a medium with preliminary deformations, two shear shock waves propagate at once: a plane-polarized wave and a circularly polarized wave.

Nevertheless, the results of this work can be useful in the formulation of non-stationary problems of the theory of large deformations, but with more complex boundary conditions, as well as when using the obtained approximate solutions in numerical finite-difference calculations at the frontal nodes on a grid along the ray.