Introduction

Genetic (or evolutionary) algorithms are often utilized to explore material design spaces and map the energy landscape [1,2,3,4,5,6,7]. Coupled with ab initio methods such as density functional theory (DFT) or empirical methods such as molecular dynamics (MD), these grand canonical algorithms perform local optimization through structure relaxation and identify basins of attraction in the design space, and global optimization through crossover and mutation operations on the best locally optimized phases. Hence, the genetic algorithm (GA) aims to pass on the desired features from the ‘parent generation’ to the ‘offspring generation,’ thereby ‘learning’ the best approaches to identify better compositions and structures along the way (as opposed to a random search). However, the most computationally expensive parts of these algorithms are the DFT calculations, which are accurate but take orders of magnitude longer to complete than the GA operations. This step creates a bottleneck in the search process, with the computational expense increasing with the number of atoms in the unit cell. Often, most of the computation time during a search may be spent performing these DFT calculations for every structure generated by the GA, which could also include many unstable structures, or structures with undesirable properties. Hence, even with modern high computational power (including GPU acceleration), performing GA searches for compositionally complex ceramics (C3) can be time- and cost-prohibitive.

Machine learning (ML) models have been successfully used to learn the results of DFT calculations and predict the properties of given input crystal structures [8,9,10,11,12,13,14]. These can act as surrogate models to map the energy and property landscapes of the given design system and quickly predict the stability and properties of a candidate structure without the need for expensive DFT calculations. In this way, they can screen all candidate structures and only pass on the high-value candidates that are predicted to be stable (and with desired attributes) for DFT calculations. However, machine learning crystal structural data present a unique challenge—an appropriate data representation technique must be selected to encode the unit cell structure into a form compatible with the ML algorithms. Additionally, a high-performing model must be selected, and its hyperparameters must be tuned before it can be deployed unsupervised into the genetic algorithm.

In this manuscript, we build on our previous work on learning the energy landscape for metallic systems [8,9,10] and extend it to map the energy and hardness of a ceramic system. The Si–C–N material system is chosen as the model design space for this study as it is known to contain many hard structures of interest to the ceramics community (SiC, Si3N4, CN, etc.), which will aid in the validation of the results as well as our approach. We particularly focus on one property, hardness, because such data can be easily determined from bond-level (intrinsic) properties [15]. At a fundamental level, hardness measures the combined resistance of chemical bonds to indentation or, simply, localized plastic deformation. Numerous studies have shown that the “intrinsic hardness” of a material can be predicted from its crystal structure, and specifically for covalent brittle materials, from its bonding environment [15,16,17,18,19,20,21,22,23,24,25,26,27]. Hence, hard phases in a given material system can be targeted through systematic searches using global optimization techniques, augmenting searches for stable phases in the system using the same methods [28].

A machine learning framework for material discovery requires several ingredients: (i) an initial learnable dataset, (ii) an objective function suitable for the selected application, (iii) an appropriate data representation for the structural data, and (iv) an optimal machine learning algorithm. In our work, GA searches are used to create datasets of structures and the associated energy and intrinsic hardness for each structure is calculated using DFT and a semi-empirical intrinsic hardness model [15], respectively. The objective function, or fitness function in the case of the GA, is based on the distance of the structure (in eV) from the convex hull in the phase diagram, shown by \(\Delta {E}_{H}\) in Fig. 1, which is a measure of the structure’s relative stability.

Figure 1
figure 1

Phase diagram of a two-element (\(n=2\)) system. Each filled circle represents an offspring structure in a generation, while unfilled circles represent structures from previous generations. The squares at the endpoints represent the elemental reference states. These structures contain atoms of only a single element. All stable structures lie on the convex hull of the system (black line). Any structure above this convex hull is unstable or metastable. The vertical distance between each structure and the convex hull (\(\Delta {E}_{H}\)) is used to define the objective function in Eq. (2). The red and green circles represent the structures in the generation with the maximum and minimum distance from the convex hull, respectively.

Full size image

Two ML algorithms, Ultra-Fast Force Field (UF3) [8] and support vector regression (SVR), are evaluated to predict the energy and hardness, respectively, of each structure. The ML algorithms take a vector \(x\in {\mathbb{R}}^{n}\) as input and return a predicted value \(y\). Hence, a vector-based data representation of the crystal structure that encodes the position and chemical identity of the atoms into constant-length vectors must be constructed before these algorithms may be used for energy and hardness predictions. The selection of this representation scheme is critical to the generation of an accurate surrogate model. Simple descriptors relying on chemical or physical attributed (atomic number/mass, density, band gap, elastic moduli, etc.) do not capture the required structural information [29, 30]. Ideally, the structural descriptor must fulfill three criteria [9]: (i) invariance with respect to the choice of unit cell and crystal symmetry, (ii) uniqueness, so no two different crystal structures have the same vector representation, and (iii) continuity, such that the energy difference between two crystal structures with vector representations \({x}_{1}\) and \({x}_{2}\) goes to zero in the limit \(\Vert {x}_{1}-{x}_{2}\Vert \to 0\).

The UF3 algorithm uses a linear combination of cubic B-spline basis functions, joined at knot positions, to represent the structural information of the system [8]. Cubic B-splines are chosen as they are globally flexible and smooth, but still maintain locally simple forms for computational efficiency. The spline coefficients are then optimized simultaneously using a regularized linear least squares method. These descriptors are inherently invariant and continuous due to their formulation. For the SVR model to predict hardness, partial radial distribution functions (RDFs) and angular distribution functions (ADFs) [9, 10] are used to represent the structures. These structural descriptors also satisfy the first and third conditions above (invariance and continuity) but may not necessarily be unique. However, the combination of these two descriptors has performed well with ML models on metallic systems and produced a rapid reduction in prediction error with smaller training set sizes [10].

The models generated using these algorithms are optimized using the datasets created by the GA. The best model parameters can then be used to create an ML-augmented GA that can be trained on-the-fly to screen candidate structures and accelerate the discovery of stable crystal structures with high hardness. An example design space consisting of three elements, Si, C, and N, was chosen to illustrate the concept and our approach to material discovery. While this study focuses on illustrating the method using this model system with hardness as the targeted property, the methodology is material-agnostic and can be applied to target a wide range of material systems and properties for tailored applications.

Results

The Si–C–N ternary system is divided into its three binary parts (Si–C, Si–N, and C–N) to create a total of three design spaces, as shown in Table 1. GA searches are performed on these three design spaces using DFT calculations to calculate each structure’s energy and the Cheenady model [27] to calculate its intrinsic hardness. To reduce computational time, structures are limited to a maximum of 16 atoms in the unit cell. The results of this search are shown in Fig. 2 for a binary and the ternary system, where the color of the diamond corresponds to the stability of the relaxed structure (distance from the convex hull) and the size of the diamond corresponds to its intrinsic hardness. Only structures with higher stability (\(\Delta {E}_{H}\le 1\) eV/atom) are plotted to prevent clutter. The GASP search successfully identifies [in Fig. 2(b)]the well-known stable phases of SiC and Si3N4, as well as experimental phases such as CN [31] in the Si–C–N system. These crystal structures serve as the input data for the ML models. A total of 6 types of models are trained—2 target properties (energy and intrinsic hardness) on 3 datasets (i.e., Si–C, C–N, Si–N), each. Representative examples of the results of these models in predicting the formation energy and intrinsic hardness of structures are shown in Figs. 3 and 4.

TABLE 1 Datasets (generated using GASP) used for training and testing the ML models. Only 10% of the unrelaxed structures within each DFT trajectory are included in the SVR datasets.
Full size table
Figure 2
figure 2

Results of a GASP search on the (a) Si–N and (b) Si–C–N systems. The color intensity of the diamonds corresponds to energy of the structure above the convex hull (lighter colored diamonds represent more stable structures). The size of the diamond corresponds to the intrinsic hardness of the structure (larger diamonds represent harder structures).

Full size image
Figure 3
figure 3

Scatter density plots for the ML-predicted vs expected (i.e., DFT-calculated) energies of structures in the (a) training and (b) testing sets for the Si–C system. Lighter colors indicate a higher density of data points in the region.

Full size image
Figure 4
figure 4

Scatter density plots for the ML-predicted vs expected (i.e., calculated by the Cheenady model [26]) hardness of structures in the (a) training and (b) testing sets for the Si–C system. Lighter colors indicate a higher density of data points in the region.

Full size image

Figure 3 compares the UF3-predicted energies in the Si–C system with the DFT calculations for the training and testing sets, which are obtained by sampling all the relaxed and all unrelaxed structures from the GA searches. Of the three binary systems, the Si–C dataset had the highest number of structures, over 4 times those of the other two (see Table 1). The predictions for the training set [Fig. 3(a)] show that the model successfully learned the data provided. The tight clustering of points around the diagonal implies that the models predicted the energy of the structures reasonably well. While it is not a measure of the predictive capability of the model, it does show that the relationship between the descriptor and target is learnable. The results from the test dataset [Fig. 3(b)] demonstrate the predictive capabilities of the model, as these are data that the model has not seen previously. While there are a greater number of outliers in this set (reasons to be discussed in the following paragraph), the overall trend of the data is captured well, and most points lie close to the diagonal. For quantitative comparison, the mean absolute error (MAE) and the root mean square error (RMSE) are presented in Table 2. Both metrics aim to capture the average error, but the RMSE is more skewed by higher errors (and is always higher than the MAE). Hence, MAE is a more robust statistic, but the RMSE gives a better measure of the model’s ability to capture the entire energy landscape within the design space.

TABLE 2 Prediction accuracy of the ML models for energy (UF3) and hardness (SVR)
Full size table

Figure 4 compares the SVR model’s predictions for intrinsic hardness to the values obtained from the Cheenady model [27], and the respective error metrics are shown in Table 2. The dataset for the SVR model contains all relaxed structures but includes only 10% of the unrelaxed structures. This is because the structures within a single relaxation trajectory are quite similar to each other, and selecting every unrelaxed structure leads to a large amount of correlation between the data points, resulting in overfitting of the SVR model (a very low error for the training set, but a high error for the testing set). Hence, only a fraction (10%) of the unrelaxed structures is chosen for the SVR database.

The datasets for the Si–N and C–N systems are smaller, resulting in training set sizes of less than 1,500 structures in both cases for the SVR model (see Table 1). However, even with the much smaller training data, the UF3 and SVR models can capture the energy and hardness landscapes in the design space. With less than a third of the data (as compared to the Si–C set), the model errors only increase slightly (see Table 2). Similar to the Si–C dataset, the largest errors in energy are for highly unstable structures (i.e., structures with a high energy). The higher hardness error for the C–N system can be attributed to the large spread (standard deviation) of the hardness values in this system.

Discussion

The prediction errors presented in Table 2 are within acceptable limits because these ML algorithms are intended to be a screening tool in the material discovery process which aims to find structures with lower energies. After obtaining an estimation of a structure’s target properties, only those predicted to be stable (low \(\Delta {E}_{H}\)) and high hardness will be passed on to the next step for more accurate DFT calculations. Additionally, most of the outliers lie at the higher energy values, which corresponds to the more unstable structures, in the region where data are more limited. A high accuracy is not necessary in this region as these structures are far from stable and will fail any screening criterion. When only considering the structures with an energy lower than -5.28 eV/atom (which corresponds to the 75th percentile) in the Si–C dataset, the RMSE and MAE drop to 94.61 meV/atom and 69.96 meV/atom, respectively (as compared to 138.25 meV/atom and 78.35 meV/atom, respectively, for the entire test dataset).

It must be noted that the UF3 model was chosen (instead of the SVR model) to predict the energy of structures due to its higher accuracy. It is possible to use the RDF + ADF descriptors and the SVR model for predictions of energy in addition to hardness; however, the errors are higher. The SVR model for energy had an RMSE and MAE of 0.4579 eV/atom and 0.2770 eV/atom, respectively, which is ~ 3.5 times that of the UF3 model. Additionally, all unrelaxed structures cannot be used in the training of the SVR model, which is a disadvantage as these structures diversify and increase the size of the training dataset. While they are not at the local minima, they are still valid datapoints in terms of the relationship between the structure and its energy or hardness. The UF3 model was trained on all unrelaxed structures in the relaxation trajectory as it did not suffer from the overfitting problem.

For the SVR model, it was found that the choice of descriptor hyperparameters does not greatly affect model performance. This is demonstrated in Fig. 5(a) for various values of \({d}_{c}\), the cutoff distance for RDF [see Eq. (8)]. The MAE and RMSE do not change considerably for the 100 iterations within the range of 3 to 10 Å. Similar results were obtained for the cutoff distance (\({d}_{k}\)) and slope parameter (\(k\)) for the ADF [see Eq. (9)] and are shown as a 2D scatter plot in Fig. 5(b). The relative insensitivity of the MAE to the descriptor hyperparameters allows the model to be generalized for a variety of different materials without the need for an additional optimization step, thereby reducing the overall computation time when running the material discovery algorithm.

Figure 5
figure 5

Prediction errors for varying descriptor hyperparameters for the (a) RDF and (b) ADF. The SVR model is insensitive to the descriptor hyperparameters.

Full size image

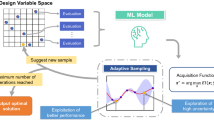
Based on the results, we estimate that the UF3 and SVR models can be used as a surrogate screening method after as few as 150 DFT relaxations. As a typical GA material discovery calculation includes between 500 and 1000 relaxations; hence, using such a screening model and only performing DFT calculation to obtain the accurate energy of promising structures can greatly reduce the amount of computational time required to discover stable structures with desired hardness in each design space. An outline of this proposed ML-augmented material discovery strategy is shown in Fig. 6. After an initial set of computationally expensive DFT calculations, the UF3 and SVR surrogate models can be used to perform an initial evaluation of each successive structure properties, and only promising stable structures (those predicted to have a high hardness and low energy) need to be evaluated using DFT. Various options are available to choose a screening criterion to select promising structures using both properties. One option is using minimum and maximum values for hardness and energy, respectively; either or both must be satisfied. Another option is a weighted objective function of the form \(f=w{f}_{E}+\left(1-w\right){f}_{H}\), where \(0\le w\le 1\). Here, \({f}_{E}\) is the objective function for the energy and \({f}_{H}\) is the objective function for hardness. As the accuracies of the ML models increase with an increase in the dataset, they can be retrained periodically as more DFT calculations are performed.

Figure 6
figure 6

Proposed material discovery strategy augmented with a machine learning model for computational efficiency.

Full size image

Further, due to the reduced computational requirements, larger design spaces can be explored. For example, the GA run in this work was restricted to a maximum of 16 atoms in the unit cell of a structure. DFT calculations generally scale up as \(O\left({N}_{a}^{3}\right)\) and the hardness calculation using the Cheenady model scales up as \(O\left({N}_{b}\right)\), where \({N}_{a}\) represents the number of atoms and \({N}_{b}\) represents the number of bonds in the unit cell (which is often proportional to \({N}_{a}\)). Hence, running a GA search for structures with larger unit cells can be prohibitively expensive. With a reduction in the number of DFT calculations due to well-trained ML models, larger unit cell structures can now be included in the search. This approach also allows for the use of more computationally expensive functionals (e.g., meta-GGAs like SCAN) that provide greater accuracy in the DFT calculations.

It is important to note that the limitation on the maximum number of atoms for the structures in the training dataset is not expected to affect the ML models’ accuracy when predicting energies and hardness of structures with larger unit cells. The structural descriptors used in this work are not simply learning the entire unit cell structure but are rather capturing local structural information. The largest cutoff radius used is 6 Å; hence, the models are learning localized structural environments within a 12 Å sphere. Reducing the maximum number of atoms would greatly reduce the computational cost; however, it would be at the cost of structural diversity in the dataset. Increasing the maximum number of atoms for the training dataset would result in the ML models learning some unique local environments; however, the increase in the dataset diversity would not scale efficiently with the increase in computational time after a certain point. The choice of 16 as the maximum number of atoms provides a suitable trade-off between dataset diversity and computational cost.

Summary

We have presented a strategy for material discovery that augments the genetic algorithm for structure prediction (GASP) with machine learning. By creating surrogate models to calculate a structure’s energy and intrinsic hardness, we can accelerate the computational discovery of structures with high hardness and stability (i.e., low energy) in a given design space. We have shown that the UF3 and SVR models can effectively learn the energy and hardness landscapes, respectively, of a given design space from as few as 150 structures generated by a genetic algorithm. These surrogate models can then be used to screen the subsequent structures created by the genetic algorithm, and the more accurate calculations (using DFT and the Cheenady model) can be performed on only the select few structures predicted to have desirable properties. The reduction in the number of expensive calculations allows for the expansion of the design space to include more structures, especially those with larger unit cells. We have also shown that the linear combination of cubic B-spline basis functions and the RDF + ADF descriptors are capable of encoding the material data for machine learning, and that the SVR model is insensitive to the descriptor hyperparameters, allowing for it to be used in material-agnostic environments. Future work will involve combining the genetic algorithm, the DFT and hardness calculations, and the surrogate models in a single package to automate the material discovery process for a variety of design space explorations.

Methodology

Dataset

The dataset is generated using the Genetic Algorithm for Structure Prediction (GASP) [4, 5], coupled with the density functional theory software VASP [32,33,34]. While the DFT calculations perform the local optimization through relaxation, GASP is a grand canonical global optimization algorithm that explores the entire design space to identify low-energy basins in the entire landscape. For each binary design space, a pool of initial stable reference elemental structures (that exist at the endpoints of the phase diagram for each design space) is mined from existing databases such as The Materials Project [35] to create the initial generation of unrelaxed structures. The relaxed structures and energies of this generation are obtained through DFT calculations, and the intrinsic hardness of the structures are obtained using the semi-empirical Cheenady [27] model (discussed below). Next, ‘offspring’ structures are generated through mutation and mating operations, using a promotion system that favors the ‘fittest parents,’ as defined by the objective function (discussed below). The DFT and hardness calculations are then run on the offspring generation, and the best offspring are selected as parents for the following generation. This process continues until a termination criterion (computation time or the number of organisms) is met. Thus, GASP acts as an intelligent global search tool to map the entire energy landscape of a given material system.

The dataset for training the ML models contains the energy and intrinsic hardness values for the relaxed structures, and 10% of the unrelaxed structures, generated during the GASP run. The data are then split into training (80%) and testing (20%) sets, as shown in Table 1. While splitting the data, we make sure that unrelaxed structures from the same relaxation run do not cross over between the trained and tested sets, as that would cause the two sets to become too correlated and underpredict the true model uncertainty.

Objective function

The objective function, or fitness function in the case of a genetic algorithm, is based on the energy per atom of the crystal structure relative to the energy of its elemental components. For a material system with \(n\) elements, this formation energy is defined as

$$E_{{\text{f}}} \, = \,E - \mathop \sum \limits_{j = 1}^{n} X_{j} E_{j}$$
(1)

where \(E\) is the energy per atom of the crystal structure (obtained through DFT calculations), \({X}_{j}\) is the molar fraction of the \(j\) th element in the structure, and \({E}_{j}\) is the energy per atom of the elemental \(j\) reference state (i.e., the endpoints of the design space). This can be visualized from the phase diagram for the design space, illustrated in Fig. 1 for \(n=2\) (binary system), where each new structure created in a generation is represented by a filled circle. Structures generated in a previous generation are represented by unfilled circles. The initial stable reference elemental structures are shown with black squares. Stable structures lie on the convex hull of the phase diagram. For the remaining structures, their distance from the convex hull in the phase diagram, termed as \(\Delta {E}_{\mathrm{H}}\) and illustrated in Fig. 1, is a measure of the structure’s relative stability. In the genetic algorithm, the fitness of each offspring in a generation of structures is defined by normalizing this parameter within the generation, as

$$f = \frac{{{\Delta }E_{{{\text{H}},{\text{max}}}} - {\Delta }E_{{\text{H}}} }}{{{\Delta }E_{{{\text{H}},{\text{max}}}} - {\Delta }E_{{{\text{H}},{\text{min}}}} }}$$
(2)

The offspring with the higher fitness values have a higher probability of being promoted to be parents and create the next generation via mating and mutation operations.

For each composition and structure thus generated, we can calculate the intrinsic hardness using the semi-empirical model recently proposed by Cheenady et al. [27]. This model was slightly modified for its pre-factor and exponents because the values for these empirical parameters in the original Cheenady equation were fit to the hardness of a set of ceramics using an electronegativity scale for covalent crystals defined by Li and Xue [36]. However, in the current study, we use the more common Pauling [37] scale of electronegativity, as the values in this scale are available for every element of the Periodic Table. Hence, the empirical pre-factor and exponents for this study, shown in Eq. (3a), were obtained by fitting the Cheenady equation to the same hardness data used by Cheenady et al. [27], with the only difference being the electronegativity scale used. The resulting equation is given as

$$H = 986 \left( {\frac{{N_{b} }}{V}} \right)^{0.844} \left[ {\mathop \prod \limits_{a,b = 1}^{{N_{b} }} Z_{ab}^{0.006} d_{ab}^{ - 3.18} e^{{ - 2.44fi_{ab} }} } \right]^{1/N}$$
(3a)

where \({N}_{b}\) is the number of bonds in the unit cell of the structure, \(V\) is the volume of the unit cell, and \({d}_{ab}\) is the bond length between the atoms \(a\) and \(b.\) For each bond, \({Z}_{ab}\) and \(f{i}_{ab}\) are defined as

$$Z_{ab} = \frac{{\chi_{a} }}{{\eta_{a} }}\frac{{\chi_{b} }}{{\eta_{b} }}$$
(3b)
$$fi_{ab} = \left( {\frac{{\chi_{a} - \chi_{b} }}{{\chi_{a} + \chi_{b} }}} \right)^{2}$$
(3c)

where \({\chi }_{a}\) and \({\chi }_{b}\) are the electronegativity values, and \({\eta }_{a}\) and \({\eta }_{b}\) are the coordination numbers, respectively, of atoms \(a\) and \(b\) that make up the bond.

To obtain the intrinsic hardness of each structure using this model, the local environment around every atom in the unit cell must be analyzed to obtain its bonding and co-ordination information (i.e., detect all the bonds in which an atom participates). For this purpose, a crystal-near-neighbor approach (CrystalNN), which uses Voronoi decomposition and solid angle weights to determine coordination environments [38], was utilized through the “local_env” module from the Pymatgen library of Python [39]. Once the bonding information for each atom in a structure is obtained, Eq. (3) can then be applied to obtain a measure of the structure’s intrinsic hardness by looping over each bond in the structure to perform the geometric average. While this analysis may be performed reasonably quickly for structures with a small number of atoms in the unit cells, the computational cost increases quadratically with an increase in the number of atoms, as the CrystalNN algorithm loops over every atom and atom-pair in the structure to detect if atoms are bonded. Hence, an ML approach that is independent of the number of atoms in the structure would greatly accelerate the hardness predictions, particularly for the more complex structures.

Machine learning algorithms

For predicting a structure’s energy, we employ the Ultra-Fast Force Field (UF3), which learns the low-order many body expansion [40] of the system’s potential energy landscape [8]. Each two- and three-body term (higher-order terms are neglected) in the expansion are represented by a set of basis functions of pairwise distances (\(r\)) as

$$E = \mathop \sum \limits_{i,j}^{{}} V_{2} \left( {r_{ij} } \right) + \mathop \sum \limits_{i,j,k}^{{}} V_{3} \left( {r_{ij} ,r_{ik} ,r_{jk} } \right)$$
(4)

where \(i\) runs over all the atoms in the unit cell and \(j,k\) run over all neighboring atoms up to a defined cutoff distance. \({V}_{2}\) and \({V}_{3}\) are expressed as linear combinations of cubic B-splines as

$$V_{2} \left( {r_{ij} } \right) = \mathop \sum \limits_{n = 0}^{K} c_{n} B_{n} \left( {r_{ij} } \right)\,V_{3} \left( {r_{ij} ,r_{ik} ,r_{jk} } \right) = \mathop \sum \limits_{l = 0}^{{K_{l} }} \mathop \sum \limits_{m = 0}^{{K_{m} }} \mathop \sum \limits_{n = 0}^{{K_{n} }} c_{lmn} B_{l} \left( {r_{ij} } \right)B_{m} \left( {r_{ik} } \right)B_{n} \left( {r_{jk} } \right)$$
(5)

where \({K}_{x}\) is the number of basis functions per spline, and \({c}_{n}\) and \({c}_{lmn}\) are the corresponding coefficients. The model is fit by simultaneously optimizing all the spline coefficients \(\mathbf{c}\) using the linear least squares method with Tikhonov regularization. This is mathematically represented as

$${\mathbf{c}} = \left( {{\mathbf{X}}^{T} {\mathbf{X}} + \lambda_{1} {\mathbf{I}} + \lambda_{2} {\mathbf{D}}_{2}^{T} {\mathbf{D}}_{2} } \right)^{ - 1} {\mathbf{X}}^{T} {\mathbf{y}}$$
(6)

where \(\mathbf{X}\) contains the B-spline values over all pair distances within the cutoff radius for all the structures in the dataset, \(\mathbf{I}\) is the identity matrix, and \(\mathbf{y}\) contains the energies of the structures. \({\lambda }_{1}\) controls the the ridge penalty and \({\lambda }_{2}{\mathbf{D}}_{2}^{T}{\mathbf{D}}_{2}\) controls the smoothness across adjacent splines with a difference penalty. The optimization problem in Eq. (6) is strongly convex, and results in an efficient and deterministic solution.

For the prediction of intrinsic hardness, we choose a support vector regression (\(\epsilon\)-SVR) model, deployed using its implementations in the sci-kit learn library for Python [41]. It implicitly uses the kernel trick to transform the input vectors \({x}_{i}\in {\mathbb{R}}^{n}\) to a higher dimensional function space \(\phi ({x}_{i})\in {\mathbb{R}}^{m}\) (\(m>n\)). A linear model is fit in this function space but is nonlinear when transformed back to the original feature space. In this work, we use the popular Gaussian radial basis kernel, defined as

$$\kappa \left( {x,x^{\prime}} \right) = \exp \left( { - \frac{{\left| {x - x^{\prime}} \right|^{2} }}{{2\sigma_{\kappa }^{2} }}} \right)$$
(7)

where \(\left| {x,\,x^{\prime}} \right|\) is the Euclidean distance (L2-norm) between two input vector variables \(x\) and \(x^{\prime}\), and \({\sigma }_{\kappa }\) is the kernel width which is optimized when fitting the model to the data. In our case, the input vectors \({x}_{i}\) are obtained by concatenating the partial radial (\({X}_{RDF}\)) and angular (\({X}_{ADF}\)) distribution functions for each structure \(i\).

The partial RDF is averaged over the entire structure and captures the average distribution of inter-atomic distances, \({d}_{kl}^{AB}=\left|{\overrightarrow{r}}_{k}^{A}-{\overrightarrow{r}}_{k}^{B}\right|\), between atoms \(k\) and \(l\) of types \(A\) and \(B\), as

$$g_{AB} \left( r \right) = \frac{1}{{N_{A} }}\mathop \sum \limits_{k = 1}^{{N_{A} }} \mathop \sum \limits_{l = 1}^{\infty } \frac{1}{{r^{2} }}\exp \left[ { - \frac{{\left( {r - d_{kl}^{AB} } \right)^{2} }}{{2\sigma_{g}^{2} }}} \right]{\Theta }\left( {d_{c} - d_{kl}^{AB} } \right)$$
(8)

where \({d}_{c}\) is the cutoff distance, enforced by the Heaviside function \(\Theta \left({d}_{c}-{d}_{kl}^{AB}\right)\). This cutoff distance is chosen such that it extends beyond the unit cell of the structure in order to capture periodicity. The width of the Gaussian distribution is controlled by \({\sigma }_{g}\).

Similarly, the ADF captures the average distribution of inter-atomic angles, \({\theta }_{klm}\), centered on atom \(l\), between atoms \(k\), \(l\), and \(m\) of types \(A\), \(B,\) and \(C\), as

$$q_{ABC} \left( x \right) = \mathop \sum \limits_{l = 1}^{{N_{B} }} \mathop \sum \limits_{k = 1}^{\infty } \mathop \sum \limits_{m = 1}^{\infty } \exp \left[ { - \frac{{\left( {r - \cos \theta_{klm} } \right)^{2} }}{{2\sigma_{g}^{2} }}} \right]f\left( {d_{kl}^{AB} } \right)f\left( {d_{lm}^{BC} } \right)$$
(9)

In this case, the logistic function, \(f\left(d\right)={\left[1+\mathrm{exp}\left\{k\left(d-{d}_{k}\right)\right\}\right]}^{-1}\), is used instead of a hard cutoff, where \({d}_{k}\) is the midpoint and \(k\) controls the fall rate (steepness) of the logistic function.

As the RDFs and ADFs result in continuous functions, they are binned to obtain discrete representations of the crystal structure. To mitigate the loss of information during binning, the bin width, \(h\), is selected such that \(h\le {\sigma }_{g}\). Hence, the final input representations for the ML models are constant-length vectors \({X}_{\mathrm{RDF}}={\widehat{g}}_{AB}^{z}\forall (z,A,B)\) and \({X}_{\mathrm{ADF}}={\widehat{q}}_{ABC}^{z}\forall (z,A,B,C)\) for each structure.

The \(\epsilon\)-SVR algorithm works by finding a surrogate function \(f\left(x\right)=\langle w,x\rangle +b\) that is allowed to deviate by a maximum of \(\epsilon\) from \(y\). This creates an “\(\epsilon\)-tube” (of diameter \(\epsilon\)) around the true value, \(y\); any points within this tube are considered as accurate predictions and not penalized by the algorithm. Slack variables \({\xi }_{i}, {\xi }_{i}^{*}\) measure the distance to points outside the tube. The optimization problem in this case is to identify a surrogate function that puts more points inside the tube while at the same time reducing the “slack.” Mathematically, it is defined as

$${\text{minimize}}\,\frac{1}{2}\left| w \right|^{2} + C\mathop \sum \limits_{i = 1}^{N} \left( {\xi_{i} + \xi_{i}^{*} } \right)$$
(10a)

subject to the following constraints

$$y_{i} \, - \,\left[ {\left\langle {w,x_{i} } \right\rangle \, + \,b} \right] \le \in \, + \,\xi _{i} {\mkern 1mu} \,\left[ {\left\langle {w,x_{i} } \right\rangle \, + \,b} \right]\, - y_{i} \le \, \in \, + \,\xi _{i}^{*}$$
(10b)

where the parameter \(C\) is the regularization parameter. The input vectors, \({x}_{i}\), are normalized by subtracting the means and dividing by the standard deviation (feature scaling) to avoid bias toward vector components with higher variance. Before determining the coefficients for (i.e., training) the ML models, the regularization parameter (\(C\)) and width of the \(\epsilon\)-tube are optimized via fivefold cross-validation with a random search using 500 iterations [42]. For each iteration, these hyperparameters are randomly sampled from exponential distributions (\(P\left(x\right)=\beta {e}^{-\beta x}\)).

For both descriptors, we set σg=0.2Å. T \(\mathrm{he}\) remaining hyperparameters for each descriptor are optimized by sampling the hyperparameter space using a random search (with 100 iterations), as shown in Fig. 5. The cutoff distances (\({d}_{c}\) and \({d}_{k}\)) are varied from 3Å to 10Å , and the slope parameter (\(k\)) is varied from 1 to 5. For the RDF, dc=6Å was chosen for the Heaviside cutoff function. The bin width (\(h\)) is selected to be 0.1Å, and hence, the length of \({X}_{\mathrm{RDF}}\) is 180 for a binary system as there are three types of atom pairs (A–A, A–B, B–B). For the ADF, the range is taken as \([-\mathrm{1,1}]\) for the cosine of six types of angles in the binary system (A–A–A, A–A–B, A–B–A, A–B–B, B–A–B, B–B–B), and the bin width (\(h\)) is selected as 0.1, resulting in a length of 120 for \({X}_{\mathrm{ADF}}\). For the logistic cutoff function, dc=6Å and k=2.5Å−1 were the chosen hyperparameters.