Introduction

Plasticity in polycrystalline metals and alloys is governed by intragranular dislocation activity, such as dislocation motion and dislocation interactions within a grain interior, and intergranular dislocation activity, such as slip transmission through grain boundaries (GBs) [1, 2]. Dislocations impinging on a GB can be: (a) transmitted through the GB, (b) deposited on or absorbed by the GB, (c) absorbed and re-emitted from an adjacent region of the GB, or (d) reflected back into the incoming grain [3,4,5,6]. Focusing on slip transfer, dislocation propagation across GBs depends on the geometry of the opposing lattice regions [7, 8]. Slip transfer without the production of a residual dislocation at the interface is known as direct transmission. Coherent transmission is accompanied by the formation of residual dislocations, when the incoming and outgoing slip traces intersect along a common line, but the incoming and outgoing Burgers vectors are different. In the most general case, slip transmission involves realignment of dislocations with the outgoing slip trace and the formation of residual dislocations to ensure Burgers continuity.

Classical studies on slip transfer [3,4,5, 9] provided a macro-scale analysis of slip transmission accounting for the geometric misalignment between slip systems across the neighboring grains and the stress-state in the system; however, mechanisms operating at the atomistic scale can influence slip transmission and were not accounted for in these works. Dislocation transmission is inherently dependent on the atomic structure of the GB and its subsequent evolution due to interactions with lattice defects during intergranular plastic deformation [10]. The atomic structures of many equilibrium GBs (EGBs) can be characterized by intrinsic secondary grain boundary dislocations (IGBDs), which accommodate the deviation in misorientation from vicinal reference boundaries [11,12,13]. The ordered arrangement of IGBDs causes periodic intergranular stresses that can influence the stress-state at the point of intersection between the dislocation and the GB [14]. After deposition or transmission of lattice dislocations, disordered networks of extrinsic secondary grain boundary dislocations (EGBDs) can be formed, in addition to the ordered IGBDs, leading to non-equilibrium (or disrupted) structure and complicated stress states at the GB [15, 16]. The modified stress landscape in disrupted boundaries can influence subsequent interactions between lattice dislocations and GBs.

The intricate nature of this problem has motivated numerous experimental [8, 17,18,19,20,21,22,23,24,25,26,27,28,29] and computational [14, 30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53] efforts over the last two decades to analyze slip transfer through GBs both qualitatively and quantitatively, with a focus on understanding the role of GB-mediated phenomena [54]. For example, atomistic simulations have been used to investigate the atomic processes that occur during slip transfer [14, 30,31,32, 37, 43, 49], and to identify quantitative metrics describing the likelihood of a mechanism, such as the energy barriers to slip transmission [31, 32]. At the mesoscale, discrete dislocation dynamics (DDD) [55,56,57,58,59] has been used to model dislocation interactions with GBs. These studies are limited to: (a) low-angle tilt GBs (LAGBs) [34, 38, 40, 42], which can be represented by regular arrays of edge dislocations, (b) impenetrable GBs that block dislocation transmission [41, 47, 52], or (c) penetrable interfaces with a critical barrier strength that is approximately characterized by the GB energy (which is expressed as a function of the GB misorientation angle) [35, 36, 46, 51] or the line-tension energy of the transmitting configuration [33]. With the exception of the LAGB studies, the mechanical structure of the interfaces is neglected, resulting in approximate evaluations of the role of GB structure on slip transmission.

Several methods have been proposed to describe GB structure at the mesoscale. For example, dislocation-based GB descriptions obtained via energetic [60] and atomistically informed coupled kinematic/energetic considerations [61, 62] have been proposed. Dislocation-based models are often limited to the description of GBs with small misorientation angles. Alternatively, models based on disclinations can be used to describe material interfaces, and in particular, high-angle symmetric tilt grain boundaries (STGBs). Disclination-based GB models have been used to investigate GB mechanical structure and energy [63,64,65,66,67], energetics of triple junctions [64], shear-coupled GB migration [68], and solute segregation to GBs [69] with the results of these studies in good agreement with theoretical predictions, atomistic calculations and experiments. This motivates the implementation of disclination-based models of STGBs in DDD to account for the role of GB structure on slip propagation.

Thus, the objectives of this work are (a) to introduce a framework to describe the mechanical structure of equilibrium and non-equilibrium GBs in DDD using disclinations, and (b) to assess the role of GB structure (i.e., equilibrium versus non-equilibrium configurations) on dislocation transmission and GB plasticity. First, a slip transmission algorithm is implemented in DDD to handle the transfer of dislocation lines between grains. Then, equilibrium and non-equilibrium (disrupted) high-angle symmetric tilt grain boundaries are modeled using the elastic fields characteristic of the structural defect content (disclination arrangements) in the STGBs. Slip transmission through EGBs with structural defects, and models with the same geometry but without structural defects, is compared to understand how GB stress fields influence slip transfer. Dislocation transmission through non-equilibrium GBs (NEGBs), which are constructed using the results of the EGB simulations, is analyzed to understand the effect of prior dislocation transmission events on subsequent slip transfer. Both comparisons show that the stress landscape at the GB influences important aspects of intergranular plasticity.

Specifically, the transmission of a dislocation shear loop through two high-angle \( \left[ {110} \right] \) STGBs in Al is analyzed. The details of the models used in this study are presented in the Methodology section. The slip transmission algorithm utilizes the Lee–Robertson–Birnbaum [5, 70] (LRB) criteria to predict the outgoing slip system, and a dissipation-based rule to determine the feasibility of dislocation transmission considering the local stress-state at the interface. The numerical implementation of the slip transmission algorithm is introduced in the Methodology section. To impose the stress field of each GB, the disclination structural unit model (DSUM) [71,72,73] and a model for the incorporation of EGBDs within the DSUM structure [16, 74] are coupled with DDD. DSUM-based construction of equilibrium STGBs in terms of wedge disclination dipoles [64, 69, 75, 76] (WDDs) is detailed in the Framework for Modeling Equilibrium and Non-equilibrium Grain Boundaries section. The non-equilibrium structure of a GB after absorption/deposition of a dislocation is described using a model for the incorporation of EGBDs within the intrinsic WDD network, proposed by Nazarov et al. [74]. In the Framework for Modeling Equilibrium and Non-equilibrium Grain Boundaries section, the approach used for modeling the stress fields of NEGBs using WDD-EGBD complexes is explained.

It is demonstrated that the local stress-state at GBs due to structural defects strongly influences the transmission of dislocations by providing periodically favorable sites for transmission into the neighboring grain. The dynamics of the residual dislocations that are formed during transmission are strongly aligned with the stress fields of the WDDs. Furthermore, the effect of modified stress fields on dislocation transmission is investigated to understand the role of stress heterogeneities in NEGBs on slip transmission. Dislocation transmission occurs preferentially through regions of the GB proximal to the WDD-EGBD defect complexes. The modified GB stress state in certain disrupted configurations is shown to lower the external driving stresses required for dislocation transmission. In essence, the developments and results presented here demonstrate that the current framework can be used to study dislocation-GB phenomena at the mesoscale.

The following notational scheme is adopted throughout the article: scalar quantities are represented by italicized characters, vectors are denoted by bold symbols, and second-order tensors are denoted by bold and italicized symbols. A rectangular Cartesian coordinate system with basis vectors \( {\mathbf{e}}_{1} ,{\mathbf{e}}_{2} ,{\mathbf{e}}_{3} \) is adopted in this work and all vector and tensor components are defined with respect to this basis.

Framework for modeling equilibrium and non-equilibrium grain boundaries

Representation of equilibrium grain boundaries via the disclination structural unit model

According to DSUM, which is an extension of the structural unit model of Sutton and Vitek [11, 12], the structure of a general planar STGB with misorientation angle \( \theta \) defined between two favored tilt boundaries \( \theta_{m} \) and \( \theta_{n} \) (i.e., \( \theta_{m} < \theta < \theta_{n} \)) can be represented by a contiguous sequence of \( m \) majority and \( n \) minority units [72]. The majority and minority units correspond to the structural elements of the favored boundaries. The cores of IGBDs, which are located at the positions of the minority units and accommodate the transition in atomic structure from one reference tilt boundary to another, are represented by equivalent wedge disclination dipoles (WDDs). Figure 1a shows a schematic of the elementary biaxial WDD composed of a pair of positive and negative wedge disclinations with parallel line vectors \( {\mathbf{t}} \) and anti-parallel Frank’s vectors \( {\varvec{\upomega}} \) that are aligned with the misorientation axis (\( {\mathbf{e}}_{1} \)-axis) and separated by a small distance, \( 2\xi \) [77, 78]. Note, the term biaxial indicates that the rotation axes corresponding to the individual disclinations are different and in this particular case, the rotation axes are coincident with the individual defect lines.

Figure 1
figure 1

(a) Simulation box showing an infinitely long WDD of strength \( \pm \omega \) and arm length \( 2\xi \) aligned with the \( {\mathbf{e}}_{1} \)-axis. The image cells for the analytical summation of the WDD stress fields along the \( {\mathbf{e}}_{2} \)-direction for the periodic models are shown via dashed boxes. (b) Simulation cell showing an infinitely long WDD with rotation axis shifts of \( l^{ + } \) and \( l^{ - } \). The positions of the new rotation axes are indicated by \( \bullet \). The corresponding infinitely long edge dislocations of Burgers magnitude \( b^{ + } = - \omega l^{ + } \) and \( b^{ - } = \omega l^{ - } \), resulting from the rotation axis shifts, are also shown.

Full size image

Disclination-based construction of STGBs with the \( \langle 100 \rangle \) misorientation axis has been detailed in previous works [64, 65, 69, 76, 79]. The application of DSUM for modeling equilibrium STGBs with GB normal \( {\mathbf{n}}_{\text{int}} \) and the \( \left[ {110} \right] \) misorientation axis is illustrated in this section by considering the example of the \( {\Sigma }123 \left( {\bar{5}\, 5\,1 4} \right)/\theta = 53.60^{ \circ } \) STGB in FCC Al. For this GB, the bounding majority and minority favored boundaries are \( {\Sigma }11 \left( {\bar{1}\, 1\,3} \right)/\theta_{m} = 50.48^{ \circ } \) and \( {\Sigma }3 \left( {\bar{1}\, 1\,1} \right)/\theta_{n} = 109.47^{ \circ } \), respectively. The structural elements corresponding to these boundaries are denoted by \( C \) and \( D \) [13]. The \( {\Sigma }123 \) boundary is a non-centered boundary with period vector \( \left[ {\bar{7}\,7\,\bar{5}} \right] \), while the \( C \) and \( D \) units are centered with period vectors \( \frac{1}{2}\left[ {\bar{3}\,3\,\bar{2}} \right] \) and \( \frac{1}{2}\left[ {\bar{1}\,1\,\bar{2}} \right] \). The period vectors are expressed in units of the lattice parameter for Al, \( a = 0.405 \,{\text{nm}} \) [80]. The vectorial decomposition of each period of the \( {\Sigma }123 \) boundary in terms of the periods of the \( C \) and \( D \) units can be expressed as,

$$ \begin{array}{*{20}c} {\left[ {\bar{7}\,7\,\bar{5}} \right] \to \frac{9}{4}\left[ {\bar{3}\,3\,\bar{2}} \right] + \frac{1}{4}\left[ {\bar{1}\,1\,\bar{2}} \right].} \\ \end{array} $$
(1)

Thus, the \( {\Sigma }123 \) period is composed of \( m = 9 \) majority units and \( n = 1 \) minority units resulting in the \( \left| {CCCCCCCCCD} \right| \) structure. The length of one period of this boundary is \( H = 9d_{m}^{\prime} + 1d_{n}^{\prime} \), where the dimensions \( d_{m}^{\prime} = d_{m} \cos \left( {\frac{{\theta - \theta_{m} }}{2}} \right) \) and \( d_{n}^{\prime} = d_{n} \cos \left( {\frac{{\theta_{n} - \theta }}{2}} \right) \) are the distorted lengths of the \( C \) and \( D \) structural units, computed using the corresponding rest lengths \( d_{m} = 0.475 \,{\text{nm}} \) and \( d_{n} = 0.248 \,{\text{nm}} \) [81]. The values of the parameters are determined to be \( d_{m}^{\prime} = 0.474 \, {\text{nm}} \), \( d_{n}^{\prime} = 0.219 \,{\text{nm}} \), and \( H = 4.492 \,{\text{nm}} \). Thus, WDDs of strength \( \pm \omega = 58.99^{ \circ } \) and arm length \( 2\xi = d_{n}^{\prime} = \) \( 0.219 \,{\text{nm}} \) are localized at the \( D \) unit and each dipole in the GB is separated by \( 9d_{m}^{\prime} = 4.272 \,{\text{nm}} \).

Similarly, the DSUM description of the \( {\Sigma }627 \) GB in Al can be derived. In this case, the delimiting majority and minority reference boundaries are the \( \Sigma 27 \left( {\bar{1} \,1\,5} \right)/\theta_{m} = 31.59^{ \circ } \), denoted as the \( B \) unit, and \( \Sigma 11 \left( {\bar{1}\, 1\,3} \right)/\theta_{n} = 50.48^{ \circ } \). The relevant DSUM parameters, such as the structural decomposition, characteristic lengths of the majority and minority units, dipole strength, and Burgers content of the WDDs for the \( {\Sigma }627 \) and \( {\Sigma }123 \) boundaries are listed in Table 1. Note, to ensure that the effects of the dipole periodicity on transmission characteristics are captured accurately, an average dislocation segment length of \( l_{\text{avg}} = 10a \), which is less than the spacing between WDDs in both GBs, is used in all the simulations reported here.

TABLE 1 GB period structures, characteristic dimensions of GB units, dipole strengths, and Burgers content of the WDDs for the \( {\Sigma }627 \) and \( {\Sigma }123 \) GBs.
Full size table

The stress fields \( \varvec{\sigma}^{\Delta } \) characteristic of equilibrium STGBs can be obtained by the superposition of the stresses of the individual WDDs arranged according to the set of parameters obtained using DSUM. For simplicity, the EGB stress fields are assumed to be static during the simulations. For the infinitely long biaxial WDD aligned with the \( {\mathbf{e}}_{1} \)-axis shown in Fig. 1a, the non-zero components of the elastic stress field under plane strain conditions are \( \sigma_{11} \), \( \sigma_{22} \), \( \sigma_{33} \), and \( \sigma_{23} \) [77, 82, 83]. The expressions for the stress components are listed in Supplemental Note 1. In modeling periodic volumes containing disclinations it is necessary to consider the stress at any field point \( {\mathbf{r}} \) due to the disclinations in the primary volume and their periodic images. For the infinitely long WDD aligned along the \( {\mathbf{e}}_{1} \)-axis contained in a simulation cell, shown in Fig. 1a, the stress field for the plane strain problem can be obtained by summing the contributions from the primary WDD and its periodic images along \( {\mathbf{e}}_{2} \) and \( {\mathbf{e}}_{3} \), which is referred to as the doubly periodic case [84] (2D PBCs). First, the stresses \( \sigma_{ij}^{*} \) at field point \( {\mathbf{r}} \) are mathematically determined by performing an analytical (infinite) summation of the WDD stress expressions along \( {\mathbf{e}}_{2} \), with periodicity \( {\mathcal{L}}_{2} \) [85]. The expressions for \( \sigma_{ij}^{*} \) are listed in Supplemental Note 1. Then, the doubly periodic stresses \( \sigma_{ij}^{**} \) are obtained via numerical summation along \( {\mathbf{e}}_{3} \) using a finite number of image cells, \( N = 3 \). The solutions for \( \sigma_{ij}^{*} \) and \( \sigma_{ij}^{**} \) used in this work are singular on the defect lines and a numerical cut-off parameter of = 0.7071a, which is equal to the Burgers vector magnitude for lattice dislocations in FCC Al, is used to overcome the singularities. Finally, the stress field \( \varvec{\sigma}^{\Delta } \left( {\mathbf{r}} \right) \) from the array of WDDs at the GB is obtained by the summation of the stresses due to each wedge dipole in the array, considering their doubly periodic images as well. The EGB stresses contribute to the internal stresses \( \varvec{\sigma}^{\text{int}} \) in the material.

The stress profiles of the WDD walls corresponding to the \( {\Sigma }627 \) and \( {\Sigma }123 \) boundaries are shown in Fig. 2a and b, respectively. The stress profiles have a periodic length equal to the separation distance between dipoles. The regular arrangement of dipoles in the GBs leads to mutual screening of their long-range fields. Consequently, the mechanical fields are localized to a \( \sim 6 - 10 \,{\text{nm}} \) region normal to the GB. These intergranular stresses will assist or impede the motion of dislocations approaching the GB. Moreover, the alternating tensile and compressive nature of the stresses will control the feasibility of transmission at a local scale. These effects are probed via transmission simulations in the forthcoming section.

Figure 2
figure 2

Contours of the \( \sigma_{11} \), \( \sigma_{22} \), and \( \sigma_{23} \) stress components for the DSUM description of the equilibrium structures of (a) \( {\Sigma }627 \) and (b) \( {\Sigma }123 \) GBs. The high stress regions correspond to the cores of the intrinsic WDDs, which generate intergranular stresses in grains 1 and 2.

Full size image

Representation of the stress fields of non-equilibrium grain boundaries

After dislocation transmission, residual dislocations will commonly remain at GBs. The absorption of dislocations trapped at GBs into the intrinsic WDD network can be described by the incorporation model presented by Nazarov et al. [74]. According to this model, the dislocations trapped at GBs can dissociate into EGBDs, with Burgers vector \( {\mathbf{b}}_{n}^{\text{DSC}} \) normal to the GB plane, and Burgers vector \( {\mathbf{b}}_{g}^{\text{DSC}} \) within the GB plane, where DSC refers to the displacement shift complete lattice vectors of the GB. In principle, the EGBDs with Burgers \( {\mathbf{b}}_{g}^{\text{DSC}} \) are likely to be very mobile and either mutually annihilate or rearrange leading to grain boundary sliding and plastic incompatibilities at triple junctions. On the other hand, the kinetics of delocalization of EGBDs with Burgers \( {\mathbf{b}}_{n}^{\text{DSC}} \) are strongly dependent on GB diffusion, and thus they will only locally reorganize. Therefore, they generate disorder in the intrinsic GB structure. In this work, disrupted tilt GB configurations are modeled as static arrays of intrinsic WDDs and WDD-EGBD complexes. The WDD-EGBD complexes are formed by the absorption (incorporation) of edge EGBDs, with defect lines parallel to the GB misorientation axis and Burgers \( {\mathbf{b}}_{n}^{\text{DSC}} \), into the intrinsic WDDs at the boundaries.

The WDD-EGBD complexes are created by shifting the rotation axes of the disclinations in the WDD. This concept is detailed in the work of deWit [77] and has been previously used to study transport properties [86] and crack nucleation [87] in metals. In Fig. 1b, the rotation axes of the positive and negative wedge disclinations, in the biaxial WDD, are shifted by \( l^{ + } > 0 \) and \( l^{ - } > 0 \) from their original positions, along the \( {\mathbf{e}}_{2} \)-direction. Following the framework of deWit [77], this results in infinitely long straight edge dislocations with defect lines along \( {\mathbf{e}}_{1} \) and Burgers along \( {\mathbf{e}}_{3} \) added at the positions of the original disclinations, as shown schematically in Fig. 1b. The stress field of this WDD-dislocation complex can be obtained by summing the fields of an infinitely long WDD and infinitely long straight edge dislocations, with Burgers magnitude \( b^{ + } = - \omega l^{ + } \) and \( b^{ - } = \omega l^{ - } \). The expressions for the non-zero stress components, \( \sigma_{11} \), \( \sigma_{22} \), \( \sigma_{33} \), and \( \sigma_{23} \) are listed in Supplemental Note 2. Thus, different configurations of WDD-EGBD complexes at the disrupted boundaries can be modeled by controlling the parameters \( b^{ + } \) and \( b^{ - } \), which quantify the extrinsic Burgers content added to the WDDs.

The doubly periodic stresses of WDD-EGBD complexes in periodic DDD bicrystal models are determined via the steps outlined for the EGB case. First, the analytical infinite sum formulations (along the \( {\mathbf{e}}_{2} \)-axis) of the WDD-EGBD stress expressions are obtained via the superposition of the WDD fields and the infinite sum expressions for edge dislocations, assuming plane strain conditions, which have been presented elsewhere [84, 88]. These expressions are listed in Supplemental Note 2 for reference. Then, the doubly periodic summation is performed via a numerical sum using \( N = 3 \) images along the \( {\mathbf{e}}_{3} \)-axis.

The NEGB stress field , due to the array of WDDs and WDD-EGBD complexes, is added to the internal stress field \( \varvec{\sigma}^{\text{int}} \) in the bicrystals. The screening characteristics of WDD-EGBD complexes are typically different compared to the original WDD, resulting in enhanced or reduced magnitudes of stresses [87]. As the arrangement of WDD-EGBD complexes is generally uncorrelated in the NEGB, the GB stress screening is not effectively balanced, resulting in more complicated elastic fields that decay as \( r^{ - 1/2} \), where \( r \) is the distance from the NEGB [89]. These long-range stresses can be sensed by dislocations in the bulk, and thus, the dynamics of dislocations and dislocation transmission can be affected by disruptions in the GB structure.

Analysis of slip transfer through geometric and equilibrium GBs

Simulations show that under constant external shear stress, \( \tau^{\text{ext}} \), the dislocation loop expands on the incoming slip system \( s_{\text{inc}} = \frac{1}{2}\left[ {\bar{1}10} \right]_{2} \left( {11\bar{1}} \right)_{2} \) in grain 2 until it encounters the GBs. Note, for the remainder of this article, subscripts associated with crystallographic planes and directions indicate the referenced grain. The outcome of the transmission event is then dictated by the local conditions at the interaction region between the dislocation loop and the GB. These outcomes vary depending on the combined internal and external stress states.

Low applied \( \varvec{\tau}^{{{\mathbf{ext}}}} \) simulations

In these simulations, \( \tau^{\text{ext}} \approx 500\,{\text{MPa}} \) and \( 320\,{\text{MPa}} \) for the \( {\Sigma }627 \) and the \( {\Sigma }123 \) bicrystals, respectively. The evolution of the dislocation densities in the transmission grain \( \left( {\rho_{\text{trans}} } \right) \) is compared for the \( {\Sigma }627 \) and the \( {\Sigma }123 \) bicrystals for the geometric and equilibrium GB models in Fig. 3a and b. The dislocation density \( \rho_{\text{trans}} \) is determined as the cumulative dislocation line length in the outgoing grain (grain 1) normalized by the volume of the grain. Figure 3a and b show a steady increase in \( \rho_{\text{trans}} \) for both the geometric and equilibrium \( {\Sigma }627 \) and \( {\Sigma }123 \) GBs at low \( \tau^{\text{ext}} \). The dislocation densities in the transmission grains are higher throughout the simulations for the EGB cases compared to the geometric GB simulations. The origin of differences in the \( \rho_{\text{trans}} \) curves for the equilibrium and geometric GB models is detailed below.

Figure 3
figure 3

Evolution of the dislocation density \( \left ( \rho_{\text{trans}} \right) \) in the transmission grain with time for the (a) \( {\Sigma }627 \) and (b) \( {\Sigma }123 \) GBs for low and high external shear stresses, \( \tau^{\text{ext}} \). The solid lines indicate the \( \rho_{\text{trans}} \) evolution curves for the EGB models with WDDs, while the dashed lines indicate \( \rho_{\text{trans}} \) profiles for the geometric GB models.

Full size image

In all the simulations, i.e., equilibrium and geometric \( {\Sigma }627 \) and \( {\Sigma }123 \) GBs, groups of dislocation segments originally on \( s_{\text{inc}} = \frac{1}{2}\left[ {\bar{1}10} \right]_{2} \left( {11\bar{1}} \right)_{2} \) coherently transmit onto \( s_{\text{trans}} = \frac{1}{2}\left[ {\bar{1}01} \right]_{1} \left( {111} \right)_{1} \) in the outgoing grain. Dislocation transmission onto \( s_{\text{trans}} \) proceeds according to the following reaction for the \( {\Sigma }627 \) geometry,

$$ \begin{array}{*{20}c} {\frac{1}{2}\left[ {\bar{1}10} \right]_{2} \left( {11\bar{1}} \right)_{2} \to \frac{1}{2}\left[ {\bar{1}01} \right]_{1} \left( {111} \right)_{1} + \frac{1}{418}\left[ {63\,146\,\overline{97} } \right]_{2} \left( {\bar{7}\,7\,34} \right)_{2} .} \\ \end{array} $$
(2)

Similarly, the transmission reaction for the \( {\Sigma }123 \) case is,

$$ \begin{array}{*{20}c} {\frac{1}{2}\left[ {\bar{1}10} \right]_{2} \left( {11\bar{1}} \right)_{2} \to \frac{1}{2}\left[ {\bar{1}01} \right]_{1} \left( {111} \right)_{1} + \frac{1}{82}\left[ {15\,26\,\bar{1}} \right]_{2} \left( {\bar{5}\,5\,14} \right)_{2} .} \\ \end{array} $$
(3)

Note, the residual Burgers vector in both cases has components that are parallel and perpendicular to the GB planes. In the \( {\Sigma }627 \) and \( {\Sigma }123 \) EGB simulations, dislocations consistently transmit through regions of positive shear stresses due to the GB resolved on the incoming \( \left( {\tau_{\text{inc}}^{\Delta } =\varvec{\sigma}^{\Delta } : \left( {{\mathbf{b}}_{\text{inc}} \otimes {\mathbf{n}}_{\text{inc}} } \right)} \right) \) and transmission \( \left( {\tau_{\text{trans}}^{\Delta } =\varvec{\sigma}^{\Delta } : \left( {{\mathbf{b}}_{\text{trans}} \otimes {\mathbf{n}}_{\text{trans}} } \right)} \right) \) slip systems, forming transmission nuclei. Figure 4 shows a snapshot of the transmission nuclei, superimposed on maps of \( \tau_{\text{inc}}^{\Delta } \) and \( \tau_{\text{trans}}^{\Delta } \) for the \( {\Sigma }627 \) EGB simulation. The GB stresses \( \tau_{\text{inc}}^{\Delta } \) and \( \tau_{\text{trans}}^{\Delta } \) alternate in polarity along the GB length with a periodicity equal to the period of the WDDs. Some of the transmission nuclei that are formed in regions of positive \( \tau_{\text{trans}}^{\Delta } \) spontaneously grow, coalesce with other transmitted portions of the dislocation loop, and propagate under the influence of the internal and external stresses, leading to an increase in \( \rho_{\text{trans}} \). This observation is consistent with the results of atomistic simulations reported by Bachurin et al. [14], which demonstrated that transmission through LAGBs occurred by the nucleation of transmission embryos in regions of positive shear stress (in the outgoing direction) followed by their subsequent growth and propagation.

Figure 4
figure 4

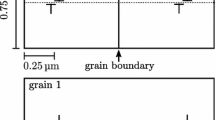
Transmission nuclei formed on the \( s_{\text{trans}} = \frac{1}{2}\left[ {\bar{1}01} \right]_{1} \left( {111} \right)_{1} \) slip system in the outgoing grain (grain 1) for the \( {\Sigma }627 \) EGB simulation at \( \tau^{\text{ext}} \approx 500\,{\text{MPa}} \). The transmission nuclei (green) are superimposed on maps of the GB shear stresses resolved on the incoming slip system in grain 2 (\( \tau_{\text{inc}}^{\Delta } \)) and on the outgoing slip system in grain 1 (\( \tau_{\text{trans}}^{\Delta } \)). Only the dislocations on the transmission slip system are shown for clarity.

Full size image

For the geometric \( {\Sigma }627 \) and \( {\Sigma }123 \) GBs, some of the dislocation segments that reach the interface are transmitted into the outgoing grain, mainly driven by \( \tau^{\text{ext}} \), and form extended transmission nuclei. However, the transmitted dislocations do not propagate in the outgoing grain as the driving stresses (and consequently, the driving forces) for propagation are insufficient to escape the opposing stresses due to dislocation–dislocation interactions and the lattice friction stress. Consequently, the transmitted dislocations remain dormant on \( s_{\text{trans}} \) and plastic dissipation is limited in the outgoing grain. Nevertheless, the dislocation line length on \( s_{\text{trans}} \) increases due to the continued formation of inactive nuclei as the loop expands along the GB, contributing to an overall increase in \( \rho_{\text{trans}} \).

In the EGB model, the residual dislocations that are deposited at the GB, glide under the action of the external and WDD stresses, leading to plastic slip on the interface. The evolution of the residual dislocationsComparison of the NEGB and is shown for the \( {\Sigma }627 \) EGB in Fig. 5. These configurations are superimposed on the maps of \( \tau_{\text{int}}^{\Delta } =\varvec{\sigma}^{\Delta } : \left( {{\mathbf{b}}_{\text{res}} \otimes {\mathbf{n}}_{\text{int}} } \right) \). The proximity of the residual dislocations to the disclination cores results in very high stresses acting on the residual dislocations. Accordingly, the glide of the residual dislocations is observed to be strongly aligned with the stress fields of the WDDs at the interface. As seen in Fig. 5, the dislocations assume a serrated profile as they move, with the serration lengths equal to the spacing between the WDDs. The heterogeneous activation of transmission nuclei on \( s_{\text{trans}} \) and evolution of the corresponding residual dislocations on the interface due to the GB stress fields, results in elongated residual dislocations deposited parallel to the misorientation axis, as shown in Fig. 5. These dislocations persist throughout the low \( \tau^{\text{ext}} \) simulations as nearly straight configurations localized in the proximity of the WDD cores. When constructing disrupted GB configurations for the NEGB simulations, it will be assumed that the out-of-plane component of these extended residual dislocations is incorporated into the neighboring wedge dipoles resulting in WDD-EGBD complexes. These features are absent in the geometric GB simulations at this level of \( \tau^{\text{ext}} \), as the residual dislocations remain stationary in their original configurations.

Figure 5
figure 5

Residual dislocation configuration on the \( \left( {\bar{7}\,7\,34} \right)_{2} \) GB plane for the \( {\Sigma }627 \) EGB simulation at \( \tau^{\text{ext}} \approx 500\,{\text{MPa}} \). The residual (cyan) dislocation lines are superimposed on the map of the GB shear stress resolved on the interface (\( \tau_{\text{int}}^{\Delta } \)). The scale bar is rescaled to highlight the positions of the WDD cores, which are indicated by the fine lines in the \( \tau_{\text{int}}^{\Delta } \) map.

Full size image

Note, the influence of numerical parameters, i.e., and \( l_{\text{avg}} \), on the formation of elongated residual configurations is assessed by performing transmission simulations for = 0.5a, \( 1.0a \) and \( l_{\text{avg}} = 5a \). In general, these configurations are observed in all cases; however, their distribution and density on the GB changes for different and \( l_{\text{avg}} \) values.

High applied \( \varvec{\tau}^{{{\mathbf{ext}}}} \) simulations

For the high stress simulations, \( \tau^{\text{ext}} \approx 600 \,{\text{MPa}} \) and \( 500\,{\text{MPa}} \) in the \( {\Sigma }627 \) and \( {\Sigma }123 \) cases. In these simulations, the expanding dislocation loop can transmit in the geometric and EGB cases according to the reactions in Eqs. (2) and (3) upon intersecting the \( {\Sigma }627 \) and \( {\Sigma }123 \) GBs. This is evident in Fig. 3a and b as \( \rho_{\text{trans}} \) evolution trajectories are very similar for geometric and EGB models. Nevertheless, differences in transmission characteristics between the geometric and EGB models are evident in the following two instances. First, the transmission pathways are different. In the geometric GB simulations, the dislocation segments reaching the interface form nuclei that coalesce and propagate uniformly under the influence of \( \tau^{\text{ext}} \). On the other hand, as in the previous lower stress simulations, transmission nuclei initially form in regions of favorable \( \tau_{\text{trans}}^{\Delta } \) for the EGB model. Groups of transmission nuclei grow, coalesce, and propagate collectively. Accordingly, the initial transmission configurations are different. However, these differences diminish as the outgoing dislocations escape the short-range fields of the interfacial WDDs and evolve largely under the influence of dislocation–dislocation interaction stresses and external loads.

Second, the evolving residual dislocation configurations are different. These profiles are compared for the \( {\Sigma }627 \) geometric and equilibrium GBs in Fig. 6a. For the EGB simulations, the glide characteristics are similar to the low stress case; serrated profiles evolve as the residual dislocations move and some extended dislocations with defect lines parallel to the misorientation axis are deposited on the interface. The elongated residual dislocations are aligned with \( \tau_{\text{int}}^{\Delta } \) of the WDDs. On the other hand, for the geometric GB case, the deposited residual dislocations glide with a smooth (non-serrated) profile. The differences are further evident in the interfacial dislocation density \( \rho_{\text{int}} \) evolution curves compared in Fig. 6b for the \( {\Sigma }627 \) case. The dislocation density at the interface \( \rho_{\text{int}} \) is computed as the cumulative line length of the residual dislocations normalized by the GB area. In general, the quantity \( \rho_{\text{int}} \) is determined to be higher for the EGB case owing to the complicated residual dislocation configurations with elongated dislocation lines. Accordingly, the evolution of interfacial plastic activity is different in the two cases.

Figure 6
figure 6

Comparison of (a) the residual dislocation configurations and (b) the evolution of the residual dislocation densities \( \rho_{\text{int}} \) on the interface for the geometric and equilibrium \( {\Sigma }627 \) GB models.

Full size image

Overall, the collective results presented here highlight the differences in the plastic response of bicrystals with and without a mechanical description of the GBs. Importantly, including the EGB fields alters the transmission characteristics as discussed above, underlining the importance of characterizing the mechanical structure of EGBs in plasticity simulation models.

Analysis of slip transfer through non-equilibrium GBs

Construction of NEGB configurations

The extended residual dislocation configurations formed after dislocation transmission through the EGBs at low \( \tau^{\text{ext}} \) (e.g., Figure 5) are used to simulate non-equilibrium configurations for the \( {\Sigma }627 \) and \( {\Sigma }123 \) GBs. This is schematically depicted in Fig. 7. As a first approximation, it is assumed that the extended residual dislocations, with Burgers \( {\mathbf{b}}_{\text{res}} \), localized near WDDs lengthen indefinitely forming straight dislocation lines parallel to the GB misorientation axis, as shown in Fig. 7a. Then, the dislocations decompose into EGBDs, with defect lines parallel to \( {\mathbf{e}}_{1} \) and Burgers vectors that are DSC lattice vectors of the specific GB, schematically shown in Fig. 7b. Finally, only the infinitely long straight EGBDs with Burgers normal to the GB plane \( \left( {{\mathbf{b}}_{n}^{\text{DSC}} } \right) \), are incorporated into the vicinal WDDs, forming WDD-EGBD complexes, as shown in Fig. 7c. All other EGBDs with planar Burgers vectors \( \left( {{\mathbf{b}}_{g}^{\text{DSC}} } \right) \) are assumed to migrate and disappear due to various relaxation mechanisms.

Figure 7
figure 7

Schematic depicting the formation of non-equilibrium (or disrupted) GB configurations resulting from prior transmission events: (a) residual dislocations with Burgers \( {\mathbf{b}}_{\text{res}} \) are localized near the core of WDDs, (b) the residual dislocations decompose into EGBDs with planar \( \left( {{\mathbf{b}}_{g}^{\text{DSC}} } \right) \) and normal \( \left( {{\mathbf{b}}_{n}^{\text{DSC}} } \right) \) Burgers vectors, and (c) the EGBDs with Burgers \( {\mathbf{b}}_{n}^{\text{DSC}} \) are symmetrically absorbed into the vicinal WDDs forming WDD-EGBD complexes.

Full size image

Consider the decomposition of the residual dislocations for the \( {\Sigma }627 \) GB, with Burgers vector \( {\mathbf{b}}_{\text{res}} = \frac{1}{418}\left[ {63\,146\,\overline{97} } \right]_{2} \), into EGBDs as,

$$ \begin{array}{*{20}c} {\frac{1}{418}\left[ {63\,146\,\overline{97} } \right]_{2} \to \frac{13}{2508}\left[ {7\,\bar{7}\,\overline{34} } \right]_{2} + \frac{5}{627}\left[ {\overline{17} \,17\,\bar{7}} \right]_{2} + \frac{1}{4}\left[ {1\,1\,0} \right]_{2} .} \\ \end{array} $$
(4)

This decomposition reaction into DSC lattice vectors corresponding to the \( {\Sigma }627 \) GB is energetically favorable according to the \( b^{2} \)-criterion [88]. The partial DSC lattice vector \( {\mathbf{b}}_{n}^{\text{DSC}} = \frac{13}{2508}\left[ {7\,\bar{7}\,\overline{34} } \right]_{2} \) is normal to the GB plane while the other two reaction products in Eq. (4) are planar. Following the framework for modeling WDD-EGBD complexes, for the \( {\Sigma }627 \) GB, Burgers content \( b^{ + } = b^{ - } = - \frac{1}{2}\left\| {{\mathbf{b}}_{n}^{\text{DSC}} } \right\| = - 0.0918a \) is added at the positions of individual disclinations in the wedge dipoles to generate WDD-EGBD complexes, similar to the schematic configuration in Fig. 7c. The negative value of the Burgers is considered here since \( {\mathbf{b}}_{n}^{\text{DSC}} = \frac{13}{2508}\left[ {7\,\bar{7}\,\overline{34} } \right]_{2} \) is antiparallel to the GB normal. Similarly, the decomposition of the residual into EGBDs for the \( {\Sigma }123 \) GB can be written as,

$$ \begin{array}{*{20}c} {\frac{1}{82}\left[ {15\,26\,\bar{1}} \right]_{2} \to \frac{1}{492}\left[ {\bar{5}\,5 14} \right]_{2} + \frac{1}{123}\left[ {\bar{7}\,7\,\bar{5}} \right]_{2} + \frac{1}{4}\left[ {1\,1\,0} \right]_{2} ,} \\ \end{array} $$
(5)

where, \( {\mathbf{b}}_{n}^{\text{DSC}} = \frac{1}{492}\left[ {\bar{5}\,5 14} \right]_{2} \) is normal to the \( {\Sigma }123 \) GB plane. For this GB, the added Burgers content is \( b^{ + } = b^{ - } = 0.0159a \). The extent of disruption at the GBs is quantified via the linear (number) density of EGBDs at the GBs, which is determined as \( \rho_{\text{EGBD}} = \frac{{n_{\text{EGBD}} }}{{{\mathcal{L}}_{2} }} \), with \( n_{\text{EGBD}} \) equal to the number of EGBDs with Burgers \( {\mathbf{b}}_{n}^{\text{DSC}} \). For the \( {\Sigma }627 \) GB, \( \rho_{\text{EGBD}} = 6.15 \times 10^{6} m^{ - 1} \), while for the \( {\Sigma }123 \) GB, \( \rho_{\text{EGBD}} = 4.06 \times 10^{6} m^{ - 1} \). The values of \( \rho_{\text{EGBD}} \) used in this study are comparable to the estimates of trapped dislocation densities used in some previous studies [74, 90, 91].

Some key differences are observed between the stress fields of EGBs and NEGBs. First, the screening of the stress field is enhanced for the modified \( {\Sigma }627 \) dipoles, lowering the stress magnitudes, while the screening is weakened for the modified \( {\Sigma }123 \) dipoles, increasing the stress magnitudes. As the Burgers content added to the \( {\Sigma }627 \) WDDs is larger, the corresponding change in the magnitudes of the stresses is higher for the modified \( {\Sigma }627 \) dipoles. Second, the presence of the WDD-EGBD complexes alters the long-range stresses, as the overall screening characteristics of the array of GB structural defects are modified. Figure 8a and b show the \( \sigma_{33} \) profiles for the \( {\Sigma }627 \) and \( {\Sigma }123 \) GBs for linear sections, along the \( {\mathbf{e}}_{2} \)-coordinate, in the outgoing grain at a distance of \( 40.5\,{\text{nm}} \) from the GB plane. From these curves, it is evident that the stress fields of the NEGBs are long ranged in comparison to the stresses due to EGBs, which are zero at these distances. For the \( {\Sigma }627 \) GB, the peak magnitude of the \( \sigma_{33} \) component \( \left( {\sim 30\,{\text{MPa}}} \right) \) is greater than the lattice friction stress \( \left( {\sim 20\,{\text{MPa}}} \right) \) for Al at 100 K [80]. The stress magnitude is considerably lower for the \( {\Sigma }123 \) GB. This difference results from the addition of greater EGBD Burgers content (\( \sim 6 \) times higher \( {\mathbf{b}}_{n}^{\text{DSC}} \)) for the \( {\Sigma }627 \) GB compared to the \( {\Sigma }123 \) GB.

Figure 8
figure 8

Comparison of the NEGB and EGB \( \sigma_{33} \) profiles along the GB (\( {\mathbf {e}}_{2} \)-coordinate) for (a) the \( {\Sigma }627 \) and (b) the \( {\Sigma }123 \) GBs. The profiles are obtained via a linear section in the outgoing grain (grain 1), along the \( {\mathbf {e}}_{2} \)-direction, at a distance of \( 40.5\,{\text{nm}} \) from the GB plane.

Full size image

Results of slip transfer through NEGBs

Slip transfer through the NEGBs is analyzed for \( \tau^{\text{ext}} \approx 500\, {\text{MPa}} \) and \( 320\,{\text{MPa}} \) in the \( {\Sigma }627 \) and \( {\Sigma }123 \) cases. Plasticity in the incoming grain is largely unaffected by the long-range fields of the NEGBs. Quantitatively, this is analyzed by comparing the dislocation densities (\( \rho_{\text{inc}} \)) and the shear strains (\( \gamma_{\text{inc}} \)) in the incoming grain for the EGB and NEGB cases. The \( \rho_{\text{inc}} \) and \( \gamma_{\text{inc}} \) evolution profiles are indistinguishable between the EGB and NEGB models (\( < 1\% \) average difference) for both \( {\Sigma }627 \) and \( {\Sigma }123 \) bicrystals.

The expanding dislocation loop transmits through the \( {\Sigma }627 \) GB via the reaction in Eq. (2). Figure 9a shows the \( \rho_{\text{trans}} \) profile for the \( {\Sigma }627 \) NEGB simulation compared with the EGB case. The \( \rho_{\text{trans}} \) profiles show only minor differences, such as the density being slightly higher in the NEGB simulation. Consequently, the evolution of the plastic activity in the outgoing grains is similar. However, locally, the transmission process is observed to be uniquely influenced by the presence of WDD-EGBD complexes in the NEGB. Snapshots of the events occurring during the NEGB transmission simulation are shown in Fig. 9b for the \( {\Sigma }627 \) GB. The dislocation lines are superimposed on maps of and obtained by resolving the GB stresses on \( s_{\text{inc}} \) and \( s_{\text{trans}} \). In general, transmission nuclei are initially formed in regions of favorable GB stresses, similar to the EGB case. However, the modified screening characteristics of the GB defects generates positive hotspots near the WDD-EGBD complexes. Accordingly, the nuclei in the vicinity of the WDD-EGBD complexes are consistently observed to grow, indicating that the disrupted GB sites aid slip transfer in this particular case.

Figure 9
figure 9

(a) Comparison of the \( \rho_{\text{trans}} \) evolution profiles for the equilibrium and non-equilibrium \( {\Sigma }627 \) GBs at \( \tau^{\text{ext}} \approx 500\,{\text{MPa}} \). (b) Snapshots of the dislocation transmission events occurring during the NEGB simulation for the \( {\Sigma }627 \) GB. The dislocation lines on \( s_{\text{inc}} \) (white) and \( s_{\text{trans}} \) (green) are superimposed on maps of the GB shear stresses resolved on the respective slip systems in grain 2 ( ) and grain 1 ( ) . The scale bar is rescaled to highlight the long-range stresses induced by the WDD-EGBD complexes at the GB.

Full size image

To further quantify the differences in the slip transmission response for the equilibrium and disrupted GB states, the minimum value of the externally applied resolved shear stress \( \left( \tau_{\text{min}}^{\text{ext}} \right) \) necessary for growth and propagation of the transmission nuclei on \( s_{\text{trans}} \) is determined. For the \( {\Sigma }627 \) GB, the values of \( (\tau_{\text{min}}^{\text{ext}}) \) for the EGB and NEGB models are \( \sim 475\,{\text{MPa}} \) and \( \sim 465 \,{\text{MPa}} \), respectively, indicating that transmission can propagate at a lower external stress state in the disrupted GB relative to the EGB case. This difference in \( ( \tau_{\text{min}}^{\text{ext}} ) \) for the two cases can be understood in terms of the difference in the maximum (positive) values of and \( \tau_{\text{trans}}^{\Delta } \) at distance of \( 10 \,{\text{nm}} \) away from the GB in the outgoing grain, and within a \( 50 \,{\text{nm}} \) region along the GB (\( {\mathbf{e}}_{2} \)-direction) centered about the propagating transmission nuclei. For the EGB model, the maximum value of \( \tau_{\text{trans}}^{\Delta } \) is constant. However, for the NEGB case, the GB stress field is amplified in the transmission location \( (26.32 \,{\text{nm}} \) away from a WDD-EGBD complex) with maximum value of measured to be \( 6.82 \,{\text{MPa}} \) greater than the corresponding value of \( \tau_{\text{trans}}^{\Delta } \). Thus, the WDD-EGBD complex plays a role in assisting the growth of the transmission nuclei, even when the transmission event does not occur precisely at the disrupted location.

Transmission through the \( {\Sigma }123 \) NEGB occurs according to Eq. (3) and the evolution of \( \rho_{\text{trans}} \) is similar to the EGB case, as shown in Fig. S1a. However, the transmission pathway is altered compared to the EGB case. Figure S1b shows snapshots of the transmission process during the simulation. The modified screening of the GB defects results in amplified negative regions near the WDD-EGBD complexes and the transmission nuclei in the neighborhood of the WDD-EGBD complexes are observed to grow in some cases. The values of \( \tau_{\text {min} }^{\text{ext}} \) for the EGB and NEGB models are \( \sim 310\,{\text{MPa}} \) and \( \sim 312 \,{\text{MPa}} \), respectively. Apparently, the influence of the extrinsic defect complexes on slip transfer is not significant in this simulation. The and \( \tau_{\text{trans}}^{\Delta } \) profiles in the corresponding probe regions, where the nuclei evolve, are nearly identical. This is likely due to the small magnitude of extrinsic Burgers added to the equilibrium wedge dipoles, which results in less significant changes to the GB stress fields compared to the \( {\Sigma }627 \) GB. Moreover, the absence of clear hotspots renders it difficult to pinpoint the exact influence of the disrupted sites on slip transfer. Nevertheless, the WDD-EGBD complexes in the disrupted boundary clearly modify the transmission pathway, similar to the \( {\Sigma }627 \) GB.

In both GB models, residual dislocations are deposited on the interface and glide with slip characteristics similar to those described for the EGB. Comparison of the \( \rho_{\text{int}} \) curves for the NEGB and EGB simulations reveals minor differences. The average differences in \( \rho_{\text{int}} \) are determined to be \( \sim 14\% \) and \( \sim 5\% \) for the \( {\Sigma }627 \) and \( {\Sigma }123 \) bicrystals, respectively. Ultimately, the preceding results demonstrate that changing the equilibrium structure of GBs can influence the slip transfer pathway and provide preferential sites for slip propagation for some configurations. For the \( \rho_{\text{EGBD}} \) values considered in this study, the minimum external stress required for transmission through the \( {\Sigma }627 \) NEGB is lower compared to its equilibrium counterpart. This implies that increasing \( \rho_{\text{EGBD}} \), through additional dislocation transmission, could further lower the driving stress required for slip transfer. A more systematic investigation of this hypothesis is warranted in future work.

Conclusions

In this study, advancements to the DDD method are presented for simulating intergranular plasticity considering the mechanical structure of GBs. These developments are leveraged to investigate the influence of intergranular stresses induced by grain boundaries on dislocation slip transmission. The stress fields of equilibrium STGBs are constructed using the DSUM framework, while disrupted GBs are modeled as walls of WDDs and WDD-EGBD complexes, using the incorporation model. Slip transmission simulations, which are performed using an algorithm based on a combination of LRB and plastic dissipation criteria, reveal that GB stresses play an important role in determining the slip transmission pathway. Summarizing, the GB stress fields provide periodically favorable transmission sites, which are not present in geometric GB models. The GB stress fields can modify the growth of the transmission nuclei influencing plasticity in the transmission grain. The evolution of the residual dislocation configurations on the interface is complicated and is strongly governed by the GB stresses. In the case of NEGBs, slip transfer simulations suggest that certain non-equilibrium states can provide preferential sites for slip propagation, characterized by amplified driving stresses. The amplified driving stresses lower the minimum external shear stress needed for slip transfer.

The models presented here employ simplifications and various approximations, with scope for improvement. First, the stress state of EGBs is computed using isotropic linear elasticity and the infinitesimal deformation approximation should be validated against atomistic calculations. A numerical cut-off parameter is used to remove singularities in the stress fields of GB defects. Changes to this cut-off parameter can alter the magnitudes of the local GB stresses, which can influence the formation and growth of transmission nuclei and the residual dislocation configurations. Second, the framework does not precisely consider the accommodation of extrinsic dislocations with in-plane Burgers vectors and dynamic stress relaxation mechanisms that can occur within GBs. Experimental studies on the accommodation of extrinsic dislocations in vicinal and general GBs in FCC Ni and Cu have highlighted that the incorporation model can operate during intergranular plastic deformation; however, reorganization pathways of EGBDs can be more complex than that predicted by the original model [16, 92,93,94,95,96,97]. Finally, the mobility of residual dislocations on the GB plane should be calibrated using atomistic simulations to accurately characterize their role on plasticity at the interface.

Despite these approximations, this work presents several novel perspectives and conclusions on modeling polycrystalline plasticity at the mesoscale. First, this study provides a framework for including equilibrium and non-equilibrium stress fields in DDD using structural defect arrangements characteristic of the GBs. The incorporation model is used in DDD for the first time to describe NEGBs composed of arrays of WDDs and WDD-EGBD complexes. Moreover, simulations clearly show that including a mechanical description of the GBs results in plastic behavior distinct from models using only geometric approximations. This work also highlights the role of residual dislocation evolution on plastic activity at the GB, which warrants further investigation. In the future, the framework should be calibrated using atomistic simulation data, which can be used to derive quantitative metrics, such as the stress barriers for slip transmission. Conceivably, the approach can also be coupled with the recently developed generalized discrete defect dynamics framework [98] to consider dynamic descriptions of GB structure.

Methodology

The conventional DDD framework detailed in Refs. [99,100,101,102]. is used in this study. Briefly, dislocations are explicitly modeled by discretizing the dislocation lines into segments connected via nodes. The motion of the nodes under thermo-mechanical driving forces is simulated to evolve the dislocation configuration. The total force per unit length \( {\mathbf{f}}\left( {\mathbf{r}} \right) \) acting at any point \( {\mathbf{r}} \) along the dislocation core is obtained via the Peach–Koehler expression,

$$ \begin{array}{*{20}c} {{\mathbf{f}}\left( {\mathbf{r}} \right) = \left( {\varvec{\sigma}^{\text{total}} \left( {\mathbf{r}} \right) \cdot {\mathbf{b}}} \right) \times {\mathbf{t}},} \\ \end{array} $$
(6)

where, \( \varvec{\sigma}^{\text{total}} \left( {\mathbf{r}} \right) \) is the total stress acting at point \( {\mathbf{r}} \), \( {\mathbf{b}} \) is the Burgers vector of the dislocation, and \( {\mathbf{t}} \) is the local line tangent. The resolved shear stress \( \tau \), due to \( \varvec{\sigma}^{\text{total}} \), acting on the dislocation is \( \tau = \frac{1}{{\mathbf{b}}}\left[ {{\mathbf{f}}\left( {\mathbf{r}} \right) \cdot \left( {{\mathbf{n}} \times {\mathbf{t}}} \right)} \right] \), where \( {\mathbf{n}} \) is the glide plane normal. Broadly, the total stress \( \varvec{\sigma}^{\text{total}} \left( {\mathbf{r}} \right) \) includes internal stresses \( \varvec{\sigma}^{\text{int}} \left( {\mathbf{r}} \right) \) induced by the presence of other defects, lattice friction stress \( \varvec{\sigma}^{\text{fric}} \left( {\mathbf{r}} \right) \), and external stress \( \varvec{\sigma}^{\text{ext}} \left( {\mathbf{r}} \right) \) due to applied loads, which is homogenized across the simulation volume. Once the forces acting on the dislocation nodes are determined, the velocities of the nodes can be obtained by solving equations of motion to evolve the dislocation network.

In this work, this framework is advanced by including mechanical descriptions of interfacial defects and an algorithm for transmission of dislocations across grains. In particular, the isotropic stress field solutions for infinitely long WDDs and WDD-EGBD complexes are included, which are used to model EGBs and NEGBs. Thus, the internal stress \( \varvec{\sigma}^{\text{int}} \left( {\mathbf{r}} \right) \) is the superposition of elastic stresses due a wall of WDDs \( \left( {\varvec{\sigma}^{\Delta } \left( {\mathbf{r}} \right)} \right) \) in EGBs or an array of WDDs and WDD-EGBD complexes in NEGBs, in addition to other dislocations \( \left( {\varvec{\sigma}^{ \bot } \left( {\mathbf{r}} \right)} \right) \) in the sample. These additional contributions will influence the forces \( {\mathbf{f}} \), and consequently the dynamics of dislocations. Details pertaining to the implementation of the stress fields \( \varvec{\sigma}^{\Delta } \) and are discussed in the Framework for Modeling Equilibrium and Non-equilibrium Grain Boundaries section. The non-singular isotropic formulation of Cai et al. [103] is used for the stress field of dislocations.

Simulation setup

A cuboidal simulation cell, shown schematically in Fig. S2, with one grain sandwiched between two identical grains is used to model bicrystals. Periodic boundary conditions are applied in all directions. In order to create STGBs with the \( \left[ {110} \right] \) misorientation axis and a specific misorientation relationship between the grains, the individual grains are first oriented such that the \( \left[ {110} \right] \), \( \left[ {\bar{1}10} \right] \), and \( \left[ {001} \right] \) crystallographic directions, are aligned with the laboratory \( {\mathbf{e}}_{1} \), \( {\mathbf{e}}_{2} \), and \( {\mathbf{e}}_{3} \) axes in all three layers, then the interface misorientation is created by a symmetric rotation \( \left( { \pm \frac{\theta }{2}} \right) \) about the \( \left[ {110} \right] \) axis. The \( {\Sigma }627 \left( {\bar{7}\,7\, 3\,4} \right)/\theta = 32.47^{ \circ } \) and \( {\Sigma }123 \left( {\bar{5}\,5\, 1\,4} \right)/\theta = 53.60^{ \circ } \) STGBs are used in this work. Without a description of the GB stress field, this model is referred to as the “geometric GB” model. As both the STGBs are non-favored, their stress fields can be included conveniently using DSUM to construct EGBs and NEGBs [72]. Note, the characteristics of the disclination dipoles, such as dipole strength, arm length, and periodicity are considerably different for the two GBs, allowing the role of these differences on slip transmission to be explored.

The dimensions of the simulation cells are \( 6019.2a \times 6019.2a \times 5500a \) and \( 6088.5a \times 6088.5a \times 5500a \) for the \( {\Sigma }627 \) and \( {\Sigma }123 \) bicrystals, respectively. The simulation cell dimensions are chosen to ensure that box size-related effects, such as spurious dislocation annihilation and interference of long-range stresses are negligible. The grains are assumed to be elastically isotropic for simplicity. The values of the elastic constants and lattice friction stress derived from atomistic calculations in Al at 100 K [80] are used.

An elliptical dislocation shear loop with semi-major axis of \( 123.5a \) and semi-minor axis of \( 95a \) is introduced on the \( s_{\text{inc}} = \frac{1}{2}\left[ {\bar{1}10} \right]_{2} \left( {11\bar{1}} \right)_{2} \) slip system at the center of grain 2. The expansion of the loop is driven under a constant applied stress tensor, \( \varvec{\sigma}^{\text{ext}} \), of the form,

$$ \begin{array}{*{20}c} {\varvec{\sigma}^{\text{ext}} = \left[ {\begin{array}{*{20}c} {\sigma_{11} } & {\sigma_{12} } & {\sigma_{13} } \\ {} & 0 & 0 \\ {\text{Sym}} & {} & 0 \\ \end{array} } \right].} \\ \end{array} $$
(7)

The specific stress tensor is motivated by the following. According to the LRB criteria, which is used to predict the outgoing slip system in the transmission algorithm adopted in this work, the outgoing slip plane is chosen such that the angle \( \delta \) between the incoming and outgoing slip traces is minimized and the outgoing slip direction is chosen so as to minimize the magnitude of the residual Burgers vector (RBV) \( {\mathbf{b}}_{\text{res}} \) formed, and maximize the resolved shear stress \( \tau_{\text{trans}} \) driving the dislocation away from the GB. A preliminary analysis of the geometric LRB parameters (\( {{\delta }} \) and \( {\mathbf{b}}_{\text{res}} \)) for the 12 possible FCC slip systems in the outgoing grain for the \( {\Sigma }627 \) and \( {\Sigma }123 \) bicrystals reveals that coherent transmission is most likely to occur onto the slip system \( s_{\text{trans}} = \frac{1}{2}\left[ {\bar{1}01} \right]_{1} \left( {111} \right)_{1} \). By controlling the values of the non-zero components in \( \varvec{\sigma}^{\text{ext}} \), similar magnitudes of the resolved shear stress \( \tau^{\text{ext}} \) can be generated simultaneously on both \( s_{\text{inc}} \) and \( s_{\text{trans}} \). The value of \( \tau^{\text{ext}} \) on \( s_{\text{inc}} \) depends on \( \sigma_{12} \) and \( \sigma_{13} \), while the value of \( \tau^{\text{ext}} \) on \( s_{\text{trans}} \) is determined by all three non-zero components. For example, for the \( {\Sigma }627 \) geometry, when \( \sigma_{11} = - 450 \,{\text{MPa}} \), and \( \sigma_{12} = \sigma_{13} = 500\, {\text{MPa}} \), the resolved shear stresses are \( \tau_{\text{inc}}^{\text{ext}} = 506.10 \,{\text{MPa}} \) and \( \tau_{\text{trans}}^{\text{ext}} = 501.57 \,{\text{MPa}} \) on \( s_{\text{inc}} \) and \( s_{\text{trans}} \), respectively. To investigate transmission features under different applied loads, values of \( \tau^{\text{ext}} \approx 500 \) and \( 600 \,{\text{MPa}} \) are used for the \( {\Sigma }627 \) models and \( \tau^{\text{ext}} \approx 320 \) and \( 500 \,{\text{MPa}} \) are used for the \( {\Sigma }123 \) models. Based on the relative magnitudes of the two \( \tau^{\text{ext}} \) used for the \( {\Sigma }627 \) and \( {\Sigma }123 \) bicrystals, the simulations are categorized as low and high stress simulations. In the Analysis of Slip Transfer through Nonequilibrium GBs section, the minimum value of the resolved shear stress on \( s_{\text{trans}} \) \(( \tau_{\text{min}}^{\text{ext}} )\), which leads to slip propagation in the outgoing grain, is determined by incrementally changing the values of \( \sigma_{11} \), while keeping the values of \( \sigma_{12} \) and \( \sigma_{13} \) fixed.

The mobility of lattice dislocations is modeled using the atomistically-derived dislocation character-angle dependent mobility functions introduced by Dang et al. [104]. Mobility laws for \( 0^{ \circ } \) (screw), \( 30^{ \circ } \), \( 60^{ \circ } \), and \( 90^{ \circ } \) (edge) dislocations, accounting for linear phonon damping and non-linear radiative damping mechanisms, are used. The mobility parameters of dislocations with intermediate character angles are estimated using a linear interpolation scheme. During coherent transmission through both GBs, residual dislocations with Burgers \( {\mathbf{b}}_{\text{res}} \) are deposited on the interface. The dynamics of residual dislocations is treated similar to the work of Cho et al. [45]. The specifics of this implementation are discussed next.

Slip transmission algorithm

The details of the slip transmission algorithm introduced by Bertin [105] and subsequent advancements to the algorithm are described here. For simplicity, it is assumed that all dislocations impinging on GBs can transmit provided the governing slip transmission criteria are satisfied. First, dislocation nodes that can cross the GB (with normal \( {\mathbf{n}}_{\text{int}} \)), based on their velocity vectors, are stopped and positioned at the interface. Then, the LRB slip transmission criteria are utilized to predict the most favorable slip system \( s_{\text{trans}} \) in the transmitted grain [5, 70]. The LRB criteria captures the essential energetics of slip transmission using geometric and driving stress criteria [7]. Specifically, for a given incoming slip system \( s_{\text{inc}} \) with slip plane normal \( {\mathbf{n}}_{\text{inc}} \) and Burgers vector \( {\mathbf{b}}_{\text{inc}} \), the misorientation \( \delta = \arccos \left( {{\hat{\mathbf{L}}}_{\text{inc}} \cdot {\hat{\mathbf{L}}}_{\text{trans}} } \right) \) is computed between the incoming and different possible outgoing slip traces \( {\hat{\mathbf{L}}}_{\text{inc}} = \frac{{{\mathbf{n}}_{\text{inc}} \times {\mathbf{n}}_{\text{int}} }}{{\left\| {{\mathbf{n}}_{\text{inc}} \times {\mathbf{n}}_{\text{int}} } \right\|}} \) and \( {\hat{\mathbf{L}}}_{\text{trans}} = \frac{{{\mathbf{n}}_{\text{trans}} \times {\mathbf{n}}_{\text{int}} }}{{\left\| {{\mathbf{n}}_{\text{trans}} \times {\mathbf{n}}_{\text{int}} } \right\|}} \), respectively. Then, the magnitude of the residual Burgers vector \( {\mathbf{b}}_{\text{res}} = {\mathbf{b}}_{\text{inc}} - {\mathbf{b}}_{\text{trans}} \), where \( {\mathbf{b}}_{\text{inc}} \) and \( {\mathbf{b}}_{\text{trans}} \) are compared in the same coordinate system, is calculated for the incoming and different possible outgoing slip directions. Following this, the resolved shear stress is determined for all possible transmission systems. The transmission slip systems are ranked according to increasing magnitudes of \( \delta \) and \( \left\| {{\mathbf{b}}_{\text{res}} } \right\| \) and decreasing magnitude of the resolved shear stress. The slip system with the lowest mean rank is chosen as the preferred transmission slip system \( s_{\text{trans}} \). This scheme is equivalent to simultaneously minimizing the misorientation between the incoming and outgoing slip traces, the magnitude of the residual Burgers vector, and maximizing the resolved shear stress on the outgoing slip system. Collectively, the LRB criteria ensure that dislocation transmission results in the minimum increase in elastic energy and maximum dissipation.

Next, if a favorable transmission system \( s_{\text{trans}} \) is found, a trial transmission configuration is constructed in the outgoing grain and tested for favorable plastic dissipation. The nodes at the interface are moved onto \( s_{\text{trans}} \) by a distance that is computed from the velocities of the nodes projected along the outgoing direction. For coherent transmission, residual dislocations with Burgers vector \( {\mathbf{b}}_{\text{res}} \) are inserted along the interface during the construction of the trial configuration. Then, the forces \( {\mathbf{f}} \) and velocities \( {\mathbf{v}} \) on the nodes in the transmission configuration are computed to check the feasibility of the transmission event. The transmission configuration is deemed energetically favorable if the driving forces and velocities lead to motion away from the GB. In this case, the trial configuration is retained, and the end nodes are merged with previously transmitted dislocations in the neighborhood of the new transmission nucleus. The residual dislocations are also merged accordingly. This ensures continuity of dislocation lines across the GB. However, if \( {\mathbf{f}} \) and \( {\mathbf{v}} \) drive the transmitted configuration back towards the interface, transmission is deemed unfavorable and the nodes are restored to their original positions at the interface. This criterion ensures that the transmission events lead to favorable plastic dissipation. Moreover, according to this algorithm, portions of the impinging dislocations can be transmitted across the GB depending on the local conditions. Thus, the influence of the local stress state on transmission events is explicitly included in this framework. When equilibrium and non-equilibrium GBs are considered, the contributions to the internal stresses due to GB structural defects will modify the forces \( {\mathbf{f}} \) (and thus, \( {\mathbf{v}} \)), affecting the dissipation of transmitted dislocations, which is expected to influence slip transfer into the transmission grain.

The motion of the residual dislocations on the interface is handled according to the following mobility scheme. The nodal velocities \( {\mathbf{v}} \) of the residual dislocations are assumed to be related to the driving forces (per unit length) \( {\mathbf{f}} \) via a linear overdamped equation of motion (EOM),

(8)

In Eq. (8), refers to the constant-valued phonon drag coefficients that are dependent on the dislocation character angle \( \theta \) and \( \varvec{I} \) is the second-order identity tensor. In this work, the values of for Al are determined by scaling the phonon drag coefficients for lattice dislocations reported by Dang and co-workers [104] according to,

(9)

where \( \left\| {{\mathbf{b}}_{\text{lattice}} } \right\| \) corresponds to the magnitude of the Burgers vector for lattice dislocations. Thus, the drag resistance is proportional to (or the dislocation mobility is inversely proportional to) the magnitude of the RBV. As the residual dislocations are constrained to glide on the interface, only the projection of the velocity on the GB plane is considered in updating the positions of the nodes on the interface. For simplicity, it is assumed that residual dislocations with \( {\mathbf{b}}_{\text{res}} \) containing a normal (out-of-plane) component can glide freely with kinetics that are accommodated by local GB diffusion processes [10].