INTRODUCTION

Human metabolic processes undergo continuous changes during the growth and maturation stages (1, 2). It is generally accepted that human physiological and metabolic parameters (Y) do not scale linearly with bodyweight (W) but scale with a power-law function, in the form of Y = aWb, where a and b are constants. This simple allometric equation is linear in a double logarithmic plot (i.e., log Y vs. log W), which has been used to describe datasets of basal metabolic rate (BMR), glomerular filtration rate (GFR), and drug clearance (CL) (3, 4). However, if data from neonates and adults were pooled for analysis, the resulting plots are usually curved with a steeper early phase, followed by a shallower later phase (3, 5,6,7). Accordingly, simple allometry with a fixed exponent, or with a specific exponent obtained from the adult data, would systematically overestimate GFR or CL values among the youngest (3, 7, 8). In the biology field, extensive studies have shown that the metabolic pace of animals or plants shifts at certain points of organism’s life; such shifting exhibits multiple linear phases connected at one or more transitional points in log–log size-scaling plots (9,10,11,12,13). The metabolic shifting phenomenon has long been recognized in human (5), and the quest for a general quantitative model has never ceased (8, 14,15,16,17). Thus, the current study addresses the feasibility of using one unified, empirical equation, where bodyweight is the only independent variable, to quantitatively describe the maturation of human physiological and metabolic functions.

The basal metabolic rate (BMR), i.e., the rate of energy transformation within the body at rest, is perhaps the most fundamental biological rate. BMR is considered as a universal “pacemaker” for biological processes (11). Therefore, allometric scaling of BMR has gained much attention and been hotly debated for over a century. In biology, the discussion has been shifted from whether there is a universal scaling law to how intra- and interspecific scaling vary beyond the “3/4-power” law (10). In medicine, human energy requirements are important considerations in clinical and public health nutrition (4, 18,19,20,21,22). Thus, the WHO issues sex- and age-specific recommendations on human energy requirements (23). The WHO recommendations consist, for each sex, of 3 bodyweight-based linear equations for estimating BMR. The equations have different constant values for separate age groups (0–3 years, 4–10 years, and 11–18 years), suggesting that BMR varies with bodyweight in a nonlinear manner during the growth period. To date, the inherent nonlinearity in human metabolic scaling remains to be addressed by a unified quantitative model.

Glomerular filtration rate (GFR) is an important parameter of renal function. In pharmacology and toxicology, GFR determines the renal elimination capacity for xenobiotics and environmental toxicants. The information of GFR is particularly useful for dosing renally cleared drugs, especially for pediatric patients, because dosing information for children is often limited by ethical and clinical considerations in clinical trials. Accordingly, attempts have been made to predict pediatric GFR values from adult’s value using quantitative models (7). Existing data show that GFR undergoes continuous change after birth and reaches adult’s level in the early childhood (7, 24). Several models have been proposed to model the growth and maturation of GFR, with a focus on predicting GFR for neonates or children from adults (6, 7). The previous models have different levels of complexity. The simplest model has the form of simple allometry, where GFR scales with bodyweight in a single power-law function, with either fixed or variable exponents (6). More complicated models include both age and bodyweight as the input variables (7, 24). The prediction models are useful for predicting population mean values but not for individual prediction (6).

Drug clearance (CL) is an essential pharmacokinetic parameter that offers direct estimation of drug dose. The acquisition of accurate CL information is critical in drug development and in drug therapy. However, the pediatric CL data are less attainable, because of the limitation of conducting clinical trials in young subjects. Thus, various prediction models have been proposed to draw quantitative relationship between CL and age and/or bodyweight (3, 8, 25,26,27). The magnitude of CL is correlated with body size and determined by the function of drug elimination organs (i.e., the kidneys and liver). Therefore, CL values are subjected to changes of renal and hepatic functions during maturation and growth. The CL values of many drugs have been compiled from both population pharmacokinetic studies and physiologically based pharmacokinetic (PBPK) modeling (8, 28,29,30,31,32). Besides, several growth and maturation models have been evaluated for their predictive performance (17, 30, 33,34,35). Overall, the previous findings are highlighted as follows: first, CL scales with bodyweight raised to a power that is variable with age or body weight (16, 28, 30). Second, more profound changes were observed in earlier life than in later life (e.g., neonates to toddlers vs. toddlers to adolescents or adults) (28, 30). Finally, a quantitative birth-to-adulthood model usually includes both age and bodyweight as the independent variables (7, 8, 15, 31, 36, 37), although, for some drugs and in particular age groups, e.g., in younger aged children, clearance can be scaled with bodyweight alone (3, 8, 30, 38,39,40).

Taken together, human BMR, GFR, and CL values seemed to share similar rate-switching features during the human maturation and growth processes. The aim of this study is to evaluate a continuous, single, bodyweight-only equation for its potential as a unified empirical model for scaling human BMR, GFR, and CL from neonates to adults. The equation is in the form of reciprocal sum of two power-law functions of bodyweight with 4 parameters (so-called mixed-allometry or mixed-power-law equation). All the datasets evaluated in this study were either directly retrieved from the literature or generated from existing age- and bodyweight equations with published parameters. The datasets thus represent the tendency of each specific dependent variable of interest (BMR, GFR, or CL), and the overall goal is not to predict the unknown, but to infer common quantitative understanding from analysis of diverse datasets.

METHODS

BMR Datasets

The basal metabolic rate (BMR) data, in kcal/day, for males and females from birth to adulthood were obtained from the historical database compiled by Schofield (41). The BMR data in MJ/day was converted to kcal/day. The database included BMR data for 4811 males (0.02–52.3 years, 2.7–108.9 kg) and 2364 females (0.14–64 years, 2.0–96.4 kg). The data are listed according to divided bodyweight groups (separated by 1 kg up to ~100 kg). The majority of groups contain >5 subjects (up to 189 subjects).

GFR Dataset

The glomerular filtration rate (GFR) data, in mL/min, were generated using the general equation proposed by the research group of Anderson (24, 37, 42) for hypothetical human subjects:

$$P=P_{adult}\cdot F_{age}\cdot F_{size}$$
(1)

where here P is GFR and Padult is the adult GFR value (136 mL/min (7)), Fage is the age function (maturation function), and Fsize is the body size function (allometric function):

$$F_{age}=\frac{PMA^\theta}{\left({TM}_{50}\right)^\theta+{PMA}^\theta}$$
(2)
$$F_{size}=\left(\frac W{W_{adult}}\right)^\mu$$
(3)

The variables and parameters are defined as PMA, postmenstrual age (weeks); θ, the Hill coefficient; TM50, maturation half-life; W, bodyweight of the individual; Wadult, adult bodyweight (70 kg); and μ, allometric, bodyweight exponent.

The GFR dataset was generated for a hypothetical population from 0 to 20 years of postnatal age. The age–bodyweight information was mainly obtained from Annex 2 in ref. (43). Additional age–bodyweight data for infants < 0.25 years were retrieved from ref. (7). A total of 26 age groups were included for the simulation: 0, 0.083, 0.167, 0.25, 0.5, 0.75, 1, 1.5, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, and 20 years. The mean bodyweight for each age group was either directly retrieved from the reported mean values (7) or estimated from the reported median values (43). Assuming lognormal distribution (44, 45), the median (μ*) was transformed to mean (μ) using the following formula (46): μ = ln μ∗. The standard deviation (σ) of lognormal distribution was estimated as \(\sigma =\sqrt{\ln \left({CV}^2+1\right)}\), where CV is the arithmetic coefficient of variation (47). For each age group, the bodyweight was randomly generated using the age-specific μ and σ, assuming CV = 0.15 in a population (43). This sampling process was conducted using the built-in functions, RandomVariate and LogNormalDistribution, in Mathematica®. The postmenstrual ages (PMA) were calculated by adding a gestational age of 40 weeks (24) to the postnatal ages. The resulting (PMA, W) data were plugged into Equations 1–3 to generate expected GFR values, using the reported parameter values (24): θ = 3.4, TM50 = 47.7 weeks, μ = 0.75. To add variability to the GFR values, the lognormal distribution was assumed with CV = 0.2. For each age group, GFR values for 20 randomly selected subjects were simulated. The data for 26 age groups (a total of 520 data points) were pooled as the GFR dataset

Drug CL Datasets

The first CL datasets were retrieved from Björkman’s work (29) on physiologically based pharmacokinetic (PBPK) modeling for two drugs, theophylline and midazolam. The CL and bodyweight values of both sexes are directly available for neonates; children ages 0.5, 1, 2, 5, 10, and 15 years; and adults. The total CL values were estimated from PBPK-modeled hepatic CL and/or renal CL (if applicable). These CL datasets were evaluated in the initial modeling trial for drug CL.

Next, the extended modeling was applied to CL datasets of 17 drugs, which have been previously modeled using the growth and maturation model of Anderson et al. (15, 37, 42); the model parameters were directly available from the literature (15). The CL values were generated using the same general models, as described in Equations 1–3, where P and Padult are replaced by CL and CLadult. All the drug-specific parameters in the age function (Equation 2) and size function (Equation 3) were taken from the literature (15). For each drug, the CL values with random errors were generated for 26 age groups (each of 20 subjects). The procedure to generate the CL values with random errors was the same as that described above for GFR.

Finally, individual experimental data were retrieved from two pharmacokinetic studies of cefetamet in pediatric patients (48, 49). The first study included 20 infants of 0.19 to 1.44 years (48). The second study included 18 children (3 to 12 years). The adult data (50, 51) were also included to complete the cefetamet dataset.

Model Fitting and Validation

In this study, the following mixed-power equation was proposed to model the datasets mentioned above.

$$\frac1P=\frac1{A\cdot W^\alpha}+\frac1{B\cdot W^\beta}$$
(4)

or

$$P=\left(\frac1{A\cdot W^\alpha}+\frac1{B\cdot W^\beta}\right)^{-1}$$
(5)

where P is the metabolic or physiological quantity of interest, viz., BMR, GFR, or drug CL. The equation consists of two allometric coefficients (0 < A < B) and two allometric exponents (α > β > 0). For model comparison, the simple allometric model was also included for analysis:

$$P=G{W}^{\gamma }$$
(6)

where G and γ are the allometric coefficient and exponent, respectively.

Model fitting was performed using the nonlinear regression function (NonlinearModelFit) in Mathematica® (Wolfram). The model parameters were obtained by fitting the model equations to all available datasets (with suitable weighting functions, e.g., 1/y2). The comparison of the biphasic allometry (BA) model with the simple allometry (SA) model was based on the Akaike’s information criterion (AIC). Besides, the model fitting was validated using multiple measures, including residual plots, R2, and t statistic for the fitted parameters.

Estimation of the Characteristic Values

The biphasic model is characterized by continuous change of slope in the log P vs. log W plot. The weight-dependent slope (S) of the fitted biphasic curve was generated using the following equation (see Appendix for the derivation):

$$S=\alpha\left(\frac{B\cdot W^\beta}{A\cdot W^\alpha+B\cdot W^\beta}\right)+\beta\left(\frac{A\cdot W^\alpha}{A\cdot W^\alpha+B\cdot W^\beta}\right)$$
(7)

The biphasic growth and maturation curve switches at a characteristic bodyweight (i.e., the bodyweight at the phase transition, \(\widetilde w\)), which was calculated using the following expression (Appendix).

$$\widetilde w=\left(B/A\right)^{1/\left(\alpha-\beta\right)}$$
(8)

The characteristic slope (S*) at the phase transition bodyweight was calculated as the sum of the allometric exponents (Appendix), i.e.,

$${S}^{\ast }=\left(\alpha +\beta \right)/2$$
(9)

Dimensionless Analysis

To conduct a dimensionless analysis, Equation 4 is treated as follows. First, let \(X=W/\widetilde w\), where W is the exact bodyweight and \(\overset{\sim }{w}\) represents the critical bodyweight at the phase transition. Thus, X is the dimensionless, fractional number associated with bodyweight. Similarly, let \(Y=P/\overset{\sim }{p}\), where P is physiological parameters such as BMR and GFR or CL and \(\overset{\sim }{p}\) is the corresponding P value at W =\(\overset{\sim }{w}\), and according to Equation 4,

$$\frac{1}{\overset{\sim }{p}}=\frac{1}{A{\overset{\sim }{w}}^{\alpha }}+\frac{1}{B{\overset{\sim }{w}}^{\beta }}$$
(10)

Accordingly, Y is defined as the fractional value of BMR, GFR, or CL (relative to their critical value at phase transition). Then, the original Equation 4 can be expressed and rearranged as follows:

$$\frac1{\widetilde pY}=\frac1{A\left(\widetilde wX\right)^\alpha}+\frac1{B\left(\widetilde wX\right)^\beta}$$
(11)
$$\frac1Y=\widetilde p\left(\frac1{A\left(\widetilde wX\right)^\alpha}+\frac1{B\left(\widetilde wX\right)^\beta}\right)$$
(12)

By substituting \(\overset{\sim }{p}\) in the last equation from Equation 10, and after further rearrangement, the final equation is obtained:

$$\frac{1}{Y}={f}_1\left(\frac{1}{X^{\alpha }}\right)+{f}_2\left(\frac{1}{X^{\beta }}\right)$$
(13)

Where

$${f}_1=\frac{B{\overset{\sim }{w}}^{\beta }}{A{\overset{\sim }{w}}^{\alpha }+B{\overset{\sim }{w}}^{\beta }}=\frac{1}{2}$$
(14)
$${f}_2=\frac{A{\overset{\sim }{w}}^{\alpha }}{A{\overset{\sim }{w}}^{\alpha }+B{\overset{\sim }{w}}^{\beta }}=\frac{1}{2}$$
(15)

Accordingly,

$$Y=2\left(\frac{X^\alpha\cdot X^\beta}{X^\alpha+X^\beta}\right)$$
(16)

The slope of the dimensionless biphasic-scaling curves (on a log–log plot) has the following form:

$$slope=\frac{d\ln Y}{d\ln X}=\alpha\left(\frac{X^\beta}{X^\alpha+X^\beta}\right)+\beta\left(\frac{X^\alpha}{X^\alpha+X^\beta}\right)$$
(17)

At X ≪ 1, the slope is approaching the asymptotic exponent, α, whereas at the other end (i.e., X ≫ 1) the slope is approaching another exponent, β. Since α > β, the slope continuously decreases as X increases. Thus, the decrease of slope (or “deceleration”) is expressed as

$$deceleration=\frac{dslope}{d\ln X}=-\left(\alpha-\beta\right)^2\left(\frac{X^\alpha}{X^\alpha+X^\beta}\right)\left(\frac{X^\beta}{X^\alpha+X^\beta}\right)$$
(18)

The deceleration equation—which always gives a negative value—quantifies the change (i.e., continuous slowing down) of pace in the growth and maturation process. In this study, different physiological and clearance datasets were harmonized using the derived dimensionless equations and the fitted parameter values for various datasets. Specifically, the dimensionless Y values were simulated using Equation 13 with input X values ranging from 0.1 to 10 (step of increment = 0.1). The corresponding slope and deceleration curves were generated using Equation 17 and Equation 18, respectively.

RESULTS

Scaling Basal Metabolic Rate

The biphasic allometry (BA) model and the simple allometry (SA) model were fitted to the Schofield’s historical dataset of BMR (41). Figure 1 shows the fitting results for the male and female datasets. The log BMR vs. log W plot (Fig. 1A and B) reveals curvature with two obvious phases. Thus, the mixed-power equation (the biphasic model) offers better fitting results with smaller AIC values than the simple allometry equation (Table I; Fig. 1A and B). Particularly, the SA model systematically overestimates the BMR values at W <10 kg but underestimates the values at the W range of 10 to 40 kg (Fig. 1C and D). The slope of the biphasic curve decreases with increasing bodyweight; at the extreme body sizes, the slope approaches the two asymptotic allometric exponents, α and β (Fig. 2). The first exponent is about 2, whereas the second exponent is near 0.3 or 0.4 (Table I). Accordingly, the first phase has a superlinear scaling relationship (slope >1), whereas the second phase scales sublinearly (slope <1). The two phases have a characteristic transition point at 5.5 kg and 6.6 kg, for males and females, respectively (Table I). Figure 2 highlights the phase transition as the body grows. The slope at the phase transition is the mean of the two asymptotic exponents (Equation 9) (male, 1.22, and female, 1.14).

Fig. 1.
figure 1

Bodyweight scaling of BMR datasets. BMR data were retrieved from Schofield’s historical database (41). A Comparison of model fittings for the male dataset. Solid line, biphasic model (Equation 4); dashed line, simple allometry model (Equation 6). B Comparison of model fittings for the female dataset. C The residual plots for the male data. Solid symbol, biphasic model; open symbol, simple allometry. D The residual plots for the female data

Full size image
Table I Model Fitting Results for Basal Metabolic Rate
Full size table
Fig. 2.
figure 2

The slope plots for the biphasic model. The changes of the slope on the log–log biphasic plots of the BMR datasets were quantified using Equation 7. The slopes for the males (dashed line) and females (solid line) have a sharp turnaround around 6 kg. The shaded area highlights the transition of the two phases

Full size image

Scaling the Glomerular Filtration Rate (GFR)

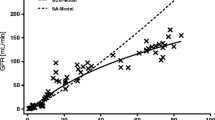
To demonstrate whether the proposed biphasic model could also be applied for scaling GFR, the (GFR, W) data were simulated for a hypothetical population with 26 age groups. In each group, the bodyweight for 20 subjects was randomly sampled from a lognormal distribution with transformed population mean and estimated standard deviation. The GFR values with random errors (CV = 20%) were generated according to Equations 1–3 and using reported parameter values (24), assuming lognormal distribution. The data of all age groups were pooled and then fitted to the biphasic mixed-power equation. Figure 3 shows again a biphasic log–log profiles. The fitted parameter values are A = 0.38 ± 0.07, α = 2.18 ± 0.15, B = 14.0 ± 3.5, β = 0.50 ± 0.06. The result is consistent with a superlinear scaling phase (slope >1) and a sublinear scaling phase (slope < 1). The scaling slope decreases with increasing bodyweight (Fig. 3A). The phase transition occurs at 8.6 kg, and the slope at the transition is 1.34. The simple allometry model overestimates GFR, again, at W < 10 kg (Fig. 3B and D). Overall, the biphasic model provides better fit with lower AIC (3774 vs. 4294) and more randomly scattered residuals (Fig. 3C).

Fig. 3.
figure 3

Bodyweight scaling of model simulated GFR. GFR values with random errors (symbol) for 26 age groups (20 datapoints for each group) were simulated using the growth and maturation model of Andersen et al. (Equations 1–3). A The log–log plot for (GFR, W) and the slope plot. The solid line represents the nonlinear best-fit for the biphasic model (Equation 4). The dashed line is a weight-dependent slope of the fitted curve (Equation 7). B The residual plot for the biphasic model. C The same data were fitted to the simple allometry model (Equation 6). D The residual plot for the simple allometry model

Full size image

Scaling Drug Clearance

Three types of drug clearance data were included for analysis. First, the proposed biphasic model was fitted to the cross-age CL data for theophylline (Fig. 4A and B) and midazolam (Fig. 4C and D), which were taken directly from a PBPK modeling study (29). The datapoints are scarcely distributed in the bodyweight range spanning neonates and adults. Nevertheless, compared with simple allometry (based on AIC and residual plots), the biphasic allometry model provides better fitting results (Table II). Again, the features of the biphasic model (i.e., 2 phases with defined phase transition) were clearly illustrated in this analysis. The two drugs have high first-phase exponents (ca. 2.6 to 3) and comparable—but less than unity—second-phase exponents (ca. 0.5 to 0.6). The results also show superlinear allometry in the early childhood and sublinear allometry in the later life. The transition occurs at 8.6 to 9.5 kg, with the corresponding slope values (S*) close to 1.6 and 1.8, for theophylline and midazolam, respectively (Table II).

Fig. 4.
figure 4

Bodyweight scaling of drug clearance. The log CL vs. log W plots and the slope plots for theophylline (A and B) and midazolam CL (C and D). Symbols are PBPK-modeled CL values directly taken from the literature (29). Lines are the best nonlinear regression fits for the biphasic model

Full size image
Table II Model Fitting Results for Theophylline and Midazolam Clearance
Full size table

Secondly, the analysis was extended to 17 drugs whose ontogeny CL data have been previously modeled using the sigmoid Emax maturation model. All the model parameters, including the maturation half-life (TM50) and the slope (Hill) coefficient, were summarized in the review article of Holford, Heo, and Anderson (15). To generate the ontogeny CL values for each drug, the drug-specific parameters were directly retrieved and plugged into the growth and maturation model (i.e., Equations 1–3, where the variable P is CL). Specifically, the CL values with random errors for 26 age groups (20 subjects/group) were simulated using the same approach described for the GFR dataset. For each drug, the population pooled (CL, W) data were then fitted to the biphasic model (Equation 4) and the simple allometry model (Equation 6). Note that the model used for generating the CL datasets is independent of the biphasic model used for model fitting.

The 17 drugs belong to 8 therapeutic categories, including antiviral agents (acyclovir, lamivudine, penciclovir), antineoplastic agents (busulfan), anticonvulsants (levetiracetam), analgesics (acetaminophen, morphine, valdecoxib), anesthetics (dexmedetomidine, levobupivacaine, propofol, midazolam, ropivacaine), antibacterial agents (vancomycin), anti-ulcer agents (pantoprazole), and antimalarials (pyrimethamine, sulfadoxine), The pharmacokinetic properties are diverse, covering drugs that are either mainly eliminated by metabolic pathways (e.g., morphine, midazolam) or by renal excretion (e.g., lamivudine, vancomycin). Moreover, while some drugs have very low adult clearance values (e.g., 0.04 L/h for sulfadoxine and 1.44 L/h for pyrimethamine), drugs such as morphine and propofol have adult CL values >100 L/h.

Table III summarizes all fitted parameters. Compared with simple allometry, biphasic allometry fits better, with universally lower AIC values (Table III). The allometric coefficients (A and B) are highly variable among drugs, because the absolute CL values span >3 orders of magnitude. However, the allometric exponents have a narrow distribution: the first exponent (α) ranges from 1.51 to 3.67 (mean = 2.36; CV = 26%), whereas the second exponent (β) is in the range of 0.40 to 0.67 (mean = 0.55, CV = 14%). The mean transitional weight is 10.0 ± 4.9 kg (range = 3.64 to 20.4 kg, CV = 49%). The mean transitional slope (S*) is 1.46 ± 0.32 (range = 1.0 to 2.0; CV = 22%). The results reveal consistent biphasic bodyweight scaling with superlinear-to-sublinear phase transition. Moreover, although the drugs are highly variable in terms of elimination pathways and the magnitude of CL value, the characteristic slope of the second phase (i.e., β) is nearly homogenous among different drugs with a CV of 14%.

Table III Fitted and Estimated Parameters for Drug CL Datasets
Full size table

Since the bodyweight at the phase transition has a wider distribution, the 17 drugs were further divided into three groups (Figs. 5, 6 and 7). The bodyweight at the phase transition is around 15 kg for the group I drugs, 10 kg for the group II drugs, and < 5 kg for the group III drugs. The grouping enables visualization and comparison of all 17 drugs with reasonable clarity in three figures. Moreover, it highlights the similarity and differences of various drugs in the maturation rate.

Fig. 5.
figure 5

Biphasic bodyweight scaling of CL (group I drugs). Group I drugs are the drugs with the largest transitional bodyweight (around 15 kg). A–E The log CL vs. log W plots (symbol) and the best-fit lines of the biphasic model. CL values with random errors (CV = 20%) were generated according to the sigmoidal maturation model (Equations 1–3). Each dataset was fitted to the biphasic model. F The slope plots (lines) and the transitional bodyweights (stars) for group I drugs

Full size image
Fig. 6.
figure 6

Biphasic bodyweight scaling of CL (group II drugs). Group II drugs are the drugs with intermediate transitional bodyweight (around 10 kg). A–E The log CL vs. log W plots (symbol) and the best-fit lines of the biphasic model. F The slope plots (lines) and the transitional bodyweights (stars) for group II drugs

Full size image
Fig. 7.
figure 7

Biphasic bodyweight scaling of CL (group III drugs). Group III drugs are the drugs with the lowest transitional bodyweight (< 5 kg). A–E The log CL vs. log W plots (symbol) and the best-fit lines of the biphasic model. F The slope plots (lines) and the transitional bodyweights (stars) for group III drugs

Full size image

Finally, to demonstrate the versatility of the biphasic model, the drug clearance values from individual pediatric subjects were retrieved from two studies of cefetamet (48, 49). Figure 8 shows that the biphasic model fits all the datapoints well, except for one point (which is from a subject that had multiple postoperative complications (49)). The fitting results are described in the figure legend. While A and B values are drug-specific, the α exponent (2.9) falls within the range of the values found for other drugs (Table III). Moreover, the beta exponent (0.47) and the transitional bodyweight (11 kg) are about the mean values estimated for the datasets of 17 drugs.

Fig. 8.
figure 8

Biphasic bodyweight scaling of individual pediatric CL data obtained from different pharmacokinetic studies. The individual CL values of cefetamet were retrieved from study 1 (20 infants, 0.19 to 1.44 years)(48) and study 2 (18 children, 3 to 12 years)(49). The adult data were from ref. (50, 51). One subject in the second study was reported to have multiple postoperative complications (coincidentally, the one that has a CL value far below the fitted line). The pooled data were fitted with the biphasic allometry and the simple allometry model. The AIC values are 269 (biphasic) vs. 313 (simple allometry). The fitted parameter values for the basic model are A = 0.049, α = 2.90, B = 16.6, and β =0.47. The estimated transition bodyweight is 11.0 kg

Full size image

Unifying All the Datasets

In this study, a total of 25 datasets were included for analysis. These data cover 3 types of human parameters (BMR, GFR, and drug CL), where the absolute values span >3 orders of magnitude. Nevertheless, some common features repeatedly appear throughout this study. To further highlight the similarities and differences among different datasets, a dimensionless analysis was performed, according to the definition of X and Y and the derived equations (Equations 13, 17, and 18). The two new variables (X, Y) are fractions or multiples of the two characteristic values (\(\overset{\sim }{w}\) and \(\overset{\sim }{p}\ \Big)\). With the dimensionless equation (e.g., Equation 13 or Equation 16), all of the 25 datasets can be compared in one figure (Fig. 9A). This composite plot clearly divides the biphasic curves into two segments at the reference point of (X, Y) = (1, 1), which is considered as a phase transition (turnaround) point. The first segment is within the region where both X and Y are below the unity, whereas the second segment locates at (X, Y) above unity. All the data in the first phase show steeper slopes than those in the second phase (i.e., α > β). Moreover, the first phase is more variable among different data than the second phase. This is consistent with the magnitude of variability reported in Table III for the drug CL (CV for α = 26.4%; for β = 14.4%).

Fig. 9.
figure 9

Unifying 25 datasets using dimensionless analysis. A The log–log plot for the dimensionless variables. B The slope plots. C The deceleration plots. The definitions of the dimensionless variables, X (fractional W) and Y (fractional P), and of the slope and deceleration are described in Section - Dimensionless Analysis. For each individual dataset, the fitted parameters of the biphasic model were used to simulate the dimensionless data, using Equations 13, 17, and 18. A total of 25 datasets (covering BMR, GFR, and drug CL) were compared in one plot

Full size image

Figure 9B further captures the essence of such disparity; while the asymptotic slope in the first phase is distributed from 1.5 to 3.5, the asymptotic slope in the second phase has a narrow distribution (ca. 0.4 to 0.7). A consistent observation is that all the data seemed to merge at X >2 (i.e., W is 2 times that of the transitional bodyweight), suggesting that the maturation and growth patterns of various human parameters are similar when the growing body is passing the critical point of transition.

Figure 9C offers further insights into the deceleration process of human development after birth. By definition, deceleration is the change of the slope of the maturation curve. The negative value suggests that, although the human function is growing, the speed of functional maturation is continuously declining, i.e., deceleration. Figure 9C shows many characteristics of the deceleration process. First, it is an inverse, symmetrical bell-shaped curve with maximal deceleration occurring at the critical turnaround point (1, 1) and, second, slow deceleration in the early life when the body size is small and when the adulthood is approaching. Third, fast deceleration starts almost universally at X = 0.3 to 0.4, reaching the maximal deceleration at X = 1. This characterizes the maturation pattern of the first phase. After passing the maximal deceleration point, the maturation enters the second phase and, again, approaches zero deceleration at the adulthood (completing the maturation process).

DISCUSSION

The current study proposes a general weight-only equation to model various ontogeny datasets of human parameters. The datasets are diverse, spanning multiple human parameters and covering extensive age groups from birth to adulthood. The data were either directly retrieved from historical datasets (including mean and individual values) or simulated from independent models with published values for specific model parameters. A statistical random sampling approach was used to add random errors to the simulated data. The results demonstrate that a biphasic, mixed-power-law equation with two limiting allometric functions adequately quantifies the developmental phase transition profiles of BMR, GFR, and drug CL. The biphasic model and the additional dimensionless analysis offer quantitative insights into the maturation and growth of human body functions.

The long-held belief that body functions develop at distinct pace in different stages of human development is well supported by extensive empirical evidence (1, 5, 52,53,54). For example, a study dated back to 1949 had shown that renal function matures with the most rapid rate in the first 6 months, followed by slower rates to reach adult values around the second year of life (52). Numerous empirical models have been proposed to scale the maturation and growth processes of body functions (6, 7, 24). These quantitative equations have been frequently developed for practical considerations, e.g., estimating children’s values (6, 14, 39). The equations are usually data-specific and age-categorized. Most equations contain bodyweight as an input variable; meanwhile, age was often included as an additional variable (6,7,8, 24, 36). The equations are either separate, discontinuous equations with cut-points at certain age thresholds (23, 40), or continuous nonlinear equations containing age and bodyweight terms (7, 8, 15, 24). The dependence of bodyweight on age (55,56,57) is often required to assume a fixed weight exponent value (i.e., 0.75) in order to estimate the age-associated parameters (e.g., maturation half-life and Hill coefficient) (15, 24, 58). Accordingly, this present study provides a different perspective where bodyweight alone in a continuous 4-parameter power-law equation is sufficient to quantitatively describe the maturation process.

A previous study has shown that the brain’s metabolic requirement starts to accelerate after the first 6-month of life and reaches a lifetime peak at about 5 years of age (1). During this particular period, the increasing demand of energy in human brain development was compensated by slow rate of body growth (1). This present study reveals that the rate switching of BMR, GFR, and CL occurs at bodyweights of around 5–20 kg, which is about the bodyweight range for children of 0.5–9 years of age. Moreover, the transitional bodyweights for different datasets center around 10 kg, which is about the weight of children at 1 year of age.

The biphasic profiles are universally reproduced in different datasets. Since other important metabolic organs, such as the liver and the kidneys, may develop similar age-related dynamics in energy demands, the biphasic profiles may be associated with the trade-off between maturation (functional development) and growth (body size development). In the first developmental phase, high blood perfusion organs (e.g., brain, liver, kidney) take up more metabolic substrate (e.g., glucose) to allow fast development of organ functions (fast maturation), which results in less energy available for the building of body mass (slow growth). Therefore, this phase is characterized by high energy needs for the maturation of vital organs, leading to the superlinear bodyweight scaling relations (exponent > 1). At birth, the major drug eliminating organs continue to mature and grow. The sizes of theses organs grow at different paces, with fractional organ size (i.e., weight per kg bodyweight) reaching the maximum at around 1 to 2 years of age (59). The organ blood flow also increases with age and bodyweight at different rates (29, 60,61,62). Moreover, the enzyme activities (per kg bodyweight) of most drug metabolizing enzymes (e.g., CYP 3A4) also undergo fast maturation and reach the adult levels at around 1–2 years of age, although some enzyme may mature faster or slower (60, 61). The above-mentioned characteristic ages of maturation correspond to average bodyweight of 9 to 13 kg (43); coincidently, the mean transition bodyweight (10.0 kg) observed for the drug CL datasets (Table III) falls within the range. Compared to the later phase, the first phase has greater variability in the estimated asymptotic (α) exponent (CV = 26%). The CV for the transitional bodyweight is even larger (49%); however, the variability levels are still surprisingly low, if one considers that the drugs differ widely both in the exact CL values and elimination mechanisms. The results suggest commonality and variability in ontogeny. While both features warrant further empirical and theoretical investigations, the variability may be attributed to variation in the maturation speed of various factors (hepatic, renal, biliary, and blood) that contribute to overall drug elimination in the maturing and growing body (59,60,61,62,63,64,65,66,67,68).

As the body size development enters into another phase, the energy supply relative to the maturing vital organs might need to be bounded or be re-shuffled to other organs, e.g., muscle. This may contribute to continuous decrease of metabolism and many other organ functions along the maturation process (69). In the present paper, equations are derived to quantify this deceleration process, which reaches the maximal deceleration at the transitional bodyweight and proceeds to the second phase. Notably, the deceleration profile is symmetrical at the transitional point (Fig. 9C). Since in the second phase, growth of body size dominates functional maturation, the phase is less variable, characterized by tightly disturbed asymptotic exponent with low CV (14%, Table III) and by highly superimposed slope profiles after passing the transitional point (Fig. 9B). Taken together, energy re-allocation between high and low energy-demanding organs may attribute to biphasic maturation and growth of organ functions. This view is consistent with the general model of West et al. (55) which suggests that the growth of body size is limited by the capacity of resource allocation networks.

As illustrated in the Appendix (Fig. 10 in the Appendix), the curvature of the biphasic profile is set by the two allometric functions. Each of the two extreme states is represented by a single allometric function of bodyweight raised to a constant power (α or β). The magnitude of the two exponents shapes the entire curve: for example, higher α together with lower β produces greater curvature and more obvious phase transitions, as indicated in the modeling of the CL values for 17 drugs (Table III and Figs. 5, 6 and 7). Moreover, the biphasic model shows that the slope of the scaling curve continuously changes during the developmental period, which agrees with previous observations (16, 28, 30).

The essence of the phase switching with deceleration is further captured by the dimensionless analysis. According to Equation 13 (or Equation 16), all unitless data will converge at (X, Y) = (1, 1), which is also the transition point of the biphasic curve. The dimensionless equations indicate that metabolic and physiological functions scale with bodyweight superlinearly at X < 1 (i.e., bodyweight < transitional weight) and sublinearly at X > 1 (i.e., bodyweight > transitional weight). The dimensionless analysis can be further elaborated as follows. Mathematically, Equation 17 can be expressed as the linear combination of two fractional terms:

$$slope=\alpha\cdot f_\beta+\beta\cdot f_\alpha$$
(19)

where

$$0<{f}_{\alpha }=\frac{X^{\alpha }}{X^{\alpha }+{X}^{\beta }}<1$$
(20)
$$0<{f}_{\beta }=\frac{X^{\beta }}{X^{\alpha }+{X}^{\beta }}<1$$
(21)

and the deceleration equation (Equation17) can be simplified as

$$deceleration=-\left(\alpha-\beta\right)^2f_\alpha\cdot f_\beta$$
(22)

In biological terms, the two fractions represent the relative contribution of the two maturation/growth phases (i.e., α and β  phases) from birth to adulthood. Phase transition occurs at the characteristic bodyweight where the two phases have equal contribution (i.e., f = 1/2). Thus, at the phase transition point, the slope is the average of the two characteristic exponents, i.e., (α + β)/2, and deceleration reaches the maximal value −0.25(α − β)2. In this study, the β exponent is around 0.5 with small variation across all 25 datasets. In contrast, the α exponent has larger variation (Table III and Fig. 9B). Thus, larger difference in the two exponents results in sharper transition and greater peak deceleration (Fig. 9C).

Bodyweight has been proposed and evaluated as the covariate in predicting pediatric CL values. It is known that a fixed exponent is insufficient to describe the change of CL with respect to bodyweight increases across the human lifespan. Given that the bodyweight exponent value is usually higher in younger (e.g., neonates and infants) than in older age groups, the bodyweight exponent has been treated as a continuous function that features continuous decline of exponent during growth—the so-called bodyweight-dependent exponent (BDE) models. Table IV compares the BDE models with the biphasic model. The first BDE model (BDE I) assumes that the decline of exponent follows a 4-parameter sigmoidal bodyweight function, with clearly defined maximal and minimal exponents. The model has been applied in the population pharmacokinetic analysis of two drugs (propofol and morphine), covering subjects with bodyweight ranging from 0.56 to 122.7 kg (2 studies)(16, 70). As demonstrated in these 2 studies, the inclusion of 4 parameters in the exponent function would have an advantage of modeling data including preterm neonates with extreme low bodyweight. However, it would be more challenging to estimate all the parameters with confidence, especially when the neonate data are not sufficient.

Table IV Comparison of Continuous Bodyweight-Dependent Exponent (BDE) Models with the Biphasic Model
Full size table

The second BDE model (BDE II) also includes a bodyweight-dependent exponent function, which itself is also a power-law function, with 2 parameters that characterize the weight-dependent decline of exponent. The model has been applied in three contexts: the population pharmacokinetic analysis of busulfan (71), predicting drug CL in children (3, 33), and scaling CL of clotting factor VIII and IX (72). Specifically, the model has been compared to other methods, including simple allometry with single fixed exponent (0.75 or data-specific), age-dependent exponent (ADE) model, segmented model, and/or maturation model (3, 33). Overall, the predictive power of the models varied with drugs or with age groups (33); however, the BDE model seemed to provide better prediction of drug CL for theophylline (3) and the clotting factors (72).

Compared with the BDE models, the biphasic model proposed in this study represents a completely different concept and methodology (Table IV). The model combines simple allometry in a form of inverse function. The two allometric exponent terms (α and β) shape the curvature of ontogeny bodyweight profiles with two distinct, definable phases. Besides, the allometric coefficient terms (A and B) determine the absolute value of human parameters (i.e., BMR, GFR, and CL of different drugs). Moreover, the model offers meaningful insights into the ontogeny dynamics of human functions. The simplicity and generality of the biphasic model are revealed in several derived terms: phase transition bodyweight, slope (rate of ontogeny), and deceleration (reduction of ontogeny rate).

Besides BDE, the age-dependent exponent (ADE) model has been previously applied to predict clearance in children. The ADE model assigns different exponent values for different age groups (3, 33, 73): 1.2 (0–3 months), 1.0 (>3 months – 2 years), 0.9 (>2–5 years), and 0.75 (>5 years). In terms of predictive performance, the ADE model appears to be comparable with BDE II (3, 33) and PBPK models (73). Since the exponent values are pre-determined, the ADE model may be useful in helping the design of first-in-child pharmacokinetic studies during new drug development (3, 33). The issue with the ADE model, however, is the designation of the same fixed exponents within the same age group for different drugs. In this study, the proposed biphasic model shows that the slope of the ontogeny curve changes continuously with bodyweight (e.g., Figs. 5F, 6H, 7F), and the slope of the early-life phase is much higher than the largest designated exponent (i.e., 1.2) in the ADE model. From this perspective, the biphasic model may help refine the ADE model by estimating the age group- and compound (or dataset)-specific exponent values using Equation 7.

Some caveats and future perspectives are noted here. The aim of this study is not to predict the unknown values from the proposed model. Instead, the study is the first attempt aiming to understand the ontogeny process of human metabolism and physiological functions by proposing a general, harmonizing model. Future studies may be directed towards building and validating the proposed model for practical applications, such as prediction of renal functions, of pediatric doses and of metabolic demands. Such studies would have broad implications in new drug development, clinical drug therapy (74,75,76,77), and clinical nutrition (78,79,80). However, it should be noted that all prediction models may be suitable for predicting mean population values but not for individual prediction, because the observed value for an individual child is erratic and uncertain (33). During pediatric new drug development, BDE and other allometric models may lack practical application due to limited availability of data (33). The biphasic model may have the same issue. However, the current study demonstrates that α and β are narrowly distributed with CV% of 26% and 14%, respectively, although the drugs differ widely in their absolute CL values (> 3 orders of magnitude) and in elimination mechanisms (metabolism-dominated vs. renal excretion-dominated). Future studies may lead to further classification of drugs according to the parameter values and drug properties, e.g., elimination mechanisms. For example, for a new investigational drug that is mainly renally excreted, the proposed dimensionless model (Equation 13 or 16) may be used for predicting pediatric CL of the drug, using the parameter values obtained from the GFR dataset. The proposed dimensionless form asks only for two parameters, i.e., α and β,. For application, it remains only to specify the phase transition bodyweight, which will then determine the CL value at this characteristic weight. The mean phase transition weight (10 kg) may be used; alternatively, specific weight may be used if the drug can be classified into specific ontogeny group. Moreover, the same reasoning and approach may be applied in population pharmacokinetic analysis and PBPK modeling. The dimensionless equation will be applied to transformed, unitless CL and weight values. Finally, this paper may inspire future attempts in finding a theoretical framework and derivation of the equation based on first principles.

CONCLUSION

In this paper, a general equation is proposed to model the maturation of BMR, GFR, and drug CL. The equation (Equation 4) is expressed in reciprocal terms of mixed allometric functions where bodyweight is the only independent variable. All the bodyweight-based profiles are biphasic on log–log coordinates. The biphasic curvature is determined by two asymptotic allometric functions, representing the maturation and growth functions, respectively. The first phase (below the critical bodyweight) is universally characterized by much steeper slopes with an asymptotic exponent >1 (superlinear scaling). The second phase (above the critical bodyweight), however, exhibits much shallower slopes with an asymptotic exponent < 1 (sublinear scaling). The proposed equation can be further expressed in a unitless form, where the relationship between the fractional physiological/metabolic quantity (Y) and the fractional bodyweight (X) can be described by a general equation with two allometric exponents, α and β. The unified equation quantitatively characterizes the curvature of the biphasic maturation and growth profiles for diverse datasets, by two characteristic parameters (α and β). In conclusion, the proposed mixed-allometry model enables a quantitative understanding of human development from birth to adulthood.