Abstract
Additive manufacturing (AM) is an innovative procedure that can quickly create complex structures. By layering a material, a three-dimensional object is created using this technique. Every deposit of liquefied or partly liquefied material abides by the previous deposit. Fused deposition modelling’s (FDM) objective is to comprehend how varied interior structures influence the bending resistance of the printed samples and to investigate the impact of various infill patterns and percentages. The term “infill” describes the pattern of solid material used to fill a 3D-printed object's interior. It is utilized to give the printed part structural support and strength. Acrylonitrile butadiene styrene (ABS) material was chosen for this study as it offers a greater and superior finished plane along with dimensional stability. The infill pattern chosen for the flexural test study was the triangular pattern which includes different densities of infill percentages precisely, 25%, 50%, 75%, and 100%. A few specimens of ABS material having 100% infill density are put through a tensile test according to the ASTM D638. The ASTM D790 standard was used to make a model and test the flexural strength of the specimen. Line and triangle patterns provided the most ideal tensile and bending strength properties. This is likely because the deposited rasters are associated with the direction of loading. For line patterns with 100% infill, scanning electron microscopy (SEM) analysis showed a convincing connection between the microstructures and the rasters (porosity, voids, gap between beads and hole due to polymer pulled out). Furthermore, SEM analysis showed matrix failure and significant voids in a triangular pattern at infill densities of 25%, 50%, 75%, and 100%.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Introduction
Inkjet printing, stereolithography (SLA), selective laser sintering (SLS), fused deposition modelling (FDM), fused filament fabrication (FFF), and laminated object manufacturing (LOM), are among the few of the several 3D printing techniques currently available on the market [1]. In AM technology, progressions are done in a variety of areas, comprising materials, machinery, and procedures. The product printed in AM is composed of layers that are bonded together to create the finished object [2,3,4,5]. Given its simplicity and low cost, the FDM has established itself as one of the most admired AM methods in the industry and the public at large. FDM has been found to be useful in various industries, like manufacturing, quick prototyping, and rapid tooling [6], as well as in the disciplines of dentistry and medicine [7,8,9,10], consumption goods [11], and the food business [12].
The layer-by-layer creation that makes an AM method distinct, makes products manufactured using FDM weaker than conventional procedures such as machining and injection molding. Complex components can be produced quickly by AM. This process uses the deposition of materials layer by layer to form a portion. The molten or lithified matter is stacked on top of its own layers. One of these more affordable methods with a variety of industrial uses is material extrusion, often known as FDM. Industries generally practice the layer-by-layer FDM approach for rapid prototyping in product design and development [13,14,15]. For the purpose of producing fully functional components and boosting the strength of the AM part, some researchers have altered the various parameters. The mass of the specimen portrays a noteworthy part in the tensile strength of the matter; according to studies on the tensile characteristics of a variety of additives produced in FDM specimens by Chisena Robert et al. [16]. To link mechanical properties to process considerations, empirical models of tensile, flexural, and impact strength along with acquaintances between air gaps, layer heights, raster widths, printing orientations, and raster angles were developed [17,18,19,20]. Letcher et al. developed a cloned prototype for investigating the impact of various printing deliberations on the flatness inaccuracy, accuracy of the dimensions, and plane texture of specimens printed using the FDM process and PLA filament. These factors included the height of the layer, orientation, feeding rate, and platform extruder traverses [21].
Other parametric studies [22,23,24] have been conducted over time as well. The impact of the print variable on the robustness of 3D-printed components was central to all previous studies. A 3-layer outer wall thickness, a 45° raster angle, and air gaps of 1–12 mm were utilized in the experiment. The findings show that the most cost-effective tensile test pieces are those with low filling density [14, 25,26,27]. The toughened CFPETG sample was demonstrated to exhibit superior characteristics [28], with the carbon fiber content and infill percentage having a direct impact on the specimen’s strength. For their mechanical characteristics, typical tensile specimens were tested experimentally based on the height of the layer, the thickness of the wall, the angle of orientation, the speed of printing, and the densities of infill. It was established that additional strength is gained by the part since the wall thickness thickens the exterior pattern. For obtaining consistent structure and improving part quality together, low layer height is advocated [29, 30]. The energy absorption is maximum for all infill schemes at a density of 85%, according to the results of the Izod impact test trials on specimens. As been revealed, the impact strength established by the microstructure’s nature serves as an equipoise amongst the component of stress intensity and the propagation of the crack.
The tensile characteristics of the PLA pieces which were printed were investigated by Malenka et al. [31]. Its results demonstrated that the 90° orientation had superior tensile strength and tensile modulus as evaluated to the 45° configuration. Tensile strength and module are reinforced by increasing the filling rate from 10 to 80%. The height of the layer was amplified by 0.1 to 0.25 mm, which also resulted in a decrease in tensile strength and tensile modulus. Torres et al. [32] examined the shear strength of PLA printed components using the properties of the height of the layer, percentage of fill, and thermal treatment time at 100 °C. By lowering the height of the layer, intensifying the fill rate, and extending the thermal treatment, the shear strength has been improved. Baich et al. [33] examined how filler patterns influence the strength and price of print items. They looked at the results of filling patterns such as solid, double dense, high, and low.
The composite’s mechanical performance is significantly impacted by the weak link between the PLA matrix and CCF. However, when the surface of the carbon fiber bundle was changed using a mixture of PLA particles glue and methylene dichloride, the adhesion and mechanical strength were increased. N. Li et al. produced a CCF-reinforced PLA composite using an FDM 3D printer and modified the carbon fiber’s surface to analyze the material's mechanical properties and reach tensile and flexural strengths of 91 MPa and 156 MPa, respectively [34]. By performing surface modification using a mixture of methylene dichloride and PLA pellets in various proportions and printing CCF-reinforced PLA composites, M. Rimauskas et al. [35] were able to generate impregnated CCF from common carbon fiber tows (1 K and 3 K). The outcomes demonstrated that the 10% concentration solution-created fiber produced the greatest results, reaching a maximum tensile strength of 165 MPa. The greatest tensile and bending strengths of the PLA thermoplastic composite components made by M. Heidari-Rarani et al. [36] using FDM technology were 61.4 MPa and 152.1 MPa, respectively. The pieces also had CCF reinforcement and 1 K carbon fiber roving.
Based on the above-mentioned literature study, researchers in very few numbers have examined various filling models with different filling densities. Most of them concentrated on the analysis of tensile strength, with only a few using FEA for numerical analysis. Yet, further research is a requisite to develop the mechanical physiognomies and quality of the components printed using the FDM. In a preceding study, the fill pattern and the fill density were found to significantly affect the characteristics of the FDM components. This study concentrates on how different fill patterns and filling percentages influence the bending strength and tensile strength of samples created using the FDM. ABS is the preferred material to create specimens since it provides superior dimensional stability and a polished surface [37,38,39,40,41,42]. Triangular infill patterns with 25%, 50%, 75%, and 100% as their filling densities were selected for testing the flexural strength in this experiment. Samples with a line filling density of 100% are generated and assessed according to ASTM D638 to analyze the tensile strength. The bending test sample was modeled and tested in compliance with ASTM D790.
Methods
In this study, test samples made of Tesseract ABS material, which is most typically used in 3D Printing, are examined for their tensile strength. ABS is a thermoplastic material with a high level of pressure, wear, and chemical resistance. ABS is the second-most accepted material for 3D printing after polylactic acid (PLA). Due to its good mechanical qualities, resistance to high temperatures, low cost, extended service life, and broad melting temperature range, it is an excellent choice for FDM manufacturing of a variety of parts.
An initial 3D model, created in the CAD software is saved with the file extension- stereolithography (STL). The STL file then advances into the program (Ultimaker Cura 5.1.1) that horizontally cuts the 3D object (Fig. 1 shows the sliced tensile specimen and Fig. 2a–d shows the sliced flexural specimens). Printing considerations including print speed, layer thickness, layer speed, height of layer, temperatures of printing, rate of the fill, orientation of the print, structure of support, and many more factors, are set up by the cutting software. Here, the elevated melting temperature of the specimens was achieved through a deliberate implementation of a glass sheet substrate, while ensuring the platform temperature remained at an elevated level in accordance with the guidelines provided by the supplier. Sections from the file created by the G-code are then provided to the FDM machine. The nozzle and built-in platform are heated before the material is extruded. On the building platform, a polymeric filament is extruded from the nozzle head of the heated extruder [43,44,45,46,47]. An illustration of an FDM machine is shown in Fig. 3 along with a 3D printer and the procedure of printing is summarized in Fig. 4.
Produced parts must, in addition to everything else, be able to tolerate repeated loads and substantial temperature changes. Unfortunately, it is not appropriate for many applications due to contraction and warping during the printing process, peeling away from the platform, and gas emissions. According to the manufacturer, the attributes in Table 1 show the filament used in this project.
Printing and process parameters
Tensile testing
The proportions of the tensile test samples are in accordance with ASTM D638-I (refer Fig. 5). The sample type 1 is having 50 mm as its gauge length and 165 mm as the gripping distance in addition to these specifications [48,49,50,51]. The tensile test specimens are created using an Ultimaker 2 + FDM machine and have the infill density as 100% in an AM facility (refer Fig. 6). To produce tensile specimens, a line infill pattern is used. The time required to print one specimen was 1 h 58 min. Table 2 shows the parameters of the printing process.
The material was measured under a forceful pull during the tensile test. To establish the tensile strength of the 3D-printed samples, this test was performed. The sample for the tensile test was made up of type 1.
Flexural testing
The ASTM D790 standard is followed in the fabrication of the flexural test samples (refer Fig. 7). The triangular infill structures used to create the flexural samples have densities of 25%, 50%, 75%, and 100%.
The manufacture of samples is done using the Ultimaker 2 + FDM machine. The triangular infill sample with an infill density of 25% took 1.02 h to print, and the specimens with 50%, 75%, and 100% infill densities took 1.20 h, 1.39 h, and 1.59 h to print, respectively.
Mechanical testing
Tensile test
The material was measured under a forceful pull during the tensile test. To establish the tensile strength of the 3D-printed samples, this test was performed. The sample for the tensile test was made up of type 1.
As shown in Fig. 8, the FSA M100 UTM tensile tester is used for the tensile strength measurement. We used a 10-kN weight cell traveling at a consistent speed of 1 mm per minute and the test was carried out at MIT World Peace University, Pune. The samples in the UTM were inserted through the handles, and the force was gradually increased until the samples failed. The resultant deformation is used for the calculation of the material’s tensile strength. Figure 9 shows the fractured tensile test samples. The load on the test samples during the test was 1674 N and the tensile strength was 32.19 N/mm2. The gauge length was recorded to be 50 mm. During testing, all the samples crack within the 1–1.4 mm strain range. The stress vs strain curve was used to determine the percentage of elongation and tensile stress values. Equations 1 and 2 were used to estimate the ultimate tensile strength (σt), and maximum strain (εt) respectively.
For Eq. 1, σt, measured in MPa stands for the ultimate strength, P which is measured in N is the load at the peak of the stress vs strain curve, and A, measured in mm2 is the cross-section area of the specimen. For Eq. 2, l0 is the strain gauge length, which is 50 mm according to the ASTM D638.
Flexural test
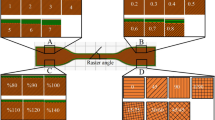
A three-point bending test was performed on an M100 high-capacity universal test machine at MIT WPU, Pune according to the ASTM D790 (refer Fig. 10). The different designs and load directions for the flexion test samples are also shown here. The sample for the bending test was type one, i.e., ASTM D790-I. The bending tests evaluate the bending force and the strain in the samples. The test was operated at a loading speed of 3 mm/min. The span length (L) amid the support pins was modified in this test to 102 mm in accordance with the test standard. A loading pin was used to apply the load (P) halfway through the span. The system automatically plots strain data in relation to the deformation of the test sample as the surface starts deforming. The bending stress (σ) is the stress resulting from the bending moment during a three-point bending test. It is computed using the formula\(\upsigma =\frac{3\mathrm{FL}}{2{\mathrm{bd}}^{2}}\), where b is the width of the tested sample whereas d is the depth of the tested sample, respectively. The nominal fractional change in an element's length on the test specimen’s outer surface at the mid-span, where the maximum strain occurs, is known as flexural strain (Ɛ). Any deflection can be determined using the formula \(\upvarepsilon = \frac{6Dd}{{L}^{2}}\), where D corresponds to the highest deviation at the center of the sample. The top surface which is in interaction with the loading roller starts compressing while tension takes place on the below surface which is in interaction with the support rollers. Once the ultimate load is attained, a fracture starts at the lower face and progresses to the above face, severely breaking or distorting the sample. Figure 11a–d demonstrates the fractured samples.
Results and discussion
Experimental results and discussion
Tensile testing
Six specimens in all were evaluated in a tensile test. As shown in Fig. 12, the average obtained tensile strength was 29.103 MPa and the average obatined yeild strength was 19.971 MPa. Tensile strength readings that were obtained were found to be within the acceptable range. The material properties obtained from the Table 1 were used to determine the tensile strength of the specimen.
Flexural testing
Flexural testing was used to determine the flexural properties of specimens made of ABS material and 3D printed with triangular infill patterns at four different infill densities. In this instance, Fig. 13 shows specimens printed with triangle infill patterns at four different density levels. The specimens printed with 75% and 100% triangle infill density exhibit the maximum level of flexural stress, according to the histogram, whereas specimens printed with 25% and 50% infill density exhibit the lowest amount of flexural stress. There are barely perceptible changes between an infill density level of 25% and 50%. The average obtained flexural strength for 25% triangular infill was 16.088 MPa. The average flexural strength values obtained for 50%, 75%, and 100% were 30.015 MPa, 49.707 MPa, and 67.961 MPa respectively.
Microstructural analysis
The rupture that occurred was inspected using SEM. Before the test, all specimens were layered with platinum making use of Auto Fine Coater, and were left in the sputter coater for 60 s to ensure that the platinum had been applied to all intended surfaces. The FEI-Nova Nano SEM 450SEM was used for the scanning and the scanning was done at Pune University. The resolution of the SEM machine was 1.0 nm at 15 kV, 1.4 nm at 1 kV, and 1.8 nm at 3 kV, and 30 Pa. To create an image, the machine scanned a surface with a focused electron beam. The samples and the electrons in the beam worked together to provide signals that could be used to learn more about the morphology for each percentage of ABS polymer. Two distinct magnifications were used for the samples’ examination and testing: flexural 200 μm and 10 μm, and tensile 300 μm. To identify matrix failure, voids, porosity, gaps between beads, and pull out breakage, samples were laid on the specimen support and concentrated on the fractured edge.
Observing the fractured surfaces using SEM micrographs, it is possible to calculate the validity of the variations in mechanical properties. The microstructures of the ruptured samples from the tensile as well as flexural tests are demonstrated in Figs. 14 and 15a–d, correspondingly, with filling percentage of 100 for tensile and filling percentages of 25, 50, 75, and 100 for flexural.
In Fig. 14, a micrograph of 100% ABS line pattern is depicted. The beads in the matrix–matrix chains were tightly packed, although there were only a few small gaps. To achieve higher mechanical characteristics, a strong bonding is needed at the polymer bead interface. Here, the resulting image was magnified × 250. The magnification was chosen to be × 250 because it gave us appropriate results. A few voids are present here, but they are large in size. There are a number of holes formed on the surface of the specimen where it cracked. This was due to the polymer being pulled-out. A part of the specimen was magnified further up to × 500. When magnified up to × 500 the gaps between the beads and the porosity of the specimen are visible. The greatest failure in FDMed systems is porosity, and greater porosity means a higher chance that failure will result from huge pores and pore clusters.
Upon conducting a thorough examination, it was ascertained that an increase in infill density directly correlated with a reduction in the porosity level exhibited by the specimens. Comparative analysis of porosity levels among specimens fabricated with varying infill densities, specifically 25%, 50%, 75%, and 100%, revealed that the highest porosity level was observed in the specimens.
with a 25% infill density, while the lowest porosity level was exhibited by the specimens with a 100% infill density. It is noteworthy that for the specimens featuring a 100% infill density, the porosity level can be considered negligible or even zero, as the porosity exists solely between the layers of the specimen and not within the infill pattern.
In Fig. 15a shows the SEM image for the flexural test of 25% infill. The resulting image was magnified × 500. A number of voids were visible here. We then considered a void and magnified it up to × 5000 (figure is attached adjacent to Fig. 15a). The number of voids decreased as the infill percentage increased (Fig. 15b–d). The magnification for Fig. 15b–d was × 500. The magnification was chosen to be × 500 because it was showing apt results. The specimens for all types of infills displayed matrix failure. The voids are present in all flexural samples, as presented in Fig. 15a–d, but their sizes and numbers are reduced for triangular infill patterns with 75% and 100%, indicating stronger and more effective bonding between the casters. The results of the mechanical testing show that this results in a higher strength. The flexural triangle infill patterns with a 25% and 50% fill rate have more voids and are more in number as compared to the 75% and 100% infills.
In the scope of this current investigation, the presence of voids between each sequential layer of the printed specimen was taken into consideration. This approach was employed due to the inherent layer-by-layer fabrication process utilized during the printing procedure.
Conclusions
-
i.
In triangular configuration, higher the infill, higher are the mechanical properties.
-
ii.
The tensile strength for a filling density of 100%, achieved during the tensile test was 29.103 MPa having the maximum deformation as 3.99 mm.
-
iii.
With a filling density of 25%, 50%, 75%, and 100% the flexural strength values obtained experimentally for the triangular model are 16.088 MPa, 38.015 MPa, 49.707 MPa, and 67.961 MPa, respectively.
-
iv.
It was observed that a stronger and more robust structure is produced by the triangle pattern’s many more infill layers, making it a superior choice for design.
-
v.
SEM micrographs for 100% line infill patterns indicated that the beads in the matrix–matrix chains, being tightly packed left very few gaps. The voids in the specimens are large in size. Holes were formed due to the polymer pulled out at the surface of the specimen where it cracked.
-
vi.
A fewer number of voids were indicated in the SEM micrographs for 75% and 100% triangular infill patterns which is a justification for the printed samples' superior mechanical characteristics at the maximum filling percentage (75% and 100% at this point). In the printed specimens of 25% and 50% triangular infill patterns, there are large voids present; which become the reason for their lower strengths as compared to 75% and 100% infill.
Availability of data and materials
The data used to support the findings of this study are included within the article and are available from the corresponding author upon request.
Abbreviations
- FDM:
-
Fused deposition modelling
- SLA:
-
Stereolithography
- SLS:
-
Selective laser sintering
- LOM:
-
Laminated object manufacturing
- FFF:
-
Fused filament fabrication
- AM:
-
Additive manufacturing
- 3D:
-
Three dimensional
- ABS:
-
Acrylonitrile butadiene styrene
- SEM:
-
Scanning electron microscopy
- PBF:
-
Powder bed fusion
- CAD:
-
Computer-aided design
- STL:
-
Stereolithography
- ASTM:
-
American Society for Testing and Materials
- PLA:
-
Polylactic acid
- mm:
-
Millimetre
- PETG:
-
Polyethylene terephthalate glycol
- CFPETG:
-
Carbon fiber reinforced polyethylene terephthalate glycol
- °C:
-
Degree Celsius
- FEA:
-
Finite element analysis
- h:
-
Hour
- min:
-
Minutes
- UTM:
-
Universal Testing Machine
- kN:
-
Kilo Newton
- N/mm2:
-
Newton per square meter
- N:
-
Newton
- Vs:
-
Versus
- mm2 :
-
Square millimetre
- MIT WPU:
-
MIT World Peace University
- mm/min:
-
Millimetre per minute
- nm:
-
Newton-meter
- kV:
-
Kilo volt
- Pa:
-
Pascal
- μm:
-
Micrometre
- MPa:
-
Mega Pascal
References
Lubombo C, Huneault MA (2018) Effect of infill patterns on the mechanical performance of lightweight 3D-printed cellular PLA parts Vol. 17 Pages 214–228, https://doi.org/10.1016/j.mtcomm.2018.09.017
N Maqsood M Rimašauskas 2022 Development and fabrication of continuous carbon fiber reinforced thermoplastic porous composite structures with different infill patterns by using additive manufacturing. https://doi.org/10.1177/08927057221088468
Shaffer S, Yang K, Vargas J, Di Prima MA, Voit W (2014) On reducing anisotropy in 3D printed polymers via ionizing radiation. Polymer 55(23):5969–5979
Mostafa N, Syed HM, Igor S, Andrew G (2009) A study of melt flow analysis of an ABS-iron composite in fused deposition modelling process. Tsinghua Sci Technol 14:29–37
Goyanes A, Buanz AB, Basit AW, Gaisford S (2014) Fusedfilament 3D printing (3DP) for fabrication of tablets. Int J Pharm 476(1):88–92
Tang Pengfei, Zhao Xianfeng, Shi Hongyan (2023) A non-supporting printing algorithm for fused filament fabrication of multi-branch structure. Int J Adv Manuf Technol. 126(7–8):2959–2974. https://doi.org/10.1007/s00170-023-11267-7
Gracias DH, McAlpine MC (2013) 3D printed bionic ears. Nano Lett 13(6):2634–2639
Roshini Yadav L, Viji Chandran S, Lavanya K, Selvamurugan N (2021) Chitosan-based 3D-printed scaffolds for bone tissue engineering. Int J Biol Macromol. 183:1925–1938. https://doi.org/10.1016/j.ijbiomac.2021.05.215
Rovira David Sabaté, Nielsen Hanne Mørck, Taboryski Rafael, Bunea Ada-Ioana (2021) Additive manufacturing of polymeric scaffolds for biomimetic cell membrane engineering. Mater Des 201:1–8. https://doi.org/10.1016/j.matdes.2021.109486
Mahale Rayappa Shrinivas, Shamanth V, Hemanth K, Nithin SK, Sharath PC, Shashanka R, Patil Adarsh, Shetty Darshan (2022) Processes and applications of metal additive manufacturing. Materials Today: Proceedings 54:228–233. https://doi.org/10.1016/j.matpr.2021.08.298
Akhoundi B, Behravesh AH, BagheriSaed A (2018) Improving mechanical properties of continuous fiber-reinforced thermoplastic composites produced by FDM 3D printer. J Reinf Plast Compos. https://doi.org/10.1177/0731684418807300
Bellehumeur C, Li L, Sun Q, Gu P (2004) Modeling of bond formation between polymer filaments in the fused deposition modeling process. J Manuf Process 6(2):170–217
Sanz de Leon, Alberto & Dominguez-Calvo, A. & Molina, Sergio. (2019). Materials & Design. doi: 182.108044.https://doi.org/10.1016/j.matdes.2019.108044
M Ziolkowski T Dyl 2020 Machines 8 4 1 34. https://doi.org/10.3390/machines8040084
Pernet, Benoit & Nagel, Jacquelyn & Zhang, Hao. (2022). Procedia CIRP 105 682–687, https://doi.org/10.1016/j.procir.2022.02.114
Chisena Robert & Chen, Lei & Shih, Albert. (2021). International Journal of Mechanical Sciences, 196. https://doi.org/10.1016/j.ijmecsci.2021.106276
B Wittbrodt JM Pearce 2015 Addit Manuf 8 110 116. https://doi.org/10.1007/s40964-022-00285-8
D Croccolo M Agostinis de 2013 and Olmi G Comput Mater Sci 79 506 518. https://doi.org/10.1016/j.commatsci.2013.06.041
Tanikella N. Wittbrodt G, B, and Pearce J. M. (2017). Additive manufacturing, vol. 15, pp. 40–47. https://doi.org/10.1016/j.addma.2017.03.005
JM Chacon M Caminero 2017 A, Garcia-Plaza E Mater Des 124 143 157. https://doi.org/10.1016/j.matdes.2017.03.065
Letcher T, Waytashek M. (2014). ASME 2014 International Mechanical Engineering Congress & Exposition, IMECE2014–39379. https://doi.org/10.1115/IMECE2014-39379
AK Sood RK Ohdar SS Mahapatra 2010 Mater Des 31 1 287 295. https://doi.org/10.1016/j.matdes.2009.06.016
Garcia Plaza E, Nunez Lopez P. J, Caminero Torija M. A (2019). Polymers (Basel), vol. 11, no. 10. https://doi.org/10.3390/polym11101581
Shuaishuai Li & Xin, Yanmei & Yu, Ying & Wang Yu. (2021). Materials & Design. 204–109664. 109664. https://doi.org/10.1016/j.matdes.2021.109664
N Fountas 2020 A, Kostazos P, Pavlidis H, Antoniou V In Procedia Structural Integrity 26 139 146. https://doi.org/10.1016/j.prostr.2020.06.017
K Kumar 2021 S, Soundararajan R, Shanthosh G Materials Today: Proceedings 45 2186 2191. https://doi.org/10.1016/j.matpr.2020.10.078
Gunasekaran, K.N. & Aravinth, Vishaal & Kumaran. (2020). Materials Today: Proceedings, 968–975. https://doi.org/10.1016/j.matpr.2020.09.041
Patil Chaitanya, Sonawwanay Puskaraj D, Naik M, and Thakur D. G. (2020). AIP Conference Proceedings, American Institute of Physics Inc., 070026(1)( 2020) 070026–1–070026–9. https://doi.org/10.1063/5.0034306
M Naik DG Thakur S Chandel 2022 Materials Today: Proceedings, Volume 62 Part 14 7391 7395. https://doi.org/10.1016/j.matpr.2022.02.305
Mishra P. K, Senthil P, Adarsh S, (2021). Composites communications, vol. 24. https://doi.org/10.1016/j.coco.2020.100605
Melenka GW, Schofield JS, Dawson MR, Carey JP (2015) Evaluation of dimensional accuracy and material properties of the MakerBot 3D desktop printer. Rapid Prototyp J 21(5):618–627
AP Gordon J Torres M Cole A Owji Z DeMastry 2016 Rapid Prototype 387–404 2014 83. https://doi.org/10.1108/RPJ-07-2014-0083
Baich L. (2016). International Journal of Physical Sciences, Vol. 7, pp. 5765–5771. https://doi.org/10.1504/IJRAPIDM.2015.074809
Li N, Li Y, Liu S (2016) Rapid prototyping of continuous carbon fiber reinforced polylactic acid composites by 3D printing. J Mater Process Technol 238:218–225
Heidari-Rarani M, Rafiee-Afarani M, Zahedi AM (2019) Mechanical characterization of FDM 3D printing of continuous carbon fiber reinforced PLA composites. Compos Part B Eng 175:107147
Rimašauskas M, Kuncius T, Rimašauskienė R (2019) Processing of carbon fiber for 3D printed continuous composite structures. Mater Manuf Process 34:1528–1536. https://doi.org/10.1177/07316844221137017
Bachhav C Y, Sonawwanay Puskaraj D. (2022) Materials today: Proceedings, Volume 62 Part 12 6727 6733. https://doi.org/10.1016/j.matpr.2022.04.806
Anoosha N M, Sachin B, Hemanth B R. (2018), Engineering and technology, Vol. 7, Issue 6, June 2018. https://doi.org/10.15680/IJIRSET.2018.0706040
H Li L Gao H Li 2020 Comput Methods Appl Mech Eng 372 0045 7825. https://doi.org/10.1016/j.cma.2020.113354
Aloyaydi Bandar & S. Sivasankaran & Alareqi, Ammar. (2020).2020.106557. https://doi.org/10.3934/matersci.2019.6.1033
ASTM D0638–14, Standard Test Method for Tensile Properties of Plastics 130. https://doi.org/10.1520/D0638-14
Yao, Tianyun, Ye, Juan, Deng, Zichen, Zhang, Kai & Ma. (2020). Composites Part B: Engineering. 188. 107894. https://doi.org/10.1016/j.compositesb.2020.107894
Aloyaydi B.A, Sivansankaran S, Ammar H.R. (2019). Mater. Sci. 6 (6) (2019) 1033–10483. https://doi.org/10.1016/j.rineng.2021.100264
T. Yao, J. Ye, Z. Deng, Composites Part B: Engineering. 188 (2020) 107894, https://doi.org/10.1016/j.compositesb.2020.107894
Dirk Fischer, Bach E, Claudia, Schonherr, Robert, Dietrich, Dagmar, Nickel, Daniela. (2022). Additive Manufacturing. https://doi.org/10.3934/matersci.2019.6.1033
R. Srinivasan, K. Nirmal Kumar, A. Jenish Ibrahim, Materials today: proceedings, Elsevier Ltd, (2020) 1801–1805. 27.https://doi.org/10.1016/j.matpr.2020.03.777
Bandar Abdullah Aloyaydi, Subbarayan Sivasankaran, Hany Rizk Ammar. (2019), AIMS Materials Science 6 6 1033 1048. https://doi.org/10.3934/matersci.2019.6.1033
ASTM D4673–02, In Encyclopedic Dictionary of Polymers, Springer, (2008). https://doi.org/10.1520/D4673-02R08
Bachhav C. Y, Sonawwanay Puskaraj D, Numerical comparison of additive manufacturing of ABS material based on infill design subjected to tensile load. Materials Today Proceedings, https://doi.org/10.1016/j.matpr.2022.04.806
Bachhav C. Y, Sonawwanay Puskaraj D, Naik Mahesh, Thakur D. G., Finite element analysis of flexural test of additively manufactured components fabricated by fused deposition modelling”, December 2020, pp.070026–1–070026–9. https://doi.org/10.1063/5.0034306
Chaitanya P (2019) Sonawwanay Puskaraj D, “FEA of additively manufactured components by fused deposition modelling – a review.” International Journal For Technological Research In Engineering 07(04):6409–6413
Acknowledgements
Na.
Funding
Na.
Author information
Authors and Affiliations
Contributions
AS conceptualized and done the experimentation. PD performed data curation and editing. MN interpreted and visualized the data. DG done the project administration. All authors have read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. The Creative Commons Public Domain Dedication waiver (http://creativecommons.org/publicdomain/zero/1.0/) applies to the data made available in this article, unless otherwise stated in a credit line to the data.
About this article
Cite this article
Karad, A.S., Sonawwanay, P.D., Naik, M. et al. Experimental study of effect of infill density on tensile and flexural strength of 3D printed parts. J. Eng. Appl. Sci. 70, 104 (2023). https://doi.org/10.1186/s44147-023-00273-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s44147-023-00273-x