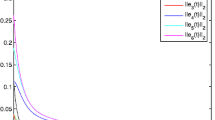1 Introduction

Synchronization as a typical and important collective behavior of dynamical networks has been extensively investigated [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]. For many networks, especially those coupled with large number of nodes, they cannot synchronize themselves or synchronize with desired goals without external controls. Therefore, different control schemes, such as feedback control, intermittent control, impulsive control, pinning control, and so on, have been developed.

Intermittent control is a kind of discontinuous control consisting of work time and rest time in a sequence of intervals. In virtue of its high efficiency and strong practicability, it has been adopted to design effective controllers in practical applications, and lots of results have been obtained. For instance, the signal will become weak in transmission, so an external control should be added to increase the strength of the signal. Zhou et al. [16] studied the exponential lag synchronization for neural networks with mixed delays via intermittent control. Zhang et al. [17] considered the intermittent control for cluster-delay synchronization in directed networks. He et al. [23] investigated the exponential synchronization of dynamical network with distributed delays via intermittent control. From practical point of view, periodically intermittent control is unreasonable in some cases. As we know, the generation of wind power is typically aperiodically intermittent [8]. The heating system of central air-conditioning can run by the aperiodically intermittent operation mode (off-preheat-occupancy-off) [2]. Therefore, aperiodically intermittent control is adopted to study the synchronization of dynamical networks. Guan et al. [4] studied the cluster synchronization of coupled genetic regulatory networks with delays via aperiodically adaptive intermittent control. Liu et al. [6] studied the finite-time synchronization of delayed dynamical networks via aperiodically intermittent control. On the other hand, for large-scale networks, it is impractical to add controllers onto all nodes. Therefore, intermittent control and pinning control are combined together to design effective controllers. That is, only a fraction of network nodes is controlled. Liu and Chen [8] studied the synchronization of nonlinear coupled networks via aperiodically intermittent pinning control. Cai et al. [12] studied the outer synchronization between two hybrid-coupled delayed dynamical networks via aperiodically adaptive intermittent pinning control.

The above results mainly concentrated on integer-order dynamical networks. Compared with integer-order dynamical networks, fractional-order dynamical networks can excellently describe the memory and hereditary properties of various models. In fact, fractional-order systems, such as viscoelastic systems, dielectric polarization, electromagnetic waves, heat conduction, robotics, finance, and so on [24,25,26,27,28,29,30], are ubiquitous in real world. Recently, synchronization of fractional-order complex networks has been investigated as well [31,32,33,34,35,36,37,38,39,40]. Particularly, Li et al. [38] studied the synchronization of fractional-order dynamical networks via periodically intermittent pinning control. Zhou et al. [40] studied the cluster synchronization of fractional-order directed networks via intermittent pinning control. Naturally, how to design aperiodically intermittent pinning controllers for achieving synchronization of fractional-order networks is an important issue and deserves further investigations. The main contribution of this paper is the design of aperiodically intermittent pinning controllers and the derivation of the sufficient conditions for achieving synchronization of fractional-order network. It is noted that the obtained results generalize some of the results in Refs. [8, 38]. For example, periodically intermittent pinning control of fractional-order dynamical network is generalized to aperiodically intermittent pinning control.

The paper is organized as follows. In Sect. 2, some necessary preliminaries about fractional calculus and the model of fractional-order networks are presented. In Sect. 3, aperiodically intermittent pinning controllers are designed and sufficient conditions for achieving synchronization are derived based on Lyapunov stability theory and mathematical analysis method. In Sect. 4, numerical simulation is performed to demonstrate the effectiveness of the obtained results. Finally, some conclusions are presented in Sect. 5.

Notations. For real matrix \(A\in \mathbb{R}^{N\times N}\), \(A^{s}=(A+A^{T})/2\) denotes the symmetric part. If all the eigenvalues of A are real, let \(\lambda _{\max }(A)\) and \(\lambda _{\min }(A)\) be its largest and smallest eigenvalues, respectively. The symbol ⊗ denotes the Kronecker product.

2 Model description and preliminaries

In this section, some definitions, lemmas, and well-known results about fractional differential equations are recalled. In addition, the mathematic model of fractional complex network is introduced.

2.1 Caputo fractional operator and Mittag-Leffler function

Caputo fractional operator plays an important role in the fractional systems, since the initial conditions for fractional differential equations with Caputo derivatives take the same form as for integer-order differential, which have well-understood physical meanings [24]. Thus, we use Caputo derivatives as a main tool in this paper. The formula of the Caputo fractional derivative is defined as follows.

Definition 1

([24])

The Caputo fractional derivative of function \(x(t)\) is defined as

$$ {}_{0}^{C}D_{t}^{\alpha }x(t)=\frac{1}{\varGamma (m-\alpha )} \int _{0}^{t}(t- \tau )^{m-\alpha -1}x^{(m)}( \tau )\,d\tau , $$

where \(m-1<\alpha <m, m\in Z^{+}\). Let \(m=1,0<\alpha <1\), then

$$ {}_{0}^{C}D_{t}^{\alpha }x(t)=\frac{1}{\varGamma (1-\alpha )} \int _{0}^{t}(t- \tau )^{-\alpha }x'( \tau )\,d\tau . $$

For simplicity, denote \(D_{t}^{\alpha }x(t)\) as \({}_{0}^{C}D_{t}^{ \alpha }x(t)\). The following properties of Caputo operators are specially provided.

Lemma 1

([24])

If \(w(t),u(t)\in C^{1}[t_{0},b]\), and \(\alpha >0,\beta >0\), then

  1. (1)

    \(D_{t}^{\alpha }D^{-\beta } w(t)=D_{t}^{\alpha -\beta } w(t)\),

  2. (2)

    \(D_{t}^{\alpha }(w(t)\pm u(t))=D_{t}^{\alpha }w(t)\pm D_{t}^{ \alpha }u(t)\).

The Mittag-Leffler function is defined by

$$ E_{\alpha ,\beta } (z):=\sum_{i=0}^{\infty } \frac{z^{i}}{\varGamma ( \alpha i+\beta )}, $$

where \(\alpha >0,\beta >0\), and \(\varGamma (\cdot )\) is the gamma function. For short, \(E_{\alpha }(z):=E_{\alpha ,1}(z)\). The following properties of Mittag-Leffler function will be used below.

Lemma 2

([38, 39])

Let \(V(t)\) be a continuous function on \([t_{0},+\infty )\) and satisfy

$$ D_{t}^{\alpha }V(t)\leq \theta V(t), $$

where \(0<\alpha <1\), θ is a constant and \(t_{0}\) is the initial time, then

$$ V(t)\leq V(t_{0}) E_{\alpha }\bigl(\theta (t-t_{0})^{\alpha } \bigr). $$

2.2 Model description

Consider a fractional-order network consisting of N individuals described by

$$\begin{aligned} D^{\alpha }_{t} x_{i}(t)=f \bigl(x_{i}(t)\bigr)+b\sum_{j=1}^{N} c_{ij}\varGamma x _{j}(t),\quad i=1,2,\ldots ,N, \end{aligned}$$
(1)

where \(0<\alpha <1 \), \(x_{i}(t)=(x_{i1}(t),x_{i2}(t),\ldots ,x_{in}(t))^{T} \in \mathbb{R}^{n}\) is the state variable of the ith node, \(f:\mathbb{R}^{n} \rightarrow \mathbb{R}^{n}\) is a continuously vector-valued function, \(b>0\) is the coupling strength, and \(\varGamma =\operatorname{diag}(\gamma _{1},\ldots ,\gamma _{n}) \in \mathbb{R}^{n\times n}\) is the inner coupling matrix, \(C=(c_{ij}) \in \mathbb{R}^{N \times N}\) is the zero-row-sum outer coupling matrix determining the topology and coupling strength of the network, which are defined as follows: if there exists a connection from node j to node \(i\ (i\neq j)\), then \(c_{ij}>0\); otherwise, \(c_{ij}=0\).

The objective here is to synchronize network (1) to the desired orbit \(\eta (t)\) by designing aperiodically intermittent pinning controllers, where \(\eta (t)\) is a solution of an isolated node satisfying \(D^{\alpha }_{t} \eta (t)=f(\eta (t))\). For simplicity, only the first node is controlled and the controlled network is written as follows:

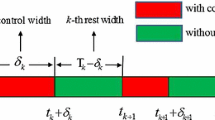
$$ \textstyle\begin{cases} D^{\alpha }_{t} x_{1}(t)=f(x_{1}(t))+b\sum_{j=1}^{N}c_{1j} \varGamma x_{j}(t)\\ \phantom{D^{\alpha }_{t} x_{1}(t)=}{}+bk\varGamma (\eta (t)-x_{1}(t)), &t\in [t_{p},s_{p}), \\ D^{\alpha }_{t} x_{i}(t)=f(x_{i}(t))+b\sum_{j=1}^{N}c_{ij} \varGamma x_{j}(t),& i=2,\ldots ,N, t\in [t_{p},s_{p}), \\ D^{\alpha }_{t} x_{i}(t)=f(x_{i}(t))+b\sum_{j=1}^{N}c_{ij} \varGamma x_{j}(t),& i=1,\ldots ,N, t\in [s_{p},t_{p+1}), \end{cases} $$
(2)

where \(p=1,2,3,\ldots , k>0\) is the control gain, \(0=t_{1}< s_{1}< t _{2}< s_{2}<\cdots <t_{p}<s_{p}<\cdots\) . Then \(s_{p}-t_{p}\) and \(t_{p+1}-s_{p}\) denote the pth control and rest width respectively.

Let \(e_{i}(t)=x_{i}(t)-\eta (t)\) be the synchronization errors. Then the error system is

$$ \textstyle\begin{cases} D^{\alpha }_{t} e_{1}(t)=f(x_{1}(t))-f(s(t))+b\sum_{j=1}^{N}c _{1j}\varGamma e_{j}(t)\\ \phantom{D^{\alpha }_{t} e_{1}(t)=}{}-bk\varGamma e_{1}(t),& t\in [t_{p},s_{p}), \\ D^{\alpha }_{t} e_{i}(t)=f(x_{i}(t))-f(s(t))+b\sum_{j=1}^{N}c _{ij}\varGamma e_{j}(t),& i=2,\ldots ,N, t\in [t_{p},s_{p}), \\ D^{\alpha }_{t} e_{i}(t)=f(x_{i}(t))-f(s(t))+b\sum_{j=1}^{N}c _{ij}\varGamma e_{j}(t),& i=1,\ldots ,N, t\in [s_{p},t_{p+1}). \end{cases} $$
(3)

Let \(\mathscr{E}(t)=(e_{1}(t)^{T},\ldots ,e_{N}(t)^{T})^{T}\) and

$$ F\bigl(\mathscr{E}(t)\bigr)=\bigl(\bigl(f\bigl(x_{1}(t)\bigr)-f\bigl( \eta (t)\bigr)\bigr)^{T},\ldots ,\bigl(f\bigl(x_{N}(t) \bigr)-f\bigl( \eta (t)\bigr)\bigr)^{T}\bigr)^{T}, $$

the error system can be rewritten as

$$\begin{aligned} \textstyle\begin{cases} D^{\alpha }_{t}\mathscr{E}(t)=F(\mathscr{E}(t))+b(\overline{C}\otimes \varGamma )\mathscr{E}(t),& t\in [t_{p},s_{p}), \\ D^{\alpha }_{t}\mathscr{E}(t)=F(\mathscr{E}(t))+b(C\otimes \varGamma )\mathscr{E}(t),& t\in [s_{p},t_{p+1}), \end{cases}\displaystyle \end{aligned}$$
(4)

where \(\overline{C}=C-\operatorname{diag}(k,0,\ldots ,0)\).

Assumption 1

([1])

Suppose that there exist two positive definite diagonal matrices \(P=\operatorname{diag}(p_{1},p_{2},\ldots ,p_{n})\) and \(\Delta =\operatorname{diag}(\delta _{1},\delta _{2},\ldots ,\delta _{n})\) such that

$$\begin{aligned} (u-v)^{T}P\bigl(f(u)-f(v)-\Delta u+\Delta v\bigr)\leq 0 \end{aligned}$$
(5)

for any \(u,v\in \mathbb{R}^{n}\).

Lemma 3

([1])

Suppose that C is an irreducible zero-row-sum matrix with nonnegative off-diagonal elements and \(\mu <0\). Then there exists a positive definite diagonal matrix \(\varPhi =\operatorname{diag}(\phi _{1},\ldots ,\phi _{N})\) such that \(C_{\mu }=C+\operatorname{diag}( \mu ,0,\ldots ,0)\) is Lyapunov stable, i.e., \(\varPhi C_{\mu }+C^{T}_{ \mu }\varPhi <0\).

Assumption 2

([2])

For the aperiodically intermittent control strategy, there exist two positive scalars σ and ψ such that

$$\begin{aligned} \textstyle\begin{cases} \inf_{p}(s_{p}-t_{p})=\sigma >0, \\ \sup_{p}(t_{p+1}-s_{p})=\psi < +\infty . \end{cases}\displaystyle \end{aligned}$$
(6)

Assumption 3

Suppose that the outer coupling matrix C is irreducible and the inner coupling matrix Γ is positive definite.

3 Main results

In this section, some sufficient conditions for achieving synchronization of the controlled network (2) are provided.

Theorem 1

Suppose that Assumptions 1–3 hold. The controlled network (2) with the intermittent pinning control can achieve synchronization if there exist positive constants \(a_{1}\), \(a_{2}\) and \(0<\varpi <1\) such that the following conditions hold:

$$\begin{aligned} &\mathrm{(i)} \quad\varPhi \otimes (P\Delta )+a_{1}\varPhi \otimes P+b \widetilde{C}_{1} \otimes (P\varGamma )\leq 0, \\ &\mathrm{(ii)}\quad \varPhi \otimes (P\Delta )-a_{2}\varPhi \otimes P+b\widetilde{C} _{2}\otimes (P\varGamma )\leq 0, \\ &\mathrm{(iii)}\quad E_{\alpha }\bigl(-a_{1}\sigma ^{\alpha } \bigr)E_{\alpha }\bigl(a_{2} \psi ^{\alpha }\bigr)< \varpi , \end{aligned}$$

where P and Δ are defined in (5), \(\widetilde{C}_{1}=( \varPhi \overline{C})^{s},\widetilde{C}_{2}=(\varPhi C)^{s}\), and Φ is defined according to Lemma 3, i.e., \(\widetilde{C}_{1}<0\).

Proof

Consider the following Lyapunov function:

$$\begin{aligned} V(t)=\frac{1}{2}\mathscr{E}^{T}(t) (\varPhi \otimes P) \mathscr{E}(t). \end{aligned}$$

Then the derivative of \(V(t)\) along the trajectories of (4) satisfies the following:

When \(t\in [t_{p},s_{p})\),

$$\begin{aligned} D_{t}^{\alpha }V(t)\leq {}&\mathscr{E}(t)^{T}(\varPhi \otimes P)D_{t}^{ \alpha }\mathscr{E}(t) \\ ={}&\mathscr{E}(t)^{T}(\varPhi \otimes P) \bigl(F\bigl(\mathscr{E}(t) \bigr)+b( \overline{C}\otimes \varGamma )\mathscr{E}(t) \bigr) \\ \leq{} &\mathscr{E}(t)^{T}\bigl[\varPhi \otimes (P\Delta )\bigr] \mathscr{E}(t)+b \mathscr{E}(t)^{T}\bigl[\varPhi \overline{C}\otimes (P \varGamma )\bigr]\mathscr{E}(t) \\ ={}&\mathscr{E}(t)^{T}\bigl[\varPhi \otimes (P\Delta )+a_{1}\varPhi \otimes P+b \widetilde{C}_{1}\otimes (P\varGamma )\bigr]\mathscr{E}(t) \\ &{} -a_{1}\mathscr{E}(t)^{T}(\varPhi \otimes P)\mathscr{E}(t) \\ \leq{} &{-}a_{1}V(t). \end{aligned}$$

Therefore, from Lemma 2,

$$\begin{aligned} V(t)\leq V(t_{p})E_{\alpha }\bigl(-a_{1}(t-t_{p})^{\alpha } \bigr). \end{aligned}$$
(7)

Similarly, when \(t\in [s_{p},t_{p+1})\),

$$\begin{aligned} D_{t}^{\alpha }V(t)\leq{}& \mathscr{E}(t)^{T}(\varPhi \otimes P)D_{t}^{ \alpha }\mathscr{E}(t) \\ ={}&\mathscr{E}(t)^{T}(\varPhi \otimes P) \bigl(F\bigl(\mathscr{E}(t) \bigr)+b(C\otimes \varGamma )\mathscr{E}(t) \bigr) \\ \leq{}& \mathscr{E}(t)^{T}\bigl[\varPhi \otimes (P\Delta )\bigr] \mathscr{E}(t)+b \mathscr{E}(t)^{T}\bigl[\varPhi C\otimes (P\varGamma )\bigr] \mathscr{E}(t) \\ ={}&\mathscr{E}(t)^{T}\bigl[\varPhi \otimes (P\Delta )-a_{2}\varPhi \otimes P+b \widetilde{C}_{1}\otimes (P\varGamma )\bigr]\mathscr{E}(t) \\ &{} +a_{2}\mathscr{E}(t)^{T}(\varPhi \otimes P)\mathscr{E}(t) \\ \leq{}& a_{2}V(t), \end{aligned}$$

which implies

$$\begin{aligned} V(t)\leq V(s_{p})E_{\alpha }\bigl(a_{2}(t-s_{p})^{\alpha } \bigr). \end{aligned}$$
(8)

For \(0=t_{1}\leq t< s_{1}\), from (7),

$$\begin{aligned} V(t)\leq V(0)E_{\alpha }\bigl(-a_{1}t^{\alpha } \bigr),\qquad V(s_{1})\leq V(0)E_{\alpha }\bigl(-a_{1}s_{1}^{\alpha } \bigr). \end{aligned}$$
(9)

For \(s_{1}\leq t< t_{2}\), from (8) and (9),

$$ \begin{aligned} &V(t)\leq V(s_{1})E_{\alpha } \bigl(a_{2}(t-s_{1})^{\alpha }\bigr)\leq V(0)E_{ \alpha }\bigl(-a_{1}s_{1}^{\alpha } \bigr)E_{\alpha }\bigl(a_{2}(t-s_{1})^{\alpha } \bigr), \\ &V(t_{2})\leq V(s_{1})E_{\alpha }\bigl(a_{2}(t_{2}-s_{1})^{\alpha } \bigr) \leq V(0)E_{\alpha }\bigl(-a_{1}s_{1}^{\alpha } \bigr)E_{\alpha }\bigl(a_{2}(t_{2}-s _{1})^{\alpha }\bigr). \end{aligned} $$
(10)

For \(t_{2}\leq t< s_{2}\), from (7) and (10),

$$ \begin{aligned} &V(t)\leq V(t_{2})E_{\alpha } \bigl(-a_{1}(t-t_{2})^{\alpha }\bigr) \\ &\phantom{V(t)}\leq V(0)E _{\alpha }\bigl(-a_{1}s_{1}^{\alpha } \bigr)E_{\alpha }\bigl(a_{2}(t_{2}-s_{1})^{ \alpha } \bigr)E_{\alpha }\bigl(-a_{1}(t-t_{2})^{\alpha } \bigr), \\ &V(s_{2})\leq V(t _{2})E_{\alpha } \bigl(-a_{1}(s_{2}-t_{2})^{\alpha }\bigr) \\ &\phantom{V(s_{2})}\leq V(0)E_{\alpha }\bigl(-a_{1}s_{1}^{\alpha } \bigr)E_{\alpha }\bigl(a_{2}(t_{2}-s_{1})^{\alpha } \bigr)E _{\alpha }\bigl(-a_{1}(s_{2}-t_{2})^{\alpha } \bigr). \end{aligned} $$
(11)

For \(s_{2}\leq t< t_{3}\), from (8) and (11),

$$ \begin{aligned} &V(t)\leq V(s_{2})E_{\alpha } \bigl(a_{2}(t-s_{2})^{\alpha }\bigr) \\ &\phantom{V(t)}\leq V(0)E _{\alpha }\bigl(-a_{1}(s_{2}-t_{2})^{\alpha } \bigr)E_{\alpha }\bigl(-a_{1}s_{1}^{ \alpha }\bigr) \\ &\phantom{V(t)\leq}{} \times E_{\alpha }\bigl(a_{2}(t_{2}-s_{1})^{\alpha } \bigr)E_{\alpha }\bigl(a_{2}(t-s _{2})^{\alpha } \bigr), \\ &V(t_{3})\leq V(s_{2})E_{\alpha }\bigl(a_{2}(t_{3}-s _{2})^{\alpha }\bigr) \\ &\phantom{V(t_{3})}\leq V(0)E_{\alpha }\bigl(-a_{1}(s_{2}-t_{2})^{\alpha } \bigr)E_{\alpha }\bigl(-a_{1}s_{1}^{\alpha }\bigr) \\ &\phantom{V(t_{3})\leq}{} \times E_{\alpha }\bigl(a_{2}(t_{2}-s_{1})^{\alpha } \bigr)E_{\alpha }\bigl(a_{2}(t _{3}-s_{2})^{\alpha } \bigr). \end{aligned} $$
(12)

By mathematical induction, for \(t_{l}\leq t< s_{l}\),

$$\begin{aligned} V(t)\leq V(0)E_{\alpha }\bigl(-a_{1}(t-t_{l})^{\alpha } \bigr)\prod^{l-1}_{p=1}E _{\alpha } \bigl(-a_{1}(s_{p}-t_{p})^{\alpha }\bigr) E_{\alpha }\bigl(a_{2}(t_{p+1}-s _{p})^{\alpha } \bigr), \end{aligned}$$
(13)

and for \(s_{l}\leq t< t_{l+1}\),

$$\begin{aligned} V(t)\leq {}&V(0)E_{\alpha }\bigl(a_{2}(t-s_{l})^{\alpha } \bigr)E_{\alpha }\bigl(-a_{1}(s _{l}-t_{l})^{\alpha } \bigr) \\ &{} \times \prod^{l-1}_{p=1}E_{\alpha } \bigl(-a_{1}(s_{p}-t_{p})^{\alpha }\bigr) E _{\alpha }\bigl(a_{2}(t_{p+1}-s_{p})^{\alpha } \bigr). \end{aligned}$$
(14)

Assume that inequalities (13) and (14) hold when \(l\leq k\). Then

$$\begin{aligned} V(t_{k+1})\leq V(0)\prod^{k}_{p=1}E_{\alpha } \bigl(-a_{1}(s_{p}-t_{p})^{ \alpha }\bigr) E_{\alpha }\bigl(a_{2}(t_{p+1}-s_{p})^{\alpha } \bigr). \end{aligned}$$

Now, for \(t_{k+1}\leq t< s_{k+1}\),

$$\begin{aligned} &V(t)\leq V(t_{k+1})E_{\alpha }\bigl(-a_{1}(t-t_{k+1})^{\alpha } \bigr) \\ & \phantom{V(t)}\leq V(0)E_{\alpha }\bigl(-a_{1}(t-t_{k+1})^{\alpha } \bigr) \\ &\phantom{V(t)\leq}{}\times \prod^{k}_{p=1}E_{\alpha } \bigl(-a_{1}(s_{p}-t_{p})^{\alpha }\bigr) E _{\alpha }\bigl(a_{2}(t_{p+1}-s_{p})^{\alpha } \bigr), \\ &V(s_{k+1})\leq V(0)E_{\alpha }\bigl(-a_{1}(s_{k+1}-t_{k+1})^{\alpha } \bigr) \\ &\phantom{V(s_{k+1})\leq}{}\times \prod^{k}_{p=1}E_{\alpha } \bigl(-a_{1}(s_{p}-t_{p})^{\alpha }\bigr) E _{\alpha }\bigl(a_{2}(t_{p+1}-s_{p})^{\alpha } \bigr), \end{aligned}$$

and for \(s_{k+1}\leq t< t_{k+2}\),

$$\begin{aligned} V(t)\leq {}& V(s_{k+1})E_{\alpha }\bigl(a_{2}(t-s_{k+1})^{\alpha } \bigr) \\ \leq {}& V(0)E_{\alpha }\bigl(a_{2}(t-s_{k+1})^{\alpha } \bigr)E_{\alpha }\bigl(-a_{1}(s _{k+1}-t_{k+1})^{\alpha } \bigr) \\ & {}\times \prod^{k}_{p=1}E_{\alpha } \bigl(-a_{1}(s_{p}-t_{p})^{\alpha }\bigr) E _{\alpha }\bigl(a_{2}(t_{p+1}-s_{p})^{\alpha } \bigr), \end{aligned}$$

that is, inequalities (13) and (14) hold for \(l=k+1\). Thus, for any l,

$$\begin{aligned} V(t_{l})\leq {}& V(0)\prod^{l-1}_{p=1}E_{\alpha } \bigl(-a_{1}(s_{p}-t_{p})^{ \alpha }\bigr) E_{\alpha }\bigl(a_{2}(t_{p+1}-s_{p})^{\alpha } \bigr) \\ \leq{} & V(0) \prod^{l-1}_{p=1}E_{\alpha } \bigl(-a_{1}\sigma ^{\alpha }\bigr) E _{\alpha } \bigl(a_{2}\psi ^{\alpha }\bigr) \\ \leq{} & V(0) \varpi ^{l-1}, \end{aligned}$$
(15)

i.e., \(V(t_{l})\to 0\) as \(l\to \infty \). And for \(t_{l}\leq t< s_{l}\),

$$\begin{aligned} V(t)\leq V(t_{l})E_{\alpha }\bigl(-a_{1}(t-t_{l})^{\alpha } \bigr), \end{aligned}$$

which implies that \(V(t)\to 0\) as \(t\to \infty \). Similarly, one can show that \(V(t)\to 0\) as \(t\to \infty \) for \(s_{l}\leq t< t_{l+1}\). Then, the synchronization is achieved and the proof is completed. □

Let \(\kappa ^{*}=\lambda _{\max }(\varPhi \otimes (P\Delta ))\), \(\vartheta ^{*}=\lambda _{\max }(\varPhi \otimes P)\), \(\vartheta _{*}=\lambda _{\min }( \varPhi \otimes P)\), \(c^{*}_{1}=\lambda _{\max }(\widetilde{C}_{1}\otimes (P\varGamma ))\), and \(c^{*}_{2}=\lambda _{\max }(\widetilde{C}_{2}\otimes (P\varGamma ))\). We have the following corollary.

Corollary 1

Suppose that Assumptions 1–3 hold. The controlled network (2) with the intermittent pinning control can achieve synchronization if there exist positive constants \(a_{1}\), \(a_{2}\), and \(0<\varpi <1\) such that the following conditions hold:

$$\begin{aligned} &\mathrm{(i)}\quad \kappa ^{*}+a_{1}\vartheta ^{*}+bc^{*}_{1} \leq 0, \\ &\mathrm{(ii)} \quad\kappa ^{*}-a_{2}\vartheta _{*}+bc^{*}_{2} \leq 0, \\ &\mathrm{(iii)}\quad E_{\alpha }\bigl(-a_{1}\sigma ^{\alpha } \bigr)E_{\alpha }\bigl(a_{2} \psi ^{\alpha }\bigr)< \varpi . \end{aligned}$$

Remark 1

If we choose \(t_{p+1}-t_{p}=T>0\) and \(s_{p}-t_{p}= \kappa T\) with \(0<\kappa <1\), then the intermittent control is periodic. And condition (iii) in Theorem 1 (or Corollary 1) is rewritten as \(E_{\alpha }(-a_{1}(\kappa T)^{\alpha })E_{\alpha }(a_{2}((1-\kappa ) T)^{\alpha })<\varpi <1\), which is similar to condition (iii) in Theorem 1 of Ref. [38]. That is, the obtained results generalize the results in Ref. [38] from periodic control to aperiodic control.

Remark 2

If we choose \(\alpha =1\), then network (2) is an integer-order network and condition (iii) in Theorem 1 (or Corollary 1) is rewritten as \(e^{-a_{1}\sigma }e^{a_{2}\psi }<\varpi \). Further, we have \(a_{2}\psi -a_{1}\sigma <\ln \varpi <0\), which is similar to the condition in Corollary 4 of Ref. [8]. That is, we generalize the results from integer-order network to fractional-order network.

4 Numerical simulations

Consider a fractional-order dynamical network consisting of 10 nodes. The node dynamics is chosen as the following fractional-order Chua circuit [41]:

$$\begin{aligned} \textstyle\begin{cases} D^{\alpha }_{t} x_{i1}=9(x_{i2}-x_{i1}-\varphi (x_{i1})), \\ D^{\alpha }_{t} x_{i2}=x_{i1}-x_{i2}+x_{i3}, \\ D^{\alpha }_{t} x_{i3}=-100/7x_{i2}, \end{cases}\displaystyle \end{aligned}$$
(16)

where \(i=1,2,\ldots ,10\), \(\alpha =0.99\), \(\varphi (x_{i1})=-5/7x_{i1}-3/14(|x _{i1}+1|-|x_{i1}-1|)\).

For simplicity, choose P as an identity matrix. Then one has

$$\begin{aligned} & (x_{i}-s)^{T}\bigl(f(x_{i})-f(s)\bigr) \\ &\quad=e_{i}^{T}\bigl(9e_{i2}-9e_{i1}-9 \bigl(\varphi (x_{i1})-\varphi (s_{1})\bigr),e _{i1}-e_{i2}+e_{i3},-100/7e_{i2} \bigr)^{T} \\ &\quad\leq 9/7e_{i1}^{2}-e_{i2}^{2}+10e_{i1}e_{i2}-93/7e_{i2}e_{i3} \\ &\quad\leq \biggl(\frac{9}{7}+5\rho \biggr)e_{i1}^{2}+ \biggl(-1+\frac{5}{\rho }+\frac{93 \beta }{14}\biggr)e_{i2}^{2}+ \frac{93}{14\beta }e_{i3}^{2}. \end{aligned}$$

Let \(\rho =1.36\) and \(\beta =0.83\), we can choose \(\Delta =\operatorname{diag}(8.19,8.19,8.19)\) such that Assumption 1 holds.

In numerical simulations, we choose \(k=1\), \(b=100\), Γ as an identity matrix and

C= [ − 3 0 1 1 1 0 0 0 0 0 1 − 5 0 1 1 1 1 0 0 0 1 1 − 5 0 1 1 1 0 0 0 1 1 0 − 4 1 0 1 0 0 0 0 1 1 1 − 4 0 1 0 0 0 1 1 1 1 0 − 4 0 0 0 0 0 1 1 0 0 0 − 4 1 1 0 1 0 0 0 0 0 0 − 2 0 1 0 0 0 0 0 0 1 0 − 2 1 0 0 0 0 0 0 0 1 1 − 2 ] .

The real parts of the eigenvalues of C are \(0, -0.7876, -2, -3.3482, -3.615, -3.615, -4.3919, -4.6587, -6.2918, -6.2918\). That is, the matrix C is irreducible. According to the discussions in [1], we choose

$$ \varPhi =\operatorname{diag}(0.4206,0.2602,0.2409,0.2764,0.2995,0.1253,0.359,0.359,0.359,0.359) $$

in Lemma 3. By simple calculations, we have \(\kappa ^{*}=3.4447\), \(\vartheta ^{*}=0.4206\), \(\vartheta _{*}=0.1253\), \(c^{*}_{1}=-0.0857\), and \(c^{*}_{2}=0\). Then we choose \(a_{1}=12\) and \(a_{2}=27.5\) such that conditions (i) and (ii) in Corollary 1 hold. Further, we choose \(\sigma =0.05\), \(\psi =0.02\), and \(\varpi =0.96\). We have \(E _{\alpha }(-12\sigma ^{\alpha }) E_{\alpha }(27.5\psi ^{\alpha })=0.9581< \varpi \), i.e., condition (iii) in Corollary 1 holds. Specially, we choose the first 7 elements of sequences \(\{t_{p}\}\) and \(\{s_{p}\}\) as \((0,0.06,0.14,0.21,0.3,0.36,0.42)\) and \((0.05,0.12,0.19,0.28,0.35,0.41,0.5)\). Figure 1 shows the orbits of the synchronization errors \(e_{ij}(t)\), \(i=1,2,\ldots ,10, j=1,2,3\).

Figure 1
figure 1

The orbits of the synchronization errors \(e_{ij}(t)\), \(i=1,2,\ldots ,10,j=1,2,3\).

Full size image

5 Conclusions

In this paper, the synchronization of complex network coupled with fractional-order dynamical systems is studied. Aperiodically intermittent control scheme is adopted to design effective controllers combining with pinning strategy. That is, only the first node is controlled. Sufficient conditions for achieving the synchronization are derived and verified by numerical example. Obviously, the obtained results for networks with only one controller are also valid for networks with more controllers. Therefore, in practical applications, especially for large-scale networks, more nodes are usually controlled to reduce the coupling strength and/or control gain.