Pinning synchronization of complex directed dynamical networks under decentralized adaptive strategy for aperiodically intermittent control

Abstract

In this paper, the problem of global synchronization for complex directed dynamical networks via adaptive aperiodically intermittent pinning control is studied. By constructing a piecewise Lyapunov function, some sufficient conditions to guarantee global synchronization are derived based on the analytical technique and theory of series with nonnegative terms. Different from previous works, the adaptive intermittent pinning control is aperiodic with non-fixed both control period and control width, and moreover, the adaptive approach is decentralized relying only on the state information of the controlled node. Hence, the adaptive intermittent pinning control strategy proposed in this paper is more practically applicable than those in previous works. Additionally, it is noted that the derived synchronization criteria are dependent on the control rates, but not the control widths or the control periods, which makes the theoretical results are less conservative than the corresponding results given in the existing works. A numerical example is finally provided to illustrate the validity of our theoretical results.

1 Introduction

In the past few decades, complex dynamical networks consisting of a number of coupled dynamical nodes connected by edges have received great attention in various fields of science and engineering. Actually, many large-scale systems in nature and human societies can be modeled as complex dynamical networks, such as power grid networks, communication networks, food webs, biomolecular networks, and social networks [1,2,3]. As a typical collective behavior of complex dynamical networks, synchronization has become a hot topic due to the potential applications in image processing, secure communication, etc. Up to now, various synchronization patterns have been studied, such as complete synchronization, phase synchronization, cluster synchronization, lag synchronization, and generalized synchronization [4,5,6].

In a dynamical network, as is well known, for forcing the states of all network nodes to synchronize with a desired objective trajectory, appropriate controllers should be added to the network nodes. Hitherto, many control techniques have been developed for synchronization problem, including pinning control [7, 8], adaptive control [9], impulsive control [10], intermittent control [11], sample-data control [12], and event-triggered control [13]. Among these control approaches, intermittent control is a discontinuous feedback control, which is activated during certain nonzero time intervals but is off during other time intervals [11, 14]. Owing to its practical and easy implementation in engineering control, intermittent control has been widely used in engineering fields, such as manufacturing, transportation and communication [11, 14, 15].

Recently, a periodically intermittent control strategy has been proposed and its application on synchronization has also been investigated [11, 14,15,16,17,18,19,20,21,22,23,24,25,26,27]. For example, the exponential synchronization of complex dynamical networks with finite distributed delays coupling via periodically intermittent control was explored in [15]. In [16, 17], the authors studied the exponential synchronization of delayed chaotic systems with parameter mismatches via periodically intermittent control. In [18], the exponential synchronization of neural networks with mixed delays and reaction diffusion was discussed by using periodically intermittent control. In [11, 19,20,21], the pinning synchronization problem for complex dynamical networks with or without delay was considered via periodically intermittent control. In [22,23,24,25], the cluster synchronization of complex dynamical networks was analyzed by means of periodically intermittent pinning control. In [26, 27], the finite-time synchronization of complex dynamical networks with or without time-varying delay under periodically intermittent control was investigated.

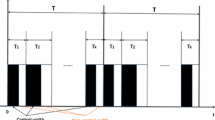
It should be noted that the intermittent control adopted in previous works [11, 14,15,16,17,18,19,20,21,22,23,24,25,26,27] is periodic, where the control period and the control width are both required to be fixed constants. Obviously, this requirement is quite restricted and may be unreasonable in practice. In fact, in practical applications, the control period and control width of intermittent control strategy are both expected to be changeable and therefore adjusted in accordance to actual requirements. In view of this, Liu and Chen [28] generalizes the periodically intermittent control strategy to aperiodically intermittent control strategy, see Fig. 1. For any time span $[t_k, t_{k+1})$ (k $\in$ $Z^+=\{1,2,\ldots \}$), $[t_k, t_k+\delta _k]$ is the kth work time and $\delta _k>0$ is called the kth control width (control duration), while $\big (t_k+\delta _k, t_{k+1}\big )$ is the kth rest time and $(t_{k+1}-t_k)-\delta _k>0$ is called the kth rest width (rest duration). In addition, $(t_{k+1}-t_k)$ is called the kth control period. Evidently, here each control period and each control width is non-fixed, and hence this control strategy is more general. In particular, when $t_{k+1}-t_k\equiv \mathrm{T}$ and $\delta _k\equiv \delta$, $k\in Z^+$, the intermittent control type becomes the periodic one, which has been studied in [11, 14,15,16,17,18,19,20,21,22,23,24,25,26,27].

Fig. 1

Sketch map of aperiodically intermittent control strategy, where $\mathrm{T}_k=t_{k+1}-t_k$, k $\in$ $Z^+$

Currently, some initial results have been reported on the synchronization of chaotic systems and complex dynamical networks via aperiodically intermittent control [28,29,30,31,32]. In [28] and [29], the authors considered the synchronization problem for complex dynamical networks with linear coupling function as well as nonlinear coupling function via aperiodically intermittent pinning control, respectively. In [30, 31], aperiodically intermittent pinning control for the exponential synchronization of complex delayed dynamical networks was investigated. In [32], the stabilization and synchronization for chaotic systems with mixed time-varying delays were considered via aperiodically intermittent control. Additionally, the synchronization of complex dynamical networks under adaptive scheme for aperiodically intermittent pinning control was also investigated in [28,29,30]. It is worth mentioning that the adaptive approach proposed in [28,29,30] is centralized, which requires the state information of all network nodes (i.e., global information of the whole network). Obviously, it is hard and costly to implement for large-scale networks. For a given node in a dynamical network, the state information of network nodes directly connected with it can be easily accessed. Therefore, a more reasonable adaptive approach is decentralized (or distributed) [21, 33,34,35], which only relies on local information instead of global information of the whole network. However, to the best of our knowledge, synchronization of complex dynamical networks under decentralized adaptive strategy for aperiodically intermittent pinning control has not been investigated, despite its importance for potential practical applications. In this paper, we will solve this problem.

Motivated by the above analysis, the purpose of this paper is to introduce a decentralized adaptive strategy for aperiodically intermittent pinning control to investigate global synchronization of complex directed dynamical networks. By employing the analytical technique and theory of series with nonnegative terms, some global synchronization criteria are obtained through constructing a piecewise Lyapunov function. Numerical simulations are also given to illustrate the effectiveness of the proposed control methodology. The main contribution of this paper lies in the following three aspects: (1) the intermittent pinning control is aperiodic with non-fixed both control period and control width, which expands intermittent control strategy’s scope; (2) the designed adaptive approach is decentralized relying only on the state information of the controlled node, which is more practically applicable than that in previous works; (3) the derived synchronization criteria are dependent on the control rates, but not the control widths or the control periods, which makes the theoretical results are less conservative than the corresponding results given in the existing works.

Throughout this paper, the following notations and definitions will be used. Let ${\mathbb {R}}=(-\infty , +\infty )$ be the set of real numbers, ${\mathbb {R}}^+=[0, +\infty )$ be the set of nonnegative real numbers, and $Z^+=\{1,2,\ldots \}$ be the set of positive integer numbers. ${\mathbb {R}}^{n}$ denotes the $n-$dimensional Euclidean space. The superscript $\top$ denotes matrix or vector transposition. For a vector $u\in {\mathbb {R}}^n$, its norm is defined as $||u||=\sqrt{u^{\top }u}$. ${\mathbb {R}}^{n\times n}$ stands for the set of $n\times n$ real matrices. $I_n\in {\mathbb {R}}^{n\times n}$ is an $n-$dimensional identity matrix, $\mathrm{diag}(\gamma _1,\gamma _2,\ldots ,\gamma _n)\in {\mathbb {R}}^{n\times n}$ is the diagonal matrix with diagonal entries $\gamma _i$ $(1\le i \le n)$. For a square matrix $A\in {\mathbb {R}}^{n\times n}$, $A^s=\frac{1}{2}(A+A^{\top })$ is its symmetric part, and $\lambda _{\min }(A)$ and $\lambda _{\max }(A)$ denote its minimum and maximum eigenvalue, respectively. For a real symmetric matrix $M\in {\mathbb {R}}^{n\times n}$, write $M>0$ $(M<0)$ if M is positive (negative) definite, and $M\ge 0$ $(M\le 0)$ if M is semi-positive (semi-negative) definite. The Kronecker product of an $N\times M$ matrix $A=(a_{ij})$ and a $p\times q$ matrix B is the $Np\times Mq$ matrix $A\otimes B$, defined as

$$\begin{aligned} A\otimes B= \left( \begin{matrix} a_{11}B\,&{} \cdots \,&{} a_{1M}B \\ \vdots \,&{}\ddots \,&{} \vdots \\ a_{N1}B \,&{} \cdots \,&{} a_{NM}B \end{matrix} \right) \end{aligned}$$

and the Kronecker product has the property

$$\begin{aligned} (A\otimes B)(C\otimes D)=(AC)\otimes (BD). \end{aligned}$$

2 Model and preliminaries

Consider a general complex network consisting of N linearly coupled identical dynamical nodes, which is described by the following equations [5]:

$$\begin{aligned} \dot{x}_{i}(t)= & {} f(t,x_{i}(t))+c\sum _{j\,=1,j\,\ne i}^{N} g_{ij}\,\Gamma \big (x_j\,(t)\nonumber \\&-x_{\,i}(t)\big ),\quad i\in \mathfrak {T}, \end{aligned}$$

(1)

where $\mathfrak {T}= \{1,2,\dots ,N\}$, $x_i(t)=(x_{i1}(t),x_{i2}(t),\ldots ,$ $x_{in}(t))^{\top }$ $\in$ ${\mathbb {R}}^{\,n}$ is the state vector of the ith node, $f(t,x_i(t))$ $=\!$ $\big ( f_1(t,x_i(t)),f_2(t,x_i(t)),\ldots ,f_n(t,$ $x_i(t))\big )^{\top }:{\mathbb {R}}^+\times {\mathbb {R}}^{\,n}\rightarrow {\mathbb {R}}^{\,n}$ is a continuous vector-valued function describing the local dynamics of each isolated node, $c>0$ is the coupling strength, $\Gamma =(\gamma _{ij})_{n\times n}\in {\mathbb {R}}^{\,n\times n}>0$ is the inner connecting matrix describing the individual coupling between nodes, $G=(g_{ij})_{N\times N}\in {\mathbb {R}}^{\,N\times N}$ is the coupling matrix representing the underlying topological structure of the whole network, in which $g_{ij}$ is defined as follows: if there is a directed link from node j to node i $(j\ne i)$, then $g_{ij}>0$; otherwise, $g_{ij}=0$. Additionally, the diagonal elements of matrix G are defined by $g_{ii}=-\sum _{j=1,j\,\ne i}^{N} g_{ij}$, $i\in \mathfrak {T}$, and therefore one has $\sum _{j=1}^{N} g_{ij}=0,$ $i\in \mathfrak {T}$. Note that the coupling matrix G is not necessarily symmetric or irreducible, which is more consistent with a realistic dynamical network.

For convenience , let $\mathrm{Deg}_\mathrm{in}(i)$ and $\mathrm{Deg}_\mathrm{out}(i)$ be the in-degree and out-degree of the ith node in network (1), respectively. By the definition of matrix G, one has

$$\begin{aligned} \mathrm{Deg}_\mathrm{in}(i)= & {} \sum _{j=1,j\,\ne i}^{N} g_{ij}=-g_{ii} \,\,\,\, \mathrm{and}\,\,\,\, \mathrm{Deg}_\mathrm{out}(i)\nonumber \\= & {} \sum _{j=1,j\,\ne i}^{N} g_{j\,i},\quad i\in \mathfrak {T}. \end{aligned}$$

(2)

In addition, define the degree difference between the out-degree and in-degree of node i as $\mathrm{Deg_{diff}}(i)=\mathrm{Deg_{out}}(i)-\mathrm{Deg_{in}}(i)$, $i\in \mathfrak {T}$. The degree-difference information of all network nodes will be used later to guide what kind of nodes should be preferentially chosen to be pinned.

Clearly, the dynamical behavior of each uncoupled node in network (1) is expressed by

$$\begin{aligned} \dot{x}(t)=f(t,x(t)), \end{aligned}$$

(3)

where x(t) $=$ $\big (x_{1}(t),\ldots ,x_{n}(t)\big )^{\top }\in {\mathbb {R}}^{n}$. This general model takes many dynamical systems as special cases, for instance, Hodgkin–Huxley models, Lorenz chaotic oscillators, Chua’s circuits, recurrently connected neural networks, cellular neural networks, and so on [9, 22].

Let s(t) be a solution of the uncoupled node dynamics $\dot{x}(t)$ $=$ f(t, x(t)). The main objective of this paper is to apply adaptive aperiodically intermittent control scheme combined with pinning strategy to make the states of all network nodes $x_i(t)$, $i\in \mathfrak {T}$ globally asymptotically synchronize with the desired trajectory s(t), i.e., for any initial conditions

$$\begin{aligned} \lim _{t\rightarrow \infty }||x_i(t)-s(t) ||=0,\quad i\in \mathfrak {T}. \end{aligned}$$

(4)

For achieving the control aim (4), some adaptive aperiodical intermittent controllers are added to partial nodes of network (1). Without loss of generality, suppose the first $l\,(1\le l <N)$ nodes are selected to be controlled; otherwise, we can rearrange the order of the network nodes. Then the controlled dynamical network can be described as:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \dot{x}_{i}(t)= f(t,x_{i}(t))+c\sum _{j=1}^{N}g_{ij}\,\Gamma x_{j\,}(t)+u_i(t),\,\,\quad 1\le i \le l, \\ \displaystyle x_{i}(t)=f(t,x_{i}(t))+c\sum _{j=1}^{N}g_{ij}\,\Gamma x_{j\,}(t),\quad \quad \, l+1\le i \le N, \end{array} \right. \end{aligned}$$

(5)

Here, the control input $u_i(t)$ is designed as an adaptive aperiodical intermittent controller, which is defined by

$$\begin{aligned} u_i(t)=d_i(t)\Gamma \big (s(t)-x_i(t)\big ), \quad 1\le i \le l, \end{aligned}$$

(6)

where

$$\begin{aligned} d_i(t)=\left\{ \begin{array}{lll} \,\,d_i(0), \quad \quad \quad \quad \quad t=0,\\ \,\,d_i\big (t_k+\delta _k\big ), \quad \quad t=t_{k+1},\\ \quad \,0, \quad \quad \quad \quad \quad \,\,\, t_k+\delta _k<t<t_{k+1}, \end{array} \right. \end{aligned}$$

(7)

and

$$\begin{aligned} \dot{d}_{i}(t)= & {} h_i \big (x_i(t)-s(t)\big )^{\top }\Gamma \big (x_i(t)\nonumber \\&-s(t)\big ),\quad t_k \le t \le t_k+\delta _k, \end{aligned}$$

(8)

where $t_1= 0$, $k\in Z^+$, $h_i$ $(1\le i \le l)$ are small positive constants, $d_i(0)\ge 0$ $(1\le i \le l)$. Without loss of generality, we assume that $\sup _{k\in Z^+}\{t_{k+1}-t_k\}$ $=$ $\mathrm{T}_{\mathrm{sup}}<\infty$ and $\inf _{k\in Z^+}\{t_{k+1}-t_k\}$ $=$ $\mathrm{T}_{\mathrm{inf}}>0$.

For $k\in Z^+$, denote $\mathrm{T}_0$ $=$ ${\hat{\mathrm{T}}}_0$ $=$ $t_1$, $\mathrm{T}_k$ $=$ $t_{k+1}-t_k$, ${\hat{\mathrm{T}}}_k$ $=$ $\sum _{j=0}^{k} \mathrm{T}_j$, and $\theta _k=\delta _k/\mathrm{T}_k$, where $\theta _k$ is called the control rate of the kth control period. Then, one can get that $t_k$ $=$ ${\hat{\mathrm{T}}}_{k-1}$ and $\delta _k$ $=$ $\theta _k \mathrm{T}_k$, k $\in$ $Z^+$. Define error variables as $e_i(t)=x_i(t)-s(t)$, $i\in \mathfrak {T}$. According to (6)–(8), we can derive the following error dynamical system:

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle \dot{e}_{i}(t)=\tilde{f}(t,x_{i},s)+c\sum _{j=1}^{N}g_{ij}\,\Gamma e_{j}(t)-d_i(t)\Gamma e_i(t), \quad {\hat{\mathrm{T}}}_{k-1} \le t \le {\hat{\mathrm{T}}}_{k-1}+\theta _{k}\mathrm{T}_{k},\,1\le i \le l,\\ \displaystyle \dot{e}_{i}(t)=\tilde{f}(t,x_{i},s)+c\sum _{j=1}^{N}g_{ij}\,\Gamma e_{j}(t),\quad \quad \quad \quad \,\, \quad {\hat{\mathrm{T}}}_{k-1} \le t \le {\hat{\mathrm{T}}}_{k-1}+\theta _{k}\mathrm{T}_{k},\,l+1\le i \le N,\\ \displaystyle \dot{e}_{i}(t)=\tilde{f}(t,x_{i},s)+c\sum _{j=1}^{N} g_{ij}\,\Gamma e_{j}(t),\,\quad \quad \quad \quad \quad \,\, {\hat{\mathrm{T}}}_{k-1}+\theta _{k}\mathrm{T}_{k}< t <{\hat{\mathrm{T}}}_{k},\,1\le i \le N, \end{array} \right. \end{aligned}$$

(9)

where $k\in Z^+$ and $\tilde{f}(t,x_{i},s)=f(t,x_{i}(t))-f(t,s(t))$. It is evident that globally asymptotical synchronization of the controlled dynamical network (5) is achieved if the error variables satisfy $\lim _{t\rightarrow \infty }||$ $e_i(t)||=0$, $i\in \mathfrak {T}$.

To derive our main results, the following assumption and lemmas are necessary.

Assumption 1

[8]: For the vector-valued function f(t, x(t)), suppose there exists a positive constant $L_0>0$ such that for any x(t), $y(t)\in {\mathbb {R}}^{\,n}$, the following condition holds:

$$\begin{aligned}&\big [x(t)-y(t)\big ]^{\top }\big [f(t,x(t))-f(t,y(t))\big ]\\&\quad \le L_0\,\big [x(t)-y(t)\big ]^{\top }\Gamma \big [x(t)-y(t)\big ]. \end{aligned}$$

Remark 1

Assumption 1 gives some requirements for the dynamics of isolated node in network (1). If the function f(t, x(t)) satisfies Lipschitz condition with respect to the time t, i.e., $||f(t,x(t))-f(t,y(t))||\le K_0 ||x(t)-y(t)||$, where $K_0>0$ is a positive constant, then one can choose $L_0=\frac{K_0}{\lambda _{\min }(\Gamma )}$ to satisfy Assumption 1. Moreover, it has been verified in [7,8,9, 31, 36] that many well-known chaotic systems such as Lorenz system, Chen system, Lü system, Rössler system, and Chua’s circuit also satisfy Assumption 1.

Lemma 1

[37]: Assume that $B_1$ and $B_2$ are two real symmetric matrices in ${\mathbb {R}}^{N\times N}$. Let $\alpha _1\ge \alpha _2\ge \ldots \ge \alpha _N$, $\beta _1\ge \beta _2\ge \ldots \ge \beta _N$ and $\gamma _1\ge \gamma _2\ge \ldots \ge \gamma _N$ be eigenvalues of matrices $B_1$, $B_2$ and $B_1+B_2$, respectively. Then, one has $\alpha _i+\beta _N\le \gamma _i \le \alpha _i+\beta _1$, $i\in \mathfrak {T}$.

Lemma 2

(Schur complement [38]): The following linear matrix inequality (LMI):

$$\begin{aligned} \left( \begin{matrix} S_{11} &{} \quad S_{12} \\ S_{12}^{\top } &{} \quad S_{22} \end{matrix} \right) <0 \end{aligned}$$

where $S_{11}=S_{11}^{\top }$, $S_{22}=S_{22}^{\top }$, and $S_{12}$ is a matrix with suitable dimensions, is equivalent to the following condition:

$$\begin{aligned} S_{22}<0, \quad S_{11}-S_{12}S_{22}^{-1}S_{12}^{\top }<0. \end{aligned}$$

3 Results

Hereinafter, let the matrix $G^s$ be defined as $G^s \overset{\mathrm{def}}{=}(G+G)/2$, and $( G^s)_l$ be the minor matrix of $G^s$ by removing its first l row–column pairs. It is easy to see that $G^s$ is a symmetric matrix with nonnegative off-diagonal elements and generally does not possess the property of zero row sums. In the following, by constructing a piecewise Lyapunov function, some sufficient conditions for globally asymptotical synchronization of the controlled dynamical network (5) under the adaptive aperiodical intermittent controllers (6)–(8) will be derived based on the analytical technique and theory of series with nonnegative terms [21, 39].

Theorem 1

Suppose that $\displaystyle \inf _{k\in Z^+} \theta _k$ $=$ $\theta _{\inf }$ > 0. Under Assumption 1, the controlled dynamical network (5) with the adaptive aperidical intermittent controllers (6)–(8) is globally asymptotically synchronized if there exist two constants $a_1>0$ and $a_2\ge 0$ such that

• (i) $L_0+a_1+c\lambda _{\max } \big (( G^s)_l\big )< 0$,

• (ii) $(L_0-a_2) I_N + c G^s \le 0,$

• (iii) $(p_1+p_2)\theta _{\inf }-p_2>0$,

where $p_1=2 a_1 \lambda _{\min }(\Gamma )$ and $p_2=2a_2 \lambda _{\max }(\Gamma )$.

Proof

Introduce a piecewise function defined as

$$\begin{aligned}&\Phi (t)\nonumber \\&\quad = \left\{ \begin{array}{lll} \displaystyle \frac{1}{2}\,\mathrm{exp}\left\{ -p_1\left( t-{\hat{\mathrm{T}}}_{k-1}\right) \right\} \displaystyle \sum _{i=1}^{l} \frac{1}{h_i}\big (d_i(t)-d_i^*\big )^2,\,\,\quad \qquad {\hat{\mathrm{T}}}_{k-1} \le t \le {\hat{\mathrm{T}}}_{k-1}+\theta _{k}\mathrm{T}_{k},\\ \displaystyle \frac{1}{2}\,\mathrm{exp}\left\{ p_2\left( t-\left( {\hat{\mathrm{T}}}_{k-1}+\theta _{k}\mathrm{T}_{k}\right) \right) -p_1\theta _{k}\mathrm{T}_{k}\right\} \displaystyle \sum _{i=1}^{l}\frac{1}{h_i}\left( d_i\left( {\hat{\mathrm{T}}}_{k-1}+\theta _{k}\mathrm{T}_{k}\right) -d_i^*\right) ^2,\\ \qquad \qquad \qquad \qquad {\hat{\mathrm{T}}}_{k-1}+\theta _{k}\mathrm{T}_{k}< t <{\hat{\mathrm{T}}}_{k}, \end{array} \right. \end{aligned}$$

(10)

where $k\in Z^+$, and $d_i^*>0$ is a sufficiently large positive constant to be determined later. Let $\varpi _{k}$ $=$ $p_2(1-\theta _{k})-p_1\theta _{k}$, $k\in Z^+$. By (7) and (10), it is easy to verify that $\Phi (t)$ is continuous except for $t={\hat{\mathrm{T}}}_{k}$ with $k\in Z^+$ and

$$\begin{aligned} \Phi \big ({\hat{\mathrm{T}}}_{k} \big )=\Phi _{+}\big ({\hat{\mathrm{T}}}_{k} \big )=\mathrm{exp}\big \{-\varpi _{k} \mathrm{T}_{k}\big \}\Phi _{-}\big ({\hat{\mathrm{T}}}_{k} \big ), \end{aligned}$$

(11)

where $\Phi _{-}\big ({\hat{\mathrm{T}}}_{k} \big )=\lim _{t\rightarrow {\hat{\mathrm{T}}}_{k}^-} \Phi (t)$ and $\Phi _{+}\big ({\hat{\mathrm{T}}}_{k} \big )=\lim _{t\rightarrow {\hat{\mathrm{T}}}_{k}^+} \Phi (t)$ represent the left-hand limit and the right-hand limit of $\Phi (t)$ at time $t={\hat{\mathrm{T}}}_{k}$, respectively.

Let e(t) $=$ $\left( e_1^{\top }(t),e_2^{\top }(t),\ldots ,e_N^{\top }(t)\right) ^{\top },$ and construct the following Lyapunov function

$$\begin{aligned} V(t)=W(t)+\Phi (t), \end{aligned}$$

(12)

where

$$\begin{aligned} W(t)=\frac{1}{2}e^{\top }(t)(I_N\otimes I_n)e(t) =\frac{1}{2}\sum _{i=1}^{N} e_{i}^{\top }(t)e_{i}(t). \end{aligned}$$

Obviously, W(t) is continuous for all $t\ge 0$, and V(t) is continuous except for t $=$ ${\hat{\mathrm{T}}}_{k}$ with $k\in Z^+$ and $V\big ({\hat{\mathrm{T}}}_{k} \big )=V_{+}\big ({\hat{\mathrm{T}}}_{k} \big )$, $k\in Z^+$.

Since $d_i(t)$ $\ge$ 0 for $t\ge 0$ which is clear from (7)–(8), using Assumption 1, the upper right derivative of V(t) with respect to the time t along the trajectories of (9) can be calculated as follows:

When ${\hat{\mathrm{T}}}_{k-1} \le t \le {\hat{\mathrm{T}}}_{k-1}+\theta _{k}\mathrm{T}_{k}$, $k\in Z^+$,

$$\begin{aligned} \dot{V}(t)= & {} \sum _{i=1}^{N} e_{i}^{\top }(t)\left[ \tilde{f}(t,x_{i},s)+c\sum _{j=1}^{N}g_{ij}\,\Gamma e_{j}(t) \right] \nonumber \\&-\,\sum _{i=1}^{l}d_i(t) e_{i}^{\top }(t)\Gamma e_i(t)\nonumber \\&-\,\frac{p_1}{2}\,\mathrm{exp}\left\{ -p_1\left( t-{\hat{\mathrm{T}}}_{k-1}\right) \right\} \displaystyle \sum _{i=1}^{l} \frac{1}{h_i}\big (d_i(t)-d_i^*\big )^2\nonumber \\&+\,\mathrm{exp}\left\{ -p_1\left( t-{\hat{\mathrm{T}}}_{k-1}\right) \right\} \displaystyle \sum _{i=1}^{l} \big (d_i(t)-d_i^*\big ) e_{i}^{\top }(t)\Gamma e_i(t)\nonumber \\\le & {} \displaystyle \sum _{i=1}^{N} L_0 e_{i}^{\top }(t)\Gamma e_{i}(t) +c\sum _{i=1}^{N} \sum _{j=1}^{N}g_{ij}e_{i}^{\top }(t)\,\Gamma e_{j}(t)\nonumber \\&-\,\mathrm{exp}\left\{ -p_1\theta _{k}\mathrm{T}_{k}\right\} \displaystyle \sum _{i=1}^{l} d_i^* e_{i}^{\top }(t) \Gamma e_i(t)\nonumber \\&-\,\frac{p_1}{2}\,\mathrm{exp}\left\{ -p_1\left( t-{\hat{\mathrm{T}}}_{k-1}\right) \right\} \displaystyle \sum _{i=1}^{l} \frac{1}{h_i}\big (d_i(t)-d_i^*\big )^2\nonumber \\= & {} \sum _{i=1}^N L_0e^\top _i(t)\Gamma e_i(t)+c e^{\top }(t) \big ( G \otimes \Gamma \big ) e(t)\nonumber \\&-\,\mathrm{exp}\big \{-p_1\theta _{k}\mathrm{T}_{k}\big \}\displaystyle \sum _{i=1}^{l} d_i^* e_{i}^{\top }(t)\Gamma e_i(t)-p_1 \Phi (t)\nonumber \\= & {} e^{\top }(t) \Big ( \big (L_0 I_N + c G^s-D_{k} \big ) \otimes \Gamma \Big ) e(t) -p_1 \Phi (t)\nonumber \\= & {} e^{\top }(t) \Big ( \big ((L_0+a_1) I_N + c G^s-D_{k} \big ) \otimes \Gamma \Big ) e(t)\nonumber \\&-\,a_1\sum _{i=1}^{N} e_{i}^{\top }(t)\Gamma e_{i}(t) -p_1 \Phi (t), \end{aligned}$$

(13)

where $D_{k}=\mathrm{diag } \Big (\mathrm{exp}\big \{-p_1\theta _{k}\mathrm{T}_{k}\big \}d_1^*,\ldots ,\mathrm{exp}\big \{-p_1\theta _{k}\mathrm{T}_{k}\big \}d_l^*,0,\ldots ,0\Big )\in {\mathbb {R}}^{N\times N}$.

For $k\in Z^+$, let $(L_0+a_1)I_N+cG^s -D_{k}$ $=$ $Q-D_{k}= \small \begin{pmatrix} E-{{\tilde{D}}}_{k} &{} S \\ S^{\top } &{} Q_l \end{pmatrix}$, where ${\tilde{D}}_{k}=\mathrm{diag} \Big (\mathrm{exp}\big \{-p_1\theta _{k}\mathrm{T}_{k}\big \}d_1^*,\ldots ,\mathrm{exp}\big \{-p_1\theta _{k}\mathrm{T}_{k}\big \}d_l^* \Big )$ and $Q_l$ is the minor matrix of Q by removing its first l row–column pairs. Evidently, $Q_l=\big ((L_0+a_1)I_N+cG^s\big )_l$ and it is a real symmetric matrix. Therefore, by Lemma 1 and condition (i), one has $\lambda _{\max }(Q_l)=\lambda _{\max }\Big ( \big ((L_0+a_1)I_N+c G^{s}\big )_l \Big )\le L_0+a_1+c\lambda _{\max } \big (( G^s)_l\big )< 0$, which means that $Q_l<0$. Consequently, when $d_i^*$ > 0, $1\le i\le l$ are sufficiently large such that $d_i^*>\mathrm{exp}\big \{p_1\mathrm{T}_{\sup }\big \}\lambda _{\max }(E-SQ_l^{-1}S^{\top })$, it is easy to see that $Q-D_{k}<0$ for $k\in Z^+$, which directly follows from Lemma 2. This combines with (13) to produce

$$\begin{aligned} \dot{V}(t)\le & {} - a_1\lambda _{\min }(\Gamma ) \sum _{i=1}^{N} e_{i}^{\top }(t) e_{i}(t) -p_1 \Phi (t)\nonumber \\= & {} - p_1 V(t),\, {\hat{\mathrm{T}}}_{k-1} \le t \le {\hat{\mathrm{T}}}_{k-1}+\theta _{k}\mathrm{T}_{k}, \,k\in Z^+,\nonumber \\ \end{aligned}$$

(14)

which implies that

$$\begin{aligned}&V(t)\le V({\hat{\mathrm{T}}}_{k-1} ) \mathrm{exp} \big \{ -p_1(t- {\hat{\mathrm{T}}}_{k-1} ) \big \}, \nonumber \\&{\hat{\mathrm{T}}}_{k-1} \le t \le {\hat{\mathrm{T}}}_{k-1}+\theta _{k}\mathrm{T}_{k}, \,\,k\in Z^+. \end{aligned}$$

(15)

Similarly, when ${\hat{\mathrm{T}}}_{k-1}+\theta _{k}\mathrm{T}_{k}< t < {\hat{\mathrm{T}}}_{k}$,   $k\in Z^+$, using condition (ii), we can obtain that

$$\begin{aligned} \dot{V}(t)= & {} \sum _{i=1}^{N} e_{i}^{\top }(t)\Big [ \tilde{f}(t,x_{i},s)+c\sum _{j=1}^{N}g_{ij}\,\Gamma e_{j}(t) \Big ] \nonumber \\&+\,p_2 \Phi (t)\nonumber \\\le & {} e^{\top }(t) \Big ( \big (L_0 I_N + c G^s \big ) \otimes \Gamma \Big ) e(t)+p_2 \Phi (t) \nonumber \\\le & {} e^{\top }(t) \Big ( \big ((L_0-a_2) I_N + c G^s \big ) \otimes \Gamma \Big ) e(t)\nonumber \\&+\, a_2 \sum _{i=1}^{N} e_{i}^{\top }(t) \Gamma e_i(t) + p_2 \Phi (t)\nonumber \\\le & {} a_2 \lambda _{\max }(\Gamma ) \sum _{i=1}^{N} e_{i}^{\top }(t) e_i(t)\!+\! p_2 \Phi (t)\!=\!p_2 V(t).\nonumber \\ \end{aligned}$$

(16)

Denote $\mathrm{T}_{k-1}^{\,\theta _{k}}={\hat{\mathrm{T}}}_{k-1}+\theta _{k}\mathrm{T}_{k}$, $k\in Z^+$, and then it follows from (16) that

$$\begin{aligned}&V(t) \le V_{+}(\mathrm{T}_{k-1}^{\,\theta _{k}})\, \mathrm{exp}\left\{ p_2\left( t-\left( {\hat{\mathrm{T}}}_{k-1}+\theta _{k}\mathrm{T}_{k}\right) \right) \right\} ,\nonumber \\&\quad \quad \quad \quad {\hat{\mathrm{T}}}_{k-1}+\theta _{k}\mathrm{T}_{k}< t < {\hat{\mathrm{T}}}_{k}, \,\,k\in Z^+. \end{aligned}$$

(17)

By (11), (12), (15), and (17), we can derive that

$$\begin{aligned} V_{-}\left( {\hat{\mathrm{T}}}_{k}\right)\le & {} \mathrm{exp}\big \{p_2\left( 1-\theta _{k}\right) \mathrm{T}_{k}\big \} V_{+}\left( \mathrm{T}_{k-1}^{\,\theta _{k}}\right) \nonumber \\= & {} \mathrm{exp}\big \{p_2\big (1-\theta _{k})\mathrm{T}_{k}\big \} V\left( \mathrm{T}_{k-1}^{\,\theta _{k}}\right) \nonumber \\\le & {} \mathrm{exp}\big \{p_2\big (1-\theta _{k})\mathrm{T}_{k}\big \} \mathrm{exp}\big \{-p_1\theta _{k}\mathrm{T}_{k}\big \} V\left( {\hat{\mathrm{T}}}_{k-1}\right) \nonumber \\= & {} \mathrm{exp}\Big \{\left( -p_1\theta _{k}+p_2\left( 1-\theta _{k}\right) \right) \mathrm{T}_{k}\Big \} V\left( {\hat{\mathrm{T}}}_{k-1}\right) \nonumber \\= & {} \mathrm{exp}\big \{\varpi _{k}\mathrm{T}_{k}\big \} V\left( {\hat{\mathrm{T}}}_{k-1}\right) , \end{aligned}$$

(18)

and

$$\begin{aligned} V\big ({\hat{\mathrm{T}}}_{k}\big )= & {} W\big ({\hat{\mathrm{T}}}_{k}\big )+\Phi \big ({\hat{\mathrm{T}}}_{k}\big )\nonumber \\= & {} W_{-}\big ({\hat{\mathrm{T}}}_{k}\big )+\mathrm{exp}\big \{-\varpi _{k}\mathrm{T}_{k}\big \}\Phi _{-}\big ({\hat{\mathrm{T}}}_{k}\big )\nonumber \\= & {} \mathrm{exp}\big \{-\varpi _{k}\mathrm{T}_{k}\big \} V_{-} \big ({\hat{\mathrm{T}}}_{k}\big )\nonumber \\&+\Big (1-\mathrm{exp}\big \{-\varpi _{k}\mathrm{T}_{k}\big \}\Big )W\big ({\hat{\mathrm{T}}}_{k}\big ). \end{aligned}$$

(19)

Combining with (18) and (19), we have

$$\begin{aligned} V\left( {\hat{\mathrm{T}}}_{k}\right) \!-\!V\left( {\hat{\mathrm{T}}}_{k-1}\right) \!\le \! \Big (1-\mathrm{exp}\big \{\!-\!\varpi _{k}\mathrm{T}_{k}\big \}\Big )W\left( {\hat{\mathrm{T}}}_{k}\right) .\nonumber \\ \end{aligned}$$

(20)

Denote $\eta =(p_1+p_2)\theta _{\inf }-p_2$. Recalling that $p_1>0$, $p_2\ge 0$, $\inf _{k\in Z^+} \theta _k=\theta _{\inf }>0$ and $\inf _{k\in Z^+}\{t_{k+1}-t_k\}=\mathrm{T}_\mathrm{inf}>0$, from condition (iii), one can obtain that $-\varpi _{k}= (p_1+p_2)\theta _{k}-p_2 \ge (p_1+p_2)\theta _{\inf }-p_2 = \eta >0$, and so $-\varpi _{k}\mathrm{T}_{k} \ge \eta \mathrm{T}_{k} \ge \eta \mathrm{T}_\mathrm{inf}>0.$ This implies that

$$\begin{aligned} V\left( {\hat{\mathrm{T}}}_{k}\right) -V\left( {\hat{\mathrm{T}}}_{k-1}\right) \le \big (1-\mathrm{exp}\{\eta \mathrm{T}_\mathrm{inf}\}\big )W\left( {\hat{\mathrm{T}}}_{k}\right) , \end{aligned}$$

(21)

and then

$$\begin{aligned} V\big ({\hat{\mathrm{T}}}_{k}\big )-V\big ({\hat{\mathrm{T}}}_{0}\big ) \le \big (1-\mathrm{exp}\{\eta \mathrm{T}_\mathrm{inf}\}\big ) \sum _{j=1}^{k}W\big ({\hat{\mathrm{T}}}_{j}\big ).\nonumber \\ \end{aligned}$$

(22)

It shows that

$$\begin{aligned} \sum _{j=1}^{+\infty }W\big ({\hat{\mathrm{T}}}_{j}\big )\le \frac{V\big ({\hat{\mathrm{T}}}_{0}\big )}{\mathrm{exp}\{\eta \mathrm{T}_\mathrm{inf}\}-1}. \end{aligned}$$

(23)

Therefore, the series of nonnegative terms $\sum _{j=1}^{+\infty } W\big ({\hat{\mathrm{T}}}_{j}\big )$ converges [39], then

$$\begin{aligned} \lim _{j \rightarrow +\infty } W\big ({\hat{\mathrm{T}}}_{j}\big )=0. \end{aligned}$$

(24)

Additionally, for ${\hat{\mathrm{T}}}_{k-1}\le t < {\hat{\mathrm{T}}}_{k}$, k $\in$ $Z^+$, according to the nonnegativity of $d_i(t)$, the following estimation of W(t) can be deduced

$$\begin{aligned} \dot{W}(t)\le & {} \sum _{i=1}^{N} e_{i}^{\top }(t)\left[ \tilde{f}(t,x_{i},s)+c\sum _{j=1}^{N}g_{ij}\,\Gamma e_{j}(t) \right] \nonumber \\= & {} e^{\top }(t) \Big ( \big ((L_0-a_2) I_N + c G^s \big ) \otimes \Gamma \Big ) e(t)\nonumber \\&+\, a_2 \sum _{i=1}^{N} e_{i}^{\top }(t) \Gamma e_i(t)\nonumber \\\le & {} a_2 \lambda _{\max }(\Gamma ) \sum _{i=1}^{N} e_{i}^{\top }(t) e_i(t)=p_2 W(t). \end{aligned}$$

(25)

Hence, one can obtain that

$$\begin{aligned}&W(t) \le W\big ({\hat{\mathrm{T}}}_{k-1}\big )\, \mathrm{exp}\Big \{p_2\big (t-{\hat{\mathrm{T}}}_{k-1}\big )\Big \}\nonumber \\&\quad \quad \quad \le W\big ({\hat{\mathrm{T}}}_{k-1}\big )\, \mathrm{exp}\big \{p_2 \mathrm{T}_{k}\big \} \le W\big ({\hat{\mathrm{T}}}_{k-1}\big )\, \nonumber \\&\quad \quad \quad \quad \mathrm{exp}\big \{p_2 \mathrm{T}_{\mathrm{sup}}\big \},\nonumber \\&\quad \quad \quad \quad {\hat{\mathrm{T}}}_{k-1} \le t < {\hat{\mathrm{T}}}_{k},\,\, k\in Z^+. \end{aligned}$$

(26)

Since $k\rightarrow +\infty$ when $t\rightarrow +\infty$, by (24) and (26), we can get

$$\begin{aligned} \lim _{t \rightarrow +\infty } W(t)=0, \end{aligned}$$

(27)

which means that $\lim _{t\rightarrow +\infty }|| e_{i}(t)||=0$, $i\in \mathfrak {T}$, that is, globally asymptotical synchronization of the controlled dynamical network (5) is achieved. This completes the proof of Theorem 1. $\square$

Remark 2

As $\delta _k \rightarrow \mathrm{T}_k$ or $\theta _k \rightarrow 1$, k $\in$ $Z^+$, the adaptive intermittent pinning control is reduced to the continuous-time adaptive pinning control which has been investigated in [8, 9]. Under such circumstance, conditions (i) and (ii) guarantee global synchronization of the controlled dynamical network (5) due to the fact that condition (iii) holds automatically.

Remark 3

It is clear from (7) and (8) that the adaptive intermittent feedback control gains $d_i(t)$ for $1\le i \le l$ are increasing in each work time but identically equal to zero in each rest time. When the synchronization is realized, the values of $d_i(t)$ $(1\le i \le l)$ will approach to some positive constants in each work time. This point will be illustrated by numerical simulations in the next section.

Letting $\varrho _0$ $=$ $L_0+c\lambda _{\max }\big ( G^s\big )$ and selecting $a_2=\max \{0,\varrho _0\}$, then condition (ii) in Theorem 1 holds. Thus, we can reduce Theorem 1 to the following Corollary.

Corollary 1

Suppose that $\displaystyle \inf _{k\in Z^+} \theta _k$ $=$ $\theta _{\inf }$ > 0. Under Assumption 1, the controlled dynamical network (5) with the adaptive aperidical intermittent controllers (6)–(8) is globally asymptotically synchronized if there exists a positive constant $a_1>0$ such that

• (i) $\lambda _{\max }\big ((G^s)_l\big )< -\displaystyle \frac{L_0+a_1}{c }$,

• (ii) $\displaystyle \frac{ p_2}{ p_1 + p_2}<\theta _{\inf } <1$,

where $p_1=2 a_1 \lambda _{\min }(\Gamma )$ and $p_2=2a_2 \lambda _{\max }(\Gamma )$ with $a_2=\max \{0,\varrho _0\}$.

When each control period and each control width is fixed, i.e., $\mathrm{T}_k$ $\equiv$ $\mathrm{T}$ and $\delta _k$ $\equiv$ $\delta$ for all $k\in Z^+$, where $\mathrm{T}$ and $\delta$ are both positive constants, the control type is adaptive periodically intermittent one [21]. Denote $\theta =\delta /\mathrm{T}$, by Corollary 1, and we can derive the following result.

Corollary 2

Under Assumption 1, the controlled dynamical network (5) with the adaptive periodical intermittent controllers (6)–(8) is globally asymptotically synchronized if there exists a positive constant $a_1>0$ such that

• (i) $\lambda _{\max }\big ((G^s)_l\big )< -\displaystyle \frac{L_0+a_1}{c }$,

• (ii) $\displaystyle \frac{ p_2}{ p_1 + p_2}<\theta <1$,

where $p_1=2 a_1 \lambda _{\min }(\Gamma )$ and $p_2=2a_2 \lambda _{\max }(\Gamma )$ with $a_2=\max \{0,\varrho _0\}$.

Remark 4

In [21], the pinning synchronization of directed dynamical networks via adaptive intermittent control was studied. However, the designed intermittent controllers in [21] are periodical, which require that all the control periods and control widths should be fixed (i.e, $t_{k+1}-t_k\equiv \mathrm{T}$ and $\delta _k\equiv \delta$, for all $k\in Z^+$). In reality, this requirement is unreasonable obviously. Moreover, in [21], the graph corresponding to the directed dynamical network is assumed to be strongly connected and balanced (that is, the coupling matrix of the directed dynamical network is irreducible, and the in-degree and the out-degree of each node in the network are equivalent), which is a very strict condition. In this paper, the adaptive intermittent control can be aperiodic with non-fixed both control period and control width, the coupling matrix is not restricted to be irreducible, and the in-degree and the out-degree of each node are not necessarily equivalent. Hence, our theoretical results extend the results in [21].

Remark 5

In [28,29,30], an adaptive scheme for aperiodically intermittent pinning control was proposed to realize the synchronization of complex dynamical networks. However, the adaptive rule in [28,29,30] is centralized, which needs the state information of all network nodes (i.e., global information of the whole network). For large-scale dynamical networks, it is clear that this adaptive rule is hard and costly to implement. In this paper, a new adaptive scheme for aperiodically intermittent pinning control is introduced. It can be observed from (6)–(8) that the designed adaptive intermittent controller depends on the state information of the controlled node itself other than all network nodes. In other words, our adaptive scheme for aperiodically intermittent pinning control is decentralized. Hence, the theoretical results established here is more practically applicable than those in [28,29,30].

Remark 6

In [28,29,30,31], in order to derive the results, an assumption that the time span of each control width should be not less than a certain positive constant $\delta _{\inf }$ and the time span of each control period should be not larger than another certain positive constant $\mathrm{T}_{\sup }$ (namely, there exist two positive constants $\delta _{\inf }$ and $\mathrm{T}_{\sup }$ such that $\inf _{k\in Z^+}\delta _k=\delta _{\inf }$ and $\sup _{k\in Z^+}\{t_{k+1}-t_k\}=\sup _{k\in Z^+}\mathrm{T}_k=\mathrm{T}_{\sup }$) has been introduced. If the method presented in [28,29,30,31] is applied to deal with the problem addressed in this paper, then condition (iii) of Theorem 1 becomes

$$\begin{aligned} (p_1+p_2)\frac{\delta _{\inf }}{\mathrm{T}_{\sup }}-p_2>0. \end{aligned}$$

(28)

Notice that for all $k\in Z^+$, $\delta _k\ge \delta _{\inf }$, $\mathrm{T}_k\le \mathrm{T}_{\sup }$, and therefore

$$\begin{aligned} \theta _{\inf }=\inf _{k \in Z^{+}}\Big \{\frac{\delta _k}{\mathrm{T}_k}\Big \}\ge \frac{\delta _{\inf }}{\mathrm{T}_{\sup }}. \end{aligned}$$

This means that condition (iii) of Theorem 1 derived by using $\theta _{\inf }$ is easier to be satisfied and less conservative than inequality (28) obtained by using ${\delta _{\inf }}/{\mathrm{T}_{\sup }}$. Therefore, the theoretical results derived in this paper are less conservative than the corresponding results given in [28,29,30,31]. For clarity, an example is given to verify the statement. Consider a special time sequence $\{t_k\}_{k=1}^{+\infty }$ $=$ $\big \{\epsilon _0, 2\epsilon _0,\ldots , (N_0-1) \epsilon _0, N_0 T_a, N_0 T_a+\epsilon _0, N_0 T_a+2\epsilon _0,\ldots , N_0 T_a+(N_0-1) \epsilon _0, 2 N_0 T_a, \ldots \big \}$, which can also be rewritten in the following form [40, 41]:

$$\begin{aligned} t_{k+1}-t_{k}=\left\{ \begin{array}{ll} \epsilon _0, &{}\quad \mathrm{if}\,\, \mathrm{mod} (k+1,N_0)\ne 0,\\ N_0(T_a-\epsilon _0)+\epsilon _0, &{}\quad \mathrm{if}\,\, \mathrm{mod} (k+1,N_0)= 0, \end{array} \right. \nonumber \\ \end{aligned}$$

(29)

where $k\in Z^+$, $\epsilon _0$ and $T_a$ are positive constants satisfying $\epsilon _0<T_a$, and $N_0$ is a positive integer. From the structure of the time sequence, one can obtain that $\inf _{k\in Z^+}\{t_{k+1}-t_{k} \} =\epsilon _0$ and $\sup _{k\in Z^+}\{t_{k+1}-t_{k} \} =N_0(T_a-\epsilon _0)+\epsilon _0$ [40]. Let the kth control period $\mathrm{T}_k=t_{k+1}-t_{k}$ satisfying Eq. (29) and the kth control width ${ \delta }_k=\theta \mathrm{T}_k$, where $k \in Z^+$ and $0<\theta <1$ is a positive constant. Then, we get

$$\begin{aligned} \delta _{\inf }=\theta \epsilon _0,\quad \mathrm{T}_{\sup }=N_0(T_a-\epsilon _0)+\epsilon _0,\quad \mathrm{and}\quad \theta _{\inf }=\theta . \end{aligned}$$

Since $0<\epsilon _0<T_a$, it is easy to see that

$$\begin{aligned} \theta _{\inf } =\theta > \theta \frac{\epsilon _0}{N_0(T_a-\epsilon _0)+\epsilon _0}= \frac{\delta _{\inf }}{\mathrm{T}_{\sup }}, \end{aligned}$$

and hence the above statement holds. Especially, when $\epsilon _0$ is sufficiently small and $N_0$ is sufficiently large, the quantity ${\delta _{\inf }}/{\mathrm{T}_{\sup }}$ will be very small. In such case, the results in [28,29,30,31] would not be applicable.

Remark 7

From Theorem 1 and Corollary 1, it can be observed that the synchronization criteria are dependent on the quantity $\theta _{\inf }$, but not the control widths $\delta _k$ $(k\in Z^+)$ or the control periods $\mathrm{T}_k$ $(k\in Z^+)$. This implies that, for achieving the global synchronization, each control period $\mathrm{T}_k$ can be arbitrarily chosen. In particular, for practical problems, the control periods $\mathrm{T}_k$, $k\in Z^+$ can be selected according to the actual requirement.

Remark 8

Corollary 1 provides a simple pinning criterion to guarantee the globally asymptotical synchronization. Evidently, to ensure pinning condition $(\mathrm{i})$ in Corollary 1 is satisfied, at least one has to choose l pinned candidates such that $\lambda _{\max }\big ((G^s)_l\big )< 0$. For a directed dynamical network, however, what kinds of nodes should be chosen as pinned candidates is still an open problem. In [8], the authors showed that the nodes whose out-degrees are bigger than their in-degrees should be selected as pinned candidates, which can result in $\lambda _{\max }\big ((G^s)_l\big )\le 0$. Based on this idea, for the controlled dynamical network (5), we first apply adaptive intermittent control to the nodes with zero in-degrees since their states are not influenced by others. Then, we continue to pick other nodes in descending order according to their degree differences as defined above until condition (i) in Corollary 1 holds. In addition, from condition (i) of Corollary 1, it can be deduced that the least number of pinned nodes $l_0$ should satisfy

$$\begin{aligned} \lambda _{\max }\big (( G^s)_{l_0-1}\big )\ge & {} \displaystyle -\frac{L_0+a_1}{c }\,\, \mathrm{and} \,\, \lambda _{\max }\big (( G^s)_{l_0}\big )\\< & {} \displaystyle -\frac{L_0+a_1}{c }. \end{aligned}$$

Remark 9

To shed light on how to design appropriate adaptive aperiodical intermittent controllers in practical application for realizing network synchronization, the following procedures are provided:

• (1) Given $a_1$, then pick l pinned nodes by means of Remark 8 such that condition (i) of Corollary 1 is satisfied.

• (2) For the given $a_1$, calculate the value of ${p_2}/(p_1+p_2)$, and then optionally choose the control rates $\theta _k$, $k\in Z^+$, only if condition (ii) of Corollary 1 holds.

• (3) Select the control periods $\mathrm{T}_k$, $k\in Z^+$ according to the actual requirement.

• (4) In the light of the above chosen pinned nodes, $\theta _k$ and $\mathrm{T}_k$, $k\in Z^+$, design the adaptive aperiodical intermittent controllers described in (6)–(8).

Remark 10

It should be pointed out that the network model (1) presented in this paper does not include time delays. Indeed, time delays are often encountered in dynamical networks because of the finite information transmission and processing speeds among the units [15, 19, 20, 30,31,32]. Hence, time delays should be taken into account in realistic modeling of dynamical networks. The main reason why the time delays are not considered here is that we do not find a rigorous proof for the aperiodically intermittent pinning control with the above adaptive rule (8) to realize global synchronization of delayed dynamical networks. It is an interesting topic to be investigated in future.

4 Numerical simulations

In this section, a numerical example is given to show the effectiveness of the obtained synchronization criteria. The Chua’s circuit is used as uncoupled node in network (1). The dynamics of Chua’s circuit is given by [8]

$$\begin{aligned} \dot{x}(t)=f(t,x(t))=Ax(t)+h(x(t)), \end{aligned}$$

(30)

where $x(t)=(x_{1}(t),x_{2}(t),x_{3}(t))^{\top }$ $\in$ $R^3$, $A= \left( \begin{matrix} -\alpha \,&{} \alpha \,&{} 0 \\ 1 \,&{}-1 \,&{} 1 \\ 0 \,&{} -\beta \,&{} 0 \end{matrix} \right)$,  $h(x(t))=\big (-\alpha \psi (x_1(t)),0, 0\big )^{\top }$ $\in$ $R^3$, $\psi (x_1(t))=\nu _1 x_1(t)+\frac{1}{2}(\nu _2-\nu _1)\big (|x_1(t)+1|-|x_1(t)-1|\big )$, and $\alpha =10,$ $\beta =17.8,$ $\nu _1=-3/4$, $\nu _2=-4/3$. The numerical simulation of system (30) is represented in Fig. 2, which indicates that system (30) displays chaotic behavior.

Fig. 2

Chaotic behavior of system (30) with initial conditions $x_1(0)=0.2$, $x_2(0)=0.6$, $x_3(0)=0.8$

Consider a scale-free network (1) consisting of 200 identical Chua’s circuit, which is described by

$$\begin{aligned} \displaystyle \dot{x}_{i}(t)= & {} Ax_i(t)+h(x_i(t))\nonumber \\&+\,c\sum _{j=1}^{200}g_{ij}\,\Gamma x_{j\,}(t),\,\,\quad 1\le i \le 200, \end{aligned}$$

(31)

where $\Gamma =\mathrm{diag}(1,1,1)$, $G=(g_{ij})_{200\times 200}$ is a diffusive coupling matrix with $g_{ij}=0$ or $1(j\ne i)$, and the coupling strength $c=20$. Here we assume that the network structure of (31) obeys the scale-free distribution of the Barabási–Albert (BA) network model [42]. The parameters of the BA network model are given by $m_0=m=5$, $N=200$. In this simulation, we obtain that $\lambda _{\max }( G^s )= 0$. In addition, it is easy to get that [8]

$$\begin{aligned}&\big [x(t)-s(t)\big ]^{\top }\big [f(t,x(t))-f(t,s(t))\big ]\\&\quad = \big [x(t)-s(t)\big ]^{\top } A\,\big [x(t)-s(t)\big ]\\&\qquad +\big [x(t)-s(t)\big ]^{\top } \big [h(x(t))-h(s(t))\big ]\\&\quad = \frac{1}{2}\big [x(t)-s(t)\big ]^{\top } (A+A^{\top })\big [x(t)-s(t)\big ]\\&\qquad +|\alpha \nu _2 | \big ( x_1(t)-s_1(t) \big )^2\\&\quad \le \lambda _{\max }(\tilde{A}) \big [x(t)-s(t)\big ]^{\top } \big [x(t)-s(t)\big ] \end{aligned}$$

where $\tilde{A}=(A+A^{\top })/{2}+\mathrm{diag}(|\alpha \nu _2|,0,0)$.

Note that $\Gamma$ $=$ $\mathrm{diag}(1,1,1)$, hence Assumption 1 can be satisfied by selecting $L_0=\lambda _{\max }(\tilde{A})=10.253$. And then we get that $\varrho _0$ $=$ $L_0+c\lambda _{\max }\big ( G^s\big )$ $=$ 10.253. If $a_1=26$ is selected, then we can obtain that $p_1=52$ and $p_2=20.506$. It follows from conditions (i) and (ii) of Corollary 1 that

$$\begin{aligned} \lambda _{\max }\big (( G^s)_l\big )<-1.8127\,\,\,\, \mathrm{and}\,\,\,\, 0.2828<\theta _{\inf }<1.\nonumber \\ \end{aligned}$$

(32)

Using the pinned-node selection scheme for the controlled dynamical network (5) in Remark 8, we rearrange nodes of network (31). Pick l from 1 to 100, and plot $\lambda _{\max }\big (( G^s)_l\big )$ in Fig. 3, which reveals that $\lambda _{\max }\big (( G^s)_l\big )$ decreases with the increase of the number of pinned nodes (l). In particular, when l $=$ 14 and l $=$ 15, we have $\lambda _{\max }\big (( G^s)_{14}\big )=-1.7792$ and $\lambda _{\max }\big (( G^s)_{15}\big )=-1.8160$. Therefore, we can only choose the first $l=15$ rearranged nodes of network (31) as pinned nodes for realizing network synchronization.

Fig. 3

$\lambda _{\max }\big (( G^s)_l\big )$ versus the number of pinned nodes (l)

Fig. 4

Time evolutions of the synchronization errors $e_{i1}(t)$, $e_{i2}(t)$, $e_{i3}(t)$ $(1\le i \le 200)$ of network (31) under the adaptive aperiodically intermittent pinning control

Fig. 5

Time evolutions of the adaptive intermittent feedback control gains $d_{i}(t)$ $(1\le i \le 15)$ of network (31) under the adaptive aperiodically intermittent pinning control

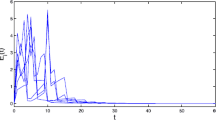
In numerical simulations, for brevity, we select the control periods $\mathrm{T}_k=t_{k+1}-t_k$, $k\in Z^+$ satisfy Eq. (29) with $T_a=0.5$, $\epsilon _0=0.2$, and $N_0=3$, the control rates $\theta _k$ $\equiv$ $\theta$ $=$ 0.3, $k\in Z^+$, and l $=$ 15, then condition (32) is satisfied. Figures 4 and 5 indicate, respectively, the time responses of the synchronization errors $e_i(t)\,(1\le i\le 200)$ and the adaptive intermittent feedback control gains $d_i(t)\,(1\le i\le 15)$, where the initial conditions of the numerical simulations are $x_i(0)=(-2+0.3i,-4+0.3i,-6+0.3i)^{\top }$, $s(0)=(1, 2 ,3)^{\top }$, $1\le i \le 200$, and $d_1(0)=\cdots =d_{15}(0)=0.01$, $h_1=\cdots =h_{15}=0.02$. It can be observed that the asymptotical synchronization is realized, and the adaptive intermittent control gains $d_i(t)\,(1\le i\le 15)$ intermittently converge to some positive constants. This implies that the synchronization of network (31) with 200 nodes can be achieved by only pinning 15 rearranged network nodes with the control rate $\theta =0.3$. Figure 6 shows the dynamics of the quantity $E(t)=\sqrt{\big (\sum _{i=1}^{200}||x_i(t)-s(t)||^2\big )/200}$, which further verifies the achievement of the asymptotical synchronization of network (31) under the adaptive aperiodically intermittent pinning control.

For the above selected control periods and control rates, according to Remark 6, one can get that $\delta _{\inf }=\inf _{k\in Z^+} \delta _k=0.06$ and $\mathrm{T}_{\sup }=\sup _{k\in Z^+}=1.1$. If the method presented in [28,29,30,31] is utilized to derive the synchronization criterion, then the synchronization of network (31) can be realized via the adaptive aperiodically intermittent pinning control when the following condition

$$\begin{aligned} \displaystyle \tilde{\eta }\mathop {=}\limits ^\mathrm{\Delta }(p_1+p_2)\frac{\delta _{\inf }}{\mathrm{T}_{\sup }}-p_2>0, \end{aligned}$$

(33)

holds. For this example, by simple computation, we get $\tilde{\eta }=-16.5511$, and so inequality (33) is not satisfied. Hence, synchronization criterion (33) derived by using ${\delta _{\inf }}/{\mathrm{T}_{\sup }}$ fails to judge whether network (31) can be synchronized under the adaptive aperiodically intermittent pinning control. This shows that results of this paper are less conservative than the corresponding results given in [28,29,30,31], which are obtained by using ${\delta _{\inf }}/{\mathrm{T}_{\sup }}$.

It is noteworthy that when the control rates $\theta _k$ $\equiv$ $\theta$ $=$ 1.0, $k\in Z^+$, the adaptive aperiodically intermittent pinning control degenerates to the continuous-time adaptive pinning control. For comparison, the dynamics of the quantity E(t) with the control rates $\theta _k$ $\equiv$ $\theta$ $=$ 1.0, $k\in Z^+$ (the other parameters are the same as those in the above simulations) is also plotted in Fig. 6. The simulation results indicate that the adaptive aperiodically intermittent pinning control is more cost-effective than the continuous-time adaptive pinning control since the latter activates the control all the times.

Fig. 6

Dynamics of the E(t) of network (31) under the adaptive aperiodically intermittent pinning control with the control rates $\theta _k$ $\equiv$ $\theta$ $=$ 0.3, $k\in Z^+$ (blue) and $\theta _k$ $\equiv$ $\theta$ $=$ 1.0, $k\in Z^+$ (red). (Color figure online)

5 Conclusion

In this paper, we have developed a decentralized adaptive aperiodically intermittent pinning control scheme for global synchronization of complex directed dynamical networks. Some effective global synchronization criteria have been established by constructing a piecewise Lyapunov function and using theory of series with nonnegative terms. It is noted that our adaptive strategy relies only on the state information of the controlled node rather than all networks nodes. Moreover, the derived synchronization criteria have been shown to be less conservative than the corresponding results presented in the existing works. Finally, some numerical simulations have been presented to verify the feasibility of the obtained theoretical results. Further research topics include the extension of the decentralized adaptive aperiodically intermittent pinning control to study the problems of synchronization and consensus for more general complex dynamical networks with time delays or uncertain perturbations.