A novel method in determining a layered periodic structure

Abstract

This paper is concerned with the inverse scattering of time-harmonic waves by a penetrable structure. By applying the integral equation method, we establish the uniform $L^{p}_{\alpha }\ (1< p\leq 2)$ estimates for the scattered and transmitted wave fields corresponding to a series of incident point sources. Based on these a priori estimates and a mixed reciprocity relation, we prove that the penetrable structure can be uniquely identified by means of the scattered field measured only above the structure induced by a countably infinite number of quasi-periodic incident plane waves.

1 Introduction

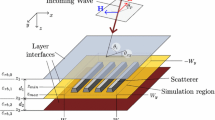
In this paper, we consider the inverse problem of determining a penetrable periodic structure in ${\mathbb{R}}^{3}$ from the scattered data measured only above the structure. This kind of problem occurs in various applications such as in radar imaging, modern diffractive optics, and non-destructive testing. For convenience, we write a point x in ${\mathbb{R}}^{3}$ for $(\widetilde{x},x_{3})$ with $\widetilde{x}:=(x_{1},x_{2})\in {\mathbb{R}}^{2}$. Assume that the penetrable profile is described by

$$\begin{aligned} \Gamma:= \bigl\{ x\in {\mathbb{R}}^{3}: x_{3}=f( \widetilde{x}) \bigr\} , \end{aligned}$$

where f is a periodic function with respect to the variable x̃, that is, $f(\widetilde{x}) = f( \widetilde{x}+2n\pi )$ for $n:=(n_{1},n_{2})\in {\mathbb{Z}}^{2}$. Assume further that the homogeneous media above and below Γ are described by

$$\begin{aligned} \Omega _{+}:= \bigl\{ x\in {\mathbb{R}}^{3}: x_{3}>f(\widetilde{x}) \bigr\} \quad \text{and}\quad \Omega _{-}:= \bigl\{ x\in {\mathbb{R}}^{3}: x_{3}< f( \widetilde{x}) \bigr\} \end{aligned}$$

with the wave numbers $k_{1}$ and $k_{2}$, respectively.

Consider the incident plane waves in the form of

$$\begin{aligned} u^{i}(x)=\exp \bigl(i\alpha _{j} \cdot \widetilde{x}-i\beta _{j}^{+}x_{3} \bigr),\quad j \in {\mathbb{Z}}^{2}, \text{with } \alpha _{j} = \alpha +j, \end{aligned}$$

(1.1)

which propagate downward from $\Omega _{+}$ with $\alpha =(\alpha _{1},\alpha _{2}): = k_{1}(\sin \theta _{1}\cos \theta _{2}, \sin \theta _{1}\sin \theta _{2})$ with the incident angle $\theta _{1}\in [0, \pi /2), \theta _{2}\in [0, 2\pi )$, and $\beta _{j}^{+}\in {\mathbb{C}}$ is given by

$$\begin{aligned} \beta _{j}^{+} = \sqrt{k_{1}^{2}- \vert \alpha _{j} \vert ^{2}} \quad\text{if } \vert \alpha _{j} \vert \leq k_{1},\qquad \beta _{j}^{+}= i\sqrt{ \vert \alpha _{j} \vert ^{2}-k_{1}^{2}} \quad\text{if } \vert \alpha _{j} \vert > k_{1}. \end{aligned}$$

Then the scattering of the incident $u^{i}$ by the periodic structure can be formulated in determining the total field $u_{1}:=u^{i}+ u^{s}$ with the scattered field $u^{s}$ and the transmitted field $u_{2}$ to the following problem:

$$\begin{aligned} & \triangle u_{1}+k_{1}^{2}u_{1}=0\quad \text{in } \Omega _{+}, \end{aligned}$$

(1.2)

$$\begin{aligned} & \triangle u_{2}+k_{2}^{2}u_{2}=0 \quad\text{in } \Omega _{-}, \end{aligned}$$

(1.3)

$$\begin{aligned} & u_{1}=u_{2}, \qquad\frac{\partial u_{1}}{\partial \nu }=\lambda \frac{\partial u_{2}}{\partial \nu } \quad\text{on } \Gamma , \end{aligned}$$

(1.4)

$$\begin{aligned} & u^{s}(x)=\sum_{n\in {\mathbb{Z}}^{2}}u_{n}^{+} \exp \bigl(i\alpha _{n} \cdot \widetilde{x}+i\beta ^{+}_{n}x_{3} \bigr),\quad x_{3}>A_{1}:= \max_{t \in {\mathbb{R}}^{2}}f(t), \end{aligned}$$

(1.5)

$$\begin{aligned} & u_{2}(x)=\sum_{n\in {\mathbb{Z}}^{2}}u_{n}^{-} \exp \bigl(i\alpha _{n} \cdot \widetilde{x}-i\beta ^{-}_{n}x_{3} \bigr),\quad x_{3}< A_{2}:= \min_{t \in {\mathbb{R}}^{2}}f(t). \end{aligned}$$

(1.6)

Here, $u_{n}^{\pm }\in {\mathbb{C}}$ are the solution sequences, λ is the transmission coefficient and the unit normal vector ν on Γ is directed into the interior of $\Omega _{-}$. Notice that the incident wave $u^{i}(\cdot )$ satisfies such an α-quasi-periodic condition $u^{i}(\widetilde{x}+2n\pi , x_{3})=e^{i 2\alpha \cdot n\pi }u^{i}( \widetilde{x}, x_{3})$ for all $n\in {\mathbb{Z}}^{2}$. Then the solution $u_{l}, l=1,2$, is also required to satisfy the same α-quasi-periodic condition, i.e., $u_{l}(\widetilde{x}+2n\pi , x_{3})=e^{i 2\alpha \cdot n\pi }u_{l}( \widetilde{x}, x_{3})$ in ${\mathbb{R}}^{3}$. Conditions (1.5) and (1.6) are known as the Rayleigh expansion conditions of the scattered field $u^{s}$ in $\Omega _{+}$ and the transmitted field $u_{2}$ in $\Omega _{-}$, respectively, with $\beta _{n}^{-}$ defined similarly as $\beta _{n}^{+}$ by the wave number $k_{2}$.

The well-posedness of problem (1.2)–(1.6) can be established by the variational method (cf. [31]) or the integral equation method (cf. [32, 33]). In the current paper we first establish the $L_{\alpha }^{p}\ (1< p \leq 2 )$ estimates for the scattered field $u^{s}$ and the transmitted field $u_{2}$. Based on these a priori estimates, we focus on the unique identification of the penetrable periodic structure from the scattered field $u^{s}$ measured only on a straight line above the periodic structure induced by a countably infinite number of quasi-periodic incident plane waves.

There are lots of results concerning the uniqueness issue for the inverse periodic transmission problems (cf. [5, 7, 12, 13, 18, 19, 23, 24, 33, 34]) and for the inverse scattering by the polygonal periodic structure (cf. [6, 11, 14]). For the special case when the medium has the energy absorption property, a uniqueness theorem was obtained in [5] from the measured scattered field for one incident plane wave in a two-dimensional space. The result of [5] was then extended to the three-dimensional case in [2]. It should be remarked that the uniqueness with one incident wave does not hold true for the inverse periodic problem for a real wave number case, that is, the medium does not has a property of energy absorption. See also [7] for a uniqueness theorem on the recovery of a smooth periodic structure with one incident plane wave under some a priori assumptions on the structure. For the case when a priori restrictions on the height of the grating surface are known in advance, a uniqueness result can be found in [18] on the identification of a smooth perfectly reflecting periodic structure from many measurements corresponding to a finite number of incident plane waves. The method of [18] was extended to the periodic transmission problem [13]. There also exist some numerical methods in reconstructing periodic structures. For example, a linear sampling method was developed in [20, 22] for determining the shape of partially coated bi-periodic structures, and in [35] a novel linear sampling method was introduced for simultaneously reconstructing dielectric grating structures in an inhomogeneous periodic medium. See also [10] for a finite element method or [3, 4, 17] for the factorization method in determining the periodic structures, or [30] for the uniquely reconstruction of a locally perturbed infinite plane. Recently, by making use of the differential sampling method, the anisotropic periodic layer can be uniquely determined in [25] under the assumption that the complement of the periodic layer in one period is connected. The analysis of sampling methods for the recovery of a local perturbation in a periodic layer can be found in [16].

For the scattering by general periodic structures case, there are several uniqueness results. We refer to [23] for a uniqueness theorem for the inverse Dirichlet problem, and to [21, 24, 32] for uniqueness results for the inverse transmission problem by means of all quasi-periodic incident plane waves. The reader is referred to [19] for a partially coated perfectly grating case with respect to infinitely many point sources, and to [34] for uniqueness results for both the partially coated perfectly reflecting grating and the periodic transmission case in a two-dimensional space, corresponding to a countably infinite number of quasi-periodic incident plane waves. In this paper we intend to develop a novel method, which differs from the approach used in [34], to prove the uniqueness on the identification of the penetrable periodic structure in the three-dimensional space from the measured data only above the structure with respect to a countably infinite number of quasi-periodic incident plane waves. The technique developed in this paper can date back to the work [27, 36] on the inverse scattering problems of determining the support of penetrable electromagnetic obstacles or to [28] for the fluid-solid interaction problem of identifying the bounded solid obstacle, [29] for the cavity scattering case.

The paper is organized as follows. In Sect. 2, the a priori estimates in the sense of $L_{\alpha }^{p}\ (1< p \leq 2)$ norm for the solution of the direct scattering problem in ${\mathbb{R}}^{3}$ are established by applying the integral equation method. Section 3 is devoted to the inverse problem of uniquely determining the periodic structure from the measured data only above the structure produced by a countably infinite number of quasi-periodic incident plane waves.

2 A priori estimates

In this section we establish some a priori estimates for the solution of the direct scattering problem by employing the integral equation method. Eliminating the incident field $u^{i}$, it is easily found that the scattered field $w_{1}:=u_{1}-u^{i}$ in $\Omega _{+}$ and the transmitted field $w_{2}:=u_{2}$ in $\Omega _{-}$ satisfy the following boundary value problem:

$$\begin{aligned} & \triangle w_{1}+k_{1}^{2}w_{1}=0 \quad\text{in } \Omega _{+}, \end{aligned}$$

(2.1)

$$\begin{aligned} & \triangle w_{2}+k_{2}^{2}w_{2}=0 \quad\text{in } \Omega _{-}, \end{aligned}$$

(2.2)

$$\begin{aligned} & w_{1}-w_{2}=f_{1},\qquad \frac{\partial w_{1}}{\partial \nu }-\lambda \frac{\partial w_{2}}{\partial \nu }=f_{2} \quad\text{on } \Gamma , \end{aligned}$$

(2.3)

$$\begin{aligned} & w_{1}(x)=\sum_{n\in {\mathbb{Z}}^{2}}w_{n}^{+} \exp \bigl(i\alpha _{n} \cdot \widetilde{x}+i\beta ^{+}_{n}x_{3} \bigr), \quad x_{3}>A_{1}, \end{aligned}$$

(2.4)

$$\begin{aligned} & w_{2}(x)=\sum_{n\in {\mathbb{Z}}^{2}}w_{n}^{-} \exp \bigl(i\alpha _{n} \cdot \widetilde{x}-i\beta ^{-}_{n}x_{3} \bigr), \quad x_{3}< A_{2} \end{aligned}$$

(2.5)

in the general case $f_{1}, f_{2}\in L^{p}_{\alpha }(\Gamma )$ with $1< p\leq 2$. $Here, L^{p}_{\alpha }(\Gamma ) (p\ge 1)$ denotes the Sobolev space of scalar functions on Γ which is assumed to be α-quasi-periodic with respect to the variable x̃, equipped with the norm in the usual Sobolev space $L^{p}(\Gamma )$.

Before going further we first introduce the basic notations that are used in the rest of this paper. For simplicity, we use $\Omega _{\pm }$ and Γ again to denote the same sets restricted to one period $0< x_{1}, x_{2}<2\pi$. For each $h>0$, denote by $\Omega _{+}(h):=\{x\in \Omega _{+}: x_{3}< A_{1}+h\}$, $\Omega _{-}(h):=\{x\in \Omega _{-}: x_{3}> A_{2}-h\}$, $\Gamma _{+}(h):=\{x\in \Omega _{+}: x_{3}= A_{1}+h\}$, and $\Gamma _{-}(h):=\{x\in \Omega _{-}: x_{3}=A_{2}-h\}$, respectively. Then, let $H^{1}_{\alpha }(\Omega _{\pm }(h))$ and $L^{p}_{\alpha }(\Omega _{\pm }(h)) (p\ge 1)$ denote the Sobolev spaces of scalar functions on $\Omega _{\pm }(h)$ which are assumed to be α-quasi-periodic with respect to the variable x̃, equipped with the norms in the usual Sobolev spaces $H^{1}(\Omega _{\pm }(h))$ and $L^{p}(\Omega _{\pm }(h))$, respectively. Let $H^{1/2}_{\alpha }(\Gamma _{\pm }(h))$ denote the trace space of $H^{1}_{\alpha }(\Omega _{\pm }(h))$, and $H^{-1/2}_{\alpha }(\Gamma _{\pm }(h))$ is the dual space of $H^{1/2}_{\alpha }(\Gamma _{\pm }(h))$.

We introduce the free space α-quasi-periodic Green function

$$\begin{aligned} G_{1}(x,y;k_{1})= \frac{i}{8\pi ^{2}}\sum_{n\in {\mathbb{Z}}^{2}} \frac{1}{\beta ^{+}_{n}}\exp \bigl(i\alpha _{n}\cdot (\widetilde{x}- \widetilde{y})+i\beta _{n}^{+} \vert x_{3}-y_{3} \vert \bigr), \quad x\neq y \end{aligned}$$

(2.6)

and the α-quasi-periodic layer-potential operators $S_{1}$, $K_{1}$, $K'_{1}$, and $T_{1}$ defined by

$$\begin{aligned} &S_{1}\xi (x)= \int _{\Gamma }G_{1}(x,y;k_{1})\xi (y)\,ds(y),\quad x \in \Gamma , \end{aligned}$$

(2.7)

$$\begin{aligned} &K_{1}\xi (x)= \int _{\Gamma }\frac{\partial }{\partial \nu (y)}G_{1}(x,y;k_{1}) \xi (y)\,ds(y),\quad x\in \Gamma , \end{aligned}$$

(2.8)

$$\begin{aligned} &K'_{1}\xi (x)=\frac{\partial }{\partial \nu (x)} \int _{\Gamma }G_{1}(x,y;k_{1}) \xi (y) \,ds(y),\quad x\in \Gamma , \end{aligned}$$

(2.9)

$$\begin{aligned} &T_{1}\xi (x)=-\frac{\partial }{\partial \nu (x)} \int _{\Gamma } \frac{\partial }{\partial \nu (y)}G_{1}(x,y;k_{1}) \xi (y)\,ds(y),\quad x\in \Gamma. \end{aligned}$$

(2.10)

Noting that $G_{1}(x,y;k_{1})-\Phi (x,y;k_{1})$ is smooth, it follows from [8] that the operators $S_{1}:H^{-\frac{1}{2}}_{\alpha }(\Gamma )\rightarrow H^{\frac{1}{2}}_{\alpha }(\Gamma )$, $K_{1}:H^{\frac{1}{2}}_{\alpha }(\Gamma )\rightarrow H^{\frac{1}{2}}_{\alpha }(\Gamma )$, $K'_{j}:H^{-\frac{1}{2}}_{\alpha }(\Gamma )\rightarrow H^{-\frac{1}{2}}_{\alpha }(\Gamma )$, and $T_{1}:H^{\frac{1}{2}}_{\alpha }(\Gamma )\rightarrow H^{-\frac{1}{2}}_{\alpha }(\Gamma )$ are all bounded, where $\Phi (x,y;k_{1})=\frac{1}{4\pi }\frac{e^{ik_{1}|x-y|}}{|x-y|}$ is the fundamental solution of the Helmholtz equation $\triangle \Phi +k_{1}^{2}\Phi =-\delta _{y}$ in the free space ${\mathbb{R}}^{3}$.

Theorem 2.1

For $f_{1},f_{2}\in L^{p}_{\alpha }(\Gamma )$ with $1< p\leq 2$, there exists a unique solution $(w_{1},w_{2})\in L^{p}_{\alpha }(\Omega _{+}(h))\times L^{p}_{\alpha }( \Omega _{-}(h))$ to the transmission problem (2.1)–(2.5) satisfying the estimate

$$\begin{aligned} \Vert w_{1} \Vert _{L^{p}_{\alpha }(\Omega _{+}(h))}+ \Vert w_{2} \Vert _{L^{p}_{\alpha }( \Omega _{-}(h))} \leq C \bigl( \Vert f_{1} \Vert _{L^{p}_{\alpha }(\Gamma )}+ \Vert f_{2} \Vert _{L^{p}_{\alpha }(\Gamma )} \bigr), \end{aligned}$$

(2.11)

where $C>0$ is a constant independent of $f_{1}, f_{2}$, and depending on $G_{j}(\cdot ,y;k_{j}), \Omega _{+}(h)$ with $j=1,2$ and the boundedness of the operators $S_{j},K_{j}, K'_{j}, j=1,2$, and $T_{2}-T_{1}$ in $L^{p}_{\alpha }(\Gamma )$.

Moreover, if $f_{1},f_{2}\in L^{p}_{\alpha }(\Gamma )$ with $\frac{4}{3}< p\leq 2$, we have

$$\begin{aligned} \Vert w_{1} \Vert _{L^{2}_{\alpha }(\Omega _{+}(h))}+ \Vert w_{2} \Vert _{L^{2}_{\alpha }( \Omega _{-}(h))} \leq C \bigl( \Vert f_{1} \Vert _{L^{p}_{\alpha }(\Gamma )}+ \Vert f_{2} \Vert _{L^{p}_{\alpha }(\Gamma )} \bigr) \end{aligned}$$

(2.12)

with a positive constant $C>0$, which is independent of $f_{1}, f_{2}$, and depending on $G_{j}(\cdot ,y;k_{j}), \Omega _{+}(h)$ with $j=1,2$ and the boundedness of the operators $S_{j},K_{j}, K'_{j}, j=1,2$ and $T_{2}-T_{1}$ in $L^{p}_{\alpha }(\Gamma )$.

Proof

We seek a solution of problem (2.1)–(2.5) in the form of combined single- and double-layer potential

$$\begin{aligned} &w_{1}(x)= \int _{\Gamma }G_{1}(x,y;k_{1})\varphi _{1}(y)\,ds(y)+ \lambda \int _{\Gamma } \frac{\partial G_{1}(x,y;k_{1})}{\partial \nu (y)}\varphi _{2}(y)\,ds(y), \end{aligned}$$

(2.13)

$$\begin{aligned} &w_{2}(x)= \int _{\Gamma }G_{2}(x,y;k_{2})\varphi _{1}(y)\,ds(y)+ \int _{ \Gamma }\frac{\partial G_{2}(x,y;k_{2})}{\partial \nu (y)}\varphi _{2}(y)\,ds(y), \end{aligned}$$

(2.14)

where $G_{2}(x,y;k_{2})$ is defined as (2.6) with the wave number $k_{1}$ replaced by $k_{2}$.

With the aid of the jump relations of the layer potentials (see [26] for the case in the $L^{p}$ norm), we obtain that the transmission problem (2.1)–(2.5) can be reduced to the system of integral equations

$$\begin{aligned} \begin{pmatrix} \varphi _{2} \\ \varphi _{1} \end{pmatrix} +L \begin{pmatrix} \varphi _{2} \\ \varphi _{1} \end{pmatrix} = \begin{pmatrix} \frac{2}{1+\lambda }f_{1} \\ -\frac{2}{1+\lambda }f_{2} \end{pmatrix} \quad\text{in } L^{p}_{\alpha }(\Gamma )\times L^{p}_{\alpha }(\Gamma ), \end{aligned}$$

(2.15)

where the operator L is given by

$$\begin{aligned} L:= \begin{pmatrix} \frac{2}{1+\lambda }(\lambda K_{1}- K_{2}) & \frac{2}{1+\lambda }(S_{1}-S_{2}) \\ \frac{2\lambda }{1+\lambda } (T_{2}-T_{1}) &\frac{2}{1+\lambda } ( \lambda K'_{2}-K'_{1}) \end{pmatrix}. \end{aligned}$$

It is easily shown that (2.15) is of Fredholm type due to the compactness of the operators $S_{j},K_{j}, K'_{j}, j=1,2$, and $T_{2}-T_{1}$ in $L^{p}_{\alpha }(\Gamma )$. This, together with the uniqueness of the scattering problem (1.2)–(1.6), implies that (2.15) has a unique solution $(\varphi _{2},\varphi _{1})^{T}\in L^{p}_{\alpha }(\Gamma )\times L^{p}_{\alpha }(\Gamma )$ with the estimate

$$\begin{aligned} \Vert \varphi _{2} \Vert _{L^{p}_{\alpha }(\Gamma )}+ \Vert \varphi _{1} \Vert _{L^{p}_{\alpha }(\Gamma )} \leq C \bigl( \Vert f_{1} \Vert _{L^{p}_{\alpha }(\Gamma )}+ \Vert f_{2} \Vert _{L^{p}_{\alpha }(\Gamma )} \bigr). \end{aligned}$$

(2.16)

We next prove the $L^{p}_{\alpha }, 1< p\leq 2$ estimates for the solution of the transmission problem (2.1)–(2.5). In fact, it can be checked that

$$\begin{aligned} & \biggl\Vert \int _{\Gamma }\Omega _{+}(h)G_{1}(\cdot ,y;k_{1}) \varphi _{1}(y)\,ds(y) \biggr\Vert _{L^{p}_{\alpha }(\Omega _{+}(h))} \\ &\quad=\sup_{g\in L^{q}_{\alpha }, \Vert g \Vert _{L^{q}_{\alpha }(\Omega _{+}(h))}=1} \biggl\vert \int _{\Omega _{+}(h)} \int _{\Gamma }G_{1}(x,y;k_{1})\varphi _{1}(y)\,ds(y)g(x)\,dx \biggr\vert \\ &\quad=\sup_{g\in L^{q}_{\alpha }, \Vert g \Vert _{L^{q}_{\alpha }(\Omega _{+}(h))}=1} \biggl\vert \int _{\Gamma } \int _{\Omega _{+}(h)}G_{1}(x,y;k_{1})g(x)\,dx \varphi _{1}(y)\,ds(y) \biggr\vert \\ &\quad\leq \vert \Gamma \vert ^{\frac{1}{q}} \sup _{g\in L^{q}, \Vert g \Vert _{L^{q}_{\alpha }( \Omega _{+}(h))}=1} \sup_{y\in \Gamma } \bigl\Vert G_{1}(\cdot ,y;k_{1}) \bigr\Vert _{L^{p}_{\alpha }(\Omega _{+}(h))} \Vert g \Vert _{L^{q}_{\alpha }(\Omega _{+}(h))} \Vert \varphi _{1} \Vert _{L^{p}_{\alpha }(\Gamma )} \\ &\quad= \vert \Gamma \vert ^{\frac{1}{q}} \sup _{y\in \Gamma } \bigl\Vert G_{1}(\cdot ,y;k_{1}) \bigr\Vert _{L^{p}_{\alpha }(\Omega _{+}(h))} \Vert \varphi _{1} \Vert _{L^{p}_{\alpha }( \Gamma )}\leq C \Vert \varphi _{1} \Vert _{L^{p}_{\alpha }(\Gamma )} \end{aligned}$$

(2.17)

and

$$\begin{aligned} & \biggl\Vert \int _{\Gamma } \frac{\partial G_{1}(\cdot ,y;k_{1})}{\partial \nu (y)}\varphi _{2}(y)\,ds(y) \biggr\Vert _{L^{p}_{\alpha }(\Omega _{+}(h))} \\ &\quad=\sup_{g\in L^{q}_{\alpha }, \Vert g \Vert _{L^{q}_{\alpha }(\Omega _{+}(h))}=1} \biggl\vert \int _{\Omega _{+}(h)} \int _{\Gamma } \frac{\partial G_{1}(x,y;k_{1})}{\partial \nu (y)}\varphi _{2}(y) \,ds(y)g(x)\,dx \biggr\vert \\ &\quad=\sup_{g\in L^{q}_{\alpha }, \Vert g \Vert _{L^{q}_{\alpha }(\Omega _{+}(h))}=1} \biggl\vert \int _{\Gamma }\frac{\partial }{\partial \nu (y)} \int _{ \Omega _{+}(h)}G_{1}(x,y;k_{1})g(x)\,dx\varphi _{2}(y)\,ds(y) \biggr\vert \\ & \quad\leq \sup_{g\in L^{q}_{\alpha }, \Vert g \Vert _{L^{q}_{\alpha }(\Omega _{+}(h))}=1} \biggl\Vert \frac{\partial }{\partial \nu (y)} \int _{\Omega _{+}(h)}G_{1}(x, \cdot;k_{1})g(x)\,dx \biggr\Vert _{L^{q}_{\alpha }(\Gamma )} \Vert \varphi _{2} \Vert _{L^{p}_{\alpha }(\Gamma )} \\ &\quad \leq \sup_{g\in L^{q}_{\alpha }, \Vert g \Vert _{L^{q}_{\alpha }(\Omega _{+}(h))}=1} C \Vert g \Vert _{L^{q}_{\alpha }(\Omega _{+}(h))}\cdot \Vert \varphi _{2} \Vert _{L^{p}_{\alpha }(\Gamma )} =C \Vert \varphi _{2} \Vert _{L^{p}_{\alpha }(\Gamma )} \end{aligned}$$

(2.18)

with $\frac{1}{p}+\frac{1}{q}=1$. Here, we have used the fact that the volume potential operator is bounded from $L^{q}_{\alpha }(\Omega _{+}(h))$ into $W^{2,q}_{\alpha }(\Omega _{+}(h))$ with $2\leq q\leq 4$ (see [15, Theorem 9.9]), and the boundary trace operator is bounded from $W^{1,q}_{\alpha }(\Omega _{+}(h))$ into $L^{q}_{\alpha }(\Gamma )$ with $2\leq q\leq 4$ (see [1, Theorem 5.36]). It is noted that (2.17)–(2.18) still holds true, with $G_{1}(x,\cdot;k_{1})$ replaced by $G_{2}(x,\cdot;k_{2})$ and $\Omega _{+}(h)$ replaced by $\Omega _{-}(h)$, respectively. Now the desired estimate (2.11) follows from (2.13)–(2.14) and (2.16)–(2.18). Furthermore, if $f_{1},f_{2}\in L^{p}_{\alpha }(\Gamma )$ with $\frac{4}{3}< p\leq 2$, by the similar arguments as those in (2.17)–(2.18), one can derive the required result (2.13). This completes the proof of the theorem. □

Corollary 2.2

For $y_{0}\in \Gamma$, define the sequence $y_{j}:=y_{0}- \frac{1}{j}\nu (y_{0})\in \Omega _{+}$, $j\in {\mathbb{N}}$. Let $(u_{1j},u_{2j})$ be the solution of the scattering problem (1.2)–(1.6) with the incident point source $u^{i}=G_{1}(x,y_{j};k_{1})$. Then, for any $h\in {\mathbb{R}}$, we have

$$\begin{aligned} \Vert u_{1j} \Vert _{L^{2}_{\alpha }(\Omega _{+}(h))}+ \Vert u_{2j} \Vert _{L^{2}_{\alpha }( \Omega _{-}(h))} \leq C \end{aligned}$$

(2.19)

uniformly for $j\in {\mathbb{N}}_{+}$, where $C>0$ is a constant depending on $G_{j}(\cdot ,y;k_{j}), \Omega _{+}(h)$ with $j=1,2$.

Proof

It is obvious that $(u_{1j}^{s},u_{2j})$ satisfies problem (2.1)–(2.5) with the boundary data

$$\begin{aligned} f_{1}(j):=-G_{1}(x,y_{j};k_{1}),\qquad f_{2}(j):=- \frac{\partial G_{1}(x,y_{j};k_{1})}{\partial \nu }\quad j\in { \mathbb{N}}. \end{aligned}$$

It is easy to see that $f_{1}(j),f_{2}(j)\in L^{p}_{\alpha }(\Gamma )$ are uniformly bounded for $j\in {\mathbb{N}}$ with $\frac{4}{3}< p<\frac{3}{2}$. Then the required result (2.19) follows from Theorem 2.1. This proves the corollary. □

Theorem 2.3

Let $(u_{1j},u_{2j})$ be the solution of the scattering problem (1.2)–(1.6) corresponding to the incident point source $u^{i}=G_{1}(x,y_{j};k_{1})$ with $y_{j}$ defined in Corollary 2.2. Then, for any $h\in {\mathbb{R}}$, it holds that

$$\begin{aligned} \Vert u_{2j} \Vert _{H^{1}_{\alpha }(\Omega _{-}(h)\setminus {\overline{B}})} \leq C \end{aligned}$$

(2.20)

uniformly for $j\in {\mathbb{N}}_{+}$. Here, $C>0$ is a constant depending on $G_{j}(\cdot ,y;k_{j}), \Omega _{+}(h)$ with $j=1,2$ and the uniform boundedness of $S_{\Gamma \setminus {B}}(j)$ and $K_{\Gamma \setminus {B}}(j)$ in the corresponding Hilbert spaces, B is a ball satisfying that $B\supset B_{\delta }$, and $B_{\delta }$ is a small ball centered at $y_{0}$ with the radius $\delta >0$.

Proof

Define $\tilde{y}_{j}:=y_{0}+\frac{1}{j}\nu (y_{0})\in \Omega _{-}$, let $w_{1}(j):=u_{1j}^{s}-G_{1}(x,\tilde{y}_{j};k_{1})$ and $w_{2}(j):= u_{2j}$, it follows that $(w_{1}(j),w_{2}(j))$ satisfies problem (2.1)–(2.5) with the boundary data

$$\begin{aligned} &f_{1}(j):=-G_{1}(x,y_{j};k_{1})-G_{1}(x, \tilde{y}_{j};k_{1}), \\ &f_{2}(j):=-\frac{\partial G_{1}(x,y_{j};k_{1})}{\partial \nu }- \frac{\partial G_{1}(x,\tilde{y}_{j};k_{1})}{\partial \nu }. \end{aligned}$$

Obviously, $f_{1}(j)\in L^{p}_{\alpha }(\Gamma )$ is uniformly bounded for $j\in {\mathbb{N}}$, where $1< p<2$. Furthermore, it is seen from [9, Lemma 4.2] that $f_{2}(j)\in C(\Gamma )$ is uniformly bounded for $j\in {\mathbb{N}}$. So $f_{2}(j)\in L^{p}_{\alpha }(\Gamma )$ is uniformly bounded for $j\in {\mathbb{N}}$, where $1< p<2$. Then, by (2.16) in Theorem 2.1, one obtains that the solution $(\varphi _{1},\varphi _{2})^{T}$ of (2.15) satisfies

$$\begin{aligned} \Vert \varphi _{1} \Vert _{L^{p}_{\alpha }(\Gamma )}+ \Vert \varphi _{2} \Vert _{L^{p}_{\alpha }(\Gamma )} \leq C \bigl( \Vert f_{1j} \Vert _{L^{p}_{\alpha }(\Gamma )}+ \Vert f_{2j} \Vert _{L^{p}_{\alpha }(\Gamma )} \bigr),\quad 1< p< 2. \end{aligned}$$

(2.21)

We next prove that the operator $S_{1j}:L^{p}_{\alpha }(\Gamma )\rightarrow L^{2}_{\alpha }(\Gamma \setminus {B})$ is uniformly bounded for $j\in {\mathbb{N}}$, where $1< p<2$. Indeed, by direct calculations, we can deduce that

$$\begin{aligned} & \biggl\Vert \int _{\Gamma }G_{1}(\cdot ,y;k_{1})\varphi _{1}(y)\,ds(y) \biggr\Vert _{L^{2}(\Gamma \setminus {B})} \\ &\quad=\sup _{\psi \in L^{2}_{\alpha }, \Vert \psi \Vert _{L^{2}_{\alpha }(\Gamma \setminus {B})}=1} \biggl\vert \int _{\Gamma \setminus {B}} \int _{\Gamma }G_{1}(x,y;k_{1})\varphi _{1}(y)\,ds(y) \psi (x)\,dx \biggr\vert \\ &\quad =\sup_{\psi \in L^{2}_{\alpha }, \Vert \psi \Vert _{L^{2}_{\alpha }(\Gamma \setminus {B})}=1} \biggl\vert \int _{\Gamma } \int _{ \Gamma \setminus {B}}G_{1}(x,y;k_{1})\psi (x)\,dx \varphi _{1}(y)\,ds(y) \biggr\vert \\ &\quad \leq \vert \Gamma \vert ^{\frac{1}{q}} \sup _{\psi \in L^{2}_{\alpha }, \Vert \psi \Vert _{L^{2}_{\alpha }(\Gamma \setminus {B})}=1} \sup_{y \in \Gamma \setminus {B}} \bigl\Vert G_{1}(\cdot ,y;k_{1}) \bigr\Vert _{L^{2}_{\alpha }( \Gamma \setminus {B})} \Vert \psi \Vert _{L^{2}_{\alpha }(\Gamma \setminus {B})} \Vert \varphi _{1} \Vert _{L^{p}_{\alpha }(\Gamma )} \\ &\quad = \vert \Gamma \vert ^{\frac{1}{q}} \sup _{y\in \Gamma \setminus {B}} \bigl\Vert G_{1}(\cdot ,y;k_{1}) \bigr\Vert _{L^{2}_{\alpha }(\Gamma \setminus {B})} \Vert \varphi _{1} \Vert _{L_{\alpha }^{p}(\Gamma )}\leq C \Vert \varphi _{1} \Vert _{L^{p}_{\alpha }(\Gamma )}. \end{aligned}$$

(2.22)

Here, we have used the fact that $G_{1}(\cdot ,y;k_{1})$ is smooth on the boundary $\Gamma \setminus {B}$ in the first inequality. Then we have that $S_{1j}:L^{p}_{\alpha }(\Gamma )\rightarrow L^{2}_{\alpha }(\Gamma \setminus {B})$ is uniformly bounded for $j\in {\mathbb{N}}_{+}$. Moreover, by using similar arguments as those in the proof of (2.22), it is seen that the operators $S_{ij}$, $K_{ij}$, $K'_{ij}$, and $T_{ij}$ are all uniformly bounded from $L^{p}_{\alpha }(\Gamma )$ into $L^{2}_{\alpha }(\Gamma \setminus {B})$ for $j\in {\mathbb{N}}_{+}$, $i=1,2$. Also notice that $f_{1}(j), f_{2}(j)\in L^{2}_{\alpha }(\Gamma \setminus {B})$ are uniformly bounded for $j\in {\mathbb{N}}_{+}$. This, combined with equation (2.15), gives that the unique solution $(\varphi _{1},\varphi _{2})^{T}$ of (2.15) satisfies that $(\varphi _{1},\varphi _{2})^{T}\in L^{2}_{\alpha }(\Gamma \setminus {B}) \times L^{2}_{\alpha }(\Gamma \setminus {B})$. It is noted from (2.14) that the solution $u_{2j}$ of the transmission problem (2.1)–(2.5) can be rewritten in the form of

$$\begin{aligned} u_{2j}(x)={}& \int _{\Gamma \setminus {B}}G_{2}(x,y;k_{2}) \varphi _{1}(y)\,ds(y)+ \int _{\Gamma \cap B}G_{2}(x,y;k_{2})\varphi _{1}(y)\,ds(y) \\ &{}+ \int _{\Gamma \setminus {B}} \frac{\partial G_{2}(x,y;k_{2})}{\partial \nu (y)}\varphi _{2}(y)\,ds(y)+ \int _{\Gamma \cap B} \frac{\partial G_{2}(x,y;k_{2})}{\partial \nu (y)}\varphi _{2}(y)\,ds(y). \end{aligned}$$

(2.23)

Define

$$ S_{\Gamma \setminus {B}}(j)\varphi _{1}:= \int _{\Gamma \setminus {B}}G_{2}(x,y;k_{2}) \varphi _{1}(y)\,ds(y). $$

It is easily seen that $S_{\Gamma \setminus {B}}(j):H^{-\frac{1}{2}}_{\alpha }(\Gamma \setminus {B})\rightarrow H^{\frac{1}{2}}_{\alpha }(\Gamma \setminus {B})$ is uniformly bounded for $j\in {\mathbb{N}}$. This in combination with the fact that $\varphi _{1}\in L^{2}_{\alpha }(\Gamma \setminus {B})$ implies that $q_{1j}(x):=S_{\Gamma \setminus {B}}(j)\varphi _{1}$ satisfies the following Dirichlet problem:

$$\begin{aligned} \textstyle\begin{cases} \triangle w+k^{2}_{2}w=0 & \text{in } \Omega _{-}\setminus {B}, \\ w=q_{1j}\in H^{\frac{1}{2}}_{\alpha }(\tilde{\Gamma }) & \text{on } \tilde{\Gamma }, \\ w(x)=\sum_{n\in {\mathbb{Z}}^{2}} w_{n}^{-} \exp (i\alpha _{n} \cdot \widetilde{x}-i\beta ^{-}_{n}x_{3}) & x_{3}< A_{2}, \end{cases}\displaystyle \end{aligned}$$

(2.24)

where $\tilde{\Gamma }=(\Gamma \setminus {B})\cup (\partial B\cap \Omega _{-})$. Then the well-posedness of the Dirichlet problem (2.24) yields that, for any $h\in {\mathbb{R}}$, $q_{1j}\in H^{1}(\Omega _{-}(h)\setminus {\overline{B}})$ uniformly for $j\in {\mathbb{N}}_{+}$.

We now define

$$ q_{2j}(x):= \int _{\Gamma \cap B}G_{2}(x,y;k_{2})\varphi _{1}(y)\,ds(y). $$

Since the region $\Omega _{-}\setminus {B}$ has a positive distance from $y_{0}$, it is found that $q_{2j}(x)\in H^{1}(\Omega _{-}(h)\setminus {\overline{B}})$ uniformly for $j\in {\mathbb{N}}_{+}$. We further define

$$ K_{\Gamma \setminus {B}}(j)\varphi _{2}:= \int _{\Gamma \setminus {B}} \frac{\partial G_{2}(x,y;k_{2})}{\partial \nu (y)}\varphi _{2}(y)\,ds(y). $$

Obviously, $K_{\Gamma \setminus {B}}(j):H^{-\frac{1}{2}}_{\alpha }(\Gamma \setminus {B})\rightarrow H^{\frac{1}{2}}_{\alpha }(\Gamma \setminus {B})$ is uniformly bounded for $j\in {\mathbb{N}}_{+}$. Then, by the fact that $\varphi _{2}\in L^{2}_{\alpha }(\Gamma \setminus {B})$, we obtain that $q_{3j}(x):=K_{\Gamma \setminus {B}}(j)\varphi _{2}$ satisfies the Dirichlet problem (2.24), with the boundary data $w=q_{1j}$ replaced by $w=q_{3j}$ on Γ̃. Then using similar arguments as those in the proof of $q_{1j}\in H^{1}_{\alpha }(\Omega _{-}(h)\setminus {\overline{B}})$ yields that $q_{3j}\in H^{1}_{\alpha }(\Omega _{-}(h)\setminus {\overline{B}})$ uniformly for $j\in {\mathbb{N}}_{+}$. We also define

$$ q_{4j}(x):= \int _{\Gamma \cap B} \frac{\partial G_{2}(x,y;k_{2})}{\partial \nu (y)}\varphi _{2}(y)\,ds(y). $$

The uniform boundedness of $q_{4j}\in H^{1}_{\alpha }(\Omega _{-}(h)\setminus {\overline{B}})$ for $j\in {\mathbb{N}}_{+}$ can be concluded from the positive distance between the region $(\Omega _{-}(h)\setminus {\overline{B}})$ and $y_{0}$. Finally, the desired result (2.20) follows from the discussions below (2.24). The proof of the theorem is thus completed. □

3 Uniqueness of the inverse problem

In this section we mainly focus on the inverse problem of determining the periodic interface by means of the near-field data measured from one side of the periodic interface. To address this issue, we first introduce a mixed-reciprocity relation between the incident plane wave (1.1) and the incident point source (2.6). To accomplish this, we let $\hat{\alpha }: = -\alpha$ and consider an incident point source located at $z\in \Omega _{+}$ taking the form

$$\begin{aligned} G_{1}(x,z;k_{1})= \frac{i}{8\pi ^{2}}\sum_{n\in {\mathbb{Z}}^{2}} \frac{1}{\hat{\beta }^{+}_{n}}\exp \bigl(i\hat{\alpha }_{n}\cdot ( \widetilde{x}-\widetilde{z})+i\hat{ \beta }^{+}_{n} \vert x_{3}-z_{3} \vert \bigr),\quad x\neq z \end{aligned}$$

(3.1)

with the coefficients $\hat{\alpha }_{n}, \hat{\beta }_{n}^{+}$ defined by $\alpha _{n}, \beta _{n}^{+}$ with α replaced by α̂, respectively. Then the inverse scattering of the incident point source $G_{1}(\cdot ,z;k_{1})$ by the two-layered periodic interface can be formulated as the following α̂-quasi-periodic problem:

$$\begin{aligned} & \triangle \hat{v}_{1}+k_{1}^{2} \hat{v}_{1}=0\quad \text{in } \Omega _{+}\setminus \{z\}, \end{aligned}$$

(3.2)

$$\begin{aligned} & \triangle \hat{v}_{2}+k_{2}^{2} \hat{v}_{2}=0 \quad\text{in } \Omega _{-}, \end{aligned}$$

(3.3)

$$\begin{aligned} & \hat{v}_{1}= \hat{v}_{2},\qquad \frac{\partial \hat{v}_{1}}{\partial \nu }=\lambda \frac{\partial \hat{v}_{2}}{\partial \nu }\quad \text{on } \Gamma , \end{aligned}$$

(3.4)

$$\begin{aligned} & \hat{v}^{s}(x)=\sum_{n\in {\mathbb{Z}}^{2}} \hat{v}_{n}^{+}\exp \bigl(i \hat{\alpha }_{n} \cdot \widetilde{x}+i\hat{\beta }^{+}_{n}x_{3} \bigr),\quad x_{3}>A_{1}, \end{aligned}$$

(3.5)

$$\begin{aligned} & \hat{v}_{2}(x)=\sum_{n\in {\mathbb{Z}}^{2}} \hat{v}_{n}^{-}\exp \bigl(i \hat{\alpha }_{n} \cdot \widetilde{x}-i\hat{\beta }^{-}_{n}x_{3} \bigr),\quad x_{3}< A_{2}. \end{aligned}$$

(3.6)

Here, both $\hat{v}_{1}$ in $\Omega _{+}$ and $\hat{v}_{2}$ in $\Omega _{-}$ satisfy the α̂-quasi-periodic condition

$$\begin{aligned} \hat{v}_{j}(\widetilde{x}+2n\pi , x_{3})=e^{i 2\hat{\alpha }\cdot n \pi } \hat{v}_{j}(\widetilde{x}, x_{3}),\quad j=1,2. \end{aligned}$$

Moreover, we write the scattered field $\hat{v}^{s}( \cdot , z):=\hat{v}_{1} (\cdot , z)-G_{1}(\cdot ,z;k_{1})$ indicates the dependance of the wave field on the location of the point source, and let $v(\cdot;m)$ and $u^{s}(\cdot;m)$ be the scattered solution to problem (1.2)–(1.6) with respect to the incident wave $u^{i}(x;m)=\exp (i\alpha _{m}\cdot \widetilde{x}-i\beta _{m}^{+}x_{3}), m\in {\mathbb{Z}}^{2}$. Therefore, we have the following mixed-reciprocity relation (for a proof, we refer to [34, Lemma 4.1]).

Lemma 3.1

For $z_{0}\in \Omega _{+}$, let $\hat{v}_{n}^{+}(z_{0})$ be the Rayleigh coefficients of $\hat{v}_{1}^{s}(\cdot;z_{0})$. Then it holds that

$$\begin{aligned} u_{1}^{s}(z_{0};m)=-8 \pi ^{2}i\hat{\beta }_{-m}^{+}\hat{v}_{-m}^{+}(z_{0}) \quad\textit{for all }m\in {\mathbb{Z}}^{2}. \end{aligned}$$

(3.7)

Now we are in a position to present a uniqueness theorem for our inverse problem. The proof mainly depends on the a priori estimates established in Sect. 2 and a construction of a well-posed transmission problem in a sufficiently small domain.

Theorem 3.2

Let $u_{1}^{s}(\cdot;m)$ and $\widetilde{u}_{1}^{s}(\cdot;m)$ be the scattered fields corresponding to problem (1.2)–(1.6) with respect to the different bi-periodic interfaces Γ and Γ̃, respectively, induced by the same incident field $u^{i}(x;m)=\exp (i\alpha _{m}\cdot \widetilde{x}-i\beta _{m}^{+}x_{3}), m\in {\mathbb{Z}}^{2}$. If $u_{1}^{s}(\cdot;m)|_{\Gamma _{+}(h)}=\widetilde{u}_{1}^{s}(\cdot;m)|_{ \Gamma _{+}(h)}$ for all incident fields $u^{i}(x;m) m\in {\mathbb{Z}}^{2}$, then we have $\Gamma =\widetilde{\Gamma }$.

Proof

We shall prove the assertion by contradiction. Assume contrarily that $\Gamma \neq \widetilde{\Gamma }$. Without loss of generality, we can choose a point $z^{*}\in \Gamma \setminus \widetilde{\Gamma }$ satisfying that $f(\widetilde{z}^{*}) >\widetilde{f}(\widetilde{z}^{*})$ with $z^{*}=(\widetilde{z}^{*},z_{3})$. Then we define the sequence

$$\begin{aligned} z_{j}: = z^{*} - \frac{\delta }{j}\nu \bigl(z^{*} \bigr) \quad\text{for }j=1,2, \ldots \cdots \end{aligned}$$

(3.8)

with sufficiently small $\delta >0$ such that $z_{j}\in B_{\varepsilon _{0}}(z^{*})\subseteq (\Omega _{+}\cap \widetilde{\Omega }_{+})$ for all $j\in {\mathbb{N}}_{+}$, where $B_{\varepsilon _{0}}(z^{*})$ is a small ball centered at $z^{*}$ with the radius $\varepsilon _{0}>0$.

Let $(\hat{v}_{1}(\cdot;z_{j}),\hat{v}_{2}(\cdot;z_{j}))$ and $(\hat{\widetilde{v}}_{1}(\cdot;z_{j}),\hat{\widetilde{v}}_{2}( \cdot;z_{j}))$ be the solutions to problem (3.2)–(3.6) corresponding to the same α̂-quasi-periodic incident point source $\hat{v}^{i} = \hat{G}(\cdot ,z_{j})$ with $z_{j}$ defined by (3.8). Then one obtains from Lemma 3.1 that

$$\begin{aligned} u_{1}^{s}(z_{j};m)=-8 \pi ^{2}i\hat{\beta }_{-m}^{+}\hat{v}_{-m}^{+}(z_{j}) \quad\text{and}\quad \widetilde{u}_{1}^{s}(z_{j};m)=-8\pi ^{2}i \hat{\beta }_{-m}^{+}\hat{ \widetilde{v}}_{-m}^{+}(z_{j}) \end{aligned}$$

(3.9)

for all $m\in {\mathbb{Z}}^{2}$, where $\hat{v}_{-m}^{+}(z_{j})$ and $\hat{\widetilde{v}}_{-m}^{+}(z_{j})$ denote the Rayleigh coefficients of the scattered fields $\hat{v}^{s}(\cdot;z_{j})$ and $\hat{\widetilde{v}}^{s}(\cdot;z_{j})$, respectively. By the assumption that $u_{1}^{s}(\cdot;m)|_{\Gamma _{+}(h)}=\widetilde{u}_{1}^{s}(\cdot;m)|_{ \Gamma _{+}(h)}$ for all incident fields $u^{i}(x;m) m\in {\mathbb{Z}}^{2}$, we arrive at that $\hat{v}_{-m}^{+}(z_{j}) = \hat{\widetilde{v}}_{-m}^{+}(z_{j})$, $m\in {\mathbb{Z}}^{2}$. This in combination with the Rayleigh expansions and the unique continuation principle implies that

$$\begin{aligned} \hat{v}_{1}(\cdot;z_{j}) = \hat{ \widetilde{v}}_{1}(\cdot;z_{j}) \quad\text{in }\Omega ^{+}\cap \widetilde{\Omega }^{+} \end{aligned}$$

(3.10)

for all $j\in {\mathbb{N}}_{+}$.

Denote $D_{0}: = B_{\varepsilon _{0}}(z^{*})\cap \Omega ^{-}$ with sufficiently small $\varepsilon _{0}>0$ such that $D_{0}\subseteq (\Omega _{-}\cap \widetilde{\Omega }_{+})$. Let $U_{j}:=\hat{\widetilde{v}}_{1}(\cdot;z_{j})$ and $W_{j}:=\hat{v}_{2}(\cdot;z_{j})$, it is observed that $(U_{j}, W_{j})$ satisfies the following modified interior transmission problem:

$$\begin{aligned} \textstyle\begin{cases} \triangle U_{j}-U_{j}=g_{1,j}& \text{in } D_{0}, \\ \triangle W_{j}-W_{j}= g_{2,j} & \text{in } D_{0}, \\ U_{j}-W_{j}=h_{1,j} & \text{on } \partial D_{0}, \\ \frac{\partial U_{j}}{\partial \nu }-\lambda \frac{\partial W_{j}}{\partial \nu }= h_{2,j} & \text{on } \partial D_{0} \end{cases}\displaystyle \end{aligned}$$

(3.11)

with the right terms and the boundary data

$$\begin{aligned} &g_{1,j}:=- \bigl(k_{1}^{2}+1 \bigr)\hat{ \widetilde{v}}_{1}(\cdot;z_{j}),\qquad g_{2,j}:=- \bigl(k_{2}^{2}+1 \bigr)\hat{v}_{2}( \cdot;z_{j}), \\ &h_{1,j}:=\hat{\widetilde{v}}_{1}(\cdot;z_{j})- \hat{v}_{2}(\cdot;z_{j}),\qquad h_{2,j}:= \frac{\partial \hat{\widetilde{v}}_{1}(\cdot;z_{j})}{\partial \nu }- \lambda \frac{\partial \hat{v}_{2}(\cdot;z_{j})}{\partial \nu }. \end{aligned}$$

Clearly, one has that $h_{1,j}=h_{2,j}$ on $\partial D_{0}\cap \Gamma$. Since $Z^{*}$ has a positive distance from Γ̃, we obtain that $\hat{\widetilde{v}}^{s}(\cdot;z_{j})\in H^{1}(D_{0})$ uniformly for all $j\in {\mathbb{N}}_{+}$. In view of the fact that $\hat{G}(\cdot ,z_{j})\in L^{2}(D_{0})$ uniformly for all $j\in {\mathbb{N}}_{+}$, it is deduced that $g_{1,j}\in L^{2}(D_{0})$ uniformly for all $j\in {\mathbb{N}}_{+}$. The uniform boundedness of $g_{2,j}$ in $L^{2}(D_{0})$ for all $j\in {\mathbb{N}}_{+}$ is a direct consequence of Corollary 2.2 in Sect. 2. Moreover, arguing similarly as in [36, Theorem 2.9], one derives from the fact that $h_{1,j}=h_{2,j}$ on $\partial D_{0}\cap \Gamma$ that $h_{1,j}\in H^{1/2}(\partial D_{0})$ and $h_{2,j}\in H^{-1/2}(\partial D_{0})$, respectively, uniformly for all $j\in {\mathbb{N}}_{+}$. Therefore, by the well-posedness of problem (3.11), we have

$$\begin{aligned} \bigl\Vert \hat{G}(\cdot ,z_{j}) \bigr\Vert _{H^{1}(D_{0})} - \bigl\Vert \hat{\widetilde{v}}^{s}( \cdot;z_{j}) \bigr\Vert _{H^{1}(D_{0})}\leq \bigl\Vert \hat{ \widetilde{v}}(\cdot;z_{j}) \bigr\Vert _{H^{1}(D_{0})}= \Vert U_{j} \Vert _{H^{1}(D_{0})} \leq C. \end{aligned}$$

However, the above inequality is a contradiction since $\|\hat{\widetilde{v}}^{s}(\cdot;z_{j})\|_{H^{1}(D_{0})}$ is uniformly bounded and $\|\hat{G}(\cdot ,z_{j})\|_{H^{1}(D_{0})}\to \infty$ as $j\to \infty$. Therefore, one concludes that $\Gamma =\widetilde{\Gamma }$. This completes the proof of the theorem. □