Design of sampled-data controller for T–S fuzzy system with the refined fractional delayed-state and its applications

Abstract

The paper is concerned with the development of a sampled-data (SD) controller designed for Takagi–Sugeno (T–S) fuzzy systems. A key highlight is the incorporation of a refined fractional delayed-state into this control approach. The primary aim is to establish criteria for system stabilization, thereby ensuring the asymptotic stability of the considered systems. This objective is pursued within the framework of the newly designed control methodology. The core contribution of work explains in the introduction of an innovative Lyapunov–Krasovskii functional (LKF) tailored to T–S fuzzy systems. This novel approach capitalizes on the efficacy of sampling intervals. The LKF design takes advantage of variable attributes tied to the real sampling pattern, effectively reducing the conservatism of the outcomes. Moreover, the paper introduces a sophisticated fractional delayed-state concept, which plays a pivotal role in shaping a modified looped functional-based LKF. The stability criteria are then formulated through the utilization of linear matrix inequalities (LMIs) and integral inequalities. These criteria perform dynamic part in establishing the asymptotic stability of considered systems when subjected to the designed control approach.

1 Introduction

Renewable energy, often termed as clean energy, emanates from natural sources that replenish consistently. Notably, wind energy stands out as an exceptionally valuable form of renewable energy due to its capacity to provide abundant, pollution-free power [1]. The PMSM has garnered significant attention in the research community, particularly from a practical perspective within the low-to-medium-power range. This interest is attributed to its distinct advantages such as a compact form factor, a high ratio of torque to inertia, a useful the ratio of torque to weight, and the absence of rotor losses [2]. As a result, exploring PMSM-based wind turbine models becomes essential. Additionally, the authors have delved into the domain of wind energy conversion systems, utilizing passivity theory as a framework [3] particularly focusing on Permanent Magnet Synchronous Generators. Furthermore, the authors have recently tackled the issue of stability analysis for dissipative systems employing the Lyapunov function approach [4].

In recent times, there has been a substantial focus on the development of fuzzy logic theory within both academic and industrial circles. Notably, the T–S fuzzy method has gained significant traction within the field of control. This is primarily due to its ability to succinctly represent nonlinear systems using a series of local subsystems intertwined with their corresponding membership functions [5]. Consequently, T–S fuzzy controller based systems investigated via stability theory. Given the inherently nonlinear nature of real-world processes, the design of complicated systems becomes a rather intricate endeavour [6] and [7]. Hence, the exploration of fuzzy systems becomes imperative. A multitude of control strategies have been explored to comprehend the dynamic behaviors of nonlinear models. These include techniques such as $H_{\infty }$ control [8], reliable control [9], passivity-based sliding-mode control [3], event-triggered control [10], sampled-data (SD) control [11], and dissipative control [12].

Over the last few decades, numerous researchers have dedicated their efforts to exploring nonlinear models through fuzzy model and parallel distributed compensation control. Additionally, the authors explored $H_{\infty }$ control for fuzzy model [13], where the similar premise variables are engaged in both the plant and control rules. Moreover, investigations have extended to the realm of stability criteria for complex models [14], utilizing identical premise variables in complex model and the control rule. Building on the inspiration derived from these previous works, for fuzzy model employing SD control, our study delves into the establishment of stabilization conditions.

Digital controllers have evolved significantly alongside the progress of modern communication networks, digital technology, and high-speed computers. Moreover, in the physical realm [15], there has been a notable reduction in the quantity of transmitted information, leading to increased efficiency in control systems. However, there are different kinds of techniques utilized to study the stability analysis of nonlinear models with SD control. For example, the impulsive systems approach [16], discrete-time method [17], and input-delay approach [18]. In the consequence of the extensive utilization of the direct LKF method in [19], the authors investigated the stability of nonlinear models. Moreover, a variety of LKF methods considered to study the stability of nonlinear models, for example time-dependent LKF approach [9] and discontinuous LKF method [20]. In [21], a time-dependent LKF technique is anticipated to study stability condition of the nonlinear model through the SD control. Besides, improved stability criterion is found in [22] by utilizing the time-dependent discontinuous LKF technique via Wirtinger inequality. Also, in [20], the authors analyzed SD controller for nonlinear systems by utilizing a free-matrix-based discontinuous LKF. Besides that, by utilizing a looped-functional based LKF approach, the stabilization criterion for nonlinear systems with SD control has been deliberated in [23]. Recently, the problem of SD control systems by employing the two-side looped-functional-based LKF technique to improve stability criteria is investigated in [24].

The study conducted by [12], introduces the concept of a looped functional. This innovation entails relaxing the necessity for positivity and incorporates a boundary condition at sampling instants. The primary objective of this modification is to mitigate conservatism and amplify the systems flexibility. From a practical perspective, larger sampling intervals encompass additional operational considerations such as communication capacity, load limitations, and computational burdens. Hence, optimizing sampling intervals becomes crucial to achieve less conservative outcomes in SD-based systems.

Inspired by the insights shared earlier, we embark on the design of control strategies to achieve stability in T–S fuzzy systems, building upon the foundation of the refined fractional-delayed state. In contrast to existing research, this paper introduces several distinctive contributions, which can be encapsulated as follows:

• A novel modified looped functional-based LKF has been developed to streamline the design process for T–S fuzzy systems. This innovative framework integrates a wide range of valuable insights, including information from the fuzzy membership function, the specific sampling configuration, and the fractional delayed state throughout the entire sampling duration.

• Furthermore, the control methodology established in this paper effectively addresses the challenges posed by delayed states and variable sampling within nonlinear models. Through the implementation of the proposed control strategy, the SD controller ensures the stability of the considered model. This achievement is especially noteworthy in the context of complex nonlinear dynamics.

• Utilizing a fuzzy-dependent control strategy coupled with the integral inequality technique, we employ an innovative approach to establish less conservative stabilization conditions for considered systems. This is achieved by extending the upper limit of the sampling period. Comparatively, when contrasted with prior investigations such as those in Refs. [25,26,27,28,29], the unique merits of the devised control approach are illuminated. These advantages are substantiated through numerical examples, showcasing the control methods effectiveness in securing the largest feasible sampling period.

The following sections of this manuscript are organized as follows:

Section 2—in this section, an overview of the model formulation is presented, accompanied by an introduction to the essential preliminary concepts. Section 3—here, the design of the SD control for fuzzy model is comprehensively detailed. Section 4—this section is dedicated to presenting three numerical examples aimed at demonstrating the practical applicability of the derived theoretical outcomes. Section 5—the manuscript concludes with a summary and conclusions in this section.

Notations: In this paper, n-dimensional Euclidean space is denoted by ${\mathbb {R}}^{n}$; ${\mathbb {R}}^{n \times m}$, $0_{n,m}$, and $I_{n}$ represent a set of all $n \times m$ real matrices, an $n \times m$ null matrix, and an identity matrix of size $n \times n$, respectively. Also, the block diagonal matrix is represented by $diag\{ \cdot \}$. In a matrix, the notation $*$ denotes the symmetric term. $A > 0 (< 0)$ denotes a positive definite (negative definite) matrix.

2 System formulation

Consider the following model:

Model Rule i: IF $\theta _{1}(t)$ is $M_{i1}$ and $\dots$ $\theta _{p}(t)$ is $M_{ip}$,

THEN

$$\begin{aligned} {\dot{x}}(t)=A_{i}x(t)+B_{i}u(t), \end{aligned}$$

(1)

here $x(t)\in R^{n}$ is the state, and $u(t)\in R^{m}$ is input. The premise variables are represented by $\theta _{i1}$, $\dots$, $\theta _{ip}$. The fuzzy sets are denoted by $M_{ij}$, $\dots$, $M_{ip}$, the parameter p stands for the number of rules. $A_{i}$, $B_{i}$ represent the matrices of the considered model. Hence, by employing the fuzzy rule, the model (1) can be rewritten as:

$$\begin{aligned} {\dot{x}}(t)=\sum \limits _{i=1}^{r} h_{i}(\theta (t)) [A_{i}x(t)+B_{i}u(t)], \end{aligned}$$

(2)

the membership function are given by

$$\begin{aligned} h_{i}(\theta (t)) = \frac{\prod \nolimits _{j=1}^{p}M_{ij}(\theta (t))}{\sum \limits _{i=1}^{r}\prod \nolimits _{j=1}^{p}M_{ij} (\theta (t))}, \end{aligned}$$

Here, $h_{i}(\theta (t))$ denote the weights of the sub-systems within the master model, subject to the conditions $h_{i}(\theta (t)) \ge 0$, and $\sum \nolimits _{i=1}^{r} h_{i}(\theta (t)) =1$. And, $\theta (t)=[\theta _{1}(t) \dots \theta _{p}(t)]^{T}$, for all $t>0$. $M_{ij} (\theta (t))$) denotes the membership grade of $\theta _{j}(t)$ in the fuzzy set $M_{ij}$.

The control signal between $t_{k}$ and $t_{k+1}$ is sustained at a constant value using the ZOH method. Subsequently, the considered model described in equation (2) is subjected to a fuzzy-based controller. This controller is implemented by employing the PDC structure, while considering the influence of the premise variable. More, specifically, j is formulated as follows

Controller rule j: IF $\theta _{j1}(t_k)$ is $\eta _{j1}$ and $\dots$ $\theta _{p}(t_k)$ is $\eta _{jp}$,

THEN

$$\begin{aligned} u(t)=K_{j}x(t_{k}),\; t_{k}\le t<t_{k+1}, \end{aligned}$$

Here, $K_{j}\in {\mathbb {R}}^{m \times n}$, with j ranging from 1 to r, represents the control gain matrices. Additionally, sequence of sampling periods is denoted by $t_{k}(k=1,2,\dots )$. Also, sampling intervals are assumed to be satisfied in the following:

$$\begin{aligned} t_{k+1}-t_{k}=h_{k}, \; h_{k} \in [h_{L},h_{U}]. \end{aligned}$$

(3)

Here, $h_{L}>0$ and $h_{U}>0$, which satisfies $0< h_{L}\le h_{U}$. Then

$$\begin{aligned} u(t)=\sum \limits _{j=1}^{r} h_{j}(\theta (t_{k}))K_{j}x(t_{k}),\; t_{k}\le t<t_{k+1}. \end{aligned}$$

(4)

By the combination of (2) with (4), one can obtain the following SD control model:

$$\begin{aligned} {\dot{x}}(t)=\sum \limits _{i=1}^{r} \sum \limits _{j=1}^{r} h_{j}(\theta (t)) h_{j}(\theta (t_{k})) [A_{i}x(t)+B_{i}K_{j}x(t_{k})]. \end{aligned}$$

(5)

The primary objective of this manuscript is to establish a SD control approach for the considered model presented in equation (5), ensuring both global asymptotic stability and the attainment of the largest feasible sampling interval. This objective is accomplished by introducing the following lemma:

Additionally, considering the fractional-delayed states as the state-space models are:

$$\begin{aligned}&{\dot{x}}(t-\alpha \tau _1(t))=\sum \limits _{i=1}^{r} \sum \limits _{j=1}^{r} h_{i}(\theta (t)) h_{j}(\theta (t_{k})) [A_{i}x(t-\alpha \tau _1(t)) +B_{i}K_{j}x(t_{k})], \\&{\dot{x}}(t+\beta \tau _2(t))=\sum \limits _{i=1}^{r} \sum \limits _{j=1}^{r} h_{i}(\theta (t)) h_{j}(\theta (t_{k})) [A_{i}x(t+\beta \tau _2(t))+B_{i}K_{j}x(t_{k})]. \end{aligned}$$

Lemma 1

[30] Let x be a differentiable function: $[a,b] \rightarrow {\mathbb {R}}^{n}$. For any vector $\xi \in {\mathbb {R}}^{n}$, symmetric matrices $M \in {\mathbb {R}}^{n \times n}$, and $Z_{1}, Z_{3} \in {\mathbb {R}}^{m \times m}$, and any matrices $Z_{2} \in {\mathbb {R}}^{m\times m}$, and $N_{1}, N_{2} \in {\mathbb {R}}^{m\times n}$ satisfying

$$\begin{aligned} \left[ \begin{array}{ccc} Z_1 &\quad Z_2 &\quad N_1 \\ * &\quad Z_3 &\quad N_2 \\ * &\quad * & \quad M \end{array} \right] \ge 0, \end{aligned}$$

the following inequality holds:

$$\begin{aligned}&-\int \limits _{a}^{b}{\dot{x}}^{T}(s)M {\dot{x}}(s)ds \le (b-a)\xi ^{T}\Big [Z_1+\frac{(b-a)^{2}}{3}Z_3\Big ] \xi \\&\quad +2 \xi ^T \Big [N_1(x(b)-x(a))-2N_2 \int \limits _{a}^{b} {x}(s)ds \Big ] +2 (b-a) \xi ^T N_2[x(b)+x(a)]. \end{aligned}$$

Remark 1

In [31] the authors extended the idea by introducing fractional-delayed states $x(t-\alpha \tau _1(t))$ and $x(t-\beta \tau _2(t))$, $0<\alpha$, $\beta <1$, $\tau _1(t)=t-t_{k}$, $\tau _2(t)=t_{k+1}-t$, $t\in [t_k,t_{k+1})$ tailored for SD control systems. This method incorporates information not only from $x(t_k)$ to x(t) however from $x(t_{k+1})$ to x(t). Also, the authors introduced a novel system [32] by utilizing the fractional-delayed state $x(t-\alpha \tau (t))$, $\alpha$ varies from 0 to 1, $\tau (t)=t-t_{k}$, $t\in [t_k,t_{k+1})$, specifically tailored for SD systems. This concept is particularly relevant for non-uniform partitioning of the sampling interval. It is crucial to note that the state $x(t-\alpha \tau (t))$ only captures information from $x(t_k)$ to x(t). Inspired by these concepts, we introduce fractional-delayed states and their associated state-space models to considered systems. The primary focus of this manuscript is to design an SD controller for the considered model presented in equation (5). This controller harnesses the refined concept of fractional delayed-states, guaranteeing the stability of the systems under consideration.

Problem 1

To tackle the stabilization aspects of the fuzzy model outlined in equation (5), the following objectives are pursued:

• With the specified system matrices and control gains provided, this study aims to establish sufficient criterion ensuring the stability of the considered model. This objective is achieved through the utilization of the modified looped LKF approach.

• In order to achieve the maximum feasible sampling interval and compute the appropriate control gains, the stabilization criterion are expressed through LMIs within the context of the SD control scheme.

3 Main results

This section focuses on deriving the necessary conditions for considered model by (5). These conditions aim to provide a solution to Problem 1 as outlined earlier. $e_{g}=[0_{n\times (g-1)n} \quad I_{n} \quad 0_{n\times (12-g)n}]$, $g=1,2, \ldots 12$ are block entry matrices, g ranges from 1 to 12.

Theorem 1

Given $0<h_{L}\le h_{U}$, $0<\alpha$, $\beta <1$, the T–S fuzzy systems (5) is asymptotically stable if there exist matrices $P>0$, $U_{s}>0$, $Q \in {\mathbb {R}}^{2n\times 2n}$, $R_{p}$, $S_{p}$, $T_{p}$ $V_p$, $W_p$, $G_q$, $N_{l} \in {\mathbb {R}}^{12n\times n}$, $M_{l} \in {\mathbb {R}}^{12n\times n}$, ${\bar{N}}_{l} \in {\mathbb {R}}^{12n\times n}$, ${\bar{M}}_{l} \in {\mathbb {R}}^{12n\times n}$, $Z_{p} \in {\mathbb {R}}^{12n\times 12n}$, $Y_{p} \in {\mathbb {R}}^{12n\times 12n}$, ${\bar{Z}}_{p} \in {\mathbb {R}}^{12n\times 12n}$, ${\bar{Y}}_{p} \in {\mathbb {R}}^{12n\times 12n}$, $s=1,2,3,4$, $p=1,2,3$, $q=1,2,\dots , 9$, $l=1,2$ such that for any $h_k\in \{h_{L},h_{U}\}$,

$$\begin{aligned}&{\Xi _{1}}_{i,i} <0, i=1,2 \dots r \end{aligned}$$

(6)

$$\begin{aligned}&{\Xi _{1}}_{i,j}+{\Xi _{1}}_{j,i}<0, 1 \le i<j \le r, \end{aligned}$$

(7)

$$\begin{aligned}&{\Xi _{2}}_{i,i} <0, i=1,2 \dots r \end{aligned}$$

(8)

$$\begin{aligned}&{\Xi _{2}}_{i,j}+{\Xi _{2}}_{j,i}<0, 1 \le i<j \le r, \end{aligned}$$

(9)

$$\begin{aligned}&\left[ \begin{array}{cccccc} Z_1 &\quad Z_2 &\quad N_1 \\ * &\quad Z_3 &\quad N_2 \\ * & \quad * &\quad U_1 \end{array} \right] \ge 0, \quad \left[ \begin{array}{cccccc} Y_1 &\quad Y_2 &\quad M_1 \\ * &\quad Y_3 &\quad M_2 \\ * &\quad * &\quad U_2 \end{array} \right] \ge 0, \end{aligned}$$

(10)

$$\begin{aligned}&\left[ \begin{array}{cccccc} {\bar{Z}}_1 &\quad {\bar{Z}}_2 &\quad {\bar{N}}_1 \\ * &\quad {\bar{Z}}_3 &\quad {\bar{N}}_2 \\ * &\quad * &\quad U_3 \end{array} \right] \ge 0, \quad \left[ \begin{array}{cccccc} {\bar{Y}}_1 &\quad {\bar{Y}}_2 &\quad {\bar{M}}_1 \\ * &\quad {\bar{Y}}_3 &\quad {\bar{M}}_2 \\ * &\quad * &\quad U_4 \end{array} \right] \ge 0, \end{aligned}$$

(11)

where

$$\begin{aligned}{\Xi _{1}}_{i,j} & ={\phi _{1}}_{i,j}+h_{k}{\phi }_{2}, {\Xi _{2}}_{i,j}={\phi _{1}}_{i,j}+h_{k} {\phi }_{3}, {\phi _{1}}_{i,j}=e_1^{T}Pe_1 -(e_1-e_2)^{T}S_1 (e_1-e_2)- (e_2-e_3)^{T} S_2 (e_2-e_3)\\ &\quad -(e_1-e_3)^{T}S_3 (e_1-e_3) + (e_6-e_1)^{T}V_1 (e_6-e_1)+(e_7-e_6)^{T} V_2 (e_7-e_6)+ (e_7-e_1)^{T}V_3 (e_7-e_1)\\ &\quad +e_{1}^{T}(G_{1}A_{i}+A_{i}^{T}G_{1}^{T})e_1-e_{10}^{T}(G_{3}+G_{3}^{T})e_{10} +e_{2}^{T}(G_{4}A_{i}+A_{i}^{T}G_{4}^{T})e_4 -e_{11}^{T}(G_{6}\\ &\quad +G_{6}^{T})e_{11}+e_{6}^{T}(G_{7}A_{i} +A_{i}^{T}G_{7}^{T})e_6-e_{12}^{T}(G_{9}+G_{9}^{T}) e_{12} +e_{3}^{T}(G_2 B_{i} K_j +K_j^{T}B_{i}^{T}G_{2}^{T}\\ &\quad +G_5 B_{i} K_j+K_j^{T}B_{i}^{T}G_{5}^{T} +G_8 B_{i} K_j+K_j^{T}B_{i}^{T} G_{8}^{T}) e_{3} +\text {He}\Big \{ e_1^{T}Pe_{10} -(e_1-e_2)^{T}T_1e_1\\ &\quad -(e_2-e_3)^{T}T_2e_2 -(e_1-e_3)^{T}T_3e_3+(e_6-e_1)^{T}W_1e_1 +(e_6-e_1)^{T}W_2e_6 +(e_7-e_1)^{T}W_3e_7\\ &\quad -e_1^{T}G_{1}e_{10} +e_1^{T}G_{1}B_{i}K_{j}e_3-e_{3}^{T}G_{2}e_{10} +e_3^{T}G_{2}A_{i}e_{1}+e_{10}^{T}G_{3}A_{i}e_{1} +e_{10}^{T}G_{3}B_{i}K_{j}e_{3} -e_2^{T}G_{4}e_{11}\\ &\quad +e_2^{T}G_{4}B_{i}K_{j}e_3-e_{3}^{T}G_{5}e_{11} +e_3^{T}G_{5}A_{i}e_{2}+e_{11}^{T}G_{6}A_{i}e_{2} +e_{11}^{T}G_{6}B_{i}K_{j}e_{3} -e_6^{T}G_{7}e_{12} +e_6^{T}G_{7}B_{i}K_{j}e_3\\ &\quad -e_{3}^{T}G_{8}e_{12} +e_3^{T}G_{8}A_{i}e_{6}+e_{12}^{T}G_{9}A_{i}e_{6} +e_{12}^{T}G_{9}B_{i}K_{j}e_{3} +N_{1}^{T}(e_1-e_2)-2N_{2}^{T}e_4 +M_{1}^{T}(e_2-e_3)\\ &\quad -2M_{2}^{T}e_5+{\bar{N}}_{1}^{T}(e_6-e_1)-2{\bar{N}}_{2}^{T}e_8 +{\bar{M}}_{1}^{T}(e_7-e_6)-2{\bar{M}}_{2}^{T}e_9 +(e_1-e_2)^{T}\\&\quad \times R_1 [(1-\beta ) e_{12}-e_{10}] +(e_{10}-(1-\alpha )e_{11})^{T} R_1(e_{6}-e_{1}) +(e_2-e_3)^{T} R_2 (1-\beta ) e_{12}\\&\quad +(1-\alpha )e_{11}^{T} R_2(e_{7}-e_{6}) +(e_1-e_3)^{T} R_3 (- e_{10}) +e_{10}^{T} R_3(e_{7}-e_{1})\Big \},\\ {\phi }_{2} &= e_{10}^{T}U_1e_{10}-(1-\alpha )e_{11}^{T}(R_1-R_2)e_{11} +\text {He}\Big \{(e_10-(1-\alpha )e_{11})^{T}[S_1(e_1-e_2)+T_1e_1]\\ &\quad +(e_1-e_2)^{T}T_1e_{10} +((1-\alpha )e_{11})^{T}[S_2(e_2-e_3)+T_2e_2] +(1-\alpha )(e_2-e_3)^{T}T_2e_{11}\\ &\quad+e_{10}^{T}[S_3(e_1-e_3)+T_3e_3]+\beta {\bar{N}}_{2}(e_6+e_1) +(1-\beta ) {\bar{M}}_{2}(e_7+e_6)\Big \}\\ &\quad +\beta {\bar{Z}}_1+\frac{\beta ^3h_u^2}{3} {\bar{Z}}_3+ (1-\beta ) {\bar{Y}}_1+\frac{(1-\beta )^3h_u^2}{3} {\bar{Y}}_3 + [e_3\; e_7]Q [e_3\; e_7]^{T},\\ {\phi }_{3} & =e_{10}^{T}U_3e_{10}-(1-\beta )e_{12}^{T}(U_3-U_4)e_{12} +\text {He}\Big \{((1-\beta )e_{12}-e_10)^{T}[V_1(e_6-e_1) +W_1e_1]+(e_6-e_1)^{T}\\ &\quad W_1e_{10} +(-(1-\beta )e_{12})^{T}[V_2(e_7-e_6)+W_2e_6] +(1-\beta )(e_7-e_6)^{T}W_2e_{12}-e_{10}^{T}[V_3(e_7-e_1)+W_3e_7]\\ &\quad +\alpha {N}_{2}(e_1+e_2) +(1-\alpha ) {M}_{2}(e_2+e_3)\Big \} +\alpha {Z}_1+\frac{\alpha ^3h_u^2}{3} {Z}_3 + (1-\alpha ){Y}_1+\frac{(1-\alpha )^3h_u^2}{3} {Y}_3 + [e_3\; e_7]Q [e_3\; e_7]^{T}. \end{aligned}$$

Proof

Let us consider the LKF:

$$\begin{aligned} V(t)=\sum \limits _{a=1}^{5}V_{a}(t), \end{aligned}$$

where

$$\begin{aligned} V_{1}(t) & = x^{T}(t)Px(t), \\ V_{2}(t) & =(t_{k+1}-t)(t-t_k) \left[ \begin{array}{c} x(t_k) \\ x(t_{k+1}) \end{array} \right] ^{T} Q \left[ \begin{array}{c} x(t_k) \\ x(t_{k+1}) \end{array} \right] ,\\V_{3}(t) & =2\xi _{1}^{T}(t)R_1\xi _{4}(t) + 2\xi _{2}^{T}(t)R_2\xi _{5}(t)+ 2\xi _{3}^{T}(t)R_3\xi _{6}(t), \\ V_{4}(t) & = (t_{k+1}-t)\Big \{\xi _{1}^{T}(t) \big [S_1\xi _{1}(t)+2T_1x(t)\big ] +\xi _{2}^{T}(t) \big [S_2\xi _{2}(t)+2T_2x(t-\alpha \tau _{1}(t))\big ] +\xi _{3}^{T}(t) \big [S_3\xi _{3}(t)+2T_3x(t_k)\big ] \\ &\quad+ \int _{t-\alpha \tau _{1}(t)}^{t} {\dot{x}}^{T}(s)U_1{\dot{x}}(s)ds + \int _{t_k}^{t-\alpha \tau _{1}(t)} {\dot{x}}^{T}(s)U_2{\dot{x}}(s)ds \Big \}, \\ V_{5}(t) &= (t-t_k)\Big \{\xi _{4}^{T}(t) \big [V_1\xi _{4}(t)+2W_1x(t)\big ] +\xi _{5}^{T}(t) \big [V_2\xi _{5}(t)+2W_2x(t+\beta \tau _{2}(t))\big ] +\xi _{6}^{T}(t) \big [V_3\xi _{6}(t)+2W_3x(t_k+1)\big ]\\ &\quad - \int _{t}^{t+\beta \tau _{2}(t)} {\dot{x}}^{T}(s)U_3{\dot{x}}(s)ds - \int _{t+\beta \tau _{2}(t)}^{t_{k+1}} {\dot{x}}^{T}(s)U_4{\dot{x}}(s)ds \Big \}, \end{aligned}$$

where

$$\begin{aligned} \xi _{1}(t)&=x(t)-x(t-\alpha \tau _1(t)), \quad \xi _{2}(t)=x(t-\alpha \tau _1(t))-x(t_k), \\ \xi _{3}(t)&=x(t)-x(t_k), \quad \xi _{4}(t)=x(t+\beta \tau _2(t))-x(t), \\ \xi _{5}(t)&=x(t_{k+1})-x(t+\beta \tau _2(t)), \quad \xi _{6}(t)=x(t_{k+1})-x(t). \end{aligned}$$

Taking the derivative of the considered LKF, one can obtain the following:

$$\begin{aligned} {\dot{V}}_{1}(t)&=2 x^{T}(t)P{\dot{x}}(t), \end{aligned}$$

(12)

$$\begin{aligned} {\dot{V}}_{2}(t)&=(t_{k+1}-t) \left[ \begin{array}{c} x(t_k) \\ x(t_{k+1}) \end{array} \right] ^{T} Q \left[ \begin{array}{c} x(t_k) \\ x(t_{k+1}) \end{array} \right] - (t-t_k) \left[ \begin{array}{c} x(t_k) \\ x(t_{k+1}) \end{array} \right] ^{T} Q \left[ \begin{array}{c} x(t_k) \\ x(t_{k+1}) \end{array} \right] , \end{aligned}$$

(13)

$$\begin{aligned}&\quad {\dot{V}}_{3}(t)= 2[\xi _{1}^{T}(t)R_1{\dot{\xi }}_{4}(t) +{\dot{\xi }}_{1}^{T}(t)R_1{\xi }_{4}(t) + \xi _{2}^{T}(t)R_2\dot{\xi _{5}}(t)+{\dot{\xi }}_{2}^{T}(t)R_2\xi _{5}(t) + \xi _{3}^{T}(t)R_3\dot{\xi _{6}}(t)+{\dot{\xi }}_{3}^{T}(t)R_3\xi _{6}(t),\end{aligned}$$

(14)

$$\begin{aligned}{\dot{V}}_{4}(t)=&- \Big \{\xi _{1}^{T}(t) \big [S_1\xi _{1}(t)+2T_1x(t)\big ] +\xi _{2}^{T}(t) \big [S_2\xi _{2}(t) +2T_2x(t-\alpha \tau _{1}(t))\big ] +\xi _{3}^{T}(t) \big [S_3\xi _{3}(t)+2T_3x(t_k)\big ]\\ & + \int _{t-\alpha \tau _{1}(t)}^{t} {\dot{x}}^{T}(s)U_1{\dot{x}}(s)ds + \int _{t_k}^{t-\alpha \tau _{1}(t)} {\dot{x}}^{T}(s)U_2{\dot{x}}(s)ds \Big \} + (t_{k+1}-t)\Big \{2\xi _{1}^{T}(t) S_1{\dot{\xi }}_{1}(t)\nonumber \\&\quad +2 {\dot{\xi }}_{1}^{T}(t) T_1 {x}(t) +2 {\xi }_{1}^{T}(t) T_1 {\dot{x}}(t) +2\xi _{2}^{T}(t) S_2{\dot{\xi }}_{2}(t) +2 {\dot{\xi }}_{2}(t) T_2 x(t-\alpha \tau _1(t)) +2 {\xi }^{T}_{2}(t) T_2 \frac{d}{dt}{x}(t-\alpha \tau _1(t)) \\& +2\xi _{3}^{T}(t) S_3{\dot{\xi }}_{3}(t)+2 {\dot{\xi }}_{3}(t) T_3 x(t_k) +{\dot{x}}^{T}(t)U_1{\dot{x}}(t) -(1-\alpha){\dot{x}}^{T}(t-\alpha \tau _1(t)) (R_1-R_{2}){\dot{x}}(t-\alpha \tau _1(t)) \Big \}. \end{aligned}$$

(15)

Based on (10) and applying Lemma 1 to the integral terms of ${\dot{V}}_4(t).$ one can obtain the following:

$$\begin{aligned} -\int _{t-\alpha \tau _{1}(t)}^{t} {\dot{x}}^{T}(s)U_1{\dot{x}}(s)ds \le & \,\alpha \tau _1(t) \xi ^{T}(t)\Big [Z_1+\frac{(\alpha h_u)^2}{3}Z_3 \Big ] \xi (t) + 2 \xi ^{T}(t)\Big [N_1 \xi _{1}(t)- 2 N_2 \int _{t-\alpha \tau _1 (t)}^{t}x(s)ds \Big ] \\ & + 2 \alpha \tau _1(t) \xi ^{T}(t)N_2 \Big [x(t)+x(t-\alpha \tau _1(t)) \Big ]. \end{aligned}$$

Applying Lemma 1 to the integral terms of ${\dot{V}}_4(t)$, one can obtain the following:

$$\begin{aligned} -\int _{t_k}^{t-\alpha \tau _1(t)} {\dot{x}}^{T}(s)U_2{\dot{x}}(s)ds \le &\,(1-\alpha ) \tau _1(t) \xi ^{T}(t) \Big [Y_1+\frac{((1-\alpha ) h_u)^2}{3}Y_3 \Big ] \xi (t)\\ &\, + 2 \xi ^{T}(t) \times \Big [M_1 \xi _{2}(t)- 2 M_2 \int _{t_k}^{t-\alpha \tau _1(t)}x(s)ds \Big ] \\ &\, + 2 (1-\alpha ) \tau _1(t) \xi ^{T}(t)M_2 \Big [x(t-\alpha \tau _1(t))+x(t_k) \Big ] {\dot{V}}_{5}(t)\\ =&\, \Big \{\xi _{4}^{T}(t) \big [V_1\xi _{4}(t)+2W_1x(t) +\xi _{5}^{T}(t) \big [V_2\xi _{5}(t)+2W_2x(t+\beta \tau _{2}(t))\big ] \\ &\, + \xi _{6}^{T}(t) \big [V_3\xi _{6}(t)+2W_3x(t_k+1)\big ] - \int _{t}^{t+\beta \tau _{2}(t)} {\dot{x}}^{T}(s)U_3{\dot{x}}(s)ds \\ & - \int _{t+\beta \tau _{2}(t)}^{t_{k+1}} {\dot{x}}^{T}(s)U_4{\dot{x}}(s)ds \Big \} + (t-t_k) \Big \{2\xi _{4}^{T}(t) V_1{\dot{\xi }}_{4}(t)+2{\dot{\xi }}_{4}^{T}(t)W_1x(t) \\&\, +2{\xi }_{4}^{T}(t)W_1 {\dot{x}}(t)+2\xi _{5}^{T}(t) V_2{\dot{\xi }}_{5}(t) +2{\dot{\xi }}_{5}^{T}(t)W_2x(t+\beta \tau _{2}(t)) \\ &\, +2 {\xi }^{T}_{5}(t) W_2 \frac{d}{dt}{x}(t+\beta \tau _{2}(t)) +2\xi _{6}^{T}(t) V_3{\dot{\xi }}_{6}(t)+2 {\dot{\xi }}_{6}(t) W_3 x(t_k+1)\\ &\,+{\dot{x}}^{T}(t)U_3{\dot{x}}(t) -(1-\beta ){\dot{x}}^{T}(t+\beta \tau _2(t))(U_3-U_{4}){\dot{x}} (t+\beta \tau _2(t)) \Big \}. \end{aligned}$$

(16)

Applying Lemma 1 to the integral terms of ${\dot{V}}_5(t)$, one can obtain the following:

$$\begin{aligned}- \int _{t}^{t+\beta \tau _{2}(t)} {\dot{x}}^{T}(s)U_3{\dot{x}}(s)ds \le &\,\beta \tau _2(t) \xi ^{T}(t) \Big [{\bar{Z}}_1+\frac{(\beta h_u)^2}{3}{\bar{Z}}_3 \Big ] \xi (t) + 2 \xi ^{T}(t) \Big [{\bar{N}}_1 \xi _{4}(t) - 2 {\bar{N}}_2 \int _{t}^{t+\beta \tau _{2}(t)}x(s)ds \Big ] \\ &\, + 2 \beta \tau _2(t) \xi ^{T}(t){\bar{N}}_2 \Big [x(t+\beta \tau _2(t)+x(t)) \Big ]. \end{aligned}$$

(17)

Applying Lemma 1 to the integral terms of ${\dot{V}}_5(t)$, one can obtain the following:

$$\begin{aligned}- \int _{t+\beta \tau _{2}(t)}^{t_{k+1}} {\dot{x}}^{T}(s)U_4{\dot{x}}(s)ds \le&\, (1-\beta ) \tau _2(t) \xi ^{T}(t) \Big [{\bar{Y}}_1+\frac{((1-\beta ) h_u)^2}{3}{\bar{Y}}_3 \Big ] \xi (t) \\ &\, + 2 \xi ^{T}(t)\Big [{\bar{M}}_1 \xi _{4}(t)- 2 {\bar{M}}_2 \int _{t}^{t+(1-\beta ) \tau _{2}(t)}x(s)ds \Big ]\\ &\, + 2 (1-\beta ) \tau _2(t) \xi ^{T}(t){\bar{M}}_2 \Big [x(t+\beta \tau _2(t)+x(t)) \Big ]. \end{aligned}$$

(18)

Now, we introduce the slack variables $G_f$, $f=1,2, \dots , 9$ by the following equations

$$\begin{aligned}&2 \sum \limits _{i=1}^{r}\sum \limits _{j=1}^{r}h_{i}(\theta (t))h_{j}(\theta (t_{k})) \Big [{x}^{T}(t)G_{1} +{x}^{T}(t_k)G_{2} +{\dot{x}}^{T}(t)G_{3}\Big ] \times \Big [A_{i}x(t)+B_{i}K_{j}x(t_{k})-{\dot{x}}(t)\Big ]=0. \end{aligned}$$

(19)

$$\begin{aligned}&\quad 2 \sum \limits _{i=1}^{r}\sum \limits _{j=1}^{r}h_{i}(\theta (t))h_{j}(\theta (t_{k})) \Big [{x}^{T}(t-\alpha \tau _1(t))G_{4} +{x}^{T}(t_k)G_{5} +{\dot{x}}^{T}(t-\alpha \tau _1(t))G_{6}\Big ] \\ &\qquad \Big [A_{i}x(t-\alpha \tau _1(t)) +B_{i}K_{j}x(t_{k})-{\dot{x}}(t-\alpha \tau _1(t))\Big ]=0. \end{aligned}$$

(20)

$$\begin{aligned}& 2 \sum \limits _{i=1}^{r}\sum \limits _{j=1}^{r}h_{i}(\theta (t))h_{j}(\theta (t_{k})) \Big [{x}^{T}(t+\beta \tau _2(t))G_{7}+{x}^{T}(t_k)G_{8} +{\dot{x}}^{T}(t+\beta \tau _2(t))G_{9}\Big ] \\ &\qquad\Big [A_{i}x(t+\beta \tau _2(t)) +B_{i}K_{j}x(t_{k})-{\dot{x}}(t-\alpha \tau _1(t))\Big ]=0. \end{aligned}$$

(21)

Now, adding from (12) to (21), one can obtain the following:

$$\begin{aligned} & {\dot{V}}(t)\le \sum \limits _{i=1}^{r}\sum \limits _{j=1}^{r}h_{i}(\theta (t))h_{j}(\theta (t_{k})) \xi ^{T}(t) \Big [ \frac{t_{k+1}-t}{h_{k}} {\Xi _{1}}_{i,j} + \frac{t-t_{k}}{h_{k}} {\Xi _{2}}_{i,j} \Big ]\xi (t), \end{aligned}$$

(22)

where

$$\begin{aligned} \xi (t) = &\,\left[x^{T}(t), \; x^{T}(t-\alpha \tau _1(t)), \; x^{T}(t_k), \int _{t-\alpha \tau _{1}(t)}^{t} x^{T}(s)ds , \right.\\ &\, \int _{t_k}^{t-\alpha \tau _{1}(t)} x^{T}(s)ds ^{T}, \; x^{T}(t_{k+1}), \; x^{T}(t+\beta \tau _2(t)), \int _{t}^{t+\beta \tau _{2}(t)} x^{T}(s)ds, \\ &\,\left.\int _{t+\beta \tau _{2}(t)}^{t_{k+1}} x^{T}(s)ds , \; {\dot{x}}^{T}(t), {\dot{x}}^{T}(t-\alpha \tau _1(t)), \; {\dot{x}}^{T}(t+\beta \tau _2(t)) \right]^{T}, \end{aligned}$$

and ${\Xi _{1}}_{i,j}$, ${\Xi _{2}}_{i,j}$ are provided in the statement of the Theorem 1.

Thus ${\dot{V}}(t)\le 0$ if $\sum \nolimits _{i=1}^{r}\sum \nolimits _{j=1}^{r}h_{i}(\theta (t))h_{j}(\theta (t_{k})) {\Xi _{l}}_{i,j}<0$, $l=1,2$.

Moreover,

$$\begin{aligned}&\sum \limits _{i=1}^{r}\sum \limits _{j=1}^{r}h_{i}(\theta (t))h_{j}(\theta (t_{k})) {\Xi _{l}}_{i,j} =\sum \limits _{i=1}^{r} h_{i}(\theta (t))h_{i}(\theta (t_{k})) {\Xi _{l}}_{i,i} +\sum \limits _{i=1}^{r}\sum \limits _{i<j}h_{i}(\theta (t))h_{j}(\theta (t_{k})) ({\Xi _{l}}_{i,j}+{\Xi _{l}}_{j,i}). \end{aligned}$$

Thus, it becomes evident that if (6)–(9) are satisfied, the asymptotic stability of the system described in Eq. (5) is ensured. This concludes the proof. $\hfill\square$

Building on the foundation of Theorem 1, this section proceeds to formulate sufficient conditions for devising a SD control strategy for the considered model depicted in Eq. (5). It ensures that the stability for the unknown control gains.

Theorem 2

Given $0<h_{L}\le h_{U}$, $0<\alpha$, $\beta <1$, $\epsilon _k$, $k=2,3, \dots , 9$, the T–S fuzzy systems (5) is asymptotically stable if there exist matrices ${\tilde{P}}>0$, ${\tilde{U}}_{s}>0$, ${\tilde{Q}} \in {\mathbb {R}}^{2n\times 2n}$, ${\tilde{R}}_{p}$, ${\tilde{S}}_{p}$, ${\tilde{T}}_{p}$ ${\tilde{V}}_p$, ${\tilde{W}}_p$, G, ${\tilde{N}}_{l} \in {\mathbb {R}}^{12n\times n}$, ${\tilde{M}}_{l} \in {\mathbb {R}}^{12n\times n}$, $\tilde{{\bar{N}}}_{l} \in {\mathbb {R}}^{12n\times n}$, $\tilde{{\bar{M}}}_{l} \in {\mathbb {R}}^{12n\times n}$, ${\tilde{Z}}_{p} \in {\mathbb {R}}^{12n\times 12n}$, ${\tilde{Y}}_{p} \in {\mathbb {R}}^{12n\times 12n}$, $\tilde{{\bar{Z}}}_{p} \in {\mathbb {R}}^{12n\times 12n}$, $\tilde{{\bar{Y}}}_{p} \in {\mathbb {R}}^{12n\times 12n}$, ${\tilde{K}}_{j}$, $s=1,2,3,4$, $p=1,2,3$, $q=1,2,\dots , 9$, $l=1,2$, $j=1,2,\dots , r$ such that for any $h_k\in \{h_{L},h_{U}\}$,

$$\begin{aligned}&{\tilde{\Xi }}_{1i,i} <0, i=1,2 \dots r \end{aligned}$$

(23)

$$\begin{aligned}&{\tilde{\Xi }}_{1i,j}+{\tilde{\Xi }}_{1j,i}<0, 1 \le i<j \le r, \end{aligned}$$

(24)

$$\begin{aligned}&{\tilde{\Xi }}_{2i,i} <0, i=1,2 \dots r \end{aligned}$$

(25)

$$\begin{aligned}&{\tilde{\Xi }}_{2i,j}+{\tilde{\Xi }}_{2j,i}<0, 1 \le i<j \le r, \end{aligned}$$

(26)

$$\begin{aligned}&\left[ \begin{array}{cccccc} \tilde{Z}_1 & \tilde{Z}_2 & \tilde{N}_1 \\ * & \tilde{Z}_3 & \tilde{N}_2 \\ * & * & \tilde{U}_1 \end{array} \right] \ge 0, \quad \left[ \begin{array}{cccccc} \tilde{Y}_1 & \tilde{Y}_2 & \tilde{M}_1 \\ * & \tilde{Y}_3 & \tilde{M}_2 \\ * & * & \tilde{U}_2 \end{array} \right] \ge 0, \end{aligned}$$

(27)

$$\begin{aligned}&\left[ \begin{array}{cccccc} \tilde{{\bar{Z}}}_1 & \tilde{{\bar{Z}}}_2 & \tilde{{\bar{N}}}_1 \\ * & \tilde{{\bar{Z}}}_3 & \tilde{{\bar{N}}}_2 \\ * & * & \tilde{U}_3 \end{array} \right] \ge 0, \quad \left[ \begin{array}{cccccc} \tilde{{\bar{Y}}}_1 & \tilde{{\bar{Y}}}_2 & \tilde{{\bar{M}}}_1 \\ * & \tilde{{\bar{Y}}}_3 & \tilde{{\bar{M}}}_2 \\ * & * & \tilde{U}_4 \end{array} \right] \ge 0, \end{aligned}$$

(28)

where

$$\begin{aligned}{\tilde{\Xi }}_{1i,j}=&\,{\phi _{1}}_{i,j}+h_{k}{\phi }_{2}, {\tilde{\Xi }}_{2i,j}={\phi _{1}}_{i,j}+h_{k} {\phi }_{3}, {\tilde{\phi }}_{1i,j} =e_1^{T}\tilde{P}e_1 -(e_1-e_2)^{T}\tilde{S}_1 (e_1-e_2) \\ &- (e_2-e_3)^{T}\tilde{S}_2 (e_2-e_3) -(e_1-e_3)^{T}\tilde{S}_3 (e_1-e_3) + (e_6-e_1)^{T}\tilde{V}_1 (e_6-e_1)+(e_7-e_6)^{T}\tilde{V}_2 (e_7-e_6) \\ &+ (e_7-e_1)^{T}\tilde{V}_3 (e_7-e_1) +e_{1}^{T}(A_{i}\tilde{G}+\tilde{G}A_{i}^{T})e_1-2\epsilon _3 e_{10}^{T}\tilde{G}e_{10} +\epsilon _4 e_{2}^{T}(A_{i}\tilde{G}+\tilde{G}A_{i}^{T})e_4-2\epsilon _6 e_{11}^{T}\tilde{G}e_{11}\\ &+\epsilon _7 e_{6}^{T}(A_{i}\tilde{G}+\tilde{G}A_{i}^{T})e_6-2\epsilon _9 e_{12}^{T}\tilde{G}e_{12} + (\epsilon _2+\epsilon _5+\epsilon _8)e_{3}^{T}(B_{i} \tilde{K}_j+\tilde{K}_j^{T}B_{i}^{T}) e_{3}\\ &+\text {He}\Big \{ e_1^{T}\tilde{P}e_{10}-(e_1-e_2)^{T}\tilde{T}_1e_1-(e_2-e_3)^{T}\tilde{T}_2e_2 -(e_1-e_3)^{T}\tilde{T}_3e_3\\ &+(e_6-e_1)^{T}\tilde{W}_1e_1+(e_6-e_1)^{T}\tilde{W}_2e_6+(e_7-e_1)^{T}\tilde{W}_3e_7 -e_1^{T}\tilde{G}e_{10}+e_1^{T}B_{i}\tilde{K}_{j}e_3 -\epsilon _2 e_{3}^{T} \tilde{G} e_{10} +\epsilon _2 e_3^{T}A_{i} \tilde{G} e_{1}\\ &+ \epsilon _3 e_{10}^{T}A_{i} \tilde{G} e_{1} +\epsilon _3 e_{10}^{T}B_{i}\tilde{K}_{j}e_{3} -\epsilon _4 e_2^{T}\tilde{G} e_{11}+ \epsilon _4 e_2^{T} B_{i}\tilde{K}_{j}e_3 - \epsilon _5 e_{3}^{T} \tilde{G} e_{11} + \epsilon _5 e_3^{T}\tilde{G} A_{i}e_{2}\\ &+ \epsilon _6 e_{11}^{T}A_{i} \tilde{G} e_{2}+ \epsilon _6 e_{11}^{T}B_{i}\tilde{K}_{j}e_{3} -\epsilon _7 e_6^{T} \tilde{G} e_{12} +\epsilon _7 e_6^{T} B_{i}\tilde{K}_{j}e_3 - \epsilon _8 e_{3}^{T}\tilde{G} e_{12} +\epsilon _8 e_3^{T}A_{i} \tilde{G} e_{6}\\ &+\epsilon _9 e_{12}^{T}A_{i} \tilde{G}e_{6} +\epsilon _9 e_{12}^{T} B_{i}\tilde{K}_{j}e_{3} +\tilde{N}_{1}^{T}(e_1-e_2)-2\tilde{N}_{2}^{T}e_4 +\tilde{M}_{1}^{T}(e_2-e_3)-2\tilde{M}_{2}^{T}e_5\\ &+\tilde{{\bar{N}}}_{1}^{T}(e_6-e_1)-2\tilde{{\bar{N}}}_{2}^{T}e_8 +\tilde{{\bar{M}}}_{1}^{T}(e_7-e_6)-2\tilde{{\bar{M}}}_{2}^{T}e_9 +(e_1-e_2)^{T} \tilde{R}_1 [(1-\beta ) e_{12}-e_{10}]\\ &+(e_{10}-(1-\alpha )e_{11})^{T} \tilde{R}_1(e_{6}-e_{1}) +(e_2-e_3)^{T} \times \tilde{R}_2 (1-\beta ) e_{12}\\ & +(1-\alpha )e_{11}^{T} \tilde{R}_2(e_{7}-e_{6}) +(e_1-e_3)^{T} \tilde{R}_3 (- e_{10}) +e_{10}^{T} \tilde{R}_3(e_{7}-e_{1})\Big \}, \\ {\tilde{\phi }}_{2}=&e_{10}^{T}\tilde{U}_1e_{10}-(1-\alpha )e_{11}^{T}(\tilde{R}_1-\tilde{R}_2)e_{11} +\text {He}\Big \{(e_10-(1-\alpha )e_{11})^{T}[\tilde{S}_1(e_1-e_2) +\tilde{T}_1e_1] +(e_1-e_2)^{T}\tilde{T}_1e_{10}\\ & +((1-\alpha )e_{11})^{T}[\tilde{S}_2(e_2-e_3)+\tilde{T}_2e_2] +(1-\alpha )(e_2-e_3)^{T}\tilde{T}_2e_{11} +e_{10}^{T}[\tilde{S}_3(e_1-e_3)+\tilde{T}_3e_3]\\ &+\beta \tilde{{\bar{N}}}_{2}(e_6+e_1) +(1-\beta ) \tilde{{\bar{M}}}_{2}(e_7+e_6)\Big \}\\ & +\beta \tilde{{\bar{Z}}}_1 +\frac{\beta ^3h_u^2}{3} \tilde{{\bar{Z}}}_3 + (1-\beta ) \tilde{{\bar{Y}}}_1 +\frac{(1-\beta )^3h_u^2}{3} \tilde{{\bar{Y}}}_3+ [e_3\; e_7]\tilde{Q} [e_3\; e_7]^{T},\\ {\tilde{\phi }}_{3}=&\,e_{10}^{T}\tilde{U}_3e_{10}-(1-\beta )e_{12}^{T} (\tilde{U}_3-\tilde{U}_4)e_{12} +\text {He}\Big \{((1-\beta )e_{12}-e_10)^{T}[\tilde{V}_1(e_6-e_1)+\tilde{W}_1e_1]\\ & +(e_6-e_1)^{T}\tilde{W}_1e_{10} +(-(1-\beta )e_{12})^{T}[\tilde{V}_2(e_7-e_6)+\tilde{W}_2e_6] +(1-\beta )(e_7-e_6)^{T}\tilde{W}_2e_{12}\\ & -e_{10}^{T}[\tilde{V}_3(e_7-e_1)+\tilde{W}_3e_7] +\alpha \tilde{{N}}_{2}(e_1+e_2) +(1-\alpha ) \tilde{{M}}_{2}(e_2+e_3)\Big \} \\ & +\alpha \tilde{Z}_1+\frac{\alpha ^3h_u^2}{3} \tilde{Z}_3 + (1-\alpha )\tilde{Y}_1+\frac{(1-\alpha )^3h_u^2}{3} \tilde{Y}_3 + [e_3\; e_7]\tilde{Q} [e_3\; e_7]^{T}. \end{aligned}$$

In this case the controller gain is given by ${K}_{j}={\tilde{K}}_{j}\tilde{G}^{-1}$.

Proof

Define $G_{1}=G>0$,  $G_{k}=\epsilon _k G,$ $k=2,3, \dots 9,$ $\tilde{G}=G^{-1}$,  $\tilde{P}=G^{-1}PG^{-1}$,  $\tilde{Q}=diag\{G^{-1}\,G^{-1}\}{Q}diag\{G^{-1}\,G^{-1}\}$,  $\tilde{R_p}=G^{-1}R_{p}G^{-1}$,  $\tilde{S_p}=G^{-1}S_{p}G^{-1}$,  $\tilde{T_p}=G^{-1}T_{p}G^{-1}$,  $\tilde{W_p}=G^{-1}W_{p}G^{-1}$,  $\tilde{V_p}=G^{-1}V_{p}G^{-1}$,  $\tilde{U_p}=G^{-1}U_{p}G^{-1}$,  $\tilde{N}_l=G^{-1}N_l \lambda$,  $\tilde{M}_l=G^{-1}M_l \lambda$,  $\tilde{{\bar{N}}}_l=G^{-1}{\bar{N}}_l \lambda$,  $\tilde{{\bar{M}}}_l=G^{-1}{\bar{M}}_l \lambda$,  $\tilde{{\bar{Z}}}_s=\lambda {\bar{Z}}_s \lambda$,  $\lambda =diag\{G^{-1}, \dots \,G^{-1}\}_{12n \times 12n}$. Utilizing a congruent transformation with respect to $\lambda$ on equations (6)–(9) leads to equations (23)–(26). $\hfill\square$

Remark 2

In SD-based control systems, the choice of a sampling interval holds a pivotal role as it significantly influences the trade-off between system conservatism and efficiency. To achieve the maximum feasible sampling interval, several approaches have been explored in literature. Firstly, researchers have derived sufficient conditions for considered systems using time-dependent continuous Lyapunov functionals [25], employing the LMI technique. These endeavors focus on optimizing the sampling interval to enhance system performance. Furthermore, the concept of looped-functional, as presented in [5, 31, 33], contributes to relaxing the positivity constraints of the Lyapunov functional. This leads to less conservative results while integrating comprehensive information from $x(t_k)$ to x(t) and $x(t_{k+1})$ to x(t). Inspired by the advancements enabled by looped functionals, we have developed a looped-functional based LKF in this work. This novel approach is instrumental in establishing stability conditions for the proposed systems, thereby diminishing traditionalism and enhancing the overall system performance.

4 Numerical simulation and results

In this section, to show the efficiency and superiority of the proposed methods, three nonlinear systems are considered. In this connection, a nonlinear model of PMSM is considered and illustrated with the acquired stabilization condition in Theorem 2, and it is provided in the design Example. Next, a Rossler’s model and Lorenz system are considered and illustrated with the acquired sufficient condition in Theorem 2, which is compared with existing works, and it is provided in the comparison Examples (see Example 4.1 and Example 4.2)

4.1 Design example

In PMSM, the $d-q$ axis representation is commonly used for analysis and control. This representation simplifies the mathematical model of the motor by transforming the three-phase system into a two-dimensional system, where the d axis represents the magnetic flux produced by the permanent magnet and the q axis represents the quadrature axis.

The state-space model of a PMSM on the $d-q$ axis typically consists of equations that describe the dynamics of the motors electrical and mechanical behavior. These equations can include equations for the stator and rotor flux linkages, electromagnetic torque, and electrical currents. The state-space representation is valuable for designing control algorithms, such as field-oriented control, which enables precise control of the motor’s torque and speed.

Here a general outline of the state-space model for a PMSM on the $d-q$ axis: The PMSM can described as in the following [11]:

$$\begin{aligned} \left\{ \begin{array}{cl} \frac{d}{dt}i_d =&\frac{-R_s i_d+n_p\nu L_q i_q+u_d}{L_d} \\ \frac{d}{dt}i_q =&\frac{-R_s i_q-n_p\nu L_d i_d-n_p \nu \phi +u_q}{L_q}\\ \frac{d}{dt}\omega =&\frac{n_p\{(L_d-L_q)i_di_q+\phi i_q\}-{{\hat{\beta }}} \nu -T_L}{\mathcal {J}} \end{array} \right. \end{aligned}$$

In this scenario, the stator currents in the d and q axes ($i_d$ and $i_q$), along with$\omega$ representing the rotor’s angular velocity. The external load torque is labeled as $T_L$, and $\mathcal {J}$ denotes the polar moment of inertia. The $d-q$ voltages are denoted as $u_d$ and $u_q$, while the stator inductances on the $d-q$ axis are represented by $L_d$ and $L_q$. Stator resistance is indicated by $R_s$. The coefficient of viscous friction is denoted by ${{\hat{\beta }}}$, and the permanent magnet flux linkage is symbolized as $\phi$. The number of pole pairs is expressed as$n_p$. Figure 1 illustrates the configuration of a PMSM-based wind energy system. Additionally, by leveraging the concepts of affine transformation and time-scaling transformation described in [34], the following relationships can be obtained:

PMSM-based wind energy system is shown in Fig. 1. Furthermore, based on the affine transformation and time-scaling transformation in one can get the following:

$$\begin{aligned} \left\{ \begin{array}{cl} {\dot{x}}_1(t) =&-\frac{L_q}{L_d}x_1(t)+x_2(t)x_3(t)+{\hat{u}}_d\\ {\dot{x}}_2(t) =&-x_2(t)-x_1(t)x_3(t)+{\bar{\gamma }} x_3(t)+{\hat{u}}_q\\ {\dot{x}}_3(t) =& {{\hat{\vartheta }}} (x_2(t)-x_3(t))+\varsigma x_1(t) x_2(t)-{\hat{T}}_L \end{array} \right. \end{aligned}$$

(29)

where ${\bar{\gamma }}=\frac{n_p \phi ^2}{R_s{{\hat{\beta }}}},$ ${{\hat{\vartheta }}}=\frac{L_q {{\hat{\beta }}}}{R_s \mathcal {J}},$ ${\hat{u}}_q =\frac{n_p L_q \phi u_q}{R_s^2 {{\hat{\beta }}}},$ ${\hat{u}}_d =\frac{n_p L_q \phi u_d}{R_s^2 {{\hat{\beta }}}},$ $\varsigma =\frac{(L_d-L_q){\hat{\beta }}^2 L_q }{L_d \mathcal {J}n_p\phi ^2},$ ${\hat{T}}_L = \frac{L_q^2 T_L}{R_s^2 \mathcal {J}},$ $n_p=1$, $[x_1(t) \ x_2(t) \ x_3(t)]^{T} =[i_d \ i_q \ \omega ]^{T}$. Here, let us assume ${\bar{\gamma }}$ and ${{\hat{\vartheta }}}$ to be positive constants. In the smooth air-gap case, $L_q = L_d$ and the external inputs are vanish, thus, ${\hat{u}}_d = {\hat{u}}_q = {\hat{T}}_L =0.$ Let $x(t)=[x_1(t)\; x_2(t)\; x_3(t)]^{T}$, and control input u(t), to establish the control design of (29) on $d-q$ axis. Thus, based on these parameter assumptions, one can obtain the following:

$$\begin{aligned} \left\{ \begin{array}{cl} {\dot{x}}_1(t) =&-x_1(t)+x_2(t)x_3(t)+u(t)\\ {\dot{x}}_2(t) =&-x_2(t)+x_3(t)({\bar{\gamma }}-x_1(t))+u(t) \\ {\dot{x}}_3(t) =& {{\hat{\vartheta }}} (x_2(t)-x_3(t)). \end{array} \right. \end{aligned}$$

(30)

Fig. 1

PMSM-based wind energy system

Due to its notable attributes like high power density, improved efficiency, and reduced maintenance costs, the dynamical system of PMSM has garnered substantial attention in existing literature. Nevertheless, a distinctive aspect of this work is the exploration of the stabilization problem within the background of the PMSM model based fuzzy approach coupled with the SD controller. In this pursuit, the non-linear PMSM model is converted into a linear subsystem using if-then rules. The central focus of this research lies in the application of the fuzzy model, which is highly suitable for modeling nonlinear systems. To exemplify the scope of obtained results, the PMSM model is employed. The state-space representation of the PMSM model described by (30) can be succinctly depicted as follows:

$$\begin{aligned} {\dot{x}}(t)=&\sum \limits _{i=1}^{2}\mu _i(x_3(t))[A_i x(t)+B_iu(t)], \end{aligned}$$

(31)

$$\begin{aligned}{} & {} \text {where} \quad A _{1}= \left[ \begin{array}{ccc} -1 & d_1 & 0 \\ - d_1 & -1 &{\bar{\gamma }} \\ 0 &{{\hat{\vartheta }}} & -{{\hat{\vartheta }}} \end{array} \right] , B _{1}= \left[ \begin{array}{c} 1 \\ 1 \\ 0 \end{array} \right] , A _{2}= \left[ \begin{array}{ccc} -1 & -d_1 & 0 \\ d_1 & -1 & {\bar{\gamma }} \\ 0 & {{\hat{\vartheta }}} & -{{\hat{\vartheta }}} \end{array} \right] , B _{2}= \left[ \begin{array}{c} 1 \\ 1 \\ 0 \end{array} \right] . \end{aligned}$$

Moreover, the considered model parameters are taken as $d_1=5,$ ${\bar{\gamma }}=1.1,$ and ${{\hat{\vartheta }}}=5.46$. Let us assume that the membership functions are $\mu _1(x_3(t))=\frac{1}{1+e^{-2 x_{3}(k)}},$ and $\mu _2(x_3(t))=1-\mu _1(x_3(t))$.

Fig. 2

State responses of system (31) under control gain matrices (32)

Fig. 3

Control response of system (31) under control gain matrices (32)

By taking $\epsilon _{l}=0.000001$, $l=1,2, \dots , 9$, $\alpha =0.01$, $\beta =0.02$ and sampling interval is 0.035, which still keeps the considered model to be stable. The below control gains are attained by solving the LMIs in Theorem 2:

$$\begin{aligned} K_{1} =[-0.7610 \; 1.8723 \; -11.8339], \nonumber \\ K_{2} =[-0.7610 \; 1.8722 \; -11.8339]. \end{aligned}$$

(32)

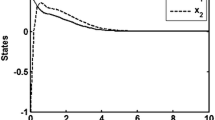
Let $x(0) = [-0.5\; 0.1\; 0.1]^T$, the simulation outcomes are presented in Figs. 2 and 3. Figure 2 illustrates the state responses of the PMSM system, affirming the stability of the controlled system. Additionally, Fig. 3 showcases the behavior of u(t). These visualizations clearly indicate that the proposed controller effectively stabilizes the considered model presented in equation (31).

4.2 Comparison examples

Example 1

To demonstrate the efficiency of the developed controller in contrast to established methods, we will analyze the model [5] formulated as follows:

$$\begin{aligned} \left\{ \begin{array}{lll} {\dot{x}}_{1}(t)=-x_{2}(t)-x_{3}(t) \\ {\dot{x}}_{2}(t)=x_{1}(t)+ax_{2}(t) \\ {\dot{x}}_{3}(t)=bx_{1}(t)-(c-x_{1}(t))x_{3}(t)+u(t) \end{array} \right. \end{aligned}$$

(33)

Here, it is assumed that $x_{1}(t)\in [c-d,c+d]$. Subsequently, we utilize the Rossler’s system (33) to establish the following T–S fuzzy model:

$$\begin{aligned} {\dot{x}}(t)=\sum \limits _{i=1}^{2}\mu _{i}(\theta (t))[A_{i} x(t)+B_{i} u(t)], \end{aligned}$$

where $A _{1}= \left[ \begin{array}{cccc} 0 & -1 & -1 \\ 1 & a & 0 \\ b & 0 & -d \end{array} \right] , B _{1}= \left[ \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right] , A _{2}= \left[ \begin{array}{cccc} 0 & -1 & -1 \\ 1 & a & 0 \\ b & 0 & d \end{array} \right] , B _{2}= \left[ \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right] ,$ and let $\mu _{1}(x_{1}(t))=\frac{c+d-x_{1}(t)}{2d}$ and $\mu _{2}(x_{1}(t))=1-\mu _{1}(x_{1}(t))$, $a = 0.3$, $b = 0.5$, $c = 5$ and $d = 10$.

Table 1 Maximum $h_U$, Control gains, and tuning parameters when $h_L = 0.00005$ in Example 1

Table 2 Maximum upper bound of sampling intervals $h_U$ when $h_{L}=h_{U}$ by various methods in Example 1

Setting $\epsilon _{l}=0.01$, $l=1,2, \dots , 9$, along with $\alpha =0.1$, $\beta =0.2$, yields a maximum sampling interval of 0.13, maintaining stability within the considered model. Solving the LMIs in Theorem 2 yields the following control gains:

$$\begin{aligned} K_{1} =[-335.1776 \; -158.1693 \; -335.7430],\\ K_{2} =[-335.2391 \; -158.2207 \; -335.7049]. \end{aligned}$$

The maximum value of $h_U$ along with the corresponding control gains can be obtained using Theorem 2, with the tuning parameters specified in Table 1. The maximum sample period bound calculated by Theorem 2 is presented in Table 2 for the case when $h_{L}=h_{U}$. In comparison, the upper bounds obtained from existing works are also included in Table 2. This table clearly indicates that our method offers larger ranges of sampling intervals for h compared to the existing works. Compared with [15, 19, 25, 35, 36, 5]. It is provided in Table 2. It is provided in Table 2. Table 2 demonstrates that our anticipated approaches yield less conservative results compared to existing methods. This clarifies the effectiveness of our proposed SD controller scheme.

Fig. 4

State responses of the open-loop system (35)

Fig. 5

State responses of system (35) under control gain matrices (36)

Fig. 6

Control response of system (35) under control gain matrices (36)

Example 2

To illustrate the superiority of the designed control approach with existing methods, in [27] model which is formulated as in the following:

$$\begin{aligned} \left\{ \begin{array}{lll} {\dot{x}}_{1}(t)=-a_1x_{1}(t)+a_1x_{2}(t)+u_1(t) \\ {\dot{x}}_{2}(t)=a_3x_{1}(t)-x_{2}(t)-x_1(t)x_{3}(t) \\ {\dot{x}}_{3}(t)=x_1(t)x_{2}(t)-a_2x_{3}(t) \end{array} \right. \end{aligned}$$

(34)

with $x_{1}(t)\in [-a_4,a_4].$ Then, we use the above Lorenz system (34):

$$\begin{aligned} {\dot{x}}(t)=\sum \limits _{i=1}^{2}\mu _{i}(\theta (t))[A_{i} x(t)+B_{i} u(t)], \end{aligned}$$

(35)

where $A _{1}= \left[ \begin{array}{ccc} -a_1 & a_1 & 0 \\ -a_3 & -1 & -a_4 \\ 0 & a_4 & -a_2 \end{array} \right] , B _{1}= \left[ \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \right] , A _{2}= \left[ \begin{array}{ccc} -a_1 & a_1 & 0 \\ -a_3 & -1 & a_4 \\ 0 & -a_4 & -a_2 \end{array} \right] , B _{2}= \left[ \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \right] ,$ and let us consider the membership functions as $\mu _{1}(x_{1}(t))=\frac{a_4+x_{1}(t)}{2a_4}$ and $\mu _{2}(x_{1}(t))=1-\mu _{1}(x_{1}(t))$. The parameters are provided as $a_1 = 10$, $a_2=\frac{8}{3}$, $a_3=28$ and $a_4=25$.

Table 3 Maximum $h_U$, Control gains, and tuning parameters when $h_L = 0.00061$ in Example 2

Table 4 Maximum upper bound of sampling intervals $h_U$ when $h_{L}=h_{U}$ by various methods in Example 2

By taking $\epsilon _{l}=0.000001$, $l=1,2, \dots , 9$, $\alpha =0.01$, $\beta =0.02$. It is possible to get that the maximum sample period is 0.12, which still keeps the considered model to be stable. By solving the LMIs in Theorem 2, one can obtain the following control gain matrices:

$$\begin{aligned} K_{1} =[7.5299 \; 3.3959 \; -3.7089], \nonumber \\ K_{2}=[7.5299 \; 3.3958 \; -3.7089]. \end{aligned}$$

(36)

Using the values in Table 3, we can determine the maximum $h_{U}$ and equivalent control gains according to Theorem 2. Considering the initial conditions as $x(0) = [-0.5\; 0.1\; 0.1]^T$, the simulation results are depicted in Figs. 4, 5. The trajectories of the Lorenz system without control input are shown in Fig. 4, indicating the chaotic behavior of the system. The responses of the Lorenz model states are displayed in Fig. 5, confirming the stable nature achieved by the considered model under the proposed control.

Furthermore, the control input u(t) is depicted in Fig. 6. Additionally, the maximum sampling upper bounds are determined by [25,26,27,28], and these values are listed in Table 4 when $h = h_L = h_U$. The data listed in Table 4 clearly reveals that the anticipated approach provides the largest sampling interval. Consequently, the proposed method yields less conservative results.

5 Conclusion

This research investigates stabilization techniques for a nonlinear model using fuzzy-based SD control. The fuzzy membership rules are customized to match fuzzy premise variables, reflecting the nonlinear terms within the model. In cases where nonlinear terms are not present, these rules are amalgamated into a singular entity, leading to less conservative outcomes through the integral inequality approach. To comprehensively account for the characteristics of membership functions, fractional-delayed states, and actual sampling patterns, an enhanced looped LKF framework has been introduced, capturing these aspects simultaneously. Stability and stabilization criteria are defined by formulating an appropriate LKF for the nonlinear model under investigation in terms of LMIs. Furthermore, Lyapunov stability theory is utilized to derive stability conditions for the nonlinear system under consideration. To highlight the advancements of this study, a comparative analysis is conducted against existing literature. Additionally, numerical examples are presented to illustrate the applicability and effectiveness of the proposed nonlinear models under the SD control scheme. In future work, the nonfragile fuzzy proportional retarded sampled-data scheme will be taken into account for multiagent systems