Large-scale longitudinal distortions of Marangoni wave patterns in the non-isothermal liquid layer covered by surfactant

Abstract

In the present paper, we consider single traveling waves (STW) generated by the oscillatory instability of Marangoni convection in the thin non-isothermal liquid layer with deformable free surface. The layer is covered by insoluble surfactant that plays an active role in the pattern selection together with inhomogeneity of temperature along the interface and surface deformability. Using the weakly nonlinear analysis we derived the modified complex Ginzburg–Landau equation describing the large-scale distortions of STWs near the bifurcation point. Linear stability analysis reveals existence of two modulational modes: one is for the amplitude and another one for the phase (Benjamin–Feir). Numerically, we found that STWs are stable with respect to longitudinal modulations in the case without surfactant. In the presence of the insoluble surfactant both modulational modes are found. The stability maps for different values of the surfactant concentration are plotted.

1 Introduction

Pattern formation is a very common phenomenon that is seen in many natural systems from the desert sand ripples to fascinated shapes of snowflakes. A wide variety of patterns are found in physical systems, including chemically active media, liquid interfaces, liquid crystals, etc. [1,2,3,4]. In many processes, such as crystal growth, paint drying, wetting processes and in other phenomena studied by thin film physics, the pattern formation relates to Marangoni effect [5,6,7,8]. The patterns grow beyond the instability threshold characterized by the critical wavenumber $k_c$ and, in the case of oscillatory instability, by the critical frequency $\omega _c$ [9]. Two sorts of patterns are possible, stationary ones and oscillatory ones. The most widespread patterns in the first group are hexagons, rolls, and squares. Wave patterns, like single traveling waves (STWs), are typical for the second group.

Recently, an interest in Marangoni patterns was stimulated by the work of Shklyaev et al. [10]. The authors showed that long-wave disturbances with wavenumber $k\sim O(Bi^{1/2})$ $(Bi\ll 1$ is the Biot number, ratio of heat transfer resistances inside and at the surface of the liquid) in a heated from below thin liquid layer can form stationary and wave periodic structures. In this paper we explore the action of an additional factor, insoluble surfactant spread over liquid interface, that can significantly modify the onset of Marangoni convection, as well as behavior of periodic structures. In extended systems, the periodicity of structures can be distorted by disturbances with wavenumbers close to the critical one, $k_c,$ [11, 12]. Earlier, [13, 14], we considered modulation of stationary patterns using the Newell–Whitehead–Segel approach [15, 16]. The result of the modulation of stationary patterns is the appearance of the Eckhaus instability.

In the present paper, we analyze the Marangoni convection that occurs in a thin liquid layer on a heated substrate with small heat conductivity. The upper liquid surface is deformable and covered by insoluble surfactant. Unlike the problem studied in [17], the considered problem contains three active variables: deviation of the flat surface, perturbation of the temperature field and distribution of surfactant concentration. In the region of the parameters characterized by the oscillatory instability of the conductive state, we investigate the propagation of a modulated one-dimensional traveling wave (STW). We obtain the corresponding complex Ginzburg–Landau equation (CGLE) modified due to the presence of the surfactant. It leads to the change of the criterion for the appearance of longitudinal phase-modulation (Benjamin–Feir) instability, as well the appearance of a new, amplitude–modulation, instability.

The structure of the paper is as follows. Section 2 describes the underlying physical problem. Unmodulated one-dimensional traveling wave is considered in Sect. 3. The modulation of STW is considered in Sect. 4. Here we present the derivation of the modified CGLE. Analysis of modulational STW instability is performed in Sect. 5. In Sect. 6 the influence of the insoluble surfactant is discussed, followed by Sect. 7 with conclusions.

2 Problem formulation

We consider an infinite thin horizontal liquid layer with a mean thickness $d_0,$ thermal diffusivity $\chi ,$ kinematic viscosity $\nu ,$ density $\rho ,$ dynamic viscosity $\eta =\rho \nu ,$ and thermal conductivity $\Lambda ,$ confined between a deformable free upper surface on the top and a solid substrate on the bottom. The layer is heated from below with transverse temperature gradient $-a (a>0).$ At the upper surface the liquid is covered by the insoluble surfactant. It is advected by interfacial velocity field and diffuses over the interface but not into the bulk. The reference value of the surfactant concentration is $\Gamma _0.$ The surface tension is a linear function of the temperature and surfactant concentration, $\sigma =\sigma _0-\sigma _1(T-T_0)-\sigma _2(\Gamma -\Gamma _0)$ ($\sigma _0$ is the reference value of the surface tension, $\sigma _1=-\partial _T\sigma ,$ $\sigma _2=-\partial _{\Gamma }\sigma ,$ $T_0$ is reference value of temperature at the surface in the absence of convection.)

The problem has the following governing parameters: $M=\sigma _1ad_0^2/\eta \chi$ is the Marangoni number, $N=\sigma _2d_0\Gamma _0/\eta \chi$ is the elasticity number, $L=D_0/\chi$ is the Lewis number ($D_0$ is the surface diffusivity), $G=gd_0^3/\nu \chi$ is the Galileo number, $\Sigma =\sigma _0d_0/\eta \chi$ is the inverse capillary number, and $Bi=qd_0/\Lambda$ is the Biot number (q is the heat transfer coefficient). The Biot number is defined as the ratio of heat-transfer resistances inside of and at the surface of the liquid.

Recently, Shklyaev et al. [10] showed that the interaction of temperature disturbances and surface deformations can generate large-scale monotonic and oscillatory instabilities in the case of poor heat transfer, $Bi\ll 1,$ and strong surface tension, $\Sigma \sim Bi^{-1}\gg 1.$ The interval $\Delta k$ of perturbation wavenumbers where the instability can appear, is $O(Bi^{1/2}).$ Therefore, the ratio between the mean thickness of the liquid $d_0$ and the typical horizontal scale of disturbances $\epsilon \sim Bi^{1/2}\ll 1.$ The appropriate scaling of Bi and $\Sigma$ is $\Sigma =\epsilon ^{-2}S,$ $Bi=\epsilon ^2\beta ,$ where $S=O(1)$ and $\beta =O(1).$ The influence of insoluble surfactants on those instabilities was formerly considered in [13, 14, 18].

The system of equations describing a long-wave Marangoni convection in the liquid layer covered by insoluble surfactant was derived in [18]. That system governs the evolution of the local film thickness $H(X,Y,\tau ),$ the surfactant concentration $\Gamma (X,Y,\tau )$ and the temperature perturbation $F(X,Y,\tau )$:

$$\begin{aligned} \partial _{\tau }H=\nabla \cdot \textbf{J}_1, \quad \textbf{J}_1 =\left( \frac{H^3}{3}\nabla R+\frac{MH^2}{2}\nabla \theta +\frac{NH^2}{2}\nabla \Gamma \right) \end{aligned}$$

(1)

$$\begin{aligned} \partial _{\tau }\Gamma =\nabla \cdot \textbf{J}_2,\quad \textbf{J}_2 =\Gamma H\left( \frac{H}{2}\nabla R+M\nabla \theta +N\nabla \Gamma \right) +L\nabla \Gamma , \end{aligned}$$

(2)

$$\begin{aligned} H\partial _{\tau }F=\nabla \cdot (H\nabla F)-\frac{1}{2}(\nabla H)^2-\beta \theta +\textbf{J}_1\cdot \nabla \theta +\nabla \cdot \left( \frac{H^4}{8}\nabla R+\frac{MH^3}{6}\nabla \theta +\frac{NH^3}{6}\nabla \Gamma \right) , \end{aligned}$$

(3)

where X, Y are new spatial coordinates $(X=\epsilon x,$ $Y=\epsilon y),$ $\tau$ is the rescaled temporal coordinate $(\tau =\epsilon ^2 t),$ $R=GH-S\nabla ^2H$ is the pressure disturbance and $\theta =F-H$ is the temperature disturbance at the free surface, $\nabla =(\partial _X,\partial _Y).$ This system of equations (1)–(3) describes following effects: in the right-hand side of (1) damping of the surface deflection due to gravity, surface tension and influence of both thermocapillary and solutocapillary flows on the thickness of the layer; the first term in the right-hand side of (3) relates to heat conductivity in the longitudinal direction, the second term describes the enhancement of heat flux due to the growth of the surface area by the surface deformation, the third term is responsible for heat losses from the surface, other terms describe the advective heat transfer by the flow. The Eq. (2) for the surfactant concentration was in details described in our work [19].

The linear stability analysis of (1)–(3) around the base state solution $H_0=1,$ $F_0=1,$ and $\Gamma _0=1$ was performed in [18], where the existence of two instability modes, monotonic one and oscillatory one, was shown. For rescaled wavenumbers $K=\epsilon ^{-1}k,$ the influence of the insoluble surfactant on the monotonic $(M_m)$ and oscillatory $(M_o)$ neutral curves, respectively is described by formulas:

$$\begin{aligned} M_m=\frac{(48+12N/L)(G+K^2S)(\beta +K^2)}{K^2(72+G+K^2S)} \end{aligned}$$

(4)

and

$$\begin{aligned} M_{o}=\frac{12 \left( \beta +K^2+i \omega _0\right) \left[ 4 i K^2 \omega _0 \left( G+K^2 S+3 (L+N)\right) +K^4 (4 L+N) \left( G+K^2 S\right) -12 \omega _0^2\right) }{K^2 \left( K^2 L+i \omega _0\right) \left( (G+72) K^2+K^4 S+48 i \omega _0\right) }. \end{aligned}$$

(5)

The frequency of neutral oscillations is determined by the formula:

$$\begin{aligned} \omega _0^2= & {} \frac{1}{288} \left( -K^4 \left[ G^2-9 G (N-3)\right. \right. \left. \left. +72 (2 L (L+N)+N+3)-45 \beta S\right] \right. \\{} & {} \left. +K^6 S (9 (N-3)-2 G)+9 \beta K^2 (5 G+16N-24)\right. \left. -K^8 S^2+\sqrt{{\mathcal {D}}_1}\right) , \end{aligned}$$

(6)

where

$$\begin{aligned} {\mathcal {D}}_1= & {} [K^4 (G^2-9 G (N-3)+72 (2 L (L+N) +N+3)-45 \beta S)+K^6 S (2 G-9 N+27) \\{} & {} -9 \beta K^2 (5 G+16 N-24)+K^8 S^2]^2 -144 K^6 \{K^4 S [4 (2 G+27) L^2+2 (G+18) L N \\{} & {} -N (2 G+\beta S+72)]+K^2 [4 L^2 (G (G+27) -45 \beta S+216)+L N (G (G+36)-36 \beta S+864) \\{} & {} -N (2 \beta (G+36) S+G (G+72))] -\beta [36 (5 G-24) L^2+36 (G-24) L N+G (G+72) N] \\{} & {} +K^6 S^2 (4 L^2+(L-1) N)\}. \end{aligned}$$

(7)

Marginal stability curves for different parameters are published in [18].

3 Unmodulated 1D STW

Let us consider the nonlinear dynamics in the vicinity of the oscillatory neutral curve, i.e., take

$$\begin{aligned} M=M_{o}+\delta ^2M_2, \end{aligned}$$

where the small parameter $\delta$ denotes a small deviation from the critical value of $M_{o}.$

Near the convection threshold we can expand the fields as

$$\begin{aligned} (H,F,\Gamma )= (1,1,1)+\delta (h_1,f_1,\gamma _1)+\delta ^2(h_2,f_2,\gamma _2) +\cdots ,\quad \partial _{\tau }=\partial _{\tau _0}+\delta ^2\partial _{\tau _2}+\cdots . \end{aligned}$$

(8)

Here, we introduce two different time scales. The “fast” time, $\tau _0,$ relates to the oscillation frequency $\omega _0,$ and the “slow” one, $\tau _2$ corresponds to the low growth rate proportional to $M-M_0.$

At the leading order, a single traveling wave (STW) is described by the following formula, that is

$$\begin{aligned}{} & {} (h_1,f_1,\gamma _1) \\{} & {} \quad =(A(\tau _2),\alpha _1A(\tau _2),\alpha _2A(\tau _2))\text{e}^{iKX+i\Omega _0\tau _0}+\text{c.c.}, \end{aligned}$$

(9)

“c.c.” means complex-conjugate terms, and

$$\begin{aligned}{} & {} \alpha _1=-\frac{GK^2+K^4S-72\beta -24i\omega _0}{72(K^2+\beta +i\omega _0)}, \end{aligned}$$

(10)

$$\begin{aligned}{} & {} \alpha _2=\frac{GK^2+K^4S+12i\omega _0}{6K^2L+6i\omega _0}. \end{aligned}$$

(11)

The temporal evolution of the STW amplitude near the convection threshold is governed by the amplitude equation, see [18]:

$$\begin{aligned} \partial _{\tau _2}A=\kappa _0 A+\kappa _1|A|^2A. \end{aligned}$$

(12)

Here, $\kappa _0=\kappa _{0,r}+i\kappa _{0,i}$ is the linear complex growth rate and $\kappa _1=\kappa _{1,r}+i\kappa _{1,i}$ is the complex Landau constant. The sign of $\kappa _{1,r}$ determines the type of Hopf bifurcation (for a direct one $\kappa _{1,r}<0$-supercritical bifurcation and for an inverse one $\kappa _{1,r}>0$-subcritical one).

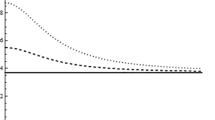
Later on, we consider the oscillatory mode of instability near the threshold of convection $M_{o}^c$ at critical wavenumber $K_c$ and frequency $\omega _c=\omega _0(K_c).$ Thus, $M=M_{o}^c+\delta ^2 M_2.$ The critical wavenumber for oscillatory instability $K_c$ is found by minimizing the Marangoni number for this instability, (5), with respect to wavenumber. In the case without surfactant the critical wavenumber was calculated in [10] and it equals $K_c=(3\beta )^{1/4},$ but surfactant can change the value of critical wavenumber. Thus, it was recalculated for each value of N. The value of the Lewis number has a significant limitation and for all our calculation is taken at fixed value as $L=0.003,$ [14]. Without loss of generality, we also fix for the calculation the inverse capillary number, $S=1,$ which corresponds to the definition of parameter $\epsilon$ as $\epsilon =\Sigma ^{-1/2}.$ The results, which demonstrate the influence of surfactant concentration, are presented in the form of stability maps in the plane $(G,\beta )$ for different values of the elasticity number. Figure 1 presents the domain of oscillatory instability for case without surfactant, [10]. The dashed line marks the boundary between subcritical and supercritical STWs.

Fig. 1

Domain of oscillatory instability without surfactant, [10]. The dashed line is the boundary between subcritical STW (above the line) and supercritical STW (below the line)

Stability maps for different values of the elasticity number N will be presented in Sect. 6.

The results of our calculations can be presented in dimensional form if we take the following typical values of the physical parameters (in SI): kinematic viscosity $\sim 10^{-6},$ density of liquid $\sim 10^3,$ thermal diffusivity $\sim 10^{-7},$ surface tension $\sim 10^{-2} {-} 10^{-1},$ heat transfer coefficient $\sim 10^2 {-} 10^3,$ surface diffusion coefficient $\sim 10^{-9}.$ It is known, [20], that low-molecular-weight surfactants in emulsions and foams form monolayers with low elasticity number $N< 1.$

4 Modulation of wave patterns

In order to consider longwave spatial modulations of a traveling wave, we introduce two spatial coordinates: $X_0$ corresponds to the pattern scale and $X_1=\delta X$ corresponds to the scale of pattern modulation due to the superposition of Fourier components within and around the instability region. For the temporal coordinate we introduce $\tau _0=\tau ,$ $\tau _1=\delta \tau ,$ $\tau _2=\delta ^2\tau ,$ i.e., $\partial _{\tau }=\partial _{\tau _0}+\delta \partial _{\tau _1}+\delta ^2\partial _{\tau _2}+\cdots .$ Note that $\partial _{XX}=\partial _{X_0X_0}+2\delta \partial _{X_0X_1}+\delta ^2\partial _{X_1X_1}.$ The variables $(H, F,\Gamma )$ near the threshold can be presented as shown in (8).

At the leading order, the system of linear stability problem is recovered, which can be written:

$$\begin{aligned}{} & {} \frac{\partial h_1}{\partial \tau _0}-\partial _{X_0X_0}\left( \frac{1}{3}R_1+\frac{M_{o}}{2}\theta _1+\frac{N}{2}\gamma _1\right) =0, \end{aligned}$$

(13)

$$\begin{aligned}{} & {} \frac{\partial \gamma _1}{\partial \tau _0}-\partial _{X_0X_0}\left( \frac{1}{2}R_1+M_{o}\theta _1+(N+L)\gamma _1\right) =0, \end{aligned}$$

(14)

$$\begin{aligned}{} & {} \frac{\partial f_1}{\partial \tau _0}-\partial _{X_0X_0}\left( \frac{1}{8}R_1+\frac{M_{o}}{6}\theta _1+\frac{N}{6}\gamma _1+f_1\right) +\beta \theta _1=0. \end{aligned}$$

(15)

The solution can be written in the form of a modulated STW:

$$\begin{aligned}{} & {} h_1=A(X_1,\tau _1,\tau _2)\text{e}^{i(K_cX_0+\omega _c\tau _0)}+\text{c.c.}, \\{} & {} f_1=\alpha _1(K_c)A(X_1,\tau _1,\tau _2)\text{e}^{i(K_cX_0+\omega _c\tau _0)}+\text{c.c.}, \\{} & {} \gamma _1=\alpha _2(K_c)A(X_1,\tau _1,\tau _2)\text{e}^{i(K_cX_0+\omega _c\tau _0)}+\text{c.c.} \end{aligned}$$

(16)

At the second order of $\delta ,$ we obtain

$$\begin{aligned}{} & {} \frac{\partial h_2}{\partial \tau _0}-\partial _{X_0X_0}\left( \frac{1}{3}R_2+\frac{M_{o}}{2}\theta _2+\frac{N}{2}\gamma _2\right) \\{} & {} \quad =-\partial _{\tau _1} h_1+\partial _{X_0}(h_1\partial _{X_0} R_1+M_{o} h_1\partial _{X_0}{\theta }_1 +Nh_1\partial _{X_0}\gamma _1)+\partial _{X_0X_1} \\{} & {} \qquad \times \left( \frac{2}{3}Gh_1-\frac{4}{3}S\partial _{X_0X_0}h_1+M_{o}(f_1-h_1)+N\gamma _1\right) , \end{aligned}$$

(17)

$$\begin{aligned}{} & {} \frac{\partial \gamma _2}{\partial \tau _0}-\partial _{X_0X_0}\left( \frac{1}{2}R_2+M_{o}\theta _2+(N+L)\gamma _2\right) \\{} & {} \quad =-\partial _{\tau _1}\gamma _1+\partial _{X_0}\left( (h_1+\frac{\gamma _1}{2})\partial _{X_0}R_1\right. \\{} & {} \qquad +M_{o}(h_1+\gamma _1)\partial _{X_0}\theta _1+N(h_1+\gamma _1)\partial _{X_0}\gamma _1\Bigr ) \\{} & {} \qquad +\partial _{X_0X_1}\Bigl (Gh_1-2S\partial _{X_0X_0}h_1 \\{} & {} \qquad +2M_{o}(f_1-h_1)+2(N+L)\gamma _1 \Bigr ), \end{aligned}$$

(18)

$$\begin{aligned}{} & {} \frac{\partial f_2}{\partial \tau _0}-\partial _{X_0X_0}\left( \frac{1}{8}R_2+\frac{M_{o}}{6}\theta _2 +\frac{N}{6}\gamma _2+f_2\right) +\beta \theta _2 \\{} & {} \quad =-\partial _{\tau _1}f_1-h_1\partial _{\tau _0}f_1+\partial _{X_0}(h_1\partial _{X_0}f_1) \\{} & {} \qquad -\frac{1}{2}(\partial _{X_0} h_1)^2+\Bigl (\frac{1}{3}\partial _{X_0}R_1+\frac{M_{o}}{2}\partial _{X_0}(f_1-h_1) \\{} & {} \qquad +\frac{N}{2}\partial _{X_0}\gamma _1\Bigr )\partial _{X_0}(f_1-h_1) \\{} & {} \qquad +\partial _{X_0}\Bigl (\frac{h_1}{2}\partial _{X_0}R_1+\frac{M_{o}h_1}{2}\partial _{X_0}(f_1-h_1) \\{} & {} \qquad +\frac{Nh_1}{2}\partial _{X_0}\gamma _1\Bigr )+\partial _{X_0X_1}\Bigl (2f_1+\frac{G}{4}h_1 \\{} & {} \qquad -\frac{S}{2}\partial _{X_0X_0}h_1+\frac{M_{o}}{3}(f_1-h_1)+\frac{N}{3}\gamma _1\Bigr ). \end{aligned}$$

(19)

Here, the solvability condition yields a wave equation for the envelope function A:

$$\begin{aligned} \partial _{\tau _1}A=\omega _1\partial _{X_1}A, \end{aligned}$$

(20)

where $\omega _1$ is a group velocity. The expression for the group velocity is given in the Appendix.

Introducing the reference frame moving with velocity $\omega _1,$ we can write for the amplitude function:

$$\begin{aligned} A=A({{\tilde{X}}}_1,\tau _2,\ldots ), \quad {{\tilde{X}}}_1=X_1+\omega _1 \tau _1. \end{aligned}$$

Later on, the tilde will be omitted.

Solution at the second order in case of modulation can be written in the form:

$$\begin{aligned} h_2= & {} a_{22}A^2\text{e}^{2i(K_cX_0+\omega _c\tau _0)}+h_{20}(X_1,\tau _2)+\text{c.c.}, \end{aligned}$$

(21)

$$\begin{aligned} f_2= b_{21}\frac{\partial A}{\partial X_1}\text{e}^{i(K_cX_0+\omega _c\tau _0)} +b_{22}A^2\text{e}^{2i(K_cX_0+\omega _c\tau _0)}+b_{20}|A|^2+\text{c.c.}, \end{aligned}$$

(22)

$$\begin{aligned} \gamma _2= c_{21}\frac{\partial A}{\partial X_1}\text{e}^{i(K_cX_0+\omega _c\tau _0)} +c_{22}A^2\text{e}^{2i(K_cX_0+\omega _c\tau _0)}+\gamma _{20}(X_1,\tau _2)+\text{c.c.} \end{aligned}$$

(23)

The coefficients $b_{20},$ $b_{21},$ and $a_{21}$ can be found as

$$\begin{aligned}{} & {} b_{20}=-\frac{K_c^2}{\beta }, \end{aligned}$$

(24)

$$\begin{aligned}{} & {} b_{21}= -i\left( \frac{\partial \alpha _1}{\partial k}\right) _{K_c} \\{} & {} \quad =\frac{2iK_c(K_c^4S+(72+G+2K_c^2S)\beta )-2K_c(24+G+2K_c^2S)\omega _c+(K_c^2(24+G+K_c^2S)-48\beta )\omega _1}{72(K_c^2+\beta +i\omega _c)^2} \end{aligned}$$

(25)

$$\begin{aligned} c_{21}= -i\left( \frac{\partial \alpha _2}{\partial k}\right) _{K_c} =\frac{K_c(-2iK_c^4LS+2(G-12L+2K_c^2S)\omega _c-K_c(G-12L+K_c^2S)\omega _1)}{6(K_c^2L+i\omega _c)^2}. \end{aligned}$$

(26)

The expressions for coefficients $a_{22},$ $b_{22},$ and $c_{22}$ are more complicated and presented in the Appendix.

For $h_{20},$ we obtain at the third order of $\delta$ the following equation:

$$\begin{aligned} \omega _1 \partial _{X_1}h_{20}=iK_c[M_{o}(\alpha _1-\alpha _1^*)+N(\alpha _2-\alpha _2^*)]\partial _{X_1}|A|^2. \end{aligned}$$

(27)

Integrating (27), we find

$$\begin{aligned} h_{20}= \frac{iK_c}{\omega _1}[M_{o}(\alpha _1-\alpha _1^*)+N(\alpha _2-\alpha _2^*)] |A|^2+C_1(\tau _2) = c_h|A|^2+C_1(\tau _2). \end{aligned}$$

(28)

Here

$$\begin{aligned} c_h= \frac{K_c\omega _c}{3\omega _1}\left( \frac{K_c^2N(G-12L+K_c^2S)}{K_c^4L^2+\omega _c^2}\right. \left. -\frac{M_{o}((G+24)K_c^2+K_c^4S-48\beta )}{12((K_c^2+\beta )^2+\omega _c^2)}\right) . \end{aligned}$$

Averaging the value of $h_{20}$ over all region $X_1$ and taking into account the conservation of the liquid’s volume, we find that the variable $h_{20}$ can be written as follows:

$$\begin{aligned} h_{20}(X_1,\tau _2)=c_h\left( |A|^2-\langle |A|^2\rangle _{X_1}\right) . \end{aligned}$$

(29)

The similar method can be applied to determine $\gamma _{20}(X_1,\tau _2)$ as

$$\begin{aligned}{} & {} \gamma _{20}=-\frac{iK_c}{2\omega _1}\left[ (G-2N+K_c^2S)(\alpha _2-\alpha _2^*)\right. \left. +2M_{o}(\alpha _1^*+\alpha _2^*-\alpha _1(1+\alpha _2^*)-\alpha _2(1-\alpha _1^*)\right] |A|^2+C_2(\tau _2) \\{} & {} \quad =c_{\gamma }|A|^2+C_2(\tau _2), \end{aligned}$$

(30)

where

$$\begin{aligned} c_{\gamma }=-\frac{K_c\omega _c}{216(K_c^4L^2+\omega _c^2)\omega _1} \left( 36K_c^2(G-12L+K_c^2S)(G-2N+K_c^2S)+\frac{{\mathcal {D}}_3M_{o}}{(K_c^2+\beta )^2+\omega _c^2}\right) , \end{aligned}$$

$$\begin{aligned} {\mathcal {D}}_3= & {} K_c^{10}(L-1)S^2+G^2K_c^4[K_c^2(L-1)-\beta ] \\{} & {} -288K_c^4(L-3)L\beta +K_c^8S[-72+6L(L+6)-S\beta ] \\{} & {} +36K_c^6[4L(L+6)-(L+2)S\beta ]+2GK_c^4[K_c^4(L-1)S \\{} & {} -18(L+2)\beta +K_c^2(-36+3L(L+6)-S\beta )]- \\{} & {} -30GK_c^2\omega _c^2+6[24K_c^2(4L+3)-5K_c^4S-144\beta ]\omega _c^2, \end{aligned}$$

(31)

and finally

$$\begin{aligned} \gamma _{20}(X_1,\tau _2)=c_{\gamma }\left( |A|^2-\langle |A|^2\rangle _{X_1}\right) . \end{aligned}$$

(32)

The solvability condition at the third order of $\delta$ gives us the equation for the envelope function $A(X_1,\tau _2)$ containing terms with $h_{20}$ and $\gamma _{20}$ as in case described in [14]:

$$\begin{aligned} \partial _{\tau _2}A= \kappa _0A+\kappa _1|A|^2A+{{\tilde{\mu }}}_1\partial _{X_1X_1}A +{{\tilde{\mu }}}_2h_{20}A+{{\tilde{\mu }}}_3\gamma _{20}A. \end{aligned}$$

(33)

The traveling wave bifurcates at $K_c$ in a supercritical way, i.e., into the region where $\kappa _{0,r}>0,$ if $\kappa _{1,r}<0,$ hence $-\kappa _{0,r}/\kappa _{1,r}>0.$ At the point $K_c$ the growth rate of the linear instability has a maximum; therefore, $\tilde{\mu }_{1r}>0.$

Using the expressions for surface distortion $h_{20}$ and distribution of the surfactant concentration we can rewrite the amplitude equation as

$$\begin{aligned} \partial _{\tau _2}A= \kappa _0A+\kappa _1|A|^2A+{{\tilde{\mu }}}_1\partial _{X_1X_1}A +{{\tilde{\kappa }}}_1 (|A|^2-\langle |A|^2\rangle )A, \end{aligned}$$

(34)

where ${{\tilde{\kappa }}}_1={{\tilde{\mu }}}_2c_h+{{\tilde{\mu }}}_3c_{\gamma }.$ Coefficients in Eq. (34) are complex.

Making the rescaling as

$$\begin{aligned} A=a\sqrt{-\frac{\kappa _{0,r}}{\kappa _{1,r}}}\text{e}^{i\kappa _{0,i}\tau _2},\quad \partial _{\tau _2}=\kappa _{0,r}\partial _t, \quad \partial _{X_1}=\sqrt{\frac{\kappa _{0,r}}{{\tilde{\mu }}_{1,r}}}\partial _x \end{aligned}$$

(35)

we obtain the standard form of the modified CGLE:

$$\begin{aligned} \partial _ta= a-(1+iv)|a|^2a+(1+iu)\partial _{xx}a +(w_r+iw_i)(|a|^2-\langle |a|^2\rangle _x)a \end{aligned}$$

(36)

with

$$\begin{aligned}{} & {} v=\kappa _{1,i}/\kappa _{1,r},\quad u={{\tilde{\mu }}}_{1,i}/{{\tilde{\mu }}}_{1,r}, \\{} & {} w_r={{\tilde{\kappa }}}_{1,r}/\kappa _{1,r},\quad w_i={{\tilde{\kappa }}}_{1,i}/\kappa _{1,r}. \end{aligned}$$

(37)

5 Linear stability of STW

Let us consider the 1D traveling wave in the form:

$$\begin{aligned} a(x,t)=r(x,t)\exp (i\phi (x,t)). \end{aligned}$$

Substituting this form of STW into Eq. (36) we obtain a system of two equations for real amplitude a(x, t) and real phase $\phi (x,t)$:

$$\begin{aligned}\partial _t r=r-r^3+\partial _{xx}r-u(2\partial _xr\partial _x\phi +r\partial _{xx}\phi )-r(\partial _x\phi )^2+w_r(r^2-\langle r^2\rangle _x)r, \end{aligned}$$

(38)

$$\begin{aligned} r\partial _t\phi =-vr^3+2\partial _xr\partial _x\phi +u(\partial _{xx}r -r(\partial _x\phi )^2)+r\partial _{xx}\phi +w_i(r^2-\langle r^2\rangle _x)r. \end{aligned}$$

(39)

Let us consider the stability of the TW solution with the amplitude independent of x (i.e., the TW with the wavenumber equal to $K_c$):

$$\begin{aligned} r_0=1, \quad \phi _0=-vt. \end{aligned}$$

(40)

Linearizing system (38)–(39) around solution (40) for small disturbances $({{\tilde{r}}},{{\tilde{\phi }}})\sim \text{e}^{\lambda t+iqx}, (q\ne 0)$ we obtain the equation for the growth rate $\lambda$:

$$\begin{aligned} \lambda ^2+2(1-w_r+q^2)\lambda +q^4(1+u^2) +2q^2[1-w_r+u(v-w_i)]=0. \end{aligned}$$

(41)

That equation has two roots. In the limit $|q|\ll 1,$ the first one describes the amplitude mode: $\lambda =2(w_r-1)+O(q^2)$ and the second one is the phase mode: $\lambda =q^2\left( \frac{1-w_r+u(v- w_i)}{w_r-1}\right) .$ Thus, the stability conditions with the longitudinal disturbances are

$$\begin{aligned} w_r<1, \quad 1-w_r+u(v-w_i)>0. \end{aligned}$$

(42)

For the standard CGLE $(w=0)$ the criterion of phase modulation (Benjamin–Feir) instability, $1+uv<0,$ coincides with the classic result of Yamada and Kuramoto [21].

6 Influence of insoluble surfactant

Without the surfactant STW is stable with respect both amplitude and phase modulation. The same result was obtained in [17]. Addition of the surfactant changes the position of the boundary between the supercritically excited STWs (this region is denoted as “STW” on the $(G,\beta )$-stability map) and the subcritically excited ones, denoted as “sub.STW” region on the map. Only “STW”-region, where $\kappa _{1,r}<0,$ is actual for our consideration, because is a region of stability of traveling rolls. Figure 2 shows how these boundaries for the three different values of the surfactant concentration $N=0.01$ (blue one), $N=0.1$ (red one), and $N=0.5$ (purple one). It is shown that the region of subcritical bifurcated STW shrinks when the surfactant concentration increases.

Fig. 2

Domain of oscillatory instability for different values of surfactant concentration. The dashed line is the boundary between subcritical STW, marked as “sub.STW” (above the line) and supercritical STW, marked as “STW” on the map (below the line). Blue, red, and purple lines correspond to $N=0.01,$ $N=0.1,$ and $N=0.5,$ respectively

To find the regions stable with respect to amplitude and phase modulation we calculate the coefficients $w_r,$ $w_i,$ u, ,  and v using the parameters of the problem for the domain of the stable traveling rolls (region “STW” on the stability map) at different values of the elasticity number N. Figure 3 on two panels (a) and (b) depicts the domains of stable traveling rolls at $N=0.01$ [panel (a)] and $N=0.1$ [panel (b)]. As we see in both these cases exist both regions: the region of amplitude modulational instability marked as “AM” and the region of phase modulational instability (Benjamin–Feir instability) marked as “BF”.

Fig. 3

Domains of stability for traveling rolls for longitudinal modulation for different values of surfactant concentration. The dashed line is the boundary between subcritically excited (“sub. STW”) and stable STWs, marked as “STW” on the map. Panel a: $N=0.01,$ panel b: $N=0.1.$ Amplitude modulational instability and phase modulation (Benjamin–Feir) instability marked as “AM” and “BF”, respectively

Note, that earlier the modulational instability was studied only in the framework of the CGLE and the phase modulation instability was discussed only. Thus, this work, together with the paper [17], for the first time demonstrates the appearance of the amplitude modulation instability as a result of the interaction with the stable soft modes.

7 Conclusion

In the present paper, we analyzed the influence of the insoluble surfactant on the modulation instability of large-scale Marangoni convection. Applying the weakly nonlinear analysis we derived a set of the CGLE-like equations for the amplitude of stable wave patterns that described the interaction of three active variable of the problem: amplitude of the wave pattern a,  surface thickness deflection h and perturbations of the surfactant concentration $\gamma .$ Near the threshold point of the oscillatory Marangoni convection onset, the linear analysis of the modulation instability of the stable traveling waves was performed. Two possible modes of instability have been revealed, the phase modulation (Benjamin–Feir) instability and the amplitude modulation instability. The criteria of their existence have been found. We reproduced the results of [17] showing that without a surfactant, the traveling waves are stable with respect to modulation. In the presence of the surfactant, both kinds of instabilities were found numerically in a tiny range of parameters at two values of the elasticity number ($N=0.01$ and $N=0.1$).

Appendix A

$$\begin{aligned}{} & {} \omega _1={\mathcal {D}}_{11}/{\mathcal {D}}_{10} \end{aligned}$$

(A1)

$$\begin{aligned} {\mathcal {D}}_{11}&=-i k \{3 K_c^2 M_0 (K_c^2 L+i \omega _0) [24 \alpha _1+3 G +6 K_c^2 S+4 (\alpha _1-1) M_o+4 \alpha _2 N] \\ & \quad -2 (K_c^2 (M_o+6)+6 (\beta +i \omega _0)) [G K_c^2 (4 L+N) +4 i G \omega _0+2 K_c^4 S (4 L+N) \\ & \quad +K_c^2 (6 (\alpha _1-1) L M_o+8 i S \omega _0) +6 i \omega _0 ((\alpha _1-1) M_o+\alpha _2 N)] +2 K_c^4 M_o N (G+2 K_c^2 S-6 \alpha _2 L)\}, \\{} & {} {\mathcal {D}}_{10}=6 \{(\alpha _2-2) K_c^4 M_o N -6 \alpha _1 K_c^2 M_o (K_c^2 L+i \omega _0)+(K_c^2 (M_o+6)\\ & \quad +6 (\beta +i \omega _0)) (K_c^2 (2 (L+N)-\alpha _2 N)+2 i \omega _0)\}. \\ a_{22} &=\frac{{\mathcal {D}}_{21}+\omega _c{\mathcal {D}}_{22}+\omega _c^2{\mathcal {D}}_{23}}{{\mathcal {D}}_{00} +{\mathcal {D}}_{01}\omega _c+{\mathcal {D}}_{02}\omega _c^2+36i\omega _c^3}, \end{aligned}$$

(A2)

$$\begin{aligned} {\mathcal {D}}_{23}&=-18 k^2 [2 G+2 (K_c^2 S+\alpha _2 N)+(\alpha _1-2) M_o], \\ {\mathcal {D}}_{22}&=3 i K_c^2 [6 \beta G+2 G K_c^2 (12 L-\alpha _1 M_o-3 \alpha _2 N +6 N+12)+2 K_c^4 S (12 L-\alpha _1 M_o-3 \alpha _2 N+6 N \\ & \quad +12)+K_c^2 (3 M_o (4 \alpha _1 (L+N+1)-8 L-4 N-7) +12 \alpha _2 N (2 L-\alpha _2 N+N+2)+((4-3 \alpha _1) \alpha _1-1) \\{} & {} \quad \times M_o^2+(13-15 \alpha _1) \alpha _2 M_o N+6 \beta S) +6 \beta ((\alpha _1-1) M_o+\alpha _2 N)], \\ {\mathcal {D}}_{21}&=3 K_c^4 [-4 G K_c^2 (L (\alpha _1 M_o-12) +3 (\alpha _2-2) N)+12 \beta G L-3 (\alpha _2-2) \beta G N \\{} & {} \quad -4 K_c^4 S (L (\alpha _1 M_o-12)+3 (\alpha _2-2) N) -2 K_c^2 L M_o ((\alpha _1-1) (3 \alpha _1-1) M_o+3 \alpha _1 (\alpha _2 N-4) \\{} & {} \quad -\alpha _2 N+21)+48 \alpha _2 K_c^2 L N+12 \beta K_c^2 L S -24 (\alpha _2-1) K_c^2 N ((\alpha _1-1) M_o+\alpha _2 N) -3 (\alpha _2-2) \beta K_c^2 N S \\{} & {} \quad +6 \beta (2 L-\alpha _2 N+N) ((\alpha _1-1)M_o+\alpha _2 N)], \\{\mathcal {D}}_{00}&=2 K_c^6 [G L (M_o-48)-12 G N+4 K_c^2 S (L (M_o-48)-12N) +72 L M_o]-6 \beta K_c^4 (4 L+N)(G+4K_c^2 S), \\ {\mathcal {D}}_{01}&=-i K_c^2 [K_c^2 (G (48 L-M_o+12 N+48) +4 K_c^2 S (48 L-M_o+12 N+48)-48 L (M_o-3) \\ & \quad -72 (M_o-2 N))+12 \beta (G+4 K_c^2 S+3 (L+N))], \\ {\mathcal {D}}_{02}&=24K_c^2(3+G+3L-M_{osc}+3N+4K_c^2S)+18\beta , \\ b_{22}&=\frac{{\mathcal {D}}_{31}+{\mathcal {D}}_{32}\omega _c+{\mathcal {D}}_{33}\omega _c^2-36i\alpha _1\omega _c^3}{2({\mathcal {D}}_{00}+{\mathcal {D}}_{01}\omega _c+{\mathcal {D}}_{02}\omega _c^2+36i\omega _c^3)}, \end{aligned}$$

(A3)

$$\begin{aligned} {\mathcal {D}}_{31}&=K_c^4 [G^2 K_c^2 (4 (4 \alpha _1-1) L+N (4 \alpha _1+\alpha _2-2)) +G (5 K_c^4 S (4 (4 \alpha _1-1) L+N (4 \alpha _1+\alpha _2-2)) \\ & \quad +2 K_c^2 (6 L (8 \alpha _1+\alpha _1 (2 \alpha _1-5) M_o+M_o +2 \alpha _1 \alpha _2 N-\alpha _2 N-2)+N (12 \alpha _1 \\{} & {} \quad +(3 \alpha _1+\alpha _2-2) ((\alpha _1-1)M_o+\alpha _2 N)-3)) +18 \beta (4 L-(\alpha _2-2) N))+4 K_c^6 S^2 (4 (4 \alpha _1-1) L \\ &\quad +N (4 \alpha _1+\alpha _2-2))+8 K_c^4 S (3 L (16 \alpha _1 +(\alpha _1 (4 \alpha _1-7)+2) M_o+4 \alpha _1 \alpha _2 N-2 \alpha _2 N-4) \\ & \quad +N (12 \alpha _1+(3 \alpha _1+\alpha _2-2) ((\alpha _1-1) M_o+\alpha _2 N)-3)) +6 K_c^2 (-2 L M_o (12 \alpha _1+3 \alpha _1^2 M_o \\ & \quad -4 \alpha _1 M_o+M_o+(3 \alpha _1-1) \alpha _2 N-3)+12 \beta L S-3 (\alpha _2-2) \beta N S) \\ &\quad +36 \beta (2 L-\alpha _2 N+N) ((\alpha _1-1) M_o+\alpha _2 N)], \\ {\mathcal {D}}_{32}&=2 i K_c^2 [(4 \alpha _1-1) G^2 K_c^2+18 \beta G +5 (4 \alpha _1-1) G K_c^4 S+3 G K_c^2 (8 \alpha _1+4 (3 \alpha _1+2) L \\& \quad +\alpha _1 (2 \alpha _1-5) M_o+M_o+N (2 \alpha _1 (\alpha _2+3)-3 \alpha _2+4)-2) +4 (4 \alpha _1-1) K_c^6 S^2 \\ & \quad +12 (9 \alpha _1+2) K_c^4 L S+6 K_c^4 S (16 \alpha _1+(\alpha _1 (4 \alpha _ 1-7)+2) M_o +N (4 \alpha _1 \alpha _2+6 \alpha _1-3 \alpha _2+2)-4) \\ & \quad +3 K_c^2 (6 L (4 \alpha _1+((\alpha _1-2) \alpha _1-1) M_o +(\alpha _1+1) \alpha _2 N-1)+((4-3 \alpha _1) \alpha _1-1) M_o^2 \\ & \quad +M_o (-12 \alpha _1+N (\alpha _1 (6 \alpha _1-7 \alpha _2-4) +5 \alpha _2-2)+3)+2 N (3 \alpha _1 (\alpha _2 N+4) \\ & \quad +\alpha _2 (1-2 \alpha _2) N-3)+6 \beta S)+18 \beta ((\alpha _1-1) M_o+\alpha _2 N)], \\ {\mathcal {D}}_{33}&=6 K_c^2 [-2 (3 \alpha _1+2) G-2 (9 \alpha _1+2) K_c^2 S -3 (4 \alpha _1 (L+N+1)+((\alpha _1-2) \alpha _1-1) M_o \\ & \quad +(\alpha _1+1) \alpha _2 N)+3], \\ c_{22}&=\frac{{\mathcal {D}}_{41}+{\mathcal {D}}_{42}\omega _c+{\mathcal {D}}_{43}\omega _c^2}{2({\mathcal {D}}_{00}+{\mathcal {D}}_{01}\omega _c+{\mathcal {D}}_{02}\omega _c^2+36i\omega _c^3)}, \end{aligned}$$

(A4)

$$\begin{aligned} {\mathcal {D}}_{41}&=-K_c^4 (-12 (\alpha _2-1) \beta G^2 +G^2 K_c^2 (M_o (4 \alpha _1+\alpha _2-2)-48 (\alpha _2-1))\\ & \quad +5 G K_c^4 S (M_o (4 \alpha _1+\alpha _2-2)-48 (\alpha _2-1))+2 (\alpha _1-1) G K_c^2 M_o^2 (3 \alpha _1\\ & \quad +\alpha _2-2)+2 G K_c^2 M_o (3 \alpha _1 (\alpha _2 (N-16)+12) +\alpha _2 ((\alpha _2-2) N+84)-99)+48 \alpha _2 (1-2 \alpha _2) G K_c^2 N\\ & \quad -60 (\alpha _2-1) \beta G K_c^2 S +12 (1-2 \alpha _2) \beta G ((\alpha _1-1) M_o+\alpha _2 N)+4 K_c^6 S^2 (M_o (4 \alpha _1+\alpha _2-2)-48 (\alpha _2-1))\\ & \quad +8 (\alpha _1-1) K_c^4 M_o^2 S (3 \alpha _1+\alpha _2-2) +8 K_c^4 M_o S (3 \alpha _1 (\alpha _2 (N-16)+12)+\alpha _2 ((\alpha _2-2) N+57)-45)\\ & \quad +192 \alpha _2 (1-2 \alpha _2) K_c^4 N S -48 (\alpha _2-1) \beta K_c^4 S^2+48 K_c^2 ((\alpha _1-1) M_o\\ & \quad +\alpha _2 N) (3 (\alpha _2-1) M_o+(1-2 \alpha _2) \beta S)),\\ {\mathcal {D}}_{42}&=6 i K_c^2 [4 (\alpha _2-1) G^2 K_c^2+3 (\alpha _2+2) \beta G +2 G K_c^2 (2 (5 (\alpha _2-1) K_c^2 S+\alpha _2 (2 \alpha _2 N-N+3)+6)\\ & \quad +M_o (\alpha _1 (4 \alpha _2-5)-6 \alpha _2+6))+16 (\alpha _2-1) K_c^6 S^2 +4 K_c^4 S (M_o (8 \alpha _1 \alpha _2-7 \alpha _1-9 \alpha _2+6)\\ & \quad +\alpha _2 (8 \alpha _2 N-4 N+3)+6)+K_c^2 (-2 (\alpha _1-1) M_o^2 (3 \alpha _1 +4 \alpha _2-5)-2 M_o (\alpha _2 (3 \alpha _1 (N-4)-5 N+12)\\ & \quad +4 \alpha _2^2 N+9)+24 \alpha _2 (\alpha _2+1) N+3 (\alpha _2+2) \beta S) +6 (\alpha _2+1) \beta ((\alpha _1-1) M_o+\alpha _2 N)], \\ {\mathcal {D}}_{43}&=-36K_c^2[2N\alpha _2(\alpha _2+1) +(G+K_c^2S)(\alpha _2+2)+2M_{o}(\alpha _2(\alpha _1-1)-1)]. \end{aligned}$$