1 Introduction

The idea of Maxwell demon has put forth the possibilities of work extraction from a single heat bath through the process of information processing [1, 2]. There is no violation of the second law of thermodynamics here. The new element is Landauer’s principle where heat is dissipated as information is erased from a memory (i.e., memory is reset to a particular state) [3], with the implication of the converse: conversion of heat from the heat bath to work when the memory is randomized. These telltale features of thermodynamics of information processing have been exhibited in feedback-controlled systems [4,5,6], or in systems that interact with an information reservoir [7,8,9,10,11]. The latter takes the form of an autonomous information ratchet which rectifies heat to deliver work independent of any external driving sources. On the other hand, work expenditure is required to erase information in the information reservoir (represented by an infinite tape) with a concomitant dissipation of heat.

Recently, we considered an information ratchet that interacts with a finite-tape while being connected to a work and a heat reservoir [12]. Such a system could correspond to real-world natural systems like DNA transcription [13], or to the artificial nanoscale heat engine [14]. While the finite-tape information ratchet can act functionally as an engine or as an eraser, it eventually equilibrates into a “dud ” due to its limited informational capacity [12]. Nonetheless, useful work can be accrued during the transient phase and we found that by harnessing correlation, a memoryful ratchet accumulates more work. Moreover, correlation is observed to have the effect of driving the ratchet to a nonequilibrium steady state, where work is continuously drawn down from the work reservoir and converted to heat which is dissipated wastefully into the heat reservoir [15].

In our earlier papers [12, 15], we studied the stochastic dynamics of the finite-tape information ratchet through a Markovian transition process, and proved that the ratchet obeys the information processing second law (IPSL) at both the transient and steady-state regime. We also demonstrated that correlation enhances work extraction through two ratchet designs by direct evaluation of the stochastic energetics. However, we have not framed the investigations in these papers from the formal perspective of stochastic thermodynamics which would give clear constraints on allowable transition between equilibrium or nonequilibrium states. By examining the finite-tape information ratchet through stochastic thermodynamics in the present paper, we aim to gain a more comprehensive view on the thermodynamics of information processing of this paradigmatic example. This is to be achieved by determining the entropic production of the information ratchet from the framework, where we first derive the IPSL obeyed by the system and then express the work done on the system explicitly in terms of thermodynamic and informational quantities. We show that the results of [12, 15] follows directly from this framework and are consistent with it, with the latter giving more precise description of the analytical outcome and the underlying physical mechanism involved. The organization of the paper is as follows. In Sect. 2, we first introduce the operation of the finite-tape information ratchet, and then in Sect. 3, describe its evolution in terms of stochastic thermodynamics. In Sect. 4, we determine the entropy production of the ratchet, and from which derive the Information Processing Second Law (IPSL) obeyed by it in both the transient and stationary regime. By examining the adiabatic and non-adiabatic components of entropy production in Sect. 5, we studied into the different entropic production behaviour of the ratchet as it converges towards either the equilibrium or nonequilibrium stationary state. Through the notion of the nonequilibrium free energy, we uncover the generic thermodynamic behaviour and function of the finite-tape information ratchet by connecting entropy production to the work output of the tape-ratchet system in Sect. 6. Finally, Sect. 7 gives a brief discussion before we conclude the paper.

2 Finite-tape information ratchet

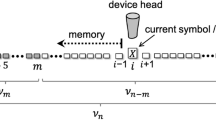
A schematic of the finite-tape information ratchet is illustrated in Fig. 1. It shows a ratchet interacting with a work reservoir and a heat reservoir, in addition to a tape with a string of bits that circulates back to itself. Our convention is that heat Q and work W are positive when they flow to their reservoir, respectively. Qualitatively, the tape operates cyclically as follows.

Fig. 1
figure 1

Schematic of the finite-tape information ratchet

Full size image

Initially, the ratchet and the tape have no interaction with each other. At this stage, we assume that the ratchet and the tape do not retain any energy individually. The first process of the cycle is the attachment of the ratchet to a bit of the tape. During this process, the ratchet is connected to the work reservoir. Work is then extracted by the ratchet to be converted to the internal energy of the tape-ratchet system. Let this amount of work performed by the work reservoir during the attachment process be \(-W_a\). The next stage of the cycle is the thermal transition process. During this process, the tape-ratchet system interacts with the heat bath or heat reservoir, changing the combined bit-ratchet state. This process is mediated by the transfer of an amount of heat \(-Q\) from the heat reservoir to the tape-ratchet system, corresponding to the change of internal energy of the tape-ratchet system. At the end of this process, the total internal energy of the tape-ratchet system is \(-W_a-Q\). After thermal transition, the next process of the cycle is the detachment of the ratchet from the earlier attached bit. In this process, the ratchet is connected to the work reservoir once more. Because the ratchet and the tape do not retain any energy individually when not attached to each other, all of the internal energy \(-W_a-Q\) is transferred to the work reservoir. Therefore, the work performed by the work reservoir during the detachment process is \(-W_d=W_a+Q\). The final step of the cycle is the shifting of the tape by one bit so that the ratchet will interact with the next bit of the tape in the next cycle. We refer to this process as switching. During switching, there is no interaction whatsoever between the ratchet, tape, heat reservoir, and work reservoir. Therefore, there is no exchange or flow of energy during the switching process. The total amount of work performed by the work reservoir in one cycle is, therefore, \(-W=-W_a-W_d=-W_a+W_a+Q=Q\). In other words, the work reservoir loses an amount of mechanical energy equivalent to the amount of heat gained by the heat reservoir. Note that the converse is also true, i.e., \(W=-Q\). In this case, the amount of mechanical energy gained by the work reservoir is equal to the amount of heat lost by the heat reservoir. Thus, the work production is equivalent to the heat \(-Q\) extracted from the heat reservoir.

3 Stochastic Thermodynamics

Let us now characterize the discrete-time stochastic evolution of the finite-tape information ratchet. First, we specify the joint tape-ratchet states of the ratchet by the probability distribution \({{\textbf {p}}}\). For an information ratchet with \(N_R\) ratchet states and a tape of L bits, \({{\textbf {p}}}\) is a \(2^{L} N_R \times 1\) vector. Second, the cyclical operation of the ratchet interacting with a bit is captured by the matrix \(O^{(L)}\). This operation involves both a thermal transition sub-step and a switching sub-step. In the thermal transition sub-step, a transition matrix \(M^{(L)}\) of a discrete-time Markov chain accounts for the stochastic transition of the bit-ratchet state due to thermal transition. On the other hand, during the switching sub-step, a switching matrix \({\mathcal {S}}^{(L)}\) moves the tape one-step to the left, with the output bit shifts from the leftmost end to the rightmost end of the tape. Thus, the operation \(O^{(L)}\) is a composite two-step process:

$$\begin{aligned} O^{(L)}={\mathcal {S}}^{(L)}M^{(L)} , \end{aligned}$$
(1)

where the matrices \(O^{(L)}\), \(M^{(L)}\) and \({\mathcal {S}}^{(L)}\) all have the same dimension of \(2^{L} N_R \times 2^{L} N_R\). The stochastic evolution is thus given by

$$\begin{aligned} {\mathbf {p'}}=O^{(L)}{\textbf{p}}, \end{aligned}$$
(2)

where

$$\begin{aligned} \mathbf {\tilde{p}}= & {} M^{(L)}{\textbf{p}}, \end{aligned}$$
(3)
$$\begin{aligned} \mathbf {p'}= & {} {\mathcal {S}}^{(L)}\mathbf {\tilde{p}} . \end{aligned}$$
(4)

Note that the \(M^{(L)}\) matrix is constructed from the \(M^{(1)}\) matrix, which is a left stochastic matrix of the 1-bit tape. Furthermore, we assume that \(M^{(1)}\) is a tridiagonal matrix. See Ref. [12, 15] for the construction of \(M^{(L)}\) and \({\mathcal {S}}^{(L)}\).

As our finite-tape ratchet system is autonomous without external energy perturbation, there is no overall change to the energy level of the system due to work considering both the thermal and switching sub-steps together. The ratchet essentially mediates energy transfer between the heat reservoir and the work reservoir as described in the last section. The energy that is effectively being transferred is heat when the tape-ratchet system interacts with the heat reservoir during the thermal transition sub-step. This heat energy is converted to (or from) the gravitational potential energy which is capable of doing work in the work reservoir.

We assume that the mediation of energy transfer by the tape-ratchet system is performed through its energy levels. In the design of the tape-ratchet system, there is interaction energy resulting from the coupling between the ratchet and a bit from the tape. The magnitude of this interaction energy depends on the combined bit-ratchet state. Therefore, different bit-ratchet states can be designed to have different levels of energy. The interaction energy can also be thought of as the internal energy of the tape-ratchet system.

In our set-up, we have fixed the energy levels \(\Delta E_{ji} \equiv E_j-E_i\) of our tape-ratchet system, where \(E_i\) corresponds to the energy of the interacting bit-ratchet state i of the tape-ratchet system. Then, the transition from state i to state j corresponds to an exchange of heat with the heat reservoir. Hence, we expect the fulfillment of the condition of detailed balance:

$$\begin{aligned} M_{ji}^{(1)}{ p_i^{\text {eq}}} = M_{ij}^{(1)}{ p_j^{\text {eq}}}, \end{aligned}$$
(5)

by the stochastic transition from state i to state j quantified by the transition probability \(M_{ji}^{(1)}\), which is the (j, i)-entry of the left stochastic thermal transition matrix \(M^{(1)}\) for a 1-bit tape. Note that the probabilities

$$\begin{aligned} { p_i^{\text {eq}}} = \frac{e^{-\beta E_i}}{\sum _k e^{-\beta E_k}} = \exp \left[ \beta (F-E_i)\right] , \end{aligned}$$
(6)

are given by the canonical ensemble in equilibrium statistical mechanics with \(\beta \equiv 1/k_B T_r\) being the inverse temperature, \(T_r\) the temperature of the heat bath, and F its Helmholtz free energy. These equations then lead to

$$\begin{aligned} \frac{M_{ij}}{M_{ji}}=\frac{{ p_i^{\text {eq}}}}{{ p_j^{\text {eq}}}}=\exp \left[ \beta (E_j-E_i)\right] , \end{aligned}$$
(7)

where we have withheld the superscript (1) to simplify notation. In fact, Eq. (7) continues to hold for the matrix \(M^{(L)}\) since detailed balance holds within the interacting bit-ratchet and not with the non-interacting bits. Note that subsequent \(M_{ij}\) is assumed to contain the superscript (L) unless otherwise specified. This equation implies

$$\begin{aligned} \Delta E_{ji} \equiv E_j - E_i = k_B T_r \, \ln \left( \frac{M_{ij}}{M_{ji}}\right) . \end{aligned}$$
(8)

Specifically, the interaction with the work reservoir to accumulate (or expend) the mechanical energy from the work conversion (with \(-Q=W\) earlier) occurs during the attachment of input bit to and detachment of output bit from the ratchet.

Thus, the expected work production W in a single bit-ratchet interaction at any arbitrary time can be expressed as

$$\begin{aligned} W = \Delta E = k_B T_r \,\sum _{i,\,j} M_{ji}p_i \ln \left( \frac{M_{ij}}{M_{ji}}\right) , \end{aligned}$$
(9)

which is the sum of the respective work \(W_{ji} \equiv k_B T_r\,\ln (M_{ij}/M_{ji})\) (originating from thermal transition \(i\rightarrow j\)) weighted by the corresponding probability \(M_{ji}p_i\) for such a transition to occur. By setting \(k_B T_r=1\) to simplify the W expression, we have

$$\begin{aligned} W = \sum _{i,\,j} M_{ji}p_i \ln \left( \frac{M_{ij}}{M_{ji}}\right) . \end{aligned}$$
(10)

We emphasise that the probabilities \(p_i\) here are the instantaneous probability distribution which is continuously evolving as the information ratchet operates. It is not the canonical distribution \(p_i^{\text {eq}}\) above which is used to define the energy level of the tape ratchet system.

Next, the change in entropy of the tape-ratchet system is evaluated by the Shannon entropy:

$$\begin{aligned} \Delta H = H\left( \mathbf {p'}\right) - H\left( {\textbf{p}}\right) = \sum _i p_i \ln p_i - \sum _j p'_j \ln p'_j . \end{aligned}$$
(11)

Because \({\mathcal {S}}^{(L)}\) is a permutation matrix, its operation according to Eq. (4) is basically a reordering of probabilities in \(\mathbf {\tilde{p}}\) without changing its values. Thus, \(\mathbf {\tilde{p}}\) and \(\mathbf {p'}\) have the same elements, and \(H\left( \mathbf {\tilde{p}}\right) =H\left( \mathbf {p'}\right)\). Hence, we have

$$\begin{aligned} \Delta H = \sum _i p_i \ln p_i - \sum _j \tilde{p}_j \ln \tilde{p}_j . \end{aligned}$$
(12)

Now, by inserting \(\sum _j M_{ji}=1\) into the first-term on the right of Eq. (12) and applying Eq. (3) to the second-term on the right, we obtain

$$\begin{aligned} \Delta H= & {} \sum _i\left( \sum _j M_{ji}\right) p_i \ln p_i - \sum _j \left( \sum _i M_{ji} p_i\right) \ln \tilde{p}_j ,\nonumber \\= & {} \sum _{i,j} M_{ji} p_i \ln \left( \frac{p_i}{\tilde{p}_j}\right) . \end{aligned}$$
(13)

Note that the symbol \(\Delta\) represents the change of its associated variable within a thermal transition sub-step. The variable is not to be taken as additive within the full time-step.

Let us illustrate the operation of the finite-tape information ratchet through an explicit example. For this, we consider a two-state ratchet, i.e., \(N_R=2\), with the following tridiagonal thermal transition matrix M for \(L=1\):

$$\begin{aligned} \begin{aligned} M_{\text {1-bit}}^{\text {T2S}} = \bordermatrix {&0\otimes A&0\otimes B&1\otimes A&1\otimes B \\ 0\otimes A&\epsilon&1-p&0&0 \\ 0\otimes B&1-\epsilon&0&q&0 \\ 1\otimes A&0&p&0&1-\epsilon \\ 1\otimes B&0&0&1-q&\epsilon }, \end{aligned} \end{aligned}$$
(14)

where the interacting bit-ratchet state \(\textrm{B}\otimes \textrm{R}\) is indicated with \(\textrm{B}=\{0,1\}\) and \(\textrm{R}=\{A,B\}\). Figure 2 illustrates the Markov transitions between these interacting bit-ratchet states in the form of a state transition diagram with transition probabilities parametrized by \((p,q,\epsilon )\). This ratchet design is termed the T2S tape-ratchet system, which has also been exemplified in [12, 15].

Because we assume that \(O^{(L)}\) is a regular matrix, the stochastic dynamics will converge to a stationary distribution, i.e., \(\varvec{\pi }=O^{(L)}\varvec{\pi }\), in the long time limit by the Perron-Frobenius theorem. In consequence, \(\Delta H = 0\) in the steady state. Moreover, the stationary state is observed to take either of the following two forms through Eqs. (2), (3) and (4):

$$\begin{aligned} \varvec{\pi }=M^{(L)}\varvec{\pi },\;\;\;\varvec{\pi }=S^{(L)}\varvec{\pi } \end{aligned}$$
(15)

or

$$\begin{aligned} \varvec{\tilde{\pi }}=M^{(L)}\varvec{\pi },\;\;\;\varvec{\pi }=S^{(L)}\varvec{\tilde{\pi }}. \end{aligned}$$
(16)

Eq. (15) implies that \(\varvec{\pi }=\mathbf {p^{\text {eq}}}\). Therefore, the T2S tape-ratchet system is at equilibrium in the steady state if it takes the first form (Eq. 15), since the thermal transition sub-step has converged to the canonical distribution. On the other hand, if the tape-ratchet system were to take the second form (Eq. 16), it would have reached a nonequilibrium stationary state whose out-of-equilibrium dynamics results from the switching operation.

Fig. 2
figure 2

Transition state diagram of the interacting bit-ratchet state \(\textrm{B}\otimes \textrm{R}\) of the T2S tape-ratchet system with the corresponding transition probabilities

Full size image

4 Information processing second law

By considering the information ratchet with its finite-tape, heat reservoir, and work reservoir as an isolated system, its total entropy production is given as follows:

$$\begin{aligned} \Delta S_{\text {tot}} = k_B\Delta H + \frac{Q}{T_r} \ge 0 . \end{aligned}$$
(17)

Note that the first term describes the entropy change due to the tape-ratchet system, while the second term indicates the entropy change of the heat reservoir (with temperature \(T_r\)) due to an amount of heat Q flows into it. There is no entropy change for the work reservoir.

Because \(Q=-W\), and by making the system of equation dimensionless (i.e. leaving out \(k_B T_r\)), we have:

$$\begin{aligned} \Delta H - W \ge 0, \end{aligned}$$
(18)

which is the information processing second law for the finite-tape information ratchet [12].

Alternatively, we can also consider the tape-ratchet sub-system of the finite-tape information ratchet as a non-isolated system. In this context, the entropy change \(\Delta S\) of the tape-ratchet system can be expressed as a sum of two components:

$$\begin{aligned} \Delta S = \Delta _e S + \Delta _i S . \end{aligned}$$
(19)

The first component \(\Delta _e S\) is the entropy flow into the tape-ratchet system, while the second component \(\Delta _i S\) is the entropy production of the tape-ratchet system.

With \(\Delta S = \Delta H\), \(\Delta _e S =-Q\) (where we have again left out \(k_B\) and \(T_r\) to the respective entropies), and using \(W=-Q\), we obtain the entropy production \(\Delta _i S\) from Eq. (19) as follows:

$$\begin{aligned} \Delta _i S = \Delta H - W . \end{aligned}$$
(20)

Because

$$\begin{aligned} \Delta _i S \ge 0 , \end{aligned}$$
(21)

we again obtain the information processing second law given by Eq. (18). Moreover, by inserting Eqs. (10) and (13) into Eq. (20), we observe that the entropy production \(\Delta _i S\) of the tape-ratchet system takes the form:

$$\begin{aligned} \Delta _i S = \sum _{i,j} M_{ji}p_i \ln \left( \frac{M_{ji} p_i}{M_{ij} \tilde{p}_j}\right) . \end{aligned}$$
(22)

5 Adiabatic and non-adiabatic entropy production

We can break the entropy production given by Eq. (22) into a discrete-time version of adiabatic entropy production \(\Delta _a S\) and non-adiabatic entropy production \(\Delta _{\text {na}} S\) [16,17,18,19] as follows:

$$\begin{aligned} \Delta _i S = \Delta _a S + \Delta _{\text {na}} S , \end{aligned}$$
(23)

where

$$\begin{aligned} \Delta _a S = \sum _{i,j} M_{ji} p_i \ln \left( \frac{M_{ji} p_i^{\text {st}}}{M_{ij} p_j^{\text {st}}}\right) , \end{aligned}$$
(24)

and

$$\begin{aligned} \Delta _{\text {na}} S = \sum _{i,j} M_{ji} p_i \ln \left( \frac{p_j^{\text {st}} p_i}{\tilde{p}_j p_i^{\text {st}}}\right) . \end{aligned}$$
(25)

Our purpose of decomposing entropy production into these two basic components is to observe the manner in which the finite-tape information ratchet system is being brought out of equilibrium. Specifically, non-adiabatic entropy production results from the system being driven out of equilibrium while adiabatic entropy production arises from the action of steady nonequilibrium constraints.

It is straightforward to show that \(\Delta _a S \ge 0\) and \(\Delta _{\text {na}} S \ge 0\) (see Appendix A.1 for a proof), which conforms with Eq. (21). With \(p_i^{\text {st}}\) being the stationary distribution of the thermal transition sub-step M which is a tridiagonal matrix in our design as indicated in Sect. 3, we have

$$\begin{aligned} p_i^{\text {st}}=p_i^{\text {eq}} , \end{aligned}$$
(26)

where \(p_i^{\text {eq}}\) is the thermal equilibrium distribution. In consequence, \(\Delta _a S = 0\), because \(M_{ji} p_i^{\text {eq}}=M_{ij} p_j^{\text {eq}}\) due to detailed balance, which shows that the information ratchet is not subjected to any nonequilibrium constraint in the steady state. This implies that

$$\begin{aligned} \Delta _i S = \Delta _{\text {na}} S , \end{aligned}$$
(27)

with the out-of-equilibrium dynamics of the system being driven by the initial state and the switching operation.

It is possible to split \(\Delta _{\text {na}} S\) into the following entropic terms:

$$\begin{aligned} \Delta _{\text {na}} S = \Delta S_{\text {ex}} + \Delta H , \end{aligned}$$
(28)

where \(\Delta S_{\text {ex}}\) is the excess entropy change and it is equal to

$$\begin{aligned} \Delta S_{\text {ex}} = \sum _{i,j} M_{ji} p_i \ln \left( \frac{p_j^{\text {st}}}{p_i^{\text {st}}}\right) . \end{aligned}$$
(29)

Furthermore, \(\Delta S_{\text {ex}}=Q_{\text {ex}}/T_r\), where \(Q_{\text {ex}}\) is the excess heat [18, 20, 21]. It is easy to see that Eq. (25) is obtained by combining Eqs. (13) and (29). Note that \(\Delta _{\text {na}} S \ge 0\) implies \(\Delta S_{\text {ex}} + \Delta H \ge 0\) which is the second law of steady-state thermodynamics of Hatano and Sasa [22]. At the steady state, \(\Delta H = 0\) for the finite-tape information ratchet, leading to

$$\begin{aligned} \Delta _{\text {na}} S = \Delta S_{\text {ex}} , \end{aligned}$$
(30)

which is illustrated in the insets of Figs. 3 and 4.

Fig. 3
figure 3

Non-adiabatic entropy production of the memoryful T2S tape-ratchet system [12, 15] with stochastic dynamics that converges to the equilibrium stationary state. The transition probabilities of the ratchet are fixed at \((p,q,\epsilon )=(0.2,0.3,0.25)\). Entropy production is observed to be larger for longer tape length as it converges to zero in the steady state. The inset shows the entropic evolution of the system for \(L=3\). The ratchet is observed to operate as an engine here with \(\Delta H > 0\) and positive work (\(W=-\Delta S_{\text {ex}}>0\)) accrued. Note that \(\Delta _{\text {na}} S = \Delta S_{\text {ex}} + \Delta H\) at each time point

Full size image
Fig. 4
figure 4

Non-adiabatic entropy production of the memoryful T2S tape-ratchet system [12, 15] with transition probabilities fixed at \((p,q,\epsilon )=(0.2,0.3,0.9)\). The stochastic dynamics of the ratchet converges to an equilibrium stationary state for \(L=1\) and to a non-equilibrium stationary state for \(L \ne 1\). Entropy production is observed to maintain at a positive value both in the transient and steady state regime for the nonequilibrium stationary states. The inset shows the entropic evolution of the system for \(L=2\). The ratchet is observed to act as an eraser here with \(\Delta H < 0\) and an expenditure of work (i.e., \(W=-\Delta S_{\text {ex}}<0\)). Note that \(\Delta _{\text {na}} S = \Delta S_{\text {ex}} + \Delta H\) at each time point

Full size image

There are two stochastic behaviour for the finite-tape information ratchet. It either converges to an equilibrium stationary state (see Fig. 3) or a nonequilibrium stationary state (see Fig. 4 for \(L\ne 1\)). In the former case, we have \(\Delta _{\text {na}} S = \Delta S_{\text {ex}} = 0\) in the steady state where the excess heat \(Q_{\text {ex}}\) is zero. But before reaching the steady state, \(\Delta _{\text {na}} S > 0\) in the transient phase as the information ratchet relaxes to the steady state from a nonequilibrium initial state [18]. For the latter case where the ratchet approaches the non-equilibrium stationary state (except for \(L=1\)), we again observe transient relaxation to the steady state with \(\Delta _{\text {na}} S > 0\). However, unlike the former case, \(\Delta _{\text {na}} S\) continues to be positive at the steady state. This results from the switching operation which drives the system out of equilibrium leading to an irreversible flow of excess heat \(Q_{\text {ex}}\) to the heat bath. The origin of this excess heat energy is the \(-W\) from the work reservoir to be discussed in the next section.

6 Work under nonequilibrium conditions

Let us now take the perspective where the second law is applied when the system is under the condition of nonequilibrium. This is expressed by relating the entropy production \(\Delta _i S\) to the change in the nonequilibrium free energy of the information ratchet system \(\Delta F\) which is defined as follows [23,24,25]:

$$\begin{aligned} \Delta F = \Delta E - T_r \Delta S . \end{aligned}$$
(31)

Using Eq. (19), we have

$$\begin{aligned} \Delta F= & {} \Delta E - T_r \Delta _e S - T_r \Delta _i S \nonumber \\= & {} \Delta E +Q - T_r \Delta _i S \nonumber \\= & {} - T_r \Delta _i S , \end{aligned}$$
(32)

where we have employed Eq. (9) to obtain \(\Delta E + Q = W + Q\), and noting that \(Q=-W\), \(\Delta E + Q\) vanishes. This leads to:

$$\begin{aligned} \Delta _i S = - \Delta F, \end{aligned}$$
(33)

where we have suppressed \(T_r\). Noting that \(\Delta _i S \ge 0\), we have

$$\begin{aligned} \Delta F \le 0 . \end{aligned}$$
(34)

Using the fact that the nonequilibrium free energy differs from the equilibrium free energy by a change in an informational term I [26], we can express \(\Delta F\) in the following manner:

$$\begin{aligned} \Delta F - \Delta F^{\text {eq}} = T_r\Delta I, \end{aligned}$$
(35)

with

$$\begin{aligned} I = k_B\sum _i p_i \ln \left( \frac{p_i}{p^{\text {eq}}_i}\right) . \end{aligned}$$
(36)

I is also known as the relative entropy between the distribution \(p_i\) and the distribution \(p^{\text {eq}}_i\). Because \(\Delta F^{\text {eq}}=0\) due to the finite-tape information ratchet being autonomous and interact with a single heat reservoir, we have

$$\begin{aligned} \Delta F = \Delta I , \end{aligned}$$
(37)

where we again suppress the temperature \(T_r\). Thus,

$$\begin{aligned} \Delta _i S = -\Delta I , \end{aligned}$$
(38)

or

$$\begin{aligned} \Delta I \le 0 . \end{aligned}$$
(39)

Note that

$$\begin{aligned} \Delta I = \sum _i \tilde{p}_i \ln \left( \frac{\tilde{p}_i}{p^{\text {eq}}_i}\right) - \sum _j p_j \ln \left( \frac{p_j}{p^{\text {eq}}_j}\right) , \end{aligned}$$
(40)

where \(k_B\) has been suppressed.

Moreover, according to Eqs. (27) and (28), together with Eq. (38), we have

$$\begin{aligned} \Delta I = - \Delta S_{\text {ex}} - \Delta H . \end{aligned}$$
(41)

For the equilibrium stationary state of the finite-tape information ratchet [15] where it obeys

$$\begin{aligned} \mathbf {p^{\text {eq}}} = M \mathbf {p^{\text {eq}}} , \end{aligned}$$
(42)

with \(\mathbf {p^{\text {eq}}}\) being its equilibrium probability, Eq. (39) implies that the ratchet tends towards the canonical distribution since \(I \ge 0\). On the other hand, in the case of nonequilibrium stationary state [15] where

$$\begin{aligned} \mathbf {\tilde{p}^{\text {neq}}} = M \mathbf {p^{\text {neq}}} , \end{aligned}$$
(43)

with \(\mathbf {p^{\text {neq}}}={\mathcal {S}}\mathbf {\tilde{p}^{\text {neq}}}\) and \(\mathbf {\tilde{p}^{\text {neq}}}\ne \mathbf {p^{\text {neq}}}\), the ratchet maintains in the nonequilibrium steady state with \(\Delta I < 0\). Overall, the result in Eq. (34) indicates that the tape-ratchet system tends to lower its free energy. And because of Eq. (37), we see that this reduction behaviour results from its being away from equilibrium and the tendency of the ratchet relaxing towards equilibrium at a time scale that depends on the design of the ratchet system [12]. Thus, nonequilibrium initial condition of the ratchet is essential for the ratchet to act as an engine due to its autonomous nature.

Finally, equating Eqs. (20) with (33), (38), as well as Eqs. (27) and (28), we obtain

$$\begin{aligned} W = \Delta H + \Delta F = \Delta H + \Delta I = -\Delta S_{\text {ex}} . \end{aligned}$$
(44)

Note that an alternative proof of part of this equation is given in Appendix A.2. At the steady state, the finite-tape information ratchet converges to a stationary probability distribution as discussed at the end of Sect. 3, with the consequence of \(\Delta H = 0\). In this case, we have

$$\begin{aligned} W = \Delta I . \end{aligned}$$
(45)

If the stationary distribution is the equilibrium probability distribution, Eq. (45) indicates that \(W=0\). On the other hand, if the ratchet converges to a nonequilibrium stationary state, Eq. (39) shows that \(W < 0\). The latter indicates that a flux of energy flows from the work reservoir to the heat reservoir, which is a representative feature of a system out-of-equilibrium. Note that these results conform to those of [15], and we have proven them here using a different method.

Under normal operating condition, we expect the finite-tape information ratchet to assimilate heat from a single heat bath which is converted to work, i.e. (positive) work production, when \(\Delta H> -\Delta I > 0\) according to Eqs. (44) and (39). Thus, in order to extract work, the information ratchet needs to write information into the tape with an entropy increase \(\Delta H\) that exceeds the associated decrease in relative entropy \(\Delta I\). This is the engine regime of the finite-tape information ratchet. Conversely, to erase information from the tape such that \(\Delta H < 0\), Eqs. (39) and (44) imply that \(W <0\). Thus, work needs to be drawn from the work reservoir for the information ratchet to acts as an eraser, with heat generated in the erasure process being dissipated to the heat reservoir. This is where the finite-tape information ratchet makes contact with the Landauer principle. Finally, when \(-\Delta I> \Delta H > 0\), we observe that \(W < 0\). In this case, work is expended even though the entropy of the tape-ratchet system increases. This is the regime of ‘dud’.

Interestingly, we observe from Eq. (44) that the work is negative of the excess entropy, or more precisely, the negative of the excess heat \(Q_{\text {ex}}\). In the case when the finite-tape information ratchet operates as an engine and converges to the equilibrium stationary state, \(-Q_{\text {ex}}\) flows from the heat reservoir to the work reservoir (see inset of Fig. 3) before it approaches zero in the steady state. The extracted work is thus obtained through the accumulation of \(-Q_{\text {ex}}\). Conversely, if the finite-tape information ratchet were to act as an eraser while approaching a nonequilibrium stationary state, we notice that \(-W=Q_{\text {ex}}\) flows from the work reservoir to the heat reservoir in both the transient and steady-state regime (see inset of Fig. 4). Thus, heat dissipation here is that of the excess heat \(Q_{\text {ex}}\).

7 Discussion and conclusion

By determining the entropy production of the finite-tape information ratchet, we uncovered Eq. (44) and from which obtain the expected result that the inaccessible part of work is given by the entropy production \(\Delta _i S\). To reach optimal work \(W= \Delta H\), we require \(\Delta _i S = 0\) but this would imply the system is in the equilibrium state since \(\Delta _i S = - \Delta I\). At the equilibrium state, \(W = \Delta H = 0\) and the system acts as a dud.

For our finite-tape information ratchet system, it is more precise to express the change of entropy as follows: \(\Delta H = \Delta H_{\text {BR}} + \Delta C\), where \(\Delta H_{\text {BR}}\) is the entropy change of the interacting bit-ratchet state, and \(\Delta C\) is the change in correlation between the interacting bit-ratchet state and the rest of the non-interacting bits. This formulation leads to

$$\begin{aligned} W = \Delta H_{\text {BR}} + \Delta C +\Delta I , \end{aligned}$$
(46)

through Eq. (44). Next, let us apply two of our results in [15]: (i) \(W \le \Delta H_{\text {BR}}\) and (ii) \(\Delta C \ge 0\). The result in (i) leads to

$$\begin{aligned} \Delta C \le -\Delta I \end{aligned}$$
(47)

through Eq. (46). Considering the steady state with \(\Delta C > 0\), Eq. (47) indicates that \(-\Delta I > 0\), which signifies the presence of a nonequilibrium stationary state. On the other hand, if the finite-tape information ratchet were to converge to an equilibrium stationary state, we will have \(-\Delta I = 0\), and this implies through Eq. (47) and (ii) that \(\Delta C=0\). Interestingly, we have proven the same two key outcome of [15] here using a different approach. Moreover, \(\Delta C\) is known to have the connotation of modularity dissipation [27, 28]. Modularity dissipation arises from the loss of global correlations during modular operation. Because our information ratchet operates modularly with interaction occurs mainly between bit B and ratchet R, it suffers from modularity dissipation. This is exhibited by the additional positive contribution of \(\Delta C\) in the entropy production of the information ratchet system: \(\Delta _i S = \Delta H_{\text {BR}} - W + \Delta C\).

In conclusion, the stochastic thermodynamic formalism provides key insights into the physical consequences of nonequilibrium conditions on the thermodynamic functioning of the information ratchet system, which is as yet unaccounted for in our earlier works [12, 15]. First, the formalism shows that an additional amount of \(\Delta I\) (see Eq. 44) has to be included in the work done on the information ratchet system as a result of nonequilibrium effects. Second, it demonstrates that the entropy production in our information ratchet system is given solely by the non-adiabatic component, with the out-of-equilibrium dynamics of the system driven by the switching operation and the nonequilibrium initial state. Moreover, the fact that the entropy production of the information ratchet is non-adiabatic implies that the flow of heat into (or out) of the information ratchet when it functions as an engine (or eraser) is the excess heat \(-Q_{\text {ex}}\) (\(Q_{\text {ex}}\)) of nonequilibrium thermodynamics [20]. In particular, when the information ratchet operates at the nonequilibrium stationary state, the formalism reveals that the process of conversion of work into excess heat is irreversible [29]. These outcome from stochastic thermodynamics clearly illustrate the out-of-equilibrium operations of the information ratchet system, and we expect even more interesting results if we were to expand our treatment to ratchet design where the adiabatic entropy production is positive with nonzero housekeeping heat [30]. We believe further investigation along this line with Markovian dynamics that violate detailed balance will yield new organizing principles and thermodynamic behaviour from the finite-tape information ratchet system, which we will pursue as future work.