Coherence resonance modulated by hybrid synapses and time delay in modular small-world neuronal networks with E–I balanced state

Abstract

Neurons communicate primarily through synapses. A neuron is usually affected by multiple synapses, which could be chemical/electrical or excitatory/inhibitory ones at the same time. Here, we make the realistic assumption that a excitatory and inhibitory balanced modular small-world network is established and focuses on the effects of hybrid chemical and electrical synapses, noise and time delay on coherence resonance of the constructed network. It is found that when the ratio f of chemical synapses to electrical synapses approaches odd ratios, coherence resonance is better than those f close to even ratios for appropriate noise intensities. Furthermore, with f increasing, it is observed that effects of chemical and electrical synapses on coherence resonance are nearly opposite. It indicates that electrical synapses are more efficient than chemical ones. Meanwhile, multiple coherence resonances are observed when time delay is introduced into the network, and it is independent of f. Finally, we demonstrate that coherence resonance decreases as the number of subnetworks increases, and when the number of subnetworks is larger, the resonance behaviour weakens or vanishes with increasing f.

1 Introduction

Noise possesses great significance in the investigation of brain and nonlinear dynamical systems. Especially in systems of neurons, the transmission of information by neurons in a noisy environment induces a variety of collective dynamic behaviours [1, 2], the most prominent of which are stochastic resonance (SR) and coherence resonance (CR). The former is the scenario where the ratio of the output signal to the noise in a nonlinear system is optimal when driven by both noise and a weak external signal [3, 4]. The latter refers to the system’s response to pure noise without external signal [5, 6], also known as autonomous SR. In the past decades, SR and CR in biological and neuronal systems have been an interesting topic and have been extensively investigated [7, 8]. Intriguingly, coherence resonance could indeed enhance neural communication or enhance weak signal detection by processing information and encoding between brain regions [9,10,11]. Therefore, investigation of coherence resonance is critical to a deeper understanding of the brain and neural networks. The research on CR was initially conducted in an excitable system with Fitz Hugh–Nagumo neuron [5]. Further development has broadened the scope to a variety of complex systems and networks consisting of different neuron models with realistic elements. It has been observed as spatial coherence resonance in excitable medium with additive noise [12], the double coherence resonance with FitzHugh–Nagumo neuron [13], and multiple firing coherence resonance with HodgkinCHuxley neurons [14]. On the other hand, it was revealed that phase noise, bounded noise, and white noise all have significant effects on coherence resonance [15,16,17]. Further topologies have shown that coherence resonance exists in small-world networks, lattice networks and one or two layers of networks [18,19,20].

Neurophysiological studies have reported that networks of cortical neurons in cats and macaque monkeys exhibit properties of modularity [21, 22]. A modular network consists of a number of clusters, where most modules are made up of nearby neurons and the connections within each cluster are densely than among clusters [23]. It is recognized as a fundamental organization of neural activity in the brain. Recently, some investigations have provided novel insights that community structure could facilitate the availability of information transmission and predict brain age [24,25,26]. Furthermore, the existence of small-world structures in neuron assemblies was confirmed by the modular characteristic [27]. However, there has been less research on modular neural networks with small-world topology in the past, and their dynamic behavior is primarily focused on synchronization or stochastic resonance or stochastic multi-resonance. [28,29,30,31]. Therefore, it makes great sense to explore the phenomenon of coherence resonance in modular neural networks with small-world topology.

Especially, in the brain, neuronal communication occurs primarily through two different types of synapses: chemical and electrical, each of which can be further subdivided into two types of coupling: excitatory and inhibitory coupling [32, 33]. Early studies focused on coupling of electrical or chemical excitable synapses [34, 35]. Subsequent evidences proved that electrical synapses and chemical synapses could coexist in the nervous system [36,37,38]. In this vein, the influences of hybrid electrical and chemical synapses on neuronal dynamics were the subject of widespread interest. For example, Kopel et al. found that chemical and electrical synapses play a supplementary role in adjusting synchronization [39]; Yu et al. reported that hybrid electrical and chemical synapses promoted the transmission of information in neuronal activities [40]. However, these studies of hybrid electrical and chemical synapses only considered the excitatory synaptic input. More interesting evidence has recently confirmed that the normal function of cortical neuronal networks requires a homeostatic control that relies on a functional balance of excitatory–inhibitory synaptic inputs in a ratio of approximately 4 : 1 [41,42,43]. Here, we refer to it as the E–I balanced state for simplicity. Yet, corresponding to this, studies of hybrid excitatory–inhibitory synapses have focused solely on chemical coupling [14, 44] or electrical coupling [19, 45], without taking into account the E–I balanced state or the coexistence of electrical and chemical synapses. Given these issues, questions are automatically brought out what are the effects of the hybrid electrical and chemical synapses on coherence resonance in the E–I balanced state and how they affect the behaviors of modular small-world neuronal networks.

In addition, time delay is designed to account for as an significant factor in our work. For biological neuron, the limited speed of propagation and the transmission of information from dendrites and synapses can inevitably produce time delays [46, 47]. In the nervous system, the investigation of time delays is of great value and has attracted a great deal of attention in the last few years. A large body of researches have revealed that time delay has a significant impact on dynamic behaviour. For example, it was demonstrated that spatiotemporal order of coupled neural networks could be enhanced or destroyed by time delay [48, 49], as well as synchronization transitions could be induced by time delay in neural networks [50,51,52]. Most importantly, time delay could induce a series of resonance behaviors, including coherence resonance [53, 54], stochastic resonance [7, 55] and stochastic multi-resonance [56, 57]. Particularly, in previous studies, we proposed the new concept of partial time delay and shown that multiple synchronization transitions and stochastic multi-resonance could be induced with changes of the probability of partial time delay [58, 59].

Inspired by these facts, to expand the scope of coherence resonance over complex neural networks and to incorporate realistic neurophysiological features into models of neural networks, we developed a modular small-world network in E–I balanced state, in which all neurons are subjected to hybrid electrical and chemical synaptic inputs simultaneously and in noisy and time delayed environments. This paper is structured as follows. In Sect. 2, we mainly present the mathematical model and measurement method of characterizing the coherence resonance behavior. The results of the neural network are exhibited in detail in Sect. 3. Finally, there is a brief discussion in Sect. 4 and some conclusions in Sect. 5.

2 Mathematical model and measure

2.1 The topology of neuronal network

In these contexts, then how do we evolve a modular network with hybrid electrical and chemical synapses in E–I balanced state? Since subnetworks of modular network can be regular networks, small-world networks or scale-free networks, we implement the small-world topology on both inter and intra-subnetwork. Firstly, for the intra-subnetwork topology, starting with a ring network with N nodes, each node is connected to its $K=6$ nearest neighbors. In accordance with the procedure suggested by Watts and Strogatz [60], each connection is reconnected to another node at random with probability p and without self-loop. Since $p>0.3$ rewired networks have random network characteristics [60], we set rewiring probability $p=0.1$ in each subnetwork. Then for the inter-subnetwork topology, we hypothesise that the number of subnetworks is M and that the subnetworks are also arranged in a ring, in which the neurons in each subnetwork are randomly connected to several pairs of neurons in their two closest subnetworks. Suppose that different subnetworks are connected low probability $p_{inter}$, i.e., there are $p_{inter}N^2$ links among different subnetworks. Here, the number of nodes of each subnetwork N is related to the number of subnetworks M and the size of modular network. Thus, if the size of the modular network is fixed, changes in $p_{inter}$ and M could result in changes in the number of interconnects between the different subnetworks. The size of the modular networks used in this paper was set to $MN=200$ and $p_{inter}=0.02$.

Next, the modular networks are tuned to have a hybrid of electrical and chemical synaptic coupling, and to maintain excitatory and inhibitory synapses in E–I balanced state. Initially, the network coupling takes the form of purely excitatory electrical synaptics. Subsequently, the synapse switches from excitatory to inhibitory with probability $f_{E-I}$. Given that the ratio of excitatory to inhibitory synapses is approximately 4 : 1 in the balanced state [41], we set $f_{E-I}=0.8$ to ensure that the network is in an E–I balanced state. Finally, based on this, electrical synapses are converted to chemical ones with probability f and ensure that different subnetworks are connected to each other with chemical synapses. Here, we denote f as the probability of chemical synapses, which represents the ratio of the number of chemical synapses to the number of electrical synapses roughly as $f\%:(1-f)\%$. The primary reason for this setup is differences in the structure and mechanisms of transmission between electrical and chemical synapses, with electrical synapses interconnecting at a distance of 3.5 nm compared with 30 nm for chemical synapses [61,62,63]. An example of a modular network topology for balanced small-world neural systems among $M=3$ interconnected subnetworks is shown in Fig. 1.

Fig. 1

Schematic presentation of the considered network architecture. The whole network consists of $M=3$ subnetworks, each of them containing $N=20$ neurons. Within each subnetwork, each node is connected to its $K=4$ neighbors. There are four connections amongst neurons from different subnetworks. The black line represents chemical synaptic coupling and the blue line represents electrical synaptic coupling, $f=0.9$. In the balanced state, the probability of excitatory and inhibitory synapses is approximately 4 : 1, $f_{E-I}=0.8$, where the lines labeled by the red text are the inhibitory connections and the rest are the excitatory connections

2.2 Neuronal model

The Rulkov map model [64], which has the capability to generate extraordinary complexity as well as fairly specific neural dynamics [65], is employed to describe the local single neuron and is formulated as following discrete equations:

$$\begin{aligned} {x_{_L,_i}(t+1)}=&\,\displaystyle \frac{\alpha }{1+x_{_L,_i}^2(t)}+y_{_L,_i}(t) +\sigma \xi _{_L,_i}(n)\\ &+I_{_L,_i}^{E}(t)+I_{_L,_i}^{C}(t)\\ {y_{_L,_i}(t+1)}=&\,y_{_L,_i}(t)-\beta x_{_L,_i}(t)-\gamma , \end{aligned}$$

(1)

where $x_{_L,_i}(n)$ is a fast dynamic variable associated with the membrane potential of the ith neuron in the Lth subnetworks; $y_{_L,_i}(n)$ denotes the slow dynamic variable related to gating variables. n refers to the discrete time indicator. The system parameter $\alpha$ controls the local dynamics of a individual neuron, in which all neurons occupy an excitable steady state for $0<\alpha <2$ and exhibit regular bursting oscillations or periodic spiking for $\alpha >2$. In this work, we fix $\alpha =2.3$ so that all unites are in a periodic spiking state in the absence of other stimulus. The system parameters $\beta , \gamma$ are set to 0.001. One of the stimulus is channel noise $\xi _i(n)$, which is assumed to be Gaussian noise with $\langle \xi _i(n)\xi _j(m)\rangle =\delta _{ij}\delta _{mn}$. $\sigma$ defines the noise intensity.

$I_{_L,_i}^{E}(t)$ is the coupling current received by electrical synapses, which is formulated as follows:

$$\begin{aligned} I_{_L,_i}^{E}(t)=g_e \sum _{j=1} A_{_L}(i,j)(x_{_L,_j}(t-\tau )-x_{_L,_i}(t)) \end{aligned}$$

(2)

where $g_e$ represents the coupling strength of electrical synapses between the neurons within each subnetwork. For excitatory electrically synapses, $g_e=0.005$; while for inhibitory electrically synapses $g_e=-0.005$. The matrix $A_{_L}=A_{_L}(i,j)$ is the intra-connectivity matrix of the Lth subnetwork. In the Lth subnetwork, when the ith neuron is connected to the jth neuron, we assume $A_{_L}(i,j)=A_{_L}(j,i)=1$; otherwise $A_{_L}(i,j)=A_{_L}(j,i)=0$ and $A_{_L}(i,i)=0$. $\tau$ is one of the main parameters investigated, which defines the time delay between the ith neuron and the jth neuron.

Similarly, $I_{_L,_i}^{C}(t)$ is the coupling current received by chemical synapses, which can be expressed as

$$\begin{aligned} I_{_L,_i}^{C}(t)=&\,-g_c \left[ \sum _{j=1} B_{_L}(i,j)(x_{_L,_i}(t)-v)\Gamma (x_{_L,_j}(t))\right. \\ &\left.+\sum _J \sum _{j=1} C_{_L,_J}(i,j)(x_{_L,_i}(t)-v) \Gamma (x_{_J,_j}(t))\right] \end{aligned}$$

(3)

where $g_c$ represents the coupling strength of neuronal chemical synapses within or between subnetworks, taking $g_c=0.003$. The matrix $B_{_L}=B_{_L}(i,j)$ is also an intra-connectivity matrix of the Lth subnetwork: if ith neuron is connected to jth neuron within the Lth subnetwork, $B_{_L}(i,j)=B_{_L}(j,i)=1$; otherwise $B_{_L}(i,j)=B_{_L}(j,i)=0$ and $B_{_L}(i,i)=0$. While the matrix $C_{_L,_J}=C_{_L,_J}(i,j)$ denotes the interconnection of neurons between different subnetworks: if the ith neuron within the Lth subnetwork is connected to the jth neuron within the Jth subnetwork, $C_{_L,_J}(i,j)=C_{_L,_J}(j,i)=1$; otherwise $C_{_L,_J}(i,j)=C_{_L,_J}(j,i)=0$. v is the reversal potential of the synapse. For excitatory chemically synapses, $v=0.2$; while for inhibitory chemically synapses $v=-1.9$. Chemical synaptic current with time delay is simulated by the sigmoidal function:

$$\begin{aligned} \Gamma (x_j(t))=\displaystyle 1/(1+exp(-\lambda (x_j(t-\tau )-\Theta _s))) \end{aligned}$$

(4)

where $\Theta _s$ is regarded as the threshold beyond which postsynaptic neurons are subjected to the action of presynaptic neurons, and is set as $\Theta _s =-1.0$. $\lambda =30$ is a constant rate at which excitation or inhibition onsets.

2.3 Measure

To quantitatively evaluate the intensity of the response between the output of the studied neuronal network and the input signal from the neurons, we compute the Fourier coefficient Q, which is defined as

$$\begin{aligned} Q_{sin}=&\,\displaystyle \frac{1}{N_T T} \sum _{t=1}^{N_T T}2X(t)sin(2\pi t/T),\\ Q_{cos}=&\,\displaystyle \frac{1}{N_T T} \sum _{t=1}^{N_T T}2X(t)cos(2 \pi t/T), \end{aligned}$$

(5)

$$\begin{aligned} Q=\sqrt{Q_{sin}^2+Q_{cos}^2}, \end{aligned}$$

(6)

where $X(t)=\displaystyle \frac{1}{MN} \sum\nolimits_{i=1}^{MN}x_i(t)$ is the mean-field of the network; $N_T T$ is the operation period and $N_T=300, T=820$; $2\pi /T$ is the frequency of the pulse train. We use Q as a resonance factor, and it follows that larger Q means higher degree of the resonance of the entire neuronal network. Thus, Q is also called as response amplitude of the neuronal systems.

3 Results

For simplicity, in what follows we study a modular E–I balanced neural network consisting of two small-world subnetworks, i.e., $M=2$. First, we focus on the combined effects of noise and hybrid synapses on coherence resonance for time delay $\tau =0$. Second, influences of $\tau$ on coherence resonance are investigated as the probability of chemical synapses f is different. Finally, the dependence of the coherence resonance on the electrical and chemical coupling strengths is given for different probability of chemical synapses f.

3.1 Combined effects of noise and hybrid synapses on coherence resonance for the time delay $\tau =0$

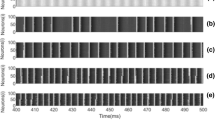
To decipher the coherence resonance, in this subsection, we focus first on the combined effects of noise and hybrid synapses with no time delay, namely, $\tau =0$. The initial values of $g_c=0.003$ and $g_e=0.005$ are set to keep the modular balanced network in a weakly coherence resonance state. The probability of chemical synapses is initially set to $f=0.1$, and Fig. 2 shows the spatiotemporal patterns of the membrane potentials for all neurons at different noise intensity $\sigma$. The obtained results present that the smaller noise intensity $\sigma$ fails to make two subnetworks spiking synchronously (Fig. 2a, b). When $\sigma$ is increased to moderate values, e.g.,$\sigma =0.025$, temporal dynamics of two subnetworks change to that of an ordered state (see panel (c)). With further increases of $\sigma$, the firing correlation of two subnetworks gradually weakens and engenders disorder. We, therefore, conjecture that there exists some intermediate noise intensities $\sigma$ to make the subnetworks spiking synchronously. The corresponding temporal evolution of the mean field X(t) is presented in Fig. 3. From this figure it can be shown much more clearly that the spiking trains from the neuron cluster between two subnetworks are stronger and more regular for the intermediate noise intensities $\sigma$ as shown in Fig. 3c); whereas the smaller and larger $\sigma$ could reduce or turbulence the spiking trains, as can be seen in Fig. 3a, b, d, e.

Fig. 2

Space-time plots of $x_i(t)$ obtained for $\tau =0$ at different noise intensity $\sigma$. a $\sigma =0.001$, b $\sigma =0.015$, c $\sigma =0.02$, d $\sigma =0.025$, e $\sigma =0.05$.$i=1-100$ indicates neurons of the first subnetwork and $i=101-200$ denotes neurons of the second subnetwork. Other parameter values: $f=0.1$, $g_c=0.003$, and $g_e=0.005$. In all panels, the system size is $MN=200$

Fig. 3

Temporal evolution of the mean field X(t) for $\tau =0$ at different noise intensity $\sigma$ corresponding to Fig. 2. (a) $\sigma =0.001$, (b) $\sigma =0.015$, (c) $\sigma =0.02$, (d) $\sigma =0.025$, (e) $\sigma =0.05$

It is of interest to assess these observations quantitatively, we plot the dependence of the Fourier coefficient Q with respect to noise intensity $\sigma$ and the probability of chemical synapses f in a two dimensional parameter space, as exhibited in Fig. 4. Clearly, there are some regions of blocks colored red or yellow, where means Q takes the larger values. Viewing this plot from the horizontal direction, i.e., $f\in [0,1]$, we then see that the regions colored by red or yellow are mostly centred in $\sigma \in [0.01,0.03]$, which is indicative of a strong resonance response. Whereas $\sigma <0.01$ as the colour shifts darker, indicating the value of Q decreases and the coherence resonance becomes weaker. A broad dark-blue band as long as $\sigma >0.03$ is observed, indicating that the coherence resonance of the system is lowest and that the noise intensity $\sigma$ and the probability of chemical synapses f have little effect on the coherence resonance. In addition, if one looks a little more closely, it happens that some closed blocky regions with a reddish yellow tinge appear at intervals around the line $\sigma =0.02$, and the ratio of the number of synapses represented by the corresponding f occurs by chance in the vicinity of the odd ratio, which is an intriguing phenomenon.

Fig. 4

Dependence of Fourier coefficient Q with respect to noise intensity $\sigma$ and the probability of chemical synapses f. Other parameter values: $g_c=0.003$ and $g_e=0.005$

To better inspect the above demonstrations, we respectively plot the variation of Q versus noise intensity $\sigma$ when the ratio f of the number of chemical to electrical synapses takes on different odd and even ratios. In this case, the critical cases for $f = 1$ (all chemistry) and $f = 0$ (all electric) are shown in the Fig. 5a, b, respectively, for the sake of comparison. Figure 5a corresponds to the case where f takes on different odd ratios, from which Q can be seen increases to rise to a maximum as $\sigma$ is increased to approximately 0.02. Then, with $\sigma$ increasing further, Q decreases to a minimum gradually. As a contrast, from Fig. 5b corresponding to different even ratios f, it can be seen that the general trend of the curve is similar to that when f is odd ratios (Fig. 5a). The obvious difference, however, is that the maximum values of Q are smaller just with the exception of $f=0$, which states that system’s coherence resonance with even ratios f is significantly weaker than that with odd ratios f. Particularly for $f=0$, where all of the neurons in the modular network are coupled via electrical synapses, an optimum noise intensity of $\sigma =0.025$ exists to ensure that the system’s coherence resonance lies at a higher level, a result which is consistent with previous findings in fully electric coupling networks(see reference [66, 67]). Moreover, from Fig. 5b, we note that as $\sigma$ increases, although the maximum of Q is much smaller than that of Fig. 5a, there are two optimal values of noise intensity $\sigma$ for Q to reach local maxima, of which one is at relatively small noise intensity $\sigma =0.015$ and the other is at relatively large noise intensity $\sigma =0.025$.

Fig. 5

a Dependence of Fourier coefficient Q on noise intensity $\sigma$ at different odd ratios f of the number of chemical to electrical synapses. b Dependence of Fourier coefficient Q on noise intensity $\sigma$ at different even ratios f of the number of chemical to electrical synapses

Furthermore, to further elucidate this detail, we take the even ratio $f = 0.2 (chemical : electrical=2:8)$ for specific presentation. Figure 6 shows the spatiotemporal patterns of membrane potentials of all neurons observed on the network for different noise intensity $\sigma$ on $f = 0.2$. The temporal evolution of the mean field X(t) corresponding to Fig. 6 is illustrated in Fig. 7. Hence, we can find a lot more that there definitely exist two best noise intensities $\sigma =0.015$ and 0.025( see Fig. 6b, d), such that the system’s coherence resonance attains a local maxima. And compared to the case where f is odd ratios, e.g., $f=0.1 (chemical : electrical=1:9)$ respectively shown in Figs. 2 and 3, it can be demonstrated that when the ratio f of the number of chemical synapses to electrical synapses is odd ratios, the coherence resonance induced by noise intensity and hybrid synapses is significantly stronger than the case when f is even ratios.

Fig. 6

Space-time plots of $x_i(t)$ obtained for $\tau =0$ at different noise intensity $\sigma$. a $\sigma =0.001$, b $\sigma =0.015$, c $\sigma =0.02$, d $\sigma =0.025$, e $\sigma =0.05$. $i=1-100$ indicates neurons of the first subnetwork and $i=101-200$ denotes neurons of the second subnetwork. Other parameter values: $f=0.2$, $g_c=0.003$, and $g_e=0.005$. In all panels, the system size is $MN=200$

Fig. 7

Temporal evolution of the mean field X(t) for $\tau =0$ at different noise intensity $\sigma$ corresponding to Fig. 6. a $\sigma =0.001$, b $\sigma =0.015$, c $\sigma =0.02$, d $\sigma =0.025$, e $\sigma =0.05$

In conclusion, combined with the above analysis, it can be seen that no matter what the ratios f of the number of chemical synapses to electrical synapses are odd or even, some intermediate noise strengths $\sigma$ exist to make the coherence resonance of subnetworks with hybrid synapses are at a higher level. In particular, at appropriate noise intensities $\sigma$, coherence resonance generated by odd ratios of chemical and electrical synapses is stronger than that generated by even ratios.

3.2 Effects of both time delay and hybrid synapses on coherence resonance.

According to the former subsection, we see that the optimal noise intensity $\sigma$ is centralized to [0.01, 0.025] for the network with hybrid synapses. Thus, in this subsection we set $\sigma =0.018$, and add time delay to the modular balanced network discussed earlier, investigating the effects of time delay and hybrid synapses on coherence resonance. We begin by calculating the dependence of the Fourier coefficient Q on $\tau$ for several different chemical synapse probabilities f, as illustrated in Fig. 8a. As can be seen, Q was able to reach four local maxima appearing roughly at $\tau =0,800, 1700, 2500$ and is independent of the value of f, which suggests that time delay may elicit the emergence of multiple coherent resonances. Indeed, the optimal value of Q appears intermittently at roughly integer multiples of the inherent oscillation period of the neuronal dynamics under consideration, equaling $T=820$. In addition, somewhat more interesting is the fact that as the time delay $\tau$ is increased, the peak heights located at approximate integer multiples of the delay are shifted to slightly higher values, except for $\tau =0$.

Furthermore, to account for the visual inspection above at a glance, the dependence of Q on f and $\tau$ is presented in Fig. 8b. One can observe that coherence resonances clearly qualify as narrow shaped regions, appearing roughly at integer multiplies of $\tau =820$. Evidently, the resonance phenomenon prevails regardless of f in $\tau -f$ parameter plane. It is clear that as the time delay $\tau$ increases, the regions of optimal $\tau$ become broader and the corresponding colors gradually turn blue and yellow, indicating that the value of Q is becoming larger. It’s worth noting that when the time delay is around $\tau =0$, the Q values are larger, either in red or blue, primarily because we set up the system initially. We can, therefore, further conclude that time delay plays a dominant role in the modulation of coherence resonance in modular networks. If the time delay $\tau$ lies at approximately an integer multiple of the intrinsic period of the oscillation, they can induce the multiple coherent resonances and have nothing to do with the ratio of the number of chemical and electrical synapses. As the integer multiple time delay $\tau$ increases, the resonance behavior is enhanced, while in other cases it could weaken or deteriorate the system’s resonant behaviour.

Fig. 8

a Dependence of Fourier coefficient Q with respect to time delay $\tau$ for different probability of chemical synapses f. b Dependence of Fourier coefficient Q both on $\tau$ and f. Other parameter values: $\sigma =0.018$, $g_c=0.003$ and $g_e=0.005$.

3.3 Effects of the coupling strength and hybrid synapses on coherence resonance

In light of the results obtained above, we knew that coherence resonance almost occurs almost when the time delay is an integer multiple of the inherent period of the system. We then take the optimally fixed value $\sigma =0.018$ as before and set the time delay $\tau =820$. The chemical coupling strength $g_c$ and the electrical coupling strength $g_e$ are regarded as control parameters. Here f is split into three cases for investigation, being small as 0.1, intermediate as 0.5 and large as 0.9, respectively. From the overall insight in Fig. 9, there are regions of band resonance with large values of Q, and these regions progressively decrease as the proportion of chemical synapses f increases. Comparing three cases, as f increases, the optimal resonant regions corresponding to $g_c$ and $g_e$ decrease gradually. Besides, the spans of the optimal electrical coupling strength $g_e$ are all wide. However, the span of the optimal chemical coupling strength $g_c$ diminishes bit by bit and the best is only in a certain interval with increasing f. It is suggested that although chemical coupling and electrical coupling are complementary, as the proportion of the chemical synapse f increases, the synergistic region between the two synapses gradually decreases. The electrical synaptic coupling is slightly influenced by the synaptic ratio f, but the chemical coupling is more sensitive and there is only a range of chemical coupling interval that allows the system to respond optimally, indicating that electrical coupling is more efficient than chemical coupling in E–I balanced modular small-world neuronal networks.

Fig. 9

Dependence of Fourier coefficient Q on the chemical coupling strength $g_c$ and the electrical coupling strength $g_e$ for different probability of chemical synapses f. a $f=0.1$; b $f=0.5$; c $f=0.9$. Other parameter values: $\tau =820$, $\sigma =0.018$

To further elucidate how f affects the coupling behaviors about the two synapse types, we respectively calculated the dependence of Q on f and $g_c$ and the dependence of Q on f and $g_e$, presented in Fig. 10. Figure 10a shows that with the increasing values of f, the optimal resonant regions with $g_c$ and f decrease gradually, it is only when $g_c$ is smaller that relatively strong resonances will appear. However, in the case of varying values of f and $g_e$ in Fig. 10b, compared with chemical coupling, most of the electrical coupling can induce the network to produce stronger resonance behaviors, and the resonant regions with $g_e$ and f increase gradually with increasing f. In this context, the coupling behavior of the two synapses is nearly opposite as f increases, and electrical coupling is more effective than chemical coupling. Thus, one can understand that the decrease of optimal resonant regions corresponding to $g_c$ and $g_e$ as f increases in Fig. 9 is primarily due to the chemical coupling. Indeed, the efficiency of electrical and chemical coupling were different in different complex network of neurons. Some studies have shown that nonlinear chemical coupling is more efficient than linear electrical coupling for vibrational resonance in hybrid small-world neuronal networks [68]. Whereas there are also studies indicated that electrical synapses are more efficient than chemical synapses for the SR in scale-free networks [69]. However, in this paper we demonstrate that electrical coupling is more efficient than chemical coupling for the CR in modular small-world neuronal networks with E–I balanced state. This is primarily due to the fact that the electrical coupling is the continuous interactions, which can better regulate the firing rate than the selective interactions among the chemically coupled neurons. Furthermore, as f increases, more chemical synapses are added to the E–I balanced modular networks, and the increase in coupling strength of chemical synapses results in subthreshold fluctuations of the mean field potential, eventually leading to decreased Q values and weaker resonance.

Fig. 10

Individual influences of electrical and chemical coupling strengths. a Variation of Fourier coefficient Q with the chemical coupling strength $g_c$ and f by a fixed chemical coupling strength $g_c= 0.003$. b Variation of Fourier coefficient Q with the electrical coupling strength $g_e$ and f by a fixed chemical coupling strength $g_e= 0.005$. Other parameter values: $\tau =820$, $\sigma =0.018$

4 Discussion

Nowadays, it is an accepted fact that clusters are often associated with specific brain regions, and the number and architecture of the subnetworks reveal how many diverse tasks it can implement [70]. In this context, we present an analysis of the number of subnetwork in the case of $M > 2$. Here, the size of the modular network is held constant, the total number of neurons stays fixed at $MN=200$, and the number of subnetworks M is taken as a control parameter. The variation of Q with respect to both M and $\tau$ for three cases of f is shown in Fig. 10. A similar result can be obtained from this graph when multiple coherent resonances appear intermittently in integer multiples of the intrinsic intrinsic period of oscillation of the system. The larger the integral time delay, the stronger the coherence resonance. However, it is worth noting that the modification depends on the number of subnetworks M. When the number of subnetworks $M\le 5$, there is a significant coherence resonance and the resonance is enhanced with increasing f; alternatively, when $M>5$, the resonance decreases with versus the variation of M and will diminish or disappear as f is sufficiently large. To more clearly observe these conclusions, Fig. 11 further illustrates that the number of subnetworks could affect the degree of resonance of the modular networks and that the degree of resonance can be diminished when the constituent neurons are dispersed over a larger number of subnetworks.

This may be explained by the fact that when there are fewer subnetworks within the modular network, many neurons are assembled together and chemical synapse activates its role in long time, at which point the neurons exhibit stronger communicative and clustering behaviour, such that as the number of chemical synapses in the network increases, the resonant behaviour of the system subsequently enhanced. Conversely, when there are more subnetworks, communication with each other is compromised as neurons are dispersed into a larger number of clusters. This is coupled with the fast signaling rate of electrical synapses, which play a major role in the network at this time. Thus, as the number of chemical synapses in the network increases, i.e., as the number of electrical synapses decreases, resonant behaviour diminishes or disappears.

Fig. 11

Contour plot of Fourier coefficient Q on the number of subnetworks M and the time delay $\tau$ for different probability of chemical synapses f. a $f=0.1$; b $f=0.5$; c $f=0.9$. Other parameter values: $\sigma =0.018$, $g_c=0.003$ and $g_e=0.005$

Fig. 12

Dependence of Fourier coefficient Q on the number of subnetworks M for different time delay $\tau$. Here, the plots corresponding to different probability of chemical synapses f are similar

5 Summary

In sum, by introducing biological features into the model, such as the properties of modules and the small-world, E–I balanced state, the hybrid electrical and chemical synapses, noise, time delay, the coupling strength as well as the number of subnetworks, we have presented how different neurophysiological factors impact the coherence resonance. The evidence has showed that there are a few intermediate noise intensities $\sigma$ to make the coherence resonance at a higher level. Yet remarkably, when the ratio f of the number of chemical synapses to electrical synapses is close to odd ratio, the resonance behaviour at appropriate noise intensities $\sigma$ is better than those near the even ratio. In addition, by introducing the time delay to the coupling scheme, it is shown that time delay can induce the multiple coherence resonance. The larger the integral time delay, the stronger the coherence resonance and independent of the ratio f of chemical and electrical synapses. Besides, although it was previously shown that nonlinear chemical coupling is more efficient than linear electrical coupling, we have demonstrated that the coupling behavior of the two synapses is nearly opposite as f increases, indicating that electrical coupling is more efficient than chemical coupling for the CR in modular small-world neuronal networks with E–I balanced state. Moreover, the coherence resonance is impacted by the number of subnetworks M. When M is the smaller, resonance behaviour becomes stronger as f increases; whereas when M is the larger, the resonance behaviour weakens or vanishes gradually with increasing f. This behavior is mainly due to the nature of the electrical and chemical synapses as well as the communication mechanism of the cluster network. Our studies expand the scope of coherence resonance and account for the fact that neuronal networks maintain an excitatory–inhibitory (E–I) balanced state as an economical choice, in addition to the fact that modular neural networks can facilitate the availability of information transmission. We, therefore, wish these results to contribute to the understanding of the role of coherence resonance behaviour in neuronal systems.