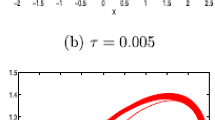1 Introduction

Flow of non-Newtonian (non-linear) fluids occurs not only in nature but also various thermal-based industries; in general, these fluids exhibit certain distinct features, for instance, time dependent response (history effects), viscoelasticity (creep or relaxation), shear-thinning or shear-thickening aspects of the fluid (shear-rate dependency of the viscosity), die-swell and rod-climbing (normal stress effects), viscoplasticity (yield stress effects) and several others [1,2,3,4,5,6,7,8,9]. Massoudi and Christie [10] presented the first study on the non-Newtonian nature of the fluid for the skin friction and heat transfer in which they focused natural convection of a homogeneous incompressible fluid of grade three between two infinite concentric vertical cylinders. They investigated the velocity and temperature profiles through numerical experimentation. Guha and Pradhan [11] explored the effective role of free convection flow of non-Newtonian power-law fluids over a horizontal plate on the basis of magnetohydrodynamics and constant heat flux. Their focused study was Hartmann number. They concluded that surface temperature and thermal boundary layer thickness decreases subject to the increment in Hartmann number. The flow of non-Newtonian fluids along an isothermal horizontal circular cylinder by means of mathematical modeling of the boundary-layer equations is studied by Bhowmick et al. [12]. They applied numerical technique, namely, implicit finite difference method with double sweep technique and emphasized their results for shear-thinning as well as shear thickening non-Newtonian fluids. Abro et al. [13] investigated the combined effects of Newtonian and non-Newtonian fluids through analytical study using Fourier analysis on the Burger fluid. They retrieved few types of non-Newtonian fluids so called second grade, Maxwell and Oldroyd-B fluids as the limitations of the problem. Mohsan et al. [14] presented the viscoelastic polydimethylsiloxane non-Newtonian nanofluid on the basis of flow of natural convection in presence of nanoparticles. The nanoparticles showed high performance for temperature profile and the rate of heat transfer and proved to be efficacious in comparison tiny size particles to large particles. The studies on non-Newtonian fluids can be continued but we end here by adding recent attempts for different types of non-Newtonian fluids [15,16,17,18,19,20,21,22,23,24,25] therein. As this manuscript has core objective to analyze chaotic analysis of thermal convection problem based on non-Newtonian fluid saturated by porosity by means of Caputo–Fabrizio fractal–fractional differential operator in Caputo sense; this is because fractional order models have the potential to capture non-local relationships in time and space with the memory kernels of the exponential, power and Mittag–Leffler type laws even to handle phenomena with high complexities [26,27,28,29]. Kashif et al. [30] studied the free convection flow of nanofluid via new fractional derivatives within magnetite nanoparticles in which A-Band C–F fractional operators have been compared for the heat transfer in presence and absence of magnetic effects. Atangana and Goufo in [31], presented analysis of nonlinear partial differential equation through numerical simulations in which Caputo–Fabrizio fractional derivative is invoked on garden equation. They investigated on existence and uniqueness of the exact solution using the Laplace iterative methods. Very interested work has been presented for the extension of fractional derivative so called fractal–fractional derivative by an African professor of University of the Free, South Africa [32] in which fractional derivative is more generalized for fractal–fractional derivatives. Keeping the importance of newly presented fractal–fractional derivatives, Kashif and Atangana [33] applied the new concept of fractal–fractional derivatives on the convective fluid motion in rotating cavity. The rotating cavity has been analyzed by means of three types of fractal–fractional derivatives so called Atangana–Baleanu, Caputo and Caputo–Fabrizio. Ilknur [34] employed the concept of fractal–fractional derivatives on heat transfer problem, where analytical study has been emphasized by comparing the Atangana–Baleanu and Caputo–Fabrizio fractal–fractional derivatives. The studies on fractal–fractional differential operators and fractional differential operators can be continued but we end here in terms of categorical sciences as epidemiological models [35,36,37], circuits and electrical transmissions [38,39,40,41,42,43,44,45], nanofluid and fluids [46,47,48,49,50] and multi-disciplinary [51,52,53,54,55] therein. Motivating by discussion, the most attractive novelty of this investigation is to retrieve the chaotic behavior of non-Newtonian fluid saturated by porosity for the chaotic behavior Newtonian fluid saturated by porosity. The mathematical modeling of governing equations of non-Newtonian fluid saturated by porosity is constructed in terms of Caputo–Fabrizio fractal–fractional differential operator subject to the appropriate imposed conditions. For the sake of mathematical analysis, chaotic convection problem of non-Newtonian fluid is explored for dissipation, equilibrium points and criteria of stability. The numerical simulations through Adam–Bashforth method in connection with Caputo–Fabrizio fractal–fractional differential operator are performed for two cases: (1) chaotic convection of non-Newtonian fluid in presence of porosity and (2) chaotic convection of Newtonian fluid in presence of porosity. Finally, the phase portraits have been depicted to identify the similarities and differences among non-Newtonian and Newtonian fluids in presence of porosity.

2 Mathematical modeling for convection of non-Newtonian fluid

We assume non-Newtonian fluid (viscoelastic fluids) so called Oldroydian fluid saturated porous medium of height \(d\) and width \(l\) that is cooled from above and heated from below. The upper surface temperature \({T}_{\mathrm{u}}\) and lower surface temperature \({T}_{\mathrm{l}}\), respectively, in which vertical walls are adiabatic. We assume that the convective fluid and porous medium are in local thermodynamic equilibrium; due to this fact Boussinesq approximation is applied. The governing equations for continuity, state, two-phase temperatures, and momentum, respectively, are described as

$$\nabla \cdot {\varvec{q}} = 0,$$
(1)
$$\rho = \rho_{{\text{R}}} - \beta \rho_{{\text{R}}} T - \rho_{{\text{R}}} \beta T_{{\text{R}}} ,$$
(2)
$$\frac{\partial T}{{\partial t}} - \frac{{\nabla^{2} T}}{\alpha }{\varvec{q}} \cdot \nabla T = 0,$$
(3)
$$\frac{K}{\mu }\left( {\nabla P - \rho {\mathbf{g}} + \frac{{\rho_{{\text{R}}} }}{\varepsilon }\frac{{\partial {\varvec{q}}}}{\partial t}} \right) = \frac{{\left( {\lambda_{2} \frac{\partial }{\partial t} + 1} \right)}}{{\left( {\lambda_{1} \frac{\partial }{\partial t} + 1} \right)}}{\varvec{q}}\user2{.}$$
(4)

To analyze the sustainable behavior of fluids, we employ the dimensionless quantities, transformations and also introducing the stream functions in the governing Eqs. (1–4) for continuity, state, two-phase temperatures and momentum, as defined below:

$$v=\frac{\partial \psi }{\partial x},u=-\frac{\partial \psi }{\partial y}, \left({u}^{*},{v}^{*}\right)=\frac{k\varepsilon }{\mathrm{d}\rho c},\left({x}^{*},{y}^{*}\right)=d\left(x,y\right),{t}^{*}=\frac{t{d}^{2}}{\alpha },T={T}_{u}+\theta {T}_{l}-\theta {T}_{u},$$
(5)

Also, we eliminate pressure from the momentum equation, we arrive at the following suitable expressions as

$$\begin{aligned}&\frac{1}{\mathrm{Ra}}\left\{\left({\lambda }_{2}\frac{\partial }{\partial t}+1\right)\left(\frac{{\partial }^{2}\psi }{\partial {y}^{2}}+\frac{{\partial }^{2}\psi }{\partial {x}^{2}}\right)\right. \nonumber \\ &\qquad +\left.\frac{\partial }{\partial t}\left({\lambda }_{1}\frac{\partial }{\partial t}+1\right)\left(\frac{{\partial }^{2}\psi }{\partial {y}^{2}}+\frac{{\partial }^{2}\psi }{\partial {x}^{2}}\right){\left({\mathrm{Pr}}_{D}\right)}^{-1}\right\}\nonumber \\ &\quad =\frac{\partial \theta }{\partial x}\left({\lambda }_{1}\frac{\partial }{\partial t}+1\right),\end{aligned}$$
(6)
$$\frac{{\partial }^{2}\psi }{\partial {y}^{2}}+\frac{{\partial }^{2}\psi }{\partial y\partial x}+\frac{{\partial }^{2}\psi }{\partial {x}^{2}}-\frac{{\partial }^{2}\psi }{\partial x\partial y}=\frac{\partial \theta }{\partial x}$$
(7)

where the letting parameters for Eqs. (6–7) are \({\lambda }_{2}=\frac{{k\overline{\lambda }}_{2}}{{d}^{2}}\) represents retardation time, \({\lambda }_{1}=\frac{{k\overline{\lambda }}_{1}}{{d}^{2}}\) is relaxation time, \(\mathrm{Pr}=\frac{\mu }{k\rho }\) denotes Prandtl number, \({\mathrm{Pr}}_{D}=\mathrm{Da}{\left(\varepsilon \mathrm{Pr}\right)}^{-1}\) signifies Darcy–Prandtl number, \(\mathrm{Da}=\frac{k}{{d}^{2}}\) is Darcy number and \(\mathrm{Ra}=\frac{\left({T}_{l}-{T}_{u}\right)gKd\beta {\rho }_{0}}{k\mu \varepsilon }\) suggests Darcy–Rayleigh number. Now, applying the concept of truncated Galerkin expansion on Eqs. (6–7) and then an infinite Fourier series with the series coefficients dependent on time alone is considered. Meanwhile, the temperature distribution and stream function can be obtained as

$$\theta +y=1+{B}_{02}\mathrm{sin}\left(2\pi y\right)+{B}_{11}\mathrm{sin}\left(\pi y\right)\mathrm{cos}\left(\frac{\pi x}{L}\right),$$
(8)
$$\psi ={A}_{11}\mathrm{sin}\left(\pi y\right)\mathrm{sin}\left(\frac{\pi x}{L}\right),$$
(9)

employing Eqs. (8–9) into Eqs. (6–7) and then solving their integration with respect to spatial domain, we arrive at the three differential equations for the time evolution described as below:

$$\begin{aligned}\frac{{A}_{11} \chi {\pi }^{3}}{{B}_{11} {\alpha }_{3} \mathrm{Ra}{ Pr}_{D}}\left\{\frac{{ {\alpha }_{3} Pr}_{D}}{{\pi }^{2}}\left({\alpha }_{2}{\alpha }_{1}\frac{\partial }{\partial \tau }+1\right)\right.\\ \left.+\frac{\mathrm{d}}{\mathrm{d}\tau }\left({\alpha }_{1}\frac{\partial }{\partial \tau }+1\right)\right\}=\left({\alpha }_{1}\frac{\partial }{\partial \tau }+1\right),\end{aligned}$$
(10)
$$\frac{\mathrm{d}{B}_{11}}{\mathrm{d}\tau }+{B}_{11} =\left(\frac{\pi {B}_{02}{A}_{11}+{A}_{11}}{\chi \pi }\right),$$
(11)
$$\frac{\mathrm{d}{B}_{02}}{\mathrm{d}\tau }+\frac{{B}_{11}{A}_{11}}{2\chi }+4{B}_{02}{\alpha }_{3}=0.$$
(12)

To rescale the time among Eqs. (10–12), we introduce the rheological quantities as \(\tau =\frac{{\pi }^{2}+{(\pi L)}^{2}}{{L}^{2}},{\alpha }_{3}=\frac{{L}^{2}}{1+{L}^{2}},\chi =\frac{1+{L}^{2}}{L}, {\alpha }_{5}=\frac{\mathrm{Ra}}{{(\pi \chi )}^{2}}\) and \({\alpha }_{4}=\frac{{ \gamma Pr}_{D}}{{\pi }^{2}}\). In addition, one can derive the set of non-linear governing ordinary differential equations by rescaling the amplitudes as \(\left({p}_{1},{p}_{2},{p}_{3}\right)=\left(\frac{{2}^{-1}{A}_{11}{\chi }^{-1}}{\sqrt{2{\alpha }_{5}\chi -2\chi }},\frac{{2}^{-1}\pi {B}_{11}{\alpha }_{5}}{\sqrt{2{\alpha }_{5}\chi -2\chi }},\frac{\pi {B}_{02}{\alpha }_{5}}{1-{\alpha }_{5}}\right)\), we get:

$$\begin{array}{l}\frac{\mathrm{d}{p}_{1}(t)}{\mathrm{d}t}={p}_{4}\left(t\right), \\ \begin{array}{l}\frac{\mathrm{d}{p}_{2}(t)}{\mathrm{d}t}={\alpha }_{5}{p}_{1}\left(t\right)-{p}_{2}\left(t\right)-{\alpha }_{5}{p}_{1}(t){p}_{3}(t), \\ \begin{array}{l}\frac{\mathrm{d}{p}_{3}\left(t\right)}{\mathrm{d}t}=4{\alpha }_{5}\left({p}_{1}\left(t\right){p}_{2}\left(t\right)-{p}_{3}\left(t\right)\right), \\ \frac{\mathrm{d}{p}_{4}\left(t\right)}{\mathrm{d}t}={\alpha }_{4}\left\{\left({\alpha }_{5}-{\alpha }_{1}^{-1}\right){p}_{1}\left(t\right)+\left({\alpha }_{1}^{-1}-1\right){p}_{2}\left(t\right)\right.\\ \left.-\left({\alpha }_{5}-1\right){p}_{1}\left(t\right){p}_{3}\left(t\right)-({\alpha }_{2}+{\alpha }_{1}^{-1}{\alpha }_{4}^{-1}){p}_{4}\left(t\right)\right\},\end{array}\end{array}\end{array}$$
(13)

Subject to initial conditions as

$${p}_{1}\left(0\right)={p}_{2}\left(0\right)={p}_{3}\left(0\right)={p}_{4}(0)=0.9.$$
(14)

The set of non-linear governing ordinary differential equations characterized by the dynamical system (13) is for non-Newtonian fluid (viscoelastic fluids). Meanwhile, the set of non-linear governing ordinary differential equations characterized by the dynamical system (13) contains a special case for the Newtonian fluid when \({\alpha }_{4}\to 0.\) The set of non-linear governing ordinary differential equations characterized by the dynamical system (13) for non-Newtonian fluid can be retrieved as written below:

$$\begin{array}{l}\frac{\mathrm{d}{p}_{1}(t)}{dt}={p}_{4}\left(t\right), \\ \begin{array}{l}\frac{\mathrm{d}{p}_{2}(t)}{dt}={\alpha }_{5}{p}_{1}\left(t\right)-{p}_{2}\left(t\right)-{\alpha }_{5}{p}_{1}(t){p}_{3}(t), \\ \begin{array}{l}\frac{\mathrm{d}{p}_{3}\left(t\right)}{dt}=4{\alpha }_{5}\left({p}_{1}\left(t\right){p}_{2}\left(t\right)-{p}_{3}\left(t\right)\right),\\ \frac{\mathrm{d}{p}_{4}\left(t\right)}{\mathrm{d}t}=0, \end{array} \end{array}\end{array}$$
(15)

The set of non-linear governing ordinary differential equations characterized by the dynamical system (15) is for Newtonian fluid subject to same initial conditions described in Eq. (14). In addition, the nonlinear mathematical model say (13) for non-Newtonian fluid can be fractal–fractionalized for Caputo–Fabrizio fractal–fractional differential operator in the Caputo sense as developed in the following equation:

$$\begin{array}{l}{\mathfrak{D}}_{t}^{{\phi }_{1},{\phi }_{2}}{p}_{1}(t)={p}_{4}\left(t\right), \\ \begin{array}{l}{\mathfrak{D}}_{t}^{{\phi }_{1},{\phi }_{2}}{p}_{2}(t)={\alpha }_{5}{p}_{1}\left(t\right)-{p}_{2}\left(t\right)-{\alpha }_{5}{p}_{1}(t){p}_{3}(t), \\ \begin{array}{l}{\mathfrak{D}}_{t}^{{\phi }_{1},{\phi }_{2}}{p}_{3}\left(t\right)=4{\alpha }_{5}\left({p}_{1}\left(t\right){p}_{2}\left(t\right)-{p}_{3}\left(t\right)\right), \\ {\mathfrak{D}}_{t}^{{\phi }_{1},{\phi }_{2}}{p}_{4}\left(t\right)={\alpha }_{4}\left\{\left({\alpha }_{5}-{\alpha }_{1}^{-1}\right){p}_{1}\left(t\right)\right.\\ \left.+\left({\alpha }_{1}^{-1}-1\right){p}_{2}\left(t\right)\right.\\ \left.-\left({\alpha }_{5}-1\right){p}_{1}\left(t\right){p}_{3}\left(t\right)-({\alpha }_{2}+{\alpha }_{1}^{-1}{\alpha }_{4}^{-1}){p}_{4}\left(t\right)\right\}.\end{array}\end{array}\end{array}$$
(16)

Equation (16) is set by replacing the classical derivative into the non-integer form by newly proposed fractal–fractional derivatives of Caputo–Fabrizio that is defined in Eqs. (17–18) for fractal–fractional differential and integral operators, respectively, under the suitable limitation \(0<{\phi }_{1},{\phi }_{2}<1\) [32]

$${\mathfrak{D}}_{t}^{{\phi }_{1},{\phi }_{2}}p\left(t\right)=\int\limits_{0}^{t}M\left({\phi }_{1}\right)\frac{\mathrm{d}}{\mathrm{d}{t}^{{\phi }_{2}}}\mathrm{exp}\left\{\frac{-{\phi }_{1}\left(t-r\right)}{1-{\phi }_{1}}\right\}{\left(1-{\phi }_{1}\right)}^{-1}p\left(r\right) \mathrm{d}r.$$
(17)
$${\mathcal{I}}_{t}^{{\phi }_{1}, {\phi }_{2}}p\left(t\right)=\int\limits_{0}^{t}{\phi }_{1}{\phi }_{2}M\left({\phi }_{1}\right){q}^{{\phi }_{1}-1}p\left(r\right)\mathrm{d}r+\frac{p\left(t\right){r}^{{\phi }_{2}-1}\left(1-{\phi }_{1}\right){\phi }_{1}}{M\left({\phi }_{1}\right)}.$$
(18)

3 Dissipation, point of equilibrium and criteria of stability for nonlinear mathematical model of non-Newtonian fluid

3.1 Dissipation

Dissipation signifies a physical process in which energy becomes irrecoverable. The phenomenon of dissipation discloses the increase and decrease in volume with respect to time. To analyze these aspects, we consider the fractal-fractionalized dynamical system (16) is dissipative, since

$$\begin{array}{c}\nabla V=\frac{\partial \dot{{p}_{1}\left(t\right)}}{\partial {p}_{1}\left(t\right)}+\frac{\partial \dot{{p}_{2}\left(t\right)}}{\partial {p}_{2}\left(t\right)}+\frac{\partial \dot{{p}_{3}\left(t\right)}}{\partial {p}_{3}\left(t\right)}+\frac{\partial \dot{{p}_{4}\left(t\right)}}{\partial {p}_{4}\left(t\right)},\\ =-\left({\alpha }_{1}^{-1}+{\alpha }_{2}{\alpha }_{4}+4{\alpha }_{3}+1\right),\end{array}$$
(19)

For the sake of the endpoints of the corresponding trajectories, a set of initial points in the phase space can occupy a region and the volume can be filled as

$$V\left(\tau \right)=V\left(0\right){e}^{-\left({\alpha }_{1}^{-1}+{\alpha }_{2}{\alpha }_{4}+4{\alpha }_{3}+1\right)\tau }.$$
(20)

Thus, Eq. (20) indicates that the volume decreases monotonically with time.

3.2 Equilibrium points

The stare of art of equilibrium points of non-linear system is at which the dynamical system will stay if it starts from that point. We can have the equilibrium points of fractal–fractional system of equations say (16) by the letting \({\mathfrak{D}}_{t}^{{\phi }_{1},{\phi }_{2}}{p}_{1}\left(t\right)={\mathfrak{D}}_{t}^{{\phi }_{1},{\phi }_{2}}{p}_{2}\left(t\right)={\mathfrak{D}}_{t}^{{\phi }_{1},{\phi }_{2}}{p}_{3}\left(t\right)={\mathfrak{D}}_{t}^{{\phi }_{1},{\phi }_{2}}{p}_{4}\left(t\right)=0\), we get:

$$\begin{array}{l}{p}_{4}\left(t\right)=0, \\ \begin{array}{l}{\alpha }_{5}{p}_{1}\left(t\right)-{p}_{2}\left(t\right)-{\alpha }_{5}{p}_{1}\left(t\right){p}_{3}\left(t\right)=0, \\ \begin{array}{l}4{\alpha }_{5}\left({p}_{1}\left(t\right){p}_{2}\left(t\right)-{p}_{3}\left(t\right)\right)=0, \\ {\alpha }_{4}\left\{\left({\alpha }_{5}-{\alpha }_{1}^{-1}\right){p}_{1}\left(t\right)+\left({\alpha }_{1}^{-1}-1\right){p}_{2}\left(t\right)\right.\\ \left.-\left({\alpha }_{5}-1\right){p}_{1}\left(t\right){p}_{3}\left(t\right)-({\alpha }_{2}+{\alpha }_{1}^{-1}{\alpha }_{4}^{-1}){p}_{4}\left(t\right)\right\}=0,\end{array}\end{array}\end{array}$$
(21)

Equation (21) suggests the equilibrium points as \({{p}_{1}\left(t\right)}_{\mathrm{1,2},3}=\left(\mathrm{0,1},-1\right),{{p}_{2}\left(t\right)}_{\mathrm{1,2},3}=\left(\mathrm{0,1},-1\right)\),\({{p}_{3}\left(t\right)}_{\mathrm{1,2},3}=\left(\mathrm{0,1},1\right)\) and \({{p}_{4}\left(t\right)}_{\mathrm{1,2},3}=\left(\mathrm{0,0},0\right)\). In addition, it is noted that one trivial solution is obtained for the origin in phase space \({{p}_{1}\left(t\right)}_{1}={{p}_{2}\left(t\right)}_{1}={{p}_{3}\left(t\right)}_{1}={{p}_{4}\left(t\right)}_{1}=0\); this trivial solution corresponds a pure heat conduction.

3.3 Criteria of stability

Stability plays critical role of non-linear mathematical model, because it assures that unstable a system in which small perturbations give rise to large variations and stable a system in which small perturbations give rise to small variations. Now, differentiating the non-linear model of non-Newtonian fluid (21), we traced out the Jacobian matrix \({\varvec{J}}\) as

$${\varvec{J}}=\left[\begin{array}{ccc}0& 0& \begin{array}{cc}0& 0\end{array}\\ {\alpha }_{5}{p}_{3}\left(t\right)-{\alpha }_{5}{p}_{3}\left(t\right)-{\alpha }_{5}& -1& \begin{array}{cc}{p}_{1}\left(t\right)-{\alpha }_{5}{p}_{1}\left(t\right)& 0\end{array}\\ \begin{array}{l}4{\alpha }_{3}{p}_{2}\left(t\right)\\ {\alpha }_{1}\left({p}_{3}\left(t\right)-{\alpha }_{5}{p}_{3}\left(t\right)\right)-{\alpha }_{4}({\alpha }_{1}^{-1}-{\alpha }_{5})\end{array}& \begin{array}{l}4{\alpha }_{3}{p}_{1}\left(t\right)\\ {\alpha }_{1}^{-1}{\alpha }_{4}-{\alpha }_{4}\end{array}& \begin{array}{ll}\begin{array}{l}4{\alpha }_{3}\\ {\alpha }_{4}{\alpha }_{5}{p}_{1}\left(t\right)+{\alpha }_{5}{p}_{1}\left(t\right)\end{array}& \begin{array}{l} 0\\ {\alpha }_{1}^{-1}+{\alpha }_{4}{\alpha }_{2}\end{array}\end{array}\end{array}\right].$$
(22)

Generating the characteristics equation for the Eigen values (\({\lambda }_{1},{\lambda }_{2},{\lambda }_{3}\, \mathrm{and }\, {\lambda }_{4}\)) with the help of Eq. (22) for two types (i) pure conduction solution, and (ii) convection solution, we arrived at

$$\left(\lambda -4{\alpha }_{3}\right)\left[{\lambda }^{3}+\left(1+{\alpha }_{2}{\alpha }_{4}+{\alpha }_{1}^{-1}\right){\lambda }^{2}+\left({\alpha }_{1}^{-1}{\alpha }_{4}+{\alpha }_{2}{\alpha }_{4}+{\alpha }_{1}^{-1}-{\alpha }_{5}{\alpha }_{4}\right)\lambda +{\alpha }_{1}^{-1}{\alpha }_{4}(1-{\alpha }_{5})\right]=0,$$
(23)
$$\begin{aligned}\begin{array}{l}{\lambda }^{4}+\left(1+{\alpha }_{4}{\alpha }_{2}+4{\alpha }_{3}+{\alpha }_{1}^{-1}\right){\lambda }^{3}\\ +\left\{{\alpha }_{1}^{-1}\left(1+{\alpha }_{4}+4{\alpha }_{3}\right)+{\alpha }_{5}\left(4{\alpha }_{3}-{\alpha }_{4}\right)+{\alpha }_{4}{\alpha }_{2}\left(4{\alpha }_{3}+1\right)\right\}{\lambda }^{2}\\ +\left\{4{\alpha }_{3}{\alpha }_{1}^{-1}\left({\alpha }_{4}+{\alpha }_{5}\right)+4{\alpha }_{3}{\alpha }_{4}\left({\alpha }_{5}+{\alpha }_{2}-2\right)\right\}\lambda \\ +8{\alpha }_{1}^{-1}{\alpha }_{3}{\alpha }_{4}\left({\alpha }_{5}-1\right)=0, \end{array}\nonumber \\ \end{aligned}$$
(24)

In addition, for Eq. (23), the stability of the fixed point associated with the pure conduction solution \(\left\{{{p}_{1}\left(t\right)}_{1}={{p}_{2}\left(t\right)}_{1}={{p}_{3}\left(t\right)}_{1}={{p}_{4}\left(t\right)}_{1}=0\right\}\) is controlled by the zeros for the eigenvalues (\({\lambda }_{1},{\lambda }_{2},{\lambda }_{3} \mathrm{and }{\lambda }_{4}\)) and the origin loses its stability to the two other steady-state solutions. On the contrary, there is an exchange of stability for Eq. (24), the stability depends on the value of \({\alpha }_{1}\) for which \({\alpha }_{1}<\frac{1+{\alpha }_{4}}{(1-{\alpha }_{2}){\alpha }_{4}}\). While, if \({\alpha }_{1}>\frac{1+{\alpha }_{4}}{(1-{\alpha }_{2}){\alpha }_{4}}\) there is a pair of pure imaginary roots representing over-stability.

4 Generation of numerical scheme for Caputo–Fabrizio fractal–fractional model

To generate the numerical scheme of the nonlinear mathematical model say (13) for non-Newtonian fluid, the methodology takes place as

$$\begin{array}{c}{\mathfrak{D}}_{t}^{{\phi }_{1},{\phi }_{2}}{p}_{1}(t)={\phi }_{1}{t}^{{\phi }_{1}-1}{\omega }_{1}\left({p}_{1},{p}_{2},{p}_{3},{p}_{4},t\right), \\ \begin{array}{c}{\mathfrak{D}}_{t}^{{\phi }_{1},{\phi }_{2}}{p}_{2}(t)={\phi }_{1}{t}^{{\phi }_{1}-1}{\omega }_{2}\left({p}_{1},{p}_{2},{p}_{3},{p}_{4},t\right),\\ \begin{array}{c}{\mathfrak{D}}_{t}^{{\phi }_{1},{\phi }_{2}}{p}_{3}(t)={\phi }_{1}{t}^{{\phi }_{1}-1}{\omega }_{3}\left({p}_{1},{p}_{2},{p}_{3},{p}_{4},t\right),\\ {\mathfrak{D}}_{t}^{{\phi }_{1},{\phi }_{2}}{p}_{4}(t)={\phi }_{1}{t}^{{\phi }_{1}-1}{\omega }_{3}\left({p}_{1},{p}_{2},{p}_{3},{p}_{4},t\right),\end{array}\end{array}\end{array}$$
(25)

Utilizing Eq. (18) on Eq. (25), we have transferred format of Eq. (25) as

$$\begin{array}{l}{p}_{1}(t)={p}_{1}(0)+\frac{{\phi }_{2}{t}^{{\phi }_{2}-1}\left(1-{\phi }_{1}\right)}{M\left({\phi }_{1}\right)}{\omega }_{1}\left({p}_{1},{p}_{2},{p}_{3},{p}_{4},t\right)\\ +\frac{{\phi }_{1}{\phi }_{2}}{M\left({\phi }_{1}\right)}\displaystyle\int\limits_{0}^{t}{\Psi }^{{\phi }_{2}-1}{\omega }_{1}\left({p}_{1},{p}_{2},{p}_{3},{p}_{4},\Psi \right)\mathrm{d\Psi }, \\ \begin{array}{l}{p}_{2}(t)={p}_{2}(0)+\frac{{\phi }_{2}{t}^{{\phi }_{2}-1}\left(1-{\phi }_{1}\right)}{M\left({\phi }_{1}\right)}{\omega }_{2}\left({p}_{1},{p}_{2},{p}_{3},{p}_{4},t\right)\\ +\frac{{\phi }_{1}{\phi }_{2}}{M\left({\phi }_{1}\right)}\displaystyle\int\limits_{0}^{t}{\Psi }^{{\phi }_{2}-1}{\omega }_{2}\left({p}_{1},{p}_{2},{p}_{3},{p}_{4},\Psi \right)\mathrm{d\Psi }, \\ \begin{array}{l}{p}_{3}(t)={p}_{3}(0)+\frac{{\phi }_{2}{t}^{{\phi }_{2}-1}\left(1-{\phi }_{1}\right)}{M\left({\phi }_{1}\right)}{\omega }_{3}\left({p}_{1},{p}_{2},{p}_{3},{p}_{4},t\right)\\ +\frac{{\phi }_{1}{\phi }_{2}}{M\left({\phi }_{1}\right)}\displaystyle\int\limits_{0}^{t}{\Psi }^{{\phi }_{2}-1}{\omega }_{3}\left({p}_{1},{p}_{2},{p}_{3},{p}_{4},\Psi \right)\mathrm{d\Psi }, \\ {p}_{4}(t)={p}_{4}(0)+\frac{{\phi }_{2}{t}^{{\phi }_{2}-1}\left(1-{\phi }_{1}\right)}{M\left({\phi }_{1}\right)}{\omega }_{4}\left({p}_{1},{p}_{2},{p}_{3},{p}_{4},t\right)\\ +\frac{{\phi }_{1}{\phi }_{2}}{M\left({\phi }_{1}\right)}\displaystyle\int\limits_{0}^{t}{\Psi }^{{\phi }_{2}-1}{\omega }_{4}\left({p}_{1},{p}_{2},{p}_{3},{p}_{4},\Psi \right)\mathrm{d\Psi }, \end{array}\end{array}\end{array}$$
(26)

By the setting at \({t}_{\xi +1}\) in Eq. (26), we obtained the numerical scheme as

$$\begin{array}{l}{{p}_{1}}_{\xi +1}\left(t\right)\\ ={p}_{1}(0)+\frac{{\phi }_{2}{t}^{{\phi }_{2}-1}\left(1-{\phi }_{1}\right)}{M\left({\phi }_{1}\right)}{\omega }_{1}\left({{p}_{1}}^{\xi },{{p}_{2}}^{\xi },{{p}_{3}}^{\xi },{{p}_{4}}^{\xi },{t}_{\xi }\right)\\ +\frac{{\phi }_{1}{\phi }_{2}}{M\left({\phi }_{1}\right)}\displaystyle\int\limits_{0}^{{t}_{\xi +1}}{\Psi }^{{\phi }_{2}-1}{\omega }_{1}\left({p}_{1},{p}_{2},{p}_{3},{p}_{4},\Psi \right)\mathrm{d\Psi }, \\ \begin{array}{l}{{p}_{2}}_{\xi +1}\left(t\right)\\ ={p}_{2}(0)+\frac{{\phi }_{2}{t}^{{\phi }_{2}-1}\left(1-{\phi }_{1}\right)}{M\left({\phi }_{1}\right)}{\omega }_{2}\left({{p}_{1}}^{\xi },{{p}_{2}}^{\xi },{{p}_{3}}^{\xi },{{p}_{4}}^{\xi },{t}_{\xi }\right)\\ +\frac{{\phi }_{1}{\phi }_{2}}{M\left({\phi }_{1}\right)}\displaystyle\int\limits_{0}^{{t}_{p+1}}{\Psi }^{{\phi }_{2}-1}{\omega }_{2}\left({p}_{1},{p}_{2},{p}_{3},{p}_{4},\Psi \right)\mathrm{d\Psi }, \\ \begin{array}{l}{{p}_{3}}_{\xi +1}\left(t\right)\\ ={p}_{3}(0)+\frac{{\phi }_{2}{t}^{{\phi }_{2}-1}\left(1-{\phi }_{1}\right)}{M\left({\phi }_{1}\right)}{\omega }_{3}\left({{p}_{1}}^{\xi },{{p}_{2}}^{\xi },{{p}_{3}}^{\xi },{{p}_{4}}^{\xi },{t}_{\xi }\right)\\ +\frac{{\phi }_{1}{\phi }_{2}}{M\left({\phi }_{1}\right)}\displaystyle\int\limits_{0}^{{t}_{p+1}}{\Psi }^{{\phi }_{2}-1}{\omega }_{3}\left({p}_{1},{p}_{2},{p}_{3},{p}_{4},\Psi \right)\mathrm{d\Psi }, \\ {{p}_{4}}_{\xi +1}\left(t\right)\\ ={p}_{4}(0)+\frac{{\phi }_{2}{t}^{{\phi }_{2}-1}\left(1-{\phi }_{1}\right)}{M\left({\phi }_{1}\right)}{\omega }_{4}\left({{p}_{1}}^{\xi },{{p}_{2}}^{\xi },{{p}_{3}}^{\xi },{{p}_{4}}^{\xi },{t}_{\xi }\right)\\ +\frac{{\phi }_{1}{\phi }_{2}}{M\left({\phi }_{1}\right)}\displaystyle\int\limits_{0}^{{t}_{p+1}}{\Psi }^{{\phi }_{2}-1}{\omega }_{4}\left({p}_{1},{p}_{2},{p}_{3},{p}_{4},\Psi \right)\mathrm{d\Psi },\end{array}\end{array}\end{array}$$
(27)

After simplification and solving Eq. (27), we invoked the approximation subject to the defined interval \(\left[{t}_{\xi },{t}_{\xi +1}\right]\) as

$$\begin{array}{l}\begin{array}{l}{{p}_{1}}_{\xi +1}\left(t\right)\\ ={{p}_{1}}_{\xi }+\frac{{\phi }_{2}{t}^{{\phi }_{2}-1}\left(1-{\phi }_{1}\right)}{M\left({\phi }_{1}\right)}{\omega }_{1}\left({{p}_{1}}^{\xi },{{p}_{2}}^{\xi },{{p}_{3}}^{\xi },{{p}_{4}}^{\xi },{t}_{\xi }\right)\\ -\frac{{\phi }_{2}{t}_{\xi -1}^{{\phi }_{2}-1}\left(1-{\phi }_{1}\right)}{M\left({\phi }_{1}\right)}\\ {\times \omega }_{1}\left({{p}_{1}}^{\xi -1},{{p}_{2}}^{\xi -1},{{p}_{3}}^{\xi -1},{4}^{\xi -1},{t}_{\xi -1}\right)\\ +\frac{{\phi }_{1}{\phi }_{2}}{M\left({\phi }_{1}\right)}\displaystyle\int\limits_{{t}_{\xi }}^{{t}_{\xi +1}}{\Psi }^{{\phi }_{2}-1}{\omega }_{1}\left({p}_{1},{p}_{2},{p}_{3},{p}_{4},\Psi \right)\mathrm{d\Psi },\end{array}\\ \begin{array}{l}\begin{array}{l}{{p}_{2}}_{\xi +1}\left(t\right)\\ ={{p}_{2}}_{\xi }+\frac{{\phi }_{2}{t}^{{\phi }_{2}-1}\left(1-{\phi }_{1}\right)}{M\left({\phi }_{1}\right)}{\omega }_{2}\left({{p}_{1}}^{\xi },{{p}_{2}}^{\xi },{{p}_{3}}^{\xi },{{p}_{4}}^{\xi },{t}_{\xi }\right)\\ -\frac{{\phi }_{2}{t}_{\xi -1}^{{\phi }_{2}-1}\left(1-{\phi }_{1}\right)}{M\left({\phi }_{1}\right)}\\ {\times \omega }_{2}\left({{p}_{1}}^{\xi -1},{{p}_{2}}^{\xi -1},{{p}_{3}}^{\xi -1},{4}^{\xi -1},{t}_{\xi -1}\right)\\ +\frac{{\phi }_{1}{\phi }_{2}}{M\left({\phi }_{1}\right)}\displaystyle\int\limits_{{t}_{\xi }}^{{t}_{\xi +1}}{\Psi }^{{\phi }_{2}-1}{\omega }_{2}\left({p}_{1},{p}_{2},{p}_{3},{p}_{4},\Psi \right)\mathrm{d\Psi },\end{array}\\ \begin{array}{l}\begin{array}{l}{{p}_{3}}_{\xi +1}\left(t\right)\\ ={{p}_{3}}_{\xi }+\frac{{\phi }_{2}{t}^{{\phi }_{2}-1}\left(1-{\phi }_{1}\right)}{M\left({\phi }_{1}\right)}{\omega }_{3}\left({{p}_{1}}^{\xi },{{p}_{2}}^{\xi },{{p}_{3}}^{\xi },{{p}_{4}}^{\xi },{t}_{\xi }\right)\\ -\frac{{\phi }_{2}{t}_{\xi -1}^{{\phi }_{2}-1}\left(1-{\phi }_{1}\right)}{M\left({\phi }_{1}\right)}\\ {\times \omega }_{3}\left({{p}_{1}}^{\xi -1},{{p}_{2}}^{\xi -1},{{p}_{3}}^{\xi -1},{4}^{\xi -1},{t}_{\xi -1}\right)\\ +\frac{{\phi }_{1}{\phi }_{2}}{M\left({\phi }_{1}\right)}\displaystyle\int\limits_{{t}_{\xi }}^{{t}_{\xi +1}}{\Psi }^{{\phi }_{2}-1}{\omega }_{3}\left({p}_{1},{p}_{2},{p}_{3},{p}_{4},\Psi \right)\mathrm{d\Psi },\end{array}\\ \begin{array}{l}{{p}_{4}}_{\xi +1}\left(t\right)\\ ={{p}_{4}}_{\xi }+\frac{{\phi }_{2}{t}^{{\phi }_{2}-1}\left(1-{\phi }_{1}\right)}{M\left({\phi }_{1}\right)}{\omega }_{4}\left({{p}_{1}}^{\xi },{{p}_{2}}^{\xi },{{p}_{3}}^{\xi },{{p}_{4}}^{\xi },{t}_{\xi }\right)\\ -\frac{{\phi }_{2}{t}_{\xi -1}^{{\phi }_{2}-1}\left(1-{\phi }_{1}\right)}{M\left({\phi }_{1}\right)}\\ {\times \omega }_{4}\left({{p}_{1}}^{\xi -1},{{p}_{2}}^{\xi -1},{{p}_{3}}^{\xi -1},{4}^{\xi -1},{t}_{\xi -1}\right)\\ +\frac{{\phi }_{1}{\phi }_{2}}{M\left({\phi }_{1}\right)}\displaystyle\int\limits_{{t}_{\xi }}^{{t}_{\xi +1}}{\Psi }^{{\phi }_{2}-1}{\omega }_{4}\left({p}_{1},{p}_{2},{p}_{3},{p}_{4},\Psi \right)\mathrm{d\Psi },\end{array}\end{array}\end{array}\end{array}$$
(28)

Deriving Eq. (27) using the concept of integration and Lagrange polynomial piecewise interpolation, we obtain

$$\begin{array}{l}\begin{array}{l}{{p}_{1}}_{\xi +1}\left(t\right)\\={{p}_{1}}_{\xi }+\frac{{\phi }_{2}{t}^{{\phi }_{2}-1}\left(1-{\phi }_{1}\right)}{M\left({\phi }_{1}\right)}{\omega }_{1}\left({{p}_{1}}^{\xi },{{p}_{2}}^{\xi },{{p}_{3}}^{\xi },{{p}_{4}}^{\xi },{t}_{\xi }\right)\\ -\frac{{\phi }_{2}{t}_{\xi -1}^{{\phi }_{2}-1}\left(1-{\phi }_{1}\right)}{M\left({\phi }_{1}\right)} \\ \begin{array}{l}{\times \omega }_{1}\left({{p}_{1}}^{\xi -1},{{p}_{2}}^{\xi -1},{{p}_{3}}^{\xi -1},{4}^{\xi -1},{t}_{\xi -1}\right)\\ +\frac{{\phi }_{1}{\phi }_{2}}{M\left({\phi }_{1}\right)}\left\{\frac{3h}{2}{t}_{\xi }^{{\phi }_{2}-1}{\omega }_{1}\left({{p}_{1}}^{\xi },{{p}_{2}}^{\xi },{{p}_{3}}^{\xi },{{p}_{4}}^{\xi },{t}_{\xi }\right)\right.\\ \left.-\frac{h}{2}{t}_{\xi -1}^{{\phi }_{2}-1}{\omega }_{1}\left({{p}_{1}}^{\xi -1},{{p}_{2}}^{\xi -1},{{p}_{3}}^{\xi -1},{4}^{\xi -1},{t}_{\xi -1}\right)\right\}, \end{array} \end{array}\\ \begin{array}{l}\begin{array}{l}{{p}_{2}}_{\xi +1}\left(t\right)\\ ={{p}_{2}}_{\xi }+\frac{{\phi }_{2}{t}^{{\phi }_{2}-1}\left(1-{\phi }_{1}\right)}{M\left({\phi }_{1}\right)}{\omega }_{2}\left({{p}_{1}}^{\xi },{{p}_{2}}^{\xi },{{p}_{3}}^{\xi },{{p}_{4}}^{\xi },{t}_{\xi }\right)\\ -\frac{{\phi }_{2}{t}_{\xi -1}^{{\phi }_{2}-1}\left(1-{\phi }_{1}\right)}{M\left({\phi }_{1}\right)} \\ \begin{array}{l}{\times \omega }_{2}\left({{p}_{1}}^{\xi -1},{{p}_{2}}^{\xi -1},{{p}_{3}}^{\xi -1},{4}^{\xi -1},{t}_{\xi -1}\right)\\ +\frac{{\phi }_{1}{\phi }_{2}}{M\left({\phi }_{1}\right)}\left\{\frac{3h}{2}{t}_{\xi }^{{\phi }_{2}-1}{\omega }_{2}\left({{p}_{1}}^{\xi },{{p}_{2}}^{\xi },{{p}_{3}}^{\xi },{{p}_{4}}^{\xi },{t}_{\xi }\right)\right.\\ \left.-\frac{h}{2}{t}_{\xi -1}^{{\phi }_{2}-1}{\omega }_{2}\left({{p}_{1}}^{\xi -1},{{p}_{2}}^{\xi -1},{{p}_{3}}^{\xi -1},{4}^{\xi -1},{t}_{\xi -1}\right)\right\}, \end{array} \end{array}\\ \begin{array}{l}\begin{array}{l}{{p}_{3}}_{\xi +1}\left(t\right)\\ ={{p}_{3}}_{\xi }+\frac{{\phi }_{2}{t}^{{\phi }_{2}-1}\left(1-{\phi }_{1}\right)}{M\left({\phi }_{1}\right)}{\omega }_{3}\left({{p}_{1}}^{\xi },{{p}_{2}}^{\xi },{{p}_{3}}^{\xi },{{p}_{4}}^{\xi },{t}_{\xi }\right)\\ -\frac{{\phi }_{2}{t}_{\xi -1}^{{\phi }_{2}-1}\left(1-{\phi }_{1}\right)}{M\left({\phi }_{1}\right)} \\ \begin{array}{l}{\times \omega }_{3}\left({{p}_{1}}^{\xi -1},{{p}_{2}}^{\xi -1},{{p}_{3}}^{\xi -1},{4}^{\xi -1},{t}_{\xi -1}\right)\\ +\frac{{\phi }_{1}{\phi }_{2}}{M\left({\phi }_{1}\right)}\left\{\frac{3h}{2}{t}_{\xi }^{{\phi }_{2}-1}{\omega }_{3}\left({{p}_{1}}^{\xi },{{p}_{2}}^{\xi },{{p}_{3}}^{\xi },{{p}_{4}}^{\xi },{t}_{\xi }\right)\right.\\ \left.-\frac{h}{2}{t}_{\xi -1}^{{\phi }_{2}-1}{\omega }_{3}\left({{p}_{1}}^{\xi -1},{{p}_{2}}^{\xi -1},{{p}_{3}}^{\xi -1},{4}^{\xi -1},{t}_{\xi -1}\right)\right\}, \end{array} \end{array}\\ \begin{array}{l}{{p}_{4}}_{\xi +1}\left(t\right)\\ \\ ={{p}_{4}}_{\xi }+\frac{{\phi }_{2}{t}^{{\phi }_{2}-1}\left(1-{\phi }_{1}\right)}{M\left({\phi }_{1}\right)}{\omega }_{4}\left({{p}_{1}}^{\xi },{{p}_{2}}^{\xi },{{p}_{3}}^{\xi },{{p}_{4}}^{\xi },{t}_{\xi }\right)\\ -\frac{{\phi }_{2}{t}_{\xi -1}^{{\phi }_{2}-1}\left(1-{\phi }_{1}\right)}{M\left({\phi }_{1}\right)} \\ \begin{array}{l}{\times \omega }_{4}\left({{p}_{1}}^{\xi -1},{{p}_{2}}^{\xi -1},{{p}_{3}}^{\xi -1},{4}^{\xi -1},{t}_{\xi -1}\right)\\ +\frac{{\phi }_{1}{\phi }_{2}}{M\left({\phi }_{1}\right)}\left\{\frac{3h}{2}{t}_{\xi }^{{\phi }_{2}-1}{\omega }_{4}\left({{p}_{1}}^{\xi },{{p}_{2}}^{\xi },{{p}_{3}}^{\xi },{{p}_{4}}^{\xi },{t}_{\xi }\right)\right.\\ \left.-\frac{h}{2}{t}_{\xi -1}^{{\phi }_{2}-1}{\omega }_{4}\left({{p}_{1}}^{\xi -1},{{p}_{2}}^{\xi -1},{{p}_{3}}^{\xi -1},{4}^{\xi -1},{t}_{\xi -1}\right)\right\}, \end{array}\end{array}\end{array}\end{array}\end{array}$$
(29)

Writing Eq. (29), we investigated the numerical scheme for Caputo–Fabrizio fractal–fractional operator as

$$\begin{array}{c}\begin{array}{c}{{p}_{1}}_{\xi +1}\left(t\right)={{p}_{1}}_{\xi }+{\phi }_{2}{t}_{\xi }^{{\phi }_{2}-1}\left(\frac{1-{\phi }_{1}}{M({\phi }_{1})}+\frac{3{\phi }_{1}h}{2M({\phi }_{1})}\right){\omega }_{1}\left({{p}_{1}}^{\xi },{{p}_{2}}^{\xi },{{p}_{3}}^{\xi },{{p}_{4}}^{\xi },{t}_{\xi }\right)-{\phi }_{2}{t}_{\xi -1}^{{\phi }_{2}-1}\left(\frac{1-{\phi }_{1}}{M\left({\phi }_{1}\right)}+\frac{{\phi }_{1}h}{2M\left({\phi }_{1}\right)}\right)\\ \times {\omega }_{1}\left({{p}_{1}}^{\xi -1},{{p}_{2}}^{\xi -1},{{p}_{3}}^{\xi -1},{4}^{\xi -1},{t}_{\xi -1}\right), \end{array}\\ \begin{array}{c}\begin{array}{c}{{p}_{2}}_{\xi +1}\left(t\right)={{p}_{2}}_{\xi }+{\phi }_{2}{t}_{\xi }^{{\phi }_{2}-1}\left(\frac{1-{\phi }_{1}}{M({\phi }_{1})}+\frac{3{\phi }_{1}h}{2M({\phi }_{1})}\right){\omega }_{2}\left({{p}_{1}}^{\xi },{{p}_{2}}^{\xi },{{p}_{3}}^{\xi },{{p}_{4}}^{\xi },{t}_{\xi }\right)-{\phi }_{2}{t}_{\xi -1}^{{\phi }_{2}-1}\left(\frac{1-{\phi }_{1}}{M\left({\phi }_{1}\right)}+\frac{{\phi }_{1}h}{2M\left({\phi }_{1}\right)}\right)\\ \times {\omega }_{2}\left({{p}_{1}}^{\xi -1},{{p}_{2}}^{\xi -1},{{p}_{3}}^{\xi -1},{4}^{\xi -1},{t}_{\xi -1}\right), \end{array}\\ \begin{array}{c}\begin{array}{c}{{p}_{3}}_{\xi +1}\left(t\right)={{p}_{3}}_{\xi }+{\phi }_{2}{t}_{\xi }^{{\phi }_{2}-1}\left(\frac{1-{\phi }_{1}}{M({\phi }_{1})}+\frac{3{\phi }_{1}h}{2M({\phi }_{1})}\right){\omega }_{3}\left({{p}_{1}}^{\xi },{{p}_{2}}^{\xi },{{p}_{3}}^{\xi },{{p}_{4}}^{\xi },{t}_{\xi }\right)-{\phi }_{2}{t}_{\xi -1}^{{\phi }_{2}-1}\left(\frac{1-{\phi }_{1}}{M\left({\phi }_{1}\right)}+\frac{{\phi }_{1}h}{2M\left({\phi }_{1}\right)}\right)\\ \times {\omega }_{3}\left({{p}_{1}}^{\xi -1},{{p}_{2}}^{\xi -1},{{p}_{3}}^{\xi -1},{4}^{\xi -1},{t}_{\xi -1}\right), \end{array}\\ \begin{array}{c}{{p}_{4}}_{\xi +1}\left(t\right)={{p}_{4}}_{\xi }+{\phi }_{2}{t}_{\xi }^{{\phi }_{2}-1}\left(\frac{1-{\phi }_{1}}{M({\phi }_{1})}+\frac{3{\phi }_{1}h}{2M({\phi }_{1})}\right){\omega }_{4}\left({{p}_{1}}^{\xi },{{p}_{2}}^{\xi },{{p}_{3}}^{\xi },{{p}_{4}}^{\xi },{t}_{\xi }\right)-{\phi }_{2}{t}_{\xi -1}^{{\phi }_{2}-1}\left(\frac{1-{\phi }_{1}}{M\left({\phi }_{1}\right)}+\frac{{\phi }_{1}h}{2M\left({\phi }_{1}\right)}\right)\\ \times {\omega }_{4}\left({{p}_{1}}^{\xi -1},{{p}_{2}}^{\xi -1},{{p}_{3}}^{\xi -1},{4}^{\xi -1},{t}_{\xi -1}\right).\end{array}\end{array}\end{array}\end{array}$$
(30)

5 Simulated results and conclusion

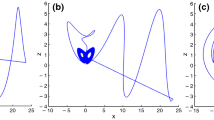
By applying the concept of non-Newtonian fluid (viscoelastic fluids) so called Oldroydian fluid saturated porous medium, we deduced governing system of non-Newtonian fluid (13), governing system of Newtonian fluid (15) and governing fractal-fractionalized system of non-Newtonian fluid (16) to describe the dynamics of thermal convection. The effects of non-Newtonian verses Newtonian fluids are performed on the basis of numerical simulations for the chaotic convection and the thermal efficiency. For the sake of industrial purpose subject to the optimization of thermal analysis, the techniques of fractal–fractional differentials can illustrate the arbitrary trajectories of a fluid particle convected by time in which considerable amount of energy consumption through the chaotic behavior can be estimated. In addition, the phase portraits for Newtonian verse non-Newtonian fluids for \({p}_{1}\left(t\right)-{p}_{2}\left(t\right),{p}_{1}\left(t\right)-{p}_{3}\left(t\right),{p}_{2}\left(t\right)-{p}_{1}\left(t\right),{p}_{3}\left(t\right)-{p}_{1}\left(t\right),{p}_{1}\left(t\right){p}_{2}\left(t\right){p}_{3}\left(t\right)\) and \({p}_{1}\left(t\right){p}_{2}\left(t\right){p}_{4}\left(t\right)\) planes with initial conditions \({p}_{1}\left(0\right)={p}_{2}\left(0\right)={p}_{3}\left(0\right)={p}_{4}(0)=0.9\) taking in consideration the parametric values as \({\alpha }_{1}=1,{\alpha }_{2}=0.2,{\alpha }_{3}=0.5,{\alpha }_{4}=100,{\alpha }_{5}=15\) have depicted. The comparative performances for chaotic configuration on the basis of phase portraits for Newtonian fluid and phase portraits for non-Newtonian fluid have been highlighted in this regard. In addition, Fig. 1 is prepared for showing the contrasting behavior of phase portraits for Newtonian fluid verses non-Newtonian fluid via Caputo–Fabrizio fractal–fractional differential operator for \({p}_{2}\left(t\right)-{p}_{1}\left(t\right)\) plane (Fig. 2). It can be observed that chaotic trajectories of non-Newtonian fluid are more complex and amorphous than chaotic trajectories of Newtonian fluid. Meanwhile, \({p}_{3}\left(t\right)-{p}_{1}\left(t\right)\) plane has also similar trend in structures. In this continuity, the comparison between phase portraits for Newtonian fluid and phase portraits for non-Newtonian fluid as depicted in Fig. 3 as \({p}_{3}\left(t\right)-{p}_{2}\left(t\right)\) has showed continuous and non-continuous states in thermal performance. Physically, non-continuous case induces a better thermal performance in comparison with the continuous case. An interested observation for non-Newtonian fluids via Caputo–Fabrizio fractal fractional differential operator is explored; this because that all characteristics of non-Newtonian fluid cannot be described due to inadequacy of Navier–Stokes equations. Figure 4 discloses the hidden aspects of purely non-Newtonian fluids in terms of chaotic behavior. It is noted that each plane \({p}_{4}\left(t\right)-{p}_{1}\left(t\right),{p}_{4}\left(t\right)-{p}_{2}\left(t\right)\) and \({p}_{4}\left(t\right)-{p}_{3}\left(t\right)\) has typical and divergent chaotic geometries for convective heat transfer. The resultant chaotic behavior observed in Fig. 4 reflects sensitivity to initial conditions and kinematic mechanisms among governing equations. The similar trend can also be seen in Fig. 5 that is illustrated for 3D planes for the observations of phase portraits for Newtonian fluid and phase portraits for non-Newtonian fluid. In brevity, it is believed that Fig. 5 has prototype chaotic comparison between fluids that confirm the thermal performances of the selected geometry as stated in problem statement. Figure 6 presents phase portrait for Newtonian fluid for \({p}_{1}\left(t\right)-{p}_{2}\left(t\right)\) plane, \({p}_{1}\left(t\right)-{p}_{3}\left(t\right)\) when fractional parameter and fractal parameter are varying. While, a similar phase portrait can be obtained for non-Newtonian fluid for \({p}_{1}\left(t\right)-{p}_{2}\left(t\right)\) plane, \({p}_{1}\left(t\right)-{p}_{3}\left(t\right)\) when fractional parameter and fractal parameter are varying. For the sake of future recommendation, some latest extensions of fractional differential operators with different domains of definitions can extend this research work in the field of fluids. The latest extensions of fractional differential operators with different domains of definitions are (i) Abu-Shady-Kaabar fractional differential operator and (ii) Yang-Abdel-Cattani fractional differential operator.

Fig. 1
figure 1

Phase portrait for Newtonian verse non-Newtonian fluids for \({p}_{1}\left(t\right)-{p}_{2}\left(t\right)\) plane with initial conditions \({p}_{1}\left(0\right)={p}_{2}\left(0\right)={p}_{3}\left(0\right)={p}_{4}(0)=0.9\) and \({\alpha }_{1}=1,{\alpha }_{2}=0.2,{\alpha }_{3}=0.5,{\alpha }_{4}=100,{\alpha }_{5}=15\)

Full size image
Fig. 2
figure 2

Phase portrait for Newtonian verse non-Newtonian fluids for \({p}_{1}\left(t\right)-{p}_{3}\left(t\right)\) plane with initial conditions \({p}_{1}\left(0\right)={p}_{2}\left(0\right)={p}_{3}\left(0\right)={p}_{4}(0)=0.9\) and \({\alpha }_{1}=1,{\alpha }_{2}=0.2,{\alpha }_{3}=0.5,{\alpha }_{4}=100,{\alpha }_{5}=15\)

Full size image
Fig. 3
figure 3

Phase portrait for Newtonian verse non-Newtonian fluids for \({p}_{1}\left(t\right)-{p}_{3}\left(t\right)\) plane with initial conditions \({p}_{1}\left(0\right)={p}_{2}\left(0\right)={p}_{3}\left(0\right)={p}_{4}(0)=0.9\) and \({\alpha }_{1}=1,{\alpha }_{2}=0.2,{\alpha }_{3}=0.5,{\alpha }_{4}=100,{\alpha }_{5}=15\)

Full size image
Fig. 4
figure 4

Phase portrait for purely non-Newtonian fluid for \({p}_{1}\left(t\right)-{p}_{4}\left(t\right)\) plane, \({p}_{1}\left(t\right)-{p}_{3}\left(t\right)\) plane and \({p}_{1}\left(t\right)-{p}_{3}\left(t\right)\) plane with initial conditions \({p}_{1}\left(0\right)={p}_{2}\left(0\right)={p}_{3}\left(0\right)={p}_{4}(0)=0.9\) and \({\alpha }_{1}=1,{\alpha }_{2}=0.2,{\alpha }_{3}=0.5,{\alpha }_{4}=100,{\alpha }_{5}=15\)

Full size image
Fig. 5
figure 5

Three-dimensional phase portrait for Newtonian verse non-Newtonian fluids for \({p}_{1}\left(t\right){p}_{2}\left(t\right){p}_{3}\left(t\right)\) plane and \({p}_{1}\left(t\right){p}_{2}\left(t\right){p}_{4}\left(t\right)\) plane, respectively, with initial conditions \({p}_{1}\left(0\right)={p}_{2}\left(0\right)={p}_{3}\left(0\right)={p}_{4}(0)=0.9\) and \({\alpha }_{1}=1,{\alpha }_{2}=0.2,{\alpha }_{3}=0.5,{\alpha }_{4}=100,{\alpha }_{5}=15\)

Full size image
Fig. 6
figure 6

Phase portrait for Newtonian fluid for \({p}_{1}\left(t\right)-{p}_{2}\left(t\right)\) plane, \({p}_{1}\left(t\right)-{p}_{3}\left(t\right)\) plane with initial conditions \({p}_{1}\left(0\right)={p}_{2}\left(0\right)={p}_{3}\left(0\right)={p}_{4}(0)=0.9\) and \({\alpha }_{1}=1,{\alpha }_{2}=0.2,{\alpha }_{3}=0.5,{\alpha }_{4}=100,{\alpha }_{5}=15\) when fractional parameter \({\phi }_{1}=0.988\) and fractal parameter is \({\phi }_{2}=0.89\)

Full size image