1 Introduction

Efficient coupling between light pulses and the acoustic phonons of a material can be realized using different types of opto-acoustic transducer, enabling the generation of coherent wave-packet of phonons with picoseconds pulse duration and nanometric spatial extent in the material. Such acoustic pulses find applications in nano-scale imaging of mechanical properties [1], or in fundamental studies on frequency-dependent sound attenuation, e.g., in disordered media [2,3,4]. Thin metallic films are frequent choices for opto-acoustic transducers [5, 6]. Due to the strong optical absorption of metals, the temperature of a metallic film is rapidly increased following its pulsed illumination resulting in thermal expansion, which launches a wave-packet of acoustic phonons propagating away from the film at the local speed of sound. The spectral content of the acoustic wave-packet is strongly dependent on the thickness of the metallic thin film and the properties of its interface with the investigated material, which determine the frequencies and damping rates of the film vibrations.

Several investigations were also conducted with size-reduced transducers, which is crucial for improving the lateral resolution in imaging applications (lateral resolution being limited by diffraction to a few hundreds of nanometers in the film case). Quantum wells were, for instance, used as acoustic sources [7]. Additionally, attempts were made for using single metallic nanoparticles as transducers, whose vibrational eigenmodes have been widely investigated [8,9,10,11,12,13,14,15,16]. Several studies confirmed the potential of nano-structures for transduction of longitudinal and transverse acoustic waves. The acoustic waves emitted by single nanodisks and nanowires in their supporting substrate could, for instance, be imaged using transmission setup [17, 18]. The propagation of longitudinal waves generated by the laser excitation of single gold nanoplates and nanorods in their supporting substrate was detected by their associated time-domain Brillouin oscillations [19, 20]. In another recent study, two close single plasmonic nanoantennas were used as emitter and receiver of surface acoustic waves [21].

Ensembles of metal nanoparticles represent an intermediate case between those discussed above (continuous film and single nanoparticle), and are expected to produce acoustic waves with more complex wavefronts. In earlier studies, near-coalescence metallic nanoislands were demonstrated as excellent candidates for fabricating nano-scale electronic components [22,23,24], surface-enhanced Raman scattering [25], and pioneering sensing approaches [26], to mention a few. Additionally, there have been numerous investigations on excitation of acoustic vibration modes on nanoparticle ensembles. These studies, mostly performed on nanoparticles embedded in a solid matrix or in solution, have in particular addressed in detail the size, shape, and environment dependence of vibrational frequencies (quantitative investigations of vibrational quality factors being challenging due to spurious inhomogeneous effects associated with inherent size and shape dispersion) [27,28,29,30,31,32,33,34]. However, the detection of coherent acoustic pulse emission by ensembles of inhomogeneous nanoparticles in their environment has not been demonstrated yet. In this context, the goal of the present work was to determine whether metal nanoparticles dispersed over a surface (constituting a non-continuous and inhomogeneous metal film) could act as an opto-acoustic transducer emitting optically detectable acoustic waves, and to clarify the role of the morphological parameters of such inhomogeneous nanoparticle ensembles in the efficiency of the acoustic wave excitation. We report here the detection of coherent acoustic pulses emitted by a layer of silver nanoparticles with broad size dispersion and propagating over several microns distances in the underlying glass substrate. Four samples with various interparticle distances and shape properties are investigated, and the attenuation of the Fourier spectral components are monitored in the acoustic frequency range of 40–50 GHz during the propagation away from the acoustic sources.

2 Experimental methods

Three TiO\(_2\):Ag:TiO\(_2\) multilayer samples with different nominal Ag thicknesses (1.5 nm, 5 nm, and 10 nm) are prepared using physical vapor deposition at room temperature on N-BK7 glass substrate. The chemical composition of the substrate is provided as 69.13 SiO\(_2\), 10.75 B\(_2\)O\(_3\), 10.40 Na\(_2\)O, 6.29 K\(_2\)O, 3.07 BaO and 0.36 Sb\(_2\)O\(_3\) in wt %. Ag layers are obtained from Ag granules, and TiO\(_2\) layers from pure TiO\(_2\) material. Due to the ultrathin Ag layers, non-spherical, near-coalescence Ag nanoislands are obtained. The thicknesses of both TiO\(_2\) layers are fixed at 30 nm in all samples. The conditions of the sample preparations and the transmittance spectra can be found in Supplementary Information.

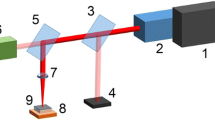
The picosecond acoustics experiment is based on a Yb:KGW femtosecond laser (PHAROS from Light Conversion) operating at 60 kHz, with a pulse duration of  200 fs, central wavelength of 1030 nm, and output power of 6 W. The pump beam is obtained from an OPA and a subsequent stage of harmonic generator (both from Light Conversion) capable of tuning the pump wavelength from 210 nm to 20 \(\upmu\)m. Pump wavelengths are chosen to directly excite the broad localized surface plasmon resonance (LSPR) of the different samples, i.e., 1100 nm, 1000 nm and 700 nm respectively for the three initial samples with decreasing Ag thicknesses, and 540 nm for an additional laser-processed sample described in the next section. The time-resolved experiments are conducted in a commercial pump-probe arrangement (HARPIA from Light Conversion). The pump is chopped and focused on the sample at nearly normal incident angle. The probe is time-delayed with respect to the pump with a maximum time delay up to 7 ns, and then frequency-doubled to produce 515 nm beam using a beta barium borate crystal. Spectrally broad white-light continuum (350–650 nm) is generated in a 4 mm-thick sapphire crystal; subsequently, the beam is focused on the sample by a parabolic mirror at normal incidence. The optical alignment of the probe beam was optimized prior to every experiment to avoid misalignment artefacts. The pump and the probe beam spot diameters are around 100 \(\upmu\)m and 90 \(\upmu\)m, respectively. The transmitted probe light is collected using a spectrograph (Kymera 193i, OXFORD instruments) equipped with an NMOS linear image sensor (HAMAMATSU S8380-256Q). The spectral resolution is  1.7 nm. The chopper allows the pump beam to be blocked half of the time to ensure the measurement of probe pulse intensity with and without pump pulse, at both states using 0.5 ms acquisition time (integrating over 32 probe pulses). One differential absorption spectrum at a fixed delay \(\varDelta A (\lambda , t)\) is a result of averaging 10,000 spectra.

The detection principle of the coherent acoustic pulse propagation is provided as follows. Each wavelength in the probe beam is partially transmitted and back-reflected by single phonon frequency component (phase-matched phonon) in the acoustic wave-packet via Brillouin scattering process, governed by the law of the momentum conservation \(k_{\text {phonon}} = 2k_{\text {photon}}\), where \(k_{\text {phonon}}\) and \(k_{\text {photon}}\) are the phonon and photon wave vectors, respectively. The back-reflected portion of the beam escapes the sample after reflection on the transducer layer, and interferes with the transmitted light in the spectrograph. As the strain pulse propagates at the local speed of sound in the substrate, the interference pattern periodically varies leading to oscillating signal with the time delay t. The temporal period of the oscillating signal is derived as

$$\begin{aligned} T = \frac{\lambda _0}{2n v}, \end{aligned}$$
(1)

where \(\lambda _0\) is the vacuum probe wavelength, v is the local sound velocity, and n is the refractive index of the medium (at \(\lambda _0\) wavelength). T corresponds to the inverse of the frequency of the phase-matched acoustic phonon. When attenuation is present during the propagation of the wave-packet, the amplitude decrease of the oscillations provides information on the attenuation of the phase-matched Fourier component.

3 Results and discussion

In Fig. 1 panel A, the first three columns contain plan-view high-angle annular dark-field scanning transmission electron microscope (HAADF-STEM) images of the samples with different initial nominal thicknesses (10 nm, 5 nm, 1.5 nm), the corresponding cross-section images, and the 2D maps of transient absorption spectra after thermal background removal. The fourth column contains an additional measurement performed on the Ag: 5 nm sample (sample with 5 nm-thick initial Ag thickness) after submission to laser processing by 515 nm wavelength using 31 mJ/cm\(^2\) laser fluence to persistently reshape the initial nanoparticle size and shape distribution. The details of the laser reshaping experiment can be found in the Supplementary information. As a result, rather spherical nanoparticles distribution with considerably smaller surface covering is achieved. In this figure, \(ff_{Ag}\) stands for surface filling factor of the Ag nanoparticles. It exhibits slightly decreasing values from 68 to 42 \(\%\) for the three initial samples with decreasing Ag thicknesses, and drastically drops to 18 \(\%\) for the laser-processed sample. As revealed by the cross-section HAADF-STEM image of this sample, the multilayer system collapses into a single layer of TiO\(_2\) with nanoparticles embedded due to the high laser-induced temperature rise in the material. In each cross-section image, massive nanoparticle traces can be observed in the TiO\(_2\) layers, which results from the TEM lamella preparation.

Fig. 1
figure 1

Investigations of acoustic pulse emission. A Plan-view and cross-section HAADF-STEM images of the different samples and the 2D maps of the corresponding transient absorption spectra after thermal background subtraction highlighting the Brillouin signals. \(ff_{Ag}\) stands for Ag filling factor. Note that even the 2D carpet of the laser-processed sample evidences small amplitude Brillouin signal between 380 and 400 nm. B Example time traces probed at 388 nm for each sample before background removal (raw experimental data). The trace of the laser-processed sample (green) is shifted vertically for clear observation of the residual Brillouin oscillation. C Plot of vibration period vs. probe wavelength for the different samples. The data from the laser-processed sample are not plotted due to the small vibration amplitude and wavelength range. D Fourier amplitude spectrum of the representative probe wavelength of 430 nm (from Ag: 10 nm sample data) indicating the presence of a single frequency component of 42.7 GHz

Full size image

The comparison of the STEM images at different nominal thicknesses reveals two main structural characteristics. First, the correlation between the Ag thickness and the average neighboring distance between the adjacent nanoparticles (nanoislands), i.e., smaller Ag thickness, results in higher nanoparticle separation. This results in smaller LSPR coupling, reflected as a blue-shifting resonance in the steady-state spectra, as observable in Supplementary Information in Fig. S2. Second, the morphology and connectivity of the film nanoparticles, i.e., the thickest sample contains highly connected complex structures, which transform into more simple distributions of clearly separated rod-like (Ag: 5 nm) and rather spherical particles (Ag: 1.5 nm and laser-processed sample). In the latter two cases, nanoparticle diameters vary on a scale from a few nm until few tens of nm (typically 30–40 nm), and the average interparticle distance is estimated in the range of 10 nm and less in all samples. The Ag: 10 nm sample is the one with the morphology closest to the one used in the traditional time-resolved Brillouin scattering experiments, where continuous metallic layers with typical thicknesses of few tens of nanometers are used as transducers.

The 2D carpets of the transient absorption spectra reveal the presence of an oscillatory signal for all samples (Fig. 1A), which is ascribed to Brillouin oscillations induced by the propagation of an acoustic pulse in the underlying glass substrate. The amplitudes of these oscillations exhibit strong probe wavelength-dependence. Beside the observed large amplitudes, Brillouin oscillations are not detected in the spectral region 540–590 nm due to low probe intensity, and the amplitude is strongly disturbed by noise in the region 450–490 nm. It is important to notice that the 2D carpet of the laser-processed sample also contains an oscillatory signal component in the reduced wavelength range of 380–400 nm. However, its amplitude is considerably smaller compared to the three intact samples. Image B shows the example time trace at 388 nm probe wavelength for the four samples (the green curve was shifted vertically for clarity). The comparison between the oscillation amplitudes in the different samples reveals no relevant difference, at the exception of the laser-processed one, which exhibits a substantially lower nanoparticle filling factor than the others. This observation suggests that \(ff_{Ag}\) is a determining factor in the efficiency of acoustic pulse generation. Image C shows that the period of the vibrations linearly increases with probe wavelength from 20.8 to 35.3 ps for the three intact samples, in agreement with Eq. (1) and the low dispersion of the glass refractive index on this probe wavelength range. The period at each probe wavelength was determined based on the raw time traces by averaging ten oscillations. Image D shows the Fourier amplitude spectrum of a representative time trace at 430 nm probe wavelength (Ag: 10 nm sample) with a single spectral peak at 42.7 GHz, i.e., the phase-matched acoustic frequency at this particular wavelength.

The sound velocity of 5993 ± 14 m/s in N-BK7 in the investigated acoustic frequency range is determined based on the expression of the oscillation period using the average of the determined period at each probe wavelength and the refractive index spectrum of N-BK7 provided by Schott. For comparison, the sound velocity in vitreous silica thin films measured by the same experimental technique reported by Ayrinhac et al., 5995 ± 10 m/s is very close to our value [35]. The similarity of these determined sound velocities is consistent with the fact that silica is the main component of N-BK7 glass.

The amplitude of the oscillations exhibits a non-monotonic decrease tendency towards longer probe wavelength, as shown in Fig. 2, for the three intact samples. The linear absorption of the different samples (observe the transmittance spectra in Fig. S2) strongly increases towards higher Ag layer thickness at the pump wavelengths which results in an unreliable quantitative comparison between the oscillation amplitudes of the different samples. Figure 2 intends to demonstrate exclusively the decreasing tendency of the oscillation amplitudes towards longer wavelengths independently of the investigated sample. The amplitude values contain the average of the first three cycles in the vibration for each wavelength. The decreasing tendency in the oscillation amplitude is not related to the excitation of the acoustic pulse, since the power of the pump laser is identical for all the probe wavelengths, nor to the spectral intensity profile of the probe laser. One should note that the probe photon energy for a shorter wavelength is higher and closer to the energy band gap of the N-BK7 glass substrate. For Schott BK7 borosilicate glass, the energy band gap was calculated from the transmission spectrum of the glass to be 4.28 eV [36]. The blue wavelength range should be more sensitive to the band-gap energy modulation induced by the traveling acoustic pulse, but less sensitivity is expected for higher probe wavelengths with lower energies. In other words, the photoelastic coupling for the N-BK7 glass is stronger for a blue probe wavelength than for a longer wavelength [37].

Fig. 2
figure 2

The probe wavelength-dependence of the Brillouin signal’s amplitude for the different samples

Full size image

Ishioka et al. studied the probe energy dependence of the coherent phonons in GaP and Si in the energy range 1.97–2.6 eV [38]. They measured that the differential reflectivity amplitude of the oscillations increased significantly for GaP approaching 2.6 eV, but moderately for Si. Baydin et al. measured drastic increase of the amplitude of Brillouin oscillations towards higher probe energy, and it is maximized near the direct optical transitions of GaP [39]. Above the direct band gap, a non-trivial wavelength-dependence was measured. Additionally, a theoretical model was developed to quantitatively explain the probe energy dependence of the oscillation amplitudes. Assuming weak strain amplitudes, i.e., strains < 10\(^4\), and that the temporal shape of the pulse can be described by derivative of a Gaussian, a simple expression was derived stating that the differential reflectivity amplitude of the oscillation is proportional to the photon energy derivative of the complex dielectric function \(\epsilon:\)

$$\begin{aligned} A_{\text {osc}} \propto \Big | \frac{\partial \epsilon }{\partial E} \Big | = \sqrt{\left( \frac{\partial \epsilon _r}{\partial E}\right) ^2 + \left( \frac{\partial \epsilon _i}{\partial E}\right) ^2}, \end{aligned}$$
(2)

where \(\epsilon _r\) and \(\epsilon _i\) are the real and imaginary parts, respectively [39]. In consequence, the dielectric function of the medium in which the acoustic pulse propagates determines the probe wavelength-dependence of the Brillouin oscillation’s amplitude. Qualitatively, the non-monotonic decreasing tendency of the measured oscillation amplitude in the present case (Fig. 2) could also be related to the \(|\frac{\partial \epsilon }{\partial E}|\) spectrum of the glass substrate. In glass, one can neglect the second term in Eq. (2) in the visible wavelength range as \(\epsilon _i<< \epsilon _r\), and therefore, the oscillation amplitudes are determined by the energy derivative of the real dielectric function (the spectra of \(\epsilon _i\) and \(\epsilon _r\), and the calculated \(|\frac{\partial \epsilon }{\partial E} |\) for N-BK7 can be found in the Supplementary Information). As pointed out in [39], the oscillation amplitude (measured in reflection configuration) is proportional to the \(|\frac{\partial \epsilon }{\partial E} |\) spectrum, even at probe photon energies far below the direct optical transition threshold in GaP. In the present work, the oscillation amplitudes are investigated far below the band gap of a dielectric medium, measured in transmission configuration, In consequence of these differences, the discussion is considered being exclusively qualitative.

Due to the rapidly decreasing vibration amplitude, the wavelength-dependent attenuation is investigated exclusively for the spectral region of 380–450 nm in the followings. The logarithm of the oscillation amplitude as a function of the oscillation number is reported in Fig. 3 using the representative example time trace at 430 nm probe wavelength, where circles show the determined amplitude of the oscillations, and red solid line shows linear fit to the data points.

Fig. 3
figure 3

The decay of the logarithm of the oscillation amplitude with increasing oscillation number for the representative example time trace at 430 nm probe wavelength (from Ag:10 nm sample). The linear fit to the measured data points is indicated by red line

Full size image

The data fit on a straight line in presence of exponential decay of the phonon frequency components during the propagation in the glass. Deviation from exponential decay would indicate acoustic pulse diffraction, i.e., spreading of the pulse during propagation, or significant density of inhomogeneities inside the glass [40]. From the fit of the experimental data to the straight line, one can conclude that the amplitude decay is exponential with propagation distance d, i.e., \(A(d)\propto e^{-\alpha d}\), where \(\alpha\) is the attenuation coefficient determined from the linear fit. The \(\alpha\) attenuation coefficient was determined for each wavelength in the range 375–460 nm for the three intact samples, covering the acoustic frequency range 39.6\(-\)48.1 GHz. The latter is obtained as the inverse of the oscillation periods. The acoustic linewidth parameters that would have been measured in a scattering experiment [41,42,43,44] were calculated as \(\varGamma /2\pi =\alpha v/\pi\), where v is the previously obtained sound velocity in N-BK7. The obtained linewidth values are reported in Fig. 4. For comparison, data measured in SiO\(_2\) using visible Brillouin light scattering (vis-BLS) technique at three scattering angles [45] and UV-BLS technique measured at two angles [46] or at two wavelengths [47] are also plotted. The similar sound attenuations in the present multicomponent glass and in chemically pure SiO\(_2\) are not surprising, because N-BK7 glass has a high percentage of SiO\(_2\) (69\(\%\) in wt\(\%\)) in its composition. The general tendency of non-monotonic increasing attenuation rate towards higher acoustic frequencies is reflected in our data on this narrow frequency range.

The acoustic frequency dependence of the sound attenuation in disordered materials originates from an interplay of several physical mechanisms from the ultrasonic to the THz frequency regions at different temperatures. The room temperature sound damping is ruled by two mechanisms, i.e., the internal friction due to anharmonic interactions of the acoustic wave with the thermal phonon bath and thermally activated relaxation (TAR) of structural inhomogeneities, in the acoustic frequency region of 10 GHz until 100s of GHz [35, 48]. At 35 GHz and room temperature, the sound damping due to anharmonicity contributes nearly twice compared to thermally activated relaxation [4]. This results in a non-trivial frequency-dependent attenuation; however, the tendency could be approximated by a quadratic scaling in agreement with the Akhiezer mechanism [49, 50]. This was supported by experimental characterizations using ultrasonics and BLS techniques [45,46,47]. Theoretical models have been developed and proposed to describe the relaxation processes of sound attenuation in glasses [3, 51,52,53]. Towards higher frequencies, the contribution of TAR exhibits saturation and anharmonicity becomes the dominant source of sound damping approaching the frequency region of 200 GHz. Further increasing acoustic frequencies around THz exhibits damping proportional to the fourth power of the acoustic frequency, as measured in densified silica and lithium diborate glasses by inelastic X-ray scattering [42, 43]. The increased rate of damping is expected for elastic scattering in a statistically disordered medium compatible with the Rayleigh law [49, 50, 54]. In the middle acoustic frequencies, in the region of hundreds of GHz until the onset of the Rayleigh regime, a non-trivial frequency dependence was reported by several experimental works [6, 35, 48, 55]. As shown in the reference [35], the data points from the BLS experiments in Fig. 4 align precisely to the theoretical prediction of the sum of anharmonicity and TAR mechanisms with nearly two times stronger contribution from anharmonicity. Based on the quantitative fit of our data points among the BLS data, we suggest that these two mechanisms rule the sound attenuation in the present N-BK7 multicomponent glass as well in the acoustic frequency region of tens of GHz.

Fig. 4
figure 4

The determined linewidths as a function of the acoustic frequency for the different samples. Data previously obtained in SiO\(_2\) measured by visible BLS [45] and UV-BLS [46, 47] techniques are plotted for comparison

Full size image

As previously discussed, our work demonstrates that a discontinuous metallic layer made of connected nanoislands or well-separated nanoparticles can generate optically detectable acoustic waves in its supporting glass substrate. In the following, we describe a simple 2D model developed to qualitatively explain this key experimental observation and better understand the relation between the morphological properties of a nanoparticle layer and the features of the acoustic waves that it produces. This model addresses the simplified case of an infinite one-dimensional chain of uncoupled, point-like acoustic emitters with non-uniform density, emitting scalar waves in a half-plane, whose attenuation upon propagation is neglected.

The density of emitters is described by a function f(a), with a the spatial coordinate along the emitter chain (located at \(z=0\)). All emitters are assumed to generate coherent acoustic pulses of same angular frequency \(\omega = 2\pi f\) and duration \(\tau\), described by the damped oscillating function of time h(t) such as (using complex notation)

$$\begin{aligned} h(t)= {\left\{ \begin{array}{ll} 0,&{} \text {if } t< 0\\ e^{-\frac{t}{\tau }}e^{i\omega t}, &{} \text {if } t\ge 0. \end{array}\right. } \end{aligned}$$
(3)

The wave created at an (x, z) point located at a distance z from the 1D emitter chain results from the interferences between the circular waves generated in the \(z>0\) half-plane by all the emitters. Its complex amplitude A(x, z, t) thus writes, introducing \(a'=a-x\)

$$\begin{aligned} A(x,z,t) = \int _{-\infty }^\infty f(a' + x) \frac{h\Big (t-\frac{\sqrt{a^{\prime 2} + z^2}}{c_L} \Big )}{\Big (a^{\prime 2} + z^2 \Big )^{1/4}}da', \end{aligned}$$
(4)

where \(c_L\) denotes the speed of sound in the \(z>0\) half-plane and \(\sqrt{a^{\prime 2} + z^2}\) corresponds to the distance between the emitter located in (a, 0) and the (x, z) point where the amplitude is calculated. Equation (4) represents the general mathematical expression describing the interferences of an infinity of propagating circular waves (whose individual amplitudes decay as the inverse of the square root of the covered distance) generated by an extended source characterized by its spatial and temporal emission profiles f(a) and h(t). Since \(h(t)=0\) for \(t<0\) (Eq. (3)), \(A (x,z,t) = 0\) when \(t<\frac{z}{c_L}\), the time needed for acoustic waves to cover the distance z. At slightly larger times \(t=\frac{z}{c_L}+t'\), such that \(t'<<\frac{z}{c_L}\), the emitters with non-zero contribution to the integral of Eq. (4) are located in a spatial region, such that

$$\begin{aligned} | a' | \le \sqrt{ ( c_L t )^2 - z^2} = a'_{\max }(z,t), \end{aligned}$$
(5)

with \(a'_{\max }(z,t)\approx \sqrt{2z c_L t'}<<z\). The \((a^{\prime 2}+ z^2 )^{1/4}\) denominator appearing in Eq. (4) can then be approximated as \(\sqrt{z}\), while the oscillating function \(h\Big (t-\frac{\sqrt{a^{\prime 2} + z^2}}{c_L} \Big )\) can be approximated as \(h\Big (t-\frac{z}{c_L}-\frac{a^{\prime 2}}{2c_Lz} \Big )\). Equation (4) then becomes

$$\begin{aligned} A(x,z,t) \approx \frac{e^{(-\frac{1}{\tau }+i\omega )t'}}{\sqrt{z}}\int _{-a'_{\max }(z,t)}^{a'_{\max }(z,t)} f(a' + x) e^{( \frac{1}{\tau } - i\omega )\frac{a^{\prime 2}}{2c_Lz}}da'. \end{aligned}$$
(6)

The f(a) density can be generally written as \(f(a)= \overline{f} + f_{\text {fluct}}(a)\), with \(\overline{f}\) being its average value. Separating the contributions of \(\overline{f}\) and \(f_{\text {fluct}} (a)\) in the integral of Eq. (6), and expressing the former one \(A_{\text {film}}\) (corresponding to a constant emitter density, as e.g., in the thin film case) as a function of the sole \(t'=t-\frac{z}{c_L}\) variable using the erf error function, Eq. (6) can be rewritten as

$$\begin{aligned} A(x,z,t) &\approx A_{\text {film}}(t') + \frac{e^{(-\frac{1}{\tau }+i\omega )t'}}{\sqrt{z}}\\ &\quad\int _{-a'_{\max }(z,t)}^{a'_{\max }(z,t)} f_{\text {fluct}}(a' + x) e^{( \frac{1}{\tau } - i\omega )\frac{a^{\prime 2}}{2c_Lz}}da', \end{aligned}$$
(7)

with

$$\begin{aligned} A_{\text {film}}(t') = \overline{f} \sqrt{\frac{2\pi c_L}{\frac{1}{\tau }-i\omega }}\text {erf}\Bigg (i\sqrt{\Big ( \frac{1}{\tau }-i\omega \Big )t'}\Bigg ) e^{(-\frac{1}{\tau }+i\omega )t'}. \end{aligned}$$
(8)

The integral appearing in Eq. (7) represents the perturbation of the spatio-temporal profile of the emitted wave induced by an inhomogeneous emitter density (non-zero \(f_{\text {fluct}}\)), as compared to the case of a homogeneous one of same average density \(\overline{f}\). Its integrand is a product of a function of zero average value \((f_{\text {fluct}}(a))\) and an oscillatory function \(a'(e^{(\frac{1}{\tau }-i\omega )\frac{a^{\prime 2}}{2c_Lz}})\). Its value is thus expected to strongly depend on the characteristic distance \(d_f\) over which the f function fluctuates, and to become much smaller than \(A_{\text {film}}\) when \(d_f\) is much smaller than the characteristic fluctuation distance of \(e^{\frac{-i\omega a^{\prime 2}}{2c_Lz}}\) (this can be seen by decomposing the integral of Eq. (7) as a sum of integrals on intervals small enough for the oscillating function to remain approximately constant, but large enough for the average value of \(f_{\text {fluct}}\) on the interval to approach its 0 overall average value). This exponential has a local wavelength \(\varLambda '=4\pi \frac{c_L z}{\omega a'}\). Since \(|a'| \le a'_{\max } \cong \sqrt{2zc_L t'}\), \(\varLambda '\) obeys \(\varLambda ' \ge \varLambda \sqrt{\frac{2z}{C_L t'}}\), where \(\varLambda = \frac{c_L}{f}\) is the acoustic wavelength. The \(d_f \ll \varLambda '\) condition is thus always fulfilled at the front of the emitted pulse, as \(\varLambda ' \rightarrow \infty\) when \(t'\rightarrow 0\). A general criterion for the whole emitted acoustic pulse to resemble that emitted by a homogeneous transducer can be obtained by replacing \(t'\) by the duration of the emitted pulse \(\tau\), leading to

$$\begin{aligned} d_f<< \varLambda \sqrt{\frac{2z}{c_L\tau }}. \end{aligned}$$
(9)

In our experiments, \(c_L\) is about 6000 m/s, and the \(f =40-50\) GHz detected acoustic frequencies correspond to acoustic wavelengths in the 120–150 nm range. As the acoustic quality factors of substrate-supported nano-objects \(Q= \pi f \tau\) are typically of the order of 10 [15], \(\tau\) is estimated to be in the order of 100 ps for an acoustic source emitting at 50 GHz. Thus, after propagation on distance of a few \(\upmu\)m, the \(\sqrt{\frac{2z}{c_L \tau }}\) factor has a value of a few units (\(\approx\) 5 for z = 6 \(\upmu\)m).

Numerical simulations of the waves produced by emitters with inhomogeneous density, based on Eq. (4), are presented in Fig. 5. A finite emitter chain (10 \(\upmu\)m length) was considered in these simulations, as required for numerically estimating the integral of Eq. (4) with random f values. Several random functions with the same average values but differing by the \(d_f\) characteristic distance over which they fluctuate were used for f. This was practically done by considering functions with independent and equiprobable random values of 0 and 2\(\overline{f}\) over successive \(d_f\) intervals (\(d_f\) values of 1, 10, and 100 nm being considered in Fig. 5). The results of these simulations confirm and illustrate the conclusions of the analytical analyses presented above. Indeed, they show that the emitted waves resemble more and more those emitted by a homogeneous transducer (shown in Fig. 5D) as \(d_f\) is decreased, and that this similarity is strong when the criterion of Eq. (9) is fulfilled, which is the case when \(d_f\)=1 nm or 10 nm (Fig. 5B, C).

Fig. 5
figure 5

Numerical simulations of the waves generated by an inhomogeneous chain of emitters. Calculations were based on the model described in the main text (Eq. (4)), considering a 10 \(\mu\)m long chain of emitters. Emitter densities with randomly chosen, equiprobable 0 or 2\(\overline{f}\) values every \(d_f\)= 100 nm (A), 10 nm (B), and 1 nm (C) intervals (and thus with same average value \(\overline{f}\)) were considered in these calculations. The case of an emitter chain with homogeneous \(\overline{f}\) density is also shown for comparison (D). A \(c_L\) = 6000 m/s sound velocity was used, and calculations were done for t = 0.5 ns delay time

Full size image

For the actual samples used in this study, \(d_f\) can be roughly estimated as the average interparticle distance in the sample, whose value is of the order of or less than 10 nm for all samples. The criterion of Eq. (9) is thus satisfied, as \(d_f\) is more than ten times smaller than \(\varLambda \sqrt{\frac{2z}{c_L \tau }}\) for acoustic propagation over distances of a few microns, which is consistent with the successful experimental detection of Brillouin oscillations for all samples. Equation (8), which shows that the amplitude of the emitted wave scales as the average emitter density, also partly explains the strongly reduced amplitude of these Brillouin oscillations for the laser-processed sample, whose filling factor is much lower than that of the other samples. Such explanation is however only partial, as the amplitude of the measured optical signals is also expected to depend on the frequency content of the emitted acoustic wave-packets, which may be very different for the laser-processed sample as compared to other ones.

4 Conclusion

Ultrafast laser excitation of a layer of randomly located plasmonic nanoparticles with broad size dispersion (diameter varying from few to few tens of nm) was shown to enable the generation of coherent acoustic pulses in its supporting N-BK7 glass substrate for all the samples tested. However, the coherent pulse generation efficiency was seen to dramatically reduce following laser reshaping of the nanoparticle layer, the pulse propagation then becoming detectable exclusively in a narrow probe spectral range where the photoelastic coupling between the photons and the acoustic phonons is the highest. The reduced pulse emission efficiency was attributed to the considerably lower nanoparticle filling factor after laser processing. The previous experimental observations were found to be qualitatively consistent with a simplified model of wave emission by an ensemble of acoustic emitters with non-uniform spatial density, showing in particular at which condition the effect of a non-uniform emitter density becomes negligible. The pulse propagation in N-BK7 was detected by means of Brillouin oscillations in time-resolved measurements. The attenuation rates of 40–50 GHz Fourier frequency components of the coherent acoustic pulses were determined, revealing their acoustic propagation over several micrometers in N-BK7, with attenuation rates very close to that previously measured on chemically pure silica and thus also dominated by anharmonic interactions with the thermal phonon bath. The similarity is attributed to the high proportion of silica in N-BK7 composition.