1 Introduction

Fractals are shapes whose fractal dimension exceed topological dimension i.e. Romanesco broccoli, clouds, lightning, leaves, rivers, the neurons in your brain, and snow flakes [1,2,3]. Some fractals that can be shown as mathematical equations that are everywhere continuous but nowhere differentiable such as the Weierstrass function and Koch curves. This is because of fractals cannot be measured in traditional ways used in ordinary calculus i.e. length and area and volume. For further explanation, to measure a non-fractal curve, its length can be measured by reducing the scale and tangent it. On the other hand, they consist of a pattern that repeats on a finer and finer scale. But this is not possible in the case of fractals since the jagged pattern appears again at an arbitrarily small scale and one can not tangent scale to them. By shrinking the scale, the length of the fractal curve increases. As a result, with this way, the length of the curve becomes infinite i.e. the fractal Koch curve has an infinite perimeter. Cantor set which is a set of points lying on a single line segment, built by iteratively deleting the open middle-\(\epsilon\) from a set of line segments [4]. The Cantor set does not have any interval of non-zero length but contains an uncountably infinite number of points, closed, not dense in any interval, self-similar, since it is equal to enlarge copies of itself. The Cantor sets have fractional dimension i.e. dimension of Cantor ternary set (\(\epsilon \,=\,1/3\)) is \(d\,=\,\log (2)/\log (3)\) [5]. Thin Cantor ternary sets have Lebesgue measures zero. Therefore, functions on the Cantor ternary set are not differential and integrable in the sense of ordinary calculus. Due to the fact that the length of the Koch curve and the Cantor sets became infinite and zero, respectively, other measures have been defined for fractals such as Hausdorff measure which is a generalization of length, area and volume to non-integer dimensions [6]. Fractals have complex dimension and discrete symmetry [7]. Dirac operators and spectral triples fractal sets were built on curves [8]. Generalized fractal comb model and Lévy processes were considered, and exact solutions for the probability distribution functions obtained in terms of the Fox H-function for a variety of the memory kernels, and the rate of the superdiffusive spreading was studied by calculating the fractional moments [9]. Optimal control theory and necessary and sufficient conditions were extended to fractal sets [10]. The asymptotic motion of a random walker on Sierpinski lattice was investigated and distribution function of the diffusion on the Sierpinski gasket was worked out [11]. Highly oscillatory behaviours of the distribution function the eigenvalues and the spectrum of the Laplacian on the finite Sierpinski gasket were described [12]. Brownian motion with Sierpinski gasket support was constructed its properties were given and corresponding diffusion process characterized by local isotropy and homogeneity properties [13]. Random walks on fractals have paths are themselves fractal and interesting kinds of behavior form of scaling laws [14]. Laplace operator, Gauss-Green’s formula on Sierpinski space with fractional Hausdorff dimension were reconstructed using the harmonic functions [15, 16]. The eigenvalues of the discrete Laplacian on pre-gaskets under the Dirichlet and Neumann boundary conditions have been completely determined applying the decimation [17].

Fractal analysis was formulated fractional space, fractional calculus, probably and measure theory and applied in physics and engineering [13, 18,19,20,21,22,23,24,25,26,27]. One of the basic equations of physics is geodesic equations in a fractal space-time framework. In this framework, the quantum feature is consequence of the fractal geometry of space-time [28]. The local and global in time solutions of multidimensional generalized Burgers-type equations with a fractional power of the Laplacian in the principal part were obtained and presented self-similar solutions in the Cauchy problems [29]. In the last decade, fractal calculus or \(F^{\alpha }\)-calculus which is a generalization of ordinary calculus to involve function with fractal support was formulated [30,31,32]. A Fokker-Planck equation on fractal curves were obtained by using Chapmann–Kolmogorov equation. The diffusion equation on fractal curves for a suitable transition probability was derived. An exact solution of this equation with the localized initial condition was obtained and shown underlying the fractal space manifests a subdiffusive behavior [33]. The random motion of a particle on a fractal curve was investigated using Langevin equation. A Langevin equation with a noise was solved using techniques of the \(F^{\alpha }\)-calculus [34]. The unbiased random walk on a fractal curve was considered and the corresponding probability distribution was found out which is gaussian-like, but shows deviation from the standard behaviour. Moments were calculated in terms of Euclidean distance for a von Koch curve. Analysis on Levy distributions demonstrate that the dimension of the fractal curve shows significant contribution to the distribution law by modifying the nature of moments [35].

Fractal calculus was used to characterize the sub-and super diffusion on fractals [32, 36, 37]. The Fractal Henstock-Kurzweil integral was formulated in order to find \(F^{\alpha }\)-integral of singular functions on the Cantor sets [32]. Random variable and stochastic differential equation on the Cantor sets are defined to model random process on fractals [38, 39]. Stability of fractal differential equations were studied [40]. Fractal calculus was used to model physical phenomena in fractal time, space and temperature [32, 41, 42]. The nonlocal fractal calculus-based Lagrange and Hamilton equations have been derived [43] and the nonlocal fractal integro-differential equations were used to describe the RL, RC, LC and RLC circuits [44].

Fractal time was described by starting from scratch with a philosophical and perceptual puzzle. The complexity of temporal perspective depends on the number of nestings performed. This temporal contextualization is described against the background of the notion of fractal time [45, 46]. According to the application of fractal space and time, which has given us new results, therefore, in the continuation of these researches, we develop physical equations and classical mechanics in fractal space and time. Newton’s and Hamilton’s equations play an important role in the study of motion and its laws in nature, therefore, in this article, their formulations are expressed in fractal space with fractional dimensions.

The outline of the paper is as follows:

In Sect. 2 we summarized the fractal calculus. Generalized classical mechanics was suggested in Sect. 3 which includes Newton, Lagrange, Hamilton, and Appell’s mechanics. Section 4 is devoted to conclusion.

2 Preliminaries

In this section we summarize the fractal calculus on fractal curve [30,31,32, 47].

Definition 1

A fractal curve F subset of \(R^{n}\) is called parameterizable if there exists a function \(\textbf{w}:[a,b]\rightarrow F\) which is continuous, one-to-one and onto F. For example, the Weierstrass function is defined by \(\textbf{w}:R\rightarrow R^{2}\) as

$$\begin{aligned} \textbf{w}(u)\,=\,\bigg (u, \sum _{k\,=\,1}^{\infty } \lambda ^{(s-2)k}\sin (\lambda ^{k}u)\bigg ), \end{aligned}$$
(1)

where \(1<s<2\) and \(\lambda >1\) and s is the box-dimension [32].

Definition 2

For a fractal curve F and a subdivision \(P_{[a,b]}, [a,b]\in [a_{0},b_{0}] \in \mathbb {R}\), the mass function is defined by

$$\begin{aligned} \gamma ^{\alpha }(F,a,b)\,=\,\lim _{\delta \rightarrow 0} \inf _{|P|\le \delta }\sum _{i\,=\,0}^{n-1} \frac{|\textbf{w}(t_{i+1})-\textbf{w}(t_{i})|^{\alpha }}{\Gamma (\alpha +1)}, \end{aligned}$$
(2)

where \(| \cdot |\) denotes the Euclidean norm on \(\mathbb {R}^{n}\), \(1\le \alpha \le n\), \(P_{[a,b]}\,=\,\{a\,=\,t_{0},...,t_{n}\,=\,b\}\), \(|P|\,=\,\max _{0\le i\le n-1}(t_{i+1}-t_{i})\) for a subdivision P and \(\Gamma (.)\) is gamma function.

Definition 3

The \(\gamma\)-dimension of F is defined by

$$\begin{aligned} \dim _{\gamma }(F)&\,=\,\inf \{\alpha :\gamma ^{\alpha }(F,a,b)\,=\,0\}\nonumber \\ {}&\,=\, \sup \{\alpha :\gamma ^{\alpha }(F,a,b)\,=\,\infty \}. \end{aligned}$$
(3)

Definition 4

The rise function of fractal curve F is defined by

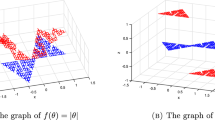
$$\begin{aligned} S_{F}^{\alpha }(u)\,=\,\left\{ \begin{array}{ll} \gamma ^{\alpha }(F,p_{0},u), &{} u\ge p_{0}; \\ -\gamma ^{\alpha }(F,u,p_{0}), &{} u<p_{0}, \end{array} \right. \end{aligned}$$
(4)

where \(u\in [a_{0},b_{0}]\), \(p_{0}\,=\,a_{0}\) is arbitrary and fixed number and \(S_{F}^{\alpha }(u)\,=\,J(\theta ), \theta \in F\) gives the mass of the fractal curve F upto point u. In Fig. 1, we have plotted the fractal curve (in blue) and corresponding rise function \(J(\theta )\) (in red).

Fig. 1
figure 1

The graph of \(J(\theta )\) (in red) for a fractal curve F (in blue)

Full size image

Remark 1

As \(\gamma ^{\alpha }\) is a monotonic function of \(\delta\). The limit exists, but could be finite or \(+\infty\). [31, 32, 47].

Definition 5

Let be a function \(f:F\rightarrow \mathbb {R}\). Then F-limit of f as \(\theta '\rightarrow \theta\) through points of F is l, if for given \(\epsilon\) there exists \(\delta>\) such that

$$\begin{aligned} \theta '\in F~~and~~|\theta '-\theta |<\delta \Rightarrow |f(\theta ')-l|<\epsilon \end{aligned}$$
(5)

or

$$\begin{aligned} \underset{ \theta '\rightarrow \theta }{F_{-}lim}f(\theta ')\,=\,l. \end{aligned}$$
(6)

Remark 2

We note that if we choose \(F\,=\,R\), then one can recover the standard definition in usual calculus [31, 32, 47].

Definition 6

A function \(f:F\rightarrow \mathbb {R}\) is said to be F-continuous at \(\theta\) if

$$\begin{aligned} \underset{ \theta '\rightarrow \theta }{F_{-}lim}f(\theta ')\,=\,f(\theta ). \end{aligned}$$
(7)

Definition 7

The fractal derivative \(F^{\alpha }\)-derivative is defined by

$$\begin{aligned} D_{F}^{\alpha }f(\theta )\,=\,\underset{ \theta '\rightarrow \theta }{F_{-}lim}~ \frac{f(\theta ')-f(\theta )}{J(\theta ')-J(\theta )}, \end{aligned}$$
(8)

where \(F_{-}lim\) indicates the fractal limit (see in [31]), and let for a point on the curve \(\textbf{w}(u)\,=\,\theta\) and \(S_{F}^{\alpha }(u)\,=\,J(\theta )\) (see for more details in [31, 32, 47]).

Remark 3

We note that the Euclidean distance from origin upto a point \(\theta \,=\,\textbf{w}(u)\) is given by \(L(\theta )\,=\,L(\textbf{w}(u))\,=\,|\textbf{w}(u)|.\)

Definition 8

The fractal integral or \(F^{\alpha }\)-integral is defined by

$$\begin{aligned} \int _{C(a,b)}f(\theta )d_{F}^{\alpha }\theta&\,=\,\sup _{P[a,b]}\sum _{i\,=\,0}^{n-1} \inf _{\theta \in C(t_{i},t_{i+1})}f(\theta )(J(\theta _{i+1})-J(\theta _{i}))\nonumber \\ {}&\,=\, \inf _{P[a,b]}\sum _{i\,=\,0}^{n-1} \sup _{\theta \in C(t_{i},t_{i+1})}f(\theta )(J(\theta _{i+1})-J(\theta _{i}))\nonumber \\ {}&\,=\, FR(f,\{\theta _{i}\}), \end{aligned}$$
(9)

where \(t_{i}\,=\,\textbf{w}^{-1}(\theta _{i})\), FR (fractal Riemann sum), and C(a, b) is the section of the curve lying between points \(\textbf{w}(a)\) and \(\textbf{w}(b)\) on the fractal curve F [31].

3 Classical mechanics on fractal spaces

Classical mechanics [48, 49] is one of the important branches of physics that explains the laws of motion in nature. which has different formulations such as Newton’s, Lagrangian’s, Hamilton’s and Appell’s approach [50], which we generalize in these sections for spaces with fractional dimensions.

3.1 Newton’s second law on Koch-like curves

Let us consider a von Koch-like curve. We can construct it by begin with a straight line, and following the given steps in below:

  1. 1.

    Divide it into three equal segments, then replace the middle segment by the two sides of an equilateral triangle of the same length as the segment being removed.

  2. 2.

    Repeat, taking each of the four resulting segments, and dividing them into three equal parts and replacing each of the middle segments by two sides of an equilateral triangle.

  3. 3.

    Continue step (2) upto infinity.

The Koch-like curves are the limiting curves obtained by applying this construction as an infinite number of times. In the following we give Newton’s equation on fractal space and time.

3.2 Newton’s second law on fractal space

The \(\alpha\)-velocity on the Koch-like curves is defined by [34]

$$\begin{aligned} v^{\alpha }(t)&\,=\,\lim _{t\rightarrow t'} \frac{S_{F}^{\alpha }(u(t))-S_{F}^{\alpha }(u(t'))}{t-t'}\nonumber \\ {}&\,=\, \frac{d}{dt}S_{F}^{\alpha }(u(t))\nonumber \\ {}&\,=\,\frac{d}{dt}J(\theta (t)). \end{aligned}$$
(10)

Consider the \(n^{th}\) iteration of constructing of the Koch-like curves. If the particle moves along straight line in this stage, then in the limiting case the \(\alpha\)-acceleration of the particle is defined by

$$\begin{aligned} a^{\alpha }(t)&\,=\,\frac{\textrm{d}}{\textrm{d}t} v^{\alpha }(t)\,=\, \lim _{t\rightarrow t'}\frac{v^{\alpha }(t)-v^{\alpha }(t')}{t-t'}\nonumber \\ {}&\,=\, \frac{\textrm{d}^{2}}{\textrm{d}t^{2}}S_{F}^{\alpha }(u(t))\nonumber \\ {}&\,=\,\frac{\textrm{d}^{2}}{\textrm{d}t^{2}}J(\theta (t)). \end{aligned}$$
(11)

Let \(f^{\alpha }\) be the component of force applied on a particle along straight line in \(n^{th}\) iteration of the Koch-like curves. The second Newton’s law on the Koch-like curves is

$$\begin{aligned} f^{\alpha }\,=\, m_{F} a^{\alpha }, \end{aligned}$$
(12)

where \(m_{F}\,=\,m\kappa\) and \([\kappa ]\,=\, Length/Mass^{\alpha }\)

The work energy theorem on the Koch-like curves is

$$\begin{aligned} w^{\alpha }&\,=\,\int _{C(a,b)}f^{\alpha }d_{F}^{\alpha }\theta \nonumber \\ {}&\,=\, \frac{1}{2} m_{F}v_{2}^{\alpha }-\frac{1}{2} m_{F}v_{1}^{\alpha }, \end{aligned}$$
(13)

where \(v_{1}^{\alpha }\) and \(v_{2}^{\alpha }\) are fractal speed of particle in point a and b, respectively.

Example 1

Consider a body of mass m that oscillates on a fractal curve so its equation of the motion is

$$\begin{aligned} m_{F} \frac{\textrm{d}^{2}}{\textrm{d}t^{2}}J(\theta (t))\,=\,-k_{F}J(\theta (t)). \end{aligned}$$
(14)

The solution of Eq. (14) is

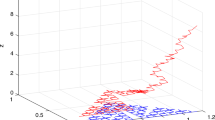
$$\begin{aligned} J(\theta (t))\,=\,A\cos (\omega _{F} t)+B\sin (\omega _{F} t). \end{aligned}$$
(15)

If \(J(0)\,=\,1\), then \(B\,=\,0\). In Fig. 2, we have sketched Eq. (15) for case of \(A\,=\,2, B\,=\,1\) and \(\omega _{F}\,=\,1\).

Fig. 2
figure 2

The graph of Eq. (15)

Full size image

3.3 Newton’s second law on fractal time and space

The \(\alpha ,\beta\)-velocity of particle moving on fractal space F with fractal time H is defined by

$$\begin{aligned} v^{\alpha ,\beta }(t)&\,=\,\lim _{t\rightarrow t'} \frac{S_{F}^{\alpha }(u(t))-S_{F}^{\alpha }(u(t'))}{S_{H}^{\beta }(t)-S_{H}^{\beta }(t')}\nonumber \\ {}&\,=\, D_{H,t}^{\beta }S_{H}^{\alpha }(u(t))\nonumber \\ {}&\,=\,D_{H,t}^{\beta }J(\theta (t)),~~~t\in H \end{aligned}$$
(16)

where \(\alpha\) is fractal dimension space and \(\beta\) is fractal dimension time. The acceleration of moving on fractal space and time is defined by

$$\begin{aligned} a^{\alpha ,\beta }(t)&\,=\,\lim _{t\rightarrow t'} \frac{v^{\alpha ,\beta }(t)-v^{\alpha ,\beta }(t')}{S_{F}^{\beta }(t)-S_{F}^{\beta }(t')}\nonumber \\ {}&\,=\, D_{F,t}^{2\beta }S_{F}^{\alpha }(u(t))\nonumber \\ {}&\,=\,D_{F,t}^{2\beta }J(\theta (t)). \end{aligned}$$
(17)

The Newton’s second law on fractal space and time is defined by

$$\begin{aligned} f^{\alpha ,\beta }\,=\,m_{F,H}D_{F,t}^{2\beta }S_{F}^{\alpha }(u(t)), \end{aligned}$$
(18)

where \(m_{F,H}\,=\,m\kappa \zeta\), and \([\zeta ]\,=\,Time^{\beta -1}\).

Example 2

The equation of damped harmonic oscillator involving fractal time is

$$\begin{aligned} m_{H}D_{F,t}^{2\beta } y(t)+c_{H}D_{F,t}^{\beta } y(t)+k_{H} y(t)\,=\,0. \end{aligned}$$
(19)

Suppose Eq. (19) has a solution of the form

$$\begin{aligned} x(t)\,=\,e^{\lambda ^{\beta } S_{F}^{\beta }(t)}. \end{aligned}$$
(20)

Substituting Eq. (20) into Eq. (19), so we have

$$\begin{aligned} m_{H}(\lambda ^{\beta })^2+c_{H}\lambda ^{\beta }+k\,=\,0. \end{aligned}$$
(21)

The roots of the quadratic auxiliary equation are

$$\begin{aligned} \lambda ^{\beta }\,=\,\frac{-c_{H}\pm \sqrt{c_{H}^2-4m_{H}k_{H}}}{2m_{H}}. \end{aligned}$$
(22)

The solution of Eq. (19) is

$$\begin{aligned} x(t)&\,=\,Ae^{-\gamma _{1}S_{F}^{\beta }(t)}+Be^{-\gamma _{2}S_{F}^{\beta }(t)},~\nonumber \\ {}&c_{H}^2-4m_{H}k_{H}>0,~Overdamped ,\nonumber \\ x(t)&\,=\,(A S_{F}^{\beta }(t)+B)e^{-\gamma S_{F}^{\beta }(t)},\nonumber \\ {}&~c_{H}^2-4m_{H}k_{H}\,=\,0,~Critically~damped ,\nonumber \\ x(t)&\,=\,e^{-\rho ^{\beta } S_{F}^{\beta }(t)}\mathcal {A}\cos \left( \omega _{1} S_{F}^{\beta }(t)-\phi \right) ,\nonumber \\ {}&~c_{H}^2-4m_{H}k_{H}<0,~Underdamped . \end{aligned}$$
(23)

By using \(S_{F}^{\beta }(t)\le t^{\beta }\) we can rewrite Eq. (23) as The solution of Eq. (19) is

$$\begin{aligned} x(t)&\propto Ae^{-\gamma _{1}t^{\beta }}+Be^{-\gamma _{2}t^{\beta })},~ c_{H}^2-4m_{H}k_{H}>0,\nonumber \\ {}&~Overdamped ,\nonumber \\ x(t)&\propto (A t^{\beta }+B)e^{-\gamma t^{\beta }},~c_{H}^2-4m_{H}k_{H}\,=\,0,\nonumber \\ {}&~Critically~damped ,\nonumber \\ x(t)&\propto e^{-\rho ^{\beta } t^{\beta }}\mathcal {A}\cos \left( \omega _{1}t^{\beta }-\phi \right) ,\nonumber \\ {}&c_{H}^2-4m_{H}k_{H}<0,~Underdamped \end{aligned}$$
(24)

where \(\rho \,=\,c_{H}/2m_{H}\), \(\omega _{1}\,=\,\sqrt{\omega _{0}^2-\rho ^2}\) and \(\omega _{0}\,=\,\sqrt{k_{H}/m_{H}}\) are constants. In Figs. 3 and 4, we have plotted Eqs. (23) and (24).

Fig. 3
figure 3

Graph of Eq. (23) for the case of fractal time with dimension \(\beta \,=\,0.63\) and Overdamped, Critically damped, and Underdamped

Full size image
Fig. 4
figure 4

Graph of Eq. (24) for different value of dimension and Overdamped, Critically damped, and Underdamped

Full size image

3.4 Fractal Langevin and fractal Fokker-Planck’s equations

Consider a particle moves on Koch-like curves so that its fractal Langevin’s equation is

$$\begin{aligned} v^{\alpha }(t)\,=\,\frac{\textrm{d}}{\textrm{d}t}J(\theta (t))\,=\,-A_{1}J(\theta (t))+\sqrt{2A_{2}} \eta (t), \end{aligned}$$
(25)

where \(\eta (t)\) is a Gaussian random noise and \(A_{1},~A_{2}\) are constants. The associated fractal Fokker-Planck’s equation is given by

$$\begin{aligned} \frac{\partial }{\partial t}P(\theta ,t)&\,=\,A_{1} D_{F,\theta }^{\alpha }(J(\theta )P(\theta ,t))+ \frac{A_{2}^2}{2}(D_{F,\theta }^{\alpha })^2 P(\theta ,t),\nonumber \\ {}&~and ~~~P(\theta ,t)\,=\,\delta (\theta -\theta '). \end{aligned}$$
(26)

The solution of Eq. (26) is

$$\begin{aligned} P(\theta ,t|\theta ',t')&\,=\,\sqrt{\frac{A_{1}}{\pi A_{2}^2(1-e^{-2 A_{1}(t-t')} )}}\nonumber \\ {}&\exp \bigg (-\frac{A_{1}}{A_{2}^2} \frac{(J(\theta )-J(\theta ')e^{-A_{1}(t-t')})^{2}}{1-e^{-2A_{1}(t-t')}}\bigg ), \end{aligned}$$
(27)

where \(P(\theta ,t|\theta ',t')\) is transition probability. The stationary solution \(\partial P(\theta ,t)/\partial t\,=\,0\) of Eq. (26) is

$$\begin{aligned} P(\theta )\,=\,\sqrt{\frac{A_{1}}{\pi A_{2}^2}}\exp \left( -\frac{A_{1} J(\theta )^{2}}{A_{2}^2}\right) . \end{aligned}$$
(28)

3.5 Lagrange’s mechanics on Koch-like curves

Let \((Z^{\alpha },L^{\alpha })\) be a mechanical system with one degrees of freedom, where \(Z^{\alpha }\) is the fractal configuration space and \(L^{\alpha }:\mathbb {R}_{t}\times TM^{\alpha }\rightarrow \mathbb {R}\) is non-relativistic fractal Lagrangian, and \(TM^{\alpha }\) fractal analogue of the tangent bundle of fractal manifold \(Z^{\alpha }\). Then, for a particle moving on Koch-like curves is defined by

$$\begin{aligned} L^{\alpha }(t,J(\theta (t)), v^{\alpha })&\,=\,T^{\alpha }-V^{\alpha }\\ {}&\,=\, \frac{1}{2}m_{F}(v^{\alpha })^{2}-V^{\alpha }(J(\theta (t)),\qquad \end{aligned}$$
(29)

where \(T^{\alpha }\) is the total kinetic energy and \(V^{\alpha }(\theta )\) is the potential energy of the particle. The fractal action functional is defined by

$$\begin{aligned} S^{\alpha }\,=\,\int _{a}^{b}L^{\alpha }(t,J(\theta (t)), v^{\alpha })\textrm{d}t. \end{aligned}$$
(30)

To obtain stationary path of Eq. (30), let

$$\begin{aligned} J(\phi _{\epsilon }(t))\,=\,J(\theta (t))+\epsilon J(\eta (t)),~~~J(\eta (a))\,=\,J(\eta (b))\,=\,0. \end{aligned}$$
(31)

Thus we write

$$\begin{aligned} S^{\alpha }_{\epsilon }\,=\,\int _{a}^{b} L^{\alpha }_{\epsilon }\big (t,J(\phi _{\epsilon }),v_{\epsilon }^{\alpha }\big ) dt. \end{aligned}$$
(32)

It follows that

$$\begin{aligned} \frac{dS^{\alpha }_{\epsilon }}{\textrm{d}\epsilon }\,=\,\int _{a}^{b} \frac{dL^{\alpha }_{\epsilon }}{\textrm{d}\epsilon }\textrm{d}t. \end{aligned}$$
(33)

Then we have

$$\begin{aligned} \frac{\textrm{d}L^{\alpha }_{\epsilon }}{\textrm{d}\epsilon }&\,=\, \frac{\textrm{d}t}{\textrm{d}\epsilon }\frac{\partial L^{\alpha }_{\epsilon }}{\partial t}+ \frac{d J(\phi _{\epsilon })}{\textrm{d}\epsilon }\frac{\partial L^{\alpha }_{\epsilon }}{\partial J(\phi _{\epsilon })}+\frac{\textrm{d} v_{\epsilon }^{\alpha } }{\textrm{d}\epsilon }\frac{\partial L^{\alpha }_{\epsilon }}{\partial v_{\epsilon }^{\alpha }}\nonumber \\ {}&\,=\, \frac{d J(\phi _{\epsilon })}{\textrm{d}\epsilon }\frac{\partial L^{\alpha }_{\epsilon }}{\partial J(\phi _{\epsilon })}+\frac{\textrm{d} v_{\epsilon }^{\alpha } }{\textrm{d}\epsilon }\frac{\partial L^{\alpha }_{\epsilon }}{\partial v_{\epsilon }^{\alpha }}\nonumber \\ {}&\,=\, J(\eta (t))\frac{\partial L^{\alpha }_{\epsilon }}{\partial J(\phi _{\epsilon })}+\frac{\textrm{d} J(\eta (t)) }{\textrm{d} t}\frac{\partial L^{\alpha }_{\epsilon }}{\partial v_{\epsilon }^{\alpha }}. \end{aligned}$$
(34)

\(S^{\alpha }_{\epsilon }\) has an extremum value, so that

$$\begin{aligned} \frac{\textrm{d}S^{\alpha }_{\epsilon }}{\textrm{d}\epsilon }\bigg |_{\epsilon \,=\,0}\,=\,\int _{a}^{b} \bigg [J(\eta (t))\frac{\partial L^{\alpha }}{\partial J(\theta )}+\frac{\textrm{d} J(\eta (t)) }{\textrm{d} t}\frac{\partial L^{\alpha }}{\partial v^{\alpha }}\bigg ]dt\,=\,0. \end{aligned}$$
(35)

Using fractal integration by parts, Eq. (35) yields

$$\begin{aligned} \int _{a}^{b} \bigg [\frac{\partial L^{\alpha }}{\partial J(\theta )}+\frac{\textrm{d}}{\textrm{d}t}\frac{\partial L^{\alpha }}{\partial v^{\alpha }}\bigg ]J(\eta (t))\textrm{d}t+\bigg [J(\eta (t))\frac{\partial L^{\alpha }}{\partial v^{\alpha }}\bigg ]_{a}^{b}\,=\,0. \end{aligned}$$
(36)

Applying the boundary conditions in Eq. (31), we get

$$\begin{aligned} \int _{a}^{b} \bigg [\frac{\partial L^{\alpha }}{\partial J(\theta )}+\frac{\textrm{d}}{\textrm{d}t}\frac{\partial L^{\alpha }}{\partial v^{\alpha }}\bigg ]J(\eta (t))\textrm{d}t\,=\,0. \end{aligned}$$
(37)

This yields the fractal Euler–Lagrange equation as follows:

$$\begin{aligned} \frac{\partial L^{\alpha } }{\partial J(\theta )}-\frac{\textrm{d}}{\textrm{d}t}\frac{\partial L^{\alpha } }{\partial v^{\alpha }}\,=\,0. \end{aligned}$$
(38)

We can derive fractal Newton’s second law from fractal Euler–Lagrange equation. Using Eq. (29), we have

$$\begin{aligned} \frac{\partial L^{\alpha }}{\partial v^{\alpha }}\,=\,m_{F}v^{\alpha },~~~~~~~~\frac{\textrm{d}}{\textrm{d}t}\frac{\partial L^{\alpha }}{\partial v^{\alpha }}\,=\,m_{F}a^{\alpha }. \end{aligned}$$
(39)

In view of Eqs. (29), (38) and (39) we arrive at

$$\begin{aligned} \frac{\partial L^{\alpha }}{\partial J(\theta )}\,=\,\frac{\partial V^{\alpha }(J(\theta ))}{\partial J(\theta )}\,=\,f\,=\,\frac{\textrm{d}}{\textrm{d}t}\frac{\partial L^{\alpha }}{\partial v^{\alpha }}\,=\,m_{F}a^{\alpha }, \end{aligned}$$
(40)

which is called fractal Newton’s second law.

3.6 Hamilton’s mechanics on Koch-like curves

In this section, we suggest Hamilton’s mechanics on Koch-like curves. Let \((Z^{\alpha },L^{\alpha })\) be a mechanical system. Then fractal momenta is defined by

$$\begin{aligned} p^{\alpha }(t,J(\theta ),v^{\alpha })\,=\,\frac{\partial L^{\alpha }}{\partial v^{\alpha }}. \end{aligned}$$
(41)

The Legendre transform of convex functional \(L^{\alpha }\) is defined by

$$\begin{aligned} H^{\alpha }(t,J(\theta ),p^{\alpha })\,=\,p^{\alpha }v^{\alpha }- L^{\alpha }(t,J(\theta ),v^{\alpha }), \end{aligned}$$
(42)

where \(H^{\alpha }(t,J(\theta ),p^{\alpha })\) is might called fractal Hamiltonian and pair \((J(\theta ),p^{\alpha })\) is might called fractal phase space coordinates. Using Eq. (42) and taking fractal total differential of \(H^{\alpha }\) we have

$$\begin{aligned} d_{F}^{\alpha }H^{\alpha }\,=\,v^{\alpha }d_{F}^{\alpha }p^{\alpha }-\frac{\partial L^{\alpha }}{\partial J(\theta )}d_{F}^{\alpha }\theta -\frac{\partial L^{\alpha }}{\partial t}\textrm{d}t. \end{aligned}$$
(43)

On the other hand, we have

$$\begin{aligned} d_{F}^{\alpha }H^{\alpha }\,=\,\frac{\partial H^{\alpha }}{\partial p^{\alpha }}d_{F}^{\alpha }p^{\alpha }+\frac{\partial H^{\alpha }}{\partial J(\theta )}d_{F}^{\alpha }\theta +\frac{\partial H^{\alpha }}{\partial t}dt. \end{aligned}$$
(44)

Comparison of Eqs. (43) and (44) we obtain

$$\begin{aligned} v^{\alpha }\,=\,\frac{\partial H^{\alpha }}{\partial p^{\alpha }},~~~-\frac{\partial L^{\alpha }}{\partial J(\theta )}\,=\,\frac{\partial H^{\alpha }}{\partial J(\theta )},~~~ -\frac{\partial L^{\alpha }}{\partial t}\,=\,\frac{\partial H^{\alpha }}{\partial t}, \end{aligned}$$
(45)

which is might called fractal Hamilton’s equations.

Example 3

Consider the fractal Lagrangian function of system as follows

$$\begin{aligned} L^{\alpha }\,=\,\frac{1}{2}m_{F}(v^{\alpha })^2-U(x). \end{aligned}$$
(46)

The Legendre transformation of Eq. (46) gives

$$\begin{aligned} H^{\alpha }\,=\,\frac{1}{2}m_{F}(v^{\alpha })^2+U(x), \end{aligned}$$
(47)

which might called the fractal Hamiltonian function of system. Since \(p^{\alpha }\,=\,m_{F}(v^{\alpha })\) we can rewrite Eq. (47) as

$$\begin{aligned} H^{\alpha }\,=\,\frac{1}{2m_{F}}(p^{\alpha })^2+U(x). \end{aligned}$$
(48)

Utilizing Hamilton’s equation we get

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t}J(\theta )\,=\,\frac{\partial H^{\alpha }}{\partial p^{\alpha }}\,=\,\frac{p^{\alpha }}{m_{F}},~~~~~~\frac{\textrm{d}p^{\alpha }}{\textrm{d}t}\,=\,-\frac{\textrm{d} U}{\textrm{d}x},\qquad \end{aligned}$$
(49)

it follows that

$$\begin{aligned} m_{F} \frac{\textrm{d}^{2}}{\textrm{d}t^{2}}J(\theta )\,=\,-\frac{\textrm{d} U}{\textrm{d}x}, \end{aligned}$$
(50)

which might be called the fractal Newton’s equation of motion.

3.7 Appell’s mechanics on fractal time

In this section, we generalize the Appell’s eq [50] on Koch-like curves.

The function \(\mathcal {S}\) for a particle is defined by

$$\begin{aligned} \mathcal {S}\,=\,\frac{1}{2}m_{F}(\textbf{a}^{\alpha }.\textbf{a}^{\alpha }), \end{aligned}$$
(51)

The Gibbs–Appell equation on Koch-like curves is defined by

$$\begin{aligned} Q^{\alpha }\,=\,\frac{\partial \mathcal {S}}{\partial \textbf{a}^{\alpha }}, \end{aligned}$$
(52)

where \(Q^{\alpha }\) is generalized force. If a force \(Q^{\alpha }\) apply to a particle during infinitesimal displacement \(d_{F}^{\alpha }\theta\) on Koch-like curves. Then

$$\begin{aligned} d_{F}^{\alpha }W^{\alpha }\,=\,Q^{\alpha }d_{F}^{\alpha }\theta , \end{aligned}$$
(53)

where \(d_{F}^{\alpha }W^{\alpha }\) is called infinitesimal work.

Example 4

For a rigid body with rotation function \(\mathcal {S}\) is defined by

$$\begin{aligned} \mathcal {S}\,=\,\frac{1}{2}\sum _{i\,=\,1}^{N}m_{i}(\textbf{a}_{i}^{\alpha }. \textbf{a}_{i}^{\alpha })\,=\,\frac{1}{2}\sum _{i\,=\,1}^{N}m_{i} \{(\pmb {\sigma }^{\alpha }\times \textbf{r}_{i})^{2}+(\pmb {\omega }^{\alpha }\times \textbf{v}_{i}^{\alpha })^{2}+2(\pmb {\sigma }^{\alpha }\times \textbf{r}_{i}).(\pmb {\omega }^{\alpha }\times \textbf{v}_{i}^{\alpha })\},\qquad \end{aligned}$$
(54)

where the fractal acceleration \(\textbf{a}_{i}^{\alpha }\), the fractal velocity \(\textbf{v}_{i}^{\alpha }\), and the positions vectors the particles of the rigid body \(\textbf{r}_{i}\) are defined by

$$\begin{aligned} \textbf{a}_{i}^{\alpha }\,=\,D_{F,t}^{2\alpha } \textbf{r}_{i},~~~\textbf{v}_{i}^{\alpha }\,=\,D_{F,t}^{\alpha } \textbf{r}_{i},~~~\pmb {\omega }^{\alpha }\,=\,D_{F,t}^{\alpha }\theta ,~~~ \pmb {\sigma }^{\alpha }\,=\,D_{F,t}^{\alpha }\pmb {\omega }^{\alpha }. \end{aligned}$$
(55)

Taking the derivative of \(\mathcal {S}\) with respect to \(\sigma\) and equating by the torque \(\pmb {\tau }^{\alpha }\,=\,(\tau _{x}^{\alpha },\tau _{y}^{\alpha },\tau _{z}^{\alpha })\), one can obtain

$$\begin{aligned} I_{xx}\sigma _{x}^{\alpha }-(I_{yy}-I_{zz})\omega _{y}^{\alpha }\omega _{z}^{\alpha }\,=\, & {} \tau _{x}^{\alpha }, \nonumber \\ \\ I_{yy}\sigma _{y}^{\alpha }-(I_{zz}-I_{xx})\omega _{z}^{\alpha }\omega _{x}^{\alpha }\,=\, & {} \tau _{y}^{\alpha },\nonumber \\ \\ I_{zz}\sigma _{z}^{\alpha }-(I_{xx}-I_{yy})\omega _{x}^{\alpha }\omega _{y}^{\alpha }\,=\, & {} \tau _{z}^{\alpha }, \end{aligned}$$
(56)

where I is the inertia tensor which is diagonal [48, 49]. Equation (56) might be called fractal Euler’s equations of rigid body. Let \(\pmb {\tau }^{\alpha }\,=\,0\) and \(I_{xx}\,=\,I_{yy}\). Then we can write

$$\begin{aligned} I_{xx}\sigma _{x}^{\alpha }-(I_{xx}-I_{zz})\omega _{y}^{\alpha }\omega _{z}^{\alpha }\,=\, & {} 0, \nonumber \\ I_{xx}\sigma _{y}^{\alpha }-(I_{zz}-I_{xx})\omega _{z}^{\alpha }\omega _{x}^{\alpha }\,=\, & {} 0,\nonumber \\ I_{zz}\sigma _{z}^{\alpha }\,=\, & {} 0. \end{aligned}$$
(57)

It follows that \(\omega _{z}^{\alpha }\,=\,constant\). Let \(\Psi ^{\alpha }\,=\,\omega _{z}^{\alpha }(I_{zz}-I_{xx})/I_{xx}\). Then Eq. (57) turns to

$$\begin{aligned} D_{F,t}^{\alpha } \omega _{x}^{\alpha }+ \Psi ^{\alpha } \omega _{y}^{\alpha }\,=\, & {} 0, \nonumber \\ D_{F,t}^{\alpha } \omega _{y}^{\alpha }- \Psi ^{\alpha } \omega _{x}^{\alpha }\,=\, & {} 0. \end{aligned}$$
(58)

The solution of Eq. (58) is

$$\begin{aligned} \omega _{x}^{\alpha }\,=\, & {} \omega _{0}\cos (\Psi ^{\alpha } S_{F}^{\alpha }(t))\approx \omega _{0}\cos (\Psi ^{\alpha } t^{\alpha }) \nonumber \\ \omega _{y}^{\alpha }\,=\, & {} \omega _{0}\cos (\Psi ^{\alpha } S_{F}^{\alpha }(t)), \approx \omega _{0}\cos (\Psi ^{\alpha } t^{\alpha }), \end{aligned}$$
(59)

where \(\omega _{0}\) is a constant. In Figs. 5 and 6, we have plotted Eq. (59) for the different valves of the dimensions of the fractal time.

Fig. 5
figure 5

Graph of \(\omega _{x}^{\alpha }\) and \(\omega _{y}^{\alpha }\) for the case of \(\omega _{0}\,=\,5\), \(\Psi ^{\alpha }\,=\,1\), and \(\alpha \,=\,1\)

Full size image
Fig. 6
figure 6

Graph of \(\omega _{x}^{\alpha }\) and \(\omega _{y}^{\alpha }\) for the case of \(\omega _{0}\,=\,5\), \(\Psi ^{\alpha }\,=\,1\), and \(\alpha \,=\,0.7\)

Full size image

Remark 4

We note that all results through the paper gives standard results if \(\alpha \,=\,\beta \,=\,1\), namely, \(S_{F}^{1}(t)\,=\,t\).

4 Conclusion

In this work, we have generalized the classical mechanics on fractal curves such as Newton, Lagrange, Hamilton and Appell’s mechanics. The fractal velocity and acceleration have defined in order to obtain Langevin equation on fractal curves. Hamilton’s mechanics on fractal curves have formulated to model non-conservative system on fractal curves. Harmonic oscillator have studied on fractal time in the case of over damping, critical damping and under damping. Suggested framework can be used to model motion of particle in fractal space and time.