Laminar mixed convection of permeable fluid overlaying immiscible nanofluid

Abstract

Immiscible flow has been extensively emerged in science and technology. Researchers and architects were delighted by the concept of multiple fluid transport by the means of shear pressure. The reliance of drag impact of the two immiscible liquids is very much aspired but yet challenging. A mathematical examination has been conveyed to understand the free convection inside a vertical vessel. There are two immiscible liquids filled in the enclosure which are synthesized as two discrete regions encompassing a nanofluid and permeable fluid. The Tiwari–Das model and Dupuit–Forchheimer is utilized to define the nanofluid and permeable fluid, respectively. Southwell over-relaxation technique subject to suitable interface and boundary conditions is bestowed to solve the conservation equations. Essential criteria defining the fluid flow and energy transfer are studied deliberately. The outcomes demonstrate that the Grashof, Brinkman and Darcy numbers augment the velocity, whereas inertial, solid volume fraction, viscosity and thermal conductivity ratios depletes the momentum. The temperature distributions are not much modulated with any of the controlling parameters. By sagging nanoparticles, the flow is not much reformed but reckoning copper nanoparticle as ethylene glycol–mineral oil base fluid regulates the supreme flow. Diamond nanoparticle dropped in water catalyzes the highest rate of heat transfer.

1 Introduction

Industrial applications’ analysts will in general utilize various techniques to drive liquids, like enforcing external forces. This work is motivated by the two layers of immiscible fluids applied in modern technology. The convective not immiscible flows are relevant in material construction because of thickness contrast of differing fluids. The subject of immiscible liquids has been explored in many fields such as oil industry, plasma physical science, and geophysics. The other applications also include film-covering, co-expulsion and greased transport mechanism. Exploration of multiple liquid momentum incorporate, yet not restricted to, cooling hardware, heat exchangers, atomic reactors, and so forth.

Most multi-facet streams happen in three distinct circumstances. To begin with, development of co-expulsion and lubricated measured, numerous polymer-composed substances are appended into the liquid polymer layer (Himmel et al. [1]). These added substances work as greases, which lie in layers between the boundaries of a conduit and the conveyed liquid (Lee et al. [2]). Second, the film-glazing includes a multi-facet, where an alternate layer is utilized on every liquid substrate (Khan et al. [3]). Third, the transmission of driving a conducting stream by a non-conducting liquid utilizing the thick shear pressure is broadly utilized in the electro-osmotic driven flow in equipment (Huang et al. [4]). Dia [5] made analyses on the gravity current initiated from a twofold layer. Golia and Viviani [6] executed a mathematical review of buoyancy-induced double-layer liquids in chambers with various composition of Prandtl and Reynolds numbers. They documented that there is a favorable compactness among analytical and numerical solutions. Koster and Nguyen [7] concentrated on free convection in not miscible liquids with density inversion in a rectangular coliseum.

Al Omari [8] and Khaled and Vafai [9] distinguished a huge energy entrust upgrade from the liquid confronting the heated boundary of a mini-channel, by co-streaming of a cool immiscible liquid with it. Hasnain et al. [10] worked on the impact of porosity on the energy on not blending liquids. They claimed that both the energy and the speed were diminished with the expansion of the third-grade parameter. To build the durability of the materials, specialists add nano-sized particles into the liquefying condition of materials, which brings nanofluids to industrialized productions. From 1995, since Sus and Ja [11] first suspended nano-sized particles into the regular fluids, the ‘nanofluid’ has been effectively applied in many fields in industries for its exclusive compound and physical qualities. Bahiraei et al. [12] inspected the flow properties of the hybrid nanofluid inside miniature channels. Milani et al. [13] scrutinized the double-pipe heat-exchanger utilizing aluminum oxide nanofluid. The homogeneous–heterogeneous reactions for the nanofluid stuffed inside a cylinder was measured by Zhao et al. [14]. Zeng and Xuan [15] probed the qualities of binary nanofluids with applications in solar plants. Numerical simulation of entropy generation driven by natural convection in a trapezoidal chamber under the influence of nonuniform temperature distribution along the vertical wall was performed using the finite-element technique by Khan et al. [16]. The observations made was that the average Nusselt number was an increasing function of the Rayleigh number and amplitude and a decreasing function of wave number. The non-uniformity of the wall temperature distribution can be considered as a passive technique for optimization of the heat transport and entropy generation.

Thermal and flow analysis was performed for free convection in a porous trapezoidal cavity considering a non-equilibrium thermal energy transport model by Khan et al. [17]. They claimed that the local Nusselt number and average Nusselt numbers showed a dominant enhancement for both fluids and solid phases assisted by Rayleigh numbers while decreased with an increase in the heating domains. A comprehensive study of ferrofluid flow of nanofluid and heat transfer enclosed in a triangle cavity was conducted numerically by Usman et al. [18]. They concluded that by enlarging the heated portion of the vertical wall, there was a significant improvement in heat transfer enclosed in a triangular domain. Further an increase of 10% in the volume fraction of Fe$_{3}$ O$_{4}$ particles increases more than 12% raise in the average Nusselt values, whereas 20% increase in the volume fraction of Fe$_{3}$O$_{4}$ particles increases more than 30% raise in the average Nusselt values. Sheikholeslami et al. [19] investigated mathematical modeling of natural convection and magnetic effects on hybrid nano-material convective transportation. The obtained results were that the isotherms were significantly affected due to an augment in applied magnetic field and increasing values of Darcy number while domain change in the streamlines pattern was perceived for the same intensity of magnetic and Darcy numbers. Hamid et al. [20] studied the heat augmentation and hydromagnetic flow of water-based carbon nanotubes (CNTs) inside a partially heated rectangular fin-shaped cavity. Their study remarked that the components of velocity were perceived maximum at a vertical corner while minimum at the horizontal corner. It was demonstrated that the local Nusselt numbers were increased by introducing both solid volume fraction of CNTs and radiation effects, while the Nusselt number noticed maximum at the corners. Khan et al. [21] examined the flow and heat transfer of hybrid nanofluid in a square cavity with a Y-shaped obstacle. The solid volume fraction of both nanoparticles reduced the temperature and increased the local and average Nusselt numbers. The Y-shaped obstacle enhanced the heat transfer rate in the cavity. Isaac Lare Animasaun [22] considered the modified version of buoyancy-induced model to investigate the flow of 47 nm alumina-water nanofluid along an upper surface of horizontal paraboloid of revolution in the of revolution in the presence of nonlinear thermal radiation, Lorentz force and quartic autocatalysis kind of homogeneous heterogeneous chemical reaction. He concluded that at large value of volume fraction/the heat capacity and other properties of 47 nm alumina-water nanofluid greatly generate more heat energy which account for the overshoot in velocity and temperature functions. Further larger values of thickness parameter correspond to higher concentration of the homogeneous bulk fluid and lower concentration of heterogeneous catalyst. He also concluded that increase in velocity index parameter corresponds to an increase in local skin friction coefficient and decrease in local Nusselt number.

Cooling problems and maintenance of products are some of the challenges in the industries due to ever-increasing heat generation. However energy saving and reduction process time have led scientists to embrace the unique nature and thermal characteristics of some fluids formed by adding solid particles (on micrometer and millimeter scales). Significance of haphazard motion and thermal migration of alumina and copper nanoparticles across the dynamics of water and ethylene glycol on a convectively heated surface was explored by Song et al. [23]. The outcome of their findings was the there was a significant difference in the temperature gradients at various haphazard motions of alumina/copper nanoparticles near the wall and free stream when the wall was highly heated convectively. Also increasing thermo-migration of nanoparticles corresponds to a growth in the square of temperature gradient, thus widen the domain of migration significantly at a more significant haphazard motion of alumina/copper nanoparticles. The partial differential equation suitable to unravel the implication of increasing partial slip and viscous dissipation on the dynamics of the mixture of (i) blood and nano-size of gold nanoparticles (ii) air and dust particles on an object with an increasing diameter was investigated by Koriko et al. [24]. They remarked that enhancement in the rate of viscous dissipation was a major factor suitable to increase the velocities of both fluids, boost temperature distribution across both fluids, and local skin friction coefficients. There existed a significant difference between the effect of partial slip on the dynamics of blood-gold nanofluid and dusty fluid.

Kefayati [25] examined non-Newtonian shear-thinning base liquid with a suspension of copper nanoparticles in a square duct. Micropolar nanofluid was inspected by Rashidi et al. [26] with the effect of uniform blowing of two equal co-axial permeable and conducting bodies. Umavathi and her collaborators measured the thermophysical characteristics of nanofluids in different geometries [27,28,29]. Free convection of nanofluids through permeable wavy cavity along with thermal dispersion was researched by Sheremet et al. [30]. A numerical investigation of natural convection heat transfer stability in cylindrical annular with discrete isoflux heat source of different lengths was carried out by Mebarek-Oudina [31]. His results showed that the increase of heat source length ratio decreased the critical Rayleigh number. The flow stability and heat transfer rate in can be controlled by varying of the length of heat source. The sensitivity analysis of the inclined magnetic field and nanoparticle aggregation effects on thermal Marangoni convection in nanoliquid was explored by Mackolil and Mahantesh [32]. The observations made was that the heat transfer rate was positively sensitive towards thermal radiation and negatively sensitive towards the linear and exponential heat sources. Among the heat sources, the heat transfer rate was enhanced more by the exponential heat source. The problem of unsteady nanofluid flow over a bidirectional stretched surface embedded in a porous medium with a magnetic field in the boundary layer region was studied by Ahmad et al. [33]. They found that the large values of the Brownian motion and thermophoresis parameters increase the width of the thermal and concentration boundary layer.

In like manner, many examinations zeroed in on the impact of type and volume part of nanoparticles in the liquid to improve heat move in fenced in areas (Tayebi [34] and Kolsi et al. [35]). Abu-Nada and Chamkha [36] explored that expanding CuO–EG nanoparticle concentration in the base liquid, the Nusselt values increased. Zargartalebi et al. [37] surveyed the natural convection in a closed conduit loaded with nanofluid concentrated on the laminar regular convection in a walled in area filled by nanofluid. The outcome shows that Nusselt number increments with increment of porosity. The average heat transfer coefficient was improved by expanding the nanoparticles volume fraction as proved in Jou and Tzeng [38]. The experimental analysis was discussed by Ho et al. [39] and Hu et al. [40] to inspect the consequences of the nanofluid on buoyancy driven flow in a rectangular chamber with a heat source at the left and cooling at the right, inculcating the upward and base of the chamber. They showed that with increment of nanoparticles in base fluid, heat transfer rate was improved. In the literature, studies reveal that the convective heat transfer is enhanced with the presence of nanoparticles and porous medium. Further examinations on the nanofluid saturated with porous bed can be counseled through the investigation [41,42,43]. Recently, Umavathi et al. [44, 45] surveyed the impacts of composite fluids in a conduit.

Industrial applications of two immiscible nanofluids in enclosures are significant in various thermal duct systems, materials processing and chemical engineering technologies. The numerical solutions on this topic in the literature is very meager. Propelled by the above work, two-layer fluid flow with the lower region filled with porous bed and the upper region saturated with nanoparticles is explored. For permeable medium, Dupuit–Forchheimer model is utilized which is an expansion of Darcy’s law model. Tiwari–Das model is incorporated for the nanofluid. Furthermore, generally, the vast majority of studies have concentrated only on one type of nanoparticles and one type of base fluid, i.e., unitary nanofluids. Mixed convection of a mixture of different base fluids (engine oil, ethylene glycol, kerosene, and water) and different nanoparticles (copper, titanium oxide, and diamond) is investigated. Graphical results on the velocity and temperature are analyzed extensively on all the governing parameters. Volumetric flow rate, skin friction and heat transfer rates are also analyzed for all the parameters.

2 Mathematical formulation

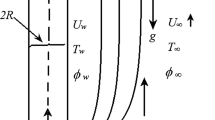
Figure 1 traces the co-ordinates, boundary and interfacial conditions. Two immiscible non-Newtonian fluids flowing inside a vertical rectangular duct are analyzed. The viscous and Darcy dissipations are also included. The height of the duct is $\left( {\frac{a_{1} }{2}\,\,+\,\,\frac{a_{2} }{2}} \right)$ and b is the thickness. The upper and underneath boundaries of the duct are isolated. The other tow sides of the duct are kept at constant temperatures $T_{w1}$ and $T_{w2}$ respectively such that $T_{w2} \,\,>\,\,T_{w1}$. The no-slip conditions is assumed at all rigid boundaries. The conditions at the interface are considered to be continuity of velocity, continuity of shear stress and continuity of heat flux. The Tiwari–Das model and Dupuit–Forchheimer model is taken into account to model the nanofluid and permeable fluid, respectively. All the physical properties of the fluid are treated to be constant. It is also assumed that the nanoparticles move consistently with the base fluid. The Zone-I contains the nanofluid having density $\rho _{nf}$, viscosity $\mu _{nf}$, thermal expansion coefficient $\beta _{nf}$, thermal conductivity $K_{nf}$ and Zone-II contains permeable fluid having density $\rho _{2}$, viscosity $\mu _{2}$, thermal expansion coefficient $\beta _{2}$, thermal conductivity $K_{2}$ and porosity $\kappa$. Copper, diamond, titanium oxide and engine oil, mineral oil, kerosene, and ethylene glycol are selected as nanoparticles and base fluids, respectively. The momentum and energy transport equations incorporating the above-mentioned assumptions along with Oberbeck–Boussinesq approximation reduces to (following Mahdi et al. [4] and Ozotop et al. [49])

Fig. 1

Physical configuration

Zone-1 (Nanofluid)

$$\begin{aligned}&\frac{\partial ^{2}W_{1} }{\partial X_{1}^{2}}\,\,+\,\,\frac{\partial ^{2}W_{1} }{\partial Y^{2}}\,\,\nonumber \\&\quad + \frac{\rho _{nf} \,\vec {{g}}\,\beta _{nf} \,\left( {T_{w1} \,-\,T_{0} } \right) \,\,}{\mu _{nf} }\,=\,\,\,\frac{1}{\mu _{nf} }\,\frac{\partial P}{\partial Z} \end{aligned}$$

(1)

$$\begin{aligned}&\frac{\partial ^{2}T_{1} }{\partial X_{1}^{2}}\,\,+\,\,\frac{\partial ^{2}T_{1} }{\partial Y^{2}}\,\,\nonumber \\&\quad + \frac{\mu _{nf} }{K_{nf} }\,\,\left[ {\left( {\frac{\partial \,W_{1} }{\partial X_{1} }} \right) ^{2}\,\,+\,\left( {\frac{\partial \,W_{1} }{\partial Y}} \right) ^{2}\,} \right] =0 \end{aligned}$$

(2)

Zone-2 (Permeable fluid)

$$\begin{aligned}&\frac{\partial ^{2}W_{2} }{\partial X_{2}^{2}}\,\,+\,\,\frac{\partial ^{2}W_{2} }{\partial Y^{2}}\,\,\nonumber \\&\quad + \frac{\rho _{2} \,\vec {{g}}\,\beta _{2} \,\left( {T_{w2} \,-\,T_{0} } \right) \,\,}{\mu _{2} } - \frac{1}{\kappa }W_{2} \,\,\nonumber \\&\quad -\,\,\frac{\rho _{2} C_{F} }{\mu _{2} \,\,\sqrt{\kappa }}\,\,W_{2}^{2}=\frac{1}{\mu _{2} }\,\frac{\partial P}{\partial Z} \end{aligned}$$

(3)

$$\begin{aligned}&\frac{\partial ^{2}T_{2} }{\partial X_{2}^{2}} + \frac{\partial ^{2}T_{2} }{\partial Y^{2}}\nonumber \\&\quad + \frac{\mu _{2} }{K_{2} }\left[ {\left( {\frac{\partial \,W_{2} }{\partial X_{2} }} \right) ^{2} + \left( {\frac{\partial \,W_{2} }{\partial Y}} \right) ^{2}\,} \right] + \frac{\mu _{2} \,}{K_{2} \,\kappa }\,W_{2}^{2} = 0 \nonumber \\ \end{aligned}$$

(4)

The reference temperature is considered as $T_{0} =\frac{\left( {T_{w1} +T_{w2} } \right) }{2}$. The convection is generated owing to the gradients of temperature. The no-slip condition is approved at the periphery. Under these assumptions, Eqs. (1)–(4) are computed using boundary and interface conditions:

Zone-1

$$\begin{aligned}&W_{1} \,=\,0,\quad T_{1} \,=\,T_{w1}\\&\quad \text{ at }\,\,Y\,=\,0\quad \text{ for }\;\;0\le \,X_{1}<\frac{a_{1} }{2}\\&W_{1} \,=\,0,\quad T_{1} \,=\,T_{w2}\\&\quad \text{ at }\,\,Y\,=\,b\quad \text{ for }\,\,\,0\le X_{1} <\frac{a_{1} }{2} \\&W_{1} \,=\,0,\quad \frac{\partial T_{1} }{\partial X_{1}}\,=\,0\\&\quad \text{ at }\,\,X_{1} =\,0\quad \text{ for }\,\,0\le \,Y\le b \end{aligned}$$

Interface

$$\begin{aligned}&W_{1} =W_{2} ,\quad \mu _{nf} \frac{\partial W_{1} }{\partial X_{1} }=\mu _{2} \frac{\partial W_{2} }{\partial X_{2} }\\&\quad \text{ at }\,\,X=\frac{a_{1} }{2}\,\,\,\,\,\,\text{ for }\,\,\,0\le \,Y\le b \\&T_{1} =T_{2} ,\quad K_{nf} \frac{\partial T_{1} }{\partial X_{1} }=K_{2} \frac{\partial T_{2} }{\partial X_{2} }\\&\quad \text{ at }\,\,X=\frac{a_{1} }{2}\quad \text{ for }\,\,\,0\le \,Y\le b \end{aligned}$$

Zone-2

$$\begin{aligned}&W_{2} =\,0,\quad T_{2} \,=\,T_{w1}\nonumber \\&\quad \text{ at }\,\,Y\,=\,0\quad \text{ for }\;\;\frac{a_{1} }{2}<X_{2} \le \frac{a_{2} }{2} \nonumber \\&W_{2} =\,0,\quad T_{2} \,=\,T_{w2}\nonumber \\&\quad \text{ at }\,\,Y\,=\,0\quad \text{ for }\;\;\frac{a_{1} }{2}<\,X_{2} \le \frac{a_{2} }{2} \nonumber \\&W_{2} =\,0,\quad \frac{\partial T_{2} }{\partial X_{2} }\,=\,0\nonumber \\&\quad \text{ at }\,\,X_{2} \,=\,\frac{a_{1} +a_{2} }{2}\quad \text{ for }\,\,\,\text{0 }\,\,\le \,Y\le b \end{aligned}$$

(5)

The dimensionless variables utilized are

$$\begin{aligned} x_{1}&=\frac{X_{1} }{b},\quad x_{2} =\frac{X_{2} }{b},\quad y = \frac{Y}{b},\quad w_{1} =\frac{\rho _{f} \,b\,}{\mu _{f} }W_{1} ,\nonumber \\ w_{2}&= \frac{\rho _{f} \,b\,}{\mu _{f} }W_{2} , \nonumber \\ \theta _{1}&= \frac{T_{1} \,-\,T_{0} }{T_{w2} \,-\,T_{w1} },\quad \theta _{2} \,=\,\frac{T_{2} \,\,-\,\,T_{0} }{T_{w2} \,-\,T_{w1} } \end{aligned}$$

(6)

Equations (1)–(4) are rewritten as

Zone-1

$$\begin{aligned}&\frac{\partial ^{2}w_{1} }{\partial x_{1}^{2}}\,\,+\,\,\frac{\partial ^{2}w_{1} }{\partial y^{2}}\,+\,\,GR\,\,\,\theta _{1} \,\,\,\,\,=\,\,p_{1} \end{aligned}$$

(7)

$$\begin{aligned}&\frac{\partial ^{2}\theta _{1} }{\partial x_{1} ^{2}}\,\,+\,\,\frac{\partial ^{2}\theta _{1} }{\partial y^{2}}\,\,\nonumber \\&\quad +\,\,BR\,\,\left[ {\left( {\frac{\partial \,w_{1} }{\partial x_{1} }} \right) ^{2}\,\,+\,\left( {\frac{\partial \,w_{1} }{\partial y}} \right) ^{2}\,} \right] \,\,\,\,=\,\,0 \end{aligned}$$

(8)

Zone-2

$$\begin{aligned}&\frac{\partial ^{2}w_{2} }{\partial x_{1}^{2}}\,\,+\,\,\frac{\partial ^{2}w_{2} }{\partial y^{2}}\,+\,\,\frac{Gr\,\,n\,\,\beta }{\lambda }\,\,\,\theta _{2} \,\nonumber \\&\quad -\,\,\frac{1}{Da}\,\,w_{2} \,\,-\,\,\frac{I\,\,n}{\lambda }\,w_{2}^{2}\,\,\,\,=\,\,\,\frac{p}{\lambda } \end{aligned}$$

(9)

$$\begin{aligned}&\frac{\partial ^{2}\theta _{2} }{\partial x_{2}^{2}}\,\,+\,\,\frac{\partial ^{2}\theta _{2} }{\partial y^{2}}\,\,\nonumber \\&\quad +\,\,\frac{Br\,\,\lambda }{K}\,\,\left[ {\left( {\frac{\partial \,w_{2} }{\partial x_{2} }} \right) ^{2}\,\,+\,\left( {\frac{\partial \,w_{2} }{\partial y}} \right) ^{2}\,} \right] \,\,\nonumber \\&\quad +\,\,\frac{Br\,\,\lambda }{Da\,\,K}\,w_{2}^{2}\,\,\,\,=\,\,0 \end{aligned}$$

(10)

Substituting Eq. (6) in Eq. (5), the conditions on the borderline and at the interface become

Zone-1

$$\begin{aligned}&w_{1} \,=\,0\,,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\theta _{1} =\,-\frac{1}{2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\\&\quad \text{ at }\,\,\,\,\,Y\,=\,0\,\,\,\,\,\,\,\,\,\text{ for }\;\;0\le \,x_{1}<A_{1} \\&w_{1} \,=\,0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\theta _{1} \,=\,\frac{1}{2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\\&\quad \text{ at }\,\,\,\,\,Y\,=\,1\,\,\,\,\,\,\,\,\,\,\text{ for }\,\,\,0\le x_{1} <A_{1} \\&w_{1} \,=\,0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{\partial \theta _{1} }{\partial x_{1} }\,=\,0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\\&\quad \text{ at }\,\,\,\,\,x_{1} \,=\,0\,\,\,\,\,\,\,\text{ for }\,\,\,0\le \,y\le 1 \end{aligned}$$

Interface

$$\begin{aligned}&w_{1} =w_{2} ,\,\,\,\,\,\,\,\,\,\,\,\frac{\partial w_{1} }{\partial x_{1} }=\frac{\lambda }{\left( {1\,-\,\phi } \right) ^{2.5}}\,\,\frac{\partial w_{2} }{\partial x_{2} }\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\\&\quad \text{ at }\,\,\,x=A_{1} \,\,\,\,\,\,\text{ for }\,\,\,0\le \,y\le 1 \\&\theta _{1} =\theta _{2} ,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{\partial \theta _{1} }{\partial x_{1} }=\frac{K\,K_{f} }{K_{nf} }\frac{\partial \theta _{2} }{\partial x_{2} }\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\\&\quad \text{ at }\,\,\,x=A_{1} \,\,\,\,\,\,\,\text{ for }\,\,\,0\le \,Y\le 1 \end{aligned}$$

Zone-2

$$\begin{aligned}&w_{2} =\,0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\theta _{2} \,=\,-\frac{1}{2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\nonumber \\&\quad \text{ at }\,\,\,\,\,y\,=\,0\,\,\,\,\,\,\,\,\,\,\text{ for }\;\;A_{1}<\,x_{2} \le A_{2} \nonumber \\&w_{2} =\,0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\theta _{2} \,=\,\frac{1}{2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\nonumber \\&\quad \text{ at }\,\,\,\,\,y\,=\,0\,\,\,\,\,\,\,\,\,\text{ for }\;\;A_{1} <x_{2} \le A_{2} \nonumber \\&w_{2} =\,0,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{\partial \theta _{2} }{\partial x}\,=\,0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\nonumber \\&\quad \text{ at }\,\,\,\,\,x\,=A_{1} \,+A_{2} \,\,\,\,\,\,\,\,\text{ for }\,\,\,\text{0 }\,\,\le \,y\le 1 \end{aligned}$$

(11)

where

$$\begin{aligned} Gr&=\frac{g\,\,\beta _{f} b^{3}\left( {T_{w2} \,-\,T_{w1} } \right) }{\nu _{f}^{2}},\,\,\,\,\,Da\,\,\,=\,\,\,\frac{\kappa }{b^{2}},\,\,\,\,\,\nonumber \\&I= \frac{C_{F} \,\,b}{\sqrt{\kappa }},\,\,\,\,\,\,p\,=\,\frac{\rho _{f} \,\,b^{3}}{\mu _{f} ^{2}}\,\frac{\partial P}{\partial Z},\,\,p_{1} \,\,=\,\,p\,\,\left( {1\,-\,\phi } \right) ^{2.5}, \nonumber \\ Br&= \frac{\mu _{f}^{3}}{K_{f} \,\,\rho _{f}^{2}\,\,b^{2}\,\,\left( {T_{w2} \,-\,T_{w1} } \right) \,\,},\,\,\,\,\nonumber \\ GR&= Gr\,\,\left( {\left( {1\,-\,\phi } \right) \,\,+\,\,\phi \,\,\frac{\left( {\rho \beta } \right) _{s} }{\left( {\rho \beta } \right) _{f} }} \right) \,\,\left( {1\,-\,\phi } \right) ^{2.5}, \nonumber \\ BR&= \frac{Br}{\left( {1\,-\,\phi } \right) ^{2.5}}\,\,\left( {\frac{K_{s} \,\,+\,\,2\,K_{f} \,\,+\,\,\phi \,\,\left( {K_{f} \,\,-\,\,K_{s} } \right) }{K_{s} \,\,+\,\,2\,K_{f} \,\,-2\,\,\,\,\phi \,\,\left( {K_{f} \,\,-\,\,K_{s} } \right) }} \right) ,\,\,\,\,\nonumber \\ \beta&\frac{\beta _{2} }{\beta _{f} },\,\,\,\,\,n=\frac{\rho _{2} }{\rho _{nf} },\,\,\,\, \nonumber \\ \lambda&=\frac{\mu _{2} }{\mu _{f} },\,\,K=\frac{K_{2} }{K_{f} },\,\,\,\,\,A_{1} =\frac{a_{1} }{2b},\,\,\,\,\,A_{2} =\frac{a_{2} }{2b} \end{aligned}$$

(12)

Following Brinkman [46] and Maxwell [47], correlations between the carrier fluid and the solid particles used in deriving the above equations are

$$\begin{aligned}&\left( \rho \right) _{nf} =\left( {1-\phi } \right) \rho _{f} +\phi \,\rho _{s} \end{aligned}$$

(13)

$$\begin{aligned}&\left( \beta \right) _{nf} =\left( {1-\phi } \right) \beta _{f} +\phi \,\beta _{s} \end{aligned}$$

(14)

$$\begin{aligned}&\mu _{nf} =\mu _{f} \left( {1-\phi } \right) ^{-2.5} \end{aligned}$$

(15)

$$\begin{aligned}&K_{nf} =K_{f} \left( {\frac{K_{s} +2K_{f} -2\phi \left( {K_{f} -K_{s} } \right) }{K_{s} +2K_{f} +\phi \left( {K_{f} -K_{s} } \right) }} \right) \end{aligned}$$

(16)

3 Numerical solutions

The solutions of Eqs. (7)–(11) which are coupled and nonlinear along with two-fluid interface and boundary conditions are evaluated numerically employing finite-difference method. A Taylor series expansion is employed to derive the first, second and central difference approximations neglecting higher order terms of the series. The finite mesh is attained by dividing zone-1 $\left( {x_{i}^{\left( 1 \right) } \,\,,\,\,y_{j} } \right)$ into Nx1, zone-II $\left( {x_{i}^{\left( 2 \right) } \,\,,\,\,y_{j} } \right)$ into Nx2 divisions along $x-$direction with the step length $\Delta x$ and Ny divisions along y-direction with the step length $\Delta y$. Substituting the finite difference approximations into Eqs. (7)–(11) results in the following finite-difference equations:

Zone-1

$$\begin{aligned}&\,\left( {\frac{w_{1(i+1,j)} -2w_{1(i,j)} +{w_{1\,\,\,(}} _{i-1,j)} }{\left( {\Delta x_{1} } \right) ^{2}}} \right) \,\,\nonumber \\&\quad +\,\,\left( {\frac{w_{1(i,j+1)} -2w_{1(i,j)} +w_{1(i,j-1)} }{\left( {\Delta y} \right) ^{2}}} \right) \,\,\,\,\nonumber \\&\quad +\,\,GR\,\,\theta _{1(i,j)} \,-\,\,p_{1} \,\,=\,\,0 \end{aligned}$$

(17)

$$\begin{aligned}&\,\left( {\frac{\theta _{1(i+1,j)} -2\theta _{1(i,j)} +\theta _{1(i-1,j)} }{\left( {\Delta x_{1} } \right) ^{2}}} \right) \,\,\nonumber \\&\quad +\,\,\left( {\frac{\theta _{1(i,j+1)} -2\theta _{1(i,j)} +\theta _{1(i,j-1)} }{\left( {\Delta y} \right) ^{2}}} \right) \nonumber \\&\quad + BR\,\,\left[ \left( {\frac{w_{1(i+1,j)} -w_{1(i-1,j)}}{2\,\,\Delta x_{1} }} \right) ^{2}\right. \nonumber \\&\quad \left. +\left( {\frac{{{w}_{1(i,j+1)}}-{w}_{{1(i,j-1)}} }{2\,\,\Delta y}} \right) ^{2} \right] \,\,\,=\,\,0 \end{aligned}$$

(18)

Zone-2

$$\begin{aligned}&\left( {\frac{w_{2(i+1,j)} -2w_{2(i,j)} +w_{2(i-1,j)} }{\left( {\Delta x_{2} } \right) ^{2}}} \right) \,\,\nonumber \\&\quad +\,\,\left( {\frac{w_{2\,(i,j+1)} -2w_{2(i,j)} +w_{2(i,j-1)} }{\left( {\Delta y} \right) ^{2}}}\right) \,\,\,\,\nonumber \\&\quad +\,\,\frac{Gr\,\,\beta \,n\,}{\lambda }\,\theta _{2(i,j)} \, \nonumber \\&\quad -\frac{1}{Da}\,\,w_{2(i,j)} \,\,\,-\,\,\,\frac{I\,\,n}{\lambda }\,\,\,w_{2}^{2}\,\,-\,\,\frac{p\,}{\lambda }\,=\,\,0 \end{aligned}$$

(19)

$$\begin{aligned}&\left( {\frac{\theta _{2(i+1,j)} -2\theta _{2(i,j)}+\theta _{2(i-1,j)} }{\left( {\Delta x_{2} } \right) ^{2}}}\right) \,\,\nonumber \\&\quad +\,\,\left( {\frac{\theta _{2(i,j+1)} -2\theta _{2(i,j)} +\theta _{2(i,j-1)} }{\left( {\Delta y}\right) ^{2}}} \right) \nonumber \\&\quad +\frac{Br\,\,\lambda }{K}\left[ \left( {\frac{w_{2(i+1,j)}-w_{2(i-1,j)} }{2\Delta x_{2} }} \right) ^{2}\right. \nonumber \\&\quad \left. +\left( {\frac{w_{2(i,j+1)} -w_{2(i,j-1)} }{2\Delta y}}\right) ^{2} \right] \,\,+\,\,\frac{Br\,\,\lambda }{Da\,\,K}\,\,w_{2}^{2}=\,\,0 \nonumber \\ \end{aligned}$$

(20)

The associated boundary conditions are

Zone-1

$$\begin{aligned}&w_{1(i,0)} \,=\,\,-w_{1(i,1)} \theta _{1(i,0)} \,=\,\,-1-\theta _{1(i,1)}\\&\quad \text{ at }\,Y\,=\,0 \text{ for }\;\;0\le \,x_{1}<A_{1} \\&w_{1} \,_{\,\,(i,Ny+1)} \,=\,\,-w_{1(i,Ny)}\theta _{1(i,Ny+1)}\,\\&=\,\,1-\theta _{1(i,Ny)} \text{ at }\,Y\,=\,1\\&\quad \text{ for }\,\,\,0\le x_{1} <A_{1} \\&w_{1(0,j)} \,=\,\,-w_{1(1,j)}\theta _{1(1,j)} \,=\,\,\theta _{1(0,j)} \\&\quad \text{ at }\,\,\,\,\,x_{1}\,=\,0 \text{ for }\,\,\,0\le \,y\le 1 \end{aligned}$$

Interface

$$\begin{aligned}&\left. {\begin{array}{l}w_{2(Nx2+1,j)} =w_{1(Nx+1,j)} \,\,+\,w_{1(Nx1,j)} \,-w_{2(Nx2,j)} \\ w_{1(Nx+1,j)} =\lambda \frac{\Delta x_{1} }{\,\,\Delta x_{2}}\\ \quad \left( {w_{2(Nx2,j)} \,\,-\,w_{2(Nx2+1,j)} }\right) +w_{1(Nx1,j)} , \\ \end{array}} \right\} \\&\quad \text{ at } x=A_{1} \text{ for } 0\le \,y\le 1\\&\left. {\begin{array}{l}\theta _{2(Nx2+1,j)} =\theta _{1(Nx+1,j)} \,\,+\,\theta _{1(Nx1,j)} \,-\theta _{2(Nx2,j)} \\ \theta _{1(Nx+1,j)} =K\frac{\Delta x_{1} }{\,\Delta x_{2} }\\ \quad \left( {\theta _{2(Nx2,j)} \,\,-\,\theta _{2(Nx2+1,j)} }\right) +\theta _{1(Nx1,j)} , \\ \end{array}} \right\} \\&\quad \text{ at } \,\,\,x=A_{1} \text{ for }\,\,\,0\le \,Y\le 1 \end{aligned}$$

Zone-2

Table 1 Grid independence test $\left[ {\frac{{\text {d}}\theta }{{\text {d}}y}} \right] _{y=0} Br=0.1,\,\,Gr\,\,=\,\,10,\,\,P\,\,=\,\,-\,1.0,\,\,\phi \,\,=\,\,0.01,\,\,Da\,\,=\,\,0.01,\,\,I\,\,=\,\,4.0$ water-copper

Table 2 Similarity of $\left[ {\frac{{\text {d}}\theta }{{\text {d}}y}} \right] _{y\,\,=\,\,0}$ for $Br\,\,=\,\,0.1,\,\,Gr\,\,=\,\,10,\,\,P\,\,=\,\,-0.1\,$

$$\begin{aligned}&w_{2(i,0)} \,=\,\,-w_{2(i,1)} ,\,\,\,\,\theta _{2(i,0)} \,=\,\,-1-\theta _{2(i,1)} \nonumber \\&\quad \text{ at }\,y\,=\,0\,\text{ for }\;\;A_{1}<\,x_{2} \le A_{2} \nonumber \\&w_{2(i,Ny+1)} \,=\,\,-w_{2(i,Ny)} ,\,\,\theta _{2(i,Ny+1)} \,=\,\,1-\theta _{2(i,Ny)} \nonumber \\&\quad \text{ at }y\,=\,0\text{ for }\;\;A_{1} <x_{2} \le A_{2} \nonumber \\&w_{2(0,j)} \,=\,\,-w_{2(1,j)} \theta _{2\,(1,j)} \,=\,\,\theta _{2(0,j)} \nonumber \\&\quad \text{ at }x\,=A_{1} \,+A_{2} \text{ for }\,\,\,\text{0 }\,\,\le \,y\le 1 \end{aligned}$$

(21)

Equations (17)–(21) are computed using the Southwell over-relaxation method (SOR). The iterations are stopped till the tolerance value is as of $10^{-8}$is achieved. Double-precision arithmetic is employed in the coding. The validation of the code is carried with grid independence and comparing the solutions with the published work. The average Nusselt values are laid out in Table 1 for different grid size. This table report that the values of Nusselt number are almost equal for 101 $\times$ 101 or 201 $\times$ 201 grids. Therefore, 101 $\times$ 101 grids are chosen for the evaluation. The computations for the values of solid volume fraction $\phi \,\,=\,\,0$, $Da\,\,=\,\,0$ and $I\,\,=\,\,0$, agree with Umavathi and Bég [48]. The results in Umavathi and Bég [48] was achieved via careful benchmarking with the finite-element solutions of Oztop et al. [49], finite volume solutions of Moshkin [50] for two-layer system and finite-difference computations of De Vahl Davis [51, 52]. The code is further is justified by observing the nature of the values of the average rate of heat transfer in Table 2. The present model consists of nanofluid in zone-I and permeable fluid in zone-2. The values in zone-1 and zone-2 are almost equal to the values of Umavathi and Bég [48]. Hence the numerical solutions computed can be considered as grid independence and the validation are satisfied.

4 Results and discussion

In this section, to understand the behavior of Grashof number $\left( {Gr} \right)$, Brinkman number $\left( {Br} \right)$, Darcy number $\left( {Da} \right)$, inertial parameter $\left( I \right)$, nanoparticle volume fraction $\left( \phi \right)$, viscosity ration $\left( \lambda \right)$, conductivity ration $\left( K \right)$, different nanoparticle, different base fluid on the flow and heat distributions are sketched in three, two, one-dimension patterns. The one-dimensional graphs are plotted at $x\,\,=\,\,0.5$ for variations of y from 0 to 1. The study have been performed over reasonable ranges $-25\,\,\le \,\,Gr\,\,\le \,\,25$, $0\,\,\le \,\,Br\,\,\le \,\,2$, $0.000001\,\,\le \,\,Da\,\,\le \,\,1.0$, $0\,\,\le \,\,I\,\,\le \,\,8$, $0\,\,\le \,\,\phi \,\,\le \,\,0.5$, $0\,\,\le \,\,\lambda \,\,\le \,\,8$, $0\,\,\le \,\,K\,\,\le \,\,1$, the nanoparticles used are copper, diamond and titanium oxide using water as base fluid, the combinations of engine oil–mineral oil, ethylene glycol–kerosene, ethylene glycol–mineral oil in zone-1 and zone-2, respectively, using copper as nanoparticle with fixed values of $Gr\,\,=\,\,10,\,\,Br\,\,=\,\,0.1,\,\,Da\,\,=\,\,0.01,\,\,I\,\,=\,\,4.0,\,\,\phi \,\,=\,\,0.01,\,\,\lambda \,\,=\,\,1,\,\,K\,\,=\,\,1,\,\,P\,\,=\,\,1$ for the numerical computations.

The exploration of Grashof number on the velocity and temperature are presented in Fig. 2a–c (velocity) and d–f (temperature). As the Grashof number increases, flow increases in both the upper and lower zones $\left( {3D} \right)$. However, for $Gr\,\,=\,\,-25$ and $Gr\,\,=\,\,-1$, the number of contours are more in the lower region. For $Gr\,\,=\,\,0$ (the flow occurs only due to forced convection), there is only one cell formation and the contours are dense at the left wall of the duct. But for $Gr\,\,=\,\,0.01$, there are two cell formations indicating that the flow is due to convection. For $Gr\,\,=\,\,25$ and $Gr\,\,=\,\,1$, the number of contours are more in the upper zone and there are two cell formation. However, the contours are dense at the right plate for $Gr\,\,=\,\,1$ and dense at the left plate for $Gr\,\,=\,\,25$. The 3D graph shows that curvature is convex in the upper and lower directions for $Gr\,\,=\,\,\pm 25$, however, the convexity occurs at the lower part and then switches to the upper part for $Gr\,\,=\,\,-25$ and the reversal pattern is attained for $Gr\,\,=\,25$. For forced convection, the convexity occurs only in the upper part and flat in the lower part as seen in Fig. 2a. Figure 2b shows that there is no convexity in the lower region for $Gr\,\,=\,\,-1$ but it starts appearing slightly for $Gr\,\,=\,\,0.01$ and grows for $Gr\,\,=\,\,1$ indicating that as Grashof number increases flow increases. This is the similar result obtained by Isaac Issac Lare Animasaun [53] in his analysis while studying dynamics of unsteady magnetohydrodynamic convective fluid flow with radiation and thermophoresis of particles past a vertical porous plate moving through a binary mixture in an optically thin environment. The observations made by him was that the velocity increased with increasing value of temperature-dependent viscosity parameter when Grashof number is greater than 1; velocity decreased with increasing values of temperature-dependent viscosity parameter when Grashof number is less than 1 and the two effects existed when Grashof number is moderately small.

Fig. 2

Momentum (a–c) and energy (d–f) contours for various Gr

Figure 2c demonstrates that the velocity increases at the left wall and decreases at the right wall for $Gr\,\,=\,\,-25$ and reversal flow occurs for $Gr\,\,=\,25$. For forced convection $Gr\,\,=\,\,0$, the velocity profile is almost linear. There are two reasons for having this type of profiles. The flow reversal occurs because of mixed convection as the velocity depends on the values of the pressure and Grashof number. The second reason is that the physical properties are different at the interface though the assumption of continuity of velocity and skin friction is assumed. Further it is also assumed that the constant temperature at the left wall is less than the temperature at the right wall. Figure 2d–f illustrates the temperate distributions. The 3D plot shows that there is no significant variations for any value of Gr. The number of temperature contours $\left( {2D} \right)$ are similar, linear and symmetric. The one-dimensional graph (Fig. 2f) also depicts that the Gr does not transform in a wider range for the impact of Gr; however, when the graph is magnified, the temperature is enhanced as Gr increases and the magnitude is high for $Gr\,\,=\,25$ in comparison with $Gr\,\,=\,\,-25$. The reasons for having less influence on $\theta$ is due to the insulating temperature conditions adopted at the top and bottom plates of the duct. Figure 2c, e shows that in the absence of thermal buoyancy force, the velocity curve is parabolic and the temperature curve is a straight line. As Grashof number increases, the velocity increases in the range of $0.5\le y \le 1$ (flow acceleration) and decreases (flow deceleration) in the range of $0.0 \le y \le 0.5$. The 1-D graphs are plotted at the location $x = 0.5$ and y ranging from 0 to 1. Figure 2f shows that the temperature profiles are boosted by increasing Grashof number. This is a classical result for the influence of buoyancy forces. Increasing the buoyancy forces physically implies the increase in convection currents which energizes the duct flow.

The consequence of Br on the momentum and thermal fields are exhibited in Fig. 3a–c, respectively. The 3D visualization confers the convexity in curvature in both the zones; however, the steepness of the curve is large in the upper zone in comparison with the lower zone. There are two cell formation for all values of Br. The number of contours are more in the upper zone and dense at the left wall of the duct. One-dimension graph expose that the velocity increases as Br increases. The velocity (Fig. 3b) and temperature (Fig. 3c) increase as Br increases. The large values of Br heighten the viscous heating and Darcy dissipations and, therefore, increases the velocity and temperature. The large values of Br uphold the kinetic energy within the fluid. Further kinetic energy converted into thermal energy results in the elevation of the temperature, and hence, the velocity is also intensified by the presence of Br. Figure 3c also shows that the temperature profile is linear (straight line) for $Br\,\,=\,\,0$ and tends to nonlinear for $Br\,\,\ne \,\,0$, because the distribution of temperature for $Br\,\,=\,\,0$ is purely by conduction and become hyperbolic for $Br\,\,\ne \,\,0$.

Fig. 3

Momentum a, b and energy c contours for various Br

The repercussion of Da on the velocity and heat fields are laid out in Fig. 4a–c. As Da increases the curvature of the velocity changes from convexity to flat in the lower region only. For $Da\,\,=\,\,0.00001$ , there are no velocity contours in the range $0.5\,\,\le \,\,x\,\,\le \,\,1$. The small values of Da implies that the permeability is very small (porous matrix is densely packed), hence, there is negligible velocity for $Da\,\,=\,\,0.00001$. For $Da\,\,=\,\,0.1,\,\,1.0$, the contours are flattened and the number of contours in the upper zone (nanofluid) are large in comparison with the lower zone (porous medium). It is also clear in 3D view that the curvature in the upper zone is vigilant and flat in the lower zone. Figure 4b also reveals that the velocity profile is almost linear for $Da\,\,=\,\,0.00001$ and the velocity increases as Da increases. The significance of Da on temperature is negligible as seen in Fig. 4c. When magnified the figure shows that as Da increases, temperature is also accelerated. The large Da implies the corresponding reduction in friction drag which results in the increase of velocity in the porous region in comparison with viscous nanofluid region.

Fig. 4

Momentum a, b and energy c contours for various Br

Figure 5 accomplishes the inertial parameter on the momentum fields. It is observed from 3D view that the convexity is fierce in zone-1 in comparison with zone-2. The number of contours are more in zone-1 and dense at the left plate when compared with zone-2. The 3D and 2D plots looks similar for all values of I. Table 3 provides the values of velocity and temperature at $x\,\,=\,\,0.5$ for variations of y. The values are almost equal to three decimal places for velocity and no variation in temperature. The values of velocity are decreasing for increasing values of I. This is for the reasons that the inertial parameter induces the dragging effect and hence decelerates the flow and the heat is cooled.

Fig. 5

Momentum contours for various I

Table 3 Values of velocity and temperature at $x\,\,=\,\,0.5$

Figure 6a–c demonstrates the consequences of $\phi$ on the momentum and heat transfer. The curvature is convex for all values of $\phi$ as seen in 3D plots. For $\phi \,\,=\,\,0,\,\,0.1$, the steepness of the curvature looks similar, whereas for $\phi \,\,=\,\,0.5$, the lower and upper region curvatures become sharp. The number of contours are more in the upper zone and dense at the left plate of the duct for $\phi \,\,=\,\,0,\,\,0.1$, whereas the contours becomes dense at the right plate for $\phi \,\,=\,\,0.5$. The 1D graph clearly visualizes that the velocity (Fig. 6b) and temperature (Fig. 6c) decrease as $\phi$ increases. The magnitude of suppression is very less for temperature. The enlargement of $\phi$ informs that for high nanoparticle concentration (doping percentage) the base fluid cannot flow fast because of modification in the viscosity and hence decelerates the flow.

Fig. 6

Momentum a, b and energy c contours for various $\phi$

The effect of viscosity ratio $\lambda \,\,\left( {=\,\,\frac{\mu _{2} }{\mu _{f} }} \right)$ on the flow field is displayed in Fig. 7a–c. The values of $\lambda \,\,=\,\,0.1\,\,\left( {\mu _{2} \,\,=\,\,10\,\,\mu _{f} } \right)$ indicates that the saturated porous medium is ten times more viscous than the base fluid, $\lambda \,\,=\,\,0.5\,\,\left( {\mu _{2} \,\,=\,\,2\mu _{f} } \right)$ implies the viscosity of the porous medium is two times the base fluid and $\lambda \,\,=\,\,1.0\,\,\left( {\mu _{2} \,\,=\,\,\mu _{f} } \right)$ implies the viscosity is equal for the porous medium and the base fluid. The 3D plot for $\lambda \,\,=\,\,0.1$ shows the sharp convexity, $\lambda \,\,=\,\,0.1,\,\,1.0$ shows the flatness in the lower region in comparison with the upper zone. The 2D contours are more in the zone-1 when compared with zone-2 and dense at the right plate. For $\lambda \,\,=\,\,0.5,\,\,1.0$, the number of contours are more in the upper zone and dense at the left plate. Figure 7b, c shows that, as $\lambda$ increases, both the velocity and temperature decrease, however, the magnitude of diminishing is very high for velocity when compared with temperature. Owing to the difference in viscosity in both the zones, depending on the relation between the viscosities in both the zones, the flow field is varied. The effect of thermal conductivity ratio $K\,\,\left( {=\,\,\frac{K_{2} }{K_{f} }} \right)$ is visualized in Fig. 8. The 3D and 2D velocity contours resemble each other for all values of K. The number of contours in the upper zone are large in comparison with lower zone and dense at the left plate for all values of K. Table 1 displays that the values of velocity and temperature are equal upto three decimal places for various K.

Fig. 7

Momentum a, b and energy c contours for various $\lambda$

Fig. 8

Momentum contours for various K

Fig. 9

Momentum contours for various nanoparticles

Fig. 10

Momentum a, b and energy c contours for various base fluids

Table 4 Volumetric flow rate and skin friction

Table 5 Average Nusselt number

Figure 9 displays the flow characteristics induced by trickling copper, diamond and titanium oxide nanoparticles in water. The 3D and 2D plots do not speculate major variations. However, the values in Table 1 interpret that the values changes from third decimal places whose contribution is negligible. This is owing to the fact that the upper and the lower phases of the duct are shielded, and hence, the velocity is not influenced using different nanoparticles as the Grashof number and Brinkman number are fixed. For flux conditions, the momentum and energy fields are not altered using different nanoparticles. Figure 10a–c characterizes the flow properties using different base fluids. The combination of engine oil (zone-1)–mineral oil (zone-2), ethylene glycol (zone-1)–kerosene (zone-2) and ethylene glycol (zone-1)–mineral oil (zone-2) are considered. The 3D view clearly shows that the curvature is convex and steep for engine oil–mineral oil combination and flat for ethylene glycol–kerosene , ethylene glycol–mineral oil combinations. The number of contours are large in zone-1 in comparison with zone-2 and dense at the right plate for engine oil–mineral oil combinations, whereas the contours are dense at the left plate for ethylene glycol–mineral oil. It is interesting to see that the velocity contours are penetrated from zone-1 into zone-2 for ethylene glycol–kerosene combinations and dense at both left and right plate of the duct. Figure 10b, c reflects that the velocity and temperature are maximum for engine oil–mineral oil and minimum for ethylene glycol–mineral oil. The 3D and 2D temperature plots for the variations of $Br,\,\,Da,\,\,I,\,\,\phi ,\,\,\lambda ,\,\,K$, different nanoparticles and different base fluid are similar to Fig. 2b and hence not presented.

Tables 4 and 5 depict the values of volumetric flow rate $\left( Q \right)$, skin friction and average Nusselt values in both the zones at the left and right plates, respectively. The $Gr,\,\,Br,\,\,Da$ access the Q in both the zones, whereas I, $\phi$, $\lambda$, and K depletes the Q in both the zones. There is no compelling transition in Q using different nanoparticles in both the zones. The engine oil–mineral oil attains the greatest flow rate and ethylene glycol–mineral oil shows the least value of Q in both the zones as seen in Table 4. The skin friction decreases at the left and right plates with $Gr,\,\,I,\,\,\phi ,\,\,\lambda ,\,\,K$, whereas it increases with Da in zone-1 and zone-2. The Brinkman number reduces the skin friction in zone-1 and zone-2 at $y\,\,=\,\,0$, whereas it increases at $y\,\,=\,\,0$ in zone-1 and decreases at in zone-2. The copper attains the maximum and titanium oxide attains the minimum skin friction in both the zones at the left and right plates, whereas the engine oil–mineral oil shows the highest value in both the zones. The average Nusselt number at $y\,\,=\,\,0$ is declined with $Gr,\,\,I,\,\,\lambda ,\,\,$ and K in zone-1 and zone-2, whereas it increases in zone-1 and decreases in zone-2 for $\phi$. The Nusselt values at the right plate decrease with $Gr,\,\,Br,\,\,Da$ in both the zones, whereas it increase with $I,\,\,\phi ,\,\,\lambda$ and K in both the zones as shown in Table 3. The diamond nanoparticle shows the highest Nusselt values in both zones at $y\,\,=\,\,0$ and at $y\,\,=\,\,1$. The ethylene glycol–kerosene at the left plate and ethylene glycol–mineral oil at the right plate in zone-1 attain the maximum Nusselt values and engine oil–mineral oil at the left plate and ethylene glycol–kerosene at the right plate in zone-2 attain the highest values.

5 Conclusions

Two immiscible fluids flowing inside a vertical rectangular duct including the viscous and Darcy dissipation effects have been presented. The solutions computed numerically are validated with the published work with limiting conditions and conclusions drawn are

• the momentum is strengthened by incrementing $Gr,\,\,Br,\,\,Da$ and decremented with $I,\,\,\phi ,\,\,\lambda ,\,\,K$

• using copper, diamond, and titanium oxide nanoparticle in water does not develop noticeable variations on the velocity and temperature.

• the rate of heat transfer drops at the left plate by escalating $Gr,\,\,I,\,\,\lambda ,\,\,K$ in zone-1 and zone-2 and it increases in zone-1 and decreases in zone-2 for $\phi$. At the right plate, $Gr,\,\,Br,\,\,Da$ reduces the Nusselt values in both the zones, whereas $I,\,\,\phi ,\,\,\lambda ,\,\,K$ enlarges the Nusselt values in both the zones. Diamond nanoparticle produces highest rate of heat transfer in both the zones at both left and right plates of the duct.

• the solutions for regular fluid in zone-1 and clear viscous fluid in zone-2 agree with Umavathi and Beg [48].