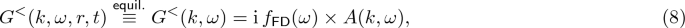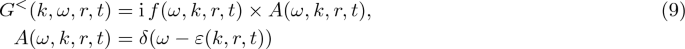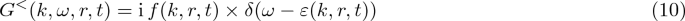Abstract
This article addresses the problem of an efficient description of the transient electron transport in (primarily small open) quantum systems out of equilibrium. It provides an overview and critical review of the use of causal Ansatzes with the accent on derivation of (quantum) transport equations from the standard Kadanoff–Baym (KB) equations for the non-equilibrium Green’s functions (NEGF). The family of causal Ansatzes originates from the well-known Generalized Kadanoff–Baym Ansatz (GKBA). The Ansatz technique has been fairly successful in practice. Recently, the scope of the method has been extended towards more “difficult” cases and its success can be assessed more precisely. This general picture is demonstrated and analyzed in detail for a variant of the generic molecular island model, an Anderson impurity linked between two bulk metallic leads by tunneling junctions. First, the KB equations are reduced to a non-Markovian generalized master equation (GME) by means of a general causal Ansatz. Further reduction to a Markovian master equation is achieved by partly relaxing the strictly causal character of the theory. For the model narrowed down to ferromagnetic leads, the transient currents are spin polarized and the tunneling functions have a complex spectral structure. This has prompted deriving explicit conditions for the use of an Ansatz. To extend the applicability range of the GME, approximate vertex corrections to the Ansatz were introduced and used with success. Finally, the relation of the GME description to possible non-equilibrium generalizations of the fluctuation–dissipation theorem is shown, extended beyond the present model within the NEGF formalism and physically interpreted in terms of a simplified kinetic theory of non-equilibrium electrons in open quantum systems.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This article deals with quantum transport theory of many electron systems, mainly open quantum systems, when far from equilibrium dynamics and quick changes of these systems are important. There are several methods in use, which deal with non-equilibrium dynamics, such as method of reduced density operators (MRDO) [1,2,3,4,5,6,7], time-dependent density-functional theory (TDDFT) [8,9,10,11,12,13,14,15,16,17], dynamical mean-field theory (DMFT) [18,19,20,21,22,23,24,25], Floquet formalism [26,27,28], density matrix renormalization group (DMRG) [29,30,31,32,33,34,35,36] or real-time quantum Monte Carlo (RTQMC) [37, 38]. Each of these methods has its own advantages as well as problems and limitations. They compete with non-equilibrium green function (NEGF) technique [1, 2, 39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80], the method we will concentrate on.
The article is partly of a review character. It addresses some important problems from general many body physics, non-equilibrium statistical physics and transport theory [81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117] using the NEGF methods.
It first summarizes the experience regarding the use of NEGF for the description of non-equilibrium single-particle dynamics of various quantum systems. Second, it demonstrates the usefulness of simplified NEGF description for quantum transport theory. Specifically, this article provides an overview and critical review of the use of an Ansatz with the accent on derivation of (quantum) transport equations.
1.1 NEGF, the Ansatz and transport equations
Well defined approximations of the full set of NEGF equations permit to formulate quantum transport theory using simpler quantum kinetic equations, either of the Boltzmann type for quasiparticle distribution function [45, 62, 63, 65, 72], of the generalized master equation (GME) form [1, 2, 72, 113] or even master equation (ME) [112,113,114,115,116], for the single particle density matrix instead of the full NEGF. The field is rather broad; our approach will be to present our personal view and place it among the recent parallel developments. The main framework of this article are the foundations of quantum transport theory deriving from the non-equilibrium Green functions formalism introduced by Schwinger [39,40,41,42,43,44], Kadanoff–Baym [45] and Keldysh [50, 51]. This formalism has been used to describe non-equilibrium dynamics of quantum many-body, closed or open, systems with various particles (such as electrons, phonons, and photons) and interactions (e.g., electron–electron or electron–phonons) and requests to describe rich physics, such as electron transport, heat transfer, changes of boundary conditions, influence of initial conditions or dissipation processes, involved. It is nowadays used in many areas of physics: in condensed matter physics including nanosystems, ultracold atoms, strongly correlated electron and lattice systems, quantum thermodynamics, quantum optics, plasma physics, nuclear physics and even astrophysics. Overviews of the recent use of the NEGF in various fields of physics and contexts can be found in [118,119,120,121,122,123,124] and references therein.
The general aim is to find a trustworthy but practicable description of single-particle transport properties of a given class of quantum systems. Since the full calculation of the NEGF equations is rather demanding, special effort has been devoted to simplification of the theory right from the beginnings of the NEGF method.
The first successful attempt was the Kadanoff–Baym Ansatz (KBA) used by Kadanoff and Baym (KB) in their well-known book [45]. This Ansatz enabled them to derive the quantum Boltzmann equation (QBE) for the first time using a well controlled approximation based on the non-equilibrium generalization of the fluctuation dissipation theorem (FDT) for the NEGF. Later on, their Ansatz was used in many areas of physics and even improved [47, 48, 65, 72, 125,126,127,128,129,130,131,132,133,134].
The range of validity of the KBA was limited, however, by the use of the quasiclassical approximation and by the fact that KBA does not have the innate causal structure of the NEGF. An improvement was reached by the proposal of the generalized Kadanoff–Baym Ansatz (GKBA—or sometimes in this text only the Ansatz) [135], which is formulated directly in the two-time representation and has the causal structure of the NEGF [65, 72]. The GKBA has been used successfully for the description of the non-equilibrium properties of various systems, often modified to a broader class of the so-called causal Ansatzes. At the same time these studies have shed a light on properties, advantages and limits of the GKBA or its modifications [135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184]. Exact criteria of the Ansatz validity for various non-equilibrium systems and situations remain unclear and further investigations of this aspect are needed.
The introduction of the GKBA raised also a renewed interest in the problem of the reconstruction of the one particle two time correlation function from the density matrix in general, as the GKBA is the leading term of the exact reconstruction equations (RE) [2, 63, 65, 67, 72, 135, 175]. These reconstruction equations enable to view the Ansatz as a tool for developing a closed transport equation for the One particle density matrix (OPDM) \(\rho \), and notably, its possible generalization by including some corrections beyond the Ansatz, the first term of RE.
The real obstacle on the way towards the use of the reconstruction equations beyond their GKBA term represents the complex structure of these additional terms, two transport vertex corrections [65, 67, 72, 175, 176, 178]. One approximate correction relying on a possible quasiparticle behavior of the studied system, has worked well in a number of cases [67, 140,141,142,143,144,145,146,147,148,149, 174, 176]. In general, however, we need to approximate both vertex corrections. The second one resisted so far any approximate treatment. Recently we proposed and made a piloting test of a “corrected” GKBA [180, 181], which covers both vertex corrections simultaneously.
When employed in computations, it leads to a significant improvement, perhaps because the exact RE are a necessary condition for the non-equilibrium Ward identity [67, 177] to hold, while the simple Ansatz fails in this respect [67, 177].
1.1.1 Preliminary comment on the use of the Ansatz method
Historically, the use of the Ansatz technique went along two main directions of effort:
\(\diamond \) to develop efficient time saving procedures for numerically solving the equations of motion (EOM) for the NEGF (the Kadanoff–Baym equations) and to use the resulting particle correlation function to calculate the observables. This has been the majority direction.
\(\diamond \) to derive, from the EOM for the NEGF, more simple quantum transport (kinetic) equations (QTE), i.e., closed equations which are subsequently solved for the OPDM \(\rho \). This is the approach we will concentrate on in this text.
\(\diamond \) A third direction gradually branches off the Ansatz-based theory of quantum transport equations. It employs the reconstruction equations and other exact relations to not only judge the validity range of the Ansatzes, but also to go beyond them, aiming at a solid base for constructing transport equations for single-particle density, their improvements, and actually, to an exact proof of existence summed up in the reconstruction and fluctuation–dissipation theorems.
1.2 NEGF for open systems with initial conditions: partitioning
The NEGF method applies to closed systems; this is hidden in the real-time formalism, but clearly apparent from the definition and properties of the underlying Schwinger-Keldysh loop [1, 2, 62, 63, 68, 71, 72, 77]. The Keldysh loop, in particular, permits to develop a perturbation theory based purely on functions of real time at the cost of extending their definition range to the whole time axis, starting at \(t=-\infty \). Such framework is directly suited for many problems, like stationary non-equilibrium processes in extended systems.
It also serves as the most natural point of departure for the study of a much wider range of processes, running in open systems on the one hand, and starting as transient processes at a finite initial time from an arbitrary initial condition on the other hand.
The open system is singled out of a broader closed system as “the relevant subsystem”, while the environment is formed by its complement. Similarly, a process starting at a selected initial time \(t_{\scriptstyle \mathrm{I}}\) defines “our” transient process which thus comes out as a process embedded in the host process, the latter running for all times from the remote past. This twin choice should be formalized in the language of the NEGF. The universal means for the class of problems treated in this paper is a projection technique known as partitioning. It allows to neatly separate the system from its surroundings without suppressing their mutual coherences.
1.2.1 Partitioning in Hilbert space
First, we formalize the task of separation of the system and its environment. The total system is associated with a linear space and the two subsystems with subspaces spanning the projectors P and Q, \(P+Q=1\). All matrix algebra is then written in terms of block projections. This technique goes by the name of PQ partitioning. It was pioneered by Feshbach [185, 186] for nuclear resonances, later applied to polarons, Fano resonances and an application to QED appears in some textbooks [187]. In all this work, the partitioning concerned a Fock space.
For electrons in nanoscopic systems consisting typically of a small relevant system attached to massive electrical leads by junctions, the projection technique has a different meaning. The one-electron Green’s function (GF) for the entire system is expanded in an orbital basis separating the nanoscopic component from the leads and the “relevant” part of the full GF is described by the corresponding square matrix. Similarly for the selfenergy and other single-particle operators. The partitioning then serves to express the effective selfenergy of electrons within the relevant area in terms of various blocks of the complete GF and the inverse GF, including the \({\varSigma }\) matrix. The resulting effective selfenergy then contains blocks representing virtual excursions from the relevant area into the environment and describes the coherent link of the system with its surrounding. This additional selfenergy, which mimics interactions, enters the scheme even in the case of non-interacting electrons.
The outlined procedure follows the archetypal papers by Löwdin [188,189,190,191,192] and forms an implicit basis of the canonical (Jauho)–Meir–Wingreen theory [193, 194]. Closely related is the Newns–Grimley model description of the atomic chemisorption on solid surfaces [195, 196].Footnote 1
1.2.2 Partitioning in time
It may be preferable to treat the relevant process as self-contained, rather than as an embedded part of the host process. To this end, a formal device called time partitioning was introduced in [178]. The idea is to view the GF and the selfenergies as square matrices in their two time arguments and partition these matrices into blocks whose separating borders are specified by a chosen initial time \(t_{\scriptstyle \mathrm{I}}\). One diagonal block of the Green’s function corresponds to the future (the relevant block). The other one encompasses the history whose decisive role for the formation of the initial state at \(t_{\scriptscriptstyle { \mathrm I}}\) is mediated to the future by the off-diagonal blocks of the selfenergy. The resulting formal expressions will be quoted below.
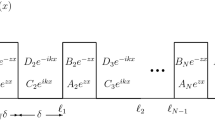
1.3 Molecular bridge model
After we will analyze the above-mentioned aspects in general, we will explore them on the particular example of a molecular bridge model. This model, which can represent well nanoscopic systems [197,198,199], enables us, because of its simplicity, to compare the full NEGF calculations with their simplified version based on transport equations.
The interest in studies of short time electronic transients in nanoscopic systems of the molecular bridge type is increasing and the NEGF are often the method of choice for theoretical calculations [113, 168, 173, 179, 193, 194, 197,198,199,200,201,202,203,204,205,206,207,208,209,210,211,212,213,214]. They are not really practicable for longer “short” times and then enters their reduction to quantum kinetic equations. The usual device for such reduction is the GKBA decoupling or its clones. Unfortunately, this only works for a limited range of parameters [179], as we will demonstrate. This creates a bottleneck for the computational effort and it is related to the approximation of the reconstruction equations, too crude in this case.
The example of the bridge model also demonstrates that the simplification of the full NEGF formalism to single-time transport equations for the density matrix has its significance not only for easier and faster calculations, but also for better understanding of the physics involved.
1.4 Outline
Following the Introduction, the article has four parts. First, the basic scheme is introduced for the construction of simplified transport theory based on the use of Ansatzes in the NEGF equations of motion in Sect. 2. Second, we discuss the features and limitations of this approach together with the related perturbation theory and the reconstruction equations in Sect. 3. Reconstruction equations and corrections to the Ansatz are discussed in Sect. 4. The following Sect. 5 deals with the theory of quantum transport equations and its relation to the reconstruction and fluctuation–dissipation theorems. Third, we introduce the problem of the inclusion of correlated initial conditions into the NEGF formalism in Sect. 6. The following Sect. 7 presents a discussion of the conditions under which the NEGF equations can be reduced to simplified quantum transport equations in this general case. Fourth, in Sect. 8 we turn our attention to open systems. The use of the Ansatz-based approach to the transport equations for the case of open systems is documented on the molecular bridge models which represent well the general features of open systems, but, at the same time, their simplicity permits to demonstrate in detail the important aspects of the Ansatz-based transport theory and make a comparison with the full NEGF approach. Final discussion follows.
2 Ansatz as a doorway to the quantum transport theory
In this section, we will briefly recapitulate the NEGF formalism for closed systems (and the Keldysh initial condition) and the approach, based on the Ansatz, which enables us to simplify the NEGF equations of motion to a Quantum Transport Equation (either of QKE or GME type [65]) for the single-particle density matrix \(\rho (t)\). We do not discuss here the quantum kinetic equations for quasiparticle distribution functions of the quantum Boltzmann equation type [47, 48, 65, 72, 125,126,127,128,129,130,131,132,133,134].
2.1 Non-equilibrium Green’s functions and equations of motion
We use, following Keldysh [50, 57], the standard \(2\times 2\) matrix of real-time NEGF to represent the contour-ordered NEGF employing the Langreth–Wilkins matrix [55, 56, 62, 65, 72, 175] with three components, the less-correlation function \(G^<\) and two (equivalent) propagators, \(G^A(1,2)=[G^R(2,1)]^\dagger \):
and similarly for the selfenergy and other quantities. Here, we introduce cumulative variables \(1\equiv x_1,t_1\), etc.
The basic original scheme of Kadanoff and Baym (KB) employs the equations of motion (EOM) for \(G^<\) and \(G^>\) and their conjugates, all having the structure analogous to
As apparent from the above equation to complete the set determining both functions \(G^<, G^>\), we need to know a prescription for the selfenergies \(\varSigma ^{<,>}\).
In this text, we prefer to work with the (Keldysh-) Langreth–Wilkins (LW) form of the EOM, an often used alternative to the KB arrangement. To convert the KB equations (KBE) to the LW ones, it is enough to employ the spectral identities
where \(F^S\) is the spectral function corresponding either to \(F=G\) or \(F={\varSigma }\), we get both, the LW Dyson equation (DE) for \(G^<\) and the plain DE for \(G^R\):
The matrix multiplication over the configuration space is understood here and further on. Note that in the rest of this text we will concentrate on the time structure of equations, so we will mostly suppress space coordinates in equations and only time arguments will be written explicitly.
The motivation for rewriting the KBE to the LW form is twofold: first, this form has the advantage that it has an explicit causal structure, important for a proper insertion of the Ansatz. Second, it separates as much as possible the spectral properties and the dynamics (evolution amplitude) described by retarded functions from the statistical information contained in the correlation functions. In fact, the Dyson equations (DE) for the retarded (and, consequently, advanced) functions are explicitly independent of the DE for the correlation function. Of course, all components of the NEGF are internally interconnected through the selfenergy \({\varvec{\varSigma }}={\varvec{\varSigma }}[\mathbf{G}]\), which in turn is typically a self-consistent functional of the Green’s function.
Of the two companion Eqs. (4) and (5), the equation for the double-time \(G^<(t,t^\prime )\) is by far more demanding from the computational point of view, and here enters the Ansatz permitting to replace this EOM for \(G^<(t,t^\prime )\) (an exact transport equation) by a simpler quantum transport equation (QTE), which we call sometimes also quantum kinetic equation (QKE), for the single-time quantity \(\rho (t)\). Note, as was already mentioned, in the case of open systems it is common to call the QKE for OPDM \(\rho (t)\) generalized master equation (GME).
2.2 The Ansatz fits into the formal scheme of the NEGF
The Ansatz (the Generalized Kadanoff–Baym Ansatz—GKBA) [62, 63, 65, 70, 72, 135] we will be concerned with eliminates the particle correlation function in favor of its “time diagonal”, the one-particle density matrix (OPDM) \(\rho (t)=\mathrm{i}G^<(t,t)\), and of the propagators:
All quantities entering (6) are matrices in configuration variables and the multiplication means here an equal time matrix product.
This Ansatz grew up from the KB Ansatz (KBA) [45], but it differs in two essential aspects:
\(\diamond \) It has the same correct causal structure as the NEGF themselves. In contrast, the KBA Ansatz does not possess the causal property:Footnote 2.
\(\diamond \) The factorization (6) contains directly the single-particle density matrix \(\rho \), not a distribution function f.Footnote 3
This factorization also satisfies the particle-hole symmetry and it has the correct equal time limit. The order of propagators and the density matrix corresponds to a matrix multiplication and so a diagonal representation of Green’s functions is not necessary.
In addition, this Ansatz has the following characteristics which are promising from the point of view of building up a transport theory based on this factorization, which is not limited to a quasi-classical description represented by the quantum Boltzmann equation (QBE):
\(\diamond \) The Ansatz is at the formal level quite general, since, contrary to KBA, any assumptions about small deviations from equilibrium, slowly varying disturbances or quasiparticle behavior are not a prerequisite.
\(\diamond \) It is exact for excitations far from equilibrium in the limit of non-interacting particles.
\(\diamond \) It has the correct asymptotic behavior for \(|t_1-t_2|\gg \tau ^\star \), where \(\tau ^\star \) is an important characteristic time defined by
with \(\tau _c\) the collision duration time and \(\tau _Q\) the quasiparticle formation time. Typically, \(\tau ^\star \) is assumed to be shorter than other characteristic times, like the quasiparticle life-time or the energy relaxation time.
\(\diamond \) It coincides with the KBA in the true Boltzmann limit.
Thus it is reasonable to look at possibilities which the Ansatz offers for building up effective quantum transport theories for various quantum systems.
Let us comment on the meaning of the word the Ansatz and the abbreviation GKBA: depending on the context we will use them in two slightly different ways: (1) The GKBA in the narrow meaning of the word, implies that the propagators, which are used in the Ansatz, are the exact ones, (2) The Ansatz (GKBA) in a general meaning: in this case it denotes only the form of the causal factorization (6), while various approximate propagators are used.
2.3 Ansatz-based quantum transport theory
Building the transport theory upon this Ansatz factorization, we decide not to follow the Boltzmann–Landau theory and its improvements.Footnote 4 We will thus not discuss those kinetic equations which determine a single (quasi)particle distribution function instead of the one-particle density matrix (OPDM) \(\rho \)—for the differences between the OPDM and single distribution function, see [65, 72].
Without going into the details of the use of the Ansatz given in the following sections, it may be said that the basic idea is to introduce it into the NEGF equations of motion (EOM). As for the transport equations for \(\rho \), we can conveniently get them in two steps.
First step By subtraction from the differential Dyson equation (4) its conjugate, we obtain the so-called generalized Kadanoff–Baym equation (GKBE). It will be convenient at this point to introduce the mean-field Green’s function by the obvious definition
Symbolically,
In the same symbolical shorthand, the generalized Kadanoff–Baym equation (GKBE) reads
Its time diagonal represents the desired precursor quantum transport equation (PQTE) equation for \(\rho \):
Note that the name of this equation is not firmly established, sometimes it can be called also precursor quantum kinetic equation (PQKE) for obvious reasons. Its structure is already closely related to transport (kinetic) equations; the r.h.s represent the generalized collision integrals. This is not a true closed equation for \(\rho \) yet. To obtain it, we make the Second step by invoking the Ansatz. For the sake of this preliminary discussion, we substitute for \(G^<\) from (6). The result is the quantum transport equation (QTE) for \(\rho \).

On the left, we see the quantum mechanical drift term. We note that this drift term differs from the corresponding term in the Quantum Boltzmann equation (for quasiparticle distribution function) since it does not contain the quasiparticle energy renormalization; Eq. (17) is a closed equation for the OPDM \(\rho \). The right hand side contains the collision integrals, which differ in their nature: the first integral describes the back scattering processes, the second integral is proportional to \(\rho \) and thus it represents the forward scattering integrals. The propagators entering these scattering integrals are responsible for the memory effect. They have to be determined simultaneously with the density matrix, thus we have to solve a coupled system of Eqs. (17) and (5) replacing now the original system (5) and (4) as its substantial simplification. That is all we need for closed systems treated in the Keldysh style (or the equivalent imaginary stretch): we obtained the set of two coupled equations which replace approximately the NEGF equations. We have to find the retarded functions, but this is simpler than to calculate the correlation functions. Even so, it would but rarely be possible to employ it as it stands. For extended or finite closed systems, the selfenergies entering the equations have to be determined self-consistently, as they depend on the Green’s functions. This dependence may be too complex for computational purposes. Also finding the propagators stepwise together with the density matrix may be not practicable. This may call for modifications of the original Ansatz, Eq. (6).
2.3.1 A historical case study
To illustrate the procedure leading to an explicit form of the Quantum Transport Equation (17), we select a paper from the whole collection of works published by H. Haug and colleagues in the nineties and devoted to the then topical field of subpicosecond optical pulses applied to semiconductors (summarized in [62]). One of the problems considered was the buildup of screening in a model two band semiconductor illuminated by a short optical pulse. It was solved in Ref. [143], a sample case of the use of GKBA. Here, we show some of the salient steps of the solution, but we take them from a precursor paper [142] devoted to a simpler system, jellium out of equilibrium. The whole procedure is the same as that outlined above, the only difference is that the authors start from the KB equations and their scattering integral is expressed in terms of the products of \(G^<,\;G^>\ \) with \({\varSigma }^<,\;{\varSigma }^>\). The Ansatz can be applied to the GF directly. As for the selfenergies, it is necessary to develop the expression \({\varSigma }^<={\varSigma }^<[\rho |G^R,\,G^A ]\) (see (17)) for the specific approximation used, in present case the non-equilibrium RPA. All quantities are diagonal in the momentum representation, the underlying diagrams are the same as in equilibrium, we concentrate here on the less quantities:
Here, \(V^<\) is the screened interaction potential given by the sum of bubble diagrams:
\(\upsilon \) is the bare Coulomb interaction potential, the RPA polarization bubble \(\mathbf{L}\) reads, by components
A bit of manipulation with Langreth–Wilkins rules yields a more explicit expression for the screened potential reminiscent of the popular Keldysh expression \(G^<=G^r{\varSigma }^<G^a\):
All this is clearly prepared for the wholesale application of the Ansatz, collecting all expressions into the Precursor QTE, and obtaining the quantum kinetic equation for the particle distribution \(\rho \). As a small neat example, the GKBA transforms the formula (21) as follows:
Of course, the need for explicit expressions for the propagator components \(G^{r,a}\) emerges, an uneasy problem whose attempted solutions we report in Sect. 3.5. The authors of [143] were the first to decide that some approximate propagators may offer a satisfactory way out. Their choice were the free (plane wave) propagators with an imaginary part of the energy artificially added. The modified GKBA they appropriately called the FGKBA, and became so the harbingers of the later prevailing custom of modifying the GKBA to some causal Ansatz, as discussed in Sect. 4.1. Perhaps it should be mentioned that the calculations were in good agreement with experiments studying plasmon formation in an excited e–h plasma.
2.4 Generalization of QTE towards open systems with complex initial conditions
It will be useful to analyze these modifications of the original Ansatz Eq. (6) within a formalism augmented in two directions. The NEGF formalism employed so far corresponds to the simplest case of the “canonical” Keldysh theory devised for extended or finite closed systems whose interactions were turned on adiabatically from an infinitely remote past. The two necessary extensions are as follows. On the one hand, to extend the theory also to open systems, on the other hand, to develop the theory for processes starting at a finite initial time. Both these tasks have been treated exhaustively within the exact NEGF formalism as briefly reviewed below. The questions we shall concentrate on are the modifications prompted by the use of the Ansatz-based approximate theories.
Before we will deal with formal aspects of these two formalism augmentation, we will briefly introduce classification of Ansatzes according to their use in various physical situations.
2.5 Classification of GKBA Ansatzes: their use for different systems
Whether the NEGF equations of motion (EOM) simplified via the use of various GKBA factorization (6) will properly describe the dynamics of quantum systems depends on several factors, which we well now shortly mention and will discuss in more details for some special cases later on.
First, we can look at Ansatzes (GKBA factorization) from the point of view of systems, which dynamics we want to describe:
\(\diamond \) Infinite (bulk) systems where the systems are their own reservoirs
\(\diamond \) Finite, but open systems: in this case the behavior of the system is influenced by reservoirs. Specifically, we have in mind bulk leads attached to the system and serving as reservoirs of particles and energy
\(\diamond \) Finite, but closed systems
Second, in all these three cases, we need to consider carefully the following three levels of the use of the GKBA:
\(\diamond \) How the quality of the Ansatz approximation depends on the used propagator approximations
\(\diamond \) To which extent the combination of used prescription for \(\varSigma ^<\) fits together with the used propagators \(G^R\) and \(G^A\), so the spectral identity (3) works properly.
\(\diamond \) To which extent an Ansatz is suitable when we use it as an approximation of the reconstruction equations. This means: how much the non-equilibrium Ward identity is fulfilled? What is the behavior of additional parts (beyond the Ansatz) in the reconstruction equations? We will deal with these equations in Sects. 3, 4, and 5.
The question, we will deal with, arises whether we can name some general features of the Ansatz for all these cases. When we want to understand the above-mentioned aspects of the use of the Ansatz we have to turn to perturbation schemes related to the Ansatz.
3 Ansatz and NEGF perturbation schemes
In this section, we will first try to shed light on relation of the Ansatz to the NEGF perturbation schemes on a phenomenological level. This will lead us to the estimate of its range of validity and possible improvements. Later on, we will deal with the question of the Ansatz validity domain on the more fundamental level by introducing the so-called reconstruction equations (RE) [2, 63, 65, 67, 72, 135, 175], which contain the Ansatz as a source term. As we will see, the RE are formally just identities. The source term can lead us to an idea that the reconstruction equations form a basis for some perturbation scheme. However, strictly speaking, this is not the case because we do not have a useful small parameter and we cannot proceed selfconsistently in a reasonable manner. We will discuss this aspect of the RE in more detail in Sect. 4.
3.1 Consistency of Ansatz and selfenergy
As already discussed in the previous section, to simplify NEGF equations we can use the Ansatz to close these equations just for the single-particle density matrix. To reach this aim we have to proceed in two steps:
\(\diamond \) First, it is easy to formulate the Ansatz also for \(G^>\).
\(\diamond \) Second, apart from using the Ansatz directly for \(G^<. G^>\), we have to use it also in expressions for \(\varSigma \) since in general selfenergy is the functional \(\mathbf{\varSigma } [G^<, G^>]\).
By the second step we mix two different perturbation schemes: one for the selfenergy and the other one based on the Ansatz.
The natural question emerges under which circumstances (for which selfenergies and propagators used in the Ansatz) these two perturbation schemes combined together (of the selfenergy and the approximation by the use of the Ansatz and the specific approximation of propagators in it) provide a good description of the system dynamics.
We can deal with the answer either already on the level of the Ansatz alone or we can go further and we can use for the investigation of the validity of the Ansatz range also the reconstruction equations (RE)— the exact equations which contain the Ansatz as the first term as we will see in Sect. 3.3.
3.2 Ansatz: non-interacting particles
To begin with considerations how the Ansatz is related to the NEGF perturbation scheme, it is useful to discuss first the case of non-interacting particles in a closed system. Thus, we will approach the Ansatz, following [65, 72, 174], from the angle, where its predominantly dynamic nature is stressed and linked with the so-called semi-group character of the single-particle propagation.
To this end, we first consider independent particles, for which \(G^{R,A}=\mp \,{\mathrm{i}}\, S^{(1)}\vartheta _\pm \) with \(S^{(1)}\) the single-particle evolution operator, and the following equation is valid:
The propagators describe a unitary evolution which obeys the multiplication rule (“semi-group property”) shown here for \(G^R\):
Using this semi-group property in (24) we obtain, for \(t_1>t_2>t_0\),
This is just the retarded half of the Ansatz. For the converse order of times, the advanced part of the Ansatz is obtained.
The Ansatz appears here as an exact identity based on the semi-group property of free-particle propagators.
The fact that the Ansatz is exact in the case of free particles, raises a hope that there is a perturbation scheme based on the strength of the interaction as a small parameter. To see whether this is doable let us try to rewrite the NEGF equations of motion (EOM) to an exact form, which contains the Ansatz in the explicit form.
3.3 Reconstruction equations
The equation of motion (EOM) can be also rewritten in a form of an equation having, as it first term, expression which introduces as the first term the approximation of the correlation function \(G^<\) by the Ansatz (GKBA) [62, 63, 65, 70, 72, 135]. To gain the exact correlation function it is, however, necessary to add the two vertex corrections to the Ansatz, so that

These are the so-called reconstruction equations (RE) since they in principle enable us to reconstruct the whole double-time correlation function from its time diagonal elements \(\rho = G^<(t,t)\), the one-particle density matrix, by means of the propagators. For their derivation, see e.g., [65, 72, 135].
These inhomogeneous integral equations are not closed, \(\rho \) is just an input. To close the scheme, the reconstruction equations must be accompanied by an additional equation, quantum transport equation (QTE) (17), for \(\rho \), see the previous section. This set of equations is then formally fully equivalent to the Dyson equations for \(G^R, G^<\).
The free (absolute) term is the Ansatz, so it enters the game explicitly. From the form of the correction terms we can immediately see:
\(\diamond \) the Ansatz is exact in the case of free particles in closed systems,
\(\diamond \) at the same time the range of validity of the Ansatz approximation depends on the time structure of the selfenergy.
The integral terms in (27) are the vertex corrections to the Ansatz. Both these terms link the past and the future events with respect to the instant \(t'\) and describe the coherence formed between these events. They both contain the unknown correlation function \(G^<\): the first one through the functional dependence \(\varSigma ^< = \varSigma ^<[G^<]\), the second one explicitly. It is thus obvious that the use of the Ansatz is justified whenever these two vertex corrections are negligible.
Two characteristic times control their behavior: the collision duration time \(\tau _c\) determining the time span of \(\varSigma ^<\) and the quasiparticle formation time \(\tau _Q\) related to the time spread of \(\varSigma ^R\). Correspondingly, these two integral terms have a rather different character: the first one is irreducible and represents the two particle correlations which are not contained in the Ansatz. The second term describes the single-particle (polaron like) renormalization of the out channel.
It is thus apparent that the times \(\tau _c\) and \(\tau _Q\) play the decisive role in the decision whether the vertex corrections can be neglected. We will see later that because of the different character of the two vertex corrections they offer different possibilities how to improve the Ansatz.
In principle, the iteration of the reconstruction equations could yield a corrected Ansatz. It is, however, very difficult, if not impossible, to iterate these equations together to get improved transport equations, beyond the first approximation given by the Ansatz. They appear thus as unsuitable for a calculation of the full correlation functions by iteration. We will return to this question in the Sect. 5
There is another possibility, however, of using these equations for deriving effective transport theory for the single-particle density matrix, based on the Renormalized Quasiparticle Generalized Kadanoff Baym Ansatz (RQGKBA), as we will discuss in Sect. 4.
3.4 Two approaches how to use the Ansatz
Having the reconstruction equations, we can look at the use of the Ansatz from two different perspectives since there are two different ways how to use the reconstruction equations on the way towards effective description of a system dynamics:
\(\diamond \) First approach: to use the Ansatz itself (only the first term of reconstruction equation (RE) (27)) either to simplify NEGF calculations or to formulate simplified transport equations for the single-particle density matrix; the final transport equations will differ according to used retarded GF in the Ansatz.
\(\diamond \) Second approach: to analyze the validity range of the Ansatz looking at the whole RE: this means to fix the GF, but, if necessary, to use not only the Ansatz itself but also some approximation of the RE vertex corrections (27).
The first approach uses the Ansatz as a means of solving the EOM for correlation functions: this is the most often used approach [118,119,120,121,122,123,124]. It is effective from the point of view of simplification of practical calculations. In this case, various approximations of propagators are used in the Ansatz (GKBA) to obtain its variants. By this step we are returning to the phenomenological level and so we just try which approximation will work. This is a very similar situation to the various forms of the local density approximation (LDA) of the density functional theory [9]. This corresponds to the fact that regarding the dependence of Ansatz’s approach on the systems up to now experience tell us that it looks that the best estimation of the quality of the Ansatz approximation work similarly like in the description of equilibrium features: the Ansatz approximation is good according to how numerical solution works for a concrete system. Various people tried to use different propagators [3, 77, 153, 158,159,160,161,162,163] to find out the validity ranges of related variants of the Ansatzes will be discussed in the following subsection.
The second approach is going after more fundamental question: In this case we are going not only after the Ansatz as a pure computational means, but we want to use it also for the formulation of a consistent quantum transport theory, to formulate closed transport equations for OPDM \(\rho \).
3.5 Ansatz and various propagators: summary of accumulated experience
The advantage of the use of the GKBA approach to transport lies in the reduced computational complexity of this scheme in comparison with the full NEGF scheme. It is just desirable to know which many body selfenergies are compatible with various approximations of the Green’s functions (propagators) in the GKBA and provide reasonable description of the non-equilibrium evolution. All such modifications of the Ansatz have the basic property of belonging to the class of causal Ansatzes. They differ by their success in practice.
The Ansatz with different approximations of its propagators has been tested in various physical situations both for closed as well as open quantum systems. Depending on the situation, good results were obtained for the following propagators: (1) free-particle propagators (FGKBA) [150,151,152], (2) various quasiparticle propagators (QP-GKBA) [140,141,142,143,144,145,146, 148], (3) Hartree–Fock propagators (HF-GKBA) [153,154,155,156,157], propagators, which even include some correlations (correlated-GKBA) [3, 183] apart from using “exact propagators” (E-GKBA) which have been obtained by simulations of the NEGF equations [164].
For the good description of systems dynamics it is essential, apart from the quality of the used approximation of propagators in the Ansatz, the proper choice of selfenergy, which enables both, the good description of the dynamics and advantageous (not too demanding) scheme for numerical calculation. For quite a long time, the Ansatz was used mainly in combination with the second Born approximation. Recently, however, the HF-GKBA was successfully used together with the T-matrix, GW and third order selfenergies. Very recently the efficient scheme (the so-called G1–G2 scheme) for simulations of NEGF using HF-GKBA was introduced [156, 157].
The numerical tests which have been comparing various selfenergy approximations used in GKBA-like approximations of non-equilibrium systems with the full solution of the NEGF equations and even with other techniques (such as DMRG) have been developed. All these approaches shows that in many situations GKBA approach provides reasonable results and the numerical demands of the GKBA approach are lower. Main results in this direction can be found in [76, 77] and references therein.
3.5.1 Ansatz and conservation laws
For the reliability check of all above-mentioned calculations, it is important to know whether the approximations used fulfill the conservation laws. The essential criterion for NEGF EOM and selfenergy approximation to be a conserving was introduced by Kadanoff and Baym [45, 46, 71, 159, 215, 216].
By introducing the Ansatz in the EOM, the question arises which selfenergies can be used in the combination with the propagators used in the Ansatz to still get a conserving approximation. In other words, which approximation of the propagators in the Ansatz is compatible with selfenergy to get the conserving approximation.
We will now briefly comment on the problem of conservation laws; more details can be found mainly in works of the groups of Bonitz and van Leuween [3, 71, 77, 153, 157, 163, 217,218,219]. The essential problem is, which propagators used in an Ansatz are compatible with an energy conserving selfenergy approximation. The question is whether the selfenergy approximation remains conserving after the Ansatz is introduced in it. There is the problem of the choice of the proper spectral function used in the Ansatz [153, 159, 217] The problem was partly solved using conserving selfenergy approximation: in Ansatz propagators but not necessarily the same selfenergy approximation in collision integrals [217].
Recently conserving approximation schemes (based on the use of the GKBA) have been developed for the description of some complicated non-equilibrium situations. It was demonstrated that these schemes work well and provide reasonable results for quite complex systems, see [77, 163] and references therein. In general, the question of conserving approximations for propagators and selfenergies combined with the Ansatz is not answered in a completely satisfactory way.
4 Reconstruction equations and corrections to the Ansatz
Now we will turn our attention to the second possibility of how to look at the perspective of the Ansatz in the description of a system dynamics: To understand the limitations of the Ansatz, its possible generalization, and its relation to transport theories on a more fundamental level, it is natural to return to the analysis of the full Reconstruction Equations (RE).
4.1 The Ansatz by itself: the first term of reconstruction equations
Let us now first concentrate on the properties of the Ansatz itself in the case of closed systems.
First, what really matters for its use is the causal structure of the Ansatz, consistent with the causal structure of the NEGF, the feature by which it differs from the original KBA. Here, we will thus deal with the class of the so-called causal Ansatzes. Following [72] we will call them causal Ansatzes if they have the following characteristics common with the GKBA (the Ansatz):
\(\diamond \) causal structure.
\(\diamond \) particle-hole symmetry.
\(\diamond \) the correct equal time limit.
Second, we can immediately see from the reconstruction equations that the Ansatz is exact for the free particles or for effectively free particles described by Hartree–Fock (HF) mean field in the case of closed (or bulk) systems for which NEGF were originally designed.
In the case of the HF mean field (in the case of closed systems), the selfenergy has only the HF term, which is time diagonal, therefore both vertex corrections in the reconstruction equations are zero and the Ansatz is thus exact.
The question arises what happens when interactions are involved. In this case, we have to discuss the properties of the two vertex corrections in the reconstruction equations. It is apparent that the importance of these corrections depends on the time behavior of the selfenergies. As we have already seen, the two corrections have a very different nature: one can be viewed as easily treated by introducing some quasiparticle description, the second, the irreducible one, is more difficult to treat.
It is obvious, however, from the above that the Ansatz could be valid for systems where interactions will lead to some free-particle-like behavior. Therefore, people started (especially the group of H. Haug) to check Ansatz on the phenomenological level using some trial retarded GF [140,141,142,143,144,145,146, 148]. Later on efforts in this direction led to the formulation of the non-equilibrium quasiparticles and quasiparticle causal Ansatz [65, 67, 72, 174, 176], which will be discussed later.
It is necessary to point out here again that the Ansatz behaves differently in the case of closed and open systems. As mentioned above already, in the case of open systems, the additional selfenergy enters the scheme (for an example, see Sect. 8) even if the whole system and reservoirs are non-interacting. Therefore, the vertex corrections are non-zero even in the non-interacting case and the Ansatz is thus never exact in the case of open systems.
The properties of the Ansatz can be summarized as follows (separately for closed and open systems):
\(\diamond \) Closed systems: the Ansatz is exact up to the mean field.
\(\diamond \) Open systems: due to the environment, the Ansatz is not exact even in the mean-field approximation.
In addition there is, of course, still a difference between systems without and with interactions. In the case of interactions, the quality of related selfenergy decides the quality of the approximation by the Ansatz.
We will now further discuss the validity of the Ansatz from the point of view of approximation of the RE.
4.2 Reconstruction equations, Ansatz, perturbation schemes and Ward identities
To proceed further with the analysis of possible approximations of reconstruction Equations (RE), let us look at the meaning of the Ansatz from the point of view of a perturbation scheme. When we look at two vertex corrections to the Ansatz in the reconstruction equations (27) we can conclude that there is the twofold meaning of the Ansatz as the first term of the perturbation scheme:
\(\diamond \) A small parameter is the strength of interaction—the reason for this view is that the Ansatz is exact for free particles, so corrections will depend on the strength of interactions.
\(\diamond \) A small parameter is some characteristic time—this derives from the fact of the time structure of the correction terms, which in turn are dependent on the time structure of selfenergies.
The interplay of these two perturbation schemes decides about the quality of the Approximation by the Ansatz.
4.2.1 Reconstruction equations and selfenergy approximations
The Ansatz is constructed in such a formal way that, on itself, it seemingly does not depend on the selfenergy. However, since \({\varvec{\varSigma }}={\varvec{\varSigma }}[\mathbf{G}]\), when we introduce the Ansatz into the selfenergy, we can ask how the approximation of the RE by the Ansatz or its possible generalization is consistent with the selfenergy. This brings us also to the question, how the single particle and many particle level of the description (described in the Dyson equation (DE) by selfenergy) is consistent in non-equilibrium situations. Thus let us turn our attention towards the discussion of non-equilibrium Ward identities as they were formulated in [177]. They are, as we will see, closely related to the reconstruction equations.
4.2.2 Non-equilibrium Ward identity
The Ward identity plays an important role as a consistency check of approximations on the one and two particle levels. At the same time, it is necessary for the conservation of the number of particles [60, 71, 220,221,222,223,224,225].
We will now introduce the non-equilibrium version of the Ward identities as they were derived in [177]. The non-equilibrium Ward identity reads:
This non-equilibrium generalization of the Ward identity provides a relation between the single-particle selfenergy \({\varvec{\varSigma }}\) and the two particle transport vertex, so it is important for an evaluation of the approximations used in building up the NEGF quantum transport theory.
The Ward identity thus provides a more rigorous framework for the task of weighing the reliability of various Ansatzes. It is obvious that the standard GKBA literally taken will be suffering from taking the vertex corrections insufficiently into account, since it does not fulfill the Ward identities [177]. We will now shortly comment on it.
The virtue of the Ward identity (28) valid for the special case of spatially homogeneous fields is to reduce the three-terminal vertex to the two-terminal selfenergy; the three-point structure is imposed by the scalar function \(\eta (t,t';t_{\times })\). The functional derivative of \(\mathbf{G}\) has the same structure for homogeneous fields; the last equation thus reduces to [177]
This equation governing the matrix Green’s function involves one-particle (two-point) quantities only.
The first term of (29) represents the sharp factorization of the NEGF at an intermediate time \(t_x\) into two factors: propagation in the past and in the future. We will call this factorization (for obvious reason) non-equilibrium semi-group rule (NE SGR).
From the derivation of (29), it is clear that it serves as a necessary condition for the Ward identity, and hence, for the particle number conservation. It is valid for the exact Green’s function as a tautology, but it also holds for any self-consistent approximation of the selfenergy. On the other hand a selfconsistent approximation together with (29) leads to the Ward identity.
There are two different uses of Eq. (29). The traditional way of using it is to check any particular physical approximation for its internal consistency, for example, to verify that all components of the selfenergy are treated in a uniform manner.
There is, however, also the second use of Eq. (29), which represents the important check of an effective transport theory based on the use of the Ansatz. This approach to quantum transport is based on a separation of two “orthogonal” kinds of approximations:
\(\diamond \) the underlying physical approximation for the treatment of interactions, and
\(\diamond \) the approximations of the Ansatz type simplifying the dynamical aspects of the theory with the aim at a quantum kinetic equation for the single-time OPDM \(\rho \). The identity (29) judges also this other class of approximations. For this purpose, it is convenient to write the identity (29) by components.
4.2.3 Ward identity and the Ansatz
Let us first introduce “extended reconstruction” equations (components of (29)) following [177]; one for the retarded propagator, the other for the particle correlation function. First, for \(t>t_{\times }>t'\), we obtain from (29) two equations:
The first term of Eq. (30) is the composition rule for propagators (exact for free particles, Eq. (25)), in the case of Eq. (31) its first term is a “mixed” composition rule for the product \(G^RG^<\).
Formally the time \(t_{\times }\) plays a role of a gliding time (of initial condition) which divides the past from future events and vertex corrections in both extended reconstruction equations just describe a coherence between the past and the future. As time flows \(t_{\times }\) can also change.
Second, for the reverse order of times, \(t<t_{\times }<t'\), another two relations are valid. One is the analogue of (30) for the advanced propagator \(G^A\). The other one, an equation for \(G^>\), is symmetric to (31); we will refer to them as to (30’) and (31’) without writing them down explicitly. It should be noted that Eqs. (30) and (30’) differ from the other pair (31) and (31’). While all are obtained as the respective components of (29), the former two can also be derived directly from the Dyson equations for \(G^{R,A}\).
These equations provide a more rigorous framework for the task of weighing the reliability of various Ansatzes.
We will now return to the original GKBA (6) and its link with the Non-equilibrium Ward identity. Equations (31) and (31’) (components of (29)) can be considered “extended reconstruction” equations for the particle correlation function; the reconstruction equations (27) (where the GKBA represents the free term) are nothing but a limiting case obtained from (31) and (31’) by merging the two earlier times, \(t_{\times }\rightarrow t'\) or \(t_{\times }\rightarrow t\) in the respective limits. We can thus conclude that the reconstruction equations are consistent with (28), while the bare GKBA itself clearly is not. To obey the Ward identities exactly, Green’s functions have to satisfy the complete reconstruction equations. Any other causal Ansatz should be constructed so as to approximate the vertex corrections in the reconstruction equations, and thus to minimize the inaccuracy of the related Ansatz-based transport theory.
Using Eq. (31), however, we can see one of the reasons, why the GKBA transport theory has been so successful in describing dynamics of some quantum systems. According to (30), \(G^<_{\scriptscriptstyle \mathrm{GKBA}}\) satisfies the (schematically written) relation \(G^<_{\scriptscriptstyle \mathrm{GKBA}}=\mathrm{i}G^RG^<_{\scriptscriptstyle \mathrm{GKBA}}+\int \int G^R{\varSigma }^R G^<_{\scriptscriptstyle \mathrm{GKBA}}\) for any \(t_{\times }\). This is just (31) without the second vertex correction \(\int \int G^R{\varSigma }^< G^A\). This correction is zero, however, for \(t_{\times }>t''\equiv t'+2\tau _Q+\tau _c\). For the use of quantum transport equations, the long time asymptotics \(t-t'\gg \tau _Q,\;\tau _c\), is decisive, and in this time region \(G^<_{\scriptscriptstyle \mathrm{GKBA}}\) is exact except for the presumably narrow interval \(t''>t_{\times }>t'\).
4.3 Approximations for vertex corrections
Up to now, two ways were suggested, how to include at least some approximation of the vertex corrections, which are numerically tractable in a reasonable manner: to use either the Quasiparticle Generalized Kadanoff–Baym Ansatz (QGKBA) [65, 67, 72, 174, 176], or the steady-state approximation (CGKBA) of RE [180, 181].
4.3.1 Quasiparticle Ansatz
The introduction of the QGKBA was originally motivated by an additional approximation for the propagators used in the GKBA. They have always been replaced by a simplified form suppressing the short time formation process (decay of initial correlations). This experience resulted into the introduction of the QGKBA [65, 67, 72, 174, 176].
This has led to a basic question, how to define quasiparticles out of equilibrium. The motivation is to mimic the free-particle behavior (when the Ansatz is exact) and thus to define quasiparticles through an approximate semi-group property similar to the exact multiplication rule (25) for free particles. The quasiparticle approach is justified in the case that the decay of correlations is much faster than any other physical process in the system [65, 67, 176]. A formal definition of non-equilibrium quasiparticles based on a multiplicative semi-group property
was introduced in [176]. This multiplicative law is (similarly like in the case of the GKBA) closely linked with the Ansatz factorization, so the relationship quasiparticle—Ansatz seems obvious, but the basic proof is missing.
When the quasi-particle picture is used, the renormalized QCR can be satisfied almost exactly. If the quasi-particle picture and the QGKBA is valid, the polaron term of the reconstruction equations (RE) (27) is suppressed. The irreducible vertex, however, still remains untreated. Incorporation of this term by a proper renormalization of quasi-particle propagators accounting for particle interactions could be made by possible renormalized quasiparticle generalized Kadanoff–Baym Ansatz (RQGKBA) [67, 176] which will treat properly both vertex corrections. Meanwhile, there is always the option of treating these corrections in a phenomenological way. This has met with practical success already [1, 62, 140,141,142,143,144,145,146, 148]; of course there is the problem of adjustable parameters selected ad hoc.
4.3.2 Steady-state correction of RE
To formulate the steady-state correction to the RE, let us assume a free relaxation of a non-equilibrium system to a steady state out of equilibrium. In the steady state, we are able to directly obtain the true \(G^<\) in the energy representation, and \(G^<_\mathrm{GKBA}\) as well. Here, we introduce the subscript GKBA to distinguish the approximate \(G^<_\mathrm{GKBA}\) from the exact \(G^<\). Then, we may define
where the single-time \(\mathcal {F}_\infty (\tau )\) is the Fourier transform of \(\mathcal {F}_\infty (E)\). Similarly, we define
Clearly,
As the simple approximation for the vertex corrections in the RE we propose here is to extend the asymptotic coincidence, Eq. (36), also to finite times and write
By this step we will approximate at the same time both, quasiparticle and irreducible, vertices. Thus we obtain another variant of the family of causal Ansatzes, the so-called corrected GKBA (CGKBA)[180, 181]:
We will comment on how this approximation works in the case of a molecular bridge model in Sect. 8.
5 Quantum transport theory
We will now return to the central task of this text: construction of closed equations for one-particle density matrix (OPDM) \(\rho \), simplified quantum transport equations for various quantum systems (either kinetic equations or generalized master equations) based on the Ansatz approach. We will now summarize possibilities how to proceed with the construction of effective transport theories based on the use of reconstruction equations.
5.1 Reconstruction theorem
Let us first consider how to use the reconstruction equations (27) to reconstruct the full double-time correlation function \(G^<(t_1,t_2)\) from the propagators and a single-time quantity \(\rho (t)\).
Looking at the reconstruction equations we can see that the whole scheme of solving the equations of motion for the NEGF can be expressed by the following cyclic reconstruction scheme:

This scheme consists of the following steps of the iterative process, which starts in the right hand panel:
\(\diamond \) The propagators are readjusted to the newly input OPDM \(\rho \),
\(\diamond \) then the correlation function \(G^<\) is expressed in terms of this OPDM and the propagators.
\(\diamond \) All these quantities enter the left-hand panel and they generate next iteration for \(\rho \).
This process guarantees the self-consistency between the propagators and the density matrix and thus it results in a consistent form of the reconstruction equations for \(G^<\). This reformulation of the whole NEGF equation system offers no practical advantage over a direct solution of KB equations or the Dyson equations for the NEGF.
This scheme, however, reveals a privileged role of \(\rho \) and can be reformulated in the form
This is a bijective relationship between the full double-time Green’s function and a single-time single-particle density matrix. This has been called the reconstruction theorem in [65, 67, 72, 175].
5.2 Approximations of the reconstruction theorem
It is very difficult to carry out the complete reconstruction cycle in a real situation, and we need to approximate this cyclic scheme at some level. By keeping only the first (free) term of the reconstruction equation (27), we resort to the GKBA decoupling, which simplifies the cycle (39) to the following scheme:

Here, the correlation function \(G^<\) is eliminated explicitly in favor of the propagators, and the cyclic process becomes practicable. Its use is conditional on validity of the GKBA. Clearly, this does not preclude the possibility of some alternative Ansatzes leading to modified schemes of the (41) type, perhaps with more favorable properties or a wider validity range.
One of the possibilities is to use the steady-state Ansatz (CGKBA) (38). The whole process of solving the equations of motion for the NEGF then follows the cyclic scheme:

It is no more difficult to solve the equation system entering this cycle than to run the GKBA cycle (41) proper. Namely, as indicated in the scheme, the approximate vertex correction enters the cycle from outside and is known beforehand.
We shall still return to the question of validity ranges of various Ansatzes in the concluding remarks.
5.3 Fluctuation–dissipation theorems
We will now deal with the NEGF fluctuation–dissipation theorem (FDT) [71, 72, 179]. The equilibrium version of the NEGF FDT, which is, as we will see below, in fact the identity connecting propagators with correlation function, was a basic motivation already for Kadanoff and Baym on their way to the KBA and quantum Boltzmann equation [45]. They generalized this identity to the non-equilibrium situation by introducing their KBA as an approximation, which led to the successful derivation of the quantum Boltzmann equation from NEGF equations of motion. It thus became obvious that the non-equilibrium version of the NEGF FDT represents an important part of the formulation of the quantum transport theory based on approximations of NEGF equations of motions. Ever since it has played the vital role in the NEGF description of the dynamics of non-equilibrium systems. It has been successfully used not only for the formulation of various approximations, but it has been also shown to be valid for advanced approximations (as DMFT) used in complex correlated systems [23, 71, 179, 183].
Before going to non-equilibrium FDT, we will first introduce the NEGF FDT in equilibrium.
5.3.1 Fluctuation–dissipation theorems and Ansatzes in equilibrium
Fluctuation–dissipation and fluctuation theorems are known to mirror special properties of systems in thermal equilibrium and stationary states. They have been extensively used to describe equilibrium properties of systems and their linear response. In addition, they can indicate how systems thermalize and in which way reach the steady states [23, 65, 71, 88, 89, 95,96,97,98, 100, 102, 107, 108, 179].
In equilibrium, as in any stationary state, the system is homogeneous in time, all NEGF depend thus only on the difference of times and all functions can be thus written in the spectral (energy) representation. Therefore, we can rewrite the correlation function in the form:
If we introduce, following Eq. (3), the spectral function \(A(1,2)=\mathrm{i}\,(G^>(1,2)-G^<(1,2))\), the equilibrium correlation function satisfies the following identity:
Here, \(f_\mathrm{FD}\) denotes Fermi–Dirac function. This identity, which connects, in terms of GF, the fluctuation and dissipation features of the system, is the well-known Green’s function fluctuation–dissipation theorem. We can immediately see that the identity (45), in its first form, is resembled by the KBA factorization (7), and in the second form, by the GKBA (6). As hinted already in the footnote 3, the relation (45) is exactly the identity which motivated the introduction of the KBA, which can thus be also viewed as a near equilibrium approximate generalization of the NEGF fluctuation–dissipation theorem essential for the derivation of quantum transport equations for near to equilibrium systems. The GKBA represents further improvement of the approximation of the FDT out of equilibrium. It should be warned, however, that even in equilibrium FDT alone is not sufficient for deriving an Ansatz. For this, the additional requirement of sharp quasiparticle resonances in the spectral density is necessary, because only then the function of energy \(f_\mathrm{FD}(E)\) can be replaced by a constant \(f_\mathrm{FD}(E_\mathrm{QP})=\rho _\mathrm{QP}\) as required by the Ansatz factorizations. For the validity of an Ansatz is thus the equilibrium state in itself not exceptional.
5.3.2 Non-equilibrium FDT and reconstruction equations
We will now connect the above-mentioned reconstruction procedures with a generalized NEGF non-equilibrium (NE) fluctuation dissipation theorem (FDT) [179]. The scheme (39) indicates in which sense the NE FDT could be understood in general. This is, in fact, equivalent to the Reconstruction Theorem: in the reconstruction cycle all ’less’ quantities should be eliminated by expressing them in terms of the one-particle density matrix (OPDM) \(\rho \) and the propagators. This reduction of the necessary independent information in principle, play the role of the NE FDT. Without technical means for achieving such reduction, the whole “theorem” would be of a little additional value since we could just recall the reconstruction theorem. This situation just reminds us of the difference between the Runge–Gross existence theorem of the time-dependent density functional (TDDFT) [10] and the limits of the practical use of the TDDFT scheme [17].
However, we can, following [179], use the FDT to formulate precisely the statement representing an extension of the FDT out of equilibrium:
Non-equilibrium fluctuation–dissipation theorem
The information contained in the propagators \(\{G^R,\,G^A\}\) and the OPDM \(\rho \) specifies the complete NEGF \(\{G^R,\,G^A\,G^<\}\) of a given system in the parameter area and in the time range for which the Ansatz factorization (6) holds.
We may express this result also by saying that under favorable conditions, we may go from the full description in terms of two independent two-time correlation functions to a shortened, one and a half (i.e., two-time and single-time) description, which is on the level of an effective transport theory based on a quantum transport equation for OPDM \(\rho \). In principle, under some conditions, by iteration we could get an improved quantum transport equation.
5.4 Tentative appraisal of the Ansatz
Before entering the problem how to incorporate complex finite-time initial conditions into the Ansatz-based NEGF treatment, a few lines recapitulating properties of the Ansatz may be useful. No doubt the Ansatz has been used to facilitate or even make possible a numerical solution of a number of problems. As a rule, there has been no independent way of assessing the results except of comparing them with experimental data.Footnote 5 It remains nothing else but to check the properties of the Ansatz in general, and for a specific problem. We have to single out the original GKBA, in which all entering quantities are strictly related to the true NEGF, and for example, the spectral identity has a strict meaning. It is then possible to verify even some fully quantitative criteria. An interesting example is the study of spectral moments for the Falicov–Kimball and Hubbard models in a time-dependent electric field [19]. In applications, GKBA as such is usually modified to one of the causal Ansatzes specified by the choice of model propagators, as discussed at length above, and the testing of basic properties is concerned with the internal consistency of the model[76, 77, 157, 163]. There is one universal and basic requirement stated already when \(\tau ^\star \) was defined by Eq. (11): \(\tau ^\star \ \ll \ \ \)all global and external characteristic times. We shall see in Sect. 8 an example, how the Ansatz completely fails, if this condition is not satisfied. This still leaves a broad field of problems for which the Ansatz route is suited.
6 NEGF and finite-time initial conditions
Up to now, we dealt with the case when initial conditions did not play a decisive role in the description of the system dynamics, so we could use the Keldysh approach to the NEGF formalism. Complex initial condition (correlated initial state) can play an important role, e.g., in the fast transients processes and it is thus inevitable to include a correlated initial condition into the NEGF method. There is a long history of the inclusion of the correlated initial state into the NEGF method [227,228,229,230,231,232,233,234].
In general, differential equations of motion for NEGF have to be supplemented by initial conditions. This includes the initial time \(t_{\scriptscriptstyle { \mathrm I}}\) and the (many-body) initial state. A particular, but often used, initial condition is an uncorrelated one. This permits to develop a perturbation series for the NEGF for times \(t,t^\prime \ge t_{\scriptscriptstyle { \mathrm I}}\) to take account of the interactions. The correlated state only develops gradually during an initial period of time, an unrealistic feature. To overcome this, several strategies have been used. In general, there are two complementary groups of approaches, we can call them synchronous and diachronous [113, 209]. In the synchronous treatment, the initial condition is specified by the complete knowledge of the correlation function \(G^<\) at the finite initial time \(t_{\scriptscriptstyle { \mathrm I}}\). This means that all higher correlation functions and related perturbation scheme to simplify NEGF equations are involved. Diachronous treatment on the other hand follows natural evolution of the system and takes an initial state as an outcome of the preparation period of evolution before the measurement starts at some initial time \(t_{\scriptscriptstyle { \mathrm I}}\) and the initial condition is represented by only single-particle quantities. This, of course, assumes the knowledge of single-particle characteristics for some time during the preparation evolution. We will now mention some representatives of these two classes of approaches specifically.
- Keldysh::
-
The simplest idea, following the original Keldysh procedure, is to start from an uncorrelated state at a time \(t_0\rightarrow -\infty \) preceding thus \(t_{\scriptscriptstyle { \mathrm I}}\), and to turn the interactions on adiabatically. Then our process will start from the resulting correlated state at the original finite initial time \(t_{\scriptscriptstyle { \mathrm I}}\).
- Kadanoff–Baym::
-
The widely used procedure expanding on the seminal concept introduced by Kadanoff and Baym is to augment the real-time Schwinger loop delimited by \(t_{\scriptscriptstyle { \mathrm I}}\) by an imaginary stretch \([t_{\scriptscriptstyle { \mathrm I}}, t_{\scriptscriptstyle { \mathrm I}}-\mathrm{i}\beta ]\) along which the systems develops Matsubara style from the uncorrelated state to the correlated one. The NEGF and the selfenergies are defined on the extended loop and this transfers the correlations also to real-time arguments. This approach has been authoritatively worked out by Danielewicz [230] and generalized by Wagner [45].
- Kremp group::
-
They have based their approach on adding initial correlation contributions to selfenergy. This approach, which has been developed and improved over years, is based on the principle that initial condition should be consistent with the approximation of the NEGF [158, 159, 164, 232, 235,236,237]. A full treatment under the name of Generalized Wick Theorem is given in [71, 238].
- Our approach::
-
We came up to this problem from a rather different angle and introduced the so-called time partitioning method which enables to introduce a correlated initial condition into the NEGF equations in a natural way by first splitting time line into the past, present and future times and second, to propagate Green’s functions from infinite past using Keldysh approach and to use the created correlated state at a finite time (the present) as an initial condition for future evolution [67, 72, 113, 178, 209].
Despite of all these efforts, it has remained unclear how to combine properly the GKBA-based approach to transport for the case of initial correlated conditions. In other words, there is a question, how the Ansatz can be used on the whole Keldysh loop. This is, first of all, also closely related to the following observation: when system changes suddenly, Ansatz cannot be valid due to the change of propagators: which propagator are we supposed to use?
6.1 Ansatz and initial condition
The thoughts about how to include properly an initial condition into the NEGF transport theory have been followed by considerations how to use the Ansatz just from the beginning of the non-equilibrium situation. Recently, four different approaches have been suggested for answering this persistent question:
- Tuovinen et al::
-
They decided to introduce the full many body selfenergy into the NEGF transport equation, and then to use the GKBA Ansatz where HF retarded Greens functions are used. They then develop equilibrium correlated state and compare it with the result provided by the use of the GKBA [182].
- Verdozzi et al::
-
They use the GKB Ansatz to determine an equilibrium correlated state without using the procedure of an adiabatic switching-on of the correlations for its preparation [183].
- Van Leuween et al::
-
Using a standard procedure, they first formulate NEGF transport equation for single-time one-particle density matrix \(\rho \) which contain two scattering integrals, one of which, the IC integral, contains information about initial condition. They then show that this IC integral can be expressed in terms of real-time NEGF and they use the GKBA in this scattering integral [184]. Recently, they applied this technique combined with partition-free approach to dynamics of molecular junctions [173].
- Bonitz et al::
-
They first used the older idea to include initial correlations into the selfenergy and thus to formulate additional scattering integral which contains finite initial condition time \(t_0\). They then introduced the GKBA to this collisional integral according to a standard GKBA scheme to transport equations [76, 77, 157].
6.2 Partitioning in time approach to initial conditions
The partitioning in time was developed as a device for handling a natural finite-time initial condition, that is the correlated initial condition generated in the course of a Keldysh process [67, 113, 178, 209].
The time domain of a Keldysh process is divided into two parts: the initial preparatory period lasting from the distant past \(t_0 \rightarrow -\infty \) to a selected finite initial time \(t_{\scriptscriptstyle { \mathrm I}}\), and the following observation (measurement) stage. The whole time line of the process is thus split into the past and the future with respect to the chosen finite initial time \(t_{\scriptscriptstyle { \mathrm I}}\). Correspondingly, the double-time quantities treated as matrices may be split into partitions with a common corner point \((t_{\scriptscriptstyle { \mathrm I}},\,t_{\scriptscriptstyle { \mathrm I}})\) of their time domains: the past \(t\le t_{\scriptscriptstyle { \mathrm I}},\,t'\le t_{\scriptscriptstyle { \mathrm I}}\), the future \(t\ge t_{\scriptscriptstyle { \mathrm I}},\,t'\ge t_{\scriptscriptstyle { \mathrm I}}\), and two off-diagonal blocks. Introducing the corresponding projectors and applying the standard projection technique to the integral equation of motion (EOM) for the Green function, we obtain their transform for the partitions. As an example, the Dyson equation for the \(G^R\) propagator has the following future-past block:

A few comments: The equation is a renormalized semi-group multiplication rule for the full propagator. The renormalization consists in smearing the multiplication point over the actual integration range in the second line. Since \(t\ge {{\bar{\bar{t}}}}\ge {t_{\scriptscriptstyle { \mathrm I}}}\ge {\bar{t}}{\ge t'}\), it follows that the spread of the integrand cannot exceed a few \(\tau ^\star \) around \(t_{\scriptscriptstyle { \mathrm I}}\), cf. Eqs. (11) and (63) below and the discussion there. Typically, it is expected to be small.
This equation is a special case, for \(t_{\times }=t_{\scriptscriptstyle { \mathrm I}}\), of Eq. (30), which was obtained and used in an entirely different context of the reconstruction equations, and \(t_{\times }\) was a floating variable.
Our main concern is the relevant part of the whole Keldysh process, the future partition starting at \( t_{\scriptscriptstyle { \mathrm I}}\). It may be considered a process embedded in the whole host Keldysh process. By partitioning, it may be converted into a self-contained “measurement process” with the time domain coinciding with the future partition of the host process. The Green’s function will remain the same, while the EOM will be changed to incorporate the correlated initial condition, reflecting in turn the whole history contained in the past partition of the host process.
The resulting equations will now be conveniently presented by components of the NEGF.
First, the EOM for the propagators retain their form. This is evident without the projector technique from the Dyson Equation (DE) for \(G^R\),
Once \(t'>t_{\scriptscriptstyle { \mathrm I}}\), the same is true for all times entering Eq. (47). Similar reasoning holds for \(G^A\). The selfenergies belong to the host process, of course, and typically will transmit the influence of the past which soaks in through their self-consistent dependence on the complete NEGF.
The less-component of the Dyson equation (DE), in contrast, has the form

which differs from the DE for the host process, usual \(G^<=G^R{\varSigma }_{}^<G^A\) in two respects, the lower integration limits are \(t_{\scriptscriptstyle { \mathrm I}}\) compared to \(t_0\) and the host selfenergy \({\varSigma }^<\) is supplemented by additional terms respecting the missing contribution of the history preceding \(t_{\scriptscriptstyle { \mathrm I}}\), in other words taking the correlated initial condition into account:Footnote 6
The four selfenergy terms have a varying degree of singularity at the initial time. The open circles indicate a time variable fixed at \(t_{\scriptscriptstyle { \mathrm I}}\), the filled ones a time variable continuous in \((t_{\scriptscriptstyle { \mathrm I}},\infty \)). From the rear, the \({}^{\,}_{\ \bullet }\varSigma ^<_{\bullet }\) term resembles most closely the usual selfenergy, being composed of two regular functions of \(t,t'\), namely the host selfenergy \({\varSigma }^<\) and an additional regular function:

The \({}^{\,}_{\ \bullet }\varSigma ^<_{\circ }\) and \({}^{\,}_{\ \circ }\varSigma ^<_{\bullet }\) contain one \(\delta \) function:

Finally, there is the \({}^{\,}_{\ \circ }\varSigma ^<_{\circ }\) term,
which clearly has a special position. It reflects the initial correlations by the resultant one-particle density matrix (OPDM) \(\rho \) only, but it would survive even in the uncorrelated case, as will be demonstrated immediately.
Before that, we show on one example the actual structure of the selfenergy terms in (49). For \(_{ } \varLambda _\mathrm{o}^<(t,t_{\scriptscriptstyle { \mathrm I}} )\), we have
Clearly \(\overline{t}\le t_{\scriptscriptstyle { \mathrm I}}\), which means that \(t-t_{\scriptscriptstyle { \mathrm I}}=O(\tau ^\star )\), as follows from Eq. (11). The same repeats for all other terms of \({\varXi }^<\). The time arguments \(t,t'\) are either equal to \(t_{\scriptscriptstyle { \mathrm I}}\) or do not depart from it by more than a quantity on the order of \(\tau ^\star \). The importance of this result will be made apparent in further analysis. To remind, similar behavior was found for Eq. (46), although the physical meaning was different. Altogether, these are various manifestations of the Bogolyubov principle of the decay of correlations.
6.2.1 Keldysh uncorrelated initial condition
It is illuminating to treat the finite-time uncorrelated initial condition as a limiting case of the general processes specified by Eqs. (48 and 49). All that means that the uncorrelated selfenergy \({\varXi }^<\) has only two terms:
In addition, we should set \(\rho (t_{\scriptscriptstyle { \mathrm I}} )=\rho _0 (t_{\scriptscriptstyle { \mathrm I}})\), that is use the unperturbed initial particle distribution. As concerns \({\varSigma }^<(t,t')\), it belongs to the host process, but the past period of the process consists of keeping the system unperturbed in the initial uncorrelated state, so that \({\varSigma }^<(t,t')\) in the past is zero. The particle function then reads
The integral consists of two terms; the first one can be given two different forms. Either the integrals of the \(\delta \) functions are performed:
The first term describes the coherent evolution and a gradual decay of the initial condition. In the long time limit (at the kinetic stage of evolution), this term will die out and only the second term will survive.
The other form of Eq. (55) is better to be written in the symbolic form. Using the Dyson equations for the propagators and introducing
we get
This is immediately recognized as the famous Keldysh form of the particle (“less”) function for a finite-time uncorrelated initial condition [50, 62].
6.3 Reconstruction equations with initial conditions
Equations (47) and (48) can be transformed, similarly as in the case of Dyson equation (DE) without correlated initial conditions, to the reconstruction equations. Initial conditions lead to the following modification of the reconstruction equations [67, 178]:

As we can see immediately, the initial condition enters explicitly only the vertex corrections, so that the form of the Ansatz remains unchanged.
6.3.1 Ward identities
The Ward identity plays, similarly as in the case already discussed, an important role as a consistency check of approximations on the one and two particle levels also in the case when complex initial conditions are involved. At the same time, it is necessary for the conservation of the particle number. The Ward identity can be derived also for the correlated initial conditions and it has formally the same structure as in the case without initial conditions [67].
7 Initial conditions and transport equations
The starting point on the way from the double-time NGF to single time transport equations is the generalized Kadanoff–Baym Equation. We have already introduced the GKBE for the special case of Keldysh initial conditions (15). Before we discuss transport equations proper, we need to consider the influence of the initial condition on the generalized Kadanoff–Baym equation (GKBE) and the precursor quantum transport equation (PQTE).
7.1 GKBE with initial conditions and PQTE
Similarly as we derived GKBE (15) in the special case of Keldysh initial conditions, we can derive its generalization:
This differential equation, the GKBE with initial conditions, already has a structure closely related to transport equations. The four terms on the r.h.s. represent the generalized collision terms. This equation, however, differs from a common transport equation in two aspects: (1) it has the double-time structure and (2) it includes the initial conditions via the selfenergy \({\varXi }^<\).
To discuss the effect of initial conditions, we need to rewrite GKBE into the form with collision integral terms explicitly corresponding to the host process and to the initial correlation terms. Thus, using (49) and (50), we will split the selfenergy \({\varXi }^<\) into the selfenergy \({\varSigma }^<\) of the host process and the remainder \(\varTheta ^<\)

Using this decomposition, we can rewrite Eq. (60) into the following form:
Having the GKBE (61), we can immediately get the precursor transport equation (PQTE), which is the generalization of (16) (for the Keldysh initial condition) to the correlated finite-time initial conditions
We will now proceed on the way to derive a closed simplified transport equation for the one-particle density matrix (OPDM) \(\rho \).
7.2 Time structure of selfenergy and PQTE
Our aim is to derive the common transport equations. This means equations which describe the stage of the system evolution when initial correlations do not play an important role. The natural question is what are the conditions which enable us to neglect the selfenergy \(\varTheta ^<\) in (62) (the last two generalized collision terms in this equation) and this equation will thus turn to the PQTE (16) already discussed.
To proceed further to this aim, it is natural to make two assumptions:
\(\diamond \) We assume to describe evolution for times when the system is already in a steady-state condition: external disturbances do not change or change smoothly and we follow the system for times which are separated enough from the time \(t_{last}\) of the last abrupt external perturbation. This enables us to recall the following assumption about the time behavior of the selfenergy.
\(\diamond \) There exists a time \(\tau ^\star \), such that
This second assumption is a natural one since it captures in a simple manner the essential feature of a typical selfenergy to be concentrated along the time diagonal, as already hinted in Sect. 2.2, where a physically motivated definition of \(\tau ^\star \) was given by Eq. (11).
Let us now notice what are the consequences of these assumptions for Eq. (62). First, in the collision terms, which contain \(\varSigma \), the time integration range is restricted by the condition (63) to a finite interval \((t-\tau ^\star ,t)\), which is the memory depth of the system. Thus, a typical term of these first and second collision terms in (61) , \({\varSigma }^RG^<\), reads
For \(t> t_{\scriptscriptstyle { \mathrm Last}}+3\tau ^\star \), the selfenergy in (64) extends already over the steady/smooth change time span, and while the turbulent past may be reflected in the values of \(G^<\), it will in no case show in the form of the Precursor equation (61).
Second, the quick loss of the disturbance memory also means that the last two generalized collision terms of Eq. (62) which take the initial conditions into account explicitly through the selfenergy \(\varTheta ^<\), become zero as the running time t exceeds \(t_{\scriptscriptstyle { \mathrm Last}}+2\tau ^\star \).
To conclude the analysis, it is enough to wait for just \(2\tau ^\star \) past \(t_{\scriptscriptstyle { \mathrm Last}}\), and the PQTE becomes free of any IC terms:
so that it is formally equivalent to the PQTE (16) derived in Sect. 2.3.
The essential step on the way from the PQTE to an effective closed transport equation of the GME form for \(\rho \) is the choice of a proper Ansatz.
7.3 Ansatz variants and transport equations
The resulting transport equation depends on the Ansatz for factorization of \(G^<\) which approximates reconstruction equations. We will consider and discuss properties of only two kinds of Ansatzes, both of them belonging to the class of the causal Ansatzes:
\(\diamond \) The so-called XGKB Ansatzes:
\(\diamond \) Steady-state XCKBA Ansatzes:
where X stands for the corresponding propagators \(G^R_X\), \(G^A_X\) .
Each of these Ansatzes is specified by a particular choice of the propagators \(G^R_X,G^R_X\) as indicated by their labels. Various choices include, e.g., free propagators \(G^{R,A}_{\scriptscriptstyle { \mathrm 0}}\), several variants of quasiparticle propagators \(G^{R,A}_{\scriptscriptstyle { \mathrm Q}}\) or the true, fully renormalized propagators \(G^{R,A}_{\scriptscriptstyle { \mathrm G}}\). As already discussed, free propagators \(G^{R,A}_{\scriptscriptstyle { \mathrm 0}}\) and related FGKBA were used in many cases, and especially in the case of bulk systems also in deriving the Boltzmann equations. They are also convenient for getting Master equations in the second order weak coupling theory which is equivalent to the Fermi Golden rule. There are also cases when the Quasiparticle Generalized Kadanoff–Baym Ansatz (QGKBA), in which the propagators are represented by the unrenormalized pole part of the true propagators, works well. The variants of the CGKBA have been successfully tested in the case of the molecular bridge models as we will discuss in the following section.
After we discussed possible Ansatzes, we can now derive a desired transport equation.
7.4 Derivation of transport equations
To derive a single-time transport equation, i.e., a closed equation for OPDM \(\rho \) (kinetic equation or GME), from the two time NEGF structure, we have to proceed in three steps:
First step: On the way to GME we start from the precursor quantum transport equation (PQTE) (65), which we can symbolically write in the following form
where \({\mathrm{drift }}=\mathrm{i} \left[ \right. {\textstyle h_0(t)},\rho \left. \right] _{-}\) and \({\varSigma }^<={\varSigma }^<[G^R,\,G^A,G^< ]\).
Second step: A physical approximation is selected, that is, the selfenergy is composed of the coupling to reservoirs, the interactions are expressed self-consistently in terms of the GF, etc.
Third step: The l.h.s. of (68) already has the quantum transport equation form. The r.h.s., however, still contains a number of double-time quantities, which have to be eliminated. In this final step, one of causal Ansatzes (either XGKBA (66) or its steady-state variant (67))
is used to eliminate \(G^<\) in favor of its time diagonal \(\rho \).
When introduced into the PQTE (68), this leads finally to the quantum transport equation represented by a closed GME for \(\rho \):
The memory kernel at the r.h.s. can be interpreted to be the generalized collision term. The role of the propagators is essential: The memory determining the transport equation (70) is completely specified by the propagators used in the Ansatz. We can thus clearly see that the quality with which the above GME describes the dynamics of the consider systems depends on suitably selected propagators.
7.5 Towards master equations (from non-Markovian to Markovian evolution)
During the gradual relaxation, the system evolution may reach the stage when the change of the density matrix over the memory depth of the GME is minute, and it becomes possible to describe the evolution of \(\rho \) by a master equation (ME), adequate for the long time asymptotics.
To derive such master equation, it is enough to start from the already established GME and make the appropriate approximations. For the first insight, the symbolic Eq. (70) is suited. The density matrix enters the r.h.s. in a causal manner, that is back in time from the present t. Taking into account a limited memory depth on the order of \(\tau ^\star \), assumed throughout this paper, we may suppose that \(\rho (\tau )\) changes only little. The simplest approximation then is to replace it by \(\rho (t)\):
By this approximation, the GME is reduced to a differential equation for \(\rho (t)\). The approximation applies to \(\rho (t)\) as it enters the functional \(\varPhi \) both explicitly, and also through other components, like through \({\varSigma }^<\), cf. Eq. (69). The whole r.h.s. of (71) then corresponds to a stationary state of the system frozen at the time t. This is an adiabatic approximation, as indicated at the arrows.
An equation having the form of a quantum master equation can be obtained from GME of a more specific form; here we use the simplest Eq. (17) derived by an elementary use of GKBA and we further assume that the selfenergies are fixed, not self-consistently dependent on the density matrix. Then, for a system with discrete states labeled by Greek letters, \(\alpha , \beta \ldots \), the approximation (71) yields
The last EOM has the structure of a master equation with the superoperator \(\mathcal {A}\) representing the transition rate matrix. Because it involves not only the rates for occupation numbers, but also for the coherences, i.e., the off-diagonal matrix elements of \(\rho \), it is a quantum master equation. The \(\mathcal {C}\) matrix provides the coupling to the environment—the particle reservoirs. With our assumptions, \(\mathcal {C}\) and \(\mathcal {A}\) are time independent, so that the process described by Eq. (72) possesses the Markovian property.
Various improvements and extensions of the presented way to master equations suggest themselves. First, the extrapolation procedure for \(\rho (t)\) into the past can be refined. This is quite desirable, as it extends the validity range of the resulting Master Equation and improves the fit to the source GME, as will be shown and analyzed in detail in Sect. 8.3.1 on the example of a molecular bridge. Second, the time dependence brought about by an external disturbance, like an oscillating electric field, should be considered, in order to broaden the scope of the Master Equation approach, and at the same time, to put it under a more demanding test. This, within our technique, has to be done starting from a field dependent GME again. Generally speaking, our method of deriving the master equations is a “cheap” one, as they form the last link in the chain Many-body system \(\rightarrow \) NEGF \(\rightarrow \) GME \(\rightarrow \) ME. The critical step in this sequence is the transition from the Green’s functions to the GME, which depends on the validity of a GKBA-like causal Ansatz and its proper implementation. The subsequent step to the master equation consists in sampling the memory of the GME at each instant t and lumping the needed information forward in a time-local form entering the ME. It is remarkable that both these steps have as a feasibility condition the requirement that the characteristic time of the internal dynamics, \(\tau ^\star \), is the shortest of all characteristic times, that is, \(\tau ^\star \ll \tau \), and \(\tau ^\star \ll \tau _{\scriptscriptstyle \mathsf{EXT}}\). The first condition was already introduced in connection with the definition (11), the second one concerns the external disturbances and \(\tau _{\scriptscriptstyle \mathsf{EXT}}\) may typically be the period of external field oscillations. It is apparent that the transition GME \(\rightarrow \) ME is gradual and is specific for each particular problem.
The problem of master equations is still open for research, as witnessed by recent publications, even of instructional nature [116], and it would be desirable to compare our results with some other approach. In this context, we would like to single out the paper [115]. Its principal aim, simulation of a fermionic reservoir on a quantum computer, goes far beyond just deriving a master equation, but the first half of the paper solves this problem for a particular system formed by electrons on a 1D tight binding chain whose nodes are individually connected to fermionic baths. The authors derive the master equation in both the Redfield and Lindblad forms, and find the respective solutions in an external homogeneous oscillating and dc field with a remarkable success. This could have been judged exactly, as the model is unique, being soluble in terms of NEGF [114]. This opens up a special chance, to follow through our approach for this system, get GME and ME and make comparisons, both concerning the technique and the results available.
In conclusion of this discussion, we overstep the self-imposed limitation of this paper and briefly present a recent manuscript [25] devoted to the quantum Boltzmann equation. The basic point of the authors is that the QBE can be derived for systems with well separated time scales, internal and external. In the Wigner representation of the NEGF, their assumption means that for all GF components it holds that \(|\partial _t G/G|<1/\delta t\) and \(|\partial _\omega G/G|<1/\delta \omega \). Here, \(\delta t\) and \(\delta \omega \) are characteristic quantities, in terms of which the time scale separation is justified if \(\delta t \gg 1/\delta \omega \). This is identical with our conditions for the master equation, \(\tau ,\;\tau _{\scriptscriptstyle \mathsf{EXT}}\gg \tau ^\star \). The authors proceed to show that it is then meaningful to introduce the distribution function, for a homogeneous system as \(F_k(t,\omega )=G^<_k(t,\omega )/A_k(t,\omega )\) with usual definitions of \(G^<\) and A. For this quantity, the quantum Boltzmann equation can be derived. The resulting scattering integral is suited both for a perturbative and a nonperturbative treatment.
8 Molecular bridge model
We will now discuss how we can use the NEGF approach and the Ansatz to develop an effective simplified transport theory for open nanoscale non-equilibrium electronic systems. There have been many studies of non-equilibrium electronic molecular junction systems, since the importance of these systems has been increasing from the point of view of theory, experiment and nanoscale devices. They have enabled to improve our understanding of ultrafast dynamics of small open electronic systems and devices based on them, when the full time description is necessary to describe properly not only well possible long time steady-state asymptotics (after system relaxes), but also initial ultrafast phenomena (often related to switch on and switch off processes) and their dependence on the variety of parameters of these systems and their environment [113, 172, 173, 193, 194, 197,198,199, 203,204,205,206,207,208,209,210,211,212,213,214]. To this end, simplified models are extremely useful for studying general features of these complex non-equilibrium systems to develop a proper simplified picture of their behavior in time.
There are two approaches how to describe open nanoscopic systems:
\(\diamond \) Partition-free approach: the initial state is contacted (describing the system and baths together) and in a thermal equilibrium [202].
\(\diamond \) Partitioned approach: the initial state is created by a sudden or adiabatic switching of contacts between the system and its surrounding as it was originally designed in [200, 201]. We will further follow this approach.
In this section, we will be interested in dynamics of a molecular island (a single-level tunneling center) between two current leads, which are connected to the central island each by its own (left and right) tunneling junctions:

Both leads are modeled as infinite baths of electrons, which are inert with respect to island’s processes and are in equilibrium.
This molecular bridge model serves well as a simple prototype of open nanoscopic systems. Thanks to the links of the molecular island to the electrodes, this model mimicks quite well some features of behavior of many body systems and it is reasonable to treat the non-equilibrium dynamics of this model by the NEGF method, which is natural for the description of non-equilibrium many body systems. The simplicity of the model provides a possibility to test various approximations for the equations of motion of correlation functions and for the use of various Ansatzes by comparing them with the full numerical solution. In particular, this model can be used conveniently as a testing ground for Ansatz based transport theories and for the clarification of the domains of their validity. Its simplicity also enables to avoid the commonly used wide band limit (WBL) approximation.
We start with treating the simplest free-particle model without any interactions, just to show the effect of the environment on transport properties.
In the second part, we will deal with the magnetic molecular bridge: the interaction of spin states will introduce additional dynamics and limitations on the use of various approximations.
For the sake of simplicity, we mainly employ here a simple finite time initial condition (non-correlated initial state) of the Keldysh type. This permits to concentrate on the essential features of the molecular bridge model representing open systems, and the Ansatz-based transport theory. This model, however, can conveniently be used also for the studies of relaxation dynamics from a natural non-equilibrium correlated initial state [67, 113, 209, 210, 212], which is prepared by the partitioning in time method discussed in Section 6.2.
8.1 Free-particle single-level model
The one-electron Hamiltonian for the bridge model is taken in its simplest possible form:
The three individual Hamiltonians of the structure parts, left lead \(\mathcal {H}_{\scriptscriptstyle {0L}}\), island \(\mathcal {H}_{\scriptscriptstyle {0B}}\), and right lead \(\mathcal {H}_{\scriptscriptstyle {0R}}\), are time independent. The couplings between the leads and the island are specified by time independent operator amplitudes \(\mathcal {V}_{\scriptscriptstyle {L,\,R}}\) coupling the leads to the central island orbital. All time dependence in the model is concentrated into two scalar functions \(\alpha _{\scriptscriptstyle {L,\,R}}(t)\) controlling the couplings strength and/or their switch on/off state. For all components of the single-level bridge Hamiltonian, we have the following expressions:
Here, \(|b\rangle \) is the single electron orbital at the island, the decay states \(\{|a\rangle \}\) are further divided between two complementing orthogonal subspaces of the two leads: \(\{|a\rangle \}=\{|\ell \rangle \}\oplus \{|r\rangle \}\), \(\hat{\varepsilon }_\ell \) and \(\hat{\varepsilon }_r\) are the ’bare’ one-electron level in unbiased leads and the level shifts \({\varDelta }_L,\,{\varDelta }_R\), correspond to the independently floating grounding of both leads considered as extended electron reservoirs. Couplings to leads are described by
where the coupling constants \(v_\ell \) and \(v_r\) are introduced.
8.2 NEGF for the island: partitioning in Hilbert space
Now, we formulate NEGF equations of motions for the island dynamics using the partitioning in Hilbert space. We proceed in three steps:
First, we can easily write free-particle NEGF of the whole system:
Here, \(\mathcal {S}\) denotes the one-electron evolution operator. Density matrix
represents a formal solution of the time development of the bridge specified by the one-electron Hamiltonian \(\mathcal {H}(t)\), and by the initial one-electron density matrix \({\varvec{\varrho }}_{\scriptscriptstyle \mathrm{I}}\) (initial OEDM at \(t_{\scriptscriptstyle \mathrm{I}}\)).
Second, we introduce the projection operators
We will than get \(G^\natural \), the NEGF of the island, by the \(\mathcal {P}\) projection of the NEGF (79) of the whole system:
Third, we will project also the equation of motions for the NEGF of the whole system. By this procedure and by shifting the initial time to infinity, \(t_{\scriptscriptstyle \mathrm{I}}\equiv t_{-\infty }\rightarrow -\infty \). we will receive the standard integral forms of NEGF Equation of Motions (EOM)—Dyson equations:
The selfenergies are given (using (74) and (75)) by the following explicit expressions:
\(\diamond \) The whole system is a free-particle system, the island plays a role of an open system. The selfenergy is only the result of the projection, it does not describe any many particle interactions. However, as already pointed out this selfenergy mimicks quite well the presence of real interactions.
\(\diamond \) All components of selfenergy for the free bridge model have the form reflecting the presence of two leads. Each fully connected junction is thus associated with a spectral function \({\varDelta }_{_Y}\), which, together with the quasi-equilibrium Fermi function \(f_{_Y}\), specifies the Y selfenergy triplet.
8.2.1 Possibilities of the model for studies of dynamics, initial conditions
The simplicity of the model offers possibilities to study basic features of non-equilibrium dynamics of open system outside of the steady-state regime. It can be used in two ways:
-
1.
To solve the full NEGF equations to study the response to switching the junctions on and off from very early times after the initial time to long times. For the purpose of studying the correlated initial conditions the Hilbert space partitioning can be combined with the time partitioning method [113, 178, 209]. The island connected suddenly to the leads represents the case of uncorrelated initial conditions, multiple switching of connections between leads and the island creates correlated initial conditions. The details of the extended period dynamics of the model and the discussion of various versions of initial conditions formalisms can be found in [113].
-
2.
To study the range of validity of the Ansatz-based transport theory—in this case, we use the Ansatz to generate approximate transport equations for the bridge model following the scheme already introduced (see the previous section). In the following, we will concentrate on this second task.
8.3 GME for the free bridge model
We will now return to precursor quantum transport equation (PQTE) (65) and will introduce transport equation (GME), based on this equation and the use of causal Ansatzes (66), for the bridge model. Thanks to the simplicity of the model, the structure of PQTE simplifies:
First, for this one level model without interactions, operators entering the PQTE reduce to scalar functions. The Hermitian conjugation then reduces to
In addition, the drift term on the left hand side of the PQTE vanishes, as the commutator in (65) is zero.
Second, the model is not self-consistent, therefore, all parts of the selfenergy (propagators as well as correlation functions) depend only on the properties of leads, not on \(\rho \), see also (130), therefore, are not subject to approximations.
Third, we will limit the discussion only to the simplest possible case of free evolution (relaxation) of the system from the trivial (non-correlated) non-equilibrium state, which is created in a very simple way: the island completely disconnected from the leads up to a finite time \(t_0\) is suddenly connected to both leads simultaneously at the initial time \(t_0\), in correspondence with the Keldysh initial condition.
We obtain the GME for the bridge model by introducing a causal Ansatz into the PQTE and using the simplifications listed above:
This equation is not fully consistent: the propagators entering the forward scattering integrals are \(G^\natural _{\scriptscriptstyle \mathsf{X}}\), as they originate from the Ansatz, while the other two integrals not influenced by the Ansatz contain the true propagators \(G^\natural \). With the exception of the original GKBA, it it necessary to make the additional approximation of replacing the exact \(G^\natural \) by \(G^\natural _{\scriptscriptstyle \mathsf{X}}\) not to violate the spectral identity. The final version of the transport equation results.
Using the symmetries (90), it can further be rewritten in two ways using convenient definitions of \(\mu \) and \(\lambda \):
8.3.1 Reduction of the GME (92) to the Master Equation
Now, we return to the program of Sect. 7.5 and work out the reduction GME \(\rightarrow \) ME, outlined there, for the toy model of this section in more detail. The Master Equation corresponding to the model GME (92) should have the form
with a and c constants to be optimized for an agreement with the GME. This equation coincides with (72) for the special case of one-dimensional \(\mathcal A\) and \(\mathcal C\). The derivation of (72) was limited to GKBA and used the crudest approximation of \(\rho (\overline{t})=\rho (t)\) in the source GME, Eq. (17). Here, we disregard both these limitations.
As the first step, the saturation value of \(\rho \) for \(t\rightarrow +\infty \) will be determined. Setting \(\partial _t\rho =0\) in (93), we get the identity
which is a strict identity for any choice of a and c. The reference value of \(\rho _\infty \)follows from the GME (92) by the same condition \(\partial _t\rho =0\) as
where \(\mathsf X\) refers to the XGKBA Ansatz used and
Since the lower integration limits do in fact not extend beyond several \(\tau ^\star \), we may employ the spectral representation (cf. (89), with all \(\alpha \) set equal to 1)
to Fourier transform the integrals with the result
The solution of the ME (93) has the expected Markovian style; for \(\overline{t}>t\), it has the form
Our task is to extrapolate this solution to the past, introduce it into the GME and adjust the quantities \(a_{\scriptscriptstyle \mathsf{trial}}\) and \(c_{\scriptscriptstyle \mathsf{trial}}\) in an optimized fashion. This anticausal extrapolation into the past is a characteristic feature in justification of time local transport equations. It requires a close attention. We proceed in three steps. The first attempt reproduces the procedure of Sect. 7.5.
The GME reduces to the ME
where
This approximation is suitable in the weak scattering limit,
It is then justified to select the FGKBA employing the free propagators as the underlying Ansatz. The corresponding spectral density is
and the ME becomes
with the FGKBA coefficients (98) and (99) given by
Comparing \({\varSigma }^R\) as given by Eq. (97) and by the explicit partitioning expression quoted in (87), we obtain
so that (107) for \(\breve{a}_{\scriptscriptstyle \mathsf 0}\) means
in parallel with the standard (Pauli) ME.
A less stringent weak scattering requirement applies in the linear approximation for \(\rho (\overline{t})\) in the GME (93):
The resulting ME is
where
\(\breve{a}_{\scriptscriptstyle \mathsf{X}}\) and \(\breve{c}_{\scriptscriptstyle \mathsf{X}}\) are given by (96), while
In the spectral representation we obtain:

It is illuminating to resort once more to FGKBA and set (105) for \(\tilde{A}\). This A spectral density is not broadened, so that the basic features of the renormalized decay rate emerge: the first equation of (112) may be written as
This is reminiscent of the expression for a quasiparticle energy (presently—renormalized resonant island level). There is a substantial difference, however. The selfenergy is doubled at both places, compared with quasiparticles.
Finally, we proceed directly from the ME with unknown coefficients. The master equation corresponding to the model GME (92) should have the form
with coefficients which will be determined by introducing its formal solution (100) for \(\rho (\overline{t})\) into the GME:
Using (96) and setting the self-consistence condition that \(a_{\scriptscriptstyle \mathsf{trial}}\) is a root of the equation
we can rewrite (117) to
The second line equals to zero by (95) and we get
in agreement with the general relation (94). This completes the construction of the optimized Master equation. It remains to solve the integral equation (118) for \(a_{\scriptscriptstyle \mathsf{trial}}\). With writing z for the unknown, the equation may be rearranged to

The integration limits could have been extended to \(\pm \infty \) because of the retarded character of the \(\mu _{\scriptscriptstyle \mathsf{X}}(t)\) function. Instead of the unwieldy integral equation involving \(\mu \), we have to deal with its Fourier transform \(\tilde{\mu }\). The framed equation is formal, however, because \(\tilde{\mu }\) can be continued from the real axis to the upper half plane, whereas our sought root lies at the negative imaginary half-axis. It is necessary to continue \(\tilde{\mu }\) analytically to the unphysical sheet in the lower half plane. This may be facilitated by the existence of \(\tau ^\star \). The \({}_{0}a_{\scriptscriptstyle \mathsf{X}},{}_{0}c_{\scriptscriptstyle \mathsf{X}}\) and \({}_{1}a_{\scriptscriptstyle \mathsf{X}},{}_{1}c_{\scriptscriptstyle \mathsf{X}}\) approximations are seen in this context as the zeroth order and the first order solutions of (121) by Taylor expansion of \(\tilde{\mu }_{\scriptscriptstyle \mathsf{X}}\) around zero of energies.
The GME (92) and the ME (116) are, in the present simplest case, both inhomogeneous equations strictly linear in \(\rho \) and have \(\rho _\infty \) as a particular solution, so that it is possible to write their solution starting from an initial condition \(\rho _{\scriptstyle \mathrm{S}}\) at \(t_{\scriptstyle \mathrm{S}}\) as
The labels J=G, M signify GME, ME and \(\mathbb {G}_{\scriptstyle \mathrm{J}}(t-t')\) denote the standard Greenians of the corresponding homogeneous equations. Their Fourier transforms read, in the complex energy plane,
The Greenian of the Master equation has a simple pole at \(-\mathrm{i}\,a_{\scriptscriptstyle \mathsf{trial}}\), in agreement with Eq. (100). For the GME, it is enough to set \(E=-\mathrm{i}z\) to observe that the pole of its Greenian is given by the above equation (121), that is, its position is also \(-\mathrm{i}\,a_{\scriptscriptstyle \mathsf{trial}}\). The pole residuals are different, however, for both \(\tilde{\mathbb {G}_{\scriptstyle \mathrm{J}}}\), namely for \(\tilde{\mathbb {G}_{\scriptstyle \mathrm{G}}}\) we obtain
The renormalization constant Z may be shown to be real. The resulting asymptotic behavior of the two solutions (122) is thus
This remarkable result offers the following explanation: the solution of the GME represents the true \(\rho \), presently the occupation number \(\rho _{\scriptscriptstyle { \mathrm G}}\) of the island level. The solution of the ME fitted to the GME is missing the renormalization constant Z; its dynamics, on the other hand, is in agreement with the GME. The “\(\rho \)” is the saturation fraction \(\rho _{\scriptscriptstyle { \mathrm M}}\) of the pole, that is to say, the quasiparticle occupation number, if we borrow the terminology from the quantum Boltzmann equation which is known to describe the quasiparticle distribution function.
8.4 Model with Hubbard interaction on the island: Hamiltonian and NEGF
We now add to the above model the Hubbard type interaction to the island, which is thus represented by an Anderson molecule with a local electron-electron interaction and a Hubbard \(U>0\) as a model parameter. The Hamiltonian of this model reads:
The selfenergy has the form
The time-local Hartree–Fock selfenergies,
are determined self-consistently in terms of the full Green’s function, as the occupation numbers \(n_{{\sigma }}\) are spin diagonal elements of the one-particle density matrix \(\rho (t)=-\mathrm{i}G^<(t,t)\) and are thus given by
On the other hand, the selfenergies \(\varSigma _{T\sigma }^{R,A},\varSigma ^<_{\sigma }\) are, in the mean-field approximation, entirely given in terms of the coupling \(\hat{H}^\prime \) between the island and the leads. As before, leads are inert reservoirs and they thus prevent any self-consistence. It is this rigidity of the pre-determined selfenergies which makes the molecular bridge model specific. As \(\hat{H}^\prime (t)=\alpha _L(t)W_L+ \alpha _R(t)W_R\), see Eq. (126), Similarly to the case of free-particle model, each of the selfenergy components \(\varSigma _{\sigma }^{R,A,<}\) can be expressed through the electrode contributions and the full set of selfenergies reads:
Each fully connected junction Y is thus associated with two spectral (tunneling) functions \({\varDelta }_{Y\sigma }\), which, together with the quasi-equilibrium Fermi function \(f_Y\), specify the Y selfenergy triplet. It remains to specify the tunneling functions \({\varDelta }_{Y\sigma }\). we model the tunneling functions by
SDOS, the lead surface density of states, defines the spectral dependence, while \(\lambda \) measures the junction strength.
8.4.1 Specification of the model for calculations
We take the electrodes as symmetrical, so that the shape of both \({\varDelta }\) functions is identical. The whole setup is shown in Fig. 1. It corresponds to \(V_{R,L}=\pm 0.6\;\mathrm{eV}\), the temperature fixed at 300 K, and \(U=0.0\;\mathrm{eV}\). The bias will be kept throughout, while the Coulomb energy will serve as a parameter. The tunneling functions shown are a simplified fit to the ab initio calculations and their sum for each spin orientation gives the selfenergy. The resulting profiles of the stationary one electron spectral densities of the island level can be found from the spectral identity
and they are shown in the central panel of Fig. 1.
8.5 Model with Hubbard interaction: GME
The way from NEGF to a transport equation follows the already introduced procedure and is the same as in the previous case of the free model. The unknowns are the occupation numbers \(n_\uparrow (t),n_\downarrow (t)\). Written conveniently:
This precursor equation can be converted to a closed equation for the occupation numbers by an Ansatz type factorization and selfconsistently for propagators. The decouplings simplify to scalar relations here in comparison with a general case for density matrix.
Sketch of the electronic structure of our bridge model. To the left and to the right, the leads are represented by the respective tunneling functions (up spin in gray color, down spin in green). The leads are given a symmetrical bias V, as given by the shifts of the quasi-Fermi levels \(\mu _{L,\,R}=\pm V/2\) with respect to the bare electron level \(\epsilon _b\) (heavy black central line) of the island center. The tunneling functions float together with \(\mu _{L,\,R}\). The red profiles in the center are the steady-state spectral densities \(\tilde{A}_\sigma (E)\). The parameters are kept at standard values: bias \(V = 1.2\;\mathrm{eV}\), coupling constant \(\lambda = 1\). The Coulomb U used in computations is variable, \(U=0.6\;\mathrm{eV}\) in most calculations, the other values include \(U=0.0\;\mathrm{eV}\) (in this figure) and \(U=1.0\;\mathrm{eV}\)
We will discuss two types of factorization:
\(\diamond \) First, the GKBA
The resulting approximate equation has the form of a true GME:
It consists of just two scalar equations for two unknown \(n_\sigma \).
\(\diamond \) Second, the steady-state corrections, the CGKBA
The resulting corrected GME has a form similar to (135),
The forward scattering term is the same as in (135), the vertex correction formally merges into the back scattering.
The aim will be to compare calculations based on the use of the full set of the NEGF equations with the results obtained from the above transport equations to see not only the advantages but also the limits of the simplified equations used. We will discuss results for the evolution of occupation numbers and magnetic currents. First, the magnetic currents have to be defined.
8.5.1 Lead magnetic currents
We will define magnetic currents through the two junctions as a difference between the currents with opposite spins:
The \(J_{Y\sigma }\) partial currents are formally defined as the rate of loss of the total occupation \(N_{\sigma L},\;N_{\sigma R}\) of the leads. They may be expressed in terms of the island NEGF:
All junction currents are defined to flow into the island. The charges and the spins in the whole system are conserved
This implies the continuity equations for each spin, for the total charge density and the magnetization:
where we introduced the total occupancy n(t) and the spin magnetization m(t),
and defined the magnetic influx \(I^M\), a property of the island center characterizing the magnetic transient: it is the rate of variation of the local magnetization, it is equal to zero in the stationary state and its evolution equations are suitable for the reduction to a quantum transport equation.
8.6 Discussion of GME based on the GKBA and steady-state corrections
First, we will now briefly summarize the results obtained by an exact solution of NEGF as compared with the results provided by the GME based on GKBA and with the criteria of the GKBA validity approach. Second, we will discuss results based on the GME which include the steady-state corrections.
8.6.1 Steady-state asymptotics and criteria for the Ansatz validity
We will now deal with the steady-state model (long time asymptotics, \(t=\rightarrow \infty \)), which provides exact expressions for the studied observables (occupation numbers and magnetic currents) and compare them with the approximate expressions when the GKBA is used. Only the final expressions are given, for their derivation, see [179].
We can bring these two expressions to a comparable form using the Mean value theorem:
where the superscript GKBA denotes the use of the GKBA for the calculation. Written in this form, these expressions give criteria for validity of the Ansatz [179].
A sufficient condition for the Ansatz to be valid is thus the condition that
\(\diamond \) [CON] the tunneling functions \(\tilde{{\varDelta }}_\sigma \) do not vary appreciably within the energy region to which the spectral density \(\tilde{A}_\sigma \) is concentrated.
This can be fulfilled in two complementary ways, so that the condition [CON] splits into two:
\(\diamond \) [CON 1] the tunneling is weak—so that the spectral density has a sharp narrow resonance;
\(\diamond \) [CON 2] the tunneling function is flat (constant in the limit)—this latter case is the well-known wide band limit (WBL).
These two limits favorable for GKBA are of a different nature. In the first case, the tunneling strength, i.e., the magnitude of the tunneling function is decisive, in the other one, it is the energy dependence, i.e., the analytical structure of the tunneling function, which plays the dominant role.
In a similar way, we can obtain corresponding expressions for the magnetic currents:
It suffices to make use of the mean value theorem for integrals to show that the two expressions will nearly coincide once the condition [C] in either form will be fulfilled.
8.6.2 GME based on steady-state corrections
In the region where, according to the above-mentioned conditions, the GKBA-based GME fails to provide a satisfactory description of non-equilibrium observables, we can try to use the corrected Ansatz based on the steady-state corrections of the reconstruction equation, GME (135). This is the case of the standard tunneling function at Fig. 1. However, the corrected steady-state GME (137), which includes at least simple corrections to the GKBA by including partly both vertex corrections of the reconstruction equations, provides good description of the dynamics and it reproduces well the NEGF calculations, for more detail [179,180,181].
When we use the standard tunneling function, see Fig. 1, the conditions CON 1 and CON 2 are not fulfilled and the GKBA-based GME fails to describe longer time non- equilibrium dynamics properly. To reach the range of the validity of the GKBA (to fulfill the conditions) it is enough to modify the tunneling conditions mildly, first, to decrease the tunneling function by reducing the \(\lambda \) factor(to weaken tunneling junctions) in equation (131), and second, to suppress the influence of d-states. The modified tunneling functions, are shown in Fig. 2 in yellow and red colors. These tunneling functions are still far from the true WBL, yet they are sufficient for the GME to work properly.
Comparison of the standard tunneling function (Fig. 1) with a modified one, with d peaks suppressed. The standard tunneling functions shown in dark tone in the background are reduced with an overall \(\lambda = 0.5\) and the suppression coefficient for the d states \(\kappa = 0.2\). Yellow (spin up)\(\,|\,\)red (spin down). Vertical black thin line is the position of chemical potential
8.7 Summary of the molecular bridge dynamics
The broad variability of parameters of the simple molecular model can be used to elucidate general features of dynamics of open systems from its initial transient stage, characterized by the decay of initial correlations, to its kinetic stage in the late period of its dynamics. We can conveniently compare the full NEGF solution of the model dynamics with the simplified description based on the Ansatz-based transport equations and study their validity range.
Based on these studies, it is possible to conclude that we can simplify the full NEGF description following natural changes in dynamics of observables during three different stages of non-equilibrium system evolution:
\(\diamond \) Initial transient dynamics, which starts at a finite initial time by an abrupt or adiabatic change of the boundary condition (switch off or on of the leads). The following fast transient processes from non-equilibrium, generally correlated, initial state can be in most cases only described by the full set of NEGF.
\(\diamond \) Later on, after the decay of initial correlations, the system tends to slower changes, which can be characterized as a kinetic stage. This period of evolution can well be described by a simplified transport theory based on the use of some form of the Ansatz. As we have seen, there are various choices of the Ansatz (how to reconstruct the full correlation function from the OPDM \(\rho \)) and correspondingly of the GME.
\(\diamond \) Finally, the last stage (long time asymptotics) of the non-equilibrium evolution can be captured by equations without memory in its scattering integrals, by Markovian ME. There can be several levels of simplification of the GME to ME, but it is important to point out that the features of the resulting ME depend on the version of the Ansatz used to get the GME.
In this text, we concentrated mainly on the discussion of the use of the Ansatz to derive the GME, but the molecular bridge model permits to study also the role of the correlated initial conditions, including multiple switching processes, where coherence processes play an important role, and the earliest stage of evolution, as documented in [67, 113, 209, 210, 212].
9 Discussion: effective transport theory
In this article, we have summarized the present views on the construction of the quantum transport theory based on the NEGF approach. The paper deals with aspects and open questions which are important on the way to an effective and reliable description of quantum systems evolution from a non-equilibrium initial state at a finite time through fast transient processes to long time steady state asymptotics. While not unique, the Ansatz method, to our opinion, dominates the field.
The NEGF description based on equations of motion for two-time correlation functions is, in general, too complicated to be practicable for most of the far from equilibrium quantum systems and a simplified description is desirable whenever physics allows it. Many research groups have developed computational means to solve either the full NEGF equations of motion, or their simplified versions using variants and extensions of the Ansatz, for ever more complex systems. This very useful approach prevails in contemporary literature, as we have described.
Our emphasis was on the alternative route, which employs the Ansatz technique to transform the Kadanoff–Baym equations into quantum transport equations. This route is also productive, and in addition, it provides valuable insights into the physics of non-equilibrium systems and involved processes, sometimes quite directly, without big computational efforts. A promising progress has also been achieved along this direction of research, concerning both the precision of the approximations involved and the range of applicability of the quantum transport equations of the GME type. This, in fact, stimulated us to prepare this report.
The aim, to create this way a unified transport theory, which uses reliable simplifications for various periods of system evolution, is, however, far from being attained. In conclusion, we list several open issues which may have an important role in the effort to develop an effective transport theory, and which provide hints what need to be further investigated:
9.1 The Ansatz like factorization and transport equations
Various forms of factorization of the correlation functions can be used to get transport equations. We have limited the scope of the article to causal Ansatzes as the means of factorization, since they are more appropriate for truly quantum transport regimes. The quality of resulting equations (the validity range of the Ansatz) then depends on the particular Ansatz used. But there is a broader question, namely this GKBA-related causal approach vs. the anticausal form of factorization associated with the original KBA. The former approach leads to particle description (with equations for the One-particle Density Matrix (OPDM) \(\rho \)), the latter one to the quasiparticle description (with the quasiparticle distribution function). This double language is suited for extended interacting systems. It is less clear what it means for nanoscopic systems with discrete energy levels. We have seen, however, that this dichotomy causal and particle vs. anticausal and quasiparticle emerged quite naturally in deriving the master equation for our test model of a molecular bridge. This is a possible point of departure.
9.2 Various phases of non-equilibrium evolution
For a typical transient process, whether it evolves spontaneously from a prepared initial state, or was initiated by an external perturbation, like in a pump-and-probe experiment, it is customary to distinguish the early period, denoted by Bogolyubov as the decay of correlations, followed by a kinetic stage and finally by the long time relaxed state merging into equilibrium. This time structure takes place, if the system possesses characteristic times, the “collision duration time” \(\tau ^\star \) and the relaxation time \(\tau \), satisfying the condition \(\tau ^\star \ll \tau \). The \(\tau ^\star \) coincides with the time of the “correlations decay”, but its smallness also guarantees the validity of the GME regime throughout the kinetic stage. While the relaxation time has a straightforward relationship to the strength of the interactions or of the coupling to external sources, the definition of \(\tau ^\star \) is somewhat elusive. The interplay between the magnitude and the spectral features of the selfenergy appears to be decisive. That was one of the main points of our analysis of the molecular bridge model and it remains to be another still open problem.
Returning to the task of solving the equation of motions of the transient process, we have to use the full NEGF description for the fast early stage of the transient and there is no simple procedure to link it seamlessly with the GME to be solved in the kinetic stage. This difficulty is better resolved in the approach using the Ansatz to speed up the solution of the Kadanoff–Baym equations, and it poses another open question for the GME technique: to create interpolation schemes, which cover the whole evolution properly and constitute a unified effective transport theory.
9.3 Reconstruction equations and their vertex corrections
The reconstruction equations provide us with the Reconstruction and fluctuation–dissipation theorems, which represent the existence theorems for quantum transport equations. In fact, reconstruction equations (RE) are the only exact statements which incorporate the Ansatz firmly into the NEGF structure. In principle, we could thus use an iteration of the RE to get an improved transport equation. The complexity of the vertex structures makes this not practicable. We can then either limit ourselves to the first term of these equations modified to various causal clones of the GKB Ansatz to construct the transport equations, or we can try to include some approximations of the vertex corrections on the way to transport equations as represented by the quasiparticle Ansatz and the steady-state Ansatz in the main text. Improvements upon such constructions would be the best promise for the future progress. Their reliability can be checked by the degree of their conformity with the related non-equilibrium Ward identities. Further investigations of what RE can offer for the transport theory will be extremely useful.
Notes
We can see from the time arguments of KBA that this Ansatz exhibits anticausal features. This corresponds to the construction of the scattering integrals (completed collisions) in the true Boltzmann equation for a quasiparticle distribution function [65]
The above symbolic forms of the KBA and GKBA seem to be nearly equivalent in an equilibrium state—homogeneous in time. In fact, the relation between the KBA proper and the GKBA is far more complicated. To see it, let us go to the Wigner representation using variables \((\omega ,k,r,t)\). Kadanoff and Baym suggested that the form of the exact equilibrium Green’s function fluctuation–dissipation theorem (FDT), cf. para. 5.3.1 below,
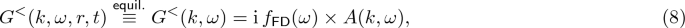
is approximately valid also in near equilibrium situations. In addition they also assumed the quasiparticle behavior of the system and they used the spectral function centered around the quasiparticle energy. Correspondingly, they suggested to use for the derivation of quantum transport equations the couple of the following approximate relations:
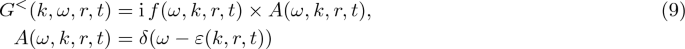
where \( \varepsilon (k,r,t)\) is the quasiparticle energy. This provides the possibility to express the energy argument of f via quasiparticle energy \(\varepsilon (k,r,t)\) and to arrive at the KBA proper:
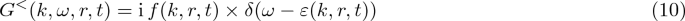
Thus, the KBA is based on the use of the quasiparticle distribution function f, which, in general, is not equal to the single particle density matrix \(\rho \) used in the GKBA. Therefore, in general the KBA and the GKBA do not coincide. They also do not represent exact identities even in equilibrium. For details about the Wigner representation and the differences between the KBA and the GKBA, see [65, 126, 134, 179].
Thus, we leave the idea of anticausal Ansatzes [45, 126, 139] and adopt different approach motivated by the causal structure of NEGF, so we will discuss causal approximations leading to effective transport theories. By this step we will leave aside equations for quasiparticle distribution function. This approach was the original approach designed already by KB, which was, however, limited to the quasiclassical approximation, moderate changes in time and long time asymptotics. We will construct transport equations of the single particle density matrix which covers also fast and abrupt dynamical processes
That may be changed in the future, at least for certain problems, for which a fast algorithm of a direct solution of the KB equations was reported in Ref. [226].
Abbreviations
- GF:
-
Green functions
- NEGF:
-
Non-equilibrium green functions
- OPDM:
-
One-particle density matrix
- FDT:
-
Fluctuation–dissipation theorem
- NE FDT:
-
Non-equilibrium fluctuation–dissipation theorem
- IC:
-
Initial condition
- KB:
-
Kadanoff–Baym
- HF:
-
Hartree–Fock
- KBA:
-
Kadanoff–Baym Ansatz
- GKBA:
-
Generalized Kadanoff–Baym Ansatz
- FGKBA:
-
Free-particle (propagators) generalized Kadanoff–Baym Ansatz
- QGKBA:
-
Quasiparticle (propagators) generalized Kadanoff–Baym Ansatz
- RQGKBA:
-
Renormalized quasiparticle generalized Kadanoff–Baym Ansatz
- XGKBA:
-
Causal Ansatz (GKBA-like) with propagators \(G^R_X\) and \(G^A_X\)
- CGKBA:
-
Corrected generalized Kadanoff–Baym Ansatz
- EOM:
-
Equations of motion
- DE:
-
Dyson equation
- RE:
-
Reconstruction equations
- KBE:
-
Kadanoff–Baym equation
- GKBE:
-
Generalized Kadanoff–Baym equation
- PQKE:
-
Precursor quantum kinetic equation
- PQTE:
-
Precursor quantum transport equation
- QTE:
-
Quantum transport equation
- QKE:
-
Quantum kinetic equation
- QBE:
-
Quantum Boltzmann equation
- GME:
-
Generalized master equation
- ME:
-
Master equation
References
M. Bonitz, Quantum Kinetic Theory (Teubner, Stuttgart, 1998)
M. Bonitz, Quantum Kinetic Theory, (Teubner-Texte zur Physik), 2nd edn. (Springer, New York, 2016)
M. Bonitz, M. Scharnke, N. Schlünzen, Time reversal invariance of quantum kinetic equations II: density matrix formalism. Contrib. Plasma Phys. 58, 1036 (2018)
I. Knezevic, D.K. Ferry, Partial-trace-free time-convolutionless equation of motion for the reduced density matrix. Phys. Rev. E 66, 016131 (2002)
I. Knezevic, D.K. Ferry, Memory effects and nonequlibrium transport in open many-particle systems for the reduced density matrix. Phys. Rev. E 67, 066122 (2003)
I. Knezevic, D.K. Ferry, Quantum transport and memory effects in mesoscopic structures for the reduced density matrix. Phys. E 19, 71 (2003)
I. Knezevic, D.K. Ferry, Open system evolution and memory dressing. Phys. Rev. A 69, 012104 (2004)
D. Joubert (ed.), Density Functionals: Theory and Applications, Lecture Notes in Phys., vol. 500 (Springer, Berlin, 1998)
D.S. Sholl, J.A. Steckel, Density Functional Theory: A Practical Introduction (Wiley, New Jersey, 2009)
E. Runge, E.K.U. Gross, Density-functional theory for time-dependent systems. Phys. Rev. Lett. 52, 997 (1984)
K. Burke, E.K.U. Gross, A guided tour of time-dependent density functional theory, in Density Functionals: Theory and Applications, Lecture Notes in Phys., ed. by D. Joubert vol. 500, p. 116 (Springer, Berlin 1998)
R. Van Leeuwen, Key concepts in time-dependent density-functional theory. Int. J. Mod. Phys. B 15, 1969 (2001)
G. Onida, L. Reining, A. Rubio, Electronic excitations: density-functional versus many-body Green’s functional approaches. Rev. Mod. Phys. 74, 601 (2002)
G. Stefanucci, C.-O. Almbladh, Time-dependent quantum transport: an exact formulation based on TDDFT. Europhys. Lett. 67, 14 (2004)
S. Kurth, G. Stefanucci, C.-O. Almbladh, A. Rubio, E.K.U. Gross, Time-dependent quantum transport: a practical scheme using density functional theory. Phys. Rev. B 72, 035308 (2005)
C. Verdozzi, D. Karlsson, M. Puig von Friesen, C.-O. Almbladh, U. von Barth, Some open questions in TDDFT: clues from lattice models and Kadanoff–Baym dynamics. Chem. Phys. 391, 37 (2011)
C. Ullrich, Time-Dependent Density-Functional Theory: Concepts and Applications (Oxford University Press, Oxford, 2012)
J.K. Freericks, V.M. Turkowski, V. Zlatic, Nonequilibrium dynamical mean-field theory. Phys. Rev. Lett 97, 266408 (2006)
V.M. Turkowski, J.K. Freericks, Spectral moment sum rules for strongly correlated electrons in time-dependent electric fields. Phys. Rev. B 73, 075108 (2006)
O.P. Matveev, A.M. Shvaika, J.K. Freericks, Optical and dc-transport properties of a strongly correlated charge-density-wave system: exact solution in the ordered phase of the spinless Falicov-Kimball model with dynamical mean-field theory. Phys. Rev. B 77, 035102 (2008)
H. Aoki, N. Tsuji, M. Eckstein, M. Kollar, T. Oka, P. Werner, Nonequilibrium dynamical mean-field theory and its applications. Rev. Mod. Phys. 86, 779 (2014)
J.K. Freericks, Transport in Multilayered Nanostructures: The Dynamical Mean-Field Theory Approach, 2nd edn. (Imperial College Press, London, 2016)
H.F. Fotso, J.K. Freericks, Characterizing the non-equilibrium dynamics of field-driven correlated quantum systems. Front. Phys. 8, 324 (2020)
M. Schüler, M. Eckstein, P. Werner, Truncating the memory time in nonequilibrium DMFT calculations. Phys. Rev. B 97, 245129 (2018). arXiv:1804.09576v1
A. Picano, J. Li, M. Eckstein, A quantum Boltzmann equation for strongly correlated electrons (2021). arXiv:2101.09037v1 (cond-mat)
M. Grifoni, P. Hänggi, Driven quantum tunneling. Phys. Rep. 304, 229 (1998)
S. Kohler, J. Lehmann, P. Hänggi, Driven quantum transport on the nanoscale. Phys. Rep. 406, 379 (2005)
N. Tsui, T. Oka, H. Aoki, Correlated electron systems periodically driven out of equilibrium: Floquet+DMFT formalism. Phys. Rev. B 78, 235124 (2008)
T.A. Costi, Renormalization group approach to non-equilibrium Green’s function. Phys. Rev. B 55, 3003 (1997)
M. Keil, H. Schoeller, The real-time renormalization group approach for the spin-boson model in nonequilibrium. Chem. Phys. 268, 11 (2001)
M.A. Cazalila, J.B. Marston, Time-dependent density-matrix renormalization group. Phys. Rev. Lett. 88, 256403 (2002)
A.J. Daley, C. Kollath, U. Schollwöck, G. Vidal, Time-dependent density-matrix renormalization-group using adaptive effective Hilbert spaces. J. Stat. Mech. P04005 (2004)
P. Schmitteckert, Nonequilibrium electron transport using the density matrix renormalization group. Phys. Rev. B 70, 121302 (2004)
S.G. Jakobs, V. Meden, H. Schoeller, Nonequilibrium functional renormalization group for interacting quantum systems. Phys. Rev. B 70, 121302 (2004)
F.B. Anders, Steady-state currents through nanodevices: a scattering states numerical renormalization group approach to open quantum systems. Phys. Rev. Lett. 101, 066804 (2008)
N. Schlünzen, J.P. Joost, F. Heidrich-Meisner, M. Bonitz, Nonequilibrium dynamics in the one dimensional Fermi–Hubbard model: comparison of the nonequilibrium Green-functions approach and the density matrix renormalization group method. Phys. Rev. B 95, 165139 (2017)
E. Gull, A.J. Millis, A.I. Lichtenstein, A.N. Rubtsov, M. Troyer, P. Werner, Continuous-time Monte Carlo methods for quantum impurity models. Rev. Mod. Phys. 83, 349 (2011)
M. Dowling, M.J. Davis, P. Drummond, J. Corney, Monte Carlo techniques for real-time quantum dynamics. J. Comput. Phys. 220, 549 (2020)
J. Schwinger, Quantum electrodynamics III. The electromagnetic properties of the electron-radiative corrections to scattering. Phys. Rev. 76, 796 (1949)
P.C. Martin, J. Schwinger, Theory of many particle systems I. Phys. Rev. 115, 1342 (1959)
J. Schwinger, Brownian motion of a quantum oscillator. J. Math. Phys. 2, 407 (1961)
F. Cooper, Nonequilibrium problems in quantum field theory and Schwinger’s closed time path formalism (1995). arXiv:hep-th/9504073
P.C. Martin, Quantum kinetic equations, in Progress in Non-equilibrium Green’s Functions Bonitz M. (ed.) (World Scientific, Singapore, 2000), p. 2
S.S. Schweber, The sources of Schwinger’s Green’s functions. PNAS 102, 7783 (2005)
L.P. Kadanoff, G. Baym, Quantum Statistical Mechanics (Benjamin, New York, 1962)
G. Baym, Conservation laws and the quantum theory of transport: the early days, in Progress in Non-equilibrium Green’s Functions, ed. by M. Bonitz (World Scientific, Singapore, 2000), p.17
R.E. Prange, L.P. Kadanoff, Transport theory for electron-phonon interactions in metals. Phys. Rev. 134, A566 (1964)
R.E. Prange, A. Sachs, Transport phenomena in the simple metals. Phys. Rev. 158, 672 (1967)
O.V. Konstantinov, V.I. Perel, A diagram technique for evaluating transport quantities. Sov. Phys. JETP 12, 142 (1961)
L.V. Keldysh, Diagram technique for nonequilibrium processes. Sov. Phys. JETP 20, 1018 (1965)
L.V. Keldysh, Real-time nonequilibrium Green’s functions, in Progress in Non-equilibrium Green’s Functions II, ed. by M. Bonitz, D. Semkat (World Scientific, Singapore, 2003), p. 2
V. Korenman, Non-equilibrium quantum statistics: applications to the laser. Ann. Phys. 39, 72 (1966)
R.A. Craig, Perturbation expansion for real time Green’s functions. J. Math. Phys. 9, 605 (1968)
R. Mills, Propagators for Many-particle Systems (Gordon and Branch, New York, 1969)
D.C. Langreth, G. Wilkins, Theory of spin resonance in dilute magnetic alloys. Phys. Rev. B 6, 3189 (1972)
D.C. Langreth, Linear and non-linear response theory with applications, in Linear and Nonlinear Electron Transport in Solids, ed. by J.T. Devreese, E. van Boren (Plenum, New York, 1976)
E.M. Lifshitz, L.P. Pitaevskii, Physical Kinetics, L.D. Landau and E.M. Lifshitz Course of Theoretical Physics, vol. 10 (Pergamon Press, 1981)
K. Chou, Z. Su, B. Hao, L. Yu, Equilibrium and nonequilibrium formalism made unified. Phys. Rep. 118, 1 (1985)
J. Rammer, H. Smith, Quantum field-theoretical methods in transport theory of metals. Rev. Mod. Phys. 58, 323 (1986)
G. Strinati, Application of the Green’s functions method to the study of the optical properties of semiconductors. Riv Il Nuovo Cim 11, 1 (1988)
W. Botermans, R. Malfliet, Quantum transport theory of nuclear matter. Phys. Rep. 198, 115 (1990)
H. Haug, A.P. Jauho, Quantum Kinetics in Transport and Optics of Semiconductors (Springer, Berlin, 1997)
H. Haug, A.P. Jauho, Quantum Kinetics in Transport and Optics of Semiconductors, 2nd edn. (Springer, Berlin, 2008)
D. Kremp, M. Schlanges, W.D. Kraeft, Quantum Statistics of Nonideal Plasmas (Springer, Berlin, 2005)
V. Špička, B. Velický, A. Kalvová, Long and short time dynamics: I. Between Green’s functions and transport equations, II. Kinetic regime, III. Transients. Phys. E 29, 154 (2005). ibid 175, ibid 196
M. Bonitz, D. Semkat (eds.), Introduction to Computational Methods in Many Body Physics (Rinton Press Inc, New Jersey, 2006)
V. Špička, A. Kalvová, B. Velický, Dynamics of mesoscopic systems: non-equilibrium Green’s functions approach. Phys. E 42, 525 (2010)
T. Kita, Introduction to nonequilibrium statistical mechanics with quantum field mechanics. Prog. Theor. Phys. 123, 581 (2010)
A. Kamenev, Field Theory of Non-Equilibrium Systems (Cambridge University Press, Cambridge, 2011)
K. Balzer, M. Bonitz, Nonequilibrium Green’s Functions Approach to Inhomogeneous Systems (Springer, Berlin, 2013)
G. Stefanucci, R. van Leeuwen, Nonequilibrium Many-Body Theory of Quantum Systems: A Modern Introduction (Cambridge University Press, Cambridge, 2013)
V. Špička, B. Velický, A. Kalvová, Electron systems out of equilibrium: nonequilibrium Green’s functions approach. Int. J. Mod. Phys. B 28, 1430013 (2014)
N.J.M. Horing, Quantum Statistical Field Theory: An Introduction to Schwinger’s Variational Method with Green’s Function Nanoapplications, Graphene and Superconductivity (Oxford University Press, Oxford, 2017)
C. Aron, G. Biroli, L.F. Cugliandolo, (Non) equilibrium dynamics: a (broken) symmetry of the Keldysh generating functional. SciPost Phys. 4, 008 (2018)
M.R. Hirsbrunner, T.M. Philip, B. Basa, Y. Kim, M.J. Park, M.J. Gilbert, A review of modeling interacting transient phenomena with non-equilibrium Green functions. Rep. Prog. Phys. 82, 046001 (2019)
M. Bonitz, K. Balzer, N. Schlünzen, M.R. Rasmussen, J-P. Joost, Ion impact induced ultrafast electron dynamics in correlated materials and finite graphene clusters. Phys. Status Solidi B 256, 1800490 (2019). arXiv:1808.07868v1
N. Schlünzen, S. Hermanns, M. Scharnke, M. Bonitz, Ultrafast dynamics of strongly correlated fermions—nonequilibrium green functions and selfenergy approximations. J. Phys. Condens. Matter 32, 103001 (2020)
M. Esposito, M.A. Ochoa, M. Galperin, Quantum thermodynamics: a nonequilibrium Green’s function approach. Phys. Rev. Lett. 114, 080602 (2015)
N. Bergmann, M. Galperin, Green’s functions perspective on nonequilibrium thermodynamics of open quantum systems strongly coupled to baths. arXiv:2004.05175v1 [cond-mat.mes-hall]
W. Dou, J. Batge, A. Levy, M. Thoss, Universal approach to quantum thermodynamics of strongly coupled systems under nonequilibrium conditions and external driving. Phys. B 101, 184304 (2020)
A.L. Fetter, J.D. Walecka, Quantum Theory of Many Particle Systems (McGraw-Hill, New York, 1971)
G.D. Mahan, Many Particle Physics (Plenum Press, New York, 1990)
X.-G. Weng, Quantum Field Theory of Many-Body Systems (Oxford University Press, Oxford, 2004)
H. Bruus, K. Flensberg, Many Body Quantum Theory in Condensed Matter Physics (Oxford Un. Press, Oxford, 2004)
H. Kleinert, Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets, 5th edn. (World Scientific, Singapore, 2009)
E. Fradkin, Field Theories of Condensed Matter Physics, 2nd edn. (Cambridge University Press, Cambridge, 2013)
P. Coleman, Introduction to Many-Body Physics (Cambridge University Press, Cambridge, 2015)
R. Kubo, Statistical-mechanical theory of irreversible processes. I. General theory and simple applications to magnetic and conduction problems. J. Phys. Soc. Jpn. 12, 570 (1957)
R. Kubo, The fluctuation-dissipation theorem. Rep. Prog. Phys. 29, 255 (1966)
R. Kubo, M. Toda, N. Hashitsume, Statistical Physics II, 2nd edn. (Springer, Berlin, 1991)
N.N. Bogolyubov, in Studies in Statistical Mechanics, Vol.1, ed. by G. Uhlenbeck, J. DeBoer (North-Holland, Amsterdam, 1962)
G.V. Chester, The theory of irreversible process. Rep. Prog. Phys. 26, 411 (1963)
R. Balescu, Equilibrium and Nonequilibrium Statistical Mechanics (Wiley, New York, 1975)
A.I. Akhiezer, S.V. Peletminskij, Methods of Statistical Physics (Pergamon, New York, 1980)
P. Hänggi, H. Thomas, Stochastic processes: time evolution, symmetries, and linear response. Phys. Rep. 88, 207 (1982)
R.L. Liboff, Kinetic Theory, Classical, Quantum and Relativistic Descriptions, 3rd edn. (Prentice Hall, London, 1990)
R. Balian, From Microphysics to Macrophysics, vol. II (Springer, Berlin, 1992)
T. Dittrich, P. Hänggi, G.-L. Ingold, B. Kramer, G. Schön, W. Zwerger, Quantum Transport and Dissipation (Wiley-WCH, Weinheim, 1998)
R. Zwanzig, Nonequilibrium Statistical Mechanics (Oxford University Press, New York, 2001)
H.P. Breuer, F. Petruccione, The Theory of Open Quantum Systems (Oxford, New York, 2002)
F. Benatti, R. Floreanini (ed.), Irreversible Quantum Dynamics (Springer, 2003)
C.M. Van Vliet, Equilibrium and Non-equilibrium Statistical Mechanics (World Scientific, Singapore, 2008)
U.M.B. Marconia, A. Puglisi, L. Rondonic, A. Vulpiani, Fluctuation–dissipation: response theory in statistical physics. Phys. Rep. 461, 111 (2008)
M. Di Ventra, Electrical Transport in Nanoscale Systems (Oxford University Press, Oxford, 2008)
Y.V. Nazarov, Y.M. Blunter, Quantum Transport (Cambridge University Press, Cambridge, 2009)
J.C. Cuevas, E. Scheer, Molecular Electronics (World Scientific, Singapore, 2010)
M. Campisi, P. Hänggi, P. Talkner, Colloquium: quantum fluctuation relations: foundations and applications. Rev. Mod. Phys. 83, 771 (2011)
R. Klages, W. Just, C. Jarzynski (eds.), Nonequilibrium Statistical Physics of Small Systems: Fluctuation Relations and Beyond (Wiley-VCH, Weinheim, 2012)
S. Datta, Lessons from Nanoelectronics (World Scientific, Singapore, 2012)
D.K. Ferry, An Introduction to Quantum Transport in Semiconductors (Stanford Publishing, Singapore, 2018)
A.D. Zaikin, D.S. Golubev, Dissipative Quantum Mechanics of Nanostructures (Jenny Stanford Publishing, Singapore, 2019)
C.F. Li, G.C. Guo, J. Piilo, Non-Markovian quantum dynamics: what does it mean? Europhys. Lett. 127, 5001 (2019)
V. Špička, A. Kalvová, B. Velický, Fast dynamics of molecular bridges. Phys. Scr. T 151, 014037 (2012)
J.E. Han, Solution of electric-field-driven tight-binding lattice coupled to fermion reservoirs. Phys. Rev. B 87, 085119 (2013)
L. Del Re, B. Rost, A.F. Kemper, J.K. Freericks, Driven-dissipative quantum mechanics on a lattice: simulating a fermionic reservoir on a quantum computer. Phys. Rev. B 102, 125112 (2020)
D. Manzano, A short introduction to the Lindblad master equation. AIP Adv. 10(2), 025106 (2020). arXiv:1906.04478
P. Talkner, P. Hänggi, Colloquium: statistical mechanics and thermodynamics at strong coupling: quantum and classical. Rev. Mod. Phys. 92, 041002 (2020)
M. Bonitz, R. Nareyka, D. Semkat (eds.), Progress in Nonequilibrium Green’s Functions (World Scientific, Singapore, 2000)
M. Bonitz, D. Semkat (eds.), Progress in Nonequilibrium Green’s Functions II (World Scientific, Singapore, 2003)
M. Bonitz, A. Filinov (eds.), Progress in Nonequilibrium Green’s Functions III. Journal of Physics: Conference Series, vol. 35, no. 1 (2006)
M. Bonitz, K. Balzer (eds.), Progress in Nonequilibrium Green’s Functions IV. Journal of Physics: Conference Series, vol. 220, no. 1, p. 011001 (2010)
R. van Leeuwen, R. Tuovinen, M. Bonitz (eds.), Progress in Nonequilibrium Green’s Functions V. Journal of Physics: Conference Series, vol. 427, no. 1, p. 011001 (2013)
C. Verdozzi, A. Wacker, C.O. Almbladh, M. Bonitz (eds.), Progress in Nonequilibrium Green’s Functions VI. Journal of Physics: Conference Series, vol. 696, no. 1, p. 011001 (2016)
G. Stefanucci, A. Marini, S. Bellucc (eds.), Progress in Nonequilibrium Green’s Functions VII, Phys. Stat. Sol. B7, vol. 256, p. 1900335 (2019)
V. Špička, P. Lipavský, Quasi-particle Boltzmann equation in semiconductors. Phys. Rev. Lett 73, 3439 (1994)
V. Špička, P. Lipavský, Quasi-particle Boltzmann equation in semiconductors. Phys. Rev. B 29, 14615 (1995)
Th Bornath, D. Kremp, W.D. Kraeft, M. Schlanges, Kinetic equations for a nonideal quantum system. Phys. Rev. E 54, 3274 (1996)
D. Kremp, M. Bonitz, W.D. Kraeft, M. Schlanges, Non-Markovian Boltzmann equation. Ann. Phys. 258, 320 (1997)
V. Špička, P. Lipavský, K. Morawetz, Quasi-particle transport equation with collision delay: I. Phenomenological approach. Phys. Rev. B 55, 5084 (1997)
V. Špička, P. Lipavský, K. Morawetz, Quasi-particle transport equation with collision delay: II. Microscopic theory. Phys. Rev. B 55, 5095 (1997)
V. Špička, P. Lipavský, K. Morawetz, Space-time versus particle-hole symmetry in quantum Enskog equations. Phys. Rev. E 64, 046107 (2001)
V. Špička, P. Lipavský, K. Morawetz, Nonlocal corrections to the Boltzmann equation for dense Fermi systems. Phys. Lett. A 240, 160 (1998)
J. Koide, Quantum kinetic equation in the closed-time-path formalism. Phys. Rev. E 62, 5953 (2000)
P. Lipavský, K. Morawetz, V. Špička, Kinetic equation for strongly interacting dense Fermi systems. Ann. Phys. Fr. 26, 1 (2001)
P. Lipavský, V. Špička, B. Velický, Generalized Kadanoff–Baym ansatz for deriving quantum transport equations. Phys. Rev. B 29, 6933 (1986)
H. Chim Tso, N.J.M. Horing, Exact functional differential variant of the generalized Kadanoff–Baym ansatz. Phys. Rev. B 44, 1451 (1991)
M. Bonitz, D. Kremp, D.C. Scott, R. Binder, W.D. Kraeft, H.S. Kohler, Numerical analysis of non-Markovian effects in charge-carrier scattering: one-time versus two-time kinetic equations. J. Phys. Cond. Matter 8, 6057 (1996)
D. Kremp, Th Bornath, M. Bonitz, M. Schlanges, Quantum kinetic theory of plasmas in strong laser fields. Phys. Rev. B 60, 4725 (1999)
P. Lipavský, V. Špička, K. Morawetz, Approximative constructions of the double-time correlation function from the single-time distribution function, in Progress in Non-equilibrium Green’s Functions, ed. by M. Bonitz (World Scientific, Singapore, 2000), p.63
H. Haug, Interband quantum kinetics with LO-phonon scattering in a laser-pulse-excited semiconductor. Phys. Stat. Sol. (b) 173, 139 (1992)
L. Banyai, D.B. Tran Thoai, C. Remling, H. Haug, Interband quantum kinetics with LO-phonon scattering in a laser-pulse-excited semiconductor II. Numerical studies. Phys. Stat. Sol. (b) 173, 149 (1992)
H. Haug, C. Ell, Coulomb quantum kinetics in a dense electron gas. Phys. Rev. B 46, 2126 (1992)
K. El Sayed, S. Schuster, H. Haug, F. Herzel, K. Henneberger, Subpicosecond plasmon response—buildup of screening. Phys. Rev. B 49, 7337 (1994)
L. Banyai, D.B. Tran Thoai, E. Reitsamer, H. Haug, D. Steinbach, M.U. Wehner, M. Wegener, T. Marschner, W. Stolz, Exciton—KLO-phonon quantum kinetics: evidence of memory effects in bulk GaAs. Phys. Rev. Lett. 75, 2188 (1995)
H. Haug, L. Banyai, Improved spectral functions for quantum kinetics. Sol. State Commun. 100, 303 (1996)
P. Gartner, L. Banyai, H. Haug, Two-time electron-LO-phonon quantum kinetics and the generalized Kadanoff–Baym approximation. Phys. Rev. B 60, 14234 (1999)
P. Gartner, L. Banyai, H. Haug, Two-time electron-LO-phonon quantum kinetics and the test of the generalized Kadanoff–Baym relation, in Progress in Non-equilibrium Green’s Functions, ed. by M. Bonitz (World Scientific, Singapore, 2000), p.464
J. Seebeck, T.R. Nielsen, P. Gartner, F. Jahnke, Polarons in semiconductor quantum dots and their role in the quantum kinetics of carrier relaxation. Phys. Rev. B 71, 125327 (2005)
M. Lorke, T.R. Nielsen, J. Seebeck, P. Gartner, F. Jahnke, Quantum kinetic effects in the optical absorption of semiconductor quantum-dot systems. J. Phys. Conf. Series 35, 182 (2006)
M. Bonitz, T. Bornath, D. Kremp, M. Schlanges, W.D. Kraeft, Quantum kinetic theory for laser plasmas. Dynamical screening in strong fields. Contrib. Plasma Phys. 39, 329 (1999)
D. Kremp, T. Bornath, M. Bonitz, Quantum kinetic theory of plasmas in strong laser fields. Phys. Rev. E 60, 4725 (1999)
H. Haberland, M. Bonitz, D. Kremp, Harmonics generation in electron-ion collisions in a short laser pulse. Phys. Rev. E 64, 026405 (2001)
M. Bonitz, S. Hermanns, K. Balzer, Dynamics of Hubbard nano-clusters following strong excitation. Contrib. Plasma Phys. 53, 778 (2013)
K. Balzer, S. Hermanns, M. Bonitz, The generalized Kadanoff–Baym ansatz. Computing nonlinear response properties of finite systems. J. Phys. Conf. Ser. 427, 012006 (2013)
S. Hermanns, K. Balzer, M. Bonitz, Few-particle quantum dynamics comparing nonequilibrium Green functions with the generalized Kadanoff–Baym ansatz to density operator theory. J. Phys. Conf. Ser. 427, 012008 (2013)
N. Schlünzen, J.P. Joost, M. Bonitz, Achieving the scaling limit for nonequilibrium Green functions simulations. Phys. Rev. Lett. 124, 076601 (2020)
J.P. Joost, N. Schlünzen, J.P. Joost, M. Bonitz, G1–G2 scheme: dramatic acceleration of nonequilibrium Green functions simulations within the Hartree–Fock generalized Kadanoff–Baym ansatz. Phys. Rev. B 101, 245101 (2020)
S. Hermanns, K. Balzer, M. Bonitz, The non-equilibrium Green function approach to inhomogeneous quantum many-body systems using the generalized Kadanoff–Baym ansatz. Phys. Scr. T 151, 014036 (2012)
K. Balzer, N. Schlünzen, M. Bonitz, Stopping dynamics of ions passing through correlated honeycomb clusters. Phys. Rev. B 94, 245118 (2016)
K. Balzer, M.R. Rasmussen, N. Schlünzen, J-P. Joost, M. Bonitz, Doublon formation by ions impacting a strongly correlated finite lattice systems. Phys. Rev. Lett. 121, 267602 (2018). arXiv:1801.05267v1
R. Tuovinen, D. Golez, M. Eckstein, M.A. Sentef, Comparing the generalized Kadanoff–Baym ansatz with the full Kadanoff–Baym equations for an excitonic insulator out of equilibrium. Phys. Rev. B 102, 115157 (2020). arXiv:2007.0780 (cond-mat)
F. Cosco, N.W. Talarico, R. Tuovinen, N. Lo Gullo, Spectral properties of correlated quantum wires and carbon nanotubes within the generalized Kadanoff–Baym Ansatz. arXiv:2007.0890 [cond-mat]
D. Karlsson, R. van Leeuwen, Y. Pavlyukh, E. Perfetto, G. Stefanucci, Fast Green’s function method for ultrafast electron-boson dynamics (2021). arXiv:2006.14956 [cond-mat]
N. Kwong, M. Bonitz, R. Binder, H. Köhler, Semiconductor Kadanoff Baym equation results for optically excited electron-hole plasmas in quantum wells. Phys. Status Solidi B 206, 197 (1998)
M.P. von Friesen, C. Verdozzi, C.O. Almbladh, Successes and failures of Kadanoff–Baym dynamics in Hubbard nanoclusters. Phys. Rev. Lett. 103, 176404 (2009)
M. Bonitz, S. Hermanns, K. Balzer, Dynamics of Hubbard nano-clusters following strong excitation. Contrib. Plasma Phys. 53, 778 (2013)
S. Hermanns, N. Schlünzen, M. Bonitz, Hubbard nanoclusters far from equilibrium. Phys. Rev. B 90, 125111 (2014)
S. Latini, E. Perfetto, A.M. Uimonen, R. van Leeuwen, G. Stefanucci, Charge dynamics in molecular junctions: nonequilibrium Green’s function approach made fast. Phys. Rev. B 89, 075306 (2014)
E. Perfetto, A. Uimonen, R. van Leeuwen, S. Stefanucci, First principles nonequilibrium Green’s-function approach to transient photoabsorption: application to atoms. Phys. Rev. A 92, 033419 (2015)
P.M.M.C. de Melo, A. Marini, Unified theory of quantized electrons, phonons, and photons out of equilibrium: a simplified ab initio approach based on the generalized Baym-Kadanoff ansatz. Phys. Rev. B 93, 155102 (2016)
Jun Koide, Perturbative method for the derivation of quantum kinetic theory based on closed-time-path formalism. Phys. Rev. E 65, 026101 (2002)
E. Perfetto, G. Stefanucci, CHEERS: a tool for correlated hole-electron evolution from real time simulation. J. Phys. Cond. Matt. 30, 465901 (2018)
R. Tuovinen, R. van Leeuwen, E. Perfetto, G. Stefanucci, Electronic transport in molecular junctions: the generalized Kadanoff Baym ansatz with initial contact and correlations (2020). arXiv:2012.08247v1
B. Velicky, A. Kalvova, Build-up and decoherence of optical transients in disordered semiconductors. Phys. Stat. Sol. (b) 188, 515 (1995)
B. Velický, A. Kalvová, V. Špička, Between Green’s functions and transport equations: reconstruction theorems and the role of initial conditions. J. Phys. Conf. Ser. 35, 1 (2006)
B. Velický, A. Kalvová, V. Špička, Quasiparticle states of electron systems out of equilibrium. Phys. Rev. B 75, 195125 (2007)
B. Velický, A. Kalvová, V. Špička, Ward identity for nonequilibrium Fermi systems. Phys. Rev. B 77, 041201(R) (2008)
B. Velický, A. Kalvová, V. Špička, Correlated initial condition for an embedded process by time partitioning. Phys. Rev. B 81, 235116 (2010)
V. Špička, B. Velický, A. Kalvová, Non-equilibrium dynamics of open systems and fluctuation-dissipation theorems. Fortschritte der Physik 65, 1700032 (2017)
A. Kalvová, B. Velický, V. Špička, Generalized master equation for a molecular bridge improved by vertex correction to the Generalized Kadanoff–Baym Ansatz. Eur. Phys. Lett 121, 67002 (2018)
A. Kalvová, B. Velický, V. Špička, Beyond the generalized Kadanoff–Baym Ansatz. Phys. Sat. Sol. B 256, 1800594 (2019)
R. Tuovinen, D. Golez, M. Schüler, P. Werner, M. Eckstein, M.A. Sentef, Adiabatic preparation of a correlated symmetry-broken initial state with the generalized Kadanoff–Baym Ansatz. Phys. Stat. Sol. B. 256, 1800469 (2019)
M. Hopjan, C. Verdozzi, Initial correlated states for the generalized Kadanoff–Baym Ansatz without adiabatic switching-on of interactions in closed systems. Eur. Phys. J. Spec. Top. 227, 1939 (2019). arXiv:1808.03520
D. Karlsson, R. van Leeuwen, E. Perfetto, G. Stefanucci, The generalized Kadanoff–Baym Ansatz with initial correlations. Phys. Rev. B. 98, 115–148 (2018). arXiv:1806.05639v1
H. Feshbach, Unified theory of nuclear reactions. Ann. Phys. 5, 357 (1958)
H. Feshbach, Unified theory of nuclear reactions. II. Ann. Phys. 19, 287 (1962)
A. Messiah, Quantum Mechanics Two volumes in One (Dover Publications Inc., Mineola, New York, 2014)
P.O. Löwdin, A note on the quantum-mechanical perturbation theory. J. Chem. Phys. 19, 1396 (1951)
P.O. Löwdin, Studies in perturbation theory. IV. Solution of Eigenvalue problem by projection operator formalism. J. Math. Phys. 3, 969 (1962)
P.O. Löwdin, Studies in perturbation theory: part I. An elementary iteration-variation procedure for solving the Schrödinger equation by partitioning technique. J. Mol. Spectr. 10, 12 (1963)
A.D. Bochevarov, C.D. Sherrill, Some simple results following from Löwdin’s partitioning technique. J. Math. Chem. 42, 59 (2007)
L. Jin, Z. Song, Partitioning technique for discrete quantum systems. Phys. Rev. A 83, 062118 (2011)
Y. Meir, N.S. Wingreen, Landauer formula for the current through an interacting electron region. Phys. Rev. Lett. 68, 2512 (1992)
A.P. Jauho, N.S. Wingreen, Y. Meir, Time-dependent transport in interacting and noninteracting resonant tunneling systems. Phys. Rev. B 50, 5528 (1994)
D.M. Newns, Self-consistent model of hydrogen chemisorption. Phys. Rev. 178, 1123 (1969)
T.B. Grimley, Electronic structure of adsorbed atoms and molecules. J. Vac. Sci. Technol. 8, 31 (1971)
M. Galperin, M.A. Ratner, A. Nitzan, Molecular transport junctions: vibrational effects. J. Phys. Condens. Matter 19, 10 (2007)
N.A. Zimbovskaya, M.K. Pedersen, Electron transport through molecular junctions. Phys. Rep. 509, 1 (2011)
F. Evers, R. Korytar, S. Tewari, J.M. van Ruitenbeek, Advances and challenges in single-molecule electron transport. Rev. Mod. Phys. 92, 035001–2 (2020)
C. Caroli, R. Combescot, P. Nozieres, D. Saint-James, Direct calculation of the tunneling current. J. Phys. C Solid State Phys. 4, 916 (1971)
C. Caroli, R. Combescot, D. Lederer, P. Nozieres, D. Saint-James, A direct calculation of the tunnelling current. II. Free electron description. J. Phys. C Solid State Phys. 4, 2598 (1971)
M. Cini, Time-dependent approach to electron transport through junctions: General theory and simple applications. Phys. Rev. B 22, 5887 (1980)
T.L. Schmidt, P. Werner, L. Mühlbacher, A. Komnik, Transient dynamics of the Anderson impurity model out of equilibrium. Phys. Rev. B 78, 235110 (2008)
D.F. Urban, R. Avriller, A. Levy Yeyati, Nonlinear effects of phonon fluctuations on transport through nanoscale junctions. Phys. Rev. B 82, 121414(R) (2010)
S. Latini, E. Perfetto, A.M. Uimonen, R. van Leeuwen, G. Stefanucci, Charge dynamics in molecular junctions: nonequilibrium Green’s function approach made fast. Phys. Rev. 89, 075306 (2014)
R. Seoane Souto, R. Avriller, R. C. Monreal, A. Martín-Rodero, A. Levy Yeyati, Transient dynamics and waiting time distribution of molecular junctions in the polaronic regime. Phys. Rev. B 92, 125435 (2015)
M. Ridley, A. MacKinnon, L. Kantorovich, Current through a multilead nanojunction in response to an arbitrary time-dependent bias. Phys. Rev. B 91, 125433 (2015)
M.M. Odashima, C.H. Lewenkopf, Time-dependent resonant tunneling transport: Keldysh and Kadanoff–Baym nonequilibrium Green’s functions in an analytically soluble problem. Phys. Rev. B 95, 104301 (2017)
B. Velický, A. Kalvová, V. Špička, Single molecular bridge as a testing ground for using NGF outside of the steady state current regime. Phys. E 42, 539 (2010)
A. Kalvová, V. Špička, B. Velický, Fast transient current response to switching events in short chains of molecular islands. J. Superconduct. Novel Magn. 26, 773 (2013)
A. Kalvová, V. Špička, B. Velický, Transient magnetic tunneling mediated by a molecular bridge in the junction region. EPJ Web Conf. 02004 (2014)
A. Kalvová, V. Špička, B. Velický, Transient magnetic tunneling mediated by a molecular bridge. J. Supercond. Novel Magn. 28, 1087 (2015)
A. Kalvová, B. Velický, V. Špička, Transient magnetic currents through a molecular bridge: limits to reduction of nonequilibrium Green’s functions to a generalized master equation. J. Supercond. Novel Magn. 30, 807 (2017)
G. Cohen, M. Galperin, Green’s function methods for single molecule junctions. J. Chem. Phys. 152, 090901 (2020)
G. Baym, L.P. Kadanoff, Conservation laws and correlation functions. Phys. Rev. 124, 287 (1961)
G. Baym, Self-consistent approximation in many-body systems. Phys. Rev. 127, 1391 (1962)
S. Hermans, N. Schlünzen, M. Bonitz, Hubbard nanoclusters far from equilibrium. Phys. Rev. B 90, 125111 (2014)
N. Schlünzen, M. Bonitz, M. Scharnke, Time reversal invariance of quantum kinetic equations: nonequilibrium Green functions formalism. J. Math. Phys. 58, 061903 (2017)
D. Karlsson, R. van Leeuwen, Partial self-consistency and analyticity in many-body perturbation theory: particle number conservation and a generalized sum rule. Phys. Rev. B 94, 125124 (2016)
M. Revzen, T. Toyoda, Y. Takahashi, F.C. Khanna, Baym–Kadanoff criteria and the Ward–Takahashi relations in many-body theory. Phys. Rev. B 40, 769 (1989)
A. Gonis, Theoretical Materials Science (Materials Research Society, Warrendale, 2000)
P. Gartner, L. Banyai, H. Haug, Coulomb screening in the two time Keldysh–Green-function formalism. Phys. Rev. B 62, 7116 (2000)
R. Ramazashvili, Ward identities for disordered metals and superconductors. Phys. Rev. B 66, 220503(R) (2002)
J. Peralta-Ramos, E. Calzetta, Two-particle irreducible effective action approach to nonlinear current-conserving approximations in driven systems. J. Phys. Condens. Matter 21, 215601 (2009)
A.S. Kondratyev, N. Shahid, Different forms of the Kadanoff–Baym equations in quantum statistical mechanics. Low Temp. Phys. 37, 777 (2011)
J. Kaye, D. Golež, Low rank compression in the numerical solution of the nonequilibrium Dyson equation (2021). arXiv:2010.06511v3 [cond-mat.str-el]
S. Fujita, Resolution of the hierarchy of Green’s functions for fermions. Phys. Rev. A 4, 1114 (1971)
A.G. Hall, Non-equilibrium Green functions: generalized Wick’s theorem and diagrammatic perturbation theory with initial correlations. J. Phys. A 8, 214 (1975)
Yu. A. Kukharenko, S.G. Tikhodeev, Diagram technique in the theory of relaxation processes. Sov. Phys. JETP 56, 831 (1982)
P. Danielewicz, Quantum theory of nonequilibrium processes, I, II. Ann. Phys. (N.Y.) 152, 239 (1984)
M. Wagner, Expansions of nonequilibrium Green’s functions. Phys. Rev. B 44, 6104 (1991)
D. Semkat, D. Kremp, M. Bonitz, Kadanoff–Baym equations with initial correlations. Phys. Rev. E 59, 1557 (1999)
V.G. Morozov, G. Röpke, The “mixed” Green’s function approach to quantum kinetics with initial correlations. Ann. Phys. 278, 127 (1999)
K. Morawetz, M. Bonitz, V.G. Morozov, G. Röpke, D. Kremp, Short-time dynamics with initial correlations. Phys. Rev. E 63, 020102(R) (2001)
D. Semkat, D. Kremp, M. Bonitz, Kadanoff–Baym equations and non-Markovian Boltzmann equation in generalized T-matrix approximation. J. Math. Phys. 41, 7458 (2000)
D. Semkat, M. Bonitz, D. Kremp, Relaxation of a quantum many-body system from a correlated initial state. A general and consistent approach. Contrib. Plasma Phys. 43, 321 (2003)
D. Kremp, D. Semkat, M. Bonitz, Short-time kinetics and initial correlations in quantum kinetic theory. J. Phys. Conf. Ser. 11, 1 (2005)
R. van Leeuwen, G. Stefanucci, Wick theorem for general initial states. Phys. Rev. B 85, 115119 (2012)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Špička, V., Velický, B. & Kalvová, A. Relation between full NEGF, non-Markovian and Markovian transport equations. Eur. Phys. J. Spec. Top. 230, 771–808 (2021). https://doi.org/10.1140/epjs/s11734-021-00109-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1140/epjs/s11734-021-00109-w