A novel study on hybrid model of radiative Cu–$\hbox {Fe}_3\hbox {O}_4$/water nanofluid over a cone with PHF/PWT

Abstract

The fascinating properties of hybrid nanofluid consisting of chemical and mechanical strength, excellent thermal and electrical conductivity, lower cost, high heat transfer rates, and physico-chemical reliability make it a desirable fluid in thermal energy system. Bearing in mind such exhilarating features of hybrid nanofluid, our intention in current research is to examine the heat and flow transfer rates in water-based hybrid nanofluid with suspension of hybrid nanoparticles (Cu–$\hbox {Fe}_{3}\hbox {O}_{4}$) past a vertical cone enclosed in a porous medium. The effects of external magnetic field, thermal radiation, and non-uniform heat source/sink are additional features to the innovation of the constructed mathematical model. The set of nonlinear coupled equations supported by related initial and boundary conditions is executed numerically using finite difference method. In the analysis of coupled distribution, the impact of various controlling parameters on velocity and temperature are scrutinized and the obtained results are exhibited graphically. The physically important quantities such as heat transfer coefficient and wall shear stress are evaluated versus governing constraints. In addition, the heat transfer performance of (Cu–$\hbox {Fe}_{3}\hbox {O}_{4}$)–water hybrid nanofluid is compared with ${\hbox {Fe}_{3}\hbox {O}_{4}}$–water and Cu–water, and their results are summarized in the tables. For both types of nanofluids, solo and hybrid, it is witnessed that the temperature of the system increases in the presence of magnetic field and thermal radiation. Moreover, the velocity of the fluid increases due to high permeability effects. It is also observed that the Nusselt number increases by increasing nanoparticles concentrations in the fluid; however, it decreases in presence of internal heat source. A striking highlight of the executed model is the validation of the findings by comparing them with a content already reported in the literature. In this respect, a venerable coexistence is achieved.

1 Introduction

Convectional heat transfer is one of the most important phenomena in modern technology because of its broad applications in heat exchangers, electronics, cooling and various thermal system. It has wide range of application from simple process of heating and cooling to advanced concept of thermo-dynamical concepts. It has significantly contributed in modern technology. If we talk about industry, 99% manufacturing involves some process of heat transfer in form of combustion, humidifying, electric machinery, etc. In most of the heat transfer applications, different types of fluids are used as a heat carrier, like, power generation, mechanical engineering, air conditioning, micro-electronics, chemical production. On the other hand, thermal conductivity is the cardinal thermophysical property that defines the characteristics of heat transfer in thermal system. But, unfortunately, the most common convectional fluid such as water, kerosene, ethanol, ethylene glycol (EG), etc. do not have sufficient thermal conductivity which limits the efficiency of these heat carrier fluid. Therefore, high performance heat transfer fluid has been the subject of numerous research in recent decades. One of the efficient methods to increase the thermal conductivity is the dispersing of metal particles in convectional heat fluid. Maxwell was the first who predicted the effectively thermal conductivity by dispersion of particles theoretically and his theory was extended from millimeter to micrometer suspension. Thereafter, Choi and Eastman [1] presented the novel concept of nanofluid. Nanofluid is intended to describe a liquid suspended by manometer sized particles which are substantially smaller than 100nm. Nowadays, nanofluids are emerging fluids in nanotechnology. For instant, for direct solar absorption, a plasmonic mixture formed with suspension of three different shapes (rod, star, spherical) of silver nanoparticles in water is experimentally analyzed by Duan et al. [2]. Their results showed that an increment in the temperature of the fluid can be exceeded 17.8 K and 21.5 K on adding 0.01%vol. of star- and rod-shaped nanoparticles, respectively. They also claimed that the disparity between the temperature rise of nanofluid is due to extinction properties. The particles shape affects the extinction properties and therefore the increment level in the temperature is subconsciously influenced by the shape of the particles. For solar energy systems, nanofluids were also integrated for direct solar absorption. Sharafeldin et al. [3] showed that the total efficiency of the solar absorber can be improved by 13.48% using ${\hbox {WO}_{3}}$–water nanofluid for direct absorption. Nazari et al. [4] discussed the thermal efficiency in pulsating heat pipe (PHP) by adding graphene oxide GO in water. They showed that the addition of GO nanosheets to deionized (DI) water can increase the thermal conductivity of DI water by 1.62% and reduce the thermal resistance of PHP by more than 40%. Said et al. [5] conducted an exergy study of flat-plate solar sector using water-based ${\hbox {TiO}_{2}}$ nanofluid with surfactant (polythene glycol) to improve the stability. Their results of showed that the energy efficiency of device could be improved by 76.6% and efficiency of exergy increased by 16.9% on adding 0.1% volume concentration of ${\hbox {TiO}_{2}}$ nanoparticles.

In addition to quality, the most of the issues faced by manufacturing in the production are time and cost reduction. Moghadassi et al. [6] conducted research on free convectional heat transfer by developing a computational fluid dynamics modal of horizontal circular tube, and obtained maximum heat transfer rates for hybrid nanofluid. Moreover, when comparing the ${\hbox {Al}_{2}\hbox {O}_{3}}$–Cu/water with pure water and ${\hbox {Al}_{2}\hbox {O}_{3}}$/water, the average Nusselt number increased by 13.64% and 4.73%, respectively. Esfe et al. [7] measured the thermal conductivity (SWCNT-Mg)–EG exponentially by employing artificial neural networking. The analysis revealed a significantly higher thermal conductivity of hybrid nanofluid than those of SWCNT–EG, MgO–EG nanofluids. Sun et al. [8] experimentally analyzed that the heat transfer coefficient in convectional swirling and impinging jets having Ag-MWCNT/water hybrid nanofluid is better than MWCNT/water nanofluid. They observed that in comparison with DI water, the heat transfer coefficient of Ag-MWCNT/water hybrid nanofluid in swirling and impinging jets increased by 29.37% and 29.45%, respectively. Esfe et al. [9] performed an experiment to evaluate the sensitivity analyzation and artificial neural networking modeling for thermal conductivity of EG–water-based ZNO hybrid nanofluid. They showed that hybrid nanofluid possessed 28% high thermal conductivity than based fluid by suspending 1% volume concentration of nanoparticle at 50$^{\circ }$C. They also claimed that the hybrid nanofluid is much more cost-effective than ZNO and MWCNT nanofluid. Arunkumar et al. [10] performed an experiment to analyze the heat transfer performance of auto-mobile radiation by utilizing two different types of hybrid nanofluid, namely, $\hbox {Al}_{2}\hbox {O}_{3}$–$\mathrm{TiO}_{2}$, $\mathrm{Al}_{2}\mathrm{O}_{3}$–Mg in based fluid (water + 20% EG). They showed that addition of ${\hbox {AlTiO}_{5}}$ and ${\hbox {MGAl}_{2}\hbox {O}_{4}}$ rise the heat transfer efficiency up to 19.8% and 25.24%, respectively, compared with water at volume concentration of 0.12%.

Thermal radiation has significant importance especially in high thermal process, space technology, polymer industry, and control heat transfer process. Ghadikolaei et al. [11] studied magnetohydrodynamic (MHD) flow in micropolar dusty fluid with suspension of $\hbox {Al}_{2}\hbox {O}_{3}$–Cu nanoparticles past a stretching sheet in presence of non-linear thermal radiation. A comparative investigation is performed by Iqbal et al. [12] on the shape effects of nanoparticles in water-based ${\hbox {SiO}_{2}}$ nanofluid and $\hbox {MoS}_{2}$–$\hbox {SiO}_{2}$ hybrid nanofluid in the presence of thermal radiation. They concluded that thermal radiation elevates the temperature distribution. In addition, the blade shape nanoparticles possess high temperature rates for hybrid nanofluid compared with other shapes of nanoparticles (cylindrical, platelets, bricks). Sheikholeslami and Ghasemi [13] studied thermal radiation effects in process of heat transfer solidification of water based CuO nanofluid. They imposed finite element method to study the behavior of physical parameters, and observed that the cold wall is much more effective for higher values of thermal radiation. Also, the average temperature decreases; whereas, the solid fraction increases when radiation parameter increases. Dogonchi et al. [14] analyzed the aspects of thermal radiation in water based ${\hbox {Fe}_{3}\hbox {O}_{4}}$ nanofluid in an annulus by mean of natural convection. They observed an increment in average Nusselt number with respect to nanoparticle concentration and radiation parameter. Khan et al. [15] studied entropy analysis in water-based nanofluid over a moving needle under nonlinear radiation for three types of nanoparticles, namely, ${\hbox {TiO}_{2}}$, Cu, ${\hbox {Al}_{2}\hbox {O}_{3}}$. Alkanhal et al. [16] investigated radiation effects in MHD nanofluid in a wavy shape cavity enclosed square obstacle surrounded by porous medium. Alizadeh et al. [17] studied heat transfer characteristics of micropolar nanofluid through a channel with combined effects of MHD and thermal radiation. Safaei et al. [18] discussed radiative heat transfer in ${\hbox {Al}_{2}\hbox {O}_{3}}$ nanofluid inside shallow cavity using Lattice Boltzmann method. Ghadikolaei et al. [19] analyzed convective heat transfer in Carreau nanofluid over a cone in rotating frame in the presence of thermal radiation. They studied the effects of hybrid nanoparticle (${\hbox {TiO}_{2}}$–Cu) in hybrid base fluid (EG–water) in the presence of magnetic field.

Fig. 1

Thermal conductivity of metals and fluids

Fig. 2

Problem schematic and geometrical coordinates

The current research demonstrates the radiation effects on heat transfer characteristics of Cu–$\hbox {Fe}_{3}\hbox {O}_{4}$/water hybrid nanofluid flow over a vertical cone encapsulated in a porous medium. The flow is executed in the presence of magnetic field and internal heat source/sink. In addition, two different temperature boundary conditions; prescribed heat flux (PHF) and prescribed wall temperature (PWT) are taken into account. The solutions of coupled equations are obtained numerically by implementing a finite difference technique. Moreover, a comparison is made between the thermal performance of ${\hbox {Fe}_{3}\hbox {O}_{4}}$/water, Cu/water, and ${\hbox {Fe}_{3}\hbox {O}_{4}}$/water. The thermal conductivity of the materials and fluid considered are exhibited graphically in Fig. 1. The rest of the paper is designed in the following way. In Sect. 2, a controllable force is incorporated in into the basic hydrodynamic equations that are designed to support active physical properties. The problem solution, accuracy and reliability of numerical method are discussed in Sect. 3. The variational effects of governing parameters on temperature distribution, velocity field, Nusselt number and wall shear stress are depicted with the aid of graphs and tables in Sect. 4. Finally, Sect. 5 summarizes the study accomplishments and provides a way to enhance the efficiency of thermal system by using hybrid nanofluid.

2 Description of problem

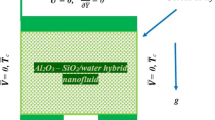
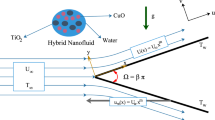
Let us consider an unsteady, mixed convectional flow and heat transfer of hybrid nanofluid past a vertical cone confined in a porous medium. Initially, the fluid is supposed to be at rest with constant temperature $T_\infty$. The physical structure is defined in a way that the x-axis is considered along the surface of the geometry and y-axis is taken normal to the geometry. The radius and half angle of the cone are represented by r and $\alpha$, respectively. An external magnetic field $(0, B_0, 0)$ is implemented in y-direction, as shown in Fig. 2. The flow is influenced by radiative flux $q_\mathrm{{r}}$ and the temperature-dependent heat source/sink ($q''$) effects. The fluid is water-based hybrid nanofluid with dilute suspension of Cu–$\hbox {Fe}_{3}\hbox {O}_{4}$ hybrid nanoparticles whose thermal physical properties are listed in Table 1. In combination of above assumptions together with boundary layer and Boussinesq approximation, the governing equations of proposed model are followed by [20]:

$$\begin{aligned}&(ru)_x+(rv)_y=0, \end{aligned}$$

(2.1)

$$\begin{aligned}&\rho _{hnf}(u_t+uu_x+vu_y)=\mu _{hnf}u_{yy} -\sigma _{hnf}B^2u\nonumber \\&-\mu _{hnf}k_0^{-1}u+g(\rho \beta )_{hnf}(T-T_\infty )\text {cos}\alpha , \end{aligned}$$

(2.2)

$$\begin{aligned}&(\rho C_\mathrm{{p}})_{hnf}(T_t+uT_x+vT_y)=k_{hnf}T_{yy}-(q_\mathrm{{r}})_y+q'',\nonumber \\ \end{aligned}$$

(2.3)

Table 1 Mathematical expressions for thermophysical properties of hybrid nanofluid [20]

subject to the following initial and boundary conditions

$$\begin{aligned} \begin{array}{rcllll} &{}t\le 0: u=0,\quad v=0, T=T_\infty ,\quad \text { for all}\ (x,y), \\ &{}t> 0: u=u_\mathrm{{w}}, \quad v=0,\quad k_{hnf}T_y=-q_\mathrm{{w}} \quad (\text {PHF}), \\ &{} T=T_\mathrm{{w}}=T_\infty +cx^n \quad (\text {PWT}) \text { at}\ y=0,\\ &{}u=0, T=T_\infty \quad \text { at}\ x=0\\ &{} u\rightarrow 0, T \rightarrow T_\infty \quad \text { as}\ y\rightarrow \infty . \end{array} \end{aligned}$$

(2.4)

Table 2 Thermal and mechanical properties of water and nanoparticles [20]

Here, (u, v) are the velocity components in (x, y) direction and T is the temperature of hybrid nanofluid, $q_\mathrm{{w}}$ refers to wall heat flux, g denotes the acceleration due to gravity. $\rho _{hnf}$, $\mu _{hnf}$, $\beta _{hnf}$, $\sigma _{hnf}$, and $(C_\mathrm{{p}})_{hnf}$ represent the density, dynamic viscosity, thermal expansion, electrical conductivity, thermal conductivity, and heat capacitance of hybrid nanofluid, respectively, and their corresponding mathematical expressions are outlined in Table 2. The temperature-dependent heat source/sink ($q''$) is modeled as [21]:

$$\begin{aligned} q''= & {} \dfrac{k_{hnf}\mathrm{{Gr}}^{\frac{1}{5}}}{L^2}\big (A\Delta Te^{-ay}\nonumber \\&+B\Delta T \big (T-T\infty \big )\mathrm{{Gr}}^{\frac{1}{5}}\big ), \end{aligned}$$

(2.5)

where $a=\dfrac{\mathrm{{Gr}}^{\frac{1}{5}}}{L}$ is a constant, $\mathrm{{Gr}}=\dfrac{g\beta \Delta T L^3}{\nu _{f}^2}$ is the Grashof number, L is the reference length of geometry, $V_f$ is the kinematic viscosity of the fluid, and $\varDelta {T}$ represents reference temperature which is equal to $qwL/K_f$ for PHF case and equal to $(T_w - T_{\infty })$ for PWT case. A and B are the space-dependent and temperature-dependent coefficients of heat source/sink, respectively. In view of Rosseland approximation, radiative flux is given by

$$\begin{aligned} q_\mathrm{{r}}=-\frac{4\sigma _\mathrm{{b}}}{3k_\mathrm{{b}}}\frac{\partial T^4}{\partial y}, \end{aligned}$$

(2.6)

where $\sigma _\mathrm{{b}}$ and $k_\mathrm{{b}}$ refer to Stefan–Boltzmann constant and absorption coefficient, respectively. Assuming that the difference between the temperature of hybrid nanofluid T and free stream $T_\infty$ is sufficiently small and expanding $T^4$ using Taylor series, we obtained an approximation by neglecting higher terms as follows

$$\begin{aligned} {T}^4\approx T^4_\infty +4T^3_\infty ({T}-T_\infty ). \end{aligned}$$

(2.7)

Together with this, using Eq. (2.6) in Eq. (2.3), we have

$$\begin{aligned}&(\rho C_\mathrm{{p}})_{hnf}(T_t+uT_x+vT_y)\nonumber \\&\quad =\Big (k_{nf}+\frac{16\sigma _\mathrm{{b}}}{3k_\mathrm{{b}}}T^3_\infty \Big )T_{yy}+q''. \end{aligned}$$

(2.8)

To be able to fully understand the physics of the flow in easy way, we need a nondimensionalized form of our proposed model. For the sake, the following parameters are introduced

$$\begin{aligned}&x^*=\dfrac{x}{L}, \quad y^*=\dfrac{y}{L}(\mathrm{{Gr}})^{\frac{1}{5}},\nonumber \\&r^*=\dfrac{r}{L},\quad t^*=\dfrac{\nu _{f} t}{L^2}(\mathrm{{Gr}})^{\frac{2}{5}}\nonumber \\&u^*=\dfrac{uL}{\nu _{f}}(\mathrm{{Gr}})^{\frac{-2}{5}},\quad v^*=\dfrac{vL}{\nu _{f}}(\mathrm{{Gr}})^{\frac{-1}{5}},\nonumber \\&T^*=\dfrac{(T-T_\infty )}{\Delta T}(\mathrm{{Gr}})^{\frac{1}{5}}, \quad u_\mathrm{{w}}^*=\dfrac{u_\mathrm{{w}}L}{\nu _f}\mathrm{{Gr}}^{\frac{-1}{2}}. \end{aligned}$$

(2.9)

The non-dimensional forms of Eqs. (2.1), (2.2), (2.8) are obtained using the non-dimensional parameters (2.9) together with mathematical expressions for thermophysical properties of hybrid nanofluid as given in Table 2, and given as follows (for the sake of simplicity $*$ is ignored.)

$$\begin{aligned}&\frac{\partial }{\partial x}\big (ru\big )+\frac{\partial }{\partial y}\big (rv\big )=0, \end{aligned}$$

(2.10)

$$\begin{aligned}&\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}\nonumber \\&\quad =\phi _1\bigg (\phi _2\frac{\partial ^2 u}{\partial y^2}-\phi _2Ku-\phi _3Mu+\phi _4T\cos \alpha \bigg ), \end{aligned}$$

(2.11)

$$\begin{aligned}&\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}\nonumber \\&\quad =\frac{\phi _5}{Pr}\bigg (\big (\phi _6+Rd\big )\frac{\partial ^2T}{\partial y^2}+\phi _6\big (Ae^{-y}+BT\big )\bigg ), \end{aligned}$$

(2.12)

where hybrid nanofluid constants $\phi _1-\phi _5$, porosity parameter K, magnetic parameter M, Prandtl number Pr, and radiation parameter Rd are defined as follows:

$$\begin{aligned}&\phi _1=(1-\varphi _{s_2})+\varphi _{s_2} a_1, \quad a_1=\dfrac{\rho _{s_2}}{\rho _{bf}},\nonumber \\&\phi _2=\big [(1-\varphi _{s_1})(1-\varphi _{s_2})\big ]^{-2.5},\quad \phi _3=\dfrac{\sigma _{hnf}}{\sigma _f},\nonumber \\&\phi _4=(1- \varphi _{s_2})+\varphi _{s_2} a_2, \quad a_2=\dfrac{(\rho \beta _T)_{s_2}}{(\rho \beta _T)_{bf}},\nonumber \\&\phi _5=(1- \varphi _{s_2})+\varphi _{s_2} a_3, \quad a_3= \dfrac{(\rho C_\mathrm{{p}})_{s_2}}{(\rho C_\mathrm{{p}})_{bf}},\nonumber \\&\phi _6=\dfrac{k_{hnf}}{k_f}, K=\dfrac{L^2}{k_0}\mathrm{{Gr}}^{\frac{-2}{5}},\quad M=\dfrac{\sigma _f B_0^2L^2}{\mu _f}\mathrm{{Gr}}^{\frac{-2}{5}},\nonumber \\&\text {Pr}=\dfrac{(\mu C_\mathrm{{p}})_f}{k_f}, \mathrm{{Rd}}=\dfrac{16\sigma _\mathrm{{b}}T_\infty ^3}{3k_\mathrm{{b}}k_f}. \end{aligned}$$

(2.13)

The related initial and boundary conditions:

$$\begin{aligned} \begin{array}{rcllll} &{}t\le 0: u=0,\quad v=0, T=0,\quad \text { for all}\ (x,y), \\ &{}t> 0: u=u_\mathrm{{w}},v=0,\quad \phi _6T_y=-x^n \quad (\text {PHF}),\\ &{} T=x^n \quad (\text {PWT})\text { at}\ y=0,\\ &{}u=0, T=0 \quad \text { at}\ x=0,\\ &{}u\rightarrow 0, T \rightarrow 0\quad \text { as}\ y\rightarrow \infty . \end{array} \end{aligned}$$

(2.14)

The physically important quantities: Nusselt number and wall shear stress are defined as follows

$$\begin{aligned} \mathrm{{Nu}}_x=\frac{xq_\mathrm{{w}}}{k_f(T_\mathrm{{w}}-T_\infty )}, \quad \tau _x=\mu _{hnf}\Big (\dfrac{\partial u}{\partial y}\Big )_{y=0},\nonumber \\ \end{aligned}$$

(2.15)

where $q_\mathrm{{w}}=-k_{hnf}\Big (\dfrac{\partial T}{\partial y}\Big )_{y=0}$, is the wall heat flux. The non-dimensional form of above quantities are

$$\begin{aligned}&\mathrm{{Nu}}_x=\dfrac{x^{n+1}}{T_{y=0}} \quad \text {(PHF)},\quad \mathrm{{Nu}}_x=-\phi _6x\Big (\dfrac{\partial T}{\partial y}\Big )_{y=0}\quad \text {(PWT)}, \nonumber \\&\tau _x=\phi _1\Big (\dfrac{\partial u}{\partial y}\Big )_{y=0}. \end{aligned}$$

(2.16)

Fig. 3

Comparison of some limited cases with peer reviewed results

3 Numerical solution

3.1 Solution method

The discrete form of non-dimensional, coupled, nonlinear system of Eqs. (2.10), (2.11), (2.12) assisted by initial boundary conditions (2.14) is attained by employing an implicit finite difference, specifically, Crank Nicolson method. This method was proposed by Crank and Nicolson [22] for solving the heat-type parabolic partial differential equations. It is not only one of the most reliable, convergent and unconditionally stable schemes, but also a second-order accurate in space and time. After discretization, the algebraic difference equations are evaluated using Thomas algorithm with the aid of MATLAB software. The limits of the rectangular domain are $x_\mathrm{{max}}=1$ and $y_\mathrm{{max}}=20$, where $y_\mathrm{{max}}$ refers to $y\rightarrow \infty$. The time level $\Delta t$, mesh sizes ( $\Delta x, \Delta y$) along (x, y) direction are considered as $\Delta t= 0.001$, $\Delta x=0.05$ and $\Delta x=0.05$. After some initial investigation, $y_\mathrm{{max}}$ is selected as 20 which lies very well away from the momentum and thermal boundary layers. The iterations are repeated several times until the solutions at two consecutive time level is met with in the tolerance rate 1$e^{-5}$.

Fig. 4

Variational effects of nanoparticle volume concentration on thermal conductivity of various fluids

Fig. 5

Surface plots for PHF case

3.2 Validation of method

In numerical analysis, validation of the method is an important step which can never be ignored. For this purpose, Fig. 3 is displayed which ensures validation in certain limited cases of existing numerical solution with existing research carried out by Kannan et al. [23] (for PHF case) and Hanif et al. [20] (for PWT case). We found a perfect correlation between the results of peer reviewed literature and the current research. It guarantees the precision of the acquired results in accordance with the numerical approach employed in this analysis.

Fig. 6

Variational effects of $\varphi _{hnf}$ on velocity distribution

Fig. 7

Variational effects of K on velocity distribution

4 Results and discussion

The most crucial step is the stable preparation of solo/hybrid nanofluid for measuring and comparing the performance of convectional heat transfer and fluid flow behavior of hybrid nanofluid. For this purpose, two different solo nanofluid, namely, ${\hbox {Fe}_{3}\hbox {O}_{4}}$–water and Cu–water and one hybrid nanofluid Cu(5%)–${\hbox {Fe}_{3}\hbox {O}_{4}}$–water are considered in this study. The thermal conductivity of solo nanofluid and hybrid nanofluid for various volume concentration of nanoparticles are compared and illustrated via column bars in Fig. 4. In this figure, it is perceived that the thermal conductivity of hybrid nanofluid is found maximum than ${\hbox {Fe}_{3}\hbox {O}_{4}}$–water but less than Cu–water nanofluid. The reason behind such a midst behavior of hybrid nanofluid is the 50:50 vol.% of $\hbox {Cu}$-$\hbox {Fe}_{3}\hbox {O}_{4}$. Overall, the thermal conductivity of fluid is significantly accrued by increasing nanoparticle volume concentration.

Variational effects of governing parameters on temperature and velocity profiles are portrayed and discussed in details. Also, Nusselt number and skin transfer coefficient are computed for PHF and PWT cases. The fixed parameters for numerical computations are taken at $\varphi _{s_1}=\varphi _{s_2}=0.005$, $K=0.5$, $M=1$, $\mathrm{{Rd}}=2$, $A=0.5$, $B=0.5$, $n=0.25$, $\alpha =\pi /4$, and $u_\mathrm{{w}}=0.1$, except where specified. The numerical ranges of parameters considered in figures and tables are: $\varphi _{s_1}=0, 0.005, 0.015, 0.025, 0.035$, $K=0.5, 1, 1.5, 2, 2.5$, $M=0, 1, 3, 5, 7$, $\mathrm{{Rd}}=0, 1, 2, 3, 4$, and $A=B=-0.5, -0.1, 0, 0.1, 0.5$. In Fig. 5, the surface plots for the velocity and temperature of hybrid nanofluid are displayed for PHF case.

Fig. 8

Variational effects of M on velocity distribution

Fig. 9

Variational effects of Rd on velocity distribution

Fig. 10

Variational effects of A and B on velocity distribution

Fig. 11

Velocity contours for Newtonian fluid and hybrid nanofluid when $K=0.5$, $M=3$, $\mathrm{{Rd}}=2$, $A=B=0$, $u_\mathrm{{w}}=0.01$, and $x=1$ a PHF case; b PWT case

Fig. 12

Velocity contours for various values of K when $M=3$, $\mathrm{{Rd}}=2$, $A=B=0$, $u_\mathrm{{w}}=0.01$, and $x=1$ a PHF case; b PWT case

4.1 Velocity profile

This section is designed to discuss the behavior of the velocity field under the effects of pertinent parameters, nanoparticle volume fraction $\varphi _{hnf}=\varphi _{s_1}+\varphi _{s_2}$, porosity parameter K, magnetic parameter M, radiation parameter Rd, and heat source/sink parameters (A, B). Figure 6 explains the pattern of axial velocity for different values of nanoparticle volume concentration $\varphi _{hnf}$ . It is evident from this figure that the velocity decreases on increasing the volume concentration of hybrid nanoparticles. This is partly due to the fact that the fluid becomes more viscous by increasing the volume concentration of nanomaterials inside the fluid. The variational change in the area of fluid flow due to porosity parameter are drawn in Fig. 7. In general, porosity is linked with the permeability of a porous medium. It indicates the ability of medium to allow the passage of the fluid, and an increased porosity enhances the permeability which leads to increased fluid flow. This is evident from Fig. 7, which shows an increase in the velocity profile for growing values of K. Figure 8 demonstrates the behavior of magnetic parameter M on velocity profiles. Through these plots, it is examined that when magnetic effect is elevated, the velocity of the hybrid nanofluid decreases. This is due to strong Lorentz force which is resistant to the motion of fluid and reduces the velocity of the fluid. Figure 9 is drawn to see the variational effects of radiation parameter Rd on velocity profile. The pattern of this figure shows that the velocity of hybrid nanofluid rises up by increasing the thermal radiation effects. The effects of heat source/sink parameters A and B on velocity field are depicted in Fig. 10. This figure shows that the heat source (heat sink) causes an increment (reduction) in buoyant forces which buoyed up (down) the fluid flow rates due to that the velocity field increases (decreases). The velocity contours for Newtonian fluid and hybrid nanofluid are presented in Fig. 11. From these velocity contours, it is perceived that the velocity of the Newtonian fluid is higher than hybrid nanofluid in any case, whether PHF or PWT. Figure 12 displays the contours for different values of porosity parameter K. It is clear from the figure that the momentum of the hybrid nanofluid increases for increasing values of K. This trend is theoretically expected as an improvement in porosity reduces the obstacles in the flow which result an increment in velocity.Another interesting point is that the velocity profile attains higher values for PHF case.

4.2 Temperature profile

In this section, the variations in the temperature of hybrid nanofluid under the effects of active governing parameters are presented through Figs. 13, 14, 15, 16 and 17. A change in the temperature due to nanoparticle volume fraction $\varphi _{hnf}$ is illustrated in Fig. 13. The pattern of this figure shows that the rising estimates of volume concentration of hybrid nanoparticles increases the temperature profile. This is all due to the exaggerated thermal conductivity of hybrid nanofluid which is the main cause of increased temperature. Figure 14 demonstrates the change in the temperature distribution by increasing the numeric values of K. It is evident from the figure that the temperature decreases gradually for higher values of K. The major reason for the temperature depreciation is heat capacitance and thermal conductivity which decline as a result of porosity. In Fig. 15, the behavior of temperature under the magnetic parameter M is portrayed. Through this plot, it is examined that when magnetic effect is elevated, the temperature of hybrid nanofluid increases. This is due to the friction forces in the fluid generated by Lorentz force which ultimately rise the temperature. Figure 16 is drawn to see the variational effects of radiation parameter Rd on temperature profile. It is determined that the higher values of thermal radiation produces more energy, which eventually brings up the fluid’s temperature. In Fig. 17, the variational effects of heat source/sink parameter A and B are examined on the temperature distribution of hybrid nanofluid. Like velocity profile, temperature of hybrid nanofluid reduces when $(A,B)<0$ and gradually increases for $(A,B)>0$. The isotherms of hybrid nanofluid for different values of M are portrayed in Fig. 18 for PHF and PWT case. From these isotherms, it is witnessed that temperature of the fluid increases when magnetic field is applied. This is partly due to the resistive Lorentz force which encourages the friction forces and, in consequence, temperature of the fluid increases. The isotherms for certain values of radiation parameter Rd are drawn in Fig. 19. Like magnetic field, the presence of thermal radiation also rises the temperature of the hybrid nanofluid. In addition, the highest temperature is observed in PHF case.

Fig. 13

Variational effects of $\varphi _{hnf}$ on temperature distribution

Fig. 14

Variational effects of K on temperature distribution

Fig. 15

Variational effects of M on temperature distribution

Fig. 16

Variational effects of Rd on temperature distribution

Fig. 17

Variational effects of A and B on temperature distribution

4.3 Nusselt number and wall shear stress

This section presents the variations in Nusselt number and wall shear stress due to active governing parameters. In addition, The Nusselt number and wall shear stress of hybrid nanofluid are compared with those of nanofluids for certain governing parameters. Figure 20 proved a strong correlation between Nusselt number and volume concentration for solo/hybrid nanoparticles. The heat transfer rates are risen rapidly due to increased volume concentration of nanoparticles. Moreover, the heat transfer rates obtained by hybrid nanofluid are comparatively higher than ${\hbox {Fe}_{3}\hbox {O}_{4}}$–water but less than Cu–water. The highest Nusselt number in Cu–water nanofluid is because of its significant improvement in the thermal conductivity by Cu nanoparticles. On the other hand, the Nusselt number of hybrid nanofluid decreases on increasing the concentration of nanoparticles in presence of heat source, see Fig. 21. The reason behind this behavior is that the convectional heat transfer frequency at every position does not only depend on thermal conductivity but also depends on the temperature gradient. However, the highest Nusselt number is attained by hybrid nanofluid in PHF cases. The solution of another physically important quantity, wall shear stress, for different types of fluid are analyzed under the effects of volume concentration for both PHF and PWT cases. The computed results are presented in tabular form, see Table 3. From the tabulated results, it is perceived that the maximum wall shear stress is possessed by solo nanofluid with ${\hbox {Fe}_{3}\hbox {O}_{4}}$ nanoparticles. When the fluid comes in contact with the surface of the cone, a friction force is applied to it. Such friction force is much more strengthened in contrast with nanoparticles. Due to that friction force, the shear stress decreases. It is noticed that when Cu is added to ferromagnetic nanofluid, the shear stress rate decreases more. In Fig. 22, the effects of porosity parameter on wall shear stress of hybrid nanofluid for PHF and PWT cases are displayed, and an increment can be seen clearly in shear rates due to increased porosity factor. Moreover, the maximum shear stress is observed for PHF case. Variational effects of K on Nusselt number for different fluids are tabulated in Table 4. The results show that the heat transfer coefficient increases due to increased porosity.

Fig. 18

Temperature contours for different values of M when $K=0.5$, $\mathrm{{Rd}}=2$, $A=B=0$, $u_\mathrm{{w}}=0.01$, and $x=1$ a PHF case; b PWT case

Fig. 19

Temperature contours for different values of Rd when $K=0.5$, $M=3$, $A=B=0$, $u_\mathrm{{w}}=0.01$, and $x=1$ a PHF case; b PWT case

In Fig. 23, the variations in wall shear stress are plotted against x for various estimates of magnetic parameter M for PHF and PWT cases. From this figure, it is evident that the shear stress increases as x approaches at maximum value. In addition, fluid shows less friction with wall in PWT case compared to PHF case when x increases. However, shear stress is a decreasing function of M for both cases. The variations in Nusselt number due to M are tabulated in Table 5. Like wall shear stress, the Nusselt number is also depreciated by magnetic effects. The higher Nusselt number is owned by solo nanofluid with Cu particles followed by Cu–$\hbox {Fe}_{3}\hbox {O}_{4}$–water and ${\hbox {Fe}_{3}\hbox {O}_{4}}$–water. The effects of radiation parameter Rd on Nusselt number are illustrated in Fig. 24. The results showed that there is a negative correlation between Nusselt number and radiation parameter. Unlike Nusselt number, the wall shear stress showed a positive relation with Rd, see Table 6. The effects of heat source/sink parameters (A, B) on Nusselt number and wall shear stress are depicted in Figs. 25 and 26, respectively. From these plots, it is evident that Nusselt number decreases for increasing estimates of A and B, whereas a contrary behavior is noticed for wall shear stress.

Fig. 20

Correlation between nanoparticle volume concentration and Nusselt number for PHF case

Fig. 21

Variational effects of $\varphi _{hnf}$ on Nusselt number

5 Concluding remarks

In the current research, the water-based nanofluid containing solo and hybrid nanoparticles over an inverted cone characterized by persuaded magnetic field in a porous medium is expounded numerically. The analysis is accomplished in the presence of radiative heat flux and non-uniform heat source/sink. The set of constitutive equations is supported by PHF and PWT boundary conditions. The key features of the conducted research are:

• For both solo and hybrid nanofluids, the temperature of the fluid escalates with growing estimates of magnetic and radiation parameter.

• Higher heat transfer rates are witnessed for PHF case.

• The velocity of the fluid grows up with permeability effects.

• Nusselt number showed a negative correlation with radiation parameter.

• Wall shear stress is a decreasing and increasing function of the magnetic and porosity parameter, respectively.

Table 3 Variational effects of nanoparticle volume fraction on wall shear stress when $K=0.5$, $M=3$, $\mathrm{{Rd}}=2$, $A=B=0$, $u_\mathrm{{w}}=0.01$, and $x=1$

Fig. 22

Variational effects of K on wall shear stress

Table 4 Variational effects of porosity parameter on Nusselt number when $M=3$, $\mathrm{{Rd}}=2$, $A=B=0$, $u_\mathrm{{w}}=0.01$, and $x=1$

Fig. 23

Variational effects of M on wall shear stress

Table 5 Variational effects of magnetic parameter on Nusselt number when $K=0.5$, $\mathrm{{Rd}}=2$, $A=B=0$, $u_\mathrm{{w}}=0.01$, and $x=1$

Fig. 24

Variational effects of Rd on Nusselt number

Table 6 Variational effects of radiation parameter on wall shear stress when $K=0.5$, $M=3$, $A=B=0$, $u_\mathrm{{w}}=0.01$, and $x=1$

Fig. 25

Variational effects of A and B on wall shear stress

Fig. 26

Variational effects of A and B on wall shear stress

The present article is hoped to serve as an incentive for further hybrid flow models. This research can be used in various industrial processes such as heating and cooling, nuclear reactors, biomedical processes.