1 Introduction

Hybrid nanofluids are very new kind of nanofluids, which can be prepared by suspending (i) different types (two or more than two) of nanoparticles in base fluid, and (ii) hybrid (composite) nanoparticles in base fluid (Adriana 2017). The advantage in heat transfer enhancement of hybrid nanofluid is due to its synergistic effect compared to nanofluid containing one nanoparticle. Turcu et al. (2006) possibly the first who reported the synthesis of hybrid nanocomposite particles including two different hybrids of the polypyrrole-carbon nanotube (PPY-CNT) nano-composite and multi-walled carbon nanotube (MWCNT) on magnetic Fe2O3 nanoparticles. However, the thermal conductivity of hybrid nanofluid such as carbon nanotube-gold nanoparticles (CNT-AuNP) and carbon nanotube-copper nanoparticles (CNT-CuNP) shows lower values as compared to single nanoparticle due to compatibility effect of the nanoparticles (Ny et al. 2016). Within the same year, Turcu et al. (2007) conducted a comprehensive experiment on the physiochemical properties of hybrid nanostructures for biotechnology application. In 2007, Jana et al. (2007) compared thermal conductivity enhancement of single and hybrid nano-additives. Interestingly, the results show that the used CNT-AuNP and CNT-CuNP hybrid nanofluid does not increase the thermal conductivity compared to single nanofluid. After 2 years, in 2009, Jha and Ramaprabhu (2009) performed similar research using hybrid of silver and multi-wall carbon nanotube, while they observed that thermal conductivity increases remarkably compared to the single nanofluids (Sidik et al. 2017). In 2011, Han and Rhi (2011) performed a comparative study on thermal performance of a grooved heat pipe using various nanofluids and hybrid nanofluids as the working fluids. They reported that by increasing the nanoparticle concentration, the thermal resistance increases and deteriorate the performance of heat pipe system. They also concluded that the hybrid nanofluids were not much effective compared with the pure nanoparticle nanofluid system. Nevertheless, a study by Selvakumar and Suresh (2012) found the opposite to be true. They used Al2O3–Cu/water hybrid nanofluid as a heat transfer fluid in an electronic heat sink. Numerical study of the enhancement of heat transfer for Ag/HEG hybrid nanofluid flowing in a circular pipe with constant heat flux was conducted by Zainal et al. (2016). There are many parameters that highly contributed to the heat transfer enhancement of hybrid nanofluid such as base fluid selection, nanoparticles size, viscosity, fluid temperature and stability, dispersibility of the nanoparticles, purity of nanoparticles, preparation method, size and shape of nanoparticles and compatibility of the nanoparticles that leads to harmonious mixture of the nanofluid (Sidik et al. 2016a, b; Li et al. 2009). Among all the parameters, thermal conductivity is the key parameter that contributed immensely to heat transfer enhancement (Sidik et al. 2017). In general, nanofluids can be prepared by two different methods, i.e. single-step and two-step method. In the single-step method, the nanoparticles are synthesized and simultaneously dispersed in the base fluid. Preparation with the single-step process is recommended for the high thermal conductivity of metal nanoparticles in order to avoid oxidation effect. However, this method is unpractical for commercial use due to the small scale in the production of nanofluids, due to the process requires a vacuum, slowing down the rate of production and making it expensive preparation technique. In two-step method, the nanofluids are prepared in two stages. Initially, the nanoparticles are produced in the form of powder. Then, the nanoparticles were dispersed to the base liquid to form a stable solution. The major parameters influencing the nanofluid properties are as follows: the temperature, the particle concentration, the particle size, the shape, the pH and the material properties. Researchers observed that thermal conductivity of nanofluid increases with the concentration and the temperature. However, the techniques employed for particle dispersion with the different surfactant, and the pH also affects the value of thermal conductivity and thermal stability of the nanofluid (Das 2017). In summary, Table 1 presents the comparison of single and hybrid nanofluids.

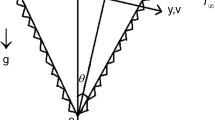
Table 1 Comparison of single and hybrid nanofluids (Jana et al. 2007; Sidik et al. 2016b, 2017; Zainal et al. 2016; Li et al. 2009; Das 2017)
Full size table

The study of a stagnation point flow toward a solid surface in a moving fluid traced back to Hiemenz (1911). He was a pioneer to analyze a two-dimensional stagnation-point flow on a stationary plate by using a similarity transformation to reduce the Navier–Stokes equations to nonlinear ordinary differential equations. Since then many investigators extended the idea to different aspects of the stagnation point flow problems (Khalili et al. 2014; Dinarvand et al. 2014, 2015; Tamim et al. 2014). The general three-dimensional stagnation point flow occurs, for example, when the fluid coming from upstream divides to pass around a finite body in the shape of a wavy cylinder (Fig. 1) (Howarth 1951; Roland 2013). At points A and C (corresponding to the maximum cylinder radius) irrotational flow near the body surface moves away from the stagnation points in all directions. On the other hand at point B (corresponding to the minimum cylinder radius), the surface flow approaches the stagnation point along one direction, but departs along the transverse direction. Points A and C are known as nodal points, but point B is called a saddle point. Both two-dimensional and axisymmetric flows were extended to three dimensional by Howarth (1951). His similarity solution of the boundary layer equations shows clearly the effect of divergence of the main stream flow in thinning the boundary layer. Further, there are appreciable changes in the direction of the velocity vector in passing through the layer at a particular station as a result of secondary flow in the boundary layer. The corresponding flow in the neighborhood of a saddle stagnation point of a body was investigated by Davey (1961). In recent years, Dinarvand et al. have been focused on Howarth’s stagnation point flow of a nanofluid. They studied the unsteady convective heat and mass transfer of a nanofluid in Howarth’s stagnation point by Buongiorno’s model (Dinarvand et al. 2015a; b). Moreover, the steady Howarth’s stagnation point flow of a nanofluid by Tiwari–Das nanofluid model has been investigated by this team (Dinarvand et al. 2013).

Fig. 1
figure 1

Flow toward a circular cylinder that has a sinusoidal radius variation and plan view of streamlines (Howarth 1951)

Full size image

Most phenomena in our world are essentially nonlinear and are described by nonlinear equations. The numerical techniques generally can be applied to nonlinear problems in complicated computation domain; this is an obvious advantage of numerical methods over analytic ones that often handle nonlinear problems in simple domains. However, numerical methods give discontinuous points of a curve and thus it is often costly and time-consuming to get a complete curve of results. Besides, from numerical results, it is hard to have a whole and essential understanding of a nonlinear problem. Numerical difficulties additionally appear if a nonlinear problem contains singularities or has multiple solutions. The numerical and analytic methods of nonlinear problems have their own advantages and limitations, and thus it is unnecessary for us to do one thing and neglect another (Abbasbandy et al. 2015; Nojavana et al. 2018; Dinarvand and Pop 2017; Yang and Liao 2017).

Considering above-mentioned matters, the well-known homotopy analysis method (HAM) as a strong novel analytic technique (Liao 1992, 2003; Yang and Liao 2017; Abbasbandy 2007; Dinarvand et al. 2017) and also a straightforward finite difference code (by Matlab-bvp4c) are considered to investigate the steady three-dimensional stagnation point flow of a hybrid nanofluid past a circular cylinder with sinusoidal radius variation. Hybrid nanofluid is considered by suspending two different nanoparticles (CuO and Ag) in pure water. A comparison with the single nanoparticle nanofluid is provided in the terms of the skin friction and heat transfer rate.

2 Mathematical formulation

2.1 Analytic modeling of hybrid nanofluid

We have considered copper oxide (CuO) and silver (Ag) nano-size particles with water as base fluid. In this model, copper oxide is initially scattered into the base fluid to make nanofluid CuO/water. Therefore, it will be chosen subscript (1) in relations for foregoing nanoparticle. Besides, to develop the targeted hybrid nanofluid CuO–Ag/water, silver is dispersed in CuO/water nanofluid and subscript (2) is applied for it. Now a one-phase model of single-particle nanofluid can be used for CuO–Ag/water, where CuO/water nanofluid has the role of base fluid for this hybridization. However, the idea seems simple, but the methodology can lead to reasonable results for a complex problem. Table 1 shows the applied models for physical properties of the nanofluid (Oztop and Abu-Nada 2008; Khanafer et al. 2003; Brinkman 1952; Wasp 1977; Maxwell 1904) and hybrid nanofluid (Hayat and Nadeem 2017; Ghadikolaei et al. 2017; Nademi Rostami et al. 2018). In this table, \( \phi_{1} \) and \( \phi_{2} \) are the copper oxide and silver nanoparticle volume fractions, respectively, \( \rho_{f} \) is the density of the base fluid as well as \( \rho_{s1} \) and \( \rho_{s2} \) are the densities of the copper oxide and silver nanoparticles, \( \mu_{f} \) is the viscosity of the base fluid, \( k_{f} \), \( k_{s1} \) and \( k_{s2} \) are the thermal conductivity of the base fluid, of the copper oxide and silver nanoparticles, respectively, \( k_{hnf} \) is the effective thermal conductivity of the hybrid nanofluid approximated by the Maxwell–Garnett model [see Oztop and Abu-Nada (2008)]. In Table 2 we can see physical properties of the base fluid and the nanoparticles at 25° C and atmospheric pressure (Nayak et al. 2010; Kamyar et al. 2012). Moreover, in present study, it is assumed that the nanoparticles are in thermal equilibrium and no slip occurs between them.

Table 2 Physical properties
Full size table

2.2 Convective transport equations of a hybrid nanofluid

The plane and axisymmetric stagnation points are very special cases. To introduce a more general way in which a flow meets a body, let us to consider the steady three-dimensional stagnation point flow of an aqueous CuO–Ag/water hybrid nanofluid past a circular cylinder that has a sinusoidal radius variation as shown in Fig. 2. Here, the nanofluid has ambient uniform temperature \( T_{\infty } , \) where the body surface is kept at a constant temperature \( T_{w} \). The analysis of the boundary layer flow in the neighborhood of the nodal stagnation point A is the first target. We introduce a coordinate system with x-axis in the upward direction, y in the longitudinal direction and z normal to the surface, while \( A \) taken as the origin. Flow near \( A \) has velocity components as follows (Howarth 1951).

Fig. 2
figure 2

The problem schematic and coordinate system. Hybrid nanofluid contains copper oxide (CuO, 29–50 nm) and silver (Ag, 2–5 nm) nanoparticles with water as base fluid

Full size image
$$ u_{e} = ax,\,\quad v_{e} = by, $$
(1)

where a and b are constants depending on the free stream velocity and the size and shape of the body. It may be noted that the quantities \( u_{e} \) and \( v_{e} \) do not in themselves satisfy the equation of continuity, but do so after due account is taken of the outflow from the boundary layer. There is no loss of generality in requiring that \( \left| a \right| \ge \left| b \right| \) with \( a\text{ > }0. \) Clearly, \( b = 0 \) corresponds to the plane stagnation flow case, while \( b = a \) is the axisymmetric case. The streamlines in the external flow are given by the equation (Howarth 1951)

$$ x_{e} = \gamma \,y\,^{1/c} , $$
(2)

where

$$ c \equiv b/a, $$
(3)

and \( \gamma \) is a constant that gives a specific streamline. The cases \( \text{0 < }c{ \le 1} \) display nodal stagnation points of attachment, \( c = 0 \) is the plane flow case, and the cases \( \text{-1 < }c{ \le 0} \) display saddle stagnation points of attachment.

Under these assumptions and following the model proposed by Tiwari and Das (2007), the governing equations for the continuity, momentum and energy in laminar incompressible boundary layer flow in a hybrid nanofluid can be written as (Howarth 1951)

$$ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} = 0 $$
(4)
$$ u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} + w\frac{\partial u}{\partial z} = a^{2} x + \nu_{nf} \frac{{\partial^{2} u}}{{\partial z^{2} }} $$
(5)
$$ u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} + w\frac{\partial v}{\partial z} = b^{2} y + \nu_{nf} \frac{{\partial^{2} v}}{{\partial z^{2} }} $$
(6)
$$ u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} + w\frac{\partial T}{\partial z} = \alpha_{nf} \frac{{\partial^{2} T}}{{\partial z^{2} }}. $$
(7)

The corresponding boundary conditions are (Howarth 1951)

$$ \begin{aligned} u = v = 0,\quad \,w = 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,T = T_{w} = {\text{Constant }}\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{at }}\,\,\,\,\,\,\,\,\,\,\,\,\,\,z\, = \,0, \hfill \\ u \to u_{e} ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,v \to v_{e} ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,T \to \,T_{\infty } \, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{as }}\,\,\,\,\,\,\,\,\,\,\,\,\,\,z \to \infty .\,\, \hfill \\ \end{aligned} $$
(8)

In above equations, \( u,\,\,v\,\,{\text{and}}\,\,w \) are the velocity components along \( x,\,\,y\,\,{\text{and}}\,\,z \) axes, respectively, T is the temperature, \( \nu_{hnf} ,\alpha_{hnf} \) are the kinematic viscosity and the thermal diffusivity of the hybrid nanofluid, respectively, which are given by Table 1.

3 Steps of solution procedure

3.1 First step: similarity equations for hybrid nanofluid boundary layer

For steady three-dimensional stagnation point flow past a wavy cylinder, Howarth (1951) has been introduced a dimensionless normal distance \( \eta \) given by

$$ \eta = z(a/\nu_{f} )^{1/2} . $$
(9)

The introduction of the similarity transformations (Howarth Howarth 1951; Dinarvand et al. 2015a; Abbasbandy et al. 2015)

$$ \begin{aligned} u = a\,xf^{\prime} (\eta ),\quad v = byg^{\prime} (\eta ),\quad w = - (av_{f} )^{1/2} (f + cg), \hfill \\ \theta (\eta ) = (T - T\infty )/(T_{w} - T\infty ), \hfill \\ \end{aligned} $$
(10)

reduced Eqs. (4)–(7) to a system of dimensionless non-linear ordinary differential equations

$$ f^{{\prime \prime \prime }} - A_{1} \left[ {f^{{\prime 2}} - f^{{\prime \prime }} (f + cg) - 1} \right] = 0 $$
(11)
$$ g^{{\prime \prime \prime }} - A_{1} \left[ {cg^{{\prime 2}} - c - g^{{\prime \prime }} (f + cg)} \right] = 0 $$
(12)
$$ \left( {\frac{{K_{hnf} }}{{K_{f} }}} \right)\,\,\theta^{\prime\prime} + \Pr \,A_{2} \,\,\,\left( {f + c\,g} \right)\,\,\theta^{\prime} = 0 $$
(13)
$$ \begin{aligned} A_{1} & \, = \,\,\,\left( {1 - \phi_{1} } \right)^{2.5} \left( {1 - \phi_{2} } \right)^{2.5} \left\{ {\left( {1 - \phi_{2} } \right)\,\left[ {\left( {1 - \phi_{1} } \right) + \phi_{1} \left( {\frac{{\rho_{s1} }}{{\rho_{f} }}} \right)} \right] + \phi_{2} \left( {\frac{{\rho_{s2} }}{{\rho_{f} }}} \right)} \right\}\,\,\,\, \\ \,A_{2} & = \,\,\,\left( {1 - \phi_{2} } \right)\left( {\left( {1 - \phi_{1} } \right) + \phi_{1} \left( {\frac{{(\rho C_{p} )_{s1} }}{{(\rho C_{p} )_{f} }}} \right)} \right) + \phi_{2} \left( {\frac{{(\rho C_{p} )_{s2} }}{{(\rho C_{p} )_{f} }}} \right)\,\,. \\ \end{aligned} $$

subject to boundary conditions

$$ f(0) = 0,\quad f\prime (0) = 0,\quad \,f\prime (\infty ) = 1 $$
(14)
$$ g(0) = 0,\quad g\prime (0) = 0,\quad g\prime (\infty ) = 1 $$
(15)
$$ \theta (0) = 1,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\theta (\infty ) = 0, $$
(16)

where the primes denote differentiation with respect to \( \eta , \)\( f\,\,{\text{and}}\,\,g \) are functions related to the velocity field, and \( \theta \) is the dimensionless temperature in the hybrid nanofluid.

Two important physical quantities of present problem are the skin friction coefficients \( C_{fx} \) and \( C_{fy} \), along the \( x\,\,{\text{and}}\,y\, \) directions, respectively, and the local Nusselt number, which are defined as (Dinarvand et al. 2013)

$$ C_{fx} = \frac{{\tau_{wx} }}{{\rho_{f} \,u_{w}^{2} }},\,\quad C_{fy} = \frac{{\tau_{wy} }}{{\rho_{f} \,u_{w}^{2} }},\quad Nu_{x} = \frac{{xq_{w} }}{{k_{f} (T_{w} - T_{\infty } )}}. $$
(17)

In above equations, \( \tau_{wx} \) and \( \tau_{wy} \) are the surface shear stresses along the \( x\,\,{\text{and}}\,y\, \) directions, respectively, and \( q_{w} \) is the surface heat flux, which are given by Dinarvand et al. (2013)

$$ \tau_{wx} = \mu_{hnf} \left( {\frac{\partial u}{\partial z}} \right)_{z = 0} ,\quad \tau_{wy} = \mu_{hnf} \left( {\frac{\partial v}{\partial z}} \right)_{z = 0} ,\quad q_{w} = - k_{hnf} \left( {\frac{\partial T}{\partial z}} \right)_{z = 0} . $$
(18)

Using Eqs. (10) and (18), we obtain

$$ Re_{x}^{\,1/2} C_{fx} = \frac{1}{{(1 - \phi_{1} )^{2.5} (1 - \phi_{2} )^{2.5} }}f^{\prime\prime}(0),\quad Re_{x}^{\,1/2} C_{fy} = \frac{c(y/x)}{{(1 - \phi_{1} )^{2.5} (1 - \phi_{2} )^{2.5} }}g^{\prime\prime}(0),\,\quad Re_{x}^{\, - 1/2} Nu_{x} = - \frac{{k_{hnf} }}{{k_{f} }}\theta^{\prime}(0).\, $$
(19)

3.2 Second step: analytical solution of similarity equations by HAM

The homotopy analysis method (HAM) (Liao 1992, 2003) is rather general and valid for nonlinear ordinary and partial differential equations in many different types. It has been successfully applied to many nonlinear problems of boundary layer flows (Dinarvand and Pop 2017; Dinarvand et al. 2017). According to the standard form of HAM, we choose the initial guesses and auxiliary linear operators as

$$ f_{\text{0}} (\eta ) = \eta - 1 + \exp ( - \eta ),\,\quad g_{\text{0}} (\eta ) = \eta - 1 + \exp ( - \eta ),\quad \theta_{\text{0}} (\eta ) = \exp ( - \eta ) $$
(20)
$$ {\mathcal{L}}_{1} [f] = f^{\prime\prime\prime} - f^{\prime},\,\quad {\mathcal{L}}_{2} [g] = g^{\prime\prime\prime} - g^{\prime},\quad {\mathcal{L}}_{3} [\theta ] = \theta^{\prime\prime} - \theta $$
(21)
$$ {\mathcal{L}}_{1} [c_{1} + c_{2} \exp (\eta ) + c_{3} \exp ( - \eta )] = {\mathcal{L}}_{2} [c_{4} + c_{5} \exp (\eta ) + c_{6} \exp ( - \eta )] = {\mathcal{L}}_{3} [c_{7} \exp (\eta ) + c_{8} \exp ( - \eta )] = 0, $$
(22)

where \( \,\,c_{i} ,\,\,i = 1 - 8,\, \) are constants,\( p \in [0,1] \) denotes the embedding parameter and \( \hbar \) indicate the non-zero auxiliary parameter. Based on Eqs. (4)–(8), we then construct the following zeroth-order deformation problems

$$ \begin{aligned} (1 - p){\mathcal{L}}_{1} \left[ {f(\eta ;\,p) - f_{0} (\eta )} \right] = p\hbar {\mathcal{N}}_{1} \left[ {f(\eta ;\,p),g(\eta ;\,p)} \right] \hfill \\ (1 - p){\mathcal{L}}_{2} \left[ {g(\eta ;\,p) - g_{ 0} (\eta )} \right] = p\hbar {\mathcal{N}}_{2} \left[ {f(\eta ;\,p),g(\eta ;\,p)} \right] \hfill \\ (1 - p){\mathcal{L}}_{3} \left[ {\theta (\eta ;\,p) - \theta_{0} (\eta )} \right] = p\hbar {\mathcal{N}}_{3} \left[ {f(\eta ;\,p),g(\eta ;\,p),\theta (\eta ;\,p)} \right] \hfill \\ \end{aligned} $$
(23)
$$ \begin{aligned} f(0;p) = 0,\,\,\,\,\,\,\,\,\,\,\,f\prime (0;p) = 0,\,\,\,\,\,\,\,\,\,\,\,\,f\prime (\infty ;p) = 1 \hfill \\ g(0;p) = 0,\,\,\,\,\,\,\,\,\,\,g\prime (0;p) = 0,\,\,\,\,\,\,\,\,\,\,\,g\prime (\infty ;p) = 1 \hfill \\ \theta (0;p) = 1,\,\,\,\,\,\,\,\,\,\,\,\theta (\infty ;p) = 0, \hfill \\ \end{aligned} $$
(24)
$$ \begin{aligned} {\mathcal{N}}_{1} \left[ {f(\eta ;\,p),g(\eta ;\,p)} \right] = \frac{{\partial^{3} f(\eta ;\,p)}}{{\partial \eta^{ 3} }} - A_{1} \,\,\left[ {\left( {\frac{\partial f(\eta ;\,p)}{\partial \eta }} \right)^{2} - \frac{{\partial^{2} f(\eta ;\,p)}}{{\partial \eta^{ 2} }}\left( {f(\eta ;\,p) + c\,g(\eta ;\,p)} \right) - 1} \right]\,\, \hfill \\ {\mathcal{N}}_{2} \left[ {f(\eta ;\,p),g(\eta ;\,p)} \right] = \,\frac{{\partial^{3} g(\eta ;\,p)}}{{\partial \eta^{ 3} }} - A_{1} \,\,\,\left[ {c\,\left( {\frac{\partial g(\eta ;\,p)}{\partial \eta }} \right)^{2} - c - \frac{{\partial^{2} g(\eta ;\,p)}}{{\partial \eta^{ 2} }}\left( {f(\eta ;\,p) + cg(\eta ;\,p)} \right)} \right]\,\,\, \hfill \\ {\mathcal{N}}_{3} \left[ {f(\eta ;\,p),\,\,g(\eta ;\,p),\,\,\theta (\eta ;\,p)} \right] = \left( {\frac{{K_{hnf} }}{{K_{f} }}} \right)\,\,\frac{{\partial^{2} \theta (\eta ;\,p)}}{{\partial \eta^{2} }} + Pr\,A_{2} \,\,\,\left( {f(\eta ;\,p) + cg(\eta ;\,p)} \right)\,\,\frac{\partial \theta (\eta ;\,p)}{\partial \eta }. \hfill \\ \end{aligned} $$
(25)

For \( \,p = 0\, \) and \( \,p = 1 \) we have

$$ \begin{aligned} f(\eta ;0) = f_{0} (\eta ),\,\,\,\,\,\,\,\,g(\eta ;0) = g_{\text{0}} (\eta ),\,\,\,\,\,\,\,\,\theta (\eta ;0) = \theta_{0} (\eta ) \hfill \\ f(\eta ;1) = f(\eta ),\,\,\,\,\,\,\,\,g(\eta ;1) = g(\eta ),\,\,\,\,\,\,\,\,\theta (\eta ;1) = \theta (\eta ). \hfill \\ \end{aligned} $$
(26)

Due to Tailor’s series with respect to p, one obtains

$$ \begin{aligned} f(\eta ;\,p) = f_{0} (\eta ) + \sum\limits_{m = 1}^{ + \infty } {\,\,f_{m} (\eta )p^{m} } ,\,\,\,\,\,\,\,\,\,\,\,\,\,as\,\,\,\,\,\,\,\,\,\,\,\,f_{m} (\eta ) = \left. {\frac{1}{m!}\frac{{\partial^{m} f(\eta ;\,p)}}{{\partial p^{m} }}} \right|_{p = 0} \hfill \\ g(\eta ;\,p) = g_{ 0} (\eta ) + \sum\limits_{m = 1}^{ + \infty } {\,\,g_{m} (\eta )p^{m} } ,\,\,\,\,\,\,\,\,\,\,\,as\,\,\,\,\,\,\,\,\,\,\,\,g_{m} (\eta ) = \left. {\frac{1}{m!}\frac{{\partial^{m} g(\eta ;\,p)}}{{\partial p^{m} }}} \right|_{p = 0} \,\,\,\,\,\,\,\,\, \hfill \\ \theta (\eta ;\,p) = \theta_{ 0} (\eta ) + \sum\limits_{m = 1}^{ + \infty } {\,\,\theta_{m} (\eta )p^{m} } ,\,\,\,\,\,\,\,\,\,\,\,\,\,as\,\,\,\,\,\,\,\,\,\,\,\,\theta_{m} (\eta ) = \left. {\frac{1}{m!}\frac{{\partial^{m} \theta (\eta ;\,p)}}{{\partial p^{m} }}} \right|_{p = 0} \,\,. \hfill \\ \end{aligned} $$
(27)

In continuation, mth-order deformation problems could be written as [see Liao (2003)]

$$ \begin{aligned} {\mathcal{L}}_{1} \left[ {f_{m} (\eta ) - \chi_{m} \,\,f_{m - 1} (\eta )} \right] = \hbar R_{m}^{f} (\eta ) \hfill \\ {\mathcal{L}}_{2} \left[ {g_{m} (\eta ) - \chi_{m} \,\,g_{m - 1} (\eta )} \right] = \hbar R_{m}^{g} (\eta ) \hfill \\ {\mathcal{L}}_{3} \left[ {\theta_{m} (\eta ) - \chi_{m} \,\,\theta_{m - 1} (\eta )} \right] = \hbar R_{m}^{\theta } (\eta ), \hfill \\ \end{aligned} $$
(28)
$$ \begin{aligned} f_{m} (0) = 0,\,\,\,\,\,\,\,\,\,\,\,\,\,f_{m}^{\prime } (0) = 0,\,\,\,\,\,\,\,\,\,\,\,\,f_{m}^{\prime } (\infty ) = 0 \hfill \\ g_{m} (0) = 0,\,\,\,\,\,\,\,\,\,\,\,\,\,g_{m}^{\prime } (0) = 0,\,\,\,\,\,\,\,\,\,\,\,\,g_{m}^{\prime } (\infty ) = 0 \hfill \\ \theta_{m} (0) = 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\theta_{m} (\infty ) = 0, \hfill \\ \end{aligned} $$
(29)
$$ \begin{aligned} R_{m}^{f} (\eta ) = f_{m - 1}^{\prime \prime \prime } (\eta ) - A_{1} \,\,\,\left[ {\sum\limits_{n = 0}^{m - 1} {\left[ {f_{n}^{\prime } (\eta )f_{m - 1 - n}^{\prime } (\eta ) - f_{n} (\eta )f_{m - 1 - n}^{\prime \prime } (\eta ) - cg_{n} (\eta )f_{m - 1 - n}^{\prime \prime } (\eta )} \right]} - (1 - \chi_{m} )} \right] \hfill \\ R_{m}^{g} (\eta ) = g_{m - 1}^{\prime \prime \prime } (\eta ) - A_{1} \,\left[ {\sum\limits_{n = 0}^{m - 1} {\left[ {cg_{n}^{\prime } (\eta )g_{m - 1 - n}^{\prime } (\eta ) - f_{n} (\eta )g_{m - 1 - n}^{\prime \prime } (\eta ) - cg_{n} (\eta )g_{m - 1 - n}^{\prime \prime } (\eta )} \right]} - c(1 - \chi_{m} )} \right] \hfill \\ R_{m}^{\theta } (\eta ) = \left( {\frac{{K_{hnf} }}{{K_{f} }}} \right)\,\theta_{m - 1}^{\prime \prime } (\eta ) + Pr\,A_{2} \,\sum\limits_{n = 0}^{m - 1} {\left[ {f_{n} (\eta )\theta_{m - 1 - n}^{\prime } (\eta ) + cg_{n} (\eta )\theta_{m - 1 - n}^{\prime } (\eta )\,} \right],} \hfill \\ \end{aligned} $$
(30)

where

$$ \chi_{m} = \left\{ {_{{1,\,\,\,\,\,\,\,\,\,\,m{ > 1,}}}^{0,\,\,\,\,\,\,\,\,\,m \le 1,} } \right. $$
(31)

and \( \hbar \) is chosen in such a way that these four series are convergent at \( \,p = 1 \), therefore we have through Eqs. (31) and (32) that

$$ f(\eta ) = f_{0} (\eta ) + \sum\limits_{m = 1}^{ + \infty } {\,\,f_{m} (\eta )} ,\quad \,g(\eta ) = g_{ 0} (\eta ) + \sum\limits_{m = 1}^{ + \infty } {\,\,g_{m} (\eta )} ,\,\quad \theta (\eta ) = \theta_{0} (\eta ) + \sum\limits_{m = 1}^{ + \infty } {\,\,\theta_{m} (\eta )} . $$
(32)

In this way, it is easy to solve the linear Eqs. (28)–(31), one after the other in the order \( m = 1,\,\,2,\,\,3,\, \ldots \), especially by means of the symbolic computation software, such as Mathematica, Maple and so on.

The explicit analytic solution given in Eq. (28) contains the auxiliary parameter \( \hbar \) which gives the convergence region and rate of approximation for the HAM solution. Proper values for this auxiliary parameter can be found by plotting the so-called \( \,\hbar {\text{ - curve}} \). Our calculations for the present investigation indicate that the convergent results could be achieved for whole region of \( \eta \) when \( - 0.60 \le \hbar \le - 0.15. \) The reader is referred to Liao (2003) for the detailed discussion regarding the role of auxiliary parameters on the convergence region.

3.3 Third step: numerical solution by finite difference code and validation

The governing Eqs. (11)–(13) subject to the boundary conditions (14)–(16) are solved numerically for some values of the governing parameters \( \phi_{1} , \)\( \phi_{2} , \)c and Pr using the function bvp4c from MATLAB software (see Shampine et al. (Shampine et al. 2003; Kierzenka and Shampine 2001, 2008)). In order to apply the bvp4c routine, we have to rewrite the boundary value problem as systems of first-order ODEs. The function bvp4c is a finite difference code that implements the 3-stage Lobatto IIIa formula. This is a collocation formula and the collocation polynomial gives us a \( C^{1} - \,continuous \) solution, which is fourth order accurate uniformly in the interval where the function is integrated (Roşca et al. 2016; Hu et al. 2015). In this approach, we have chosen a suitable finite value of \( \eta \to \infty \) namely \( \eta = \eta_{\infty } \) between 1.5 and 4.5, where the relative tolerance was set as default (\( 10^{ - 3} \)). Mesh selection and error control are based on the residual of the continuous solution.

To validate our numerical procedure, the value of the dimensionless skin friction coefficients and the local Nusselt number for two special cases, pure water and \( {\text{CuO/water}} \) nanofluid, are shown in Table 3. It is seen that the present results are in good agreement with the solutions obtained by Bhattacharyya and Gupta (1998), Bachok et al. (2010) and Dinarvand et al. (2013) for pure water case.

Table 3 Comparison with results of the previously published studies, when \( Pr = 6.2 \)
Full size table

4 Results and discussion: boundary layers behavior, skin friction coefficient and heat transfer rate

Here, nodal/saddle stagnation-point boundary layer flow and heat transfer of CuO–Ag/water hybrid nanofluid is investigated while; results are shown and compared with both regular Newtonian fluid (water) and single-particle nanofluid (CuO/water) cases. In our study, the value of the cumulative nanoparticle volume fraction \( \phi_{c} \) varies from 0 (regular Newtonian fluid, when \( \phi_{1} = \,\phi_{2} = 0 \)) to 0.2 (for hybrid nanofluid, when \( \phi_{1} = 0.1,\,\,\phi_{2} = 0.1 \)) as pointed out by Oztop and Abu-Nada for single-particle nanofluid (Oztop and Abu-Nada 2008). Moreover, the value of the Prandtl number Pr is equal to 6.2 (for water at atmospheric pressure and 25 °C).

The velocity profile \( f^{\prime}(\eta ) \) for regular fluid \( (\phi_{1} = \phi_{2} = 0), \) nanofluid \( (\phi_{1} = 0.1,\,\,\phi_{2} = 0) \) and hybrid nanofluid \( (\phi_{1} = 0.1,\,\,\phi_{2} = 0.1), \) has been shown in Fig. 3. It is observed that the highest value of \( f^{\prime}(\eta ) \) is related to hybrid nanofluid and the lowest one belongs to regular fluid, for both the nodal and saddle points.

Fig. 3
figure 3

\( f^{\prime}(\eta ) \) for the regular fluid, nanofluid and hybrid nanofluid, when \( Pr = 6.2 \)

Full size image

This means the presence of nanoparticles leads to further thickening of the hydrodynamic boundary layer in the problem conditions. Figure 4 illustrates the velocity profile \( g^{\prime}(\eta ) \) for the regular fluid, nanofluid and hybrid nanofluid, where same trend with the first component of velocity profile \( f^{\prime}(\eta ), \) for both the nodal and saddle points, can be demonstrated. For the regular fluid, nanofluid and hybrid nanofluid, temperature profile \( \theta (\eta ) \) has been shown in Fig. 5. This figure depicts that the lowest temperature occurs when fluid is pure water and the highest one is related to CuO–Ag/water hybrid nanofluid. This is since the hybridity boosts the temperature distribution in the boundary layer. The result also agrees with the physical behavior, when the volume of nanoparticles enhances the thermal conductivity increases, and then the thermal boundary layer thickness increases.

Fig. 4
figure 4

\( g^{\prime}(\eta ) \) for the regular fluid, nanofluid and hybrid nanofluid, when \( Pr = 6.2 \)

Full size image
Fig. 5
figure 5

\( \theta (\eta ) \) for the regular fluid, nanofluid and hybrid nanofluid, when \( Pr = 6.2 \)

Full size image

Here, our focus will be on a nodal point \( (c = 0.5). \) Therefore,\( f^{\prime}(\eta ) \),\( g^{\prime}(\eta ) \) and \( \theta (\eta ) \) have been illustrated, for different values of Ag volume fraction \( (\phi_{2} = 0,\,\,0.05,\,\,0.1) \) and a fixed value of CuO volume fraction \( (\phi_{1} = \,0.1) \) in Fig. 6. Clearly, the velocity profiles and temperature distribution grow as the value of the Ag volume fraction increases. In point of fact, the presence of Ag nanoparticle leads to further thinning of the hydrodynamic boundary layer in hybrid nanofluid flow under the problem conditions. Moreover, the thermal conductivity enhances and consequently the thermal boundary layer thickness grows, as the Ag volume fraction increases. This issue is in compliance with the primary proposes of employing nanofluids (Bachok et al. 2012).

Fig. 6
figure 6

The variation of \( f^{\prime}(\eta ) \),\( g^{\prime}(\eta ) \) and \( \theta (\eta ) \) with \( \phi_{2} \), when \( \phi_{1} = 0.1,\,\,c = 0.5 \) and \( Pr = 6.2 \)

Full size image

The effect of nodal/saddle indicative parameter c on both the first and second components of velocity profile \( f^{\prime}(\eta ) \) and \( g^{\prime}(\eta ) \) has been depicted in Fig. 7. Clearly, velocity components grow with the nodal/saddle indicative parameter \( c, \) however, the positive and negative values of \( c \) have much stronger effect on \( f^{\prime}(\eta ) \) and \( g^{\prime}(\eta ), \) respectively. As a matter of fact, the geometrical effect of the nodal and saddle points on velocities boundary layer behavior can be an acceptable reason on the subject.

Fig. 7
figure 7

The variation of \( f^{\prime}(\eta ) \) and \( g^{\prime}(\eta ) \) with \( c \), when \( \phi_{1} = 0.1 \) and \( Pr = 6.2 \)

Full size image

The skin friction coefficients \( \,\,C_{fx} [Re_{x} ]^{1/2} ,\, \)\( C_{fy} [Re_{x} ]^{1/2} (x/y) \) and the Nusselt number \( [Re_{x} ]^{ - 1/2} Nu_{x} \) versus Ag volume fraction \( \phi_{2} \) have been plotted for a fixed value of CuO volume fraction \( (\phi_{1} = \,0.1) \) in Fig. 8. The results have been presented for both the nodal \( (c = \,0.5) \) and saddle \( (c = \, - 0.5) \) points. Obviously, for both the nodal and saddle points, skin friction coefficients and local Nusselt number grow almost linearly with increasing the Ag volume fraction \( \phi_{2} \). One can observe that the skin friction coefficient in x-direction is larger in comparison to y-direction. However, the geometry of wavy cylinder can justify the matter from a physical point of view. On the increasing trend of the Nusselt number, Ag has the high thermal conductivity (see Table 2) that can increase the effective thermal conductivity of hybrid nanofluid and cause the higher enhancements in heat transfer. However, it is worth to mentioning that the Ag nanoparticles have high values of thermal diffusivity and, therefore, this reduces temperature gradients which will affect the performance of Ag nanoparticles. In spite of this point, when the Ag volume fraction \( \phi_{2} \) is increased from 0 to 0.1, we can see that the Nusselt number grows significantly.

Fig. 8
figure 8

\( \,\,C_{fx} [Re_{x} ]^{1/2} \), \( C_{fy} [Re_{x} ]^{1/2} (x/y) \) and \( [Re_{x} ]^{ - 1/2} Nu_{x} \) versus \( \phi_{2} \), when \( \phi_{1} = 0.1 \) and \( Pr = 6.2 \)

Full size image

Figure 9 shows \( \,\,C_{fx} [Re_{x} ]^{1/2} \) and \( C_{fy} [Re_{x} ]^{1/2} (x/y) \) versus the nodal/saddle indicative parameter \( c \) for the regular fluid, CuO/water nanofluid, and CuO–Ag/water hybrid nanofluid. It is observable that the nodal/saddle indicative parameter \( c \) has a very slow incremental effect on the skin friction coefficient in x-direction, while their influence on the skin friction coefficient in y-direction can be egregious and interesting. Besides, for saddle point area \( {(-}\,{0.5 \le }\,c\text{ 0)} \) and nodal point area \( \text{(0 < }c{ \le 0}\text{.5),} \) the hybrid nanofluid has the lowest and highest values of \( C_{fy} [Re_{x} ]^{1/2} (x/y) \), respectively.

Fig. 9
figure 9

\( \,\,C_{fx} [Re_{x} ]^{1/2} \) and \( C_{fy} [Re_{x} ]^{1/2} (x/y) \) versus \( c \) for the regular fluid, nanofluid and hybrid nanofluid, when \( Pr = 6.2 \)

Full size image

The Nusselt number \( [Re_{x} ]^{ - 1/2} Nu_{x} \) versus the nodal/saddle indicative parameter \( c \) for same cases of regular fluid, CuO/water nanofluid, and CuO–Ag/water hybrid nanofluid has been plotted in Fig. 10. Clearly, the highest local Nusselt number is obtained for the case of CuO–Ag/water hybrid nanofluid. Moreover, the Nusselt number grows almost linearly with increasing the nodal/saddle indicative parameter \( c \) within nodal point area \( \text{(0 < }c{ \le 0}\text{.5).} \)

Fig. 10
figure 10

\( [Re_{x} ]^{ - 1/2} Nu_{x} \) versus \( c \) for the regular fluid, nanofluid and hybrid nanofluid, when \( Pr = 6.2 \)

Full size image

The comparison of the Nusselt number \( [Re_{x} ]^{ - 1/2} Nu_{x} \) for various cases of regular fluid, CuO/water nanofluid and CuO–Ag/water hybrid nanofluid has been presented in Fig. 11. It can be observed that the Nusselt number grows with increasing the volume fraction of CuO and Ag for all cases. Because of the larger thermal conductivity value of Ag (according to Table 4), NF4 has the highest Nusselt number (\( [Re_{x} ]^{ - 1/2} Nu_{x} = 1.62262 \)) between the cases of nanofluids. Besides, it is obvious that the lowest heat transfer rate between the cases of nanofluids is obtained for NF1 (\( [Re_{x} ]^{ - 1/2} Nu_{x} = 1.42932 \)), while HNF3 has the highest heat transfer rate between all cases (\( [Re_{x} ]^{ - 1/2} Nu_{x} = 1.90156 \)). Consequently, we can analytically realize that hybrid nanofluids have higher values of Nusselt number relative to single nanoparticle nanofluids and conventional pure fluids.

Fig. 11
figure 11

\( [Re_{x} ]^{ - 1/2} Nu_{x} \) for various cases of the regular fluid, nanofluid and hybrid nanofluid according to the enclosed list, when \( Pr = 6.2 \) and \( c = 0.5 \)

Full size image
Table 4 Physical properties of nanoparticles and base fluid at 25° C (Nayak et al. 2010; Kamyar et al. 2012)
Full size table

5 Conclusion

Nodal/saddle stagnation-point boundary layer flow and heat transfer of a CuO–Ag/water hybrid nanofluid past a circular cylinder that has a sinusoidal radius variation has been investigated. The dimensional non-linear governing PDEs (mass, momentum and energy conservation) are altered to a set of dimensionless non-linear ODEs with help of similarity transformation method which are then solved analytically by the well-known homotopy analysis method and numerically using bvp4c function from MATLAB. Here, hybrid nanofluid is synthesized by suspending two different nanoparticles copper oxide (CuO 29–50 nm) and silver (Ag 2–5 nm) in pure water. The effects of CuO and Ag nanoparticle volume fractions \( \phi_{1} \) and \( \phi_{2} \) and also the nodal/saddle indicative parameter \( c \) on dimensionless velocities and temperature distribution, skin friction coefficient and local Nusselt number were presented graphically and discussed in details.

Conclusions of the present study can be summarized as follows:

  1. (a)

    The highest value of velocity components is related to the hybrid nanofluid and the lowest one belongs to the regular fluid, for both the nodal and saddle points.

  2. (b)

    The adding of Ag nanoparticle (as second nanoparticle) leads to further thinning of the hydrodynamic boundary layer in hybrid nanofluid flow.

  3. (c)

    The velocity components grow with the nodal/saddle indicative parameter \( c. \)

  4. (d)

    Hybridity boosts the temperature distribution as well as the heat transfer rate at surface. Therefore, the highest Nusselt number is obtained for the case of CuO–Ag/water hybrid nanofluid.

  5. (e)

    For both the nodal and saddle points, skin friction coefficients and local Nusselt number grow almost linearly with increasing the Ag volume fraction \( \phi_{2} \).

  6. (f)

    Hybrid nanofluids can be suggested to improve the thermophysical properties of regular fluid and nanofluid for heat transfer applications but our challenge will be increasing the skin friction simultaneously.

  7. (g)

    The present novel algorithm for analytically modeling of hybrid nanofluids can be used in various problems with great confidence.