Numerical investigation of MHD natural convection in a hexagonal enclosure with heated corrugated cylinder

Abstract

The MHD natural convection with nanofluids has a wide range of applications in engineering, industries, environmental sciences, and material sciences. In this paper, a detailed numerical investigation is carried out for the magnetohydrodynamic (MHD) natural convection of a Newtonian ferrofluid within a hexagonal enclosure containing a heated corrugated cylinder. The parallel (upper and lower) walls of hexagonal enclosure are adiabatic and the other two walls are kept cold, while the inner corrugated cylinder is heated at constant temperature. The physical problem is described by the mathematical model of differential equations by using Boussinesq approximation. The finite element method is employed for the numerical solution of dimensionless system of the differential equations with dimensionless parameters such as the Hartmann number, Rayleigh number, and number of corrugations. We examine the multiple factors, such as the applied magnetic field, ferrofluid properties, and number of corrugations. This study comprehensively explains the distribution of velocity and temperature profile in the presence of magnetic field within the enclosure. The average Nusselt number is investigated with respect to the variations in physical parameters and is treated as a significance of indicated results. Moreover, as the Hartmann number increases, the average Nusselt number significantly decreases within the range of Rayleigh number $({10}^{3}-{10}^{6})$ which shows the interference of the magnetic field. Hereafter, the system exhibits a progressively increasing behavior in heat transfer with an increase in the volume fraction of the ferrofluid. The average Nusselt number demonstrates a 2.59% decline by introducing the Hartman number. Conversely, the presence of nanoparticles leads to a significant increase of 6.12%. However, this increase is suppressed by 3.47% when a magnetic field is introduced against nanoparticles. Additionally, the highest average Nusselt number of 5.3% is observed at eight corrugations, while the lowest value of 3.4% is seen at  “3” corrugations. These results are well matched with the previous results which is the evident of the proposed study and can be implemented for the other complex geometries.

1 Introduction

The optimization of the efficiency of the thermal transport has become a global priority due to the microheat apparatus. The thermal transport in various systems can be improved by dynamic and idle techniques. The dynamic techniques involve the use of external agents such as body forces including suction, injection, electric or magnetic field, which act as mechanical aids to enhance thermal distribution, while the passive approaches focus on modifying material domains, enhancing surface characteristics, and incorporating permeability.

Choi et al. [1] introduced a novel approach to address heat transfer and thermal conductivity, consisting of metallic nanoparticles suspended in conventional fluids. This innovation will enhance heat transfer efficiency and potentially reduce the power required for heat exchangers. Evaluating the thermal performance of conventional coolants and emphasizing the benefits of copper's high thermal conductivity, Leong et al. [2] investigated copper nanofluids as coolants for automobile radiators. Saidur et al. [3] comprehensively analyze solar PV/T systems with loop-pipe and nanofluid, demonstrating their potential to enhance energy output and overcome barriers. Yousafi et al. [4] Scrutinized the implications of ($Al$ ₂ $O$ ₃) nanofluid as a heat-absorbing material in a solar power water heater featuring a flat plate. They discovered the influence of mass flow flux, nanoparticle mass ratio, and surfactant presence on collector efficiency, providing valuable insights into optimizing the system's performance. The numerical assessment of enhancing the effectiveness of heat transmission in a two-dimensional enclosure using nanofluids is studied in [5], and the study also analyzed the implication of the volume fraction on nanofluid heat transfer and compared different nanofluid models based on physical properties.

The basic idea behind the nanofluids is discussed in detail by [6]. The investigation of the buoyancy-driven flow is carried out in a chamber which is partially heated with the incorporation of nanoparticles with different properties by Oztop and Nada in [7]. Mahdavi et al. [8] performed a comprehensive investigation of the dynamical and thermal features of laminar natural convective flow through combined experimental and numerical techniques in a rectangular cavity using different working fluids. Ghasemi et al. [9] examined the features of heat transmission and prospects for enhancing the efficiency of heat dissipation through free convection in an inclined cavity filled with water-$CuO$ nanofluid. The computation of different nanoparticles, and adjustments to their volume fractions could optimize thermal transfer rate in an automotive radiator by Mahmoodi in [10]. The investigation of the convective transport of water in a square geometry with $1\%$ volume percentage of $TiO$ ₂ nanoparticles is presented by Rahmati and Tahery in [11]. The computation of the (${Nu}_{avg}$) number is utilized to observe that the higher amounts of particles in nanofluid optimize the heat transport within the enclosure by Boualit et al. in [12]. The study conducted by Lee [13] covers various Rayleigh numbers within ($10$ ³ $\le Ra \le 10$ ⁶) to investigate the existence of heated tube placed horizontally or diagonally within a cold square enclosure. Kishor et al. [14] executed experimental research to comprehend the convective heat exchanger phenomena occurring in a vertically oriented enclosed cavity with varying temperatures. They employed Mach Zehnder interferometry, a laser-based measurement technique, to analyze and interpret the data obtained from their study. The factors that can optimize the thermal conductivity of liquids revealed the thermal dissipation enhancement altered by the scale outline of the particles and arrangement of particles introduced by Keblinski et al. in [15]. Experimental validation of the $25 nm$ $SiO$ ₂ particles was performed to accumulate the influences modifications in elevated thermal transport efficiency in [16].

The influence of microparticles $(\phi )$ and heat source position on natural convection has been investigated by applying the $Al$ ₂ $O$ ₃ particles to the base fluid by Tinnaluri and Devanuri in [17]. Sajjadi et al. [18] examined thermal buoyancy-driven convection in a permeable enclosure with a oscillating temperature pattern using a novel double multi-relaxation time (MRT) lattice Boltzmann method (LBM), focusing on a copper/water nanofluid within the cavity. Mehryan et al. [19] studied the natural convection of Ag-MgO hybrid/water nanofluid in a permeable chamber using the LTNE model. The Darcy model and GFEM method were utilized to analyze and solve the flow dynamics.

The effects of the magnetic field and the concentration of nanoparticles on the flow and heat transfer properties are discussed inside the enclosure and conclude that a higher concentration of the nanoparticles improved the rate of heat transmission, while the rate of heat transmission was reduced as a result of applying a magnetic field by Seyyedi et al. in [20]. Comprehensive investigations were conducted on hybrid nanofluids ($Au-Ag$/blood and $Cu-Fe$ ₃ $O$ ₄/blood) between rotating disks in [21], while Raza et al. formed a mathematical model to study the impact of nanolayers on fluid flow across a permeable surface using a SWCNT-nanoparticle in an expanding and contracting conduit [22]. Maneengam et al. executed a numerical simulation on thermal transfer in a lid-driven chamber using a 4% $Al$ ₂ $O$ ₃-$Cu$ nanoparticle-based hybrid nanofluid, considering various influential factors [23]. Kasaeian et al. [24] (Fig. 1) reviewed solar cavity receivers for dish concentrators, optimizing their performance for solar thermal power plants. Hamad et al. [25] highlighted the importance of fluid motion and thermal transport in rotor–stator systems for applications like wind generators. Cai et al. [26] analyzed cavity ignition in supersonic flow, investigating non-reacting flows and ignition methods. Shah et al. [27] studied thermal convection in a star-shaped cavity with Casson fluid and corrugations. Tilehnoee et al. [28] numerically investigated thermal and fluid flow in concentrated annuli of a gas transmission line. Heat transport in an isothermal hot surface with laminar slot-jet impingement was analyzed in [29], considering different fluids and a magnetic field.

Fig. 1

Real-world application of the hexagonal geometry in the form of the telescope and heat exchanger devices

The numerical and experimental analyses of the hydrothermal characteristics in cavities are extensively studied with obstacles in [30]. The computational approach is applied to study the steady-state convective flow within a well-defined domain to investigate the efficiency in closed systems by utilizing external heating methods by Kalita et al. in [31]. The density variations on the flow field and convection by employing a quadrature scheme are studied by Shu and Wee in [32]. The investigation of heat transmission model and the occurrence of natural convection within a fluid flow by the incorporating discrete heat sources are discussed by Deng in [33]. The Pirmohammadi et al. explored the impact of magnetization-induced resistive forces on heat transmission within the free convective motion of fluid confined in a square cavity [34]. Gumir et al. [35] explore convective heat transfer in a permeable chamber filled with mixture of microparticles $(35\%MWCNT-65\% Fe$ ₃ $O$ ₄)/water, considering the presence of a solid wavy wall. In recent literature, studies have examined convective heat transfer within confined domains, nanofluids, and the enhancement of thermodynamic properties. This current investigation aims to contribute to the existing body of research by focusing on the enhancement of thermodynamic properties. Specifically, the study explores the thermodynamics properties within a hexagonal enclosure, which demonstrates practical applications and notable efficiency in heat transfer.

Novelty This paper presents a novel study on the combined effects of magnetohydrodynamics (MHD) and corrugation in heat transfer. By exploring the interplay between magnetic fields, natural convection, and geometric features, the research offers valuable insights into the complex fluid flow and thermal behavior within the system. This study contributes to the existing knowledge by providing compact findings relevant to thermal management and design optimization in engineering applications.

Objective The objective of the present investigation is to explore and understand the heat transfer characteristics and fluid flow behavior in a system which combines magnetohydrodynamics (MHD), natural convection, and a heated corrugated cylinder within a hexagonal enclosure. The study aims to investigate the influence of MHD and corrugation on heat transfer performance and provide insights into the complex interaction between magnetic fields, natural convection, and geometric features. The ultimate goal is to contribute to the knowledge and understanding of thermal management and design optimization in relevant engineering applications.

Application Some potential engineering applications of hexagonal cavities include:

• 1. Heat Exchangers: Hexagonal cavities can be utilized as heat exchangers in thermal systems. The geometry allows for amplification of heat dissipation due to increased surface area and improved fluid flow characteristics.

• 2. Microfluidics: Hexagonal microfluidic channels are used in lab-on-a-chip devices for applications such as chemical analysis, drug delivery, and biomedical diagnostics. The hexagonal shape enables efficient mixing and transport of fluids on a small scale.

• 3. Structural Design: Hexagonal cavities can be incorporated into structural elements to enhance their strength and load-bearing capacity. Honeycomb structures, for example, utilize hexagonal cells to provide lightweight yet robust construction materials.

• 4. Acoustic Enclosures: Hexagonal cavities can be employed in the design of acoustic enclosures or noise barriers. The geometric properties of hexagons help to reduce sound transmission and improve acoustic insulation.

• 5. Optics and Photonics: Hexagonal cavities are utilized in optical devices, such as laser resonators and photonic crystals. The hexagonal shape allows for precise control of light propagation and confinement, enabling applications in telecommunications, sensing, and optical signal processing.

Motivation The present work is motivated by the quest for a deeper understanding of heat transfer phenomena in complex systems. The combination of magnetohydrodynamics (MHD), natural convection, and a heated corrugated cylinder within a hexagonal enclosure presents a unique and challenging configuration. By delving into this system, the researchers aim to uncover the intricate fluid flow behavior and heat exchanger behavior, with the ultimate goal of optimizing thermal management and design strategies in diverse engineering implementations. The outcomes of this study have the ability to heighten energy efficiency, advance heat transfer technologies, and foster innovation in engineering design. The rest of our proposed study is presented as follows,

In Sect. 2, we described the Problem formulation. In Sect. 3, we discussed the solution methodology followed by finite element method and validation of results. In Sect. 4, we computed the results and drawn some numerical examples to visualize our proposed study. In Sect. 5, we illustrated some conclusions and remarks.

2 Problem formulation

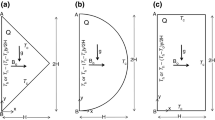
In this section, we discuss the problem description of MHD nanofluid in a hexagonal enclosure with inner corrugated circular cylinder. The inner corrugated circular cylinder is kept isothermally hot, the left and right walls of the cavity are cold, and the top and bottom walls are adiabatic. We assumed some physical restrictions concerned with the flow characteristics and mathematical model which are presented as follows:

We have examined a 2D hexagonal enclosure filled with a viscous fluid (water) and introduced a symmetrical heated corrugated round cylinder inside the cavity. The boundaries of the enclosure, which are not parallel to each other, are kept cold temperature with temperature (${T}_{c}$), while the upper and lower surfaces are maintained as adiabatic surfaces. To ensure convective potential within the domain, uniform temperature (${T}_{h}$) is applied to the surface of the corrugated circular cylinder. Water serves as the base fluid, and additional particles from a ferrofluid ($Fe$ ₃ $O$ ₄) are introduced. A uniform magnetic field with a specified strength ${B}_{o}$ is applied in an inclined direction. The geometric representation of the domain is portrayed in Fig. 2.

Fig. 2

Geometry of the problem

2.1 Thermal and material parameters of Newtonian ferrofluid.

The ferroparticles are composed of $Fe$ ₃ $O$ ₄ which have been introduced into a carrier fluid based on water. The choice of ${Fe}_{3}{O}_{4}$ particles in our study on MHD natural convection in a hexagonal cavity is due to the magnetic properties of ${Fe}_{3}{O}_{4}$ exhibits strong magnetism, making it suitable for studying MHD effects in a magnetic field. The ${Fe}_{3}{O}_{4}$ nanoparticles disperse uniformly in the ferrofluid, ensuring consistent properties throughout the experiment. The ${Fe}_{3}{O}_{4}$ nanoparticles have biocompatible properties and have industrial applications in various fields. The ${Fe}_{3}{O}_{4}$ nanoparticles can be synthesized with different sizes and coatings, allowing for control over the ferrofluid properties.

Table 1 offers a comprehensive listing of the thermo-physical properties associated with both the ferroparticles and water. The thermo-physical properties extracted from Table 1 can be used to calculate the overall thermo-physical attributes of the resulting ferrofluid. We identify and quantify varies properties including effective density as follows [36, 37]:

Table 1 Values of thermo-physical properties [38,39,40]

$${\rho }_{ff}=\left(1-\phi \right){\rho }_{f}+\phi {\rho }_{s}.$$

(1)

In this context, ${\rho }_{f}$ represents the density of the base fluid, ${\rho }_{s}$ represents the density of the solid particles, and $\phi$ represents the volume fraction of the nanoparticles. To determine the specific heat capacity ${(\rho Cp)}_{ff}$ and the expansion coefficient of thermal expansion ${(\rho \beta )}_{ff}$ of the ferrofluid, we apply the following approximation method [36].

$${(\rho Cp)}_{ff}={\left(\rho Cp\right)}_{f}\left(1-\phi \right)+{\left(\rho Cp\right)}_{s}\phi ,$$

(2)

$${(\rho \beta )}_{ff}={\left(\rho \beta \right)}_{f}\left(1-\phi \right)+{\left(\rho \beta \right)}_{s}\phi .$$

(3)

In accordance with the Maxwell–Garnetts (MG) model, one can derive both the electrical performance ${(\sigma }_{ff})$ and the effective thermal diffusivity $(K_{ff})$ of the ferrofluid.

$${\sigma }_{ff}={\sigma }_{f}\left[1+\frac{3\left(\frac{{\sigma }_{s}}{{\sigma }_{f}}-1\right)\phi }{\left(\frac{{\sigma }_{s}}{{\sigma }_{f}}+2\right)-\left(\frac{{\sigma }_{s}}{{\sigma }_{f}}-1\right)\phi }\right],$$

(4)

$${K}_{ff}={K}_{f}\left(\frac{{K}_{s}+2{K}_{f}-2\phi ({K}_{f}-{K}_{s})}{{K}_{s}+2{K}_{f}+\phi ({K}_{f}-{K}_{s})}\right).$$

(5)

The dynamic viscosity ${(\sigma }_{ff})$ of the $({Fe}_{3}{O}_{4})$ can be defined as

$${\mu }_{ff}=\frac{{\mu }_{f}}{{(1-\phi )}^{2.5}}.$$

(6)

The calculation for the thermal diffusivity ${(\alpha }_{ff})$ is performed as follows.

$${\alpha }_{ff}=\frac{{K}_{ff}}{{(\rho Cp)}_{ff}}.$$

(7)

2.2 Governing equation in dimensional form

Considering the stated assertion and utilizing the Boussinesq approximation, governing Eqs. (1)-(7) depict the physical properties of the nanofluid of the present work in the following manner with the help of continuity equation, momentum equation, and energy equation [41, 42].

$$\frac{\partial \mathcalligra{u}}{\partial \mathcalligra{x}}+\frac{\partial \mathcalligra{v}}{\partial \mathcalligra{y}}=0,$$

(8)

$${\rho }_{ff}\left(\mathcalligra{u}\frac{\partial \mathcalligra{u}}{\partial \mathcalligra{x}}+\mathcalligra{v}\frac{\partial \mathcalligra{u}}{\partial \mathcalligra{y}}\right)=-\frac{\partial \mathcalligra{p}}{\partial \mathcalligra{x}}+{\mu }_{ff}\left(\frac{{\partial }^{2}\mathcalligra{u}}{{\partial x}^{2}}+\frac{{\partial }^{2}\mathcalligra{u}}{{\partial \mathcalligra{y}}^{2}}\right)+{{B}_{0}}^{2}{\sigma }_{ff}\left(-u{sin}^{2}\gamma +\mathcalligra{v}cos\gamma sin\gamma \right),$$

(9)

$$\left.\begin{array}{c} {\rho }_{ff}\left(\mathcalligra{u}\frac{\partial \mathcalligra{v}}{\partial \mathcalligra{x}}+\mathcalligra{v}\frac{\partial \mathcalligra{v}}{\partial \mathcalligra{y}}\right)=-\frac{\partial \mathcalligra{p}}{\partial \mathcalligra{y}}+{\mu }_{ff}\left(\frac{{\partial }^{2}\mathcalligra{v}}{{\partial x}^{2}}+\frac{{\partial }^{2}\mathcalligra{v}}{{\partial \mathcalligra{y}}^{2}}\right)+g{\left(\rho \beta \right)}_{ff}\left(\mathcalligra{T}-{\mathcalligra{T}}_{c}\right)\\ +{{B}_{0}}^{2}{\sigma }_{ff}\left(-\mathcalligra{v}{cos}^{2}\gamma +\mathcalligra{u}cos\gamma sin\gamma \right),\end{array}\right\}$$

(10)

$$\mathcalligra{u}\frac{\partial \mathcalligra{T}}{\partial \mathcalligra{x}}+\mathcalligra{v}\frac{\partial \mathcalligra{T}}{\partial \mathcalligra{y}}={\alpha }_{ff}\left(\frac{{\partial }^{2}\mathcalligra{T}}{{\partial \mathcalligra{x}}^{2}}+\frac{{\partial }^{2}\mathcalligra{T}}{{\partial \mathcalligra{y}}^{2}}\right).$$

(11)

In this context, $\mathcalligra{u}$ and $\mathcalligra{v}$ represent velocities in the $\mathcalligra{x}$ and $\mathcalligra{y}$ directions, while $\mathcal{T}$, ${\mathcal{T}}_{c}$, $\mathcalligra{g}$, and $\mathcalligra{p}$ are the ferrofluid temperature, surrounding temperature, gravitational acceleration, and pressure, respectively. Additionally, ${B}_{0}$ and $\gamma$ describe the strength of the magnetic field and orientation of the magnetic field, respectively. For the model mentioned above, the initial conditions are set as follows:

Outer boundaries:

$$\mathcalligra{u}= \mathcalligra{v}=0, \mathcalligra{T}={\mathcalligra{T}}_{c}=0.$$

(12)

Inner boundaries:

$$\mathcalligra{u}= \mathcalligra{v}=0, \mathcalligra{T}={\mathcalligra{T}}_{h}=1.$$

(13)

To convert the dimensional equations into a dimensionless form, we introduce the following non-dimensional variables:

$$\mathcalligra{X}=\frac{\mathcalligra{x}}{L},\mathcalligra{Y}=\frac{\mathcalligra{y}}{L}, \mathcalligra{U}=\frac{\mathcalligra{u}L}{{\alpha }_{f}},\mathcalligra{V}=\frac{\mathcalligra{v}L}{{\alpha }_{f}}, \mathcalligra{P}=\mathcalligra{p}\frac{{L}^{2}}{{\rho }_{ff}{{\alpha }_{f}}^{2}} ,\Theta =\frac{\mathcalligra{T}-{\mathcalligra{T}}_{c}}{{\mathcalligra{T}}_{h}-{\mathcalligra{T}}_{c}} ,$$

(14)

$$Ha=\sqrt{\frac{{\sigma }_{f}}{{\mu }_{f}}}{B}_{0}L, { \alpha }_{f}=\frac{{K}_{f}}{{(\rho Cp)}_{f}} , { \nu }_{f}=\frac{{\mu }_{f}}{{\rho }_{f}},$$

(15)

$$Pr=\frac{{\nu }_{f}}{\alpha }, Ra=\frac{\mathcal{g}{\beta }_{f}\Delta \mathcal{T}{L}^{3}}{{\nu }_{f}{ \alpha }_{f}} , \Delta \mathcal{T}={\mathcal{T}}_{h}-{\mathcal{T}}_{c}.$$

(16)

By employing the relationships provided in Eqs. (14) to (16), we can convert the dimensional governing equations into their dimensionless form [41, 42].

$$\frac{\partial \mathcal{U}}{\partial \mathcal{X}}+\frac{\partial \mathcal{V}}{\partial \mathcal{Y}}=0,$$

(17)

$$\left.\begin{array}{c}U\frac{\partial \mathcal{U}}{\partial \mathcal{X}}+V\frac{\partial \mathcal{U}}{\partial \mathcal{Y}}=-\frac{\partial \mathcal{P}}{\partial \mathcal{X}}+\frac{Pr}{{\left(1-\phi \right)}^{2.5}}\left(\frac{{\partial }^{2}\mathcal{U}}{{\partial \mathcal{X}}^{2}}+\frac{{\partial }^{2}\mathcal{U}}{{\partial \mathcal{Y}}^{2}}\right) \\ +{Ha}^{2}Pr\frac{{\sigma }_{ff}}{{\sigma }_{f}}\left(-\mathcal{U}{sin}^{2}\gamma +\mathcal{V}cos\gamma sin\gamma \right),\end{array}\right\}$$

(18)

$$\left.\begin{array}{c}U\frac{\partial \mathcal{V}}{\partial \mathcal{X}}+V\frac{\partial \mathcal{V}}{\partial \mathcal{Y}}=-\frac{\partial \mathcal{P}}{\partial \mathcal{Y}}+\frac{Pr}{{\left(1-\phi \right)}^{2.5}}\left(\frac{{\partial }^{2}\mathcal{V}}{{\partial \mathcal{X}}^{2}}+\frac{{\partial }^{2}\mathcal{V}}{{\partial \mathcal{Y}}^{2}}\right)+\text{Pr}Ra\Theta \\ +{Ha}^{2}Pr\frac{{\sigma }_{ff}}{{\sigma }_{f}}\left(-\mathcal{V}{sin}^{2}\gamma +\mathcal{U}cos\gamma sin\gamma \right), \end{array}\right\}$$

(19)

$$\mathcal{U}\frac{\partial\Theta }{\partial \mathcal{X}}+\mathcal{V}\frac{\partial\Theta }{\partial \mathcal{Y}}=\frac{{\alpha }_{ff}}{{\alpha }_{f}}\left(\frac{{\partial }^{2}\Theta }{{\partial \mathcal{X}}^{2}}+\frac{{\partial }^{2}\Theta }{{\partial \mathcal{Y}}^{2}}\right).$$

(20)

Boundary conditions:

Outer boundaries:

$$\mathcal{U}= \mathcal{V}=0,\Theta =0.$$

(21)

Inner boundaries:

$$\mathcal{U}= \mathcal{V}=0,\Theta =1.$$

(22)

The dimensionless representation of the $({Nu}_{avg})$ at the heated inner corrugated wall is expressed as:

${Nu}_{{\varvec{a}}{\varvec{v}}{\varvec{g}}}=\frac{1}{s}\underset{0}{\overset{s}{\int }}Nu(\eta )d\eta$ where

$$Nu\left(\eta \right)=-\frac{{K}_{ff}}{{K}_{f}}\frac{\partial\Theta }{\partial \eta }.$$

(23)

Here $\eta$ is the radial coordinate and $s$ denotes the surface area of inner cavity.

3 Solution methodology

Computational methodologies are basically used to get the numerical solutions of the engineering and other field problems. These methodologies are used for different partial differential system of equations to make them the algebraic system of equations with the help of the analytical techniques, while extending their applicability to complex systems. In the literature, there are three dominant computational methodologies which are Finite Difference, Finite Element, and Finite Volume method. The Finite Element Method (FEM) stands out as a prominent choice, primarily to its remarkable ability to solve problems containing discontinuities. The advantages of FEM over the Finite Difference Method are given below:

• 1. Flexibility in handling complex geometries.

• 2. Local approximation and adaptivity for improved accuracy and efficiency.

• 3. Convergence and error analysis ensure reliable results.

• 4. Versatility across various physics and complex material properties.

• 5. Handles complex boundary conditions effectively.

• 6. Robustness and scalability for large-scale simulations.

4 Galerkin finite element discretization

The GFEM method is used for solving the system of partial differential Eqs. (18–20) correspondingly. Continuity Eq. (17) is employed as a constraint, generating the pressure dispersion due to the mass conservation [43]. By utilizing the FEM to solve Eqs. (18–20), where the pressure $\mathcal{P}$ is reduced by an extra parameter and the incompressibility constraints are specified by Eq. (17) (see Reddy and Ali [44, 45]) which generates as follows:

$$\mathcal{P}=-\mathfrak{R}\left(\frac{\partial \mathcal{U}}{\partial \mathcal{X}}+\frac{\partial \mathcal{V}}{\partial \mathcal{Y}} \right).$$

(24)

Consistency Eq. (16) is obviously valid for the big values of $\mathfrak{R}$. The prevalent values of $\mathfrak{R}$ produce a reliable result which is ${10}^{7}$. By employing Eq. (24), the momentum dimensionless Eqs. (17) and (18) are reduced as follows:

$$\left. {\begin{array}{*{20}c} {U\frac{{\partial {\mathcal{U}}}}{{\partial {\mathcal{X}}}} + V\frac{{\partial {\mathcal{V}}}}{{\partial {\mathcal{Y}}}} = R\frac{\partial }{{\partial {\mathcal{X}}}}\left( {\frac{{\partial {\mathcal{U}}}}{{\partial {\mathcal{X}}}} + \frac{{\partial {\mathcal{V}}}}{{\partial {\mathcal{Y}}}}} \right) + \frac{Pr}{{\left( {1 - \phi } \right)^{2.5} }}\left( {\frac{{\partial^{2} {\mathcal{U}}}}{{\partial {\mathcal{X}}^{2} }} + \frac{{\partial^{2} {\mathcal{U}}}}{{\partial {\mathcal{Y}}^{2} }}} \right)} \\ { + Ha^{2} Pr\frac{{\sigma_{ff} }}{{\sigma_{f} }}\left( { - {\mathcal{U}}{\text{sin}}^{2} \gamma + {\mathcal{V}}{\text{cos}}\gamma {\text{sin}}\gamma } \right),} \\ \end{array} } \right\}$$

(25)

$$\left. {\begin{array}{*{20}c} {U\frac{{\partial {\mathcal{U}}}}{{\partial {\mathcal{X}}}} + V\frac{{\partial {\mathcal{V}}}}{{\partial {\mathcal{Y}}}} = R\frac{\partial }{{\partial {\mathcal{Y}}}}\left( {\frac{{\partial {\mathcal{U}}}}{{\partial {\mathcal{X}}}} + \frac{{\partial {\mathcal{V}}}}{{\partial {\mathcal{Y}}}}} \right) + \frac{Pr}{{\left( {1 - \phi } \right)^{2.5} }}\left( {\frac{{\partial^{2} {\mathcal{V}}}}{{\partial {\mathcal{X}}^{2} }} + \frac{{\partial^{2} {\mathcal{V}}}}{{\partial {\mathcal{Y}}^{2} }}} \right) + PrRa\Theta } \\ { + Ha^{2} Pr\frac{{\sigma_{ ff} }}{{\sigma_{f} }}\left( { - {\mathcal{V}}{\text{sin}}^{2} \gamma + {\mathcal{U}}{\text{cos}}\gamma {\text{sin}}\gamma } \right),} \\ \end{array} } \right\}$$

(26)

The velocity ingredients ($\mathcal{U}$,$\mathcal{V}$) and temperature ($\Theta$) are expressed by employing basis set ${\left\{{\Psi }_{k}\right\}}_{k=1}^{N}$ as follows:

$$\mathcal{U}\approx \sum_{k=1}^{N}{\mathcal{U}}_{k}{\Psi }_{k}\left(\mathcal{X}, \mathcal{Y}\right), \mathcal{V}\approx \sum_{k=1}^{N}{\mathcal{V}}_{k}{\Psi }_{k}\left(\mathcal{X}, \mathcal{Y}\right),$$

and

$$\Theta \approx \sum_{k=1}^{N}{\Theta }_{k}{\Psi }_{k}\left(\mathcal{X}, \mathcal{Y}\right),$$

(27)

For $0\le \mathcal{X},\mathcal{Y}\le 1.$

The nonlinear residual expression for Eqs. (25), (26), and (20) was generated by the Galerkin finite element method at the nodes within the internal domain. $\varpi$:

$$\left. {\begin{array}{*{20}c} {R_{j}^{1} = \mathop \sum \limits_{k = 1}^{N} {\mathcal{U}}_{k} \int\limits_{\varpi } {\left[ {\left( {\mathop \sum \limits_{k = 1}^{N} {\mathcal{U}}_{k} \Psi_{k} } \right)\frac{{\partial \Psi_{k} }}{{\partial {\mathcal{X}}}} + \left( {\mathop \sum \limits_{k = 1}^{N} {\mathcal{V}}_{k} \Psi_{k} } \right)\frac{{\partial \Psi_{k} }}{{\partial {\mathcal{Y}}}}} \right]\Psi_{i} {\text{d}}{\mathcal{X}}{\text{d}}{\mathcal{Y}}} } \\ \begin{gathered} \quad + \Re \left[ {\mathop \sum \limits_{k = 1}^{N} {\mathcal{U}}_{k} \mathop \smallint \limits_{\varpi } \frac{{\partial \Psi_{i} }}{{\partial {\mathcal{X}}}}\frac{{\partial \Psi_{k} }}{{\partial {\mathcal{X}}}}{\text{d}}{\mathcal{X}}{\text{d}}{\mathcal{Y}} + \mathop \sum \limits_{k = 1}^{N} {\mathcal{V}}_{k} \mathop \smallint \limits_{\varpi } \frac{{\partial \Psi_{i} }}{{\partial {\mathcal{X}}}}\frac{{\partial \Psi_{k} }}{{\partial {\mathcal{Y}}}}{\text{d}}{\mathcal{X}}{\text{d}}{\mathcal{Y}}} \right] \hfill \\ \quad + \frac{\Pr }{{\left( {1 - \phi } \right)^{2.5} }}\mathop \sum \limits_{k = 1}^{N} {\mathcal{U}}_{k} \mathop \smallint \limits_{\varpi } \left[ {\left[ {\frac{{\partial \Psi_{i} }}{{\partial {\mathcal{X}}}}\frac{{\partial \Psi_{k} }}{{\partial {\mathcal{X}}}} + \frac{{\partial \Psi_{i} }}{{\partial {\mathcal{Y}}}}\frac{{\partial \Psi_{k} }}{{\partial {\mathcal{Y}}}}} \right]{\text{d}}{\mathcal{X}}{\text{d}}{\mathcal{Y}}} \right] \hfill \\ \quad - Ha^{2} \Pr \frac{{\sigma_{ff} }}{{\sigma_{f} }}\left( { - \mathop \sum \limits_{k = 1}^{N} {\mathcal{U}}_{k} \Psi_{k} \sin^{2} \gamma + \mathop \sum \limits_{i = 1}^{M} {\mathcal{V}}_{k} \Psi_{k} \cos \gamma \sin \gamma } \right)\Psi_{i} , \hfill \\ \end{gathered} \\ \end{array} } \right\}$$

(28)

$$\left. {\begin{array}{*{20}l} {R_{j}^{2} = \mathop \sum \limits_{k = 1}^{N} {\mathcal{V}}_{k} \int\limits_{\varpi } {\left[ {\left( {\mathop \sum \limits_{k = 1}^{N} {\mathcal{U}}_{k} \Psi_{k} } \right)\frac{{\partial \Psi_{k} }}{{\partial {\mathcal{X}}}} + \left( {\mathop \sum \limits_{k = 1}^{N} {\mathcal{V}}_{k} \Psi_{k} } \right)\frac{{\partial \Psi_{k} }}{{\partial {\mathcal{Y}}}}} \right]\Psi_{i} {\text{d}}{\mathcal{X}}{\text{d}}{\mathcal{Y}} } } \\ \begin{gathered} \quad + \Re \left[ {\mathop \sum \limits_{k = 1}^{N} {\mathcal{U}}_{k} \mathop \smallint \limits_{\varpi } \frac{{\partial \Psi_{i} }}{{\partial {\mathcal{X}}}}\frac{{\partial \Psi_{k} }}{{\partial {\mathcal{X}}}}{\text{d}}{\mathcal{X}}{\text{d}}{\mathcal{Y}} + \mathop \sum \limits_{k = 1}^{N} {\mathcal{V}}_{k} \mathop \smallint \limits_{\varpi } \frac{{\partial \Psi_{i} }}{{\partial {\mathcal{X}}}}\frac{{\partial \Psi_{k} }}{{\partial {\mathcal{Y}}}}{\text{d}}{\mathcal{X}}{\text{d}}{\mathcal{Y}}} \right] \hfill \\ \quad + \frac{\Pr }{{\left( {1 - \phi } \right)^{2.5} }}\mathop \sum \limits_{k = 1}^{N} {\mathcal{V}}_{k} \mathop \smallint \limits_{\varpi } \left[ {\left[ {\frac{{\partial \Psi_{i} }}{{\partial {\mathcal{X}}}}\frac{{\partial \Psi_{k} }}{{\partial {\mathcal{X}}}} + \frac{{\partial \Psi_{i} }}{{\partial {\mathcal{Y}}}}\frac{{\partial \Psi_{k} }}{{\partial {\mathcal{Y}}}}} \right]{\text{d}}{\mathcal{X}}{\text{d}}{\mathcal{Y}}} \right] - \begin{array}{*{20}l} {Ra\Pr \int_{\varpi } {\left( {\sum\limits_{k = 1}^{N} {\Theta_{k} } \Psi_{k} } \right)\Psi_{i} } } \\ \end{array} \hfill \\ \quad - Ha^{2} \Pr \frac{{\sigma_{ff} }}{{\sigma_{f} }}\left( { - \mathop \sum \limits_{k = 1}^{N} {\mathcal{U}}_{k} \Psi_{k} \sin^{2} \gamma + \mathop \sum \limits_{i = 1}^{M} {\mathcal{V}}_{k} \Psi_{k} \cos \gamma \sin \gamma } \right)\Psi_{i} , \hfill \\ \end{gathered} \\ \end{array} } \right\}$$

(29)

$$\left. \begin{gathered} R_{j}^{3} = \sum\limits_{k = 1}^{N} {\Theta_{k} } \int\limits_{\varpi } {\begin{array}{*{20}c} {\left[ {\left( {\sum\limits_{k = 1}^{N} {{\mathcal{U}}_{k} } \Psi_{k} } \right)\frac{{\partial \Psi_{k} }}{{\partial {\mathcal{X}}}} + \left( {\sum\limits_{k = 1}^{N} {{\mathcal{V}}_{k} } \Psi_{k} } \right)\frac{{\partial \Psi_{k} }}{{\partial {\mathcal{Y}}}}} \right]\Psi_{i} {\text{d}}{\mathcal{X}}{\text{d}}{\mathcal{Y}}} \\ \end{array} } \hfill \\ + \Re \left[ {\mathop \sum \limits_{k = 1}^{N} {\mathcal{U}}_{k} \mathop \smallint \limits_{\varpi } \frac{{\partial \Psi_{i} }}{{\partial {\mathcal{X}}}}\frac{{\partial \Psi_{k} }}{{\partial {\mathcal{X}}}}{\text{d}}{\mathcal{X}}{\text{d}}{\mathcal{Y}} + \mathop \sum \limits_{k = 1}^{N} {\mathcal{V}}_{k} \mathop \smallint \limits_{\varpi } \frac{{\partial \Psi_{i} }}{{\partial {\mathcal{X}}}}\frac{{\partial \Psi_{k} }}{{\partial {\mathcal{Y}}}}{\text{d}}{\mathcal{X}}{\text{d}}{\mathcal{Y}}} \right] \hfill \\ + \frac{{\alpha_{ff} }}{{\alpha_{f} }}\mathop \sum \limits_{k = 1}^{N} \Theta_{k} \mathop \smallint \limits_{\varpi } \left[ {\left[ {\frac{{\partial \Psi_{i} }}{{\partial {\mathcal{X}}}}\frac{{\partial \Psi_{k} }}{{\partial {\mathcal{X}}}} + \frac{{\partial \Psi_{i} }}{{\partial {\mathcal{Y}}}}\frac{{\partial \Psi_{k} }}{{\partial {\mathcal{Y}}}}} \right]{\text{d}}{\mathcal{X}}{\text{d}}{\mathcal{Y}}} \right]. \hfill \\ \end{gathered} \right\}$$

(30)

The integrals in the residual equations are evaluated numerically by using Gaussian quadrature for the three-point bi-quadratic basis functions. The second term carrying the penalty parameter ($\mathfrak{R}$) is assessed with two points in Eqs. (28) and (29). Equations (28)–(30) are residuals which are represented in the matrix vector representation by finite element procedure as follows:

$$\left({\Pi }_{1}+\Upsilon {\Pi }_{2} \right)\textbf{b}=\textbf{F}.$$

(31)

Π₁, Π₂ are the matrices derived from the Jacobian of the residuals where ${\varvec{b}}$ indicates the indeterminate vector. The constraint equation is well satisfied, as $\mathfrak{R}$ occurs to a significant plenty ($\sim {10}^{7}$). The result of the extension of the Π₁ is negligible when compared to ${\mathfrak{R}\Pi }_{2}$.

$${\Pi }_{2}{\varvec{b}}=\frac{{\varvec{F}}}{\mathfrak{R}}.$$

(32)

The Newton–Raphson method is applied for solving the nonlinear residual Eqs. (28)–(30) in order to ascertain the expansion coefficient in Eq. (27). The linear $(3N \times 3N)$ system is illustrated at each iteration.

$$\textbf{J}\left({\textbf{b}}^{\text{n}}\right) \left[{\textbf{b}}^{\text{n}}-{\textbf{b}}^{\text{n}+1}\right]=\textbf{R}\left({\textbf{b}}^{\text{n}}\right).$$

(33)

where n denotes the number of iterations index. The Jacobian matrix element $\textbf{J}\left({\textbf{b}}^{\text{n}}\right)$ contains the velocity component derivatives of the residual equations, and the residual vector is represented by $\textbf{R}\left({\textbf{b}}^{\text{n}}\right)$.

The flow potential $\psi$ is created from the velocity ingredients $\mathcal{U}$ and $\mathcal{V}$, which is employed to convey the flow dynamic. For the two-dimensional flow, the connection between flow potential,$\psi$, and velocity ingredients are as follows:

$$\mathcal{U}=\frac{\partial \psi }{\partial \mathcal{Y}} , \mathcal{V}=\frac{\partial \psi }{\partial \mathcal{X}}.$$

(34)

That produce a singular equation.

$$\frac{{\partial }^{2}\psi }{\partial {\mathcal{X}}^{2}}+\frac{{\partial }^{2}\psi }{\partial {\mathcal{Y}}^{2}}=\frac{\partial \mathcal{U}}{\partial \mathcal{Y}}-\frac{\partial \mathcal{V}}{\partial \mathcal{X}}.$$

(35)

According to the description of the stream function given above, the positive sign of $\psi$ indicates anti-clockwise circulation, while a negative value of $\psi$ signifies clockwise circulation. The Galerkin finite element approach produces the subsequent linear residual equation for Eq. (27) through the expansion of the stream function ($\psi )$ with the basis set $\{{\Psi }_{i} {\}}_{k=1}^{N}$ as

$$\psi =\sum_{k=1}^{N}{\psi }_{k}{\Psi }_{i}(\mathcal{X},\mathcal{Y}).$$

and the incorporating the relationship for $\mathcal{U}, \mathcal{V}$ from Eq. (48).

$$\left. \begin{gathered} R_{i}^{s} = \mathop \sum \limits_{k = 1}^{N} \psi_{k} \mathop \smallint \limits_{{\Omega }} \left[ {\frac{{\partial {\Psi }_{i} }}{{\partial {\mathcal{X}}}}\frac{{\partial {\Psi }_{k} }}{{\partial {\mathcal{X}}}} + \frac{{\partial {\Psi }_{i} }}{{\partial {\mathcal{Y}}}}\frac{{\partial {\Psi }_{k} }}{{\partial {\mathcal{Y}}}}} \right]{\text{d}}{\mathcal{X}}{\text{d}}{\mathcal{Y}} + \mathop \sum \limits_{k = 1}^{N} {\mathcal{U}}_{k} \mathop \smallint \limits_{\varpi } {\Psi }_{i} \frac{{\partial {\Psi }_{k} }}{{\partial {\mathcal{Y}}}}{\text{d}}{\mathcal{X}}{\text{d}}{\mathcal{Y}} \hfill \\ \quad - \mathop \sum \limits_{k = 1}^{N} {\mathcal{V}}_{k} \mathop \smallint \limits_{\varpi } {\Psi }_{i} \frac{{\partial {\Psi }_{k} }}{{\partial {\mathcal{Y}}}}{\text{d}}{\mathcal{X}}{\text{d}}{\mathcal{Y}}. \hfill \\ \end{gathered} \right\}$$

(36)

Since there is no cross-flow and the no-slip criteria hold true at all boundaries, ϔ$=0$ is employed as the residual equation at the boundary nodes.

4.1 Advantages of Galerkin finite element in fluid dynamics

The implementation of the Galerkin finite element discretization method in fluid dynamics offers several advantages. This numerical method allows for the accurate approximation of the solution of a PDE’s by discretizing the domain into finite elements. The Galerkin method enables the construction of an approximate solution by decreasing the deviation between true solution and the finite element solution. This technique offers a flexible approach to the discretization of complicated geometries and irregular domains. Furthermore, the Galerkin method can handle problems with complex boundary conditions and provides high accuracy for problems with strong solutions. In summary, the Galerkin FEM discretization is a powerful tool for solving problems in fluid dynamics that require high accuracy and flexibility.

4.2 Numerical solution procedure

In the study, the commercial software COMSOL Multiphysics is used to generate the mesh and plot contour plots. COMSOL Multiphysics provides a comprehensive platform for Multiphysics simulations and offers built-in tools for mesh generation and visualization, including contour plots. The study is conducted using a level 8 (package) mesh, indicating a high level of refinement and accuracy in the computational grid. Table 2 shows a visual representation that effectively illustrates the intricate iterative process undertaken during the study. Additionally, it provides valuable insights of D.O.F associated with different refinement level and the corresponding CPU times recorded throughout the research.

Table 2 Mesh statistics at different refinement levels

4.3 Mesh generation

The main aim is to determine the optimal mesh size which provides a significant solution for the accuracy and efficiency of computational simulations. We determine the mesh sensitivity by measuring the ${{\varvec{N}}{\varvec{u}}}_{{\varvec{a}}{\varvec{v}}{\varvec{g}}}$ by fixing the value of non-dimensional parameters, $\left(Pr=0.863\right), \left(Ra={10}^{5}\right), (Ha=10$), and $(\phi =0.03)$. These specific conditions allow us to evaluate the reliability and validity of our computational framework thoroughly. Table 2 provides valuable data on the efficiency and stability of our numerical procedure. Our goal is to identify the optimal mesh and their effects on the ${{\varvec{N}}{\varvec{u}}}_{{\varvec{a}}{\varvec{v}}{\varvec{g}}}$ for a reliable solution.

Figure 3 presents a visual representation of the computational grid, characterized by rectangular elements at the boundaries and triangular elements in the internal geometry.

Fig. 3

Meshing refinement

4.4 Validation of result

The validation of our results is effectively demonstrated in Fig. 4, where a visual comparison reveals a strong agreement between the findings of the present work and the experimental and numerical research conducted by Kishor [14]. This visuals representation serves as solid evidence that our current study aligns well with the previous work and further strengthens the credibility and reliability of the present work.

Fig. 4

Comparison of result validation the present result with the experimental and numerical work by Kishor et al. [14]

The validation of our findings is based on comparing average Nusselt numbers with the standard values offered by Kishor et al., which are listed in Table 3. The outcomes demonstrated a favorable level of conformity with the accordance statistics reported by Kishor et al. [14].

Table 3 Comparison of the average Nusselt number $({Nu}_{avg})$ of the present work and Kishor et al. [14]

5 Results and discussions

This section showcases the computational findings of temperature field (Isotherms) and velocity field (streamlines) in a hexagonal enclosure. We explore the results of average Nusselt number by fixing the ranges of Rayleigh number $(Ra={10}^{3}, {10}^{4}, {10}^{5}, {10}^{6}),$ volume fraction $\left(\phi =0, 0.03, 0.06 and 0.09\right)$, Prandtl number fixed at $(Pr=6.8377)$, and angle of magnetic field being $\gamma =\frac{\pi }{4}$. These specifications provide us to gain a comprehensive understanding of the heat transfer phenomenon and create a stable groundwork for the further exploration discernment in complex geometries.

5.1 The impact of varying inner cylinder shapes on streamlines and isotherms.

In this experiment, we compute the pattern distribution of streamlines and isotherms for different value of corrugation number ($\lambda$). This numerical investigation is conducted by taking Hartman number$(Ha=10)$, volume fraction$(\phi =0.03)$, Prandtl number$(Pr=6.8377)$, Rayleigh number $(Ra={10}^{5})$, and angle $\gamma =\frac{\pi }{4}$. Figure 5 represents the influence of different cavity shapes $(\lambda )$ on the velocity field and temperature distribution. In order to investigate the underlying mechanisms across a range of $\lambda$ values, the remaining physical parameters are kept constant. Figure 5 clearly demonstrates that the magnitude of the velocity is increasing corresponds to increasing in $\lambda$ values, as $\lambda$ = 0, 3, 4, 8, 12, and 16 give us the velocity magnitudes as 7.5, 8.47, 7.09, 18.9, 19, and 19 and 20.5, respectively. Similarly, the temperature magnitude aligns with the respective lambda ($\lambda )$ values. These findings have significant variations in the flow patterns and temperature distribution within the cavity, which provides a valuable impact on different cavity shapes.

Fig. 5

Impact of number of corrugations $(\lambda )$ of cylinder on velocity and temperature profile

Figure 6 provides a comprehensive comparison between different $\lambda$ values and their corresponding average Nusselt numbers against a spectrum of Rayleigh numbers. The findings from the figure distinctly demonstrate that as the corrugation number lambda $\lambda$ increases, the average heat transfer coefficient $(Nu$ _avg) exhibits a proportional increase as well. This relationship indicates that the higher values of lambda $\lambda$ correspond to enhanced the heat transfer rates within the system. Notably, when lambda $\lambda$ approaches infinity, the behavior of the system closely resembles that of $\lambda$ equal to zero. This suggests that when $\lambda$ tends to $\infty$, then the heat transfer has a similar characteristic as lambda $\lambda$ approaches to zero, which indicates an interesting limit concept in the system's response.

Fig. 6

Variation in average Nusselt number $({Nu}_{avg})$ against Rayleigh number $(Ra)$ for number of corrugations $(\lambda )$ of cylinder

5.2 Impact of ${\varvec{R}}{\varvec{a}}$ on streamlines and isotherms.

Figure 7 portraits the significance of the Rayleigh number $(Ra)$ on the temperature and velocity profiles, While the non-dimensional quantities are kept constant, i.e., Hartman number $(Ha=10)$, volume fraction $(\phi =0.06)$, and Prandtl number $Pr=6.8377$. Figure 7 visually presents the flow behavior and thermal profile within the cavity as the Rayleigh number varies from ${10}^{3}$ to ${10}^{6}$. A clear observation can be made regarding the behavior of the streamlines as the Rayleigh number escalating. The streamlines become denser and exhibit irregular patterns in the upper section of the cavity. Additionally, with the escalation of the Rayleigh number, it is observed that the fluid in the lower section of the cavity, positioned beneath the heated cylinder, exhibits an upward flow due to the buoyancy forces triggered by thermal convection. Regarding the rotational behavior characterized by the formation of vortices, clockwise and counterclockwise eddies arise in the proximity of the left and right regions of the enclosure. When considering the fluctuations in isotherm distribution, it becomes apparent that augmenting the Rayleigh number $(Ra)$ gives rise to enhanced temperature gradients, amplifying the extent of the heated region surrounding the circular cylinder and compelling the isotherms contours toward the enclosure boundaries. Consequently, with the augmentation of the Rayleigh number, the thermal layer thickness expands near the cylinder's surface and its extremities.

Fig. 7

Impact Rayleigh number $(Ra)$ on velocity and temperature profile

Figure 8 exhibits the behavior of the local Nusselt number for temperature distribution along the hot surface with constant temperature, considering different values of the $(Ra)$ number. It is observed that the local Nusselt number exhibits both maximum and minimum values for $Ra={10}^{6}$ in specific regions along the hot surface. This behavior suggests the existence of distinct heat transfer characteristics in the region.

Fig. 8

Impact of Rayleigh number $(Ra)$ on local Nusselt number (${Nu}_{local}$)

5.3 Impact of ${\varvec{H}}{\varvec{a}}$ on streamlines and isotherms.

The graphical representation in Fig. 9 holds significant importance, as it effectively demonstrates the ramification of varying the Hartman field parameter $(Ha)$ on both momentum and thermal distributions. The rest of the non-dimensional parameters are kept constant to achieve the following results.

Fig. 9

Impact of Hartmann number $(Ha)$ on velocity and temperature profile

When $Ha= 0$, the velocity distribution is without a magnetic field, which leads to a symmetric distribution of velocity, and when the intensity of the Hartman field is increases as $(Ha)$ goes up, then this change causes a decrease in the flow pattern and the magnitude of velocity from $(20.9-11)$ for corresponding values of magnetic flow control parameter $(Ha=0, 10, 20,$ and $40).$ The observed phenomena can be explained physically by the resistive nature of the magnetic field, which acts against the motion of the fluid. Consequently, the revealed behavior can be attributed to this inherent resistance of the Hartman field. The contour plots of the isotherms have been presented for various magnetic flow parameter, with a volume fraction of $\phi =0.03$. A noticeable pattern is observed among the isotherms for different magnetic flow control parameter $(Ha)$. The isotherms for $Ha=0$ indicate a more significant curvature than those for $(Ha=10$ $\&$ $20),$ indicating that the convectional heat dissipation is more prominent when the magnetic flux strength is absent. The temperature flow becomes more controlled when $(Ha)$ is increased. Enhanced values of $(Ha)$ correspond to potent Hartman field, acknowledged as the Lorentz force field, which acts counter to fluid flow, convection and heat transport. Enhancing the heat dissipation and transfer performance of the system is attainable by introducing a magnetic field. In relation to the ramification of the Hartmann number $(Ha)$ on the temperature distribution, it is evident that the temperature decreases throughout the domain. This behavior can be attributed to the dominance of convection over conduction at lower Hartmann number values, leading to particle motion and an accompanying increase in kinetic energy, ultimately resulting in an elevation of the temperature.

Figure 10 comprehensively represents the variation in the Hartman number $(Ha)$ portrayed by the graph of the Nusselt number against the Rayleigh number $(Ra).$ A clear and significant trend is noticed for Hartman number; there is a pronounced and remarkable decline in the associated Nusselt number as the Hartman number $(Ha)$ increases. The presence of a Hartman field weakens the ability of the fluid to transfer heat through convection. The average heat transfer rate ($Nu$ _avg) signifies the efficiency of convective heat flow.

Fig. 10

Variation in average Nusselt number $({\text{Nu}}_{\text{avg}})$ against Rayleigh number $(\text{Ra})$ and Hartmann number $(\text{Ha})$

5.4 Impact of ${\varvec{\phi}}$ on streamlines and isotherms.

Figure 11 visually represents the relationship between volume fraction $(\phi )$ and the Rayleigh number $(Ra)$ for the velocity streamlines and temperature isotherms contours which provide a comprehensive view of the velocity and temperature profiles. Figure 11 effectively demonstrates the temperature and velocity profiles across a range of Rayleigh numbers $(Ra={10}^{3}-{10}^{6})$ for varying values of volume friction $(\phi )$.

Fig. 11

Effect of nanoparticle volume fraction $(\phi )$ on velocity and temperature profiles

The $(\phi )$ values correspond to the concentration of volume fraction, for $(\phi =0)$ represents the simple fluid, while the other values of $(\phi )$ represent the nanofluid with different concentrations. This visual representation illustrates the behavior of the velocity profile change with changing conditions. The streamlines of the velocity profile exhibit stability and same flow pattern across the entire domain as the value of $(\phi )$ increases, although the fluid's velocity increases gradually when the value of $(\phi )$ increases. This suggests a clear and proportional relationship between $(\phi )$ and the fluid's velocity. Across all $(\phi )$ values, augmenting the volume fraction of nanoparticles induces a rise in fluid viscosity, leading to the attenuation of both buoyancy force and flow velocity. Consequently, this leads to a decline in the stream function values as the fluid's resistance to motion intensifies due to increased nanoparticle concentration. The temperature isotherms in the profile exhibit an exponential increase with the value of $(\phi )$. This pattern of behavior reveals the substantial effect that a change in volume fraction $(\phi )$ on the fluid's temperature distribution provides informative and creative information on heat transfer. A positive correlation is observed between the isotherm maps and the fractional volume $(\phi )$ of nanoparticles, as the augmentation and accumulation of nanoparticles elevate the thermic transmission of the base fluid due to their inherent characteristics, leading to an amplification in convection and heat transfer rate.

Figure 12 comprehensively compares different values of $(\phi )$ and their corresponding average Nusselt numbers, plotted against a range of Rayleigh numbers. These findings demonstrate that with an increase in the value of $(\phi )$, proportional elevation in average Nusselt number also exhibits a proportional increase. This relationship indicates that higher $(\phi )$ values correspond to enhanced heat transfer rates within the system.

Fig. 12

Variation in average Nusselt number $(\text{Nu}$ _avg $)$ against nanoparticle volume fraction $\upphi$ and Rayleigh number (Ra)

5.5 Impact of Ha and ${\varvec{\phi}}$ on streamlines and isotherms.

Figures 13, 14 provide a visual representation of the isotherms and streamlines for the correlation between the volume fraction $(\phi )$ of nanofluid and the magnitude of the Hartman field (Hartman number) while the other parameters are kept constant. This visualization showcases a comprehensive understanding of the velocity (streamlines) and temperature (isotherms) profiles. The values of the MHD parameter $(Ha)$ represent the strength of the Hartman field, while $(\phi )$ represents the concentration of nanoparticles. The velocity profile exhibits symmetric and regular behavior in the absence of the magnetic field$(Ha=0)$. However, introducing the magnetic field disrupts the pattern of velocity streamlines. When the Hartman number $(Ha)$ increases for the constant concentration of nanoparticles $\left(\phi =0\right)$, the velocity profile decreases, and velocity magnitude at$(Ha=0)$,$(Ha=10)$, and $(Ha=20)$ measures 19.8, 17.9 and 15.3, respectively, while for $(\phi =0.09)$ and at$(Ha=0 ,Ha=10$, and $Ha=20)$ the velocity magnitudes are 24.2, 21.3, and 17, respectively. An escalating in the Hartmann number $(Ha)$ results causes a reduction in velocity magnitude, indicating a weakening of convection strength. Concurrently, the growth of $Ha$ leads to an increase in boundary layer thickness. Moreover, as the intensity of ferroparticles increases from $0.0$ to 0.09, the velocity field strength diminishes along with the convective force due to the amplified effective viscosity of the mixture.

Fig. 13

Effect of nanoparticles volume fraction on the velocity profile in the presence of magnetic field

Fig. 14

Effect of nanoparticles volume fraction on the temperature profile in the presence of magnetic field

Isotherms at $(\text{Ha}=0)$ display more pronounced curvature than those at $(\text{Ha}=20)$. When $(\text{Ha}=0)$, the convective thermal transport is stronger and the flow becomes more regular with an increase in the Hartmann number. The stronger Hartman field is introduced by an escalate in $(\text{Ha})$, which counteracts fluid flow, convection, and heat transfer. Additionally, increasing magnetic field and the level of ferroparticles concentration rises from $0.0$ to $0.09,$; then, the thickness of the buoyancy layer decreases which causes the cooling system. Higher Hartmann numbers $(\text{Ha})$ generate a stronger Lorentz force field that opposes fluid flow, convection, and heat transfer. Additionally, increasing ferroparticle concentration from 0.0 to 0.09 reduces the buoyancy layer thickness, resulting in less curved isotherms that align closely with the inner cylinder.

Figure 15 presents a brief visual of the magnetic strength parameter $(Ha)$ by the graph of the average convective heat transfer rate ($Nu$ _avg) for two different Rayleigh numbers $(Ra={10}^{5},{10}^{6})$. The visuals demonstrate the inverse relationship between the increasing Hartman number $(Ha)$ and the decreasing average Nusselt number, indicating a reverse trend. This behavior is observed for two different Rayleigh numbers, with $Ra={10}^{5}$ demonstrating a gradual decrease and $Ra={10}^{6}$ exhibiting a significant decline. For $(Ra={10}^{5})$ and $(Ha=\text{0,10} \& 20)$ equal space-decreasing behavior can be seen, while for $(Ra={10}^{6})$, a drastic decrease occurs for the same values for $Ha$.

Fig. 15

Variation in average Nusselt number ${(Nu}_{avg})$ against nanoparticle volume fraction $(\phi )$ and Hartman number $(Ha)$

Figure 16 depicts average heat transfer coefficient ($Nu$ _avg) for different values of $(Ha)$ and $(\phi )$; it is clearly demonstrated that the behavior of average Nusselt number decreases by increasing $(Ha)$ number with the influence of $(\phi )$.

Fig. 16

Variation in average Nusselt number $(Nu$ _avg $)$ against nanoparticle volume fraction $(\phi )$ and Hartman number $(Ha).$

5.6 Residue versus iteration

Figures 17, 18 depicting the residue versus the number of iterations present a comprehensive view of the iterative process and its impact on reducing computational error. The residue progressively decreases as the number of iterations increases, demonstrating the efficiency of the iterative process in improving the outcome and attaining greater precision.

Fig. 17

Velocity and temperature residue plots

Fig. 18

Residue vs iteration plot

6 Conclusion

This section contains a summarized discussion of the numerical investigation of natural convection in a hexagonal-shaped cavity filled with a Newtonian ferrofluid containing a corrugated circular cylinder. The study explored various parameters $(Ra)$, $(Ha)$, and $(\phi )$ values while keeping the Prandtl number $(Pr=6.8377)$. Graphics and tabulated presentations were utilized to present qualitative and quantitative depiction from the numerical results. Additionally, relevant literature could be referenced to validate the experimental findings. The following points from the findings and investigation are illustrated.

• The heat transfer rate $\left({Nu}_{avg}\right)$ increased in proportion to the increase in the Rayleigh number $(Ra).$

• As the number of corrugations in the inner circular cylinder increased, the associated enhancement in the heat transfer rate is occurred.

• An increase in the Hartman number $(Ha)$ leads to a reduction in the heat transfer through natural convection.

• The heat transfer becomes more efficient when the concentration of nanoparticles rises.

• Under the influence of a magnetic field, the heat transfer demonstrates higher effectiveness in simple fluids when compared to ferrofluids.

7 Future recommendations

The future recommendations are: including the exploration of various geometric positions within the hexagonal cavity, conducting parametric studies to analyze the effects of different parameters, considering experimental validation to the complement of the numerical findings, and exploring optimization and design considerations to enhance the heat transfer efficiency and the fluid flow characteristics. These directions will contribute to advancing our understanding of the subject matter and have practical implications for engineering applications.