1 Introduction

Thermal energy transport improvement in energy devices has received significant attention for its importance and direct implication in many engineering applications and has been studied widely in the last decade in the literature. Many researchers have considered nanofluids as a working medium for the simple reason that the presence of nanoparticles boosts the thermal conductivity of the mixture, making it a viable candidate for heat removal techniques. It is one of the best solutions, which was discovered for the first time by Choi et al. [1].

In addition to employing nanofluids, we discovered that there is another alternative, depicted in a mixture of various mediums. It depicts a confined area that has been partially filled with a porous layer with a permeable interface and saturated by a nanofluid, which can be divided vertically or horizontally depending on the applications. Numerous industrial and environmental applications call for these techniques. Among the uses are fuel cells, solar collectors, and fibrous thermal insulation. Beavers and Joseph [2] made the first attempts to analyze natural convection flow heat transfer between a porous medium and a homogeneous fluid experimentally and analytically by focusing on the boundary condition at the fluid/porous interface. Li and Hu [3, 4] investigated the impacts of stress jump, stress continuity, and thermal interface conditions at the fluid-porous interface of a channel, which was partially filled with porous media. According to the results, for larger Darcy numbers and stress jump coefficients, the Nusselt number anticipated by the stress jump condition differs somewhat from the value predicted by the stress continuity condition. Hu and Li [5] investigated the effects of the partially porous medium under forced convection conditions analytically, and the porous medium was modeled using the Darcy-Brinkman technique. They found precise temperature distribution solutions for both local thermal non-equilibrium (LTNE) and local thermal equilibrium (LTE) conditions. They looked at both solid and fluid heat sources and discovered that having extra source terms caused singularities in the Nusselt number. They discovered more than one singularity when the porous filling ratio was raised. In a rectangular enclosure, Mehryan et al. [6] explored the conjugate natural convection flow and heat transfer of hybrid nanofluids. Alsabery et al. [7] investigated the Darcian natural convection of a nanofluid in a trapezoidal cavity partially filled with porous media numerically. The inclusion of silver-water nanofluid boosted convection heat transfer considerably, and the heat transfer rate was controlled by the inclination angle of the cavity. The distinction between two main types of fluid flow interfacial conditions, which are depicted in clear fluid and porous medium, is investigated by Rashidi et al. [8]. Chamkha and Ismael [9] used the Darcy-Brinkman model to tackle the problem of a differentially heated and vertically partly stratified porous cavity filled with nanofluid via natural convection. Sheremet et al. [10] reported the results of a numerical study of natural convection and heat transfer within a horizontal concentric annulus filled with a porous medium and saturated with a Cu–water nanofluid. This study investigated the effects of the Rayleigh number, porosity of the porous medium, radius ratio, and the media’s solid matrix (glass balls and aluminum foam) on the Nusselt number and flow regime. Karimi et al. [11] investigated the forced convection in a channel partially filled with a porous material and exposed to a constant wall heat flux analytically. Mahmoudi et al. [12] looked at the heat behavior of a channel with a porous layer in the middle. The results revealed that an ideal porous thickness of 0.8 will optimize the Nusselt number with a suitable pressure drop under model A, which more closely resembles the LTE model than model B. Additionally, the impact of inertia factors on heat transmission under models A and B was explored. Astanina et al. [13] investigated numerically free convection in a square cavity with two adhering porous blocks in the center. The obtained results revealed that the Darcy number improves heat transfer at the hot wall, but increasing the size of the porous layers reduces the heat transfer rate at this hot wall. Chamkha and Ismael [14] analyzed the conjugate free convection-conduction heat transfer in a square domain formed of a porous cavity filled with nanofluids and heated by a triangle solid wall. Their findings suggested that heat transfer enhancement occurred when the wall thickness was greater than a critical value and that this critical value grew as the Rayleigh number rose. By using Buongiorno’s model, Tahmasebi et al. [15] investigated the natural convection heat transfer in a cavity filled with three layers of solid, porous medium, and free fluid. Yang et al. [16] compared the effects of the stress-jump condition and the B-J condition on the fluid flow in a partially filled porous channel under the Darcy model and the Brinkman-extended Darcy model and looked into the errors for the interface velocity, predicted by the velocity slip coefficient and the stress jump coefficient. Torabi et al. [17, 18] derived semianalytical solutions for temperature profiles and the Nusselt number using the LTNE model to investigate thermal performance, including entropy generation, in a partly porous channel. Saryazdi et al. [19] demonstrated that raising the particle volume fraction increases the Nusselt number. Furthermore, wall shear stresses are enhanced. Under the LTNE model, five temperature conditions with a slip velocity condition for the porous-fluid interface were examined by Yang and Vafai [20]. Bendaraa et al. [21] studied the problem of natural convection in an inclined square cavity filled with a Cu/water nanofluid under a differentially heated configuration in the presence of a magnetic field that tracks the cavity in its inclination. Foukhari et al. [35] evaluated free convection in a coaxial cylinder enclosure filled by a porous medium and filled by a nanofluid using various nanoparticle shapes, and they discovered that heat transmission is better with cylindrical nanoparticles than spherical nanoparticles. Foukhari et al. [36] explored free convection heat transfer in an annular area within two coaxial cylinders partially filled by a porous medium with a permeable interface and submerged by a nanofluid (Cu–water).

In recent years, the analysis of convection has attracted a growing interest from researchers, who have explored various aspects of convection to gain a deeper understanding of its mechanisms and behaviors. Venkatadri [37] examined the effects of flow in a partially filled porous zone on transverse magnetic flux vectors and heatline visualization. Biswas et al. [38] investigated thermal radiation and chemical reactions using a two-dimensional Maxwell magnetohydrodynamic nanofluid throughout an extended sheet. Venkatadri et al. [39, 40] investigated heat flow visualization in a trapezoidal cavity utilizing energy flux vectors with the impact of thermal radiation as a simulation of high-temperature fuel cell operations. Venkatadri et al. [41] studied several factors for measuring the increase in heat transfer in diverse practical applications by natural convection in porous media. Afikuzzaman et al. [42] used an explicit finite difference approach to analyze an unstable MHD Casson fluid flow across a parallel plate with hall current. Ahmmed et al. [43] demonstrate unstable MHD-natural nanofluid convection motion over an accelerating inclined plate inserted into a porous  medium with adjustable thermal conductivity. Afikuzzaman et al. [44] studied the natural convection of a Casson fluid bounded by two parallel non-conducting plates in the presence of a hall current. Venkatadri et al. [45] examined numerically the effect of a baffle on the natural convection of a water-Fe3O4 nanofluid in a C-shaped container in the presence of a magnetic field. Rashed et al. [46] looked at the characteristics of nanofluids surrounding a cylinder for laminar steady-state axisymmetric flow. Rashed et al. [47] examined a two-phase model for mixed convection magnetohydrodynamic (MHD) flow combining hybrid nanoparticles, using the Three Parameter Group Transformation Method to simplify the mathematical model. Biswas et al. [48] looked at MHD natural convection and heat transport flux through a vertical porous plate while a chemical reaction was present. Abu-Nab et al. [49] presented the findings of a theoretical model of the growing bubbles at small Mach number in a generalized Newtonian fluid under the influence of magnetic field and shear stress, in which they highlighted the significance of the model’s findings for the mechanism of bubble growth in a generalized Newtonian fluid at small Mach number. Over the last two years, there have been a number of studies into the dynamics of bubbles and their behavior in different cases. Abu-bakr et al. [50] examined the behavior of spherical bubbles close to a stiff wall. They concluded that the wall’s presence considerably affected bubble growth and caused a considerable difference in the velocities of the interfaces for the both cases: close to and far from the wall. Abu-Nab and Abu-Bakr [51] carefully examined the nonlinear multibubble model while taking into account the interaction between bubbles in a \(Cu-Al_{2}O_{3}\)/water hybrid nanofluid over the radius of the vapor bubble in Newtonian media. Abu-Nab et al. [52] focused on the theoretical analysis of the pressure relaxation time of N-dimensional spherical bubble dynamics submerged in \({\text{H}}_{2} {\text{O}}\)/\({\text{H}}_{2} {\text{O}}\) nanofluid. They demonstrated how the diameter and volume concentration of nanoparticles can both dramatically shorten the time required for pressure relaxation. Shalaby et al. [53] investigated the behavior of a spherical bubble in an N-dimensional fluid composed of vapor and superheated liquid. They demonstrated that as the value of N-dimensions decreases, the radius of the bubble grows. Abu-Nab et al. [54] investigated the influence of heat transmission on the temperature distribution in a superheated liquid during the formation of vapor bubbles immersed in various types of nanoparticles  in a two-phase turbulent flow.

The objective of this study was to understand how the process of natural convection works via an annular, partially porous space between two coaxial cylinders with a permeable interface saturated by a Newtonian nanofluid. The simulations discovered provide some insight into potential applications, like the development of new heat exchanger designs. This discovery could lead to the creation of new types of heat exchangers that use natural convection and porous materials to optimize heat transmission. These heat exchangers have potential uses ranging from (heating, ventilation, and air conditioning) systems to industrial operations.

2 Mathematical formulation

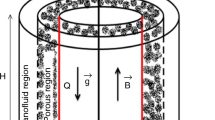
In the current research, we examined an enclosure formed of vertical concentric cylinders with a height of H. The annular space between the two vertical cylinders is partially filled with a porous medium with a thickness of Xp and located on the lateral surface of the inner cylinder Fig. 1. The porous and free regions are saturated by a Newtonian Cu–water nanofluid. The base walls are isolated and impermeable. The inner and outer cylinders are kept at a constant hot and cold temperature, respectively. The flow under consideration is steady in a laminar, incompressible, homogeneous, and isotropic porous medium. The double-domain approach is used in this study to overcome the interface’s restriction on grid localization. The governing equations are formulated based on the formulation of stream function and vorticity under the Boussinesq approximation, [22, 23]. The dimensional governing equations for continuity, momentum, and energy are defined as follows [24].

Fig. 1
figure 1

Physical problem schematic: (a) the 3D geometry (b) the cross section

Full size image

For the porous layer

$$\begin{aligned}{} & {} \frac{1}{r}\frac{\partial (rU)}{\partial r}+\frac{\partial W}{\partial z}=0, \end{aligned}$$
(1)
$$\begin{aligned}{} & {} \begin{aligned} \frac{1}{\epsilon ^{2}}\left( \frac{\partial (U\Omega )}{\partial r}+\frac{\partial (W\Omega )}{\partial z} \right)&=\frac{\mu _{{\mathrm{{{nf}}}}}}{\epsilon .\rho _{{\mathrm{{{nf}}}}}}\left( \frac{\partial ^{2}\Omega }{\partial r^{2}}-\frac{\Omega }{r^{2}}+\frac{1}{r}\frac{\partial \Omega }{\partial r}+\frac{\partial ^{2}\Omega }{\partial z^{2}}\right) -\frac{\mu _{{\mathrm{{{nf}}}}}}{K.\rho _{{\mathrm{{{nf}}}}}}\Omega \\&-\beta _{Tnf}.g\frac{\partial T}{\partial r}, \end{aligned} \end{aligned}$$
(2)
$$\begin{aligned}{} & {} \frac{\partial (UT)}{\partial r}+\frac{\partial (WT)}{\partial z}+\frac{UT}{r}= \alpha _{{\mathrm{{{eff}}}}}\left( \frac{\partial ^{2}T}{\partial r^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{\partial ^{2} T}{\partial z^{2}}\right) . \end{aligned}$$
(3)

For the nanofluid layer

$$\begin{aligned}{} & {} \frac{1}{r}\frac{\partial (rU)}{\partial r}+\frac{\partial W}{\partial z}=0, \end{aligned}$$
(4)
$$\begin{aligned}{} & {} \frac{\partial (U\Omega )}{\partial r}+\frac{\partial (W \Omega )}{\partial z} =\frac{\mu _{{\mathrm{{{nf}}}}}}{\rho _{{\mathrm{{{nf}}}}}}\left( \frac{\partial ^{2}\Omega }{\partial r^{2}}-\frac{\Omega }{r^{2}}+\frac{1}{r}\frac{\partial \Omega }{\partial r}+\frac{\partial ^{2}\Omega }{\partial z^{2}}\right) -\beta _{Tnf}g.\frac{\partial T}{\partial r}, \end{aligned}$$
(5)
$$\begin{aligned}{} & {} \frac{\partial (UT)}{\partial r}+\frac{\partial (WT)}{\partial z}+\frac{UT}{r}= \frac{\partial ^{2} T}{\partial r^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{\partial ^{2}T}{\partial z}^{2}. \end{aligned}$$
(6)

In order to normalize these governing equations, the following no-dimensional parameters are introduced, for length, velocity, vorticity, stream function, and temperature \(\left( R_{e}, \frac{\alpha _{m}}{R_{e}}, \frac{\alpha _{m}}{R_{e}^{2}},(\alpha _{m}.R_{e}),(T_{h}-T_{c})\right)\), where m refers to nf or eff. However, the nondimensional set of conservation equations can be written as [24]:


For the porous layer

$$\begin{aligned}{} & {} \frac{1}{{\overline{r}}}\frac{\partial ({\overline{rU}})}{\partial {\overline{r}}}+\frac{\partial {\overline{W}}}{\partial {\overline{z}}}=0, \end{aligned}$$
(7)
$$\frac{1}{{\epsilon^{2} }}\left( {\frac{{\partial (\overline{{U\Omega }} )}}{{\partial \bar{r}}} + \frac{{\partial (\overline{{W\Omega }} )}}{{\partial \bar{z}}}} \right) = \bar{\lambda }.\Gamma .\Sigma .{\text{Pr}}\left( {\frac{{\partial ^{2} \bar{\Omega }}}{{\partial \bar{r}^{2} }} + \frac{1}{{\bar{r}}}\frac{{\partial \bar{\Omega }}}{{\partial \bar{r}}} + \frac{{\partial ^{2} \bar{\Omega }}}{{\partial \bar{z}^{2} }}} \right) + \left( { - \bar{\lambda }.\Sigma \frac{{{\text{Pr}}}}{{{\text{Da}}}} - \bar{\lambda }.\Gamma .\Sigma \frac{{{\text{Pr}}}}{{\bar{r}^{2} }}} \right)\bar{\Omega } - \Lambda .\bar{\lambda }^{2} .{\text{Ra}}.{\text{Pr}}.\frac{{\partial \bar{T}}}{{\partial \bar{r}}},{\text{ }}$$
(8)
$$\begin{aligned}{} & {} \frac{\partial ({\overline{UT}})}{\partial {\overline{r}}}+\frac{\partial ({\overline{WT}})}{\partial {\overline{z}}}+\frac{{\overline{UT}}}{{\overline{r}}}= \frac{\partial ^{2}{\overline{T}}}{\partial {\overline{r}}^{2}}+\frac{1}{{\overline{r}}}\frac{\partial {\overline{T}}}{\partial {\overline{r}}}+\frac{\partial ^{2}{\overline{T}}}{\partial {\overline{z}}^{2}}. \end{aligned}$$
(9)

For the nanofluid layer

$$\begin{aligned}{} & {} \frac{1}{{\overline{r}}}\frac{\partial ({\overline{rU}})}{\partial {\overline{r}}}+\frac{\partial {\overline{W}}}{\partial {\overline{z}}}=0, \end{aligned}$$
(10)
$$\begin{aligned}{} & {} \frac{\partial (\overline{U\Omega })}{\partial {\overline{r}}}+\frac{\partial (\overline{W\Omega })}{\partial {\overline{z}}} =\Sigma .Pr\left( \frac{\partial ^{2}{\overline{\Omega }}}{\partial {\overline{r}}^{2}}+\frac{1}{{\overline{r}}}\frac{\partial {\overline{\Omega }}}{\partial {\overline{r}}}-\frac{{\overline{\Omega }}}{{\overline{r}}^{2}}+\frac{\partial ^{2}{\overline{\Omega }}}{\partial {\overline{z}}^{2}}\right) -\Lambda .Ra.Pr.\frac{\partial {\overline{T}}}{\partial {\overline{r}}}, \end{aligned}$$
(11)
$$\begin{aligned}{} & {} \frac{\partial ({\overline{UT}})}{\partial {\overline{r}}}+\frac{\partial ({\overline{WT}})}{\partial {\overline{z}}}+\frac{{\overline{UT}}}{{\overline{r}}}= \frac{\partial ^{2}{\overline{T}}}{\partial {\overline{r}}^{2}}+\frac{1}{{\overline{r}}}\frac{\partial {\overline{T}}}{\partial {\overline{r}}}+\frac{\partial ^{2}{\overline{T}}}{\partial {\overline{z}}^{2}}. \end{aligned}$$
(12)

The vorticity function and the velocity fields are defined as:

$$\begin{aligned} \Omega =\frac{1}{r}\left( \frac{\partial ^{2}\Psi }{\partial r^{2}}-\frac{1}{r}\frac{\partial \Psi }{\partial r}+\frac{\partial ^{2}\Psi }{\partial z^{2}}\right) , \quad \quad {\overline{U}}=\frac{1}{{\overline{r}}}\frac{\partial {\overline{\Psi }}}{\partial {\overline{z}}}, \quad \quad {\overline{W}}=-\frac{1}{{\overline{r}}}\frac{\partial {\overline{\Psi }}}{\partial {\overline{r}}}. \end{aligned}$$
(13)

Where,

$$\begin{aligned} \Gamma= & {} \frac{\mu ^{*}}{\mu _{{\mathrm{{{nf}}}}}}, \quad \quad \alpha _{{\mathrm{{{nf}}}}}=\frac{\lambda _{{\mathrm{{{nf}}}}}}{\left( \rho Cp\right) _{{\mathrm{{{nf}}}}}}, \quad \quad \alpha _{{\mathrm{{{eff}}}}}=\frac{\lambda _{\mathrm{{{eff}}}}}{\left( \rho Cp\right) _{\mathrm{{{nf}}}}},\quad \quad {\overline{\lambda }}=\frac{\lambda _{\mathrm{{{nf}}}}}{\lambda _{\mathrm{{{eff}}}}}, \end{aligned}$$
(14)
$$\begin{aligned} \Sigma= & {} \frac{(1-\phi )^{-2.5}\left( (1-\phi )+\phi \frac{(\rho C)_{np}}{(\rho C)_{bf}}\right) }{\frac{\lambda _{\mathrm{{{nf}}}}}{\lambda _{bf}}\left( (1-\phi )+\phi \frac{\rho _{np}}{\rho _{bf}}\right) }, \end{aligned}$$
(15)
$$\begin{aligned} \Lambda= & {} \frac{\left( (1-\phi )+\phi \frac{(\rho \beta )_{np}}{(\rho \beta )_{bf}}\right) }{\left( (1-\phi )+\phi \frac{\rho _{np}}{\rho _{bf}}\right) \left( \frac{\frac{\lambda _{\mathrm{{{nf}}}}}{\lambda _{bf}}}{(1-\phi )+\phi \frac{(\rho C)_{np}}{(\rho C)_{bf}}}\right) ^{2}}, \end{aligned}$$
(16)
$$\begin{aligned} \lambda _{\mathrm{{{eff}}}}= & {} (1-\epsilon )\lambda _{p}+\epsilon \lambda _{\mathrm{{{nf}}}}. \end{aligned}$$
(17)

The dimensionless numbers in the above equations are:

$$\begin{aligned} Ra=\frac{\rho _{bf}g\beta _{Th}(T_{h}-T_{c}).R_{e}^{3}}{\mu _{bf}\alpha _{bf}}, \quad \quad Pr=\frac{\mu _{bf}}{\rho _{bf}\alpha _{bf}}, \quad \quad Da=\frac{k}{R_{e}^{2}}. \end{aligned}$$
(18)

Mahian et al. [25] stated the thermo-physical properties of the nanofluid, which are dependent on both the base fluid and the nanoparticles.

$$\begin{aligned} \begin{aligned} \rho _{\mathrm{{{nf}}}}&=(1-\phi )\rho _{bf}+\phi \rho _{np},\\ \left( \rho \beta \right) _{\mathrm{{{nf}}}}&=(1-\phi )\left( \rho \beta \right) _{bf}+\phi \left( \rho \beta \right) _{np},\\ \left( \rho C_{p}\right) _{\mathrm{{{nf}}}}&=(1-\phi )\left( \rho C_{p}\right) _{bf}+\phi \left( \rho C_{p}\right) _{np}. \end{aligned} \end{aligned}$$
(19)

The following relationship was provided by Hamilton and Crosser in order to determine a nanofluid’s thermal conductivity [26].

$$\begin{aligned} \frac{\lambda _{\mathrm{{{nf}}}}}{\lambda _{bf}}=\frac{\lambda _{np}+(n-1)\lambda _{bf}+(n-1)(\lambda _{np}-\lambda _{bf})\phi }{\lambda _{np}+(n-1)\lambda _{bf}-(\lambda _{np}-\lambda _{bf}\phi }. \end{aligned}$$
(20)

Brinkman proposed the formula given below to determine the effective viscosity [27].

$$\begin{aligned} \frac{\mu _{\mathrm{{{nf}}}}}{\mu _{bf}}=\frac{1}{(1-\phi )^{-2.5}}. \end{aligned}$$
(21)

The boundary conditions

$$\begin{aligned}{} & {} {\overline{T}}=1,\, {\overline{\Psi }}=\frac{\partial {\overline{\Psi }}}{\partial {\overline{r}}}=\frac{\partial {\overline{\Psi }}}{\partial {\overline{z}}}=0,\, {\overline{\Omega }}=\frac{2}{\Delta {\overline{r}}^{2}}{\overline{\Psi }}\vert _{\Delta {\overline{r}}}. \quad {\overline{r}}=0.5\,;\, 0\le {\overline{z}} \le AL. \end{aligned}$$
(22)
$$\begin{aligned}{} & {} {\overline{T}}=0,\, {\overline{\Psi }}=\frac{\partial {\overline{\Psi }}}{\partial {\overline{r}}}=\frac{\partial {\overline{\Psi }}}{\partial {\overline{z}}}=0,\, {\overline{\Omega }}=\frac{2}{\Delta {\overline{r}}^{2}}{\overline{\Psi }}\vert _{0.5-\Delta {\overline{r}}}. \quad {\overline{r}}=1 \,;\, 0\le {\overline{z}} \le AL. \end{aligned}$$
(23)
$$\begin{aligned}{} & {} \frac{\partial {\overline{T}}}{\partial {\overline{z}}}=0,\, {\overline{\Psi }}=\frac{\partial {\overline{\Psi }}}{\partial {\overline{r}}}=\frac{\partial {\overline{\Psi }}}{\partial {\overline{z}}}=0,\, {\overline{\Omega }}=\frac{1}{\overline{r}}\frac{2}{\Delta {\overline{z}}^{2}}{\overline{\Psi }}\vert _{\Delta {\overline{z}}}.\quad 0.5\le {\overline{r}} \le 1 \,; \, {\overline{z}}=0. \end{aligned}$$
(24)
$$\begin{aligned}{} & {} \frac{\partial {\overline{T}}}{\partial {\overline{z}}}=0, \, {\overline{\Psi }}=\frac{\partial {\overline{\Psi }}}{\partial {\overline{r}}}=\frac{\partial {\overline{\Psi }}}{\partial {\overline{z}}}=0, \, {\overline{\Omega }}=\frac{1}{\overline{r}}\frac{2}{\Delta {\overline{z}}^{2}}{\overline{\Psi }}\vert _{AL-\Delta {\overline{z}}}.\quad 0.5\le {\overline{r}} \le 1 \,; \, {\overline{z}}=AL. \end{aligned}$$
(25)

The interface conditions are expressed as

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle {{\overline{T}}_{\mathrm{{{nf}}}}={\overline{T}}_{p}, \quad \frac{\partial {\overline{T}}_{\mathrm{{{nf}}}}}{\partial {\overline{r}}}=\frac{\lambda _{\mathrm{{{eff}}}}}{\lambda _{\mathrm{{{nf}}}}}\frac{\partial {\overline{T}}_{p}}{\partial {\overline{r}}}.}\\ \displaystyle {{\overline{\Psi }}_{\mathrm{{{nf}}}}={\overline{\Psi }}_{p}, \quad \frac{\partial {\overline{\Psi }}_{\mathrm{{{nf}}}}}{\partial {\overline{r}}}=\frac{\lambda_{eff}}{\lambda_{nf}}\frac{\mu _{\mathrm{{{eff}}}}}{\mu _{\mathrm{{{nf}}}}}\frac{\partial {\overline{\Psi }}_{p}}{\partial {\overline{r}}}.}\\ \displaystyle {{\overline{\Omega }}_{\mathrm{{{nf}}}}={\overline{\Omega }}_{p}, \quad \frac{\partial {\overline{\Omega }}_{\mathrm{{{nf}}}}}{\partial {\overline{r}}}=\frac{\lambda_{eff}}{\lambda_{nf}}\frac{\mu _{\mathrm{{{eff}}}}}{\mu _{\mathrm{{{nf}}}}}\frac{\partial {\overline{\Omega }}_{p}}{\partial {\overline{r}}}.} \end{array} \right. \quad At \, {\overline{r}}=0.5+X_{p}; \, 0\le {\overline{z}} \le AL. \end{aligned}$$
(26)

The average Nusselt number is used to express the rate of heat transfer coefficient at the active wall, which is given by [55]:

$$\begin{aligned} {\text{Nu}}_{\mathrm{{{Average}}}} =\frac{1}{AL}\frac{\lambda _{\mathrm{{{eff}}}}}{\lambda _{bf}}\int _{0}^{AL} \frac{\partial {\overline{T}}_{\mathrm{{{nf}}}}}{\partial {\overline{r}}}\mathrm{{d}}{\overline{z}}. \end{aligned}$$
(27)

3 Numerical methods

To derive the flow and temperature fields, the sets of dimensionless governing equations associated with the specified boundary conditions are numerically solved, and this comes down to the fact that these problems are characterized by their complexity and nonlinearity. Finite difference discretization is a method used to approximate the solutions of differential equations by discretizing the domain into a finite set of grid points. The governing equations of vorticity and energy are then approximated using the central difference scheme at each grid point. Once the equations have been discredited, the Alternation Direction Implicit (ADI) method is employed to solve the governing algebraic equations, while the stream function equation is solved using the Successive Over Relaxation (SOR) method [28]. This iterative method is a modification of the Gauss-Seidel method, which is used to solve the equations by updating the values of the unknowns at each iteration using a weighted average (typically between 1 and 2). This approach is particularly useful for solving sparse matrices, which often arise from discretizing partial differential equations. The central difference approximation is used to examine the dynamic field at each grid point for the velocity components. The flow chart of the numerical simulation is shown in Fig. 2. The procedure of iteration was continued until the highest relative change in all dependent variables exceeded the condition.

$$\begin{aligned} \frac{\sum _{i}\sum _{j}\mid f_{i,j}^{n+1}-f_{i,j}^{n}\mid }{\sum _{i}\sum _{j}\mid f_{i,j}^{n}\mid }\le 10^{-5}. \end{aligned}$$
(28)

Table 1 represents a precision check performed with the finite difference approach and several mesh grid combinations. \({\text{Nu}}_{\mathrm{{{ave}}}}\) is used to evaluate the grid mesh independence of the current FORTRAN code. It is proven that (\(61 \times 121\)) is a good mesh size that assures grid independence.

Table 1 Grid independence test
Full size table
Fig. 2
figure 2

Flow chart for the numerical procedure of solution

Full size image
Table 2 Comparison of the average Nusselt number with other published data for \(Pr=0.7\)
Full size table
Fig. 3
figure 3

Comparison of our findings to previous published studies regarding temperature (a) and axial velocity (b) for \(Al_{2}O_{3}\) (\({\text{Ra}} = 10^{5}, Pr=0.7\))

Full size image

The current numerical code is validated by comparing our numerical data for \({\text{Ra}} = 10^{5}\) and \(Pr=0.7\) with numerical data of Abu Nada et al. [29] and experimental data of Krane and Jessee [34] Fig. 3a, 3b, and other data given in the literature Table 2. The interface conditions Eqs. (26) are numerically determined by taking five points, two on the left and two on the right of the interface, and the fifth concentrated at the interface. As a result, the following difference equations are used to compute the interface potentials:

$$\begin{aligned} \begin{aligned} {\overline{\Omega }}(i,j)&=\frac{4\overline{\Omega _{\mathrm{{{nf}}}}}(i+1,j)-\overline{\Omega _{\mathrm{{{nf}}}}}(i+2,j)+\lambda_{r}\mu _{r}\left( 4\overline{\Omega _{P}}(i-1,j)-\overline{\Omega _{p}}(i-2,j)\right) }{3\left( 1+\lambda_{r}\mu _{r} \right) },\\ {\overline{T}}(i,j)&=\frac{4\overline{T_{\mathrm{{{nf}}}}}(i+1,j)-\overline{T_{\mathrm{{{nf}}}}}(i+2,j)+\lambda _{r}\left( 4\overline{T_{P}}(i-1,j)-\overline{T_{p}}(i-2,j)\right) }{3\left( 1+\lambda _{r} \right) }. \end{aligned} \end{aligned}$$
(29)

Where, \(\mu _{r}=\frac{\mu _{\mathrm{{{eff}}}}}{\mu _{\mathrm{{{nf}}}}}, \lambda _{r}=\frac{\lambda _{\mathrm{{{eff}}}}}{\lambda _{\mathrm{{{nf}}}}}\) are the effective ratio of dynamic viscosity and thermal conductivity.

4 Results and discussion

The annular space inside two coaxial cylinders with an aspect ratio \((AL=H/R_{e})\) equal to 2 has been considered for this numerical simulation. This section displays the numerical results in graphical form to demonstrate the effect of the investigated parameters on heat transport. The nanofluid is thought to be made up of water as the base fluid \((Pr=6.2)\) and Cu nanoparticles, as illustrated in Table 3. The porous layer’s porosity is fixed at \(\epsilon =0.7\), which corresponds to glass \(\lambda _{p}=0.845W/m.K.\) The nanoparticle concentration range is \(0.01 \le \phi \le 0.05\).

Table 3 Thermo-physical properties of water and Cu [14]
Full size table
Fig. 4
figure 4

The isotherms and streamlines at \(\phi =0.05\), \(Da=10^{-2}\) for a\(\mid {\overline{\Psi }}\mid = 1.1977\), b\(\mid {\overline{\Psi }}\mid = 20.4275\)

Full size image

Figure 4 displays the distributions of streamlines and isotherms. For \({\text{Ra}} =10^{4}\), the entire enclosure is filled with one clockwise circular cell with a low maximum intensity flow, and the isotherms are more compact on the left bottom part, practically vertical. The flow becomes more intense when the Rayleigh number is increased to \({\text{Ra}}= 10^{6}\) Fig. 4.b. Indeed, a rise in the Rayleigh number may be explained by an increase in the inner cylinder’s heating energy, which causes the nanofluid to escape from the hot side in order to transmit energy to the cold side. We see that the flow on the nanofluid layer is more intense than the porous layer; this is due to the porous layer’s hydrodynamic resistance, which is the consequence of many brakes as friction is created by solid particles in the porous medium.

Fig. 5
figure 5

The isotherms and streamlines at \(\phi =0.05\), \({\text{Ra}}=10^{6}\) for a\(\mid {\overline{\Psi }}\mid = 11.2319\), b\(\mid {\overline{\Psi }}\mid = 20.4275\)

Full size image

Figure 5 illustrates the streamlines and isothermal distributions for various Da numbers. For \(Da= 10^{-5}\), the isotherms are almost vertical in the lower half, whereas the convection is boosted by an intensity’s flow \((\mid {\overline{\Psi }}\mid = 11.231)\). In this state, the fluid moves more slowly within the porous layer, resulting in a slower heat transfer rate. On the other hand, when the Da number increases, the strength of the flow increases Fig. 5.b, which can be explained by the porous media becoming more permeable or decreasing the characteristic diameter of the particles. That’s allowing more nanofluid to pass through the porous layer. While the isotherms become tighter, and the temperature gradient becomes more noticeable when the Darcy number increased to \(Da = 0.01.\)

The streamlines and isotherm distributions for various porosity levels are shown in Fig. 6. We see that the flow intensity is higher in the free region than in the porous region, and this is due to the localized hydrodynamic resistance in the porous region, which plays an important role as a brake in the flow. Moreover, as the porosity of the medium decreases, the intensity increases, which leads to a rise in the velocity in the free region. To be more understanding, the reduction of the porosity causes most of the fluid to escape to the free zone, while the remaining fluid in the porous region is impeded and mixed owing to the hydraulic resistance of impediments in the porous region. As a result, the velocity in the free zone increases.

Fig. 6
figure 6

The isotherms and streamlines at \(\phi =0.05\), \({\text{Ra}} = 10^{6}\), \(Da=10^{-2}\) for a\(\mid {\overline{\Psi }}\mid = 20.4275\), b\(\mid {\overline{\Psi }}\mid = 13.5261\)

Full size image

Figure 7 depicts the axial velocity component’s radial distribution at the enclosure’s midpoint for various Ra values and various Da numbers. The velocity profile within the porous layer changes from flat to parabolic as the permeability of the porous medium increases, causing a decrease in hydrodynamic resistance. Concerning the Rayleigh number, we can observe that when \({\text{Ra}} = 10^{6}\), the fluid flow is likely to be dominated by buoyant forces over viscosity, which causes the velocity to increase. Also, the axial velocity is positive in the porous region and negative in the nanofluid region, indicating that the nanofluid rises near the inner cylinder and falls near the outer cylinder; this alternance can be explained by one clockwise cell.

Fig. 7
figure 7

Axial velocity’s radial distribution for Pr=6.2, \(\epsilon =0.7\) and \(\phi =0.05\)

Full size image

Figure 8a depicts the average Nusselt variation along the inner cylinder for various volume fractions and for different Ra numbers. We can demonstrate from the figure that the average Nusselt number increases when the Rayleigh number increases, as shown in Fig. 4. This increase implies an intensification of fluid motion due to the dominance of buoyant forces, which leads to a more efficient transfer of thermal energy, resulting in a more efficient exchange of heat between the surface and the fluid. We also note the high values of the average Nusselt number for \(\phi = 0.05\), indicating the importance of nanoparticle concentration in improving heat transfer. For Fig. 8.b, we can demonstrate that the average Nusselt number rises as the Da number rises, a relationship that may be connected to an increase in permeability. This offers the nanofluid a great deal of freedom, which improves the rate of heat transmission in the active wall. Additionally, it should be noted that high Darcy numbers and nanoparticle volume fraction values result in a higher average Nusselt number.

Fig. 8
figure 8

Some parameters effect on average Nusselt number variation for different Ra and Da numbers at, \(\epsilon =0.7\) for Da=0.01 a and \({\text{Ra}} = 10^{5}\) b

Full size image

Figure 9 illustrates the evolution of the \({\text{Nu}}_{\mathrm{{{ave}}}}\) throughout the inner cylinder for various Rayleigh numbers and different effective thermal conductivity ratio \({\overline{\lambda }}\). We can observe that the average Nusselt number drops as the effective thermal conductivity ratio grows. That can be explained by the definition of the effective thermal conductivity ratio, which depicts the ratio between the thermal conductivity of the nanofluid and the porous medium that is saturated with the nanofluid. In which, with the drops of this parameter, the thermal conductivity of porous media will be more dominant, thus the heat transfer rate will start to increase, which shows the importance of using a porous material to boost the thermal energy transfer in the active wall.

Fig. 9
figure 9

The effective thermal conductivity ratio effect on average heat transfer for various Rayleigh number for \(Da=10^{-2}\)

Full size image

The evolution of the average Nusselt number around the inner cylinder for various nanoparticle concentrations and various porosity values is shown in Fig. 10. As shown in the graph, the heat transfer rate rises as the porosity number rises. As a result, the flow becomes more intense, and convection becomes more dominant. Furthermore, there is a critical point at which the average Nusselt number increases inversely with increasing nanoparticle concentration; below the critical point, the medium becomes less porous, and the addition of nanoparticles makes the medium more viscous, allowing the conduction mode to dominate. To gain a better understanding, the nanoparticles can fill the spaces between particles in a material, which can increase the material’s density and decrease its porosity.

Fig. 10
figure 10

Porosity effect on heat transfer rate for different nanoparticle concentrations for \(Da=10^{-2}\) and \({\text{Ra}} = 10^{6}\)

Full size image

5 Conclusion

In this study, we numerically examine the impacts of certain control parameters on fluid flow induced by natural convection heat transfer in an annular zone of concentric cylinders filled with porous media, such as porosity and porous layer thickness. The study region was saturated with a nanofluid made up of Cu nanoparticles and water. The controlled equations are modeled using the finite difference method. Furthermore, the problem was solved using the numerical code FORTRAN, and numerous verification examples were explored using published numerical and experimental data that show great agreement. As a result of the findings, it is possible to conclude:

  • The intensity of nanofluid flow circulation improves with increasing Rayleigh number Ra and Darcy number Da, but drops with increasing effective thermal conductivity.

  • Because of the porous layer’s hydrodynamic resistance, the flow intensity is higher for the nanofluid layer than for the porous layer, as illustrated by the streamlines.

  • The rate of thermal energy transfer within the active wall increases as the volume fraction of solid NPs increases.

  • The average Nusselt number increases as the porosity increases; there is also a critical point of porosity at which the heat transfer rate increases inversely with the variation in nanoparticle concentration.