Introduction

The constant increase in heat transfer requirements has led the thermal science community to consider new passive intensification approaches, which consist of improving thermal-hydraulic properties, particularly thermal conductivity. Most of these studies are designed to control heat and mass transfer rates. Therefore, numerous ways are suggested to increase the heat transfer strength, of which one is known as nanofluids, which was first presented by Choi et al. [1]. Heretofore, a number of studies have been done to determine how nanofluids affect the rate of heat transmission [2,3,4,5,6,7].

Furthermore, another approach was identified by mixing several medium types, which were divided vertically or horizontally depending on the application. Li et al. [8, 9] looked into the impact of stress jump, stress continuity, and interface conditions at the interface of a canal partially filled with porous media. Hu and Li [10] studied analytically the impact of porous media under forced convection using the Darcy–Brinkman approach for modeling the porous media. Mehryan et al. [11] studied how hybrid nanofluids conjugate free convection flow and thermal transmission in a container with a rectangular shape. Alsabery et al. [12] explored numerically the free convection of a nanofluid in a trapezoidal cavity partially, in which it is occupied by a porous channel, by regulating the inclination angle of the cavity. Rashidi et al. [13] investigated the distinctions between two important categories of fluid flow interface. Chamkha and Ismael [14] employed the Darcy–Brinkman model to solve the problem of a porous cavity with differential heating and partial vertical stratification that is filled by a nanofluid under natural convection. Mahdavi et al. [15] explored entropy generation and heat transfer by convection in a conduit prefilled with porous metal foam. Karimi et al. [16] investigated the forced convection in a space that was partly filled by a porous medium and exposed to a constant heat flux analytically. Mahmoudi et al. [17, 18] looked at the thermal behavior of a canal with a porous region in the center. According to the results, an ideal porous width of 0.8 maximizes the Nu number with a suitable drop in pressure under model A, which more closely reflects the LTE (Local Thermal Equilibrium) method than model B. Chamkha and Ismael [19] investigated heat transfer in a square domain prefilled by a porous medium using conjugate free convection and heated by a triangle solid wall. Tahmasebi et al. [20] explored free convection in a space occupied by three layers of solid, porous medium, and free fluid utilizing Buongiorno’s model. Yang et al. [21] investigated how the slip parameter and the stress jump coefficient have an impact on the fluid flow in a prefilled porous medium.

Another potential effective approach to limiting and controlling the heat transfer rate was represented by the existence of a magnetic flux in the study. Numerous research projects and experiments have been realized for studying the magnetic force’s effect on heat transfer patterns in different geometries [22,23,24]. Mebarek-Oudina and Bessaih [25] evaluated the oscillation of MHD-free convection of liquid metal across overturned coaxial cylinders. They remarked that a change in the direction and amount of the applied magnetic force can regulate the heat transfer rate. Mebarek-Oudinaa et al. [26] showed a numerical analysis of MHD-free convection in a vertical porous cylindrical enclosure filled with magnetic nanofluid. They concluded that more magnetism leads to reduced mass and heat transmission. Pirmohammadi and Ghassemi [27] showed that stronger convection is caused by higher shape factor values. Furthermore, Veera Krishna et al. [28] investigated the impact of Cu and \({\text{Al}}_{{\text{2}}} {\text{O}}_{{\text{3}}}\) nanoparticles on heat transfer in an unstable nanofluid exposed to a magnetic flux. Qureshi et al. [29] evaluated the impact of nanoparticle suspension on heat transfer in MHD flow exposed to a constant-intensity magnetic field. Babazadeh et al. [30] described the simulation of magnetic nanoparticle movement within a porous region with radiation effects and shape factors. Giri et al. [31] investigated the effects of bio-convection and Stefan blowing on MHD nanofluid flow, including gyrotactic bacteria. Giri et al. [32] established the generalized Fourier and Fick’s Law for computing the heat and mass transfer processes in the Casson nanofluid flow with a magnetic field on the stretched surface. Giri et al. [33] studied the Darcy–Forchheimer flow of a nanofluid over a Riga plate with a chemical reaction. Das et al. [34] investigated the influence of a comparative composition of \({\text{Al}}_{{\text{2}}} {\text{O}}_{{\text{3}}}\) and graphene nanoparticles on the flow of a hybrid nanofluid with the Hall effect over a thin stretchable surface. Giri et al. [35] used the differential transform method to explore the chemical reaction mechanism of MHD carbon nanotube flow through a stretching cylinder with a preset heat flux. Das et al. [36] studied the convective heat transport of a viscous liquid driven by an impermeable stretched sheet. Giri et al. [37] presented the melting heat transport process in a magnetohydrodynamic nanofluid moving in a rotating configuration between two horizontally formed plates. Giri [38] investigated the flow properties of a magnetic nanofluid that was electrically conducted as it moved through a curved stretching surface. Giri et al. [39] calculated the heat and mass impacts of hydromagnetic hybrid nanofluid flow across a slick, curved surface.

From this literature review, we notice that there is a lack of studies that combine all these techniques into one study to regulate heat transfer. Nevertheless, the goal of this research could be to better comprehend the behavior of the nanofluid in this particular configuration, in addition to knowing how other parameters such as heat flux, porous layer porosity, and magnetic field intensity might influence heat transfer and fluid flow properties. This information is applicable to a wide range of industrial and technological applications, where heat transfer efficiency is important, including heat exchangers and cooling systems. The findings of this work can help in the design and optimization of such systems by providing insights into fluid flow and heat transfer behavior when magnetic fields and porous media are present. Therefore, this work investigated the magnetic force application on the natural convection within an annular gap between two coaxial cylinders, partially filled by a glass porous layer, and compared it with a metal-base porous layer immersed in (Cu–water) nanofluid and subjected to discrete heat flux.

Mathematical formulation

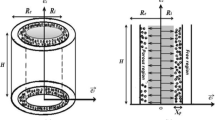
Figure 1 depicts a vertical concentric cylinder with a height of H, in which the annular gap between the two vertical cylinders is partially occupied with a porous layer with a thickness of Xp and saturated by a Newtonian (Cu–water) nanofluid. A heat flux is subjected to the inner cylinder, while the exterior cylinder is preserved at a uniform temperature. Additionally, it is hypothesized that the solid material and nanofluid are in thermal equilibrium. The flow is designed to be laminar, incompressible, homogeneous, isotropic porous medium, and with uniform physical characteristics, except for density, which is approximated by the Boussinesq approximation, in which it changes with temperature. In the present study, the dimensional mathematical formulation in vector form is based on conservation equations and Boussinesq.

Fig. 1
figure 1

Physical domain

Full size image

For the porous layer

$$\begin{aligned}{} & {} \triangledown . V=0, \end{aligned}$$
(1)
$$\begin{aligned}{} & {} \frac{1}{\epsilon ^{2}}\Omega .\triangledown \Omega =-\frac{\mu _\text{nf}}{\rho _\text{nf}.K}\Omega + \frac{\mu _\text{nf}}{\rho _\text{nf}.\epsilon }\triangledown .\left( \triangledown .\Omega \right) \nonumber \\{} & {} \quad -\beta _\text{Th}\frac{\partial T}{\partial r}\overrightarrow{g}-\frac{\sigma _\text{nf}}{\rho _\text{nf}}B_{0}^{2}\Omega ^{2}, \end{aligned}$$
(2)
$$\begin{aligned}{} & {} V.\triangledown T=\alpha _\text{eff} \triangledown .\left( \triangledown T \right) . \end{aligned}$$
(3)

For the nanofluid layer

$$\begin{aligned}{} & {} \triangledown . V=0, \end{aligned}$$
(4)
$$\begin{aligned}{} & {} \Omega .\triangledown \Omega = \frac{\mu _\text{nf}}{\rho _{\text{nf}}}\triangledown .\left( \triangledown .\Omega \right) -\beta _\text{Th}\frac{\partial T}{\partial r}\overrightarrow{g}-\frac{\sigma _{\text{nf}}}{\rho _\text{nf}}B_{0}^{2}\Omega ^{2}, \end{aligned}$$
(5)
$$\begin{aligned}{} & {} V.\triangledown T=\alpha _\text{nf} \triangledown .\left( \triangledown T \right) . \end{aligned}$$
(6)

The controlling equations in scalar form are derived from the formulations of the stream function and rotational velocity (vorticity) [40, 41]. In order to normalize the equations for continuity, momentum, and energy, the following non-dimensional parameters are introduced: length, velocity, vorticity, and temperature with m that denotes nf or eff.

$$\begin{aligned} \begin{aligned}&(\overline{r};\overline{z})=\left( \frac{r}{R_\text{e}};\frac{z}{R_\text{e}}\right) \,;\, (\overline{U};\overline{W})=\left( \frac{U.R_\text{e}}{\alpha _\text{m}};\frac{W.R_\text{e}}{\alpha _\text{m}}\right) \,;\, \overline{\Omega }=\frac{\Omega .R_\text{e}^{2}}{\alpha _\text{m}}\\&\overline{\Psi }=\frac{\Psi }{\alpha _\text{m}.R_\text{e}}\,;\, \overline{T}=\frac{(T-Tc).\lambda _\text{bf}}{Q.R_\text{e}}. \end{aligned} \end{aligned}$$
(7)

The vorticity function and the velocity fields are defined as:

$$\begin{aligned}{} & {} \Omega =\frac{1}{r}\left( \frac{\partial ^{2}\Psi }{\partial r^{2}}-\frac{1}{r}\frac{\partial \Psi }{\partial r}+\frac{\partial ^{2}\Psi }{\partial z^{2}}\right) ;\quad \overline{U}=\frac{1}{\overline{r}}\frac{\partial \overline{\Psi }}{\partial \overline{z}} \nonumber ; \\{} & {} \overline{W}=-\frac{1}{\overline{r}}\frac{\partial \overline{\Psi }}{\partial \overline{r}}. \end{aligned}$$
(8)

However, the non-dimensional set of conservation equations can be stated as.

For the porous layer

$$\begin{aligned}{} & {} \frac{1}{\overline{r}}\frac{\partial (\overline{rU})}{\partial \overline{r}}+\frac{\partial \overline{W}}{\partial \overline{z}}=0, \end{aligned}$$
(9)
$$\begin{aligned}{} & {} \begin{aligned}&\frac{1}{\epsilon ^{2}}\left( \frac{\partial (\overline{U\Omega })}{\partial \overline{r}}+\frac{\partial (\overline{W\Omega })}{\partial \overline{z}} \right) =-\Lambda \overline{\lambda }^{2}RaPr\frac{\partial \overline{T}}{\partial \overline{r}}\\&+\left( -\overline{\lambda }.\Sigma \frac{Pr}{Da}-\overline{\lambda }.\Gamma .\Sigma \frac{Pr}{\overline{r}^{2}}\right) \overline{\Omega }\\&+\overline{\lambda }.\Gamma .\Sigma .Pr\left( \frac{\partial ^{2}\overline{\Omega }}{\partial \overline{r}^{2}}+\frac{1}{\overline{r}}\frac{\partial \overline{\Omega }}{\partial \overline{r}}+\frac{\partial ^{2}\overline{\Omega }}{\partial \overline{z}^{2}}\right) \\&-\overline{\lambda }.\frac{\sigma _\text{nf}}{\sigma _\text{bf}}.Ha^{2}.Pr_\text{bf}\frac{\Sigma }{(1-\phi )^{-2.5}}\frac{\partial \overline{U}}{\partial \overline{z}}, \end{aligned} \end{aligned}$$
(10)
$$\begin{aligned}{} & {} \frac{\partial (\overline{UT})}{\partial \overline{r}}+\frac{\partial (\overline{WT})}{\partial \overline{z}}+\frac{\overline{UT}}{\overline{r}}= \frac{\partial ^{2}\overline{T}}{\partial \overline{r}^{2}}+\frac{1}{\overline{r}}\frac{\partial \overline{T}}{\partial \overline{r}}+\frac{\partial ^{2}\overline{T}}{\partial \overline{z}^{2}}. \end{aligned}$$
(11)

For the nanofluid layer

$$\begin{aligned}{} & {} \frac{1}{\overline{r}}\frac{\partial (\overline{rU})}{\partial \overline{r}}+\frac{\partial \overline{W}}{\partial \overline{z}}=0, \end{aligned}$$
(12)
$$\begin{aligned}{} & {} \begin{aligned}&\frac{\partial (\overline{U\Omega })}{\partial \overline{r}}+\frac{\partial (\overline{W\Omega })}{\partial \overline{z}} =\Sigma .Pr\left( \frac{\partial ^{2}\overline{\Omega }}{\partial \overline{r}^{2}}+\frac{1}{\overline{r}}\frac{\partial \overline{\Omega }}{\partial \overline{r}}-\frac{\overline{\Omega }}{\overline{r}^{2}}+\frac{\partial ^{2}\overline{\Omega }}{\partial \overline{z}^{2}}\right) \\&-\Lambda .Ra.Pr.\frac{\partial \overline{T}}{\partial \overline{r}}-\frac{\sigma _\text{nf}}{\sigma _\text{bf}}.Ha^{2}.Pr_\text{bf}\frac{\Sigma }{(1-\phi )^{-2.5}}\frac{\partial \overline{U}}{\partial \overline{z}}, \end{aligned} \end{aligned}$$
(13)
$$\begin{aligned}{} & {} \frac{\partial (\overline{UT})}{\partial \overline{r}}+\frac{\partial (\overline{WT})}{\partial \overline{z}}+\frac{\overline{UT}}{\overline{r}}= \frac{\partial ^{2}\overline{T}}{\partial \overline{r}^{2}}+\frac{1}{\overline{r}}\frac{\partial \overline{T}}{\partial \overline{r}}+\frac{\partial ^{2}\overline{T}}{\partial \overline{z}^{2}}. \end{aligned}$$
(14)

Where

$$\begin{aligned}{} & {} \alpha _\text{eff}=\frac{\lambda _\text{eff}}{\left( \rho Cp\right) _\text{nf}} \quad ; \quad \alpha _\text{nf}=\frac{\lambda _\text{nf}}{\left( \rho Cp\right) _\text{eff}} \quad ; \quad \Gamma =\frac{\mu _\text{eff}}{\mu _\text{nf}} \nonumber \\{} & {} \quad ; \quad \overline{\lambda }=\frac{\lambda _\text{nf}}{\lambda _\text{eff}}, \end{aligned}$$
(15)
$$\begin{aligned}{} & {} \Sigma =\frac{(1-\phi )^{-2.5}\left( (1-\phi )+\phi \frac{(\rho C)_\text{np}}{(\rho C)_\text{bf}}\right) }{\frac{\lambda _\text{nf}}{\lambda _\text{bf}}\left( (1-\phi )+\phi \frac{\rho _\text{np}}{\rho _\text{bf}}\right) }, \end{aligned}$$
(16)
$$\begin{aligned}{} & {} \Lambda =\frac{\left( (1-\phi )+\phi \frac{(\rho \beta )_\text{np}}{(\rho \beta )_\text{bf}}\right) }{\left( (1-\phi )+\phi \frac{\rho _\text{np}}{\rho _\text{bf}}\right) \left( \frac{\frac{\lambda _\text{nf}}{\lambda _\text{bf}}}{(1-\phi )+\phi \frac{(\rho C)_\text{np}}{(\rho C)_\text{bf}}}\right) ^{2}}. \end{aligned}$$
(17)
$$\begin{aligned}{} & {} \lambda _\text{eff}=(1-\epsilon )\lambda _\text{s}+\epsilon \lambda _\text{nf}. \end{aligned}$$
(18)

The dimensionless numbers in the above equations can be written as:

$$\begin{aligned}{} & {} Ra=\frac{\rho _\text{bf}g\beta _\text{Th}.Q.R_\text{e}^{4}}{\mu _\text{bf}\lambda _\text{bf}\alpha _\text{bf}} \,; \, Pr=\frac{\mu _\text{bf}}{\rho _\text{bf}\alpha _\text{bf}}\,;\,Da=\frac{k}{R_\text{e}^{2}}; \nonumber \\{} & {} \quad Ha=R_\text{e}B_{0}\sqrt{\frac{\sigma _\text{bf}}{\mu _\text{bf}}}. \end{aligned}$$
(19)

The thermophysical characteristics of the nanofluid are calculated by using the mixing law between the base fluid and the nanoparticles, as indicated by [42].

$$\begin{aligned} \begin{aligned} \rho _\text{nf}&=(1-\phi )\rho _\text{bf}+\phi \rho _\text{np},\\ \left( \rho \beta \right) _\text{nf}&=(1-\phi )\left( \rho \beta \right) _\text{bf}+\phi \left( \rho \beta \right) _\text{np},\\ \left( \rho C_\text{p}\right) _\text{nf}&=(1-\phi )\left( \rho C_\text{p}\right) _\text{bf}+\phi \left( \rho C_\text{p}\right) _\text{np}. \end{aligned} \end{aligned}$$
(20)

The formula given below was proposed by Brinkman [43]. In order to determine the effective viscosity, which can be written as:

$$\begin{aligned}{} & {} \frac{\mu _\text{nf}}{\mu _\text{bf}}=\frac{1}{(1-\phi )^{-2.5}}. \end{aligned}$$
(21)

The following expression was provided by Maxwell [44]. In order to determine the nanofluid’s thermal and electrical conductivity, which can be stated as:

$$\begin{aligned} \begin{aligned}&\frac{\lambda _\text{nf}}{\lambda _\text{bf}}=\frac{\lambda _\text{np}+(n-1)\lambda _\text{bf}+(n-1)(\lambda _\text{np}-\lambda _\text{bf})\phi }{\lambda _\text{np}+(n-1)\lambda _\text{bf}-(\lambda _\text{np}-\lambda _\text{bf})\phi },\\&\frac{\sigma _\text{nf}}{\sigma _\text{bf}}=1+\frac{3\left( \frac{\sigma _\text{np}}{\sigma _\text{bf}}-1 \right) \phi }{\left( \frac{\sigma _\text{np}}{\sigma _\text{bf}}+2 \right) -\left( \frac{\sigma _\text{np}}{\sigma _\text{bf}}-1 \right) \phi }. \end{aligned} \end{aligned}$$
(22)

The boundary conditions

In the interior cylinder:

$$\begin{aligned}{} & {} \frac{\partial \overline{T}}{\partial \overline{r}}=-\frac{\lambda _\text{bf}}{\lambda _\text{nf}} \,; \, \frac{\partial \overline{T}}{\partial \overline{r}}=0 \,;\, \overline{\Psi }=\frac{\partial \overline{\Psi }}{\partial \overline{r}}=\frac{\partial \overline{\Psi }}{\partial \overline{z}}=0 \,; \, \overline{\Omega }=\frac{2}{\Delta \overline{r}^{2}}\overline{\Psi }\vert _{\Delta \overline{r}}. \end{aligned}$$
(23)

In the exterior cylinder:

$$\begin{aligned}{} & {} \overline{T}=0 \quad ; \quad \overline{\Psi }=\frac{\partial \overline{\Psi }}{\partial \overline{r}}=\frac{\partial \overline{\Psi }}{\partial \overline{z}}=0 \quad ; \quad \overline{\Omega }=\frac{2}{\Delta \overline{r}^{2}}\overline{\Psi }\vert _{0.5-\Delta \overline{r}}. \end{aligned}$$
(24)

On the lower base:

$$\begin{aligned}{} & {} \frac{\partial \overline{T}}{\partial \overline{z}}=0 \quad ; \quad \overline{\Psi }=\frac{\partial \overline{\Psi }}{\partial \overline{r}}=\frac{\partial \overline{\Psi }}{\partial \overline{z}}=0 \quad ; \quad \overline{\Omega }=\frac{2}{\Delta \overline{r}^{2}}\overline{\Psi }\vert _{\Delta \overline{z}}. \end{aligned}$$
(25)

On the upper base:

$$\begin{aligned}{} & {} \frac{\partial \overline{T}}{\partial \overline{z}}=0 \quad ; \quad \overline{\Psi }=\frac{\partial \overline{\Psi }}{\partial \overline{r}}=\frac{\partial \overline{\Psi }}{\partial \overline{z}}=0 \quad ;\quad \overline{\Omega }=\frac{2}{\Delta \overline{r}^{2}}\overline{\Psi }\vert _{AL-\Delta \overline{z}}. \end{aligned}$$
(26)

The interface conditions are expressed as:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle {\overline{T}_\text{nf}=\overline{T}_\text{p}\quad ; \quad \frac{\partial \overline{T}_\text{nf}}{\partial \overline{r}}=\frac{\lambda _\text{eff}}{\lambda _\text{nf}}\frac{\partial \overline{T}_\text{p}}{\partial \overline{r}}}.\\ \displaystyle {\overline{\Psi }_\text{nf}=\overline{\Psi }_\text{p}\quad ; \quad \frac{\partial \overline{\Psi }_\text{nf}}{\partial \overline{r}}=\frac{\mu _\text{eff}}{\mu _\text{nf}}\frac{\partial \overline{\Psi }_\text{p}}{\partial \overline{r}}}.\\ \displaystyle {\overline{\Omega }_\text{nf}=\overline{\Omega }_\text{p}\quad ; \quad \frac{\partial \overline{\Omega }_\text{nf}}{\partial \overline{r}}=\frac{\mu _\text{eff}}{\mu _\text{nf}}\frac{\partial \overline{\Omega }_\text{p}}{\partial \overline{r}}}. \end{array} \right. \end{aligned}$$
(27)

The average Nusselt number is used to express the rate of heat transfer coefficient at the active wall [45], which is given by:

$$\begin{aligned}{} & {} Nu_\text{aver} =\frac{1}{Ls}\frac{\lambda _\text{eff}}{\lambda _\text{bf}}\int _\text{0}^{Ls}\frac{1}{\overline{T}}\mid _\text{Heat flux}d\overline{z}. \end{aligned}$$
(28)

Numerical methods

Due to their complexity and nonlinearity, the sets of dimensionless governing equations associated with the frontier conditions are numerically resolved to produce the dynamic field, fluid flow pattern, and temperature distribution. The finites differences in conjunction with SOR methods are used to approximate the solutions of the governing differential equations; the vorticity, energy, and stream function are then approximated using the central differences schemes at each grid point, while the forward and backward difference schemes are employed to approximate the boundary conditions. The alternation direction implicit (ADI) technique is employed to resolve the controlling algebraic equations, and the SOR (successive over relaxation) approach [46] to solve the stream function equation. This iterative method is a modification of the Gauss–Seidel method, which is used to solve the equations by updating the values of the unknowns at each iteration using a weighted average (typically between 1 and 2). This approach is particularly useful for solving sparse matrices, which often arise from discretizing partial differential equations. Figure 2 depicts the flow chart of the numerical simulation.

$$\begin{aligned}{} & {} \frac{\sum _\text{i}\sum _\text{j}\mid f_\text{i,j}^{\text{n}+1}-f_\text{i,j}^{\text{n}}\mid }{\sum _\text{i}\sum _\text{j}\mid f_\text{i,j}^{\text{n}}\mid }\le 10^{-5}. \end{aligned}$$
(29)
Fig. 2
figure 2

Flowchart for the algorithm followed

Full size image

Table 1 represents a precision check, which is performed with the finite difference approach and several mesh grid combinations. \(Nu_\text{aver}\) used to evaluate the grid mesh independence of the current FORTRAN code. It is proven that (\(71\times 141\)) is a good mesh size that assures grid independence.

Table 1 Grid independence test
Full size table

The interface conditions Eq. (27) are numerically determined by taking five points, two on the left and two on the right of the interface, and the fifth is concentrated at the interface. As a result, the following difference equations are used to compute the interface potentials, where \({\lambda _\text{r}=\frac{\lambda _\text{eff}}{\lambda _\text{nf}}}\) represents the effective thermal conductivity.

$$\begin{aligned}{} & {} \begin{aligned}&\overline{\Omega }(i,j)=\frac{4\overline{\Omega _\text{nf}}(i+1,j)-\overline{\Omega _\text{nf}}(i+2,j)+\Gamma \left( 4\overline{\Omega _\text{P}}(i-1,j)-\overline{\Omega _\text{p}}(i-2,j)\right) }{3\left( 1+\Gamma \right) },\\&\overline{T}(i,j)=\frac{4\overline{T_\text{nf}}(i+1,j)-\overline{T_\text{nf}}(i+2,j)+\lambda _\text{r}\left( 4\overline{T_\text{P}}(i-1,j)-\overline{T_\text{p}}(i-2,j)\right) }{3\left( 1+\lambda _\text{r} \right) }. \end{aligned} \end{aligned}$$
(30)

The current numerical program is confirmed by evaluating our data with experimental data from Krane and Jessee [47], numerical data from Abu Nada et al. [48] (Fig. 3), and Sankar et al. [49] (Fig. 4).

Fig. 3
figure 3

A comparison of our findings to other published data on temperature distribution (a) on velocity distribution (b) for \({\text{Al}}_{{\text{2}}} {\text{O}}_{{\text{3}}}\) (\({\text{Ra}} =10^{5}\), Pr = 0.7)

Full size image
Fig. 4
figure 4

Streamlines and temperature distribution at \({\text{Ra}} = 10^{4}\), and Ls = 0.25 for a Sankar et al. [49] results, b our results

Full size image

Results and discussion

For this numerical simulation, the annular space between two coaxial vertical cylinders with an aspect ratio (\(AL=H/R_\text{e}\)) of 2 was studied. This paragraph displays the numerical findings in graphical form to demonstrate the effect of several parameters on fluid flow patterns and heat transport. The nanofluid is a mixture of \({\text{H}}_{2} {\text{O}}\) as a base fluid (\(Pr=6.2\)) and nanoparticles of copper, as illustrated by their characteristics in Table 2. The porous layer’s porosity is set to \(\epsilon =0.7\), which corresponds to glass \(\lambda _\text{p}=0.845 Wm^{-1}K^{-1}\). The nanoparticle concentration range is (\(0.01 \le \phi \le 0.05\)).

Table 2 Thermo-physical properties of water and Cu [21]
Full size table
Fig. 5
figure 5

Streamlines and isotherms at Xp = 0.5, Ha = 0, \({\text{Ra}} =10^{6}\), and \(\phi =0.05\) for (a) \({\text{Da}} =10^{-5}\), (b) \({\text{Da}} =10^{-2}\)

Full size image

Figure 5 depicts the Darcy number’s effect on isotherms and streamlines for the mixture of (Cu–water) nanofluid. As seen in Fig. 5a, the Darcy effect appears to be significantly stronger, indicating that the porous material has a high flow obstruction. In this state, the fluid travels more slowly within the porous layer, resulting in a reduction in heat transfer rate. On the other hand, when the Da number increases, the medium becomes more permeable, resulting in increasing the porous matrix’s permeability or decreasing the characteristic diameter of the particles. That’s allowing more nanofluid to pass through the porous layer, which boosts the cell’s strength. Also, the interesting result from Fig. 5 is that the inclusion of nanoparticles has a better influence on the streamlines inside the porous layer with lower permeability (Fig. 5a) than the one with a higher permeability (Fig. 5b). Furthermore, the isotherms illustrate how the convection mode becomes more dominant in the porous layer when the Darcy number increases.

Fig. 6
figure 6

Streamlines and isotherms at Ha = 0, Xp = 0.5, \({\text{Da}} =10^{-5}\), and \(\phi =0.05\) for (a) \({\text{Ra}} =10^{4}\), (b) \({\text{Ra}} =10^{6}\)

Full size image

Figure 6 illustrates the temperature and the streamlines distribution for (Cu–water) nanofluid with different Ra number values. As illustrated in Fig. 6a, the isotherms are closer and oriented vertically on the upper side. In the proximity of the heat source, the isotherms become bent, and when the Ra number is increased to \({\text{Ra}} = 10^{6}\), it can be explained by the fact that increasing the Ra number generates a rise in buoyancy forces, which leads to growth in heat transfer. Figure 6b shows that the flow becomes more vigorous, indeed causing the nanofluid to move away from the hot side toward the cold side.

Fig. 7
figure 7

Streamlines and isotherms at Xp=0.5, \({\text{Ra}} =10^{5}\), \({\text{Da}} =10^{-5}\), and \(\phi =0.05\) for (a) Ha=0, (b) \({\text{Ha}} =150\)

Full size image

Figure 7 illustrates how the magnetic force expressed by the Hartmann number affects the heat transfer rate. As seen in the illustration, the circulation strength reduces as the Ha number increases. This can be explained by the fact that the maximum value of the stream function in an enclosure declines from \(\mid \Psi _\text{max}\mid =1.21\) to \(\mid \Psi _\text{max}\mid =0.46\), when the magnetic force increases because of the Lorentz force, which leads to the suppression of fluid motion, which in turn reduces the heat transfer. That means, as the magnetic force increases, the conductive heat transfer mode becomes more significant than the convective mode. The isotherms are influenced by fluctuations in the Ha number, which causes a change in the shape of the isotherms from horizontal to vertical. This indicates lower convection fluxes for larger Hartmann numbers.

Fig. 8
figure 8

Streamlines and isotherms at Ha = 50, \({\text{Ra}} =10^{5}\), \(\phi =0.05\), and \({\text{Da}} =10^{-5}\), For Ls = 0.5 (a), Ls = 1 (b) and Ls = 2 (c)

Full size image

Figure 8 represents the streamlines and temperature distributions inside the enclosure for the mixture (Cu–water) for various values of Ls. As the heater size reduces, the circulation strength of the nanofluid increases. This is due to the fact that the thermal and hydrodynamic boundary regions are being established just next to the heat source, which is causing an improvement in the thermal energy. To be more understandable, we can observe border circulation patterns and more consistent isotherms with larger heaters. This is owing to the heater’s increased surface area, which gives fluid additional space for moving upward and downward due to buoyancy forces. Thus, the flow patterns would subsequently disperse and cover a larger area of the fluid. However, with a smaller heater, this may result in more evenly distributed streamlines and temperatures. This is because the heat source’s small surface area would limit fluid flow in both the vertical and horizontal directions, constricting the flow pattern to the heater’s immediate vicinity and potentially increasing the temperature difference between the heated region and the surrounding fluid.

Figure 9 illustrates the distributions of streamlines and isotherms for several porous layer thicknesses Xp (0.25, 0.50, and 0.75). We can remark that the fluid flow pattern is manifested by only one clockwise rotating cell for all the Xp values. Its influence on the cell strength becomes more significant as the porous region thickness grows. This is due to the hydrodynamic resistance provided by the porous region, of which the variance of the penetration streamlines inside the porous region is greater for a smaller width (Fig. 9a), and as Xp grows, the cell reaches out to be vertically elongated (Fig. 9c). To be more comprehensible, we can see complex flow patterns when a porous layer covering 75% of the domain is present, with flow becoming highly concentrated in the remaining nanofluid region. This causes the streamlines to be severely deformed and significantly lower flow velocities in the porous zone. In this situation, the isotherms throughout the porous layer would exhibit significant temperature changes and gradients. Heat transmission within the porous zone would be extremely efficient at redistributing heat, causing significant variations from the isotherms in the surrounding nanofluid region.

Fig. 9
figure 9

Streamlines and isotherms at Ha = 0, \({\text{Da}} =10^{-5}\), \(\phi =0.05\), and \({\text{Ra}} =10^{5}\) for Xp = 0.25 (a), Xp = 0.5 (b), Xp = 0.75 (c)

Full size image

To understand the impacts of the studied parameters on the rate of heat transfer in the internal cylinder of the composite cavities, the following figures have been treated. Figure 10a indicates the heat transfer rate along the interior cylinder for different Da numbers and nanoparticle concentration values. As represented in the figure, the average Nusselt number grows with the growth of the Da number, which signifies more flexibility for nanofluid to travel from the warm side to the cold side, thus improving the heat transfer rate in the active wall. Furthermore, high Darcy numbers and nanoparticle volume fraction values have led to a high value of the average Nusselt number. Figure 10b represents the heat transfer rate along the heater for various nanoparticle concentrations \((0.01\le \phi \le 0.05)\) and Ra numbers. The results illustrate that as the Ra number increases, so does the average Nusselt number. Indeed, a rise in the Ra number might be interpreted as a boost in the source’s heating energy, which causes the nanofluid to migrate from the heated side to transfer energy to the coldest side. We also notice that the heat transfer rate for \(\phi = 0.05\) has a high value, demonstrating the importance of nanoparticle concentration in enhancing heat transfer.

Fig. 10
figure 10

The variation of average Nusselt number (source) according nanoparticle concentration at Xp = 0.5, and Ha = 0 for \({\text{Ra}} =10^{5}\) (a) and \({\text{Da}} =10^{-5}\) (b)

Full size image

Figure 11 demonstrates the variation of the average Nusselt number with the Hartmann number at various nanoparticle concentrations (\(0\le \phi \le 0.05\)) and for several porous matrix materials. As represented in the illustration, the average Nusselt number \(Nu_\text{Aver}\) augments with increasing of the nanoparticle concentration traduced by increasing in the thermal conductivity, which improves heat transfer by enhancing conduction and convection mechanisms, and with decreasing of the Hartmann number Ha traduced by the Lorentz forces. Furthermore, we remark that with a high thermal conductivity material value, the strength of heat transfer will be higher (Fig. 11b), and the Hartmann number effect also becomes important.

Fig. 11
figure 11

Heat transfer rate (source) for different values of Hartmann number at Xp = 0.5, \({\text{Ra}} =10^{5}\), and \({\text{Da}} =10^{-5}\) for Glass (a) and stainless-steel (b)

Full size image
Fig. 12
figure 12

Heat transfer rate(source) for different Darcy number at Ha = 0, and \({\text{Ra}} =10^{5}\) for Glass (a) and stainless-steel (b)

Full size image

Figure 12 indicates the average Nusselt number according to the Darcy number for varied porous layer thicknesses for glass in Fig. 12a and stainless steel in Fig. 12b. The rise in the Da number, which means the medium is going to be more permeable, will result in a rise in the average Nusselt number. As shown in Fig 12a, the heat transfer rate is higher for \({\text{Xp}} = 0.25\) than for the others. On the other hand, when we use stainless steel as a porous layer material instead of glass with \(\lambda _\text{s}=26\; {\text{Wm}}^{{ - 1}} {\text{K}}^{{ - 1}}\), the heat transfer rate improves for all Xp, but we note a critical point for the Darcy number \({\text{Da}} = 0.0057\), above which the heat transfer for \({\text{Xp}} = 0.5\) becomes more favorable than for \({\text{Xp}} = 0.25\). Furthermore, we can infer that there is a competition between the thermal conductivity and the viscosity effects of the porous medium. As the porous layer thickness increases, the heat transfer surface contact with the nanofluid increases, which can be traduced by an increase in the heat transfer rate, but on the other hand, this increase in porous layer thickness increases the fluid flow resistance, depending on porosity and Da number, which can be traduced by a reduction in overall heat transfer, so an optimum porous layer thickness is sought for better heat transfer.

Figure 13 indicates that the average Nusselt number decreases as the heater size increases, in which we have already interpreted the cause behind this improvement in Fig. 8. This result is in good accordance with a preceding study by Yucel [50]. For the magnetic effect, with \({\text{Ha}} = 50\) the magnetic forces begin to affect fluid flow and heat transfer, which can lead to a decrease in Nusselt numbers with increasing of the heater length. In the case of a strong magnetic field \({\text{Ha}} = 100\), convection is suppressed more strongly and magnetic forces dominate the flow behavior, tending to reduce fluid motion; as a result, the average Nusselt number should be lower than in the absence of a magnetic field. Furthermore, the slop of the curve for \({\text{Ha}} =0\) is higher than that for \({\text{Ha}} =50\, or\, 100\) and that confirms the fact that the application of magnetic force is a good controller for the heat transfer rate.

Fig. 13
figure 13

The average Nusselt number for different heater sizes

Full size image

Conclusions

The magnetic force and the composite cavities are technical methods that play an important role in controlling heat transport and providing new insights into the behavior of the nanofluid under these conditions in order to project this study into industrial and technological applications. Furthermore, the problem was solved using the numerical code FORTRAN, in which the findings are expressed as follows:

  • The power of nanofluid flow is amplified by increasing the Rayleigh number Ra, nanoparticle concentration \(\phi\), and Darcy number Da.

  • The flow intensity in the nanofluid layer is greater than in the porous region because of the porous layer’s hydrodynamic resistance.

  • The performance of the transfer is significantly improved by the heater’s size, whose reduction improves convection.

  • The application of magnetic force has a crucial role in heat transfer control, where the growth of the Hartmann number decreases the average Nusselt number \(Nu_\text{aver}\).

  • The use of a porous material with a high thermal conductivity improves the heat transfer rate.

  • For stainless steel, we observed a critical point above which the heat transfer ability is favorable for Xp = 0.5 instead of Xp = s0.25.