1 Introduction

Currently, graph theory seeks to advance and apply several contemporary scientific hypotheses in various branches of chemistry. Typically, nodes and edges make up a graph [8]. A graph consists of vertices (also known as nodes) and edges, which are the lines or arcs that connect any two or more vertices. T can be used to mathematically depict a graph. Assuming that the basic connected graph T=(V, E) is given, V shows nodes or points in the graph. Each vertex is typically labeled with a unique identifier or value, and E shows the connections or relationships between vertices in the graph. An edge connects two vertices and can be either directed (with a specific direction) or undirected (without any direction). The quantity of elements in V and the quantity of elements in E, respectively, determine the order and size of T [9]. The graph is finished, if all distinct pairs of vertices in T are in close proximity. There are no isolated vertices, loops, or multiple edges in any of the finite, undirected graphs that are being considered. The vertex degree in a graph (T) refers to the count of directly connected vertices to a specific vertex or V(T). Polynomials, matrices, and integers can all be used to represent a graph.

Zhang et. al [10] computed the topological indices of generalized molecular graphs and products of chemical graphs. Shao et.al [11] computed Zagreb indices for nanotubes. Gao et.al [12] provided the characterization of carbon graphite. Zhang et. al [13, 14] discussed the physical analysis of heat for the formation and entropy of ceria oxide. Zhang et. al [15, 16] provides an analysis of different molecular structures using topological indices. Liu et.al [27] discuss the smart grid graphs for topological analysis. Lu et.al [28] provided the details about bipolar cubic fuzzy graphs and its chemical applications. Ma et.al [29] provided the classification of integrating knowledge graphs with topological indices. Wu et.al [34] analyzed the application of graph theory teaching method in ideological and political education.

Topological indices are used in chemical graph theory to analyze the molecular topological qualities of molecules. The computation of topological indices in the domain of chemical research enables the examination of the molecular structure’s impact on the associated chemical, pharmacological, and biological characteristics of pharmaceutical. By analyzing topological indices, researchers can gain insights into the relationships between molecular topology and various properties and behaviors of pharmaceutical compounds [25]. The QSAR/QSPR research involved the integration of physiochemical characteristics and topological indices, such as the hyper-Zagreb index (which is calculated by summing the square of the vertex degree within the graph), the first multiple Zagreb index (the molecular graph’s vertex pairs are multiplied together, and their degrees are summed to compute it), and the second multiple Zagreb index (which is computed by summing the squares of the multiplication of the degrees of each pair of adjacent vertices in the graph results in the product of their degrees). These indices were utilized to analyze the molecular structures of the compounds being studied [26].

2 Motivation and interest of researchers

Topological indices are numerical descriptors that offer information about a molecule’s structure and behavior. Topological indices based on sums of vertex degrees in a molecular network, in particular, are determined. Here are some reasons why you should use sum degree-based topological indices:

1. Molecular structure–property relationships: Topological indices, which predict the characteristics and activities of molecules based on their structure, have been widely employed in chemoinformatics and drug development. Sum degree-based topological indices can give insights into molecular attributes such as boiling point, solubility, and biological activity by assessing the connectivity and degree distribution of atoms in a molecule.

2. Prediction of stereoselectivity and reactivity: The spatial arrangement of atoms in a molecule, particularly in chiral compounds, is critical in determining biological activity and reactivity. Topological indices based on sum degrees can capture a molecule’s symmetry and spatial information, making them valuable for forecasting reaction stereoselectivity.

This article discusses some established and recently developed degree-based topological indices [4, 17]. The graph invariants now known as Zagreb indices were the first vertex-degree-based structure identifiers [18, 19]. A chemical structure called a graph, denoted as T, is made up of a collection of vertices (V) and a set of edges (E). The set of vertices includes all the nodes or points in the graph, and the set of edges includes all the connections or links between the vertices. The quantity of edges at a vertex determines its degree of incidence on it (denoted by \(\mathrm{{deg}}_v\)). The collection of all vertices that are adjacent to v is known as the open neighborhood N(v) vertex constructed the degree-based indices [2, 22]. The degree sum of a vertex’s neighbors is represented by the symbol \(S_T(v)\), this is the total of all degrees of a vertex’s neighbors[30].

3 Some features of superlattice structures

In solid-state physics and materials science, a superlattice is a specialized structure composed of alternating layers of two or more different materials having distinct characteristics and crystal structures. Typically, these layered structures are created utilizing sophisticated growth methods such as molecular beam epitaxy or chemical vapor deposition.

Superlattices have unique and controllable features not seen in the basic materials. Researchers can create and regulate a wide range of physical phenomena by altering the thickness, content, and arrangement of the layers, making these structures very appealing for a variety of technological applications. The confinement and interaction of charge carriers, photons, or phonons inside the layered structure is the basic concept of a superlattice. This confinement causes quantum confinement effects, in which the characteristics of particles are altered as a result of their confinement at nanoscale dimensions.

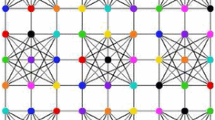
Superlattices have found use in a variety of sectors, including electronics, optoelectronics, thermoelectrics, quantum computers, and photovoltaics. They have been utilized to improve electronic devices. For more details see Fig. 1.

Fig. 1
figure 1

Superlattice structure

Full size image

Vertex sum degrees that are close to a vertex u is known as \(S_T(u)\) according to Graovac et al [21]. In other words, the sum of all the degrees of the vertices in the graph T that are directly related to vertex u is known as \(S_T(u)\). Inspired by the Graovac indices, V. R. Kulli [23, 24] introduced the general fifth M-Zagreb indices. For a molecular graph, these indices were created as polynomials. In QSAR/QSPR research, the fifth M-Zagreb indices, a particular kind of topological index, are frequently employed to examine the molecular structure of a chemical. These indices have shown their capacity to predict a number of physicochemical properties of molecules, including surface area, boiling points, and melting points. They are created by computing the total of all of the chemical network’s vertices’ degrees [1], The fifth M-Zagreb index (\(MZ_{5}\)) is a graph-theoretic topological index that describes the degree of branching of a molecule. It is a modification of the original Zagreb index, which sums the degrees of all vertices in a molecule. Quantitative structure–property relationship (QSPR) models have also been created using it to predict a number of molecular physical and chemical properties [5]. The following is a description of these indices.

$$\begin{aligned} M_1G_5(T)=\sum _{uv \epsilon {E(T)}} {(\S _{T}(u)+\S _{T}(v))}, \end{aligned}$$
(1)
$$\begin{aligned} M_2G_5(T)=\sum _{uv \epsilon {E(T)}} {(\S _{T}(u) \S _{T}(v))}. \end{aligned}$$
(2)

V. R. Kulli created the general fifth M-Zagreb indices and fifth hyper-M-Zagreb indices in reference to the aforementioned indices. Here is a description of them:

$$\begin{aligned} {M_{1} ^{a}} G_5(T)=\sum _{uv \epsilon {E(T)}} ({\S _{T}(u)+\S _{T}(v)})^a, \end{aligned}$$
(3)
$$\begin{aligned} {M_{2} ^{a}} G_5(T)=\sum _{uv \epsilon {E(T)}} ({\S _{T}(u)\S _{T}(v)})^a, \end{aligned}$$
(4)
$$\begin{aligned} {HM_{1}} G_5(T)=\sum _{uv \epsilon {E(T)}} ({\S _{T}(u)+\S _{T}(v)})^2, \end{aligned}$$
(5)
$$\begin{aligned} {HM_{2}} G_5(T)=\sum _{uv \epsilon {E(T)}} ({\S _{T}(u)\S _{T}(v)})^2. \end{aligned}$$
(6)

Furthermore, they introduced a revised version of the Zagreb index, that is alternatively referred to as the third Zagreb index or the fifth \(M_3\)-Zagreb index,

$$\begin{aligned} M_3G_5(T)=\sum _{uv \epsilon {E(T)}} {|\S _{T}(u)-\S _{T}(v)|}. \end{aligned}$$
(7)

Corresponding the above indices, they defined the General fifth \(M_{1}\)-Zagreb polynomial and the general fifth \(M_{2}\)-Zagreb polynomial of a molecular graph T.

$$\begin{aligned} {M_{1} ^{a}} T_5(T, z)=\sum _{uv \epsilon {E(T)}} z^{({\S _{T}(u)+\S _{T}(v)})^a}, \end{aligned}$$
(8)
$$\begin{aligned} {M_{2} ^{a}} G_5(T, z)=\sum _{uv \epsilon {E(T)}} z^{({\S _{T}(u)\S _{T}(v)})^a}. \end{aligned}$$
(9)

The fifth \(M_{1}\)-Zagreb polynomial and the fifth \(M_{2}\)-Zagreb polynomial of a graph T are defined

$$\begin{aligned} {M_{1}} G_5(T,z)=\sum _{uv \epsilon {E(T)}} z^{({\S _{T}(u)+\S _{T}(v)})}, \end{aligned}$$
(10)
$$\begin{aligned} {M_{2}} G_5(T,z)=\sum _{uv \epsilon {E(T)}} z^{({\S _{T}(u)\S _{T}(v)})}. \end{aligned}$$
(11)

The fifth hyper-\(M_{1}\)-Zagreb polynomial and the fifth hyper-\(M_{2}\)-Zagreb polynomial of a graph T are defined

$$\begin{aligned} {M_{1}} G_5(T,z)=\sum _{uv \epsilon {E(T)}} z^{({\S _{T}(u)+\S _{T}(v)})^2}, \end{aligned}$$
(12)
$$\begin{aligned} {M_{2}} G_5(T,z)=\sum _{uv \epsilon {E(T)}} z^{({\S _{T}(u)\S _{T}(v)})^2}. \end{aligned}$$
(13)

References provide additional resources and literature pertaining to the study of topological indices [3, 6, 7, 20, 32].

In Fig. 2, we have presented the bibliometric analysis of the fifth Zagreb M-polynomial keywords in different manners. In this analysis, it can be seen easily that fifth Zagreb M-polynomial keywords are mostly discuss in different forms.

Fig. 2
figure 2

Bibliometric value of fifth Zagreb M-polynomial with respect to other topological indices

Full size image

In Fig. 3, we have presented the bibliometric analysis of the fifth Zagreb M-polynomial by different authors in world.

Fig. 3
figure 3

Bibliometric analysis of M-polynomials by different authors

Full size image

4 Main results

An arrangement of alternating layers of several materials is known as a superlattice. Phase-change memory technology employs a material known as Ge-Sb-Te superlattice. It consists of alternating layers of germanium (Ge), antimony (Sb), and tellurium (Te) atoms [31]. The usual superlattice is quite tiny, and these layers are commonly measured in nanometers. These structures are utilized in the development of novel semiconductor forms that display characteristics distinct from those of the constituent materials. The arrangement of atoms within the Ge-Sb-Te superlattice at the molecular level can be described as a series of crystalline layers, with each layer composed of a repeating pattern of atoms[33]. The layers are arranged in a way that creates a specific atomic arrangement that allows for rapid changes in electrical conductivity. Superlattice’s composition have \(9n + 3\) vertices and 13n edges see Table 1.

Table 1 Edge vertex degree based on superlattices
Full size table

Theorem 4.1

Consider the superlattice structure, \(M_1G_5(T)\) of fifth M-Zagreb index given a molecular graph, that is equivalent to:

$$\begin{aligned} M_1G_5(T)= 258n-108. \end{aligned}$$

Proof

Let T be the superlattice structure. From Eq. (1),

$$\begin{aligned} M_1G_5(T)=\sum _{uv \epsilon {E(T)}} {(\S _{T}(u)+\S _{T}(v))}. \end{aligned}$$

Using the edge partition from Table 1

$$\begin{aligned}=\; & {} 2(9)+ 2(10)+ 2(12)+ (2n-2)(13)+ 8(15)+ 2(19)+ 2(18) \\{} & {} + (2n+2)(21)+ (n-2)(12)+ (n-2)(22)+ (6n-12)(23)+ (n-2)(18), \end{aligned}$$

we have got, by making some calculations

$$\begin{aligned} \Longrightarrow M_1G_5(T)= 258n-108. \end{aligned}$$

\(\hfill\square\)

Theorem 4.2

The Superlattice structure, \(M_2G_5(T)\) corresponds to the fifth M-Zagreb index polynomial for a given graph

$$\begin{aligned} M_2G_5(T)= 1317n-990. \end{aligned}$$

Proof

Let T be the superlattice structure. Eq. (2) can be applied using this partition to

$$\begin{aligned} M_2G_5(T)=\sum _{uv \epsilon {E(T)}} {(\S _{T}(u)\S _{T}(v))}, \end{aligned}$$

Applying edge partition of Table 1

$$\begin{aligned}=\; & {} 2(18)+2(21)+ 2(36)+ (2n-2)(42)+ 8(54)+ 2(84)+ 2(81) \\{} & {} + (2n+2)(108)+ (n-2)(27)+ (n-2)(121)+ (6n-12)(132)+ (n-2)(77), \end{aligned}$$

we have got, by making some calculations

$$\begin{aligned} \Longrightarrow M_2G_5(T)= 1317n-990. \end{aligned}$$

\(\hfill\square\)

Theorem 4.3

Consider the Superlattice structure, \({M_{1} ^{a}} G_5(T)\) of fifth M-Zagreb index, polynomial for a structural graph, that is equal to:

$$\begin{aligned} {M_{1} ^{a}} G_5(T)=\; & {} 2(9)^{a}+2(10)^{a}+2(12)^{a}+(2n-2)(13)^{a}+8(15)^{a}\\{} & {} +2(19)^{a}+2(18)^{a}+(2n+2)(21)^{a}+(n-2)(12)^{a}\\{} & {} +(n-2)(22)^{a}+ (6n-12)(23)^{a}+(n-2)(18)^{a}\\. \end{aligned}$$

Proof

Let T be the Superlattice structure. From Eq. (3),

$$\begin{aligned} {M_{1} ^{a}} G_5(T)=\sum _{uv \epsilon {E(T)}} {(\S _{T}(u)+\S _{T}(v))}^{a}, \end{aligned}$$

By implementing an edge partition on Table 1.

$$\begin{aligned}=\; & {} 2(3+6)^{a}+ 2(3+7)^{a}+ (2)(6+6)^{a}+ (2n-2)(6+7)^{a}+ 8(6+9)^{a}\\{} & {} +2(7+12)^{a}+ 2(9+9)^{a}+ (2n+2)(9+12)^{a}+ (n-2)(3+9)^{a}\\{} & {} +(n-2)(11+11)^{a}+ (6n-12)(11+12)^{a}+ (n-2)(11+7)^{a}, \end{aligned}$$

we have got, by making some calculations

$$\begin{aligned} \Longrightarrow {M_{1} ^{a}} G_5(T)=\; & {} 2(9)^{a}+2(10)^{a}+2(12)^{a}+(2n-2)(13)^{a}+8(15)^{a}\\{} & {} +2(19)^{a}+2(18)^{a}+(2n+2)(21)^{a}+(n-2)(12)^{a}\\{} & {} +(n-2)(22)^{a}+ (6n-12)(23)^{a}+(n-2)(18)^{a}\\. \end{aligned}$$

\(\hfill\square\)

Theorem 4.4

Consider the Superlattice structure \({M_{2} ^{a}} G_5(T)\) of fifth M-Zagreb index as polynomial for a molecular graph, that is equal to:

$$\begin{aligned} {M_{2} ^{a}} G_5(T)=\; & {} 2(18)^{a}+2(21)^{a}+2(36)^{a}+(2n-2)(42)^{a}+8(54)^{a}\\{} & {} +2(84)^{a}+2(81)^{a}+(2n+2)(108)^{a}+(n-2)(27)^{a}\\{} & {} +(n-2)(121)^{a}+ (6n-12)(132)^{a}+(n-2)(77)^{a}\\. \end{aligned}$$

Proof

Let T be the Superlattice structure. In Table 1, there is an frequency of T. From Eq. (4),

$$\begin{aligned} {M_{2} ^{a}} G_5(T)=\sum _{uv \epsilon {E(T)}} {(\S _{T}(u)\S _{T}(v))}^{a}, \end{aligned}$$

Through the utilization of edge partitioning with respect to Table 1

$$\begin{aligned}=\; & {} 2(3\times 6)^{a}+ 2(3\times 7)^{a}+ (2)(6\times 6)^{a}+ (2n-2)(6\times 7)^{a}+ 8(6\times 9)^{a}\\{} & {} +2(7\times 12)^{a}+ 2(9\times 9)^{a}+(2n+2)(9\times 12)^{a}+ (n-2)(3\times 9)^{a}\\{} & {} +(n-2)(11\times 11)^{a}+ (6n-12)(11\times 12)^{a}+ (n-2)(11\times 7)^{a}, \end{aligned}$$

we have got, by making some calculations

$$\begin{aligned} \Longrightarrow {M_{2} ^{a}} G_5(T)=\; & {} 2(18)^{a}+2(21)^{a}+2(36)^{a}+(2n-2)(42)^{a}+8(54)^{a}\\{} & {} +2(84)^{a}+2(81)^{a}+(2n+2)(108)^{a}+(n-2)(27)^{a}\\{} & {} +(n-2)(121)^{a}+ (6n-12)(132)^{a}+(n-2)(77)^{a}\\. \end{aligned}$$

\(\hfill\square\)

Theorem 4.5

Consider the Superlattice structure \({HM_{1}} G_5(T)\) of fifth M-Zagreb index as polynomial for a chemical graph, that is equal to:

$$\begin{aligned} {HM_{1}} G_5(T)=5346n-3888. \end{aligned}$$

Proof

Let T be the Superlattice structure. From Eq. (5),

$$\begin{aligned} {HM_{1}} G_5(T)=\sum _{uv \epsilon {E(T)}} {(\S _{T}(u)+\S _{T}(v))}^{2}, \end{aligned}$$

Through the use of Frequency as a means of partitioning table 1

$$\begin{aligned}=\; & {} 2(3+6)^{2}+ 2(3+7)^{2}+ (2)(6+6)^{2}+ (2n-2)(6+7)^{2}+ 8(6+9)^{2}\\{} & {} +2(7+12)^{2}+ 2(9+9)^{2}+ (2n+2)(9+12)^{2}+ (n-2)(3+9)^{2}\\{} & {} +(n-2)(11+11)^{2}+ (6n-12)(11+12)^{2}+ (n-2)(11+7)^{2}, \end{aligned}$$

we have got, by making some calculations

$$\begin{aligned} \Longrightarrow {HM_{1}} G_5(T)=5346n-3888. \end{aligned}$$

\(\hfill\square\)

Theorem 4.6

Consider the Superlattice structure , \({HM_{2}} G_5(T)\) of fifth M-Zagreb index, polynomial for a structural formula of graph is

$$\begin{aligned} {HM_{2}} G_5(T)=152699n-177202. \end{aligned}$$

Proof

Let T be the Superlattice structure. From Eq. (6),

$$\begin{aligned} {HM_{2}} G_5(T)=\sum _{uv \epsilon {E(T)}} {(\S _{T}(u)\S _{T}(v))}^{2}, \end{aligned}$$

By employing an edge partitioning technique on Table 1

$$\begin{aligned}=\; & {} 2(3\times 6)^{2}+ 2(3\times 7)^{2}+ (2)(6\times 6)^{2}+ (2n-2)(6\times 7)^{2}+ 8(6\times 9)^{2}\\{} & {} +2(7\times 12)^{2}+ 2(9\times 9)^{2}+ (2n+2)(9\times 12)^{2}+ (n-2)(3\times 9)^{2}\\{} & {} +(n-2)(11\times 11)^{2}+ (6n-12)(11\times 12)^{2}+ (n-2)(11\times 7)^{2} \end{aligned}$$

we have got, by making some calculations

$$\begin{aligned} \Longrightarrow {HM_{2}} G_5(T)=152699n-177202. \end{aligned}$$

\(\hfill\square\)

Theorem 4.7

Consider the Superlattice structure, \(M_3G_5(T)\) of fifth M-Zagreb index as polynomial for a molecular graph, that is equal to:

$$\begin{aligned} M_3G_5(T)= 21n+46. \end{aligned}$$

Proof

Let T be the Superlattice structure. By Eq. (7),

$$\begin{aligned} M_3G_5(T)=\sum _{uv \epsilon {E(T)}} {|\S _{T}(u)-\S _{T}(v)|}, \end{aligned}$$

From Table 1

$$\begin{aligned}=\; & {} 2|3-6|+ 2|3-7|+ 2|6-6|+ (2n-2)|6-7|+ 8|6-9|+ 2|7-12|\\{} & {} +2|9-9|+ (2n+2)|9-12|+ (n-2)|3-9|+ (n-2)|11-11|\\{} & {} +(6n-12)|11-12|+ (n-2)|11-7|, \end{aligned}$$

we have got, by making some calculations

$$\begin{aligned} \Longrightarrow M_3G_5(T)= 21n+46. \end{aligned}$$

\(\hfill\square\)

Theorem 4.8

Consider the Superlattice structure , \({M_{1} ^{a}} G_5(T,z)\) of fifth M-Zagreb index as polynomial, that is equal to:

$$\begin{aligned} {M_{1} ^{a}} G_5(T,z)=\; & {} 2{z^{(9)^{a}}}+2{z^{(10)^{a}}}+2{z^{(12)^{a}}}+(2n-2){z^{(13)^{a}}}+8{z^{(15)^{a}}}\\{} & {} +2{z^{(19)^{a}}}+2{z^{(18)^{a}}}+(2n+2){z^{(21)^{a}}}+(n-2){z^{(12)^{a}}}\\{} & {} +(n-2){z^{(22)^{a}}}+ (6n-12){z^{(23)^{a}}}+(n-2){z^{(18)^{a}}}\\. \end{aligned}$$

Proof

Let T be the Superlattice structure. Using Eq. (8),

$$\begin{aligned} {M_{1} ^{a}} G_5(T,z)=\sum _{uv \epsilon {E(T)}} z^{({\S _{T}(u)+\S _{T}(v)})^a}. \end{aligned}$$

By implementing an edge-based partitioning strategy for Table 1

$$\begin{aligned}=\; & {} 2{z^{(3+6)^{a}}}+2{z^{(3+7)^{a}}}+2{z^{(6+6)^{a}}}+(2n-2){z^{(6+7)^{a}}}+8{z^{(6+9)^{a}}}\\{} & {} +2{z^{(7+12)^{a}}}+2{z^{(9+9)^{a}}}+(2n+2){z^{(9+12)^{a}}}+(n-2){z^{(3+9)^{a}}}\\{} & {} +(n-2){z^{(11+11)^{a}}}+ (6n-12){z^{(11+12)^{a}}}+(n-2){z^{(11+7)^{a}}}\\. \end{aligned}$$

we have got, by making some calculations

$$\begin{aligned} \Longrightarrow {M_{1} ^{a}} G_5(T,z)=\; & {} 2{z^{(9)^{a}}}+2{z^{(10)^{a}}}+2{z^{(12)^{a}}}+(2n-2){z^{(13)^{a}}}+8{z^{(15)^{a}}}\\{} & {} +2{z^{(19)^{a}}}+2{z^{(18)^{a}}}+(2n+2){z^{(21)^{a}}}+(n-2){z^{(12)^{a}}}\\{} & {} +(n-2){z^{(22)^{a}}}+ (6n-12){z^{(23)^{a}}}+(n-2){z^{(18)^{a}}}\\. \end{aligned}$$

\(\hfill\square\)

Theorem 4.9

Consider the Superlattice structure , \({M_{2} ^{a}} G_5(T,z)\) of fifth M-Zagreb index, polynomial for a structural formula of given graph, that is equal to [24]:

$$\begin{aligned} {M_{2} ^{a}} G_5(T,z)=\; & {} 2{z^{(18)^{a}}}+2{z^{(21)^{a}}}+2{z^{(36)^{a}}}+(2n-2){z^{(42)^{a}}}+8{z^{(54)^{a}}}\\{} & {} +2{z^{(84)^{a}}}+2{z^{(81)^{a}}}+(2n+2){z^{(108)^{a}}}+(n-2){z^{(27)^{a}}}\\{} & {} +(n-2){z^{(121)^{a}}}+ (6n-12){z^{(132)^{a}}}+(n-2){z^{(77)^{a}}}\\. \end{aligned}$$

Proof

Let T be the Superlattice structure. From Eq. (9),

$$\begin{aligned} {M_{2} ^{a}} G_5(T,z)=\sum _{uv \epsilon {E(T)}} z^{({\S _{T}(u)\S _{T}(v)})^a}. \end{aligned}$$

Applying edge partition from Table 1

$$\begin{aligned}=\; & {} 2{z^{(3\times 6)^{a}}}+2{z^{(3\times 7)^{a}}}+2{z^{(6\times 6)^{a}}}+(2n-2){z^{(6\times 7)^{a}}}+8{z^{(6\times 9)^{a}}}\\{} & {} +2{z^{(7\times 12)^{a}}}+2{z^{(9\times 9)^{a}}}+(2n+2){z^{(9\times 12)^{a}}}+(n-2){z^{(3\times 9)^{a}}}\\{} & {} +(n-2){z^{(11\times 11)^{a}}}+ (6n-12){z^{(11\times 12)^{a}}}+(n-2){z^{(11\times 7)^{a}}}\\. \end{aligned}$$

we have got, by making some calculations

$$\begin{aligned} \Longrightarrow {M_{2} ^{a}} G_5(T,z)=\; & {} 2{z^{(18)^{a}}}+2{z^{(21)^{a}}}+2{z^{(36)^{a}}}+(2n-2){z^{(42)^{a}}}+8{z^{(54)^{a}}}\\{} & {} +2{z^{(84)^{a}}}+2{z^{(81)^{a}}}+(2n+2){z^{(108)^{a}}}+(n-2){z^{(27)^{a}}}\\{} & {} +(n-2){z^{(121)^{a}}}+ (6n-12){z^{(132)^{a}}}+(n-2){z^{(77)^{a}}}\\. \end{aligned}$$

\(\hfill\square\)

Theorem 4.10

Consider the Superlattice structure , \({M_{1}} G_5(T,z)\) of fifth M-Zagreb index as polynomial for given graph, equal to:

$$\begin{aligned} {M_{1}} G_5(T,z)=\; & {} 2{z^{(9)}}+2{z^{(10)}}+2{z^{(12)}}+(2n-2){z^{(13)}}+8{z^{(15)}}\\{} & {} +2{z^{(19)}}+2{z^{(18)}}+(2n+2){z^{(21)}}+(n-2){z^{(12)}}\\{} & {} +(n-2){z^{(22)}}+ (6n-12){z^{(23)}}+(n-2){z^{(18)}}\\. \end{aligned}$$

Proof

Let T be the Superlattice structure. By Eq. (10),

$$\begin{aligned} {M_{1}} G_5(T,z)=\sum _{uv \epsilon {E(T)}} z^{{\S _{T}(u)+\S _{T}(v)}}. \end{aligned}$$

From Edge segmentation of T Table 1

$$\begin{aligned}=\; & {} 2{z^{(3+6)}}+2{z^{(3+7)}}+2{z^{(6+6)}}+(2n-2){z^{(6+7)}}+8{z^{(6+9)}}\\{} & {} +2{z^{(7+12)}}+2{z^{(9+9)}}+(2n+2){z^{(9+12)}}+(n-2){z^{(3+9)}}\\{} & {} +(n-2){z^{(11+11)}}+ (6n-12){z^{(11+12)}}+(n-2){z^{(11+7)}}\\. \end{aligned}$$

we have got, by making some calculations

$$\begin{aligned} \Longrightarrow {M_{1}} G_5(T,z)=\; & {} 2{z^{(9)}}+2{z^{(10)}}+2{z^{(12)}}+(2n-2){z^{(13)}}+8{z^{(15)}}\\{} & {} +2{z^{(19)}}+2{z^{(18)}}+(2n+2){z^{(21)}}+(n-2){z^{(12)}}\\{} & {} +(n-2){z^{(22)}}+ (6n-12){z^{(23)}}+(n-2){z^{(18)}}\\. \end{aligned}$$

\(\hfill\square\)

Theorem 4.11

Consider the Superlattice structure, \({M_{2}} G_5(T,z)\) of fifth M-Zagreb index polynomial for a chemical graph, that is equal to:

$$\begin{aligned} {M_{2}} G_5(T,z)=\; & {} 2{z^{(18)}}+2{z^{(21)}}+2{z^{(36)}}+(2n-2){z^{(42)}}+8{z^{(54)}}\\{} & {} +2{z^{(84)}}+2{z^{(81)}}+(2n+2){z^{(108)}}+(n-2){z^{(27)}}\\{} & {} +(n-2){z^{(121)}}+ (6n-12){z^{(132)}}+(n-2){z^{(77)}}\\. \end{aligned}$$

Proof

Let T be the Superlattice structure. Through Eq. (11),

$$\begin{aligned} {M_{2}} G_5(T,z)=\sum _{uv \epsilon {E(T)}} z^{{\S _{T}(u)\S _{T}(v)}}. \end{aligned}$$

By use of Table 1

$$\begin{aligned}=\; & {} 2{z^{(3\times 6)}}+2{z^{(3\times 7)}}+2{z^{(6\times 6)}}+(2n-2){z^{(6\times 7)}}+8{z^{(6\times 9)}}\\{} & {} +2{z^{(7\times 12)}}+2{z^{(9\times 9)}}+(2n+2){z^{(9\times 12)}}+(n-2){z^{(3\times 9)}}\\{} & {} +(n-2){z^{(11\times 11)}}+ (6n-12){z^{(11\times 12)}}+(n-2){z^{(11\times 7)}}\\. \end{aligned}$$

we have got, by making some calculations

$$\begin{aligned} \Longrightarrow {M_{2}} G_5(T,z)=\; & {} 2{z^{(18)}}+2{z^{(21)}}+2{z^{(36)}}+(2n-2){z^{(42)}}+8{z^{(54)}}\\{} & {} +2{z^{(84)}}+2{z^{(81)}}+(2n+2){z^{(108)}}+(n-2){z^{(27)}}\\{} & {} +(n-2){z^{(121)}}+ (6n-12){z^{(132)}}+(n-2){z^{(77)}}\\. \end{aligned}$$

\(\hfill\square\)

Theorem 4.12

Consider the Superlattice structure, \({M_{1}} G_5(T,z)\) of fifth M-Zagreb index as polynomial for a chemical graph, that is equal to:

$$\begin{aligned} {M_{1}} G_5(T,z)=\; & {} 2{z^{(81)}}+2{z^{(100)}}+2{z^{(144)}}+(2n-2){z^{(169)}}+8{z^{(225)}}\\{} & {} +2{z^{(361)}}+2{z^{(324)}}+(2n+2){z^{(441)}}+(n-2){z^{(144)}}\\{} & {} +(n-2){z^{(484)}}+ (6n-12){z^{(529)}}+(n-2){z^{(324)}}\\. \end{aligned}$$

Proof

Let T be the Superlattice structure. From Eq. (12),

$$\begin{aligned} {M_{1}} G_5(T,z)=\sum _{uv \epsilon {E(T)}} z^{({\S _{T}(u)+\S _{T}(v)})^2}. \end{aligned}$$

By applying the concept of edge frequency to Table 1.

$$\begin{aligned}=\; & {} 2{z^{(3+6)^{2}}}+2{z^{(3+7)^{2}}}+2{z^{(6+6)^{2}}}+(2n-2){z^{(6+7)^{2}}}+8{z^{(6+9)^{2}}}\\{} & {} +2{z^{(7+12)^{2}}}+2{z^{(9+9)^{2}}}+(2n+2){z^{(9+12)^{2}}}+(n-2){z^{(3+9)^{2}}}\\{} & {} +(n-2){z^{(11+11)^{2}}}+ (6n-12){z^{(11+12)^{2}}}+(n-2){z^{(11+7)^{2}}}\\. \end{aligned}$$

we have got, by making some calculations

$$\begin{aligned} \Longrightarrow {M_{1}} G_5(T,z)=\; & {} 2{z^{(81)}}+2{z^{(100)}}+2{z^{(144)}}+(2n-2){z^{(169)}}+8{z^{(225)}}\\{} & {} +2{z^{(361)}}+2{z^{(324)}}+(2n+2){z^{(441)}}+(n-2){z^{(144)}}\\{} & {} +(n-2){z^{(484)}}+ (6n-12){z^{(529)}}+(n-2){z^{(324)}}\\. \end{aligned}$$

\(\hfill\square\)

Theorem 4.13

Consider the Superlattice structure, \({M_{2}} G_5(T,z)\) of fifth M-Zagreb index polynomial for a molecular graph, which is equal to:

$$\begin{aligned} {M_{2}} G_5(T,z)=\; & {} 2{z^{(324)}}+2{z^{(441)}}+2{z^{(1296)}}+(2n-2){z^{(1764)}}+8{z^{(2916)}}\\{} & {} +2{z^{(7056)}}+2{z^{(6561)}}+(2n+2){z^{(11664)}}+(n-2){z^{(729)}}\\{} & {} +(n-2){z^{(14641)}}+ (6n-12){z^{(17424)}}+(n-2){z^{(5929)}}\\. \end{aligned}$$

Proof

Let T be the Superlattice structure. From Eq. (13),

$$\begin{aligned} {M_{2}} G_5(T,z)=\sum _{uv \epsilon {E(T)}} z^{({\S _{T}(u)\S _{T}(v)})^2}. \end{aligned}$$

Through Table 1.

$$\begin{aligned}=\; & {} 2{z^{(3\times 6)^{2}}}+2{z^{(3\times 7)^{2}}}+2{z^{(6\times 6)^{2}}}+(2n-2){z^{(6\times 7)^{2}}}+8{z^{(6\times 9)^{2}}}\\{} & {} +2{z^{(7\times 12)^{2}}}+2{z^{(9\times 9)^{2}}}+(2n+2){z^{(9\times 12)^{2}}}+(n-2){z^{(3\times 9)^{2}}}\\{} & {} +(n-2){z^{(11\times 11)^{2}}}+ (6n-12){z^{(11\times 12)^{2}}}+(n-2){z^{(11\times 7)^{2}}}\\. \end{aligned}$$

we have got, by making some calculations

$$\begin{aligned} \Longrightarrow {M_{2}} G_5(T,z)=\; & {} 2{z^{(324)}}+2{z^{(441)}}+2{z^{(1296)}}+(2n-2){z^{(1764)}}+8{z^{(2916)}}+\\ {}{} & {} 2{z^{(7056)}}+2{z^{(6561)}}+(2n+2){z^{(11664)}}+(n-2){z^{(729)}}+\\ {}{} & {} (n-2){z^{(14641)}}+ (6n-12){z^{(17424)}}+(n-2){z^{(5929)}}\\. \end{aligned}$$

\(\hfill\square\)

The numerical and graphical representation if above computed results are depicted in Table 2 and Fig. 4, respectively.

Table 2 The Fifth Zagreb Indices, both general and degree-based of Superlattice Network for\(n=1\) to 10 with comparison of numbers
Full size table
Fig. 4
figure 4

Numerical values of indices

Full size image

5 Conclusion

In this paper, the analysis of superlattice structure with the help of fifth M-Zagreb polynomials and fifth M-Zagreb indices provides a deeper understanding of the structural and chemical and physical properties i. e such as boiling and melting points, refractive index, and dielectric constant of the superlattice. The fifth M-Zagreb polynomials and indices provide a quantitative measure of the degree of branching of the molecules in the superlattice. Using the fifth M-Zagreb polynomials and indices can provide valuable insights into the degree of branching and topological properties of the material.