1 Introduction

Rayleigh waves have enormous importance in the field of Geo-mechanics and Physics. As the Rayleigh waves are two-dimensional, their energy is not dissipated as rapidly as that of the three-dimensional P-wave and S-wave. Hence, this type of waves is the most destructive in earthquake tremors and has a particular significance in seismology. In the study of shear horizontal Rayleigh waves in seismograms, in 1911, Love [2] discovered a wave propagating at the free surface of a layer in perfect contact with a half space. Later on, Stoneley studied about the occurrences of waves localized at the surface of discontinuity between two materials [31]. In contrast with Love, Stoneley found that wave motion that is greatest at the surface of separation of the two media. Whereas, Love’s observation was the disturbances confined to the free surface. These waves are also termed as the generalized Rayleigh waves. Stoneley concluded about the existence of the of the localized waves that “we can assert that when the wave-velocities are not too widely different for two media, a wave of Rayleigh type can exist at the interface” [32].

Stoneley wave is a type of surface wave which propagates along the surfaces possessing their fields confined to neighbouring surfaces [7, 8]. This wave is different in nature than other type of primary waves. It can be generated in piezo-electric transduction, non-destructive testing to find the defects, electromagnetics, hydrodynamics and also in many other fields. The importance of the localized wave to non-destructive detection of various materials’ surface flaws is of great interest in the current era. The dispersion of localized wave and depth of penetration may be influenced deeply by the type of surfaces because of presence of various boundary conditions.

In the last few decades, many researchers have been investigated the behaviour of elastic medium in presence of the thermal effects. Thermoelasticity theories relate the nature of elastic materials with effect of non-uniform temperature, in general it presents the generalization of theory of elasticity. In the thermoelastic model owing to Fourier, the classical thermoelasticity theory, heat conduction law governed by a parabolic type partial differential equation which admit infinite speed of propagation of thermal signals. This paradox of speed of propagation of thermal signals happened due to parabolic type heat conduction equation. Biot [26] proposed coupled thermoelastic model with the incorporation of strain related term in Fourier’s law of heat conduction. This theory signify the finite speed of propagation of elastic waves but attains infinite speed of thermal signals. In later, to surmount the paradox of speed of propagation of thermal signals a generalization of thermoelasticity theories was introduced. The spectacular success of this generalization is attaining of finite speed of propagation of thermal signals.

The generalized thermoelasticity theories posses hyperbolic type heat transport equation which predicts wave like thermal signals propagate with finite speed. There are various types of model of generalized thermoelasticity which have been introduced by various researchers, among those most acceptable models which are generally used, have been developed by Lord and Shulman [21], Green and Lindsay [3], Green and Naghdi [4,5,6], Tzou [14, 15]. The finite wave speed was verified under various kind of conditions by Ignaczak and Ostoja-Starzewsk [24], Sherief and Dhaliwal [20], and Sherief [19]. A brief history regarding generalized thermoelasticity is presented in the monographs given by Chandrasekharaiah [13], Ignaczak and Hetnarski [25].

Thermal effects on transversely isotropic elastic half-space overlaid by a transversely isotropic elastic layer is a model finding a large number of applications in seismology, geophysics etc. Measures of the mechanical properties of such layers supported by transversely isotropic half-space plays a significant role in realizing the natures of these structures in applications. There are different types of measurement methods among those, the method of guided wave is mostly used as it has non-destructive property and also related to reduced cost, smaller inspection time and wider coverage. The Rayleigh wave is a type of guided wave which has versatility and it is also a convenient tool. The frequency equation of Rayleigh wave without thermal effect was formulated by Haskell [27] when both of half-space and layer are isotropic. Sotiropoulos [11] deduced the frequency equation taking both of the half-space and layer orthotropic. Considering various cases, the frequency equation of Rayleigh wave in case of elastic half-spaces overlaid by thin film, are derived by various author like steigmann and Ogden [12], Vinh and Linh [28], Pham and Vu [10]. Vinh et al [29] deduced the secular equations of Rayleigh waves for the case of orthotropic elastic half-space overlaid by an orthotropic elastic layer taking the compressible in-compressible cases into consideration. In the last decade several authors have works in numerous occasion about Rayleigh wave propagation, among them we can mention, (Liu et al [16,17,18], Shaw and Othman [33]).

In the present model, thermoelastic responses of localized wave propagating in transversely isotropic half-space overlaid by a layer, of arbitrary thickness, is investigated. To facilitate the thermal impact, one of the most accepted hyperbolic type thermoelastic models due to Lord–Shulman is used. Numerical computations are made to analyse different characteristics of the wave like attenuation coefficient, specific loss, phase velocity and frequency of wave. Numerical simulations are presented in figures and observations are made for different cases. The investigations in the present work are worthwhile in real applications like earthquake engineering, damage characterizations of materials, geophysics and seismology.

2 Statement of the problem

A transversely isotropic medium is a medium has a favored direction and is isotropic in the plane perpendicular to this direction. Among crystalline media, all materials with a hexagonal crystal system belongs to this class: they obey elastically isotropic in the plane perpendicular to the hexagonal axis.

A linear transversely isotropic medium is fully dependent by five elastic constants. For the definition of these constants, the elastic moduli and coefficient of transverse contraction are used.

If the \(x_1 x_2\)-plane is perpendicular to the favored direction of transversely isotropic medium in Cartesian coordinate system \((x_1, x_2, x_3)\), the constitutive relations of the transversely isotropic materials are:

$$\begin{aligned} \begin{aligned} \sigma _{11}&= c_{11} u_{1,1} +c_{12} u_{2,2} + c_{13} u_{3,3} - \beta _1 T, \\ \sigma _{22}&= c_{12} u_{1,1} +c_{11} u_{2,2} + c_{13} u_{3,3} - \beta _1 T, \\ \sigma _{33}&= c_{13} \Big ( u_{1,1} + u_{2,2} \Big ) + c_{13} u_{3,3} - \beta _3 T, \\ \sigma _{23}&= c_{44} \Big ( u_{2,3} + u_{3,2} \Big ), \\ \sigma _{31}&= c_{44} \Big ( u_{3,1} + u_{1,3} \Big ), \\ \sigma _{12}&= c_{66} \Big ( u_{1,2} + u_{2,1} \Big ), \end{aligned} \end{aligned}$$
(1)

where \(u_1, u_2, u_3\) are the components of displacements in \(x_1, x_2, x_3\) directions respectively; \(\sigma _{ij}\) represent the components of stress tensor; ’T’ denotes the temperature increment. \(c_{ij}\) and \(\beta _i\) are elastic and thermal modules respectively. \(c_{66} = \frac{1}{2} \big ( c_{11} - c_{12} \big )\). ’Comma’ in the subscript denotes the derivative with respect to the spacial variable.

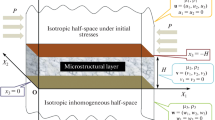
Here, we have considered a transversely isotropic elastic half-space \(x_2 \ge 0\) overlaid by a transversely isotropic elastic layer under a temperature field and with thickness h which occupy the domain \( -h\le x_2\le 0\). The layer is assumed to be perfectly bonded to the half-space. The surface \(x_2=-h\) is stress free and thermally insulated. The localized wave propagates along the interface of the layer and half-space. Same symbols are used for the quantities pertaining to half-space and the layer but a bar is used if it belongs to the layer (Fig. 1).

For the simplicity of the problem, we are interested in plane-strain problem parallel to \(x_1 x_2\)-plane in which,

$$\begin{aligned} \begin{aligned} u_i=u_i(x_1,x_2,t),\, \, \bar{u_i}=\bar{u}_i(x_1,x_2,t),\, \,u_3=\bar{u}_3=0\\ T_1=T_1(x_1,x_2,t),\,\bar{T}_1=\bar{T}_1(x_1,x_2,t); \quad i=1,2. \end{aligned} \end{aligned}$$
Fig. 1
figure 1

Schematic diagram of the problem

Full size image

In absence of body forces, the mechanical equilibrium equations for the layer are

$$\begin{aligned} \bar{\sigma }_{11,1}+\bar{\sigma }_{12,2}={\bar{\rho }}{\ddot{{\bar{u}}}_1},\,\bar{\sigma }_{12,1}+\bar{\sigma }_{22,2}={\bar{\rho }}{\ddot{{\bar{u}}}_2} \end{aligned}$$
(2)

where \(\bar{\sigma }_{ij}\) are stress components and \(\bar{\rho }\) is material density of the layer. The stress–strain relations for transversely isotropic body under thermal effect are given by

$$\begin{aligned} \begin{aligned} \bar{\sigma }_{11}&=\bar{c}_{11}\bar{u}_{1,1}+\bar{c}_{12}\bar{u}_{2,2}-\bar{\beta }_1\bar{T}, \\ \bar{\sigma }_{22}&=\bar{c}_{12}\bar{u}_{1,1}+\bar{c}_{11}\bar{u}_{2,2}-\bar{\beta }_1\bar{T}, \\ \bar{\sigma }_{12}&=\frac{1}{2}({\bar{c}_{11}-\bar{c}_{12}})({\bar{u}_{1,2}+\bar{u}_{2,1}}),\\ \end{aligned} \end{aligned}$$
(3)

where \(\bar{c}_{ij}\) are material constants; \(\bar{T}\) is the temperature increment, given by \(\bar{T}=\bar{T}_1-\bar{T}_0\) and \(\bar{T}_0\) is initial temperature of the layer.

Substituting (3) in Eq. (2s) yield,

$$\begin{aligned} \begin{aligned} \bar{c}_{11}\bar{u}_{1,11}+\frac{1}{2}(\bar{c}_{12}+\bar{c}_{11})\bar{u}_{2,12}+\frac{1}{2}({\bar{c}_{11}-\bar{c}_{12}})\bar{u}_{1,22}-\bar{\beta }_1\bar{T}_{,1}=\bar{\rho }\ddot{\bar{u}}_1, \\ \frac{1}{2}(\bar{c}_{11}+\bar{c}_{12})\bar{u}_{1,12}+\frac{1}{2}({\bar{c}_{11}-\bar{c}_{12}})\bar{u}_{2,11}+\bar{c}_{11}\bar{u}_{2,22}-\bar{\beta }_1\bar{T}_{,2}=\bar{\rho }\ddot{\bar{u}}_2. \\ \end{aligned} \end{aligned}$$
(4)

The heat conduction equation in Lord–Shulman theory for transversely isotropic body in \(x_1 x_2\) plane is

$$\begin{aligned} \bar{K_1}(\bar{T}_{,11}+\bar{T}_{,22})=\left( 1+\tau \frac{\partial }{\partial t}\right) [\bar{\rho }\bar{C_v}\dot{\bar{T}}+\bar{T_0}\bar{\beta _1} \left( \dot{\bar{u}}_{1,1}+\dot{\bar{u}}_{2,2}\right) ] \end{aligned}$$
(5)

where \(\bar{C}_v\) is the specific heat, \(\tau \) is the relaxation time, \({\bar{K}}_1\) is the thermal conductivity and \({\bar{\beta }}_1\) is defined as thermal modulo of the layer. An over-headed dot represents the time derivative.

3 Solution procedure

The displacement vector \( \big ( \bar{u}_1, \bar{u}_2 \big )\) can be decomposed by using Helmholtz decomposition theorem, in-terms of \( {\bar{\phi }}(x_1,x_2,t)\) and \( {\bar{\psi }}(x_1,x_2,t)\) in the following manner:

$$\begin{aligned} \begin{aligned} \bar{u}_1=\frac{\partial \bar{\phi }}{\partial x_1}+\frac{\partial \bar{\psi }}{\partial x_2},\\ \bar{u}_2=\frac{\partial \bar{\phi }}{\partial x_2}-\frac{\partial \bar{\psi }}{\partial x_1}. \end{aligned} \end{aligned}$$
(6)

Now substituting (6) in (4) we get the following system of equations

$$\begin{aligned} \begin{aligned} \bar{c}_{11}\bar{\phi }_{,11}+\bar{c}_{11}\bar{\phi }_{,22}-\bar{\beta _1}\bar{T}=\bar{\rho }\ddot{\bar{\phi }},\\ \frac{1}{2}({\bar{c}_{11}-\bar{c}_{12}})\bar{\psi }_{,11}+\frac{1}{2}({\bar{c}_{11}-\bar{c}_{12}})\bar{\psi }_{,22}=\bar{\rho }\ddot{\bar{\psi }}. \end{aligned} \end{aligned}$$
(7)

The heat conduction equation becomes

$$\begin{aligned} \bar{K_1}(\bar{T}_{,11}+\bar{T}_{,22})=\left( 1+\tau \frac{\partial }{\partial t}\right) [\bar{\rho }\bar{C_v}\dot{\bar{T}}+\bar{T_0}\bar{\beta _1} \left( \dot{\bar{\phi }}_{,11}+\dot{\bar{\phi }}_{,22}\right) ]. \end{aligned}$$
(8)

Now for the Stoneley wave propagating in \(x_1\) direction we shall find the solution of system of Eqs. (7) and (8) in the following form

$$\begin{aligned} \begin{aligned} \bar{\phi }=\bar{\phi } ^*(x_2)\exp (ik(x_1-ct)),\\ \bar{\psi }=\bar{\psi } ^*(x_2)\exp (ik(x_1-ct)),\\ \bar{T}=\bar{\theta } ^*(x_2)\exp (ik(x_1-ct)), \end{aligned} \end{aligned}$$
(9)

where k and c are the wave number and phase velocity of the wave respectively.

Using (9) the system of Eq. (7) we get the following system of equations

$$\begin{aligned} \begin{aligned} \bar{c}_{11}\frac{\partial ^2\bar{\phi }^*}{\partial x_2^2}+k^2(\bar{\rho }c^2-\bar{c}_{11})\bar{\phi }^*-\bar{\beta _1}\bar{\theta }^*=0,\\ \frac{\partial ^2\bar{\psi }^*}{\partial x_2^2}-{\tau _0}^2\bar{\psi }^*=0, \end{aligned} \end{aligned}$$
(10)

where \({\tau _0}^2=k^2(1-\frac{2\bar{\rho }c^2}{\bar{c}_{11}-\bar{c}_{12}})\).

From the heat conduction Eq. (8) we get the following equation

$$\begin{aligned} \frac{\partial ^2\bar{\theta }^*}{\partial x_2^2}-d_2\bar{\theta }^*=-d_3\left( \frac{\partial ^2\bar{\phi }^*}{\partial x_2^2}-k^2\bar{\phi }^* \right) , \end{aligned}$$
(11)

where \(d_2=(\frac{ikc\bar{\rho }\bar{C}_vd_1}{\bar{K_1}}-k^2) \),  \( d_3=\frac{ikcd_1\bar{T}_0\bar{\beta }_1}{\bar{K}_1} \) and \(d_1=(1-\tau ikc)\).

Here we observed that the first equation of (10) and Eq. (11) are coupled system of equations. The second equation of (10) is in decoupled form. Solving these two sets of equations we obtain:

$$\begin{aligned} \begin{aligned} \bar{\phi }^*=&\,B_1\cosh \bar{b}_1x_2+B_2\sinh \bar{b}_1x_2+B_3\cosh \bar{b}_2x_2+B_4\sinh \bar{b}_2x_2,\\ \bar{\psi }^*=&\,A_1\cosh \tau _0x_2+A_2\sinh \tau _0x_2,\\ \bar{\theta }^*=&\,\bar{\alpha }_1(B_1\cosh \bar{b}_1x_2+B_2\sinh \bar{b}_1 x_2)+ \bar{\alpha }_2 (B_3\cosh \bar{b}_2 x_2 + B_4 \sinh \bar{b}_2 x_2), \end{aligned} \end{aligned}$$
(12)

where \(A_1, A_2, B_i\) are arbitrary constants and \(\bar{b}_1\), \(\bar{b}_2\), \(\bar{\alpha }_1\), \(\bar{\alpha }_2\) are given by

$$\begin{aligned} \begin{aligned} \bar{b}_1=\sqrt{\frac{\bar{S}-\sqrt{\bar{S}^2-4\bar{P}}}{2}}, \quad \bar{b}_2=\sqrt{\frac{\bar{S}+\sqrt{\bar{S}^2-4\bar{P}}}{2}} \end{aligned} \end{aligned}$$
(13)
$$\begin{aligned} \begin{aligned} \bar{\alpha }_1=\frac{\bar{c}_{11}\bar{b}_1^2+k^2(\bar{\rho } c^2-\bar{c}_{11})}{\bar{\beta }_1}, \quad \bar{\alpha }_2=\frac{\bar{c}_{11}\bar{b}_2^2+k^2(\bar{\rho } c^2-\bar{c}_{11})}{\bar{\beta }_1} \end{aligned} \end{aligned}$$
(14)

with

$$\begin{aligned}{} & {} \bar{S}=\frac{k^2(\bar{c}_{11}-\rho c^2)-\bar{c}_{11}d_2-\bar{\beta }_1d_3}{\bar{c}_{11}}, \end{aligned}$$
(15)
$$\begin{aligned}{} & {} \bar{P}=\frac{k^2d_2(\bar{\rho }c^2-\bar{c}_{11})-k^2\bar{\beta _1}d_3}{\bar{c}_{11}}. \end{aligned}$$
(16)

Therefore, the displacement components are given by

$$\begin{aligned}{} & {} \bar{u}_1={\overline{U}}_1(x_2)exp(ik(x_1-ct)), \end{aligned}$$
(17)
$$\begin{aligned}{} & {} \bar{u}_2={\overline{U}}_2(x_2)exp(ik(x_1-ct)), \end{aligned}$$
(18)

where

$$\begin{aligned} {\overline{U}}_1(x_2)= & {} {}[ik(B_1\cosh {\bar{b}_1x_2}+B_2\sinh {\bar{b}_1x_2}+B_3\cosh {\bar{b}_2x_2}+B_4\sinh {\bar{b}_2x_2})\\{} & {} \quad +\tau _0(A_1\sinh {\tau _0x_2}+A_2\cosh {\tau _0x_2})]exp(ik(x_1-ct)), \\ {\overline{U}}_2(x_2)= & {} {}[\bar{b}_1(B_1\sinh {\bar{b}_1x_2}+B_2\cosh {\bar{b}_1x_2})+\bar{b}_2(B_3\sinh {\bar{b}_2x_2}+B_4\cosh {\bar{b}_2x_2})\\{}{} & {} \quad -ik(A_1\cosh {\tau _0x_2}+A_2\sinh {\tau _0x_2})]exp(ik(x_1-ct)). \end{aligned}$$

The stress components are

$$\begin{aligned}{} & {} \bar{\sigma }_{12}={\overline{\Sigma }}_1(x_2)exp(ik(x_1-ct)), \end{aligned}$$
(19)
$$\begin{aligned}{} & {} \bar{\sigma }_{22}={\overline{\Sigma }}_2(x_2)exp(ik(x_1-ct)), \end{aligned}$$
(20)

where

$$\begin{aligned} \begin{aligned} {\overline{\Sigma }}_1(x_2)&=\bar{\mu }_1(B_1\sinh {\bar{b}_1x_2}+B_2\cosh {\bar{b}_1x_2)}+\bar{\mu }_2(B_3\sinh {\bar{b}_2x_2}+B_4\cosh {\bar{b}_2x_2})\\&\quad +\bar{\eta }_1(A_1\cosh {\tau _0x_2}+A_2\sinh {\tau _0x_2}),\\ {\overline{\Sigma }}_2(x_2)&=\bar{\gamma }_1(B_1\cosh {\bar{b}_1x_2}+B_2\sinh {\bar{b}_1x_2)}+\bar{\gamma }_2(B_3\cosh {\bar{b}_2x_2}+B_4\sinh {\bar{b}_2x_2})\\&\quad +\bar{\eta }_2(A_1\sinh {\tau _0x_2}+A_2\cosh {\tau _0x_2}). \end{aligned} \end{aligned}$$

In which,

\(\bar{\mu }_1=ik\bar{b}_1(\bar{c}_{11}-\bar{c}_{12})\),    \(\bar{\mu }_2=ik\bar{b}_2(\bar{c}_{11}-\bar{c}_{12})\),

\(\bar{\eta }_1=\frac{(\bar{c}_{11}-\bar{c}_{12})(\tau _0^2+k^2)}{2}\),    \(\bar{\eta }_2=-ik\tau _0(\bar{c}_{11}-\bar{c}_{12})\),

\(\bar{\gamma }_1=\bar{c}_{11}b_1^2-k^2\bar{c}_{12}-\bar{\beta _1}\bar{\alpha }_1\),    \(\bar{\gamma }_2=\bar{c}_{11}b_2^2-k^2\bar{c}_{12}-\bar{\beta _1}\bar{\alpha }_2\).

3.1 Boundary conditions:

The mechanical boundary condition: The surface \(x_2=-h\) is stress free, hence we have

$$\begin{aligned} \bar{\sigma }_{12}|_{x_2=-h}=0, \quad \bar{\sigma }_{22}|_{x_2=-h}=0. \end{aligned}$$

For thermodynamic boundary condition; we consider

$$\begin{aligned} \bar{T} + m \bar{T}_{,2} =0 \end{aligned}$$

Now, stress free conditions and \(m \rightarrow \infty \) yield following system of homogeneous equations

$$\begin{aligned} \begin{aligned}&-\bar{\mu }_1B_1 \sinh {\epsilon _1} +\bar{\mu }_1B_2 \cosh {\epsilon }_1 - \bar{\mu }_2B_3 \sinh {\epsilon _2} +\bar{\mu }_2B_4\cosh {\epsilon _2}+\bar{\eta }_1A_1\cosh {\delta } \\&-\bar{\eta }_1A_2\sinh {\delta }=0, \\&\times \bar{\gamma }_1B_1\cosh {\epsilon _1}-\bar{\gamma }_1B_2\sinh {\epsilon }_1+\bar{\gamma }_2B_3\cosh {\epsilon _2}-\bar{\gamma }_2B_4\sinh {\epsilon _2}- \bar{\eta }_2 A_1 \sinh {\delta } \\&+\bar{\eta }_2A_2\cosh {\delta }=0, \\&-\bar{b}_1 \bar{\alpha }_1B_1 \sinh {\epsilon _1} +\bar{b}_1 \bar{\alpha _1}B_2 \cosh {\epsilon _1}-\bar{b}_2 \bar{\alpha _2} B_3 \sinh {\epsilon _2}+ \bar{b}_2 \bar{\alpha _2} B_4 \cosh {\epsilon _2} = 0, \end{aligned} \end{aligned}$$
(21)

where \(\epsilon _1=\bar{b}_1h\),    \(\epsilon _2=\bar{b}_2h\) and \(\delta =\tau _0h\).

Now putting \(x_2=0\) in \({\overline{U}}_1(x_2), {\overline{U}}_2(x_2), \bar{\theta }^*(x_2)\) and in \(\bar{\sigma }_{12}, \bar{\sigma }_{22}, \bar{T}_{,2}\) one can get the following relations:

$$\begin{aligned} \begin{aligned} {\overline{U}}_1(0)&=ik(B_1+B_3)+\tau _0A_2,\\ {\overline{U}}_2(0)&=\bar{b}_1B_2+\bar{b}_2B_4-ikA_1,\\ \bar{\theta }^*(0)&=\bar{\alpha }_1B_1+\bar{\alpha }_2B_3, \\ {\overline{\Sigma }}_1(0)&=\bar{\mu }_1B_2+\bar{\mu }_2B_4+\bar{\eta }_1A_1, \\ {\overline{\Sigma }}_2(0)&=\bar{\gamma }_1B_1+\bar{\gamma }_2B_3+\bar{\eta }_2A_2, \\ \bar{\theta }^{*}_{,2}(0)&=\bar{b}_1 \bar{\alpha }_1B_2 +\bar{b}_2\bar{\alpha }_2B_4, \end{aligned} \end{aligned}$$
(22)

Solving system of Eq. (22) the values of the constants are obtained as

$$\begin{aligned} A_1= & {} \frac{{\overline{\Sigma }}_1(0)-ik(\bar{c}_{11}-\bar{c}_{12}){\overline{U}}_2(0)}{\bar{\xi }} \\ A_2= & {} \frac{ik[\bar{\alpha }]{\overline{\Sigma }}_2(0)-[\bar{\alpha };\bar{\gamma }]{\overline{U}}_1(0)-ik[\bar{\gamma }]\bar{\theta }^*(0)}{ik[\bar{\alpha }]\bar{\eta }_2-[\bar{\alpha };\bar{\gamma }]\tau _0} \\ B_1= & {} \frac{\bar{\alpha }_2\bar{\eta }_2{\overline{U}}_1(0)-\tau _0\bar{\alpha }_2{{\overline{\Sigma }}}_2(0)+(\tau _0\bar{\gamma }_2-ik\bar{\eta }_2)\bar{\theta }^*(0)}{ik[\bar{\alpha }]\bar{\eta }_2-[\bar{\alpha };\bar{\gamma }]\tau _0} \\ B_2= & {} \frac{ik\bar{\alpha }_2{\overline{\Sigma }}_1(0)-\bar{\xi }\bar{\theta }^{*}_{,2}(0) + \bar{\eta }_1 \bar{\alpha }_2 {\overline{U}}_2(0)}{\bar{b}_1[\bar{\alpha }]\bar{\xi }} \\ B_3= & {} \frac{(ik\bar{\eta }_2-\bar{\gamma }_1\tau _0)\bar{\theta }^*(0)-\bar{\alpha }_1\bar{\eta }_2{\overline{U}}_1(0)+\tau _0\bar{\alpha }_1{\overline{\Sigma }}_2(0)}{ik[\bar{\alpha }]\bar{\eta }_2-[\bar{\alpha };\bar{\gamma }]\tau _0} \\ B_4= & {} \frac{\bar{\xi }\bar{\theta }^{*}_{,2}(0)-ik\bar{\alpha }_1{\overline{\Sigma }}_1(0)-\bar{\eta }_1\bar{\alpha }_1{\overline{U}}_2(0)}{\bar{b}_2[\bar{\alpha }]\bar{\xi }} \end{aligned}$$

where \(\bar{\xi }=\bar{\eta }_1-k^2(\bar{c}_{11}-\bar{c}_{12})\) and for simplicity following notations are used

$$\begin{aligned}{}[f]=(f_2-f_1),\,[f;g]=(f_2g_1-f_1g_2) \end{aligned}$$

Now using the above obtained values of \(A_1\),\(A_2\),\(B_1\),\(B_2\),\(B_3\),\(B_4\) in the system of Eq. (21) we get the following system of equations

$$\begin{aligned} \begin{aligned} a_{11}{\overline{\Sigma }}_1(0)+a_{12}{\overline{\Sigma }}_2(0)+a_{13}{\overline{U}}_1(0)+a_{14}{\overline{U}}_2(0)+a_{15}\bar{\theta }^*(0) + a_{16} \bar{\theta }^{*}_{,2}(0) = 0\\ a_{21}{\overline{\Sigma }}_1(0)+a_{22}{\overline{\Sigma }}_2(0)+a_{23}{\overline{U}}_1(0)+a_{24}{\overline{U}}_2(0)+a_{25}\bar{\theta }^*(0)+a_{26}\bar{\theta }^{*}_{,2}(0)=0 \\ a_{31}{\overline{\Sigma }}_1(0)+a_{32}{\overline{\Sigma }}_2(0)+a_{33}{\overline{U}}_1(0)+a_{34}{\overline{U}}_2(0)+a_{35}\bar{\theta }^*(0)+a_{36}\bar{\theta }^{*}_{,2}(0)=0 \end{aligned} \end{aligned}$$
(23)

where

$$\begin{aligned} \begin{aligned} a_{11}&=\frac{k^2(\bar{c}_{11}-\bar{c}_{12})[\cosh {\epsilon };\bar{\alpha }]+\bar{\eta }_1[\bar{\alpha }]\cosh {\delta }}{[\bar{\alpha }]\bar{\xi }}, \\ a_{12}&=\frac{\tau _0 [\bar{\alpha };\bar{\mu }\sinh {\epsilon }]-ik\bar{\eta }_1 [\bar{\alpha }]\sinh {\delta }}{ik[\bar{\alpha }]\bar{\eta }_2-[\bar{\alpha };\bar{\gamma }]\tau _0}, \\ a_{13}&=\frac{\bar{\eta }_2[\bar{\mu }\sinh {\epsilon };\bar{\alpha }]+\bar{\eta }_1[\bar{\alpha };\bar{\gamma }]\sinh {\delta }}{ik[\bar{\alpha }]\bar{\eta }_2-[\bar{\alpha };\bar{\gamma }]\tau _0}, \\ a_{14}&=\frac{ik(\bar{c}_{11}-\bar{c}_{12})\bar{\eta }_1([\bar{\alpha };\cosh {\epsilon }]-[\bar{\alpha }]\cosh {\delta })}{[\bar{\alpha }]\bar{\xi }}, \\ a_{15}&=\frac{-ik\bar{\eta }_2[\bar{\mu }\sinh {\epsilon }]-\tau _0[\bar{\gamma };\bar{\mu }\sinh {\epsilon }]+ik\bar{\eta }_1[\bar{\gamma }]\sinh {\delta }}{ik[\bar{\alpha }]\bar{\eta }_2-[\bar{\alpha };\bar{\gamma }]\tau _0}, \\ a_{16}&=\frac{ik(\bar{c}_{11}-\bar{c}_{12})[\cosh {\epsilon }]}{[\bar{\alpha }]}, \\ a_{21}&=\frac{ik[\bar{\gamma }\sinh {\epsilon };\bar{\alpha }\bar{b}]-\bar{b}_1\bar{b}_2[\bar{\alpha }]\sinh {\delta }}{\bar{b}_1\bar{b}_2[\bar{\alpha }]\bar{\xi }}, \\ a_{22}&=\frac{\tau _0[\bar{\gamma }\cosh {\epsilon };\bar{\alpha }]+ik\bar{\eta }_2[\bar{\alpha }]\cosh {\delta }}{ik[\bar{\alpha }]\bar{\eta }_2-[\bar{\alpha };\bar{\gamma }]\tau _0},\\ a_{23}&=\frac{\bar{\eta }_2([\bar{\alpha };\bar{\gamma }\cosh {\epsilon }]-[\bar{\alpha };\bar{\gamma }]\cosh {\delta })}{ik[\bar{\alpha }]\bar{\eta }_2-[\bar{\alpha };\bar{\gamma }]\tau _0}, \\ a_{24}&=\frac{\bar{\eta }_1[\bar{\gamma }\sinh {\epsilon };\bar{\alpha }\bar{b}]+ik\bar{\eta }_2\bar{b}_1\bar{b}_2[\bar{\alpha }](\bar{c}_{11}-\bar{c}_{12})\sinh {\delta }}{\bar{b}_1\bar{b}_2[\bar{\alpha }]\bar{\xi }}, \\ a_{25}&=\frac{-\tau _0 \bar{\gamma }_1\bar{\gamma }_2 [\cosh {\epsilon }] +ik\bar{\eta }_2 [\bar{\gamma }\cosh {\epsilon }] -ik\bar{\eta }_2 [\bar{\gamma }] \cosh {\delta }}{ik[\bar{\alpha }]\bar{\eta }_2-[\bar{\alpha };\bar{\gamma }]\tau _0}, \\ a_{26}&=\frac{[\bar{b};\bar{\gamma }\sinh {\epsilon }]}{\bar{b}_1\bar{b}_2[\bar{\alpha }]}, \\ a_{31}&=\frac{-ik\bar{\alpha }_1\bar{\alpha }_2[\cosh {\epsilon }]}{[\bar{\alpha }]\bar{\xi }}, \\ a_{32}&=\frac{-\tau _0 \bar{\alpha }_1 \bar{\alpha }_2 [\bar{b}\sinh {\epsilon }]}{ik[\bar{\alpha }]\bar{\eta }_2-[\bar{\alpha };\bar{\gamma }]\tau _0}, \\ a_{33}&=\frac{\bar{\alpha }_1\bar{\alpha }_2\bar{\eta }_2 [\bar{b}\sinh {\epsilon }]}{ik[\bar{\alpha }]\bar{\eta }_2-[\bar{\alpha };\bar{\gamma }]\tau _0}, \\ a_{34}&=\frac{- \bar{\eta }_1 \bar{\alpha }_1 \bar{\alpha }_2[\cosh {\epsilon }]}{[\bar{\alpha }] \bar{\xi }}, \\ a_{35}&= \frac{\tau _0 [\bar{b} \bar{\alpha } \sinh {\epsilon }\bar{\gamma }]-ik\bar{\eta }_2 [\bar{b} \bar{\alpha } \sinh {\epsilon }]}{ik[\bar{\alpha }]\bar{\eta }_2-[\bar{\alpha };\bar{\gamma }]\tau _0}, \\ a_{36}&=\frac{[\bar{\alpha }\cosh {\epsilon }]}{[\bar{\alpha }]}. \end{aligned} \end{aligned}$$
(24)

Since the layer and half-space are assumed to be perfectly bonded at the interface \(x_2=0\).

Thus, we have the conditions of continuity:

$$\begin{aligned} \bar{u}_1=u_1, \quad \bar{u}_2=u_2, \quad \bar{\sigma }_{12}=\sigma _{12}, \quad \bar{\sigma }_{22}=\sigma _{22}, \quad \bar{T}=T, \quad \bar{T}_{,2}=T_{,2} \end{aligned}$$

at \(x_2=0\).

Using these conditions in the system of Eq. (23) we get the following system of equations

$$\begin{aligned} \begin{aligned} a_{11}{\Sigma }_1(0)+a_{12}{\Sigma }_2(0)+a_{13}{U}_1(0)+a_{14}U_2(0)+a_{15}{\theta ^*}(0)+a_{16}{\theta }^{*}_{,2}(0)=0 \\ a_{21}{\Sigma }_1(0)+a_{22}{\Sigma }_2(0)+a_{23}U_1(0)+a_{24}U_2(0)+a_{25}{\theta ^*}(0)+a_{26}{\theta }^{*}_{,2}(0)=0 \\ a_{31}{\Sigma }_1(0)+a_{32}{\Sigma }_2(0)+a_{33}U_1(0)+a_{34}U_2(0)+a_{35}{\theta ^*}(0)+a_{36}{\theta }^{*}_{,2}(0)=0 \end{aligned} \end{aligned}$$
(25)

where \(U_1(0)\),\(U_2(0)\) and \({\Sigma }_1(0)\),\({\Sigma }_2(0)\) are amplitudes of displacements and stresses of the half-space at the interface \(x_2=0\).

4 Frequency equation

We consider the propagation of the localized waves along the surface \(x_2=0\) of the half-space possessing velocity c and have the wave number k in the direction of \(x_1\).

The displacement components \(u_1\) and \(u_2\) in the half -space \(x_2>0\) are given by

$$\begin{aligned} u_1=U_1(x_2)\exp (ik(x_1-ct), u_2=U_2(x_2)\exp (ik(x_1-ct)) \end{aligned}$$
(26)

where

$$\begin{aligned} U_1(x_2)&=ik[C_1\exp (-b_1x_2)+C_2\exp (-b_2x_2)]-\tau _0D_1\exp (-\tau _0x_2) \\ U_2(x_2)&=-[C_1b_1\exp (-b_1x_2)+C_2b_2\exp (-b_2x_2)+ikD_1\exp (-\tau _0x_2)] \end{aligned}$$

\(C_1\), \(C_2\), \(D_1\) are arbitrary constants and \(b_1\) and \(b_2\) are two roots having positive real parts of the equation:

$$\begin{aligned} b^4-Sb^2+P=0, \end{aligned}$$

in which the expressions of S and P can be found from Eqs. (15) and (16).

Thus, the components stresses become

$$\begin{aligned} \sigma _{12}={\Sigma }_1(x_2)\exp (ik(x_1-ct)), \, \sigma _{22}={\Sigma }_2(x_2)\exp (ik(x_1-ct)) \end{aligned}$$
(27)

where, \(\Sigma _1(x_2)\) and \(\Sigma _2(x_2)\) are given by

$$\begin{aligned} {\Sigma }_1(x_2)=\mu _1C_1\exp (-b_1x_2)+\mu _2C_2\exp (-b_2x_2)+\eta _1D_1\exp (-\tau _0x_2) \\ {\Sigma }_2(x_2)=\gamma _1C_1\exp (-b_1x_2)+\gamma _2C_2\exp (-b_2x_2)+\eta _2D_1\exp (-\tau _0x_2) \end{aligned}$$

The temperature T is given by

$$\begin{aligned} T=\theta ^*(x_2)\exp (ik(x_1-ct) \end{aligned}$$
(28)

where \(\theta ^*(x_2)\) is given by

$$\begin{aligned} \theta ^*(x_2)=[\alpha _1C_1\exp (-b_1x_2)+\alpha _2C_2\exp (-b_2x_2) ] \end{aligned}$$

with

$$\begin{aligned} \alpha _1=\frac{c_{11}b_1^2+k^2(\rho c^2-c_{11})}{\beta _1} ,\\ \alpha _2=\frac{c_{11}b_2^2+k^2(\rho c^2-c_{11})}{\beta _1}, \end{aligned}$$

and

\(\mu _1=-ik(c_{11}-c_{12})b_1\), \(\mu _2=-ik(c_{11}-c_{12})b_2\), \(\eta _1=\frac{(c_{11}-c_{12})({\tau _0}^2+k^2)}{2}\), \(\gamma _1=c_{11}{b_1}^2-k^2c_{12}-\beta _1\alpha _1\), \(\gamma _2=c_{11}{b_2}^2-k^2c_{12}-\beta _1\alpha _2\), \(\eta _2=ik\tau _0(c_{11}-c_{12})\).

Now putting \(x_2=0\) in \(U_1(x_2)\), \(U_2(x_2)\), \(\Sigma _1(x_2)\), \(\Sigma _2(x_2)\), \(\theta ^*(x_2)\), \(\theta ^{*}_{,2}(x_2)\) we get

$$\begin{aligned} U_1(0)&=ik(C_1+C_2)-\tau _0D_1\\ U_2(0)&=-(C_1b_1+C_2b_2+ikD_1)\\ \Sigma _1(0)&=\mu _1C_1+\mu _2C_2+\eta _1D_1\\ \Sigma _2(0)&=\gamma _1C_1+\gamma _2C_2+\eta _2D_1 \\ \theta ^*(0)&=\alpha _1C_1+\alpha _2C_2 \\ \theta ^{*}_{,2}(0)&=-(\alpha _1b_1C_1+\alpha _2b_2C_2) \end{aligned}$$

Using these obtained values of \(U_1(0)\), \(U_2(0)\), \(\Sigma _1(0)\), \(\Sigma _2(0)\), \(\theta ^*(0)\), \(\theta ^{*}_{,2}(0)\) in Eq. (25), a homogeneous system of equations in \(C_1\), \(C_2\), \(D_1\) is obtained, given by

$$\begin{aligned} \begin{aligned} r_{11}C_1+r_{12}C_2+r_{13}D_1=0\\ r_{21}C_1+r_{22}C_2+r_{23}D_1=0\\ r_{31}C_1+r_{23}C_2+r_{33}D_1=0 \end{aligned} \end{aligned}$$
(29)

On elimination of \(C_1\), \(C_2\) and \(D_1\), Eq. (29) yields the frequency equation as follows:

$$\begin{aligned} r_{11}(r_{22}r_{33}-r_{32}r_{23})+r_{12}(r_{31}r_{23}-r_{21}r_{33})+r_{13}(r_{21}r_{32}-r_{31}r_{22})=0 \end{aligned}$$
(30)

in which

$$\begin{aligned} \begin{aligned} \begin{aligned} r_{j1}&=\mu _1a_{j1}+\gamma _1a_{j2}+ika_{j3}-b_1a_{j4}+\alpha _1a_{j5}-\alpha _1b_1a_{j6},\\ r_{j2}&=\mu _2a_{j1}+\gamma _2a_{j2}+ika_{j3}-b_2a_{j4}+\alpha _2a_{j5}-\alpha _2b_2a_{j6},\\ r_{j3}&=\eta _1a_{j1}+\eta _2a_{j2}-\tau _0a_{j3}-ika_{j4}; \quad j=1(1)3. \end{aligned} \end{aligned} \end{aligned}$$
(31)

Similarly, for \(m \rightarrow 0\) and stress free boundary conditions, the frequency equation can be recast in the following form:

$$\begin{aligned} r^{\prime }_{11}(r^{\prime }_{22}r^{\prime }_{33}-r^{\prime }_{32}r^{\prime }_{23}) + r^{\prime }_{12}(r^{\prime }_{31}r^{\prime }_{23}-r^{\prime }_{21}r^{\prime }_{33})+r^{\prime }_{13}(r^{\prime }_{21}r^{\prime }_{32}-r^{\prime }_{31}r^{\prime }_{22})=0, \end{aligned}$$
(32)

where the expressions for \(r^{\prime }_{ij}\) can be obtained from \(r_{ij}\) after replacing \(a_{3j}\) by \(a^{\prime }_{3j}\); \(j=1(1)6\).

In which

$$\begin{aligned} \begin{aligned} a^{\prime }_{31}&=\frac{ik \bar{\alpha }_1 \bar{\alpha }_2}{ \bar{b}_1 \bar{b}_2[\bar{\alpha }]\bar{\xi }} [sinh{\epsilon }; \bar{b} ], \\ a^{\prime }_{32}&=\frac{\tau _0 \bar{\alpha }_1 \bar{\alpha }_2}{ik[\bar{\alpha }]\bar{\eta }_2-[\bar{\alpha };\bar{\gamma }]\tau _0} [\cosh \epsilon ], \\ a^{\prime }_{33}&=\frac{-\bar{\alpha }_1 \bar{\alpha }_2 \bar{\eta }_2}{ik[\bar{\alpha }]\bar{\eta }_2-[\bar{\alpha };\bar{\gamma }]\tau _0} [\cosh \epsilon ], \\ a^{\prime }_{34}&=\frac{\bar{\eta }_1 \bar{\alpha }_1 \bar{\alpha }_2}{\bar{b}_1 \bar{b}_2[\bar{\alpha }] \bar{\xi }} [sinh \epsilon ; \bar{b}], \\ a^{\prime }_{35}&= \frac{\big (ik \bar{\eta }_2 - \bar{\gamma }_1 \tau _0\big )}{ik[\bar{\alpha }]\bar{\eta }_2-[\bar{\alpha };\bar{\gamma }]\tau _0} [\bar{\alpha } \cosh \epsilon ], \\ a^{\prime }_{36}&=\frac{[\bar{\alpha }_1}{\bar{b}_1 \bar{b}_2[\bar{\alpha }]} [\bar{b}; sinh \epsilon ]. \end{aligned} \end{aligned}$$
(33)

4.1 Special cases:

(i) Very thin layer \((h \rightarrow 0)\): Corresponding frequency equation for adiabatic condition can be expressed as:

$$\begin{aligned} \alpha _1 b_1 (R_{12} R_{23} - R_{22} R_{13} ) + \alpha _2 b_2 (R_{11} R_{23} - R_{21} R_{13} ) = 0 \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} R_{11}&= A_{11} \mu _1 - A_{14} b_1 - a_{16} \alpha _1 b_1 \\ R_{12}&= A_{11} \mu _2 -A_{14} b_2 - A_{16} \alpha _2 b_2 \\ R_{13}&= A_{11} \eta _1 -ikA_{14} \\ R_{21}&= \gamma _1 A_{22}\\ R_{22}&= \gamma _2 A_{22} \\ R_{23}&= \eta _2 A_{22} \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} A_{11}&= \frac{ik\big ( \bar{\mu }_1 -\bar{\mu }_2 \big )}{[\bar{\alpha }] \bar{b}_1 \bar{b}_2\bar{\xi }} [\bar{\alpha } \bar{b}] + \bar{\eta }_1\\ A_{14}&= \frac{\bar{\eta }_1 \big ( \bar{\mu }_1 -\bar{\mu }_2 \big )}{[\bar{\alpha }] \bar{b}_1 \bar{b}_2\bar{\xi }} [\bar{\alpha } \bar{b}] - \frac{ik\big ( \bar{c}_{11} - \bar{c}_{12} \big ) }{\bar{\xi }} \bar{\eta }_1 \\ A_{16}&= \frac{\big ( \bar{\mu }_1 -\bar{\mu }_2\big )}{[\bar{\alpha }] \bar{b}_1 \bar{b}_2} [\bar{b}] \\ A_{22}&= \frac{[\bar{\gamma }; \bar{\alpha }] \tau _0 + ik [\bar{\alpha }]\bar{\eta }_2}{ik[\bar{\alpha }] \bar{\eta }_2 - [\bar{\alpha }; \bar{\gamma }] \tau _0} \end{aligned} \end{aligned}$$

(ii) Coupled Thermoelasticity: If \(\tau = 0\), Eq. (30) yields the corresponding frequency relation in Coupled Thermoelasticity theory.

(iii) In absence of thermal effect: We now take the thermal field to vanish in order to reduce our results to the purely elastic case. For this purpose we take \(\bar{T}=0, \bar{C}_v = 0,\bar{\beta }_1 =0\). Under this specialization the equations in (10) become identical with Ref. [8] and the governing Eq. (30) becomes,

$$\begin{aligned} \frac{\cosh (\tau _0 h) - \frac{\bar{\xi }^2 -\bar{b}_1^2}{2\bar{\xi }^2} \cosh (\bar{b}_1 h)}{\sinh (\tau _0 h) - \frac{\bar{\xi }^2 +\bar{b}_1^2}{2\bar{b}_1 \tau _0} \sinh (\bar{b}_1 h)} = \frac{\sinh (\tau _0 h) - \frac{2\bar{b}_1 \tau _0}{\bar{\xi }^2 +\bar{b}_1^2} \sinh (\bar{b}_1 h)}{\cosh (\tau _0 h) - \frac{2\bar{\xi }^2}{\bar{\xi }^2 +\bar{b}_1^2} \cosh (\bar{b}_1 h)} \end{aligned}$$

(iv) It is observed that the component of heat flux vector \(q_2\) is related to the temperature gradient \(T_{,2}\) by the following relation:

$$\begin{aligned} q_{2} = \frac{-K_1 }{(1+\tau D^\prime )} T_{,2}, \end{aligned}$$

where \(D^\prime \equiv \frac{\partial }{\partial t}\).

4.2 Particles’ motion:

In order to describe the surface particle motion during the surface wave propagation, we retain only the real parts of \(u_1\) and \(u_2\) as follows:

$$\begin{aligned} \begin{aligned} u_1 = A cosp + B sinp \\ u_2 = \Big (\frac{B}{k}\Big ) cosp - \Big (\frac{kA}{\tau _0}\Big ) sinp \end{aligned} \end{aligned}$$
(34)

where \(A = -\tau _0 D_1 \exp (-\tau _0 x_2)\), \(B = -k \big (C_1 \exp (-b_1x_2) + C_2 \exp (-b_2x_2) \big )\), \(p = k(x_1 -ct)\).

Eliminating p from \(u_1\) and \(u_2\) we get,

$$\begin{aligned} \Big (A^2 +B^2 \Big ) u_2^2 + \Big (\frac{k^2 A^2}{\tau _0^2} + \frac{B^2}{k^2} \Big ) u_1^2 + AB \Big (\frac{2k}{\tau _0}-\frac{2}{k} \Big ) u_1 u_2 = \Big ( \frac{kA^2}{\tau _0} + \frac{B^2}{k} \Big )^2 \end{aligned}$$
(35)

Equation (35) represents an ellipse in the \(u_1 u_2\) plane. The semi-major axis X, semi-minor axis Y, and the eccentricity e of the ellipse are the following:

$$\begin{aligned} \begin{aligned} X = \Bigg [\frac{\Big (\frac{kA^2}{\tau _0} + \frac{B^2}{k}\Big )^2}{a cos^2 \theta + b sin^2 \theta +h sin(2\theta ) }\Bigg ]^{\frac{1}{2}},\\ Y = \Bigg [\frac{\Big (\frac{kA^2}{\tau _0} + \frac{B^2}{k}\Big )^2}{a sin^2 \theta + b cos^2 \theta - h sin(2\theta ) }\Bigg ]^{\frac{1}{2}},\\ e = \Bigg [ 1- \frac{a cos^2 \theta + b sin^2 \theta + h sin(2\theta )}{a sin^2 \theta + b cos^2 \theta - h sin(2\theta )}\Bigg ]^{\frac{1}{2}}, \end{aligned} \end{aligned}$$
(36)

in which \(a= \Big (\frac{k^2 A^2}{\tau _0^2} + \frac{B^2}{k^2}\Big )^2\), \(b = A^2 + B^2\), \(h = AB \Big (\frac{2k}{\tau _0} - \frac{2}{k} \Big )\), \(c= -\Big ( \frac{kA^2}{\tau _0}+ \frac{B^2}{k} \Big )^2\) and \(\theta = \frac{1}{2} tan^{-1} \big ( \frac{2\,h}{a-b} \big )\).

Thus, in the presence of thermal field, when a Rayleigh wave propagates into a homogeneous, an-isotropic layer, surface particles followed an elliptical path as seen in the Eq. (35). The lengths of the major and minor axes depend on the term ’A’. Therefore, they increase or decrease exponentially. The decay of the elliptical paths of the surface particles depends on the attenuation coefficient and wave propagation speed.

5 Solution of the frequency equation

Here we shall discuss about the technique of the solution of the obtained frequency equation with various conditions. With the help of this technique we shall try to interpret and extract the contained information in this relational equation involving secular characteristic parameters.

Generally the wave number(k) and hence the phase velocity(c) of the wave are complex quantities such that

$$\begin{aligned} \frac{1}{c}=\frac{1}{V}+i\frac{Q}{\omega } \end{aligned}$$
(37)

where \(k=R+iQ\) and \(R=\frac{\omega }{V}\) with the quantities R and V are real. Now using the relation (37) the exponent term in (9) becomes \(iR(x_1-Vt)-Qx_1\). It shows V and Q are propagation speed and attenuation coefficient of the wave respectively.

As we know \(c=\frac{\omega }{k}\), so for fixed values of frequency(\(\omega \)) and the depth of the layer (h) the Eq. (30) becomes a function of k only and let the equation be \(g(k)=0\). Hereafter we shall apply iteration method on the equation \(g(k)=0\) to obtain the solution with desired level of accuracy.

5.1 Specific loss

Specific loss is defined as the ratio of dissipated energy (\(\Delta W\)) in taking a specimen through a stress cycle to the stored elastic energy (W) in a specimen in its maximum strain. It is genuinely most effective way to define internal friction for materials. For sinusoidal plane wave of small amplitude, the specific loss (\(\frac{\Delta W}{W}\)) is equals to \(4\pi \) times the absolute value of the imaginary part of k to the real part of k i.e

$$\begin{aligned} \frac{\Delta W}{W}=4\pi |{\frac{\hbox {Im}(k)}{\hbox {Re}(k)}}|=4\pi |\frac{VQ}{\omega }| \end{aligned}$$
(38)

6 Numerical results

This section includes the numerical results from the obtained frequency equation. For the numerical analysis purposes we have taken the medium and the overlaid layer both are made of carbon steel with material constants as follows:

\(c_{11}=268.1\,({\text {GPA}})\),  \(c_{12}=111.2\,({\text {GPA}})\),  \({\bar{c}}_{11}=268.1\,({\text {GPA}})\),

\({\bar{c}}_{12}=111.2\,({\text {GPA}})\),  \(\beta _1=6910112\, {\text {kg}}/({\text {Km}}\,{\text {s}}^2 )\),  \({\bar{\beta }}_1=6910112 \,{\text {kg}}/({\text {Km}}\,{\text {s}}^2 )\),

\(C_v=465 \,{\text {J}}/({\text {kg}}\,{\text {K}})\),  \({\bar{C}}_v=465 \,{\text {J}}/({\text {kg}}\,{\text {K}})\),  \(K_1=54\, {\text {W}}/({\text {m}}\,{\text {K}})\),  \({\bar{K}}_1=54\, {\text {W}}/({\text {m}}\,{\text {K}})\),

\(\rho =7833\, {\text {kg}}/{\text {m}}^3\),  \({\bar{\rho }}=7833 \,{\text {kg}}/{\text {m}}^3\),  \(T_0=293\,{\text {K}}\). ‘\(\omega \)’ in Hz.

Taking these material constants and using the above stated solution technique for frequency equation some numerical results are presented here.

Attenuation coefficients and specific loss factors for various cases are computed in the context of Lord–Shulman theory and classical thermoelasticity theory.

Figures 2 and 3 depict the nature of attenuation coefficient of the localized waves with respect to frequency for thick and comparatively thinner \(( h \rightarrow 0) \) layer respectively.

Figure 2 shows the nature of attenuation coefficient in the layered medium with respect to frequency of the wave. From this figure it is observed that for a certain relaxation time in the context of Lord–Shulman model the magnitude of attenuation coefficients increases gradually and after taking higher values in magnitudes it decreases monotonically in the region \(40\le \omega \le 100\). The nature of attenuation coefficient in context of classical thermoelasticty also follows the same fashion, it takes nearly equal values in magnitudes as of Lord–Shulman model in the region \(0\le \omega \le 75\). The difference in magnitude occurs in the higher frequency region \(75\le \omega \le 100\). In this region classical thermoelasticity attains lower magnitude of attenuation coefficient compared to Lord–Shulman model.

Fig. 2
figure 2

Nature of attenuation coefficient for thick layer

Full size image

Figure 3 depicts the nature of attenuation coefficient when the thickness of the layer tends to zero i.e \(h \rightarrow 0\). In the region \(0\le \omega \le 45\) attenuation coefficient increases very slowly with small magnitude and suddenly it takes the very high in the region \(45\le \omega \le 70\). Thereafter attenuation coefficient becomes very low in the higher frequency region \(70\le \omega \le 100\). In the whole region of frequency classical thermoelasticity theory attains low attenuation coefficient than the Lord–Shulman theory.

Fig. 3
figure 3

Nature of attenuation coefficient for thin (\(h \rightarrow 0\)) layer

Full size image

Figures 4 and 5 describe the behaviour of specific loss factor with respect to frequency in the context of both Lord–Shulman model and classical thermoelasticity theory.

Figure 4 shows the change in specific loss with respect to frequency for the layered media of a certain thickness. In lower frequency region \(0\le \omega \le 20\) specific loss increases in rapid manner and then a sharp decline occur in the region \(20\le \omega \le 30\). It is observed that specific loss gradually decreases in frequency region \(30\le \omega \le 100\) and it takes very low values in magnitudes when frequencies are high. The Lord–Shulman model and classical thermoelasticity theory follow the same fashion of change in specific loss but differs in magnitude. In the region \(10\le \omega \le 30\) Lord–Shulman model attains higher value of specific loss as compared to classical thermoelasticity theory and in remaining region both attain nearly same value of specific loss.

Fig. 4
figure 4

Comparison of specific loss for thick layer

Full size image

Figure 5 is the depiction of specific loss with respect to frequency when the depth of the layer tends to zero i.e \(h\rightarrow 0\). This figure infer that Lord–Shulman model attempts higher value of specific loss as compared to classical thermoelasticity. According to Lord–Shulman model specific loss increases in rapid manner in the frequency region \(0\le \omega \le 10\) then slow increment occur in the region \(10\le \omega \le 30\), thereafter it gradually decreases in the higher frequency region \(30\le \omega \le 100\). In the classical thermoelasticity theory specific loss increases highly in the low frequency region \(0\le \omega \le 10\) and then in the remaining region it monotonically decreases.

Here in this figure the diminishing nature of specific loss in high frequency region for both Lord–Shulman model and classical thermoelasticity theory is a noticeable fact.

Fig. 5
figure 5

Comparison of specific loss for thin (\(h \rightarrow 0 \)) layer

Full size image

Again, the obtained frequency Eq. (30) is an implicit equation of phase velocity c and depth of the layer h. From this implicit equation of c and h the nature of phase velocity of the Rayleigh wave under thermal effect depicted graphically in Fig. 6 with respect to depth of the layer. The phase velocity of the wave is very high when depth of the layer is close to zero, thereafter it decreases monotonically and become close to very low value when the depth of the layer is very high. It is also noticed that in classical thermoelasticity phase velocity of the wave diminishes faster than Lord–Shulman model of thermoelasticity.

Fig. 6
figure 6

Comparison of frequencies with the thickness of the layer

Full size image

In general, we have the relation \(c=\frac{\omega }{k}\) and hence the frequency Eq. (30) becomes equation in two variables frequency \(\omega \) and the depth of the layer h for fixed value of k. By using this fact the nature of frequency of Rayleigh wave under thermal effect with respect to depth of the layer has been shown in Fig. 7. The frequency of the wave is very high when depth of the layer close to zero and it becomes very low when depth of the layer is high. The frequency of the wave decreases monotonically and diminishes in higher depth of layer. It is observed that in the region \(0\le h \le 0.07 \), Lord–Shulman theory attains higher value of frequency than classical thermoelasticity theory and in the remaining region both coincide with each other.

Fig. 7
figure 7

Comparison of frequencies with the thickness of the layer

Full size image

7 Conclusion

In this article, the frequency equation of the localized wave propagation is achieved in a transversely isotropic elastic half-space overlaid by a transversely isotropic elastic layer with arbitrary thickness under thermal effect. The layer and half-space are assumed to be bonded perfectly to each other. Lord–Shulman model of generalized thermoelasticity for transversely isotropic media is used for derivation of frequency equation. The behaviour of attenuation coefficient and specific loss with respect to frequency are depicted in numerically simulated figures. Nature of phase velocity and Rayleigh wave frequencies with respect to the thickness of the layer are presented graphically for various cases.

By analyzing the obtained results and numerical simulations, one can highlight following salient points:

  1. (a)

    Attenuation coefficient of the wave is higher in Lord–ShulmanLord–Shulman theory as compared to classical thermoelasticity and has the diminishing nature in higher frequencies for both the cases of finite layered media as well as in thin layer.

  2. (b)

    In the lower frequency region specific loss increases in rapid manner thereafter it gradually decreases and diminishes in higher frequency region. This observation hold for both case of layered media with layer of certain thickness and when thickness of the layer tends to zero.

  3. (c)

    Phase velocity as well as frequency of the localized both are notably high for thin layer. The hyperbolic type heat conduction model can able to depict more realistic nature the Rayleigh wave as compared to the classical thermoelasticity.

  4. (d)

    It has been observed that the elliptical path of the particle is exponentially decaying with phase lag.

  5. (e)

    This theoretical model can be useful in various real applications in future like, earthquake engineering, seismology, geophysics etc.