1 Introduction

The unprecedented increase in the radiative forcing of Earth’s atmosphere over the last few decades has given rise to the threat of global warming. The anthropogenic carbon dioxide emission is the prime contributor to the increase in the radiative forcing of the Earth’s atmosphere. Every year human activities, mainly deforestation and fossil fuel burning, are putting more carbon dioxide (CO2) into the atmosphere than natural processes can remove. The excessive anthropogenic CO2 emissions have pushed the atmospheric CO2 above the level of 400 ppm, the highest at any time in the past 800,000 years [1]. Deforestation is one of the prime causes behind the upsurge in CO2 concentrations. Agricultural expansion, logging for fuel, fodder, wood, and paper-based industries, and infrastructure expansion to support the growing population and economy are mainly attributed to deforestation. Between 1990 and 2020, 420 million ha (hectare) of forest was lost because of deforestation [2]. With the growth in the world’s population and economy, the deforestation rate is expected to further increase due to agriculture and infrastructure expansion. In this scenario, restoring the forest cover is imperative to tackle the climate changes caused by enhanced levels of atmospheric carbon dioxide. Many countries are implementing forest conservation policies to enlarge their forest cover. The adoption of forest conservation policies can have a profound impact on forest biomass conservation and even cause the reversal of deforestation trends. For instance, Costa Rica has achieved success in reversing deforestation by increasing the forest cover from 24.4% in 1985 to more than 50% by 2011 by implementing the forest conservation programs [3]. Reforestation programs are prominent options to restore the forest cover; but their implementation on a desired scale involves many economical and geographical constraints [4]. One of the constraints is the economic cost of planting and managing the forests.

Apart from deforestation, fossil fuel burning for energy generation and industrial processes is another prominent source of CO2 emissions. Many countries, such as Canada, South Africa, India, Taiwan, Columbia, Costa Rica and most EU countries, have implemented environmental regulations to reduce carbon emissions by imposing taxes [5]. The taxation policy is corroborated by the government to directly price the emissions of carbon dioxide of enterprises, following the taxation principle of “who consumes, who pays” [6]. The implementation of carbon taxation is an effective option to reduce the carbon dioxide emissions from the point source. Several empirical, semi-empirical and numerical models are used to study the nexus between carbon taxation and carbon dioxide emissions from anthropogenic sources [7,8,9,10,11,12,13,14,15]. These studies pointed out that carbon taxation is effective strategy to mitigate the carbon dioxide levels. In particular, Andersson [12] has used an empirical model to quantify the effect of the implementation of a carbon tax and a value-added tax on transport fuel in Sweden and showed that the implementation of the carbon tax and a value-added tax causes a reduction of nearly 11 percent in carbon dioxide emissions from transport. Ghazounani et al. [14] have also empirically analyzed the effect of a carbon tax on the mitigation of carbon dioxide emissions in the European context and showed a significant and positive effect of adoption of a carbon tax on the reduction of CO2 emissions. However, these studies provide a quantitative analysis of the effect of carbon taxation on the control of carbon dioxide emissions and rely entirely on the data. Apart from these numerical and empirical models, theoretical models that employ qualitative methods can be used to gain an in-depth understanding of the effect of carbon taxation on the control of anthropogenic carbon dioxide emissions. In recent years, various differential equation models have been proposed and analyzed qualitatively to study the impact of human activities and forest biomass over the dynamics of carbon dioxide in the atmosphere [16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]. In particular, Misra et al. [20] have proposed a mathematical model to analyze the effect of reforestation and the delay involved in between the measurement of forest data and implementation of reforestation efforts on the control of carbon dioxide concentration in the atmosphere. Misra and Jha [27] have proposed a nonlinear model to study the effect of population pressure on the dynamics of carbon dioxide. Their study reveals that as the reduction rate coefficient of carrying capacity of forest biomass due to population pressure increases, the equilibrium level of atmospheric carbon dioxide increases. Verma and Gautam [29] have proposed and analyzed a nonlinear mathematical model to study the effect of forest management programs on the control of atmospheric carbon dioxide. This study indicates that the atmospheric carbon dioxide level can be reduced by increasing the implementation rate and maximum efficiencies of forest management options to reduce deforestation rate and increase forest biomass, respectively. Devi and Gupta [31] have proposed a mathematical model to analyze the effect of environmental tax and time lag in implementation of taxation policy on the concentration of greenhouse gases. This study shows that the concentration of greenhouse gases can be reduced to innocuous level via increasing the implementation rate of environment tax. The literature review shows that there is lack of mathematical studies that analyze the long-term effect of integrated carbon taxation-reforestation policies on the atmospheric CO2 levels. However, such a study is very important as the integration of carbon taxation and reforestation policies may aid in overcoming the economic constraints that exist in large scale tree plantation. The goal of the present work is to propose and analyze a nonlinear mathematical model to explore the effect of a mitigation policy that integrates the reforestation programs with carbon taxation on the atmospheric CO2. We assumed that the carbon tax is applied to the anthropogenic emission of carbon dioxide that result in the reduction of CO2 emissions from the point source. Further, a portion of the fund collected through taxation is spent to accelerate reforestation programs. Since the reforestation efforts are subjected to the seasonal variations, the model is further extended to incorporate seasonality in implementation of reforestation programs by taking the implementation rate of reforestation programs as periodic function of time.

The remainder of this paper is ordered as follows. The next section presents the formulation of mathematical model used to examine the effects of the integrated carbon taxation -reforestation policy on the control of carbon dioxide levels. In Sect. 3, the boundedness of model solutions is discussed. Further, the feasible equilibrium points of the model are identified and their stability properties are examined. The existence of Hopf-bifurcation is discussed by taking the deforestation rate coefficient of forest biomass as a bifurcation parameter. Section 4 offers the study of the effect of seasonal variations in reforestation rate over the system dynamics. We have demonstrated the behavior of autonomous as well as nonautonomous system through numerical simulations in Sect. 5. Finally, Sect. 6 concludes the important findings of the work. A flowchart of the methodology is given in Fig. 1.

Fig. 1
figure 1

The flowchart of the methodology

Full size image

2 The model

Let in a geographical region, C(t) denotes the atmospheric concentration of CO2 at any time t. Further, let N(t) and B(t) denote the human population and forest biomass, respectively. Let T(t) and R(t) denote the carbon tax and a measure of reforestation programs, respectively at time t. The reforestation programs are measured in terms of money invested in their implementation. We formulate a mathematical model to study the effect of the integrated carbon taxation-reforestation policy on the dynamics of atmospheric CO2 based on the following assumptions:

  1. (i)

    The natural emission rate of CO2 is constant while the anthropogenic emission rate of CO2 is proportional to the human population [32, 33].

  2. (ii)

    The removal rate of CO2 by forests during photosynthesis process depends on the carbon dioxide concentration and the forest biomass, while the removal rate of carbon dioxide by natural sinks other than forests is proportional to CO2 concentration [34].

  3. (iii)

    The population and forest biomass are assumed to evolve with time according to logistic growth law. The population clears forest for their use which feeds back to the population growth [35]. So, it is considered that the forest biomass’s growth rate declines because of increase in population and population’s growth rate boosts because of increase in forest biomass.

  4. (iv)

    It is assumed that the population declines due to the adverse impacts of climate changes caused by the enhancement in the concentration of CO2 [19].

  5. (v)

    The implementation of reforestation programs causes increase in forest biomass. Since the forest biomass can not increase indefinitely with the increase in reforestation programs, so the increment in the forest biomass due to reforestation program is taken as a increasing saturating function of reforestation programs.

  6. (vi)

    Carbon tax is assumed to be applied to the anthropogenic CO2 emission at a rate proportional to the anthropogenic CO2 emission rate. The application of carbon tax leads to the reduction in the anthropogenic CO2 emission rate. Since, the reduction in anthropogenic CO2 emission rate brought by carbon taxation can not increase indefinitely with carbon taxation, therefore it is taken as a increasing saturating function of carbon tax.

  7. (vii)

    It is assumed that some taxation policies will be scraped with time due to their inefficacy.

  8. (viii)

    The reforestation programs are executed with a rate proportional to the difference between the carrying capacity of forest biomass and its current density. A portion of carbon tax is invested on reforestation programs that enhance the implementation rate of reforestation programs. Further, it is considered that some reforestation programs are diminished due to their inefficiency or some economical barriers.

The above assumptions give rise to the following system of differential equations governing the time evolutions of the model variables:

$$\begin{aligned} \dot{C}=\, & {} Q+\lambda \left( 1-\frac{\eta T}{l+T}\right) N-\alpha C-\lambda _1 BC,\nonumber \\ \dot{N}= \,& {} sN\left( 1-\frac{N}{L}\right) -\theta CN+\xi NB, \nonumber \\ \dot{B}= \,& {} uB\left( 1-\frac{B}{M}\right) -\phi NB+\frac{\beta RB}{p+R},\nonumber \\ \dot{T}= \,& {} \gamma (\lambda N)-\gamma _0T, \nonumber \\ \dot{R}= \,& {} (\delta _1+\delta _2 T)(M-B)-\delta _0 R, \end{aligned}$$
(1)

with initial conditions \(C(0)>0, N(0)\ge 0, B(0)\ge 0, T(0)\ge 0 \text { and } R(0)\ge 0.\) The parameters used in system (1) are specified in Table 1.

Table 1 Description and values of the model parameters of system (1) with their unit and source
Full size table

3 Qualitative analysis of the system (1)

Since the model system (1) is highly non-linear, it is not possible to find the exact solution to the system. Instead, we will determine the long-term behaviour of the system by applying the stability theory of ordinary differential equations. In this regard, we will determine the feasible equilibrium states of the system (1) and examine their stability properties.

3.1 Boundedness

Boundedness of a system demonstrates that it is well behaved, and ensures that the model variables will not grow exponentially as time increases indefinitely. The results regarding the boundedness of the solution of model system (1) are given in following Lemma 1.

Lemma 1

The region of attraction [36] for the solution of the system (1) initiating in the positive cone of \(\mathbb {R}^5\) is given by the set

$$\begin{aligned} \varGamma =\{(C,N,B,T,R)\in {\mathbb {R}}^5_{+}: 0<C\le C_m; 0\le N\le N_m; 0\le B \le B_m; 0\le T\le T_m; 0\le R\le R_m\}, \end{aligned}$$

where \(C_m=\frac{Q+\lambda N_m}{\alpha }, N_m=\frac{L}{s}(s+\xi M), B_m=M, T_m=\frac{\gamma \lambda N_m}{\gamma _0} \text { and } R_m= \frac{(\delta _1+\delta _2 T_m)M}{\delta _0}\), which is invariant with respect to system (1).

Proof

From third equation of system (1), we have

$$\begin{aligned} \frac{{\mathrm{d}}B}{{\mathrm{d}}t}\le u B\left( 1-\frac{B}{M}\right) +\frac{\beta RB}{p+R}. \end{aligned}$$

From the last equation of model system (1), we note that as B increases to M, R becomes zero, suggesting that \(\frac{d B}{d t}\le 0\) for \(B \ge M\). Thus, \(B \rightarrow M\) for large \(t>0\).

$$\begin{aligned} \Rightarrow \limsup _{t\rightarrow \infty } B(t)\le M=B_m \ (say), \end{aligned}$$

From second equation of system (1), we have

$$\begin{aligned}{} & {} \frac{{\mathrm{d}}N}{{\mathrm{d}}t}\le sN-\frac{sN^2}{L}+\xi N M. \\{} & {} \Rightarrow \limsup _{t\rightarrow \infty } N(t)\le \frac{L}{s}(s+\xi M)=N_m \ (say), \end{aligned}$$

From first equation of system (1), we have

$$\begin{aligned}{} & {} \frac{{\mathrm{d}}C}{{\mathrm{d}}t}\le Q+\lambda N_m-\alpha C. \\{} & {} \Rightarrow \limsup _{t\rightarrow \infty } C(t)\le \frac{Q+\lambda N_m}{\alpha }=C_m \ (say), \end{aligned}$$

From fourth equation of system (1), we have

$$\begin{aligned}{} & {} \frac{{\mathrm{d}}T}{{\mathrm{d}}t}\le \gamma \lambda N_m-\gamma _0 T. \\{} & {} \Rightarrow \limsup _{t\rightarrow \infty } T(t)\le \frac{\gamma \lambda N_m}{\gamma _0}=T_m \ (say), \end{aligned}$$

From fifth equation of system (1), we have

$$\begin{aligned}{} & {} \frac{{\mathrm{d}}R}{{\mathrm{d}}t}\le (\delta _1+\delta _2 T_m)M-\delta _0R \\{} & {} \Rightarrow \limsup _{t\rightarrow \infty } R(t)\le \frac{(\delta _1+\delta _2 T_m)M}{\delta _0}=R_m \ (say). \end{aligned}$$

This proves the lemma. \(\hfill\square\)

3.2 Equilibria

An equilibrium point of dynamical system (1) represents the state of the system which does not change with time. The equilibrium states of system (1) are obtained by putting the rate of change of all dynamical variables with respect to time \('t'\) equal to zero. It is found that system (1) has four feasible equilibria; three boundary equilibria and one interior equilibrium.

3.2.1 Boundary equilibria

System (1) has three feasible boundary equilibria, which are given below:

  1. 1.

    \(S_1\left( \frac{Q}{\alpha },0,0,0,\frac{\delta _1 M}{\delta _0}\right)\) always exists.

  2. 2.

    \(S_2\left( \frac{Q}{\alpha +\lambda _1 M},0,M,0,0\right)\) always exists.

  3. 3.

    \(S_3 (C_3,N_3,0,T_3,R_3)\) exists provided

    $$\begin{aligned} s>\frac{\theta Q}{\alpha }, \end{aligned}$$
    (2)

The existence of the boundary equilibria \(S_1\) and \(S_2\) are obvious. In the equilibrium \(S_3(C_3,N_3,0,T_3,R_3),\) the values of \(C_3,\ N_3, \ T_3\) and \(R_3\) are found by solving the given set of differential equations:

$$\begin{aligned} Q+\lambda \left( 1-\frac{\eta T}{l+T}\right) N-\alpha C \,& = {} 0, \end{aligned}$$
(3)
$$\begin{aligned} s\left( 1-\frac{N}{L}\right) -\theta C \,& = {} 0, \end{aligned}$$
(4)
$$\begin{aligned} \gamma (\lambda N)-\gamma _0T \,& = {} 0, \end{aligned}$$
(5)
$$\begin{aligned} (\delta _1+\delta _2 T)M-\delta _0 R= \,& {} 0. \end{aligned}$$
(6)

From the equation (5), we have

$$\begin{aligned} T=\frac{\gamma \lambda N}{\gamma _0}. \end{aligned}$$
(7)

Using equation (7) in equation (6), we have

$$\begin{aligned} R=\frac{M}{\delta _0}\left( \delta _1+\frac{\delta _2\gamma \lambda N}{\gamma _0}\right) . \end{aligned}$$
(8)

Using Eq. (7) in Eq. (3), we have

$$\begin{aligned} C=\frac{1}{\alpha }\left[ Q+\lambda N\left( \frac{l\gamma _0+\gamma \lambda N(1-\eta )}{l\gamma _0+\gamma \lambda N}\right) \right] . \end{aligned}$$
(9)

Using Eq. (9) in Eq. (4), we have a two degree polynomial in N

$$\begin{aligned} \hat{a}N^2+\hat{b}N+\hat{c}=0 \end{aligned}$$
(10)

where \(\hat{a}=\frac{s\gamma \lambda }{L}+\frac{\gamma \lambda ^2\theta (1-\eta )}{\alpha }, \hat{b}= \frac{sl\gamma _0}{L}+\frac{\theta \lambda (l\gamma _0+\gamma Q)}{\alpha }-s\gamma \lambda\) and \(\hat{c}=-l\gamma _0\left( s -\frac{\theta Q}{\alpha }\right) .\) Clearly, \(\hat{a}>0\) and \(\hat{c}<0\) provided \(s-\frac{\theta Q}{\alpha }>0.\) Thus, a unique positive root of N, say \(N_3,\) of Eq. (10) exists provided condition (2)  holds. Putting \(N = N_3\) in Eqs. (7), (8) and (9), we get the positive values of \(T = T_3, \ R=R_3\) and \(C=C_3\), respectively.

3.2.2 Interior equilibrium

The components of interior equilibrium \(S^*(C^*,N^*,B^*,T^*,R^*)\) are obtained by solving the following equations:

$$\begin{aligned} Q+\lambda \left( 1-\frac{\eta T}{l+T}\right) N-\alpha C-\lambda _1 BC= \,& {} 0, \end{aligned}$$
(11)
$$\begin{aligned} s\left( 1-\frac{N}{L}\right) -\theta C+\xi B= \,& {} 0, \end{aligned}$$
(12)
$$\begin{aligned} u\left( 1-\frac{B}{M}\right) -\phi N+\frac{\beta R}{p+R}= \,& {} 0, \end{aligned}$$
(13)
$$\begin{aligned} \gamma (\lambda N)-\gamma _0T= \,& {} 0, \end{aligned}$$
(14)
$$\begin{aligned} (\delta _1+\delta _2 T)(M-B)-\delta _0 R= \,& {} 0, \end{aligned}$$
(15)

From Eq. (14), we have

$$\begin{aligned} T=\frac{\gamma \lambda N}{\gamma _0}. \end{aligned}$$
(16)

Using this value of T in Eqs. (11) and (15), we get

$$\begin{aligned} C=\frac{1}{\alpha +\lambda _1B}\left[ Q+\lambda N\left( 1-\frac{\eta \gamma \lambda N}{l \gamma _0+\gamma \lambda N}\right) \right] . \end{aligned}$$
(17)

and

$$\begin{aligned} R=\left( \frac{M-B}{\delta _0}\right) \left( \delta _1+\frac{\delta _2\gamma \lambda N}{\gamma _0}\right) . \end{aligned}$$
(18)

Using Eq. (17) in Eq. (12), we get the following equation in N and B:

$$\begin{aligned} s\left( 1-\frac{N}{L}\right) -\frac{\theta }{\alpha +\lambda _1B}\left[ Q+\lambda N\left( 1-\frac{\eta \gamma \lambda N}{l \gamma _0+\gamma \lambda N}\right) \right] +\xi B=0. \end{aligned}$$
(19)

Using Eq. (18) in Eq. (13), we get another equation in N and B as:

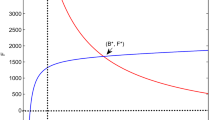
$$\begin{aligned} u\left( 1-\frac{B}{M}\right) -\phi N+\frac{\beta \left( \frac{M-B}{\delta _0}\right) \left( \delta _1 +\frac{\delta _2\gamma \lambda N}{\gamma _0}\right) }{p+\left( \frac{M-B}{\delta _0}\right) \left( \delta _1+ \frac{\delta _2\gamma \lambda N}{\gamma _0}\right) }=0. \end{aligned}$$
(20)

Now to establish the existence of \(S^*,\) we plot the isoclines given by Eqs. (19) and (20).

From Eq. (19), we may noted that:

  1. (i)

    When \(N=0,\) we get the following quadratic equation in B

    $$\begin{aligned} \xi \lambda _1B^2+(s\lambda _1+\xi \alpha )B+(s\alpha -\theta Q)=0, \end{aligned}$$

    which has negative roots under the condition (2).

  2. (ii)

    When \(B=0,\) we get the following equation in N:

    $$\begin{aligned} \left( \frac{s\gamma \lambda }{L}+\frac{\gamma \lambda ^2\theta (1-\eta )}{\alpha }\right) N^2-\left[ \left( s-\frac{\theta Q}{\alpha }\right) \gamma \lambda -l\gamma _0\left( \frac{s}{L}+\frac{\lambda \theta }{\alpha }\right) \right] N-l\gamma _0\left( s-\frac{\theta Q}{\alpha }\right) =0. \end{aligned}$$

    This equation has unique positive root, say \(N_a\) provided the condition (2) holds.

  3. (iii)

    \(\frac{dN}{dB}>0.\)

Similarly, from Eq. (20), we may noted that:

  1. (i)

    When \(N=0,\) we get \(B=M\).

  2. (ii)

    When \(B=0,\) we get the following equation in N:

    $$\begin{aligned} \frac{\delta _2\phi \gamma \lambda M}{\delta _0\gamma _0}N^2-\left[ \frac{u \delta _2\gamma \lambda M}{\delta _0\gamma _0}-\phi \left( p+\frac{\delta _1 M}{\delta _0}\right) +\frac{\beta M\delta _2\gamma \lambda }{\gamma _0\delta _0}\right] N-\left[ u\left( p+\frac{\delta _1 M}{\delta _0}\right) +\frac{\beta M \delta _1}{\delta _0}\right] =0. \end{aligned}$$

    The above equation has unique positive root, say \(N_b\).

  3. (iii)

    \(\frac{dN}{dB}<0.\)

Now, the isoclines given by (19) and (20) will intersect at a unique point \((B^*,N^*)\) in the region \(\varOmega '=\{(B,N)\in \mathbb {R}^2_{+}: 0 \le B\le M, N\ge 0\}\) of positive quadrant as shown in Fig. 2 provided

$$\begin{aligned} N_b>N_a. \end{aligned}$$
(21)

Using the values of \(N^*\) and \(B^*\) in (16), (17) and (18), we get the positive value of \(T=T^*, \ C=C^*\) and \(R=R^*\), respectively. Thus, a unique interior equilibrium \(S^*\) exists under the conditions (2) and (21).

Fig. 2
figure 2

Intersection of the isoclines (19) (shown by red colour) and (20) (shown by green colour) at a unique point \((B^*,N^*)\) in the region \(\varOmega '=\{(B,N) \in \mathbb {R}^2_{+}: 0 \le B\le M, N\ge 0\}\) of positive quadrant

Full size image

3.3 Local stability analysis

In order to examine the faith of solution trajectories of the system (1) initiating in small neighborhood of the non-negative equilibria \(S_1, \ S_2, \ S_3 \text { and } S^*\), the local stability analysis is performed. The local stability analysis tells about the faith of solution trajectories that initiated close to but not precisely at the equilibrium point. The local stability behavior of equilibrium points is investigated by determining the sign of the eigenvalues of Jacobian matrix evaluated at  the equilibrium points [37] and the following result is obtained:

Theorem 1

  1. (i)

    The equilibrium \(S_1\) is unstable.

  2. (ii)

    The equilibrium \(S_2\) is unstable whenever \(S^*\) exists.

  3. (iii)

    The equilibrium \(S_3\) is unstable whenever \(u-\phi N_3+\frac{\beta R_3}{p+R_3}>0.\)

  4. (iv)

    The equilibrium \(S^*\) is locally asymptotically stable if and only if conditions stated below hold:

    $$\begin{aligned}{} & {} A_5>0, A_1A_2-A_3>0, A_3(A_1A_2-A_3)-A_1(A_1A_4-A_5)>0, \nonumber \\{} & {} \quad A_4\{A_3(A_1A_2-A_3)-A_1(A_1A_4-A_5)\}-A_5\{A_2(A_1A_2-A_3)-(A_1A_4-A_5)\} > 0. \end{aligned}$$
    (22)

    where \(A_i's(i=1,2,3,4,5)\) are defined in the proof.

Proof

The variational matrix J for system (1) is given as

$$\begin{aligned} J= \begin{pmatrix} J_{11}&{} J_{12} &{} J_{13} &{} J_{14} &{} 0 \\ J_{21}&{} J_{22} &{} J_{23} &{} 0 &{} 0\\ 0 &{} J_{32} &{} J_{33} &{} 0 &{} J_{35} \\ 0 &{} J_{42} &{} 0 &{} J_{44} &{} 0 \\ 0 &{} 0 &{} J_{53} &{} J_{54} &{} J_{55} \\ \end{pmatrix},\\ \end{aligned}$$

where \(J_{11}=-(\alpha +\lambda _1 B), \ J_{12}=\lambda \left( 1-\frac{\eta T}{l+T}\right) , \ J_{13}=-\lambda _1 C, \ J_{14}=-\frac{\lambda \eta l N}{(l+T)^2},\)

\(J_{21}=-\theta N, \ J_{22}=s\left( 1-\frac{2N}{L}\right) -\theta C+\xi B, \ J_{23}=\xi N,\)

\(J_{32}=-\phi B, \ J_{33}=u\left( 1-\frac{2B}{M}\right) -\phi N+\frac{\beta R}{p+R}, \ J_{35}=\frac{\beta p B}{(p+R)^2},\)

\(J_{42}=\gamma \lambda , \ J_{44}=-\gamma _0, \ J_{53}=-(\delta _1+\delta _2 T), \ J_{54}=\delta _2(M-B), \ J_{55}=-\delta _0.\) Let \(J_{S_1}\), \(J_{S_2}\), \(J_{S_3}\) and \(J_{S^*}\) denote the variational matrix J evaluated at \(S_1\), \(S_2\), \(S_3\) and \(S^*\), respectively. Then we have

  1. (i)

    The eigenvalues of matrix \(J_{S_1}\) are \(-\alpha , \ s-\frac{\theta Q}{\alpha }, u+\frac{\beta \delta _1 M}{p\delta _0+\delta _1 M}, \ -\gamma _0, \ -\delta _0.\) It is clear that one value is \(u+\frac{\beta \delta _1 M}{p\delta _0+\delta _1 M},\) which is always positive and hence \(S_1\) is always unstable.

  2. (ii)

    The eigenvalues of \(J_{S_2}\) are \(-(\alpha +\lambda _1 M), \ s-\frac{\theta Q}{\alpha +\lambda _1 M}+\xi M, \ -\gamma _0\) and the other two values are the roots of the quadratic equation \(\hat{\psi }^2+ (u+\delta _0) \hat{\psi }+ u\delta _0+\frac{\beta M \delta _1}{p}=0\), which are either negative or with negative real part. It is clear that one value of \(J_{S_2}\) is \(s-\frac{\theta Q}{\alpha +\lambda _1 M}+\xi M,\) which is positive whenever \(S^*\) exists. Thus, the equilibria \(S_2\) is unstable whenever \(S^*\) exists.

  3. (iii)

    Two eigenvalues of \(J_{S_3}\) are \(u-\phi N_3+\frac{\beta R_3}{p+R_3},-\delta _0\) and the other three eigenvalues are the roots of the characteristic equation

    $$\begin{aligned} \varphi ^3+D_1\varphi ^2+D_2\varphi +D_3=0, \end{aligned}$$
    (23)

    where

    $$\begin{aligned} D_1= \,& {} \frac{s N_3}{L}+\gamma _0+\alpha , \\ D_2= \,& {} \alpha \left( \frac{sN_3}{L}+\gamma _0\right) +\frac{sN_3\gamma _0}{L}+\theta \lambda N_3\left( 1-\frac{\eta T_3}{l+T_3}\right) ,\\ D_3= \,& {} \frac{\alpha s N_3\gamma _0}{L}+\gamma _0\theta \lambda N_3\left( 1-\frac{\eta T_3}{l+T_3}-\frac{\eta l T_3}{(l+T_3)^2}\right) . \end{aligned}$$

    All \(D_i's(i=1,2,3)\) are positive. Also, we find that \(D_1 D_2-D_3>0\). Using the Routh-Hurwitz (R-H) criterion, it is concluded that all roots of equation (23) will fall in left half of the complex plane. Thus, \({S_3}\) is unstable whenever \(u-\phi N_3+\frac{\beta R_3}{p+R_3}>0.\)

  4. (iv)

    The characteristic equation of matrix \(J_{S^*}\) is given as

    $$\begin{aligned} \psi ^5+A_1\psi ^4+A_2\psi ^3+A_3\psi ^2+A_4\psi +A_5=0, \end{aligned}$$
    (24)

    where

    $$\begin{aligned} A_1 \,& = {} \alpha +\lambda _1B^*+\frac{sN^*}{L}+\frac{uB^*}{M}+\gamma _0+\delta _0, \\ A_2 \,& = {} (\alpha +\lambda _1B^*)\left( \frac{sN^*}{L}+\frac{uB^*}{M}+\gamma _0+\delta _0\right) +(\gamma _0+\delta _0)\left( \frac{sN^*}{L}+\frac{uB^*}{M}\right) + \frac{sN^*}{L}\frac{uB^*}{M}\\{} &\quad +\gamma _0\delta _0+\frac{\beta pB^*}{(p+R^*)^2}(\delta _1+\delta _2T^*)+\theta N^*\lambda \left( 1-\frac{\eta T^*}{l+T^*}\right) +\xi N^*\phi B^*, \\ A_3= \,& {} \gamma _0\delta _0\left( \alpha +\lambda _1B^*+\frac{sN^*}{L}+\frac{uB^*}{M}\right) +\left( \frac{sN^*}{L}\frac{uB^*}{M}+\xi N^*\phi B^*\right) \left( \alpha +\lambda _1B^*+\gamma _0+\delta _0\right) \\{} & {} +(\gamma _0+\delta _0)(\alpha +\lambda _1B^*)\left( \frac{sN^*}{L}+\frac{uB^*}{M}\right) +\frac{\beta pB^*}{(p+R^*)^2}(\delta _1+\delta _2T^*)\left( \alpha +\lambda _1B^*+\frac{sN^*}{L}+\gamma _0\right) \\{} & {} +\theta N^*\lambda \left( 1-\frac{\eta T^*}{l+T^*}\right) \left( \frac{uB^*}{M}+\delta _0\right) +\theta N^*\lambda \gamma _0\left( 1-\frac{\eta T^*}{l+T^*}-\frac{\eta l T^*}{(l+T^*)^2}\right) +\theta N^*\phi B^*\lambda _1C^*, \\ A_4= \,& {} \gamma _0\delta _0\left[ (\alpha +\lambda _1B^*)\left( \frac{sN^*}{L}+\frac{uB^*}{M}\right) +\frac{sN^*}{L}\frac{uB^*}{M}+\xi N^*\phi B^*\right] +(\gamma _0+\delta _0)\left[ (\alpha +\lambda _1B^*)\left( \frac{s N^*}{L}\frac{uB^*}{M}\right. \right. \\{} & {} \left. \left. +\xi N^*\phi B^*\right) +\theta N^*\phi B^*\lambda _1C^*\right] +\frac{\beta pB^*}{(p+R^*)^2}(\delta _1+\delta _2T^*) \left[ (\alpha +\lambda _1B^*)\left( \frac{sN^*}{L}+\gamma _0\right) +\frac{sN^*}{L}\gamma _0\right] \\{} & {} +\theta N^*\lambda \left( 1-\frac{\eta T^*}{l+T^*}\right) \left( \frac{uB^*}{M}\delta _0+\frac{\beta pB^*}{(p+R^*)^2}(\delta _1+\delta _2T^*)\right) +\theta N^*\lambda \gamma _0\left( \frac{uB^*}{M}+\delta _0\right) \left( 1-\frac{\eta T^*}{l+T^*}\right. \\{} & {} \left. -\frac{\eta l T^*}{(l+T^*)^2}\right) -\xi N^*\gamma \lambda \frac{\beta p B^*\delta _2(M-B^*)}{(p+R^*)^2}, \\ A_5= \,& {} \gamma _0\delta _0\left\{ (\alpha +\lambda _1B^*)\left( \frac{sN^*}{L}\frac{uB^*}{M}+\xi N^*\phi B^*\right) +\theta N^*\lambda _1C^*\phi B^*\right\} -\frac{\gamma \lambda \beta pB^*\delta _2(M-B^*)}{(p+R^*)^2}\\{} & {} \{(\alpha +\lambda _1 B^*)\xi N^*+\theta N^*\lambda _1 C^*\}+\frac{\gamma _0\beta pB^*}{(p+R^*)^2}(\delta _1+\delta _2T^*)(\alpha +\lambda _1 B^*)\frac{sN^*}{L}\\{} & {} +\theta N^*\lambda \gamma _0\left( \frac{uB^*}{M}\delta _0+\frac{\beta p B^*(\delta _1+\delta _2 T^*)}{(p+R^*)^2}\right) \left( 1-\frac{\eta T^*}{l+T^*}-\frac{\eta l T^*}{(l+T^*)^2}\right) .\\ \end{aligned}$$

    Applying the Routh-Hurwitz criterion, the roots of the characteristic equation (24) are either negative or with negative real parts iff the conditions given in (22) are satisfied.

\(\hfill\square\)

Remark 1

The conditions stated in (22) give the necessary and sufficient conditions under which the atmospheric concentration of carbon dioxide, forest biomass and other model variables settle down to a positive equilibrium state as time grows indefinitely if their initial states are close to the equilibrium state.

3.4 Global stability analysis

In the following, the stability analysis of the interior equilibrium \(S^*\) is extended to the whole region of attraction \(\varGamma\) using the Lyapunov’s direct method [38]. The basic idea of this method for determining the global stability of equilibrium point is to construct a scalar valued positive definite function, called Lyapunov function or energy function, that decreases with time along the trajectories of the system. Using Lyapunov’s direct method, we have obtained some sufficient conditions under which the solution trajectories of the system (1) initiating inside the region of attraction converge to \(S^*\) as \(t \rightarrow \infty .\) The result regarding the global stability of \(S^*\) is stated in the following theorem:

Theorem 2

The equilibrium \(S^*\), if feasible, is globally asymptotically stable inside the domain \(\varGamma\) if the inequalities given below are satisfied:

$$\begin{aligned}{} & {} \lambda _1^2{C_m}^2<\frac{\xi \lambda u}{\theta \phi M}(\alpha +\lambda _1B^*)\left( 1-\frac{\eta T^{*}}{l+T^{*}}\right) , \end{aligned}$$
(25)
$$\begin{aligned}{} & {} \frac{\beta R_m^2}{(p+R_m)^2(p+R^*)}<\frac{u\delta _0}{M(\delta _1+\delta _2T^*)}, \end{aligned}$$
(26)
$$\begin{aligned}{} & {} \max \left\{ \frac{\lambda \eta ^2 N_m^2}{(l+T^*)^2(\alpha +\lambda _1 B^*)},\frac{\xi \beta \delta _2^2M^2\left( 1-\frac{\eta T^{*}}{l+T^{*}}\right) }{\theta \phi \delta _0(p+R^*)(\delta _1+\delta _2 T^*)}\right\} <\frac{8}{9}\frac{s\gamma _0^2}{\theta \lambda ^2\gamma ^2 L}\left( 1-\frac{\eta T^{*}}{l+T^{*}}\right) . \end{aligned}$$
(27)

Proof

Consider the positive definite function \(V: \varGamma \rightarrow \mathbb {R}\) defined as:

$$\begin{aligned} V(C,N,B,T,R)= \,& {} \frac{1}{2}(C-C^*)^2+m_1\left( N-N^*-N^*\ln \frac{N}{N^*}\right) +m_2\left( B-B^*-B^*\ln \frac{B}{B^*}\right) \nonumber \\{} & {} +\frac{m_3}{2}(T-T^*)^2+\frac{m_4}{2}(R-R^*)^2, \end{aligned}$$

where \(m_1, \ m_2,\ m_3\) and \(m_4\) are positive constants.

The time derivative of V is given by

$$\begin{aligned} \dot{V}= & {} -(\alpha +\lambda _1B^{*})(C-C^*)^2-\frac{m_1 s}{L}(N-N^*)^2-\frac{m_2 u }{M}(B-B^*)^2-m_3\gamma _0(T-T^*)^2\\{} & {} -m_4\delta _0(R-R^*)^2-\lambda _1C(C-C^*)(B-B^*)+\left[ \lambda \left( 1-\frac{\eta T^{*}}{l+T^{*}}\right) -m_1\theta \right] (C-C^*)(N-N^*)\\{} & {} -\frac{\lambda \eta l N}{(l+T)(l+T^*)}(C-C^*)(T-T^*)+(m_1\xi -m_2\phi )(N-N^*)(B-B^*)\\{} & {} +\left( \frac{m_2p\beta }{(p+R)(p+R^*)}-m_4(\delta _1+\delta _2 T^*)\right) (B-B^*)(R-R^*) +m_3\gamma \lambda (N-N^*)(T-T^*)\\{} & {} +m_4\delta _2(M-B)(T-T^*)(R-R^*).\\ \end{aligned}$$

Choosing \(m_1=\frac{\lambda }{\theta }\left( 1-\frac{\eta T^{*}}{l+T^{*}}\right)\) and \(m_2=\frac{m_1\xi }{\phi }=\frac{\xi \lambda }{\theta \phi }\left( 1-\frac{\eta T^{*}}{l+T^{*}}\right)\) and \(m_4=\frac{m_2\beta }{(p+R^*)(\delta _1+\delta _2 T^*)}=\frac{\xi \lambda \beta \left( 1-\frac{\eta T^*}{l+T^*}\right) }{\theta \phi (p+R^*)(\delta _1+\delta _2 T^*)},\) we have

$$\begin{aligned} \dot{V}= & {} -(\alpha +\lambda _1B^{*})(C-C^*)^2-\frac{s \lambda }{\theta L}\left( 1-\frac{\eta T^{*}}{l+T^{*}}\right) (N-N^*)^2-\frac{\xi \lambda u}{\theta \phi M}\left( 1-\frac{\eta T^{*}}{l+T^{*}}\right) \\{} & {} (B-B^*)^2-m_3\gamma _0(T-T^*)^2-\frac{\xi \lambda \beta \delta _0\left( 1-\frac{\eta T^*}{l+T^*}\right) }{\theta \phi (p+R^*)(\delta _1+\delta _2 T^*)}(R-R^*)^2-\lambda _1C(C-C^*)(B-B^*)\\{} & {} -\frac{\lambda \eta l N}{(l+T)(l+T^*)}(C-C^*)(T-T^*)-\frac{\xi \lambda \beta R}{\theta \phi (p+R)(p+R^*)}\left( 1-\frac{\eta T^*}{l+T^*}\right) (B-B^*)\\{} & {} (R-R^*)+m_3\gamma \lambda (N-N^*)(T-T^*)+\frac{\xi \lambda \beta \delta _2(M-B)\left( 1-\frac{\eta T^*}{l+T^*}\right) }{\theta \phi (p+R^*)(\delta _1+\delta _2 T^*)}(T-T^*)(R-R^*).\\ \end{aligned}$$

Now, \(\dot{V}\) will be negative definite inside \(\varGamma\) under the following inequalities:

$$\begin{aligned}{} & {} \lambda _1^2{C_m}^2<\frac{\xi \lambda u}{\theta \phi M}(\alpha +\lambda _1B^*)\left( 1-\frac{\eta T^{*}}{l+T^{*}}\right) \end{aligned}$$
(28)
$$\begin{aligned}{} & {} m_3>\frac{3}{2}\frac{\lambda ^2\eta ^2{N_m}^2}{\gamma _0(\alpha +\lambda _1B^{*})(l+T^{*})^2} \end{aligned}$$
(29)
$$\begin{aligned}{} & {} \frac{\beta R_m^2}{(p+R^*)(p+R_m)^2}<\frac{u\delta _0}{M(\delta _1+\delta _2 T^*)} \end{aligned}$$
(30)
$$\begin{aligned}{} & {} m_3<\frac{4}{3}\frac{s\gamma _0}{\theta \lambda \gamma ^2 L}\left( 1-\frac{\eta T^{*}}{l+T^{*}}\right) \end{aligned}$$
(31)
$$\begin{aligned}{} & {} m_3>\frac{3}{2}\frac{\xi \lambda \beta \delta _2^2 M^2}{\theta \phi \gamma _0\delta _0(p+R^*)(\delta _1+\delta _2T^*)}\left( 1-\frac{\eta T^{*}}{l+T^{*}}\right) \end{aligned}$$
(32)

From inequalities (29), (31) and (32), we can choose \(m_3>0\) provided condition (27) holds. Thus, the time derivative of V is negative definite inside Γ if conditions (25), (26) and (27) are satisfied. \(\hfill\square\)

Remark 2

The conditions (25)–(27) are the sufficient conditions under which the atmospheric concentration of carbon dioxide and other model variables settle down to positive equilibrium level.

Remark 3

The conditions (25)–(27) may not hold for large values of \(\lambda ,\) \(\lambda _1\), \(\theta\) and \(\phi\), indicating that these parameters may have destabilizing effect on dynamic behavior of the system (1).

3.5 Analysis of Hopf-bifurcation

It is noted that on increasing the value of deforestation rate coefficient \(\phi ,\) the condition for local stability of interior  equilibrium \(S^*\) stated in (22) is violated. Thus, there is a possibility of occurrence of Hopf-bifurcation around the  equilibrium \(S^*\) with respect to the parameter \(\phi .\) Hopf bifurcation is a local bifurcation described by the appearance of a limit cycle around an equilibrium point of system accompanied by a sudden change in stability of the equilibrium point as a parameter of system varies [39]. In the following, we investigate the conditions for the occurrence of Hopf-bifurcation around the equilibrium \(S^*(C^*,N^*,B^*,T^*,R^*)\) by considering the deforestation rate coefficient of forest biomass ‘\(\phi\)’ as bifurcation parameter.

Theorem 3

The system (1) experiences Hopf-bifurcation around the equilibrium \(S^*(C^*,N^*,B^*,T^*,R^*)\) at \(\phi =\phi _c\) if the following conditions hold:

$$\begin{aligned}{} & {} \,(i)\quad \chi (\phi _c)\equiv \{A_3(\phi _c)-A_1(\phi _c)A_2(\phi _c)\}\{A_5(\phi _c)A_2(\phi _c)-A_3(\phi _c)A_4(\phi _c)\}\\{} & {} \quad \quad -\{A_5(\phi _c)-A_1(\phi _c)A_4(\phi _c)\}^2=0, \\{} & {} \,(ii)\quad A_1(\phi _c)>0, A_1(\phi _c)A_2(\phi _c)-A_3(\phi _c)>0,A_3(\phi _c)-A_1(\phi _c){\omega _0}_c>0,\\{} & {} \quad \quad {\omega _0}_c=\frac{A_5(\phi _c)-A_1(\phi _c)A_4(\phi _c)}{A_3(\phi _c)-A_1(\phi _c)A_2(\phi _c)}>0, \\{} & {} \,(iii)\quad \frac{d\chi (\phi )}{d\phi }\bigg |_{\phi =\phi _c}\ne 0. \end{aligned}$$

Proof

The characteristic Eq. (24) has purely imaginary roots \(\psi _{1,2}=\pm i \sqrt{\omega _0},\ \omega _0>0\) iff it can be rewritten as

$$\begin{aligned} f(\psi )=(\psi ^2+\omega _0)g(\psi )=0, where \ g(\psi )=\psi ^3+B_1\psi ^2+B_2 \psi +B_3. \end{aligned}$$
(33)

Thus, we have

$$\begin{aligned} f(\psi )=\psi ^5+B_1\psi ^4+(B_2+\omega _0)\psi ^3+(B_3+B_1\omega _0)\psi ^2+B_2\omega _0\psi +B_3\omega _0=0. \end{aligned}$$
(34)

Equating the coefficients of (24) and (34), we get

$$\begin{aligned} A_1=B_1,A_2=B_2+\omega _0, A_3=B_3+B_1\omega _0,A_4=B_2\omega _0, A_5=B_3\omega _0. \end{aligned}$$
(35)

For the consistence of above relations, we have

$$\begin{aligned} \omega _0^2-A_2\omega _0+A_4=0,A_1\omega _0^2-A_3\omega _0+A_5=0. \end{aligned}$$
(36)

The elimination of \(\omega _0^2\) gives

$$\begin{aligned} (A_3-A_1A_2)\omega _0=A_5-A_1A_4. \end{aligned}$$
(37)

Thus (24) can be written as

$$\begin{aligned} f(\psi )=\psi ^5+A_1\psi ^4+A_2\psi ^3+A_3\psi ^2+\omega _0(A_2-\omega _0)\psi +\omega _0(A_3-A_1\omega _0)=0. \end{aligned}$$
(38)

If \((A_3-A_1A_2), (A_5-A_1A_4)>0,\) then from (37), we have

$$\begin{aligned} \omega _0={\omega _0}_c=\frac{A_5-A_1A_4}{A_3-A_1A_2}>0. \end{aligned}$$
(39)

Substituting \(\omega _0={\omega _0}_c\) in (38), we find that (24) and (38) are identical if and only if

$$\begin{aligned} \chi =(A_3-A_1A_2)(A_5A_2-A_3A_4)-(A_5-A_1A_4)^2=0. \end{aligned}$$
(40)

Now, the polynomial

$$\begin{aligned} g(\psi )=\psi ^3+A_1\psi ^2+(A_2-\omega _0)\psi +A_3-A_1\omega _0=0 \end{aligned}$$
(41)

does not have zero roots iff

$$\begin{aligned} A_3-A_1\omega _0\ne 0. \end{aligned}$$
(42)

Now, using Routh-Hurwitz criteria we can infer that all roots of polynomial (41) have negative real parts iff

$$\begin{aligned} A_1>0,A_1A_2-A_3>0,A_3-A_1\omega _0>0. \end{aligned}$$
(43)

Thus the remaining roots \(\psi _{3,4,5}\) of Eq. (34) are either negative or have negative real parts under the condition (43). Now, to show the existence of Hopf-bifurcation, we need to verify the transversality condition.

The function \(\chi (\phi )\) can be written in the form of Orlando’s formula as:

$$\begin{aligned} \chi (\phi )= & {} (\psi _1+\psi _2)(\psi _1+\psi _3)(\psi _1+\psi _4)(\psi _1+\psi _5)(\psi _2+\psi _3)(\psi _2+\psi _4)(\psi _2+\psi _5) \nonumber \\{} & {} (\psi _3+\psi _4)(\psi _3+\psi _5)(\psi _4+\psi _5). \end{aligned}$$
(44)

As \(\chi (\phi _c)\) is a continuous function, there exists an open interval \(I_{\phi _c}=(\phi _c-\epsilon ,\phi _c+\epsilon ),\) where \(\psi _1\) and \(\psi _2\) are complex conjugates for all \(\phi \in I_{\phi _c}.\) Let \(\psi _1(\phi )=\zeta _1(\phi )+i\zeta _2(\phi ),\psi _2(\phi )=\zeta _1(\phi )-i\zeta _2(\phi )\) with \(\zeta _1(\phi _c)=0,\zeta _2(\phi _c)=\sqrt{\omega _0}>0\) while \({\text {Re}}(\psi _{3,4,5}(\phi _c))\ne 0.\) Then, we have

$$\begin{aligned} \chi (\phi )= & {} 2\zeta _1\{(\psi _3+\zeta _1)^2+\zeta _2^2\}\{(\psi _4+\zeta _1)^2+\zeta _2^2\}\{(\psi _5+\zeta _1)^2+\zeta _2^2\}(\psi _3+\psi _4) (\psi _3+\psi _5)(\psi _4+\psi _5),\\ \chi (\phi _c)= & {} 0. \end{aligned}$$

Differentiating \(\chi (\phi )\) with respect to \(\phi\) and then putting \(\phi =\phi _c,\) we get

$$\begin{aligned} \left[ \frac{d\chi (\phi )}{d\phi }\right] _{\phi =\phi _c}=\left[ 2(\zeta _2^2+\psi _3^2)(\zeta _2^2+\psi _4^2)(\zeta _2^2+\psi _5^2)(\psi _3+\psi _4) (\psi _3+\psi _5)(\psi _4+\psi _5)\frac{d\zeta _1(\phi )}{d\phi }\right] _{\phi =\phi _c}. \end{aligned}$$
(45)

Since, at \(\phi =\phi _c,\) roots \(\psi _{3,4,5}\) have negative real part, hence

$$\begin{aligned} \left[ \frac{d\zeta _1(\phi )}{d\phi }\right] _{\phi =\phi _c}\ne 0 \Longleftrightarrow \left[ \frac{d\chi (\phi )}{d\phi }\right] _{\phi =\phi _c}\ne 0. \end{aligned}$$
(46)

Thus the Eq. (46) is the transversality condition. Hence the claim. \(\hfill\square\)

4 Seasonally forced model

The forest plantation programs are subjected to seasonal variations. Thus, we have taken the implementation rate of reforestation programs \(\delta _1\) and the expenditure rate of carbon tax on reforestation programs \(\delta _2\) to vary seasonally. By considering time variation in \(\delta _1\) and \(\delta _2,\) system (1) takes the following form:

$$\begin{aligned} \dot{C}= \,& {} Q+\lambda \left( 1-\frac{\eta T}{l+T}\right) N-\alpha C-\lambda _1 BC,\nonumber \\ \dot{N}= \,& {} sN\left( 1-\frac{N}{L}\right) -\theta CN+\xi NB, \nonumber \\ \dot{B}= \,& {} uB\left( 1-\frac{B}{M}\right) -\phi NB+\frac{\beta RB}{p+R},\nonumber \\ \dot{T}= \,& {} \gamma (\lambda N)-\gamma _0T, \nonumber \\ \dot{R}= \,& {} (\delta _1(t)+\delta _2(t) T)(M-B)-\delta _0 R, \end{aligned}$$
(47)

Denote \(\delta _1^M=\max _{t>0}\delta _1(t), \ \delta _2^M=\max _{t>0}\delta _2(t)\) and \(\delta _1^m=\min _{t>0}\delta _1(t), \ \delta _2^m=\min _{t>0}\delta _2(t).\)

Lemma 2

Consider a non-negative, integrable and uniformly continuous function f on \([\kappa , +\infty ),\) where \(\kappa\) be a real number, then \(\lim _{t \rightarrow +\infty } f(t)=0\).

4.1 Global attractivity

Theorem 4

The positive periodic solution of (47), if exists, is unique and globally attractive if \(\exists\) \(\mu _i>0(i=1-5)\) such that the conditions stated below are satisfied:

$$\begin{aligned}{} & {} \frac{\mu _1Q}{e^{2\rho _1}}+\frac{\mu _1\lambda e^{\rho _{22}}}{e^{2\rho _1}}-\frac{\mu _1\lambda \eta e^{\rho _2+\rho _4}}{e^{2\rho _{11}}(l+e^{\rho _{44}})}-\mu _2\theta >0, \end{aligned}$$
(48)
$$\begin{aligned}{} & {} \frac{\mu _2s}{L}-\mu _1\left\{ \frac{\lambda }{e^{\rho _{11}}}+\frac{\lambda \eta e^{\rho _4}}{e^{\rho _{11}}(l+e^{\rho _{44}})}\right\} -\mu _3\phi -\frac{\mu _4\gamma \lambda }{e^{\rho _{44}}}>0, \end{aligned}$$
(49)
$$\begin{aligned}{} & {} \frac{\mu _3u}{M}-\mu _1\lambda _1-\mu _2\xi -\frac{\mu _5\delta _1^M}{e^{\rho _{55}}}-\frac{\mu _5\delta _2^M e^{\rho _4}}{e^{\rho _{55}}}>0, \end{aligned}$$
(50)
$$\begin{aligned}{} & {} \frac{\mu _4\gamma \lambda e^{\rho _{22}}}{e^{2\rho _4}}-\mu _1\frac{\lambda \eta le^{\rho _2}}{e^{\rho _{11}}(l+e^{\rho _{44}})^2}-\frac{\mu _5\delta _2^M M}{e^{\rho _{55}}}-\frac{\mu _5\delta _2^M e^{\rho _3}}{e^{\rho _{55}}}>0, \end{aligned}$$
(51)
$$\begin{aligned}{} & {} \mu _5\frac{\delta _1^m M}{e^{2\rho _5}}+\mu _5\frac{\delta _2^m M e^{\rho _{44}}}{e^{2\rho _{5}}}-\mu _5\frac{\delta _1^M e^{\rho _3}}{e^{2\rho _{55}}}-\mu _5\frac{\delta _2^M e^{\rho _3+\rho _4}}{e^{2\rho _{55}}} -\frac{\mu _3\beta p}{(p+e^{\rho _{55}})^2}>0. \end{aligned}$$
(52)

Proof

Consider that the system (47) has at least one positive periodic solution \((\overline{C}(t),\overline{N}(t),\overline{B}(t),\overline{T}(t),\overline{R}(t)).\) Let

$$\begin{aligned} e^{\rho _{11}}\le \overline{C}(t)\le e^{\rho _1},\ e^{\rho _{22}}\le \overline{N}(t)\le e^{\rho _2},\ e^{\rho _{33}}\le \overline{B}(t)\le e^{\rho _3},\ e^{\rho _{44}}\le \overline{T}(t)\le e^{\rho _4},\ e^{\rho _{55}}\le \overline{R}(t)\le e^{\rho _5}. \end{aligned}$$

Let (C(t), N(t), B(t), T(t), R(t)) be any positive periodic solution of the system (47).

We define a Lyapunov functional as,

$$\begin{aligned} V(t)= & {} \mu _1|\ln C(t)-\ln \overline{C}(t)|+\mu _2|\ln N(t)-\ln \overline{N}(t)|+\mu _3|\ln B(t)-\ln \overline{B}(t)|\\{} & {} +\mu _4|\ln T(t)-\ln \overline{T}(t)|+\mu _5|\ln R(t)-\ln \overline{R}(t)|. \end{aligned}$$

Computing the right hand Dini’s derivatives, we have

$$\begin{aligned} D^{+}V(t)= & {} \mu _1sgn(C(t)-\overline{C}(t))\left[ \frac{\dot{C}(t)}{C(t)}-\frac{\dot{\overline{C}}(t)}{{\overline{C}}(t)}\right] +\mu _2sgn(N(t)-\overline{N}(t))\left[ \frac{\dot{N}(t)}{N(t)}-\frac{\dot{\overline{N}}(t)}{{\overline{N}}(t)}\right] \\{} & {} +\mu _3sgn(B(t)-\overline{B}(t))\left[ \frac{\dot{B}(t)}{B(t)}-\frac{\dot{\overline{B}}(t)}{{\overline{B}}(t)}\right] +\mu _4sgn(T(t)-\overline{T}(t))\left[ \frac{\dot{T}(t)}{T(t)}-\frac{\dot{\overline{T}}(t)}{{\overline{T}}(t)}\right] \\{} & {} +\mu _5sgn(R(t)-\overline{R}(t))\left[ \frac{\dot{R}(t)}{R(t)}-\frac{\dot{\overline{R}}(t)}{{\overline{R}}(t)}\right] .\\ \end{aligned}$$

Now, we have

$$\begin{aligned}&\mu _1sgn(C(t)-\overline{C}(t))\left[ \frac{\dot{C}(t)}{C(t)}-\frac{\dot{\overline{C}}(t)}{{\overline{C}}(t)}\right] \le \mu _1\left[ -\frac{Q}{C(t)\overline{C}(t)}|C(t)-\overline{C}(t)|+\frac{\lambda }{\overline{C}(t)}|N(t)-\overline{N}(t)| \right. \\&\quad \left. -\frac{\lambda N(t)}{C(t)\overline{C}(t)}|C(t)-\overline{C}(t)|+\lambda _1|B(t)-\overline{B}(t)| \right. \\&\quad \left. +\lambda \eta \left\{ \frac{N(t)T(t)}{C(t) \overline{C}(t)(l+T(t))}|C(t)-\overline{C}(t)| +\frac{T(t)}{\overline{C}(t)(l+T(t))}|N(t)-\overline{N}(t)| \right. \right. \\&\quad \left. \left. +\frac{l\overline{N}(t)}{\overline{C}(t)(l+T)(l+\overline{T}(t))}|T(t)-\overline{T}(t)|\right\} \right] \\&\mu _2sgn(N(t)-\overline{N}(t))\left[ \frac{\dot{N}(t)}{N(t)}-\frac{\dot{\overline{N}}(t)}{{\overline{N}}(t)}\right] \le \mu _2\left[ -\frac{s}{L}|N(t)-\overline{N}(t)| +\xi |B(t)-\overline{B}(t)|\right. \\&\quad \left. +\theta |C(t)-\overline{C}(t)|\right] \\ \\&\mu _3sgn(B(t)-\overline{B}(t))\left[ \frac{\dot{B}(t)}{B(t)}-\frac{\dot{\overline{B}}(t)}{{\overline{B}}(t)}\right] \le \mu _3\left[ -\frac{u}{M}|B(t)-\overline{B}(t)|+\phi |N(t)-\overline{N}(t)|\right. \\&\quad \left. +\frac{\beta p}{(p+R(t))(p+\overline{R}(t))}|R(t)-\overline{R}(t)|\right] \\ \\&\mu _4sgn(T(t)-\overline{T}(t))\left[ \frac{\dot{T}(t)}{T(t)}-\frac{\dot{\overline{T}}(t)}{{\overline{T}}(t)}\right] \le \mu _4\left[ -\frac{\gamma \lambda N(t)}{T(t)\overline{T}(t)}|T(t)-\overline{T}(t)|+\frac{\gamma \lambda }{\overline{T}(t)}|N(t)-\overline{N}(t)|\right] \\&\mu _5sgn(R(t)-\overline{R}(t))\left[ \frac{\dot{R}(t)}{R(t)}-\frac{\dot{\overline{R}}(t)}{{\overline{R}}(t)}\right] \le \mu _5\left[ -\frac{\delta _1(t)(M-B(t))}{R(t)\overline{R}(t)}|R(t)-\overline{R}(t)| +\frac{\delta _1(t)}{\overline{R}(t)}|B(t)-\overline{B}(t)| \right. \\&\quad \left. +\frac{\delta _2(t)M}{\overline{R}(t)}|T(t)-\overline{T}(t)|-\frac{\delta _2(t)(M-B(t))T(t)}{R(t)\overline{R}(t)}|R(t)-\overline{R}(t)| \right. \\&\quad \left. +\frac{\delta _2(t)T(t)}{\overline{R}(t)}|B(t)-\overline{B}(t)|+\frac{\delta _2(t)\overline{B}(t)}{\overline{R}(t)}|T(t)-\overline{T}(t)| \right] . \end{aligned}$$

Thus, we have

$$\begin{aligned}{} & {} D^{+}V(t)\le -\left[ \frac{\mu _1Q}{C(t) \overline{C}(t)}+\frac{\mu _1\lambda N(t)}{C(t) \overline{C}(t)}-\frac{\mu _1\lambda \eta N(t)T(t)}{C(t) \overline{C}(t)(l+T(t))}-\mu _2\theta \right] |C(t)-\overline{C}(t)| \\{} & {} \quad -\left[ \mu _2\frac{s}{L}-\mu _1\left\{ \frac{\lambda }{\overline{C}(t)}+\frac{\lambda \eta T(t)}{\overline{C}(t)(l+T(t))}\right\} -\mu _3\phi -\frac{\mu _4\gamma \lambda }{\overline{T}(t)}\right] |N(t)-\overline{N}(t)|\\{} & {} \quad -\left[ \mu _3\frac{u}{M}-\mu _1\lambda _1-\mu _2\xi -\frac{\mu _5\delta _1(t)}{\overline{R}(t)}-\frac{\mu _5\delta _2(t)T(t)}{\overline{R}(t)} \right] |B(t)-\overline{B}(t)|\\{} & {} \quad -\left[ \frac{\mu _4\gamma \lambda N(t)}{T(t)\overline{T}(t)}-\frac{\mu _1\lambda \eta l\overline{N}(t)}{\overline{C}(t)(l+T(t))(l+\overline{T}(t))}-\frac{\mu _5\delta _2(t)M}{\overline{R}(t)} -\frac{\mu _5\delta _2(t)\overline{B}(t)}{\overline{R}(t)}\right] |T(t)-\overline{T}(t)|\\{} & {} \quad -\left[ \frac{\mu _5\delta _1(t)(M-B(t))}{R(t)\overline{R}(t)}+\frac{\mu _5\delta _2(t)MT(t)}{R(t)\overline{R}(t)} -\frac{\mu _5\delta _2(t)T(t)B(t)}{R(t)\overline{R}(t)}-\frac{\mu _3\beta p}{(p+R(t))(p+\overline{R}(t))}\right] |R(t)-\overline{R}(t)|. \end{aligned}$$

Therefore,

$$\begin{aligned} D^{+}V(t)\le & {} -k_1|C(t)-\overline{C}(t)|-k_2|N(t)-\overline{N}(t)|-k_3|B(t)-\overline{B}(t)| \nonumber \\{} & {} -k_4|T(t)-\overline{T}(t)|-k_5|R(t)-\overline{R}(t)|, \end{aligned}$$
(53)

where,

$$\begin{aligned} k_1= & {} \frac{\mu _1Q}{e^{2\rho _1}}+\frac{\mu _1\lambda e^{\rho _{22}}}{e^{2\rho _1}}-\frac{\mu _1\lambda \eta e^{\rho _2+\rho _4}}{e^{2\rho _{11}}(l+e^{\rho _{44}})}-\mu _2\theta ,\\ k_2= & {} \frac{\mu _2s}{L}-\mu _1\left\{ \frac{\lambda }{e^{\rho _{11}}}+\frac{\lambda \eta e^{\rho _4}}{e^{\rho _{11}}(l+e^{\rho _{44}})}\right\} -\mu _3\phi -\frac{\mu _4\gamma \lambda }{e^{\rho _{44}}},\\ k_3= & {} \frac{\mu _3u}{M}-\mu _1\lambda _1-\mu _2\xi -\frac{\mu _5\delta _1^M}{e^{\rho _{55}}}-\frac{\mu _5\delta _2^M e^{\rho _4}}{e^{\rho _{55}}},\\ k_4= & {} \frac{\mu _4\gamma \lambda e^{\rho _{22}}}{e^{2\rho _4}}-\mu _1\frac{\lambda \eta le^{\rho _2}}{e^{\rho _{11}}(l+e^{\rho _{44}})^2}-\frac{\mu _5\delta _2^M M}{e^{\rho _{55}}}-\frac{\mu _5\delta _2^M e^{\rho _3}}{e^{\rho _{55}}},\\ k_5= & {} \mu _5\frac{\delta _1^m M}{e^{2\rho _5}}+\mu _5\frac{\delta _2^m M e^{\rho _{44}}}{e^{2\rho _{5}}}-\mu _5\frac{\delta _1^M e^{\rho _3}}{e^{2\rho _{55}}}-\mu _5\frac{\delta _2^M e^{\rho _3+\rho _4}}{e^{2\rho _{55}}} -\frac{\mu _3\beta p}{(p+e^{\rho _{55}})^2}. \end{aligned}$$

If the conditions (48)–(52) hold, then V(t) is monotonically decreasing on \([0,\infty ).\) Now integrating the inequality (53) over [0, t],  we get

$$\begin{aligned}{} & {} V(t)+\int _{0}^{t}[k_1|C(t)-\overline{C}(t)|+k_2|N(t)-\overline{N}(t)|+k_3|B(t)-\overline{B}(t)|+k_4|T(t)-\overline{T}(t)|\\{} & {} \quad +k_5|R(t)-\overline{R}(t)|]dt\le V(0)<\infty , \forall \ t\ge 0. \end{aligned}$$

Using the Lemma 2, we have

$$\begin{aligned}{} & {} \lim _{t \rightarrow \infty }|C(t)-\overline{C}(t)|=0, \ \lim _{t \rightarrow \infty }|N(t)-\overline{N}(t)|=0, \ \lim _{t \rightarrow \infty }|B(t)-\overline{B}(t)|=0, \\{} & {} \lim _{t \rightarrow \infty }|T(t)-\overline{T}(t)|=0, \ \lim _{t \rightarrow \infty }|R(t)-\overline{R}(t)|=0. \end{aligned}$$

Hence, the positive periodic solution \((\overline{C}(t),\overline{N}(t),\overline{B}(t),\overline{T}(t),\overline{R}(t))\) is globally attractive.

To prove the uniqueness of globally attractive positive periodic solution \((\overline{C}(t),\overline{N}(t),\overline{B}(t),\overline{T}(t),\overline{R}(t))\), we consider that the system (47) has one more globally attractive solution as \((\overline{C}_1(t),\overline{N}_1(t),\overline{B}_1(t),\overline{T}_1(t),\overline{R}_1(t))\) with period 1. If this solution is different from \((\overline{C}(t),\overline{N}(t),\overline{B}(t),\overline{T}(t),\overline{R}(t)),\) then there exists at least one \(\kappa \in [0,1]\) such that \(\overline{C}(\kappa )\ne \overline{C}_1(\kappa ),\) which means \(|\overline{C}(\kappa )-\overline{C}_1(\kappa )|=\epsilon _{11}>0.\) Therefore,

$$\begin{aligned} \epsilon _{11}= & {} \lim _{n\rightarrow \infty }|\overline{C}(\kappa +n)-\overline{C}_1(\kappa +n)| \\= & {} \lim _{t\rightarrow \infty }|\overline{C}(t)-\overline{C}_1(t)|>0, \end{aligned}$$

which contradicts the fact that the positive periodic solution \((\overline{C},\overline{N},\overline{B},\overline{T},\overline{R})\) is globally attractive. Hence, \(\overline{C}(t)=\overline{C}_1(t) \ \forall t\in [0,1].\) We can use the similar arguments for the remaining components \(\overline{N}, \ \overline{B}, \ \overline{T}\) and \(\overline{R}.\) Thus, the system (47) has unique globally attractive positive periodic solution. \(\hfill\square\)

5 Numerical simulations

5.1 Simulation of system (1)

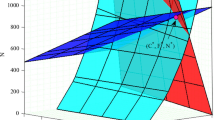
To show the impact of integrated carbon taxation-reforestation policy on the atmospheric \(CO _{2}\) and forest biomass, we have performed numerical simulations using the software environment MATLAB. MATLAB ode solver ‘ode45’ is used to integrate the system of differential equations (1) [40]. Unless until stated the parameter values in figures will be same as in Table 1. For the given set of parameter values, the eigenvalues of the variational matrix \('J'\) corresponding to the interior equilibrium \(S^*\) are given by \(-\)3.95993, \(-\)0.138065, \(-\)0.06631, \(-\)0.026177 and \(-\)0.012615. Here, we can see that all eigenvalues of \(J_{S^*}\) are negative, which means that the interior equilibrium \(S^*\) of the system (1) is locally asymptotically stable. The non-linear stability of \(S^*\) in \(C-B-R\) space is shown in Fig. 3 by taking the parameter values same as in Table 1 except \(\lambda =0.005,\ \phi =0.00008,\ \lambda _1=0.000001\) and \(\theta =0.000001.\) From this figure, we may see that the solution trajectories starting at any point inside the region \('\varGamma '\) are approaching to \(S^*,\) showing the non-linear stability behavior of the interior equilibrium \(S^*\) of system (1) in \(C-B-R\) space.

Fig. 3
figure 3

Non-linear stability of equilibrium \(S^*\) of system (1) in \(C-B-R\) space. Other parameters take same values as specified in Table 1 except \(\lambda =0.005,\ \phi =0.00008,\ \lambda _1=0.000001\) and \(\theta =0.000001\)

Full size image

Figure 4 depicts that an increase in the efficacy of carbon taxation policy to cut down the anthropogenic CO2 emission rate i.e., \(\eta\) causes a decline in equilibrium CO2 levels. A decrease in half saturation constant l representing the level of carbon taxation at which half of maximum possible reduction in CO2 emission rate is attained via CO2 taxation causes decline in the equilibrium CO2 level. This shows that the taxation policies which leads to higher cuts in CO2 emission rate at low taxation levels are more beneficial to control atmospheric CO2 concentration. In Fig. 5, we have drawn contour lines depicting changes in equilibrium CO2 concentration \(C^*\) and forest biomass \(B^*\) on varying  the imposition rate of carbon tax \(\gamma\) and CO2 emission rate from human sources \(\lambda\) at a time. It can be seen that the CO2 settles to low level for high values of imposition rate of carbon tax \(\gamma\) and low values of CO2 emission rate \(\lambda\). The equilibrium CO2 level rises with the rise in anthropogenic CO2 emission rate, while it declines with the increase in the imposition rate of carbon tax. The second plot of Fig.  5 shows that forest biomass settles to high level for high values of \(\lambda\) and \(\gamma\). This happens because a part of carbon tax which is imposed on anthropogenic CO2 emission is invested in reforestation which cause increase in forest biomass.

Fig. 4
figure 4

Variations of atmospheric carbon dioxide with time for different values of \(\eta\) and l for system (1). The other parameters take same values as specified in Table 1

Full size image
Fig. 5
figure 5

Contour plots of equilibrium level of a carbon dioxide (i.e. \(C^*\)) and b forest biomass (i.e. \(B^*\)) as functions of imposition rate of carbon tax \(\gamma\) and per capita anthropogenic emission rate \(\lambda\) for system (1). The other parameters take same values as specified in Table 1

Full size image

In Fig. 6, we have plotted the contour lines of equilibrium  values \(C^*,\ B^*,\ T^*,\) and \(R^*\) by varying the implementation rate of reforestation programs \(\delta _1\) and expenditure rate of carbon tax on reforestation programs \(\delta _2\) at a time. This figure depicts a reduction in equilibrium CO2 concentration and upsurge in equilibrium levels of forest biomass, carbon tax and reforestation programs with an increase in \(\delta _1\) and \(\delta _2.\) It can be observed that for high values of \(\delta _1\) and \(\delta _2\), the impact of increments in their value over the reduction in \(C^*\) and increment in \(B^*\) is low in comparison to the scenario when \(\delta _1\) and \(\delta _2\) are low. This shows that the impact of increase in \(\delta _1\) and \(\delta _2\) on \(B^*\) and \(C^*\) saturates at high values of \(\delta _1\) and \(\delta _2\). Fig. 7 depicts the contour plots of equilibrium levels of CO2 \(C^*\) and forest biomass \(B^*\) as a function of maximum efficiency of reforestation programs to enhance forest biomass \((\beta )\) and deforestation rate coefficient \((\phi ).\) This figure depicts that on increasing the value of \(\beta\) and decreasing the value of \(\phi ,\) \(C^*\) decreases while \(B^*\) increases. Fig. 8 is drawn to show the time evolutions of carbon dioxide and forest biomass in different carbon taxation and reforestation scenarios. From this figure, we can observe that in comparison to the scenario in which only reforestation programs are implemented and the scenario in which carbon taxation is not used to boost the reforestation rate, the increment in equilibrium level of forest biomass and decline in equilibrium level of CO2 is more in the scenario when an integrated carbon taxation-reforestation programs is used. This shows that integration of carbon taxation and reforestation policy to boost the implementation rate of reforestation efforts is beneficial to bring down the atmospheric CO2 levels.

Fig. 6
figure 6

Contour plots of equilibrium levels of a atmospheric carbon dioxide, b forest biomass, c carbon tax and d reforestation programs as functions of \(\delta _1\) and \(\delta _2\) for system (1). The other parameters take same values as specified in Table 1

Full size image
Fig. 7
figure 7

Contour plots of equilibrium level of a carbon dioxide (i.e. \(C^*\)) and b forest biomass (i.e. \(B^*\)) as functions of maximum efficiency of reforestation programs to enhance forest biomass \(\beta\) and deforestation rate coefficient \(\phi\) for system (1). The other parameters take same values as specified in Table 1

Full size image
Fig. 8
figure 8

Time evolutions of carbon dioxide and forest biomass in different carbon taxation and reforestation scenarios. The red solid lines represent the scenario when carbon taxation-reforestation policy is not applied (i.e. system (1) with \(\eta =0, \ l=0, \ \beta =0, p=0, \gamma =0, \gamma _0=0, \delta _0=0, \delta _1=0\),and \(\delta _2=0\)), the green dash-dotted lines represent the scenario when only the reforestation policy is applied (i.e. system (1) with \(\eta =0, \ l=0, \gamma =0, \gamma _0=0\), and \(\delta _2=0\)), the blue dashed lines represent the scenario when non-integrated taxation-reforestation policy is applied (i.e. system (1) with \(\delta _2=0\)), and the black lines with cross markers represent the scenario when integrated taxation-reforestation policy is applied. The other parameters take same values as specified in Table 1

Full size image

5.1.1 Sensitivity analysis

To study the effect of changes in the parameters \(\eta ,\ \beta ,\ \gamma ,\ \delta _1\) and \(\delta _2\) on the state variables of system (1), we performed the basic sensitivity analysis of differential equations for the same set of parameter values given in Table 1 following Bortz and Nelson [41]. The sensitivity systems with respect to the parameters \(\eta , \ \beta ,\ \gamma ,\ \delta _1\) and \(\delta _2\) are given by

$$\begin{aligned} \dot{C}_{\eta }(t,\eta )= & {} \lambda N_{\eta }(t,\eta )-\frac{\lambda \eta T(t,\eta )}{l+T(t,\eta )}N_{\eta }(t,\eta )-\frac{\lambda \eta lN(t,\eta )}{(l+T(t,\eta ))^2}T_{\eta }(t,\eta )-\frac{\lambda T(t,\eta )N(t,\eta )}{l+T(t,\eta )}\\ \ {}{} & {} -\alpha C_{\eta }(t,\eta )-\lambda _1B(t,\eta )C_{\eta }(t,\eta )-\lambda _1C(t,\eta )B_{\eta }(t,\eta ),\\ \dot{N}_{\eta }(t,\eta )= & {} s N_{\eta }(t,\eta )-\frac{2s}{L}N(t,\eta )N_{\eta }(t,\eta )-\theta C(t,\eta )N_{\eta }(t,\eta )-\theta N(t,\eta )C_{\eta }(t,\eta )\\ \ {}{} & {} +\xi N(t,\eta )B_{\eta }(t,\eta )+\xi B(t,\eta )N_{\eta }(t,\eta ),\\ \dot{B}_{\eta }(t,\eta )= & {} u B_{\eta }(t,\eta )-\frac{2u}{M}B(t,\eta )B_{\eta }(t,\eta )-\phi N(t,\eta )B_{\eta }(t,\eta )-\phi B(t,\eta )N_{\eta }(t,\eta )\\ \ {}{} & {} +\frac{\beta R(t,\eta )}{p+R(t,\eta )}B_{\eta }(t,\eta )+\frac{\beta p B(t,\eta )}{(p+R(t,\eta ))^2}R_{\eta }(t,\eta ),\\ \dot{T}_{\eta }(t,\eta )= & {} \gamma \lambda N_{\eta }(t,\eta )-\gamma _0T_{\eta }(t,\eta ),\\ \dot{R}_{\eta }(t,\eta )= & {} -\delta _1 B_{\eta }(t,\eta )+\delta _2MT_{\eta }(t,\eta )-\delta _2 T(t,\eta )B_{\eta }(t,\eta )-\delta _2 B(t,\eta )T_{\eta }(t,\eta )\\ \ {}{} & {} -\delta _0 R_{\eta }(t,\eta ), \end{aligned}$$
$$\begin{aligned}\dot{C}_{\beta }(t,\beta )= & {} \lambda N_{\beta }(t,\beta )-\frac{\lambda \eta T(t,\beta )}{l+T(t,\beta )}N_{\beta }(t,\beta )-\frac{\lambda \eta lN(t,\beta )}{(l+T(t,\beta ))^2}T_{\beta }(t,\beta )-\alpha C_{\beta }(t,\beta )\\ \ {}{} & {} -\lambda _1B(t,\beta )C_{\beta }(t,\beta )-\lambda _1C(t,\beta )B_{\beta }(t,\beta ),\\ \dot{N}_{\beta }(t,\beta )= & {} s N_{\beta }(t,\beta )-\frac{2s}{L}N(t,\beta )N_{\beta }(t,\beta )-\theta C(t,\beta )N_{\beta }(t,\beta )-\theta N(t,\beta )C_{\beta }(t,\beta )\\ \ {}{} & {} +\xi N(t,\beta )B_{\beta }(t,\beta )+\xi B(t,\beta )N_{\beta }(t,\beta ),\\ \dot{B}_{\beta }(t,\beta )= & {} u B_{\beta }(t,\beta )-\frac{2u}{M}B(t,\beta )B_{\beta }(t,\beta )-\phi N(t,\beta )B_{\beta }(t,\beta )-\phi B(t,\beta )N_{\beta }(t,\beta )\\ \ {}{} & {} +\frac{\beta R(t,\beta )}{p+R(t,\beta )}B_{\beta }(t,\beta )+\frac{\beta p { B}(t,\beta )}{(p+R(t,\beta ))^2}R_{\beta }(t,\beta )+\frac{R(t,\beta )B(t,\beta )}{p+R(t,\beta )},\\ \dot{T}_{\beta }(t,\beta )= & {} \gamma \lambda N_{\beta }(t,\beta )-\gamma _0T_{\beta }(t,\beta ),\\ \dot{R}_{\beta }(t,\beta )= & {} -\delta _1 B_{\beta }(t,\beta )+\delta _2MT_{\beta }(t,\beta )-\delta _2 T(t,\beta )B_{\beta }(t,\beta )-\delta _2 B(t,\beta )T_{\beta }(t,\beta )\\ \ {}{} & {} -\delta _0 R_{\beta }(t,\beta ),\end{aligned}$$
$$\begin{aligned}\dot{C}_{\gamma }(t,\gamma )= & {} \lambda N_{\gamma }(t,\gamma )-\frac{\lambda \eta T(t,\gamma )}{l+T(t,\gamma )}N_{\gamma }(t,\gamma )-\frac{\lambda \eta lN(t,\gamma )}{(l+T(t,\gamma ))^2}T_{\gamma }(t,\gamma )-\alpha C_{\gamma }(t,\gamma )\\ \ {}{} & {} -\lambda _1B(t,\gamma )C_{\gamma }(t,\gamma )-\lambda _1C(t,\gamma )B_{\gamma }(t,\gamma ),\\ \dot{N}_{\gamma }(t,\gamma )= & {} s N_{\gamma }(t,\gamma )-\frac{2s}{L}N(t,\gamma )N_{\gamma }(t,\gamma )-\theta C(t,\gamma )N_{\gamma }(t,\gamma )-\theta N(t,\gamma )C_{\gamma }(t,\gamma )\\ \ {}{} & {} +\xi N(t,\gamma )B_{\gamma }(t,\gamma )+\xi B(t,\gamma )N_{\gamma }(t,\gamma ),\\ \dot{B}_{\gamma }(t,\gamma )= & {} u B_{\gamma }(t,\gamma )-\frac{2u}{M}B(t,\gamma )B_{\gamma }(t,\gamma )-\phi N(t,\gamma )B_{\gamma }(t,\gamma )-\phi B(t,\gamma )N_{\gamma }(t,\gamma )\\ \ {}{} & {} +\frac{\beta pB(t,\gamma )}{(p+R(t,\gamma ))^2}R_{\gamma }(t,\gamma )+\frac{\beta R(t,\gamma )}{p+R(t,\gamma )}B_{\gamma }(t,\gamma ),\\ \dot{T}_{\gamma }(t,\gamma )= & {} \gamma \lambda N_{\gamma }(t,\gamma )+\lambda N(t,\gamma )-\gamma _0T_{\gamma }(t,\gamma ),\\ \dot{R}_{\gamma }(t,\gamma )= & {} -\delta _1 B_{\gamma }(t,\gamma )+\delta _2MT_{\gamma }(t,\gamma )-\delta _2 T(t,\gamma )B_{\gamma }(t,\gamma )-\delta _2 B(t,\gamma )T_{\gamma }(t,\gamma )\\ \ {}{} & {} -\delta _0 R_{\gamma }(t,\gamma ), \\ \dot{C}_{\delta _1}(t,\delta _1)= & {} \lambda N_{\delta _1}(t,\delta _1)-\frac{\lambda \eta T(t,\delta _1)}{l+T(t,\delta _1)}N_{\delta _1}(t,\delta _1)-\frac{\lambda \eta lN(t,\delta _1)}{(l+T(t,\delta _1))^2}T_{\delta _1}(t,\delta _1)-\alpha C_{\delta _1}(t,\delta _1)\\ \ {}{} & {} -\lambda _1B(t,\delta _1)C_{\delta _1}(t,\delta _1)-\lambda _1C(t,\delta _1)B_{\delta _1}(t,\delta _1),\\ \dot{N}_{\delta _1}(t,\delta _1)= & {} s N_{\delta _1}(t,\delta _1)-\frac{2s}{L}N(t,\delta _1)N_{\delta _1}(t,\delta _1)-\theta C(t,\delta _1)N_{\delta _1}(t,\delta _1)-\theta N(t,\delta _1)C_{\delta _1}(t,\delta _1)\\ \ {}{} & {} +\xi N(t,\delta _1)B_{\delta _1}(t,\delta _1)+\xi B(t,\delta _1)N_{\delta _1}(t,\delta _1),\\ \dot{B}_{\delta _1}(t,\delta _1)= & {} u B_{\delta _1}(t,\delta _1)-\frac{2u}{M}B(t,\delta _1)B_{\delta _1}(t,\delta _1)-\phi N(t,\delta _1)B_{\delta _1}(t,\delta _1)-\phi B(t,\delta _1)N_{\delta _1}(t,\delta _1)\\ \ {}{} & {} +\frac{\beta pB(t,\delta _1)}{(p+R(t,\delta _1))^2}R_{\delta _1}(t,\delta _1)+\frac{\beta R(t,\delta _1)}{p+R(t,\delta _1)}B_{\delta _1}(t,\delta _1),\\ \dot{T}_{\delta _1}(t,\delta _1)= & {} \gamma \lambda N_{\delta _1}(t,\delta _1)-\gamma _0T_{\delta _1}(t,\delta _1),\\ \dot{R}_{\delta _1}(t,\delta _1)= & {} M-B(t,\delta _1)-\delta _1 B_{\delta _1}(t,\delta _1)+\delta _2MT_{\delta _1}(t,\delta _1)-\delta _2 T(t,\delta _1)B_{\delta _1}(t,\delta _1)-\delta _2 B(t,\delta _1)T_{\delta _1}(t,\delta _1)\\ \ {}{} & {} -\delta _0 R_{\delta _1}(t,\delta _1), \end{aligned}$$

and

$$\begin{aligned} \dot{C}_{\delta _2}(t,\delta _2)= & {} \lambda N_{\delta _2}(t,\delta _2)-\frac{\lambda \eta T(t,\delta _2)}{l+T(t,\delta _2)}N_{\delta _2}(t,\delta _2)-\frac{\lambda \eta lN(t,\delta _2)}{(l+T(t,\delta _2))^2}T_{\delta _2}(t,\delta _2)-\alpha C_{\delta _2}(t,\delta _2)\\ \ {}{} & {} -\lambda _1B(t,\delta _2)C_{\delta _2}(t,\delta _2)-\lambda _1C(t,\delta _2)B_{\delta _2}(t,\delta _2),\\ \dot{N}_{\delta _2}(t,\delta _2)= & {} s N_{\delta _2}(t,\delta _2)-\frac{2s}{L}N(t,\delta _2)N_{\delta _2}(t,\delta _2)-\theta C(t,\delta _2)N_{\delta _2}(t,\delta _2)-\theta N(t,\delta _2)C_{\delta _2}(t,\delta _2)\\ \ {}{} & {} +\xi N(t,\delta _2)B_{\delta _2}(t,\delta _2)+\xi B(t,\delta _2)N_{\delta _2}(t,\delta _2),\\ \dot{B}_{\delta _2}(t,\delta _2)= & {} u B_{\delta _2}(t,\delta _2)-\frac{2u}{M}B(t,\delta _2)B_{\delta _2}(t,\delta _2)-\phi N(t,\delta _2)B_{\delta _2}(t,\delta _2)-\phi B(t,\delta _2)N_{\delta _2}(t,\delta _2)\\ \ {}{} & {} +\frac{\beta pB(t,\delta _2)}{(p+R(t,\delta _2))^2}R_{\delta _2}(t,\delta _2)+\frac{\beta R(t,\delta _2)}{p+R(t,\delta _2)}B_{\delta _2}(t,\delta _2),\\ \dot{T}_{\delta _2}(t,\delta _2)= & {} \gamma \lambda N_{\delta _2}(t,\delta _2)-\gamma _0T_{\delta _2}(t,\delta _2),\\ \dot{R}_{\delta _2}(t,\delta _2)= & {} -\delta _1 B_{\delta _2}(t,\delta _2)+\delta _2MT_{\delta _2}(t,\delta _2)+MT(t,\delta _2)-\delta _2 T(t,\delta _2)B_{\delta _2}(t,\delta _2)-\delta _2 B(t,\delta _2)T_{\delta _2}(t,\delta _2)\\ \ {}{} & {} -T(t,\delta _2)B(t,\delta _2)-\delta _0 R_{\delta _2}(t,\delta _2), \end{aligned}$$

respectively. Here, the semi-relative sensitivity function of X with respect to the parameter w is given by \(X_w(t,w)=\frac{\partial }{\partial w}X(t,w).\) The semi-relative sensitivity solutions are calculated by multiplying the sensitivity functions by the parameter w i.e., \(w X_w(t,w).\) The semi-relative sensitivity solution gives the information about the change in the state variables when a parameter value is doubled. To show the impact of doubling of parameters \(\eta ,\ \beta ,\ \gamma ,\ \delta _1\) and \(\delta _2\) on the state variables, semi- relative sensitivity solutions are plotted in Fig 9 for the time period of 100 months. The first plot in Fig. 9 shows that the positive perturbations in the parameters \(\eta ,\ \beta ,\ \gamma ,\ \delta _1\) and \(\delta _2\) have negative impact on the atmospheric carbon dioxide concentration. A doubling of the parameters \(\eta ,\ \beta\) and \(\gamma\) lead to decrease of 60.043 ppm, 149.434 ppm and 40.6334 ppm, respectively, in CO2 concentration, while the doubling of parameters \(\delta _1\) and \(\delta _2\) lead to decrease of 32.5985 ppm and 31.4580 ppm, respectively, in CO2 concentration over the period of 100 months. The second plot in Fig. 9 shows that the positive perturbations in the parameters \(\eta ,\ \beta ,\ \gamma ,\ \delta _1\) and \(\delta _2\) have positive impact on the human population. The third plot in Fig. 9 shows that the positive perturbations in the parameters \(\beta ,\ \gamma ,\ \delta _1\) and \(\delta _2\) have positive impact on the forest biomass, while the positive perturbation in \(\eta\) has negative impact on forest biomass. A doubling of the parameters \(\beta ,\ \gamma ,\ \delta _1,\ \delta _2\) lead to increase of 570.2917, 95.1760, 124.0634 and 119.6411 million tons, respectively, in the biomass, while the doubling of parameter \(\eta\) lead to decrease of 59.120 million tons, respectively, in the biomass over the period of 100 months. The fourth plot in Fig. 9 shows that the positive perturbations in all the parameters \(\eta ,\ \beta ,\ \gamma ,\ \delta _1\) and \(\delta _2\) have positive impact on the carbon taxation. The fifth plot in Fig. 9 shows that the positive perturbations in the parameters \(\eta ,\ \gamma ,\ \delta _1\) and \(\delta _2\) have positive impact on the measure of reforestation programs while the positive perturbation in \(\beta\) has negative impact on the measure of reforestation programs. The variables C(t), N(t),  B(t) and R(t) are most sensitive to changes in the parameter \(\beta\) while T(t) is most sensitive to the changes in the parameter \(\gamma\). The sensitivity analysis shows that the parameter \(\beta\) is more influential parameter than \(\eta ,\ \gamma ,\ \delta _1\) and \(\delta _2\) in respect to the control of carbon dioxide concentrations and increment in the forest biomass. This suggests that the selection of reforestation policies greatly influence the carbon dioxide concentrations in the atmosphere.

Fig. 9
figure 9

Semi-relative sensitivity solutions for the state variables of system (1) with respect to parameters \(\eta ,\ \beta ,\ \gamma ,\ \delta _1\) and \(\delta _2\)

Full size image

5.1.2 Bifurcation results

Fig. 10
figure 10

Time variations of variables of system (1) for \(\phi\)=0.0003. The other parameters take same values as specified in Table 1

Full size image
Fig. 11
figure 11

Time variations of variables of system (1) for \(\phi\)=0.0009. The other parameters take same values as specified in Table 1

Full size image
Fig. 12
figure 12

Time variations of variables of system (1) for \(\phi\)=0.0009 and \(\beta\)=0.35. The other parameters take same values as specified in Table 1

Full size image

It is observed that the variations in the deforestation rate \(\phi ,\) may significantly influence the dynamical behaviour of system (1). It is found that for \(\phi \in (0,\phi _c)\), system (1) exhibits a stable positive equilibrium state \(S^*\). At \(\phi =\phi _c\), positive equilibrium state \(S^*\) losses stability and periodic oscillations arise via Hopf-bifurcation. The Hopf-bifurcation threshold value is computed to be \(\phi _c=0.0008943\). The variation of \(C(t),\ N(t),\ B(t),\ T(t)\) and R(t) with respect to time t for \(\phi <\phi _c\) is shown in Fig. 10. This figure illustrates that when \(\phi <\phi _c,\) all the state variables settle to equilibrium values showing that positive equilibrium state \(S^*\) is stable. Further, in Fig. 11, we can see that if \(\phi >\phi _c,\) system show sustained oscillations around  equilibrium \(S^*\). These periodic oscillations may die out and positive equilibrium state \(S^*\) again becomes stable if we increase the maximum efficacy of reforestation programs to enhance forest biomass \(\beta\). Fig. 12 depicts that all the variables of system (1) attain their equilibrium values for \(\phi =0.0009(>\phi _c)\) and \(\beta =0.35.\) This means that increment in the maximum efficacy of reforestation programs to enhance forest biomass \(\beta\) exert stabilizing effect of system’s dynamics and may cause the interior  equilibrium \(S^*\) to switch from  instablity to stability. In order to present a more clear glimpse of the impact of changes in parameters \(\phi\) and \(\beta\) on the dynamics of system 1, we have drawn the bifurcation diagrams of the system by taking \(\phi\) and \(\beta\) as bifurcation parameters in Figs. 13 and 14 respectively. From Fig. 13, it can be easily seen that when \(\phi <\phi _c,\) a stable interior equilibrium exists but as \(\phi\) passes through \(\phi _c,\) the interior equilibrium losses stability and periodic oscillations of increasing amplitude developed around interior equilibrium through Hopf-bifurcation. The amplitude of the periodic oscillations declines as the value of \(\beta\) increases. Figure 14 presents the bifurcation diagram of the system by taking \(\beta\) as bifurcation parameter for \(\phi =0.001(>\phi _c)\) . From this figure, it is evident that increment in \(\beta\) decreases the amplitude of periodic oscillations that exist for high deforestation rates and after a critical threshold, the periodic oscillations die out and all the variables of system (1) approach their equilibrium values. Thus, we conclude that plantation of plants having  high biomass production may not only reduce the atmospheric CO2 concentration but may also aid in stabilization of atmospheric carbon dioxide concentrations.

5.2 Simulation of system (47)

To depict the effect of seasonality in plantation efforts on the dynamics of forest biomass and CO2 levels, we have simulated the nonautonomous system (47) by taking the seasonally forced parameters \(\delta _1(t)\) and \(\delta _2(t)\) of the form:

$$\begin{aligned} \delta _1(t)=\delta _1+\delta _{11}\sin {\omega t} \text { and } \delta _2(t)=\delta _2+\delta _{22}\sin {\omega t} \end{aligned}$$

with a period of 12 months. The benefit of considering the above form of \(\delta _1\) and \(\delta _2\) is that they  encompass both high and low seasons corresponding to positive and negative values of \(\sin {\omega t},\) respectively. Here, parameters \(\delta _{11} (0<\delta _{11}<\delta _1)\) and \(\delta _{22} (0<\delta _{22}<\delta _2)\) decide the strength of seasonal forcing in \(\delta _1(t)\) and \(\delta _2(t),\) respectively. We have plotted the solution trajectories for the nonautonomous system (47) in Fig. 15 by taking the same set of parameter values specified in Table 1 and \(\delta _{11}=0.1,\ \delta _{22}=0.0001,\ \omega =2\pi /12\). This figure shows the periodic oscillations in the non-autonomous system (47), whereas the corresponding autonomous system (1) shows a stable solution (see Fig. 10). Figure 16a and b depict the time evolutions of atmospheric carbon dioxide and forest biomass for three different initial starts for the autonomous system (1) and the non-autonomous system (47) respectively. From the Fig. 16a, it can be noted that for autonomous system, carbon dioxide and forest biomass settle to an equilibrium level irrespective of the initial start, showing the stability of interior equilibrium state of system (1). Figure 16b shows that for the non-autonomous system (47), the solutions initiating from three different initial values converge to a single periodic solution, showing that the system (47) exhibits a globally attractive positive periodic solution. This shows that the inclusion of seasonality in the system cause the translation of the system from having a globally stable interior equilibrium to have a global attractive periodic solutions. Thus, seasonality in plantation programs cause sustained oscillations in the forest biomass and atmospheric carbon dioxide levels. In Fig. 17, we set \(\phi =0.0009,\) at which the autonomous system (1) shows a simple periodic solution (see Fig. 11) and consider seasonality in \(\delta _1\) and \(\delta _2.\) It can be seen that for \(\phi =0.0009,\) the non-autonomous system shows higher periodic solutions. This shows that the enhancement in the deforestation rate affects the global stability of the nonautonomous system and may lead to generation of higher periodic solutions. The existence of the higher periodic oscillation makes it difficult to predict the future levels of carbon dioxide and forest biomass.

Fig. 13
figure 13

Bifurcation diagrams of system (1) with respect to \(\phi\). The other parameters take same values as in Table 1. In this figure, red and blue dots represent the maximum and minimum value of oscillation cycles, respectively

Full size image
Fig. 14
figure 14

Bifurcation diagrams of system (1) with respect to \(\beta\) at \(\phi =0.001 (>\phi _c)\). The other parameters take same values as in Table 1. In this figure, red and blue dots represent the maximum and minimum value of oscillation cycles, respectively

Full size image
Fig. 15
figure 15

Time series of \(C(t),\ B(t)\) and R(t) for system (47) at \(\delta _{11}=0.1, \delta _{22}=0.0001\) and \(\omega =2 \pi /12.\) The other parameters take same values as in Table 1

Full size image
Fig. 16
figure 16

 Time series of (a) atmospheric carbon dioxide and forest biomass  for system (1) and (b) atmospheric carbon dioxide and forest biomass  for system (47) at \(\delta _{11}=0.1, \delta _{22}=0.0001\) and \(\omega =2 \pi /12\) for different initial starts. The other parameters take same values as in Table 1

Full size image
Fig. 17
figure 17

Time series of \(C(t),\ B(t)\) and R(t) for system (47) at \(\delta _{11}=0.1, \delta _{22}=0.0001\) and \(\omega =2 \pi /12.\) The other parameters take same values as in Table 1 except \(\phi\) = 0.0009

Full size image

6 Conclusion

Restoring the forest cover can aid in mitigating the climate changes caused by the increase in carbon dioxide levels in the atmosphere. However, several economic and geographical constraints limit the large-scale implementation of reforestation programs. Carbon taxation is another crucial strategy adopted by policymakers that aids to limit anthropogenic carbon dioxide emissions from the point source. A part of the money generated via carbon taxation may be used to boost the implementation rate of plantation programs. Thus, an integrated carbon taxation-reforestation policy may be a better option to control atmospheric CO2 levels by cutting down anthropogenic CO2 emissions and overcoming the economic constraints that existed in large-scale plantation programs. This paper presents a mathematical framework to evaluate the effect of integrated carbon taxation-reforestation policy on the mitigation of atmospheric CO2. The model is formulated by considering five dynamical variables  namely, atmospheric concentration of CO2, human population, forest biomass, carbon tax and reforestation programs. To model the phenomenon, we have assumed that the carbon tax is implemented on the anthropogenic CO2 emissions and a part of the money generated via taxation is invested to accelerate the reforestation programs. The qualitative analysis of the model is presented and the local and global stability conditions of the system’s equilibria are investigated. Our analysis reveals that increasing the implementation rates of reforestation programs and carbon taxation causes declination in equilibrium CO2 levels. It is evident that deforestation rate coefficient ‘\(\phi\)’ may affect the stability of positive equilibrium state \(S^*\) of system (1). It is found that an increase in deforestation rate beyond a threshold value \(\phi _c\) destabilizes the positive equilibrium state \(S^*\) and system enters into sustained oscillations around \(S^*\). This shows that if deforestation rate exceeds the Hopf-bifurcation threshold \(\phi _c\), the concentration of carbon dioxide and other model variables will not settle to the equilibrium state but oscillates about the equilibrium level. The amplitude of the periodic oscillations grows as the deforestation rate increase. It is observed that an increment in the maximum efficacy of reforestation programs to enhance forest biomass ‘\(\beta\)’ can dampen the periodic oscillations and above a threshold value of ‘\(\beta\)’, periodic oscillations die out and system gets stabilized to a positive equilibrium state. This suggests that reforestation programs that focus on plantation of fast-growing trees high biomass production not only contributes to reduction in atmospheric CO2 levels but also aids in stabilization of system. It is found that integration of carbon taxation and reforestation programs to boosts the reforestation rate bringing more increment in equilibrium level of forest biomass and decline in equilibrium level of CO2 in comparison to the scenario in which only reforestation programs are implemented and the scenario in which carbon taxation is not used to boost the reforestation rate.

We have extended our model to examine the effect of seasonal variations in the application of reforestation efforts on the system’s dynamics by considering the implementation rate coefficient of reforestation programs and expenditure rate of carbon tax on reforestation programs as a periodic function of time having a period of 12 months. The conditions for the global attractivity of positive periodic solutions of the nonautonomous system are derived. Numerical simulation illustrates that the nonautonomous system possesses globally attractive positive periodic solutions whenever the corresponding autonomous system exhibits stable dynamics. It is found that the high deforestation rates can alter the global attractivity of the periodic solution and the nonautonomous system may show higher periodic solutions at critically high deforestation rates. It is shown that the solution trajectories of the system (47) for different initial starts, when the deforestation rate \(\phi\) is less than the threshold value \(\phi _c\), converge to a unique periodic solution. This depicts that for a range of deforestation rate, the positive periodic solution is globally asymptotically stable. However, if the deforestation rate is increased above a threshold value, then the system (47) exhibits higher periodic oscillations. Thus, it can be concluded that the high deforestation rate together with the seasonal forcing in application of reforestation efforts is responsible for the generation of higher periodic solution that was absent in the autonomous system. The existence of higher periodic oscillation in the system makes it difficult to predict the future atmospheric level of carbon dioxide and consequently the formulation and implementation of effective reforestation-taxation policy becomes a tedious job. The outcomes of the present investigation suggest that the application of reforestation efforts and carbon tax act as effective control parameters by reducing the equilibrium level of carbon dioxide. An increase in the efficiency of reforestation programs to increase the forest biomass can alter the prevalence of limit cycle oscillations induced by the high deforestation rate and ultimately lead the system to settle to a stable state. Moreover, the deforestation rate and seasonal variations in the application of reforestation efforts have synergism effect for inducing higher periodic oscillations in the system. For the formulation of an effective integrated carbon taxation-reforestation policy the effects of deforestation rate and seasonal variations in the application of reforestation efforts must be taken into account. Overall, the present study provides a mathematical framework to identify the carbon taxation-reforestation policies for the control of atmospheric CO2 levels. However, there are several limitations in the current modeling work. One of the main limitations of current modeling framework is that the energy factors and macroeconomic factors that influence carbon tax pricing have not been taken into account. The present work can be extended to include the impact of energy factors and macroeconomic factors on the carbon taxation.