1 Introduction

Nuclear forces indicate the main characteristic of the models employed in studying the properties of finite-nuclei and nuclear matter. In fact, ultra-dense events including heavy-ion collisions [1,2,3] and astrophysical compact objects like neutron stars (NSs) and supernovas explosions [4,5,6,7,8,9], which have stimulated impressive theoretical efforts, reflect different aspects of nuclear forces. The realistic nuclear forces obtained from nucleon–nucleon scattering data are used in microscopic models [10,11,12,13,14,15,16,17,18], while phenomenological models [19,20,21,22,23,24,25,26,27] are proposed within the mean-field (MF) approximation by the interactions whose parameters are fixed to satisfy saturation properties of nuclear matter and the experimental nuclear ground state data. Such phenomenological models include the relativistic MF approaches relying on meson-exchange interactions, and the non-relativistic MF theories using effective macroscopic interactions like different types of zero-range Skyrme, finite-range Gogny, and phase-space nuclear forces. Complying with the Thomas–Fermi (TF) approximation, the phase-space approach of nuclear forces was first introduced by Seyler and Blanchard (SB) [28,29,30] in a simplest possible model without considering density-dependent interaction terms, which give rise to the so-called rearrangement effects. Bandyopadhyay and Samaddar [20, 31] have proposed a density-dependent extension of the SB interaction in studying thermal properties of nuclear matter. In addition, Myers and Swiatecki (MS) [19, 32, 33] have formulated a new version of density-dependent SB interaction by including an inverse-momentum dependence in phase space to predict the properties of finite nuclei and nuclear matter. By using the MS interaction, different aspects in thermodynamics of nuclear matter have been successfully investigated in Refs. [27, 34, 35]. Such interaction has also shown its capability in modeling the structure of neutron stars (NSs) [36, 37] and proto-NSs [38,39,40] in agreement with the theoretical predictions and observational constraints.

Based on the local and non-local NJL models of deconfined quark matter [41,42,43], this interaction has been adopted for probing the baryon-quark phase transition (PT) in a \(2M_{\odot }\) neutron star, as the existence of a pure phase in the stellar core has been excluded. The baryon-quark PT scenario in hybrid NSs (HNSs) has gained a lot of attention over the last decades [44,45,46,47,48,49,50,51,52,53,54]. In this work, we aim to study the outcomes of the basic interaction of Seyler and Blanchard in the baryon-quark PT and HNS structure, as compared to its density-dependent extension proposed by Myers and Swiatecki. Applying the MC, we analyze such a transition in dense matter within the SU(3) version of the standard NJL model for the quark degrees of freedom. The MC indicates a limiting case of the finite-size effects with a sufficiently large value of the baryon-quark surface tension, which leads to a sharp PT. Based on the MC, the stability of a NS requires the formation of a pure quark matter core (no matter how small), as it can be recognized by the constant-sound-speed (CSS) parameters for the baron-quark PT [55, 56]. Therefore, for our purpose, it is necessary to clarify the instability of a NS at the quark onset under the MC. In light of the comments remarked above, this paper is arranged as follows. In Sect. 2, we describe our statistical formalism for the baryon EOS, using the SB interaction and its density-dependent extension given by MS. In addition, we present the standard NJL model for the quark matter EOS with the three sets RKH, HK, and LKW, which are connected to the baryonic EOSs SB and MS via the MC. Section 3 includes the expression and discussion of our results obtained for the baryon-quark PT and onset of quark matter in the HNSs structure. Finally, the summary and conclusions are presented in Sect. 4

2 Formalism

In this section, the EOS of baryonic matter is illustrated using the SB and MS interactions in a statistical MF approach, where the state of each nucleon is determined by its location and momentum in phase space. Based on a sharp baryon-quark PT in the MC, the hybrid EOS is obtained employing the quark EOS of the standard NJL model.

2.1 Baryonic model

Based on a statistical approach, we employ the phase-space SB interaction \(V_{12}^\mathrm{(SB)}\) [30] to be compared with its density-dependent extension \(V_{12}^\mathrm{(MS)}\) given by MS [19] as follows:

$$\begin{aligned}{} & {} V_{12}^\mathrm{(SB)}=-C \frac{\textrm{e}^{-r_{12} / a}}{r_{12} / a}\left[ 1-\frac{p_{12}^{2}}{p_{b}^{2}}\right] , \end{aligned}$$
(1)
$$\begin{aligned}{} & {} V_{12}^\mathrm{(MS)}=-C \frac{\textrm{e}^{-r_{12} / a}}{r_{12} / a}\left[ 1-\frac{p_{12}^{2}}{p_{b}^{2}}-\chi (\frac{2{\bar{\rho }}}{\rho _{b}})^ {\frac{2}{3}}+{\bar{\chi }}(\frac{p_{b}}{p_{12}})\right] , \end{aligned}$$
(2)

where \(r_{12}\) and \( p_{12} \) are the separation distance and relative momentum of each nucleonic pair in phase space, respectively. The mean density \({\bar{\rho }}\) in the MS interaction, which is defined in terms of the nucleonic densities \( \rho _{1} \) and \( \rho _{2} \) as \({\bar{\rho }}^{\frac{2}{3}}=\frac{1}{2}(\rho ^{\frac{2}{3}}_{1}+\rho ^{\frac{2}{3}}_{2})\), implies the density-dependent extension of the SB interaction, and therefore, leads to the rearrangement effects. Meanwhile, the addition of the inverse-momentum term in the MS case increases the attraction when the relative momentum \(p_{12}\) becomes smaller so that the two particles would like to become more correlated. By introducing the overall interaction strength C and the characteristic kinetic energy \(T_{b}=\frac{p_{b}^{2}}{2 {\bar{m}}}\) (\(p_{b}=\hbar (\frac{3}{2}\rho _{b}\pi ^{2})^{\frac{1}{3}}\)), with \({\bar{m}}=938.903\,\text {MeV}/c^{2}\) being the average nucleonic mass, the parameters of these Yukawa-type interactions (including the force range a) are fitted to the data of finite nuclei and saturation properties of nuclear matter [19, 30]. Thus, we adopt \(C= 435.1\,\text {MeV} \), \(T_{b}=89.274\,\text {MeV}\), \(a=0.557\,\)fm in the SB interaction, and \(C=173.51209\,\text {MeV} \ (\eta _{1}\,C)\), \(T_{b}= 503.58068\,\text {MeV} \), \(a=0.59542\,\)fm, \(\chi = 3.55552\,(\eta _{1}\,\chi ),\ {\bar{\chi }}= 0.01161\,(\eta _{2}\, {\bar{\chi }})\) for the interaction between the like (unlike) particles in the MS interaction. Considering \( \eta _{1}=2.57162 \) and \( \eta _{2}=1.54471 \) in MS provides a more comprehensive analysis of the nucleonic systems with lower isospin symmetry.

For cold baryonic matter, the step function is used in this statistical approach as the phase-space distribution function to calculate the baryonic energy density by,

$$\begin{aligned} e_{_{B}}=\sum _{i=n,p}\frac{2}{h^{3}} \int d^{3} p\left[ m_{i}\,c^{2}+\frac{p^{2}}{2 {\bar{m}}}+\frac{1}{2} V_{12}\right] \theta \left( {p}_{F,i}-p\right) . \end{aligned}$$
(3)

Here, \( \rho _{_{B}}=\rho _{p}+\rho _{n} \) is the baryonic density, and \( {p}_{F,i}=\hbar \left( \frac{3}{2} \pi ^{2} \rho _{i}\right) ^{\frac{1}{3}}\) is the Fermi momentum of the ith nucleon. Using Eq. (3), the baryonic energy density is obtained by

$$\begin{aligned} e_{_{B}}= & {} \sum _{i,(j \ne i)} T_{b}\kappa _{i}+\left( 4 \pi a^{3} C\right) \left\{ -\frac{ \rho _{i}^{2}}{2}+\rho _{i} \kappa _{i}\right. \left. -\frac{64 \pi ^{2} p_{b} p_{F, i}^{5}{\bar{\chi }}}{15 h^{6}}+\frac{ \rho _{b}\chi }{4}\left[ \left( \frac{2 \rho _{i}}{\rho _{b}}\right) ^{\frac{5}{3}} \rho _{i}\right] \right\} \nonumber \\{} & {} +\left( 4 \pi a^{3} C\right) \left\{ -\frac{ \rho _{i} \rho _{j}\eta _{1}}{2}+\rho _{i} \kappa _{j}\eta _{1}\right. -\frac{16 \pi ^{2} p_{b} {\bar{\chi }}}{h^{6}}\left[ \left( \frac{p_{F,<}^{3} p_{F,>}^{2}}{3} -\frac{p_{F,<}^{5}}{15}\right) \eta _{1}\eta _{2}\right] \nonumber \\{} & {} \left. +\frac{ \rho _{b}\chi }{4}\left[ \left( \frac{2 \rho _{i}}{\rho _{b}}\right) ^{\frac{5}{3}} \rho _{j}\eta _{1}\eta _{2}\right] \right\} , \end{aligned}$$
(4)

where

$$\begin{aligned} \kappa _{i}=\frac{8 \pi p_{F,i}^{5}}{5 h^{3}p_{b}^{2}}. \end{aligned}$$
(5)

Based on these interactions, the chemical potential of neutrons (protons) is given by

$$\begin{aligned} \mu _{i}=\frac{\partial e_{_{B}}}{\partial \rho _{i}}={\bar{m}} c^{2}+\frac{p_{F, i}^{2}}{2 {\bar{m}}}+\mu _{i}^{(l)}+\mu _{i}^{(u)}, \end{aligned}$$
(6)

where

$$\begin{aligned} \mu _{i}^{(l)}= \, & {} \left( 4 \pi a^{3} C\right) \bigg \{-\rho _{i}+ \rho _{i}\left( \frac{p_{F, i}}{p_{b}}\right) ^{2}+ \kappa _{i}+\chi \left( \frac{2 \rho _{i}}{\rho _{b}}\right) ^{\frac{2}{3}} \frac{4\rho _{i}}{3}-{\bar{\chi }}\left( \frac{8 \pi p_{b}}{h^{3}}\right) \left( \frac{p_{F, i}^{2}}{3}\right) \bigg \}, \end{aligned}$$
(7)
$$\begin{aligned} \mu _{i}^{(u)}= & {} \sum _{i \ne j} \left( 4 \pi a^{3} C\right) \bigg \{- \rho _{j}\eta _{1}+ \rho _{j}\left( \frac{p_{F, i}}{p_{b}}\right) ^{2}\eta _{1}+ \kappa _{j}\eta _{1}+\chi \left( \frac{2 \rho _{i}}{\rho _{b}}\right) ^{\frac{2}{3}}\left( \frac{5 \rho _{j}}{6}\right) \eta _{1}\eta _{2}\nonumber \\{} & {} +\chi \left( \frac{2\rho _{j}}{\rho _{b}}\right) ^{\frac{2}{3}} \left( \frac{\rho _{j}}{2}\right) \bigg . \eta _{1}\eta _{2}\bigg .-{\bar{\chi }}\left( \frac{8 \pi p_{b}}{h^{3}}\right) \bigg [\left( \frac{p_{F, j}^{3}}{3 p_{F, i}} \text{ for } p_{F, i} \geqslant p_{F, j}\right) \nonumber \\{} & {} \text { or }\left( \frac{p_{F, j}^{2}}{2}-\frac{p_{F, i}^{2}}{6} \text {for } p_{F, j} \geqslant p_{F, i}\right) \bigg ]\eta _{1}\eta _{2}\bigg \}. \end{aligned}$$
(8)

Using \(\mu _{n (p)}\) in the parabolic law, one can extract the nuclear symmetry energy as

$$\begin{aligned} E_{\rm sym}=\left. \frac{1}{2} \frac{\partial ^{2} \varepsilon _{_{B}}}{\partial \delta ^{2}}\right| _{\delta =0}=\lim _{\delta \rightarrow 0} \frac{\mu _{n}-\mu _{p}}{4 \delta }. \end{aligned}$$
(9)

with \(\delta =\frac{\rho _n-\rho _p}{\rho _{_{B}}}\) and \(\varepsilon _{_{B}}=\frac{e_{_{B}}}{\rho _{_{B}}}\), which are the asymmetric parameter and the baryonic energy per baryon, respectively.

To obtain the total baryonic energy density \(e=e_{_{B}}+e_{_{L}} \), the leptonic energy density contribution \(e_{_{L}} \) can be considered by

$$\begin{aligned} e_{_{L}}=\frac{2}{h^{3}}\sum _{j=e^{-},\mu ^{-}} \int _{0}^{p_{F,j}}d^{3}p\sqrt{(pc)^{2}+(m_{j}c^{2})^{2}}, \end{aligned}$$
(10)

Therefore, one can describe the structure of baryonic matter in terms of a Fermi sea of nucleons and relativistic lepton under the following \(\beta \)-equilibrium conditions:

$$\begin{aligned} y_{p}= & {} y_{e^{-}}+y_{\mu ^{-}}, \end{aligned}$$
(11)
$$\begin{aligned} \mu _{e^{-}}= & {} \mu _{n}-\mu _{p}, \end{aligned}$$
(12)
$$\begin{aligned} \mu _{e^{-}}= & {} \mu _{\mu ^{-}}. \end{aligned}$$
(13)

In the charge neutrality relation (11), \(y_{k}=\frac{\rho _{_{k}}}{\rho _{_{B}}}\) implies the particle fractions. According to the Fermi energy level, the chemical potential of electrons \(e^{-} \) (muons \(\mu ^{-}\)) can also be determined by

$$\begin{aligned} \mu _{_{j=e^{-},\mu ^{-}}}=\sqrt{(p_{F,j} \ c)^{2}+(m_{j}c^{2})^{2}}, \end{aligned}$$
(14)

where \( p_{F,j}=(\frac{3h^{3}\rho _{_{j}}}{8\pi })^{\frac{1}{3}} \). Finally, by adding the leptonic pressure \(P_{L} \) to the baryonic pressure \( P_{B} \), the total pressure of baryonic matter in \( \beta \)-equilibrium can be computed from

$$\begin{aligned} P=P_{B}+P_{L}=\sum _{k }(\mu _{_{k}}\rho _{_{k}})-e. \end{aligned}$$
(15)

2.2 Standard NJL model for the quark phase

In this work, we focus on the three-flavor version of the standard NJL model for analysis of the EOS of quark matter. The QCD Lagrangian is written as follows:

$$\begin{aligned} {\mathcal {L}}_{NJL}=\, & {} {\bar{q}}\left( i \gamma _{\mu } \partial ^{\mu }-m^{0}\right) q+G_{S} \sum _{a=0}^{8}\left[ \left( {\bar{q}} \lambda _{a} q\right) ^{2}+\left( {\bar{q}} \gamma _{5} \lambda _{a} q\right) ^{2}\right] -K\left\{ {\text {det}}\left[ {\bar{q}} \left( 1+\gamma _{5}\right) q\right] \right. \nonumber \\{} & {} \left. +{\text {det}}\left[ {\bar{q}}\left( 1-\gamma _{5}\right) q\right] \right\} -G_{V} \sum _{a=0}^{8}\left[ \left( {\bar{q}} \gamma _{\mu } \lambda _{a} q\right) ^{2}\right] . \end{aligned}$$
(16)

Here, q denotes the quark fields containing the terms from the three flavors (\( N_{f} = 3 \)) and three colors (\( N_{c} = 3 \)). In addition, the Lagrangian includes the current quark mass matrix \( m^{0} \) as

$$\begin{aligned} m^{0}={\text {diag}}\left( m_{d}^{0},m_{u}^{0}, m_{s}^{0}\right) . \end{aligned}$$
(17)

The Gell-Mann matrices of flavor SU(3) \( \lambda _{a} \ (a=1,2,...,8)\) are accompanied by \( \lambda _{0}=\sqrt{2/3} \) times the \(3\times 3\) unit matrix. This study employs the RKH, HK, and LKW interaction parameters for the EOS of deconfined quark matter, which are given in Table 1.

Table 1 Three sets of parameters in the standard (local) NJL model of quark matter
Full size table

Since the vector coupling ratio \(\eta _{_{V}}=G_{V}/G_{S}\) cannot be predicted with certainty [60], one can consider it a free parameter. Based on the MF approximation [61], one can introduce the zero-temperature grand canonical thermodynamic potential as

$$\begin{aligned} \Omega _{Q}= & {} -\sum _{i=u, d, s} \frac{3}{\pi ^{2}} \int _{0}^{\Lambda } d p p^{2}\bigg [E_{p}^{\left( M_{i}\right) }+\left( {\tilde{\mu }}_{i} -E_{p}^{\left( M_{i}\right) }\right) \Theta \left( {\tilde{\mu }}_{i}-E_{p}^{\left( M_{i}\right) }\right) \bigg ]\nonumber \\{} & {} +\sum _{i=u, d, s} 2G_{S}\left\langle {\bar{q}}_{i} q_{i}\right\rangle ^{2}-4 K\left\langle {\bar{q}}_{u} q_{u}\right\rangle \left\langle {\bar{q}}_{d} q_{d}\right\rangle \left\langle {\bar{q}}_{s} q_{s}\right\rangle -\sum _{i=u, d, s} \frac{\left( {\tilde{\mu }}_{i}-\mu _{i}\right) ^{2}}{8 G_{V}}, \end{aligned}$$
(18)

where \(E_{p}^{\left( M_{i}\right) }=\sqrt{p^{2}+M_{i}^{2}}\). The dynamic quark mass \( M_{i} \) and effective chemical potential \( {\tilde{\mu }}_{i} \) read

$$\begin{aligned} M_{i}= & {} m_{i}-4G_{S}\langle {\bar{q}}_{i}q_{i}\rangle +2K\langle {\bar{q}}_{j}q_{j} \rangle \langle {\bar{q}}_{k}q_{k}\rangle , \end{aligned}$$
(19)
$$\begin{aligned} {\tilde{\mu }}_{i}= & {} \mu _{i}-4 G_{V}\langle q_{i}^{\dagger } q_{i}\rangle . \end{aligned}$$
(20)

The cutoff parameter \(\Lambda \) in the MF grand thermodynamic potential \( \Omega _{Q} \) provides a regularization scheme due to the non-renormalizability of the standard NJL model. In Eq. (19), (i, j, k) demonstrate any permutation of (u, d, s) quarks with \(\langle {\bar{q}}_{i}q_{i}\rangle \) being the ith quark condensate. In addition, \( \langle q_{i}^{\dagger } q_{i}\rangle \) in Eq. (20) is the ith quark number density \(\rho _{i}=\frac{(p_{F}^{i})^{3}}{\pi ^{2}} \) (where \( p_{F}^{i} \) stands for the association of the Fermi momentum). According to Eqs. (19) and (20), \( \langle {\bar{q}}_{i}q_{i}\rangle \) and \( \langle q_{i}^{\dagger } q_{i}\rangle \) are determined by minimizing \( \Omega _{Q} \) with respect to \( M_{i} \) and \( {\tilde{\mu }}_{i} \), respectively (\( \tilde{\mu _{i}}\leqslant \Lambda \)):

$$\begin{aligned}{} & {} \frac{\partial \Omega _{Q}}{\partial M_{i}}=0 \Rightarrow \left\langle {\bar{q}}_{i} q_{i}\right\rangle =-\frac{3}{\pi ^{2}} \int _{0}^{\Lambda } d p p^{2} \frac{M_{i}}{E_{p}^{\left( M_{i}\right) }} \bigg [1-\Theta \left( {\tilde{\mu }}_{i}-E_{p}^{\left( M_{i}\right) }\right) \bigg ], \end{aligned}$$
(21)
$$\begin{aligned}{} & {} \frac{\partial \Omega _{Q}}{\partial {\tilde{\mu }}_{i}}=0 \Rightarrow \left\langle q_{i}^{\dagger } q_{i}\right\rangle =\rho _{i}=+\frac{3}{\pi ^{2}} \int _{0}^{\Lambda } d p p^{2}\Theta \left( {\tilde{\mu }}_{i}-E_{p}^{\left( M_{i}\right) }\right) . \end{aligned}$$
(22)

The Beta-equilibrium conditions proposed for a neutral mixture of quarks and leptons can be read as

$$\begin{aligned}{} & {} 2y_{u^{+}}-\left( y_{e^{-}}+y_{\mu ^{-}}\right) -\left( y_{d^{-}}+y_{s^{-}}\right) =0, \end{aligned}$$
(23)
$$\begin{aligned}{} & {} \mu _{u^{+}}=\mu _{_{B}}-\dfrac{2\mu _{e^{-}} }{3}, \end{aligned}$$
(24)
$$\begin{aligned}{} & {} \mu _{d^{-}}=\mu _{s^{-}}=\mu _{_{B}}+\dfrac{\mu _{e^{-}} }{3}, \end{aligned}$$
(25)
$$\begin{aligned}{} & {} \mu _{e^{-}}=\mu _{u^{-}}, \end{aligned}$$
(26)

in which \(y_{(i=u,d,s)}=\frac{\rho _{i}}{3\rho _{_{B}}}\), and \(\mu _{_{B}}=\dfrac{2\mu _{d^{-}}+\mu _{u^{+}} }{3} \) denote the ith quark fraction, and baryonic chemical potential, respectively. Moreover, in Eqs. (24), (25), and (26), \(\mu _{_{B}} \) is taken as the baryonic chemical potential, used as an input to solve the coupled equations self-consistently. Eventually, the pressure P and energy density e for quark matter in beta-equilibrium are obtained as

$$\begin{aligned}{} & {} P_{}=P_{Q}+P_{L}, \end{aligned}$$
(27)
$$\begin{aligned}{} & {} e_{}=\sum _{k} \rho _{k} \mu _{k}-P_{}, \end{aligned}$$
(28)

in which, we assume the quark pressure \(P_{Q}=\Omega _{Q}^{0}-\Omega _{Q}\), utilizing \(\Omega _{Q}^{0}\) to guarantee the condition \(P_{Q}=0\) in the vacuum.

The MC is widely used for studying the baryon-quark PT. As a result of the MC, which is a limiting case corresponding to a large enough surface tension, and a WS cell that is large compared to the electromagnetic Debye screening length, the pure baryonic and quark phases are considered to be independently charge-neutral. Therefore, a sharp PT between baryonic and quark matter occurs, leading to the disappearance of the mixed phase region in the structure of a HNS. Thus, the PT conditions can be read as

$$\begin{aligned} \mu _{n}^\mathrm{(BP)}= & {} \mu _{u}^{(Q P)}+2\,\mu _{d}^\mathrm{(QP)}=3\,\mu _{_{B}}^\mathrm{(MC)}, \end{aligned}$$
(29)
$$\begin{aligned} P^\mathrm{(BP)}= & {} P^\mathrm{(QP)}=P^\mathrm{(MC)}, \end{aligned}$$
(30)

and for the energy density of the mixed phase \( e^{(MC)} \) , we have

$$\begin{aligned} e^\mathrm{(MC)}=3\,\rho _{_{B}}\,\mu _{_{B}}^\mathrm{(MC)}-P^\mathrm{(MC)}. \end{aligned}$$
(31)

3 Results and discussions

According to the overall direction of this investigation, we utilize the baryonic interactions SB and MS, combined with the three quark interactions RKH, HK, and LKW to analyze the PT from nuclear matter to quark matter. The baryon-quark PT is examined for the three values of the vector coupling strength \(\eta _{_{V}}=G_{V}/G_{S} = 0, 0.15, 0.3\) by the MC.

It is noteworthy to present a genuine picture of our baryonic EOSs by comparing the pressure of symmetric nuclear matter (SNM) and pure nuclear matter (PNM) with the measurements acquired from the analysis of heavy-ion flow data [62] (see Fig. 1).

Fig. 1
figure 1

Pressure of SNM (left panel) and PNM (right panel) vs. baryonic density. Our findings are compared with those obtained from the flow data analysis of heavy-ion collisions [62]. The inner panel shows the nuclear symmetry energy vs. the baryonic density for the SB and MS interactions

Full size image

As shown in this figure, the baryonic interaction MS gives a softer EOS than SB, resulting in a better agreement with the flow data measurements of heavy-ion collisions. Hence, the EOS of PNM in SB (MS) is stiffer (softer) than the one in SNM due to the stiffness (softness) effects of the nuclear symmetry energy, which is also shown in this figure.

To examine the causality condition in our quark EOSs, the ratio of the sound velocity to the light speed \(v_{s}/c=\sqrt{(\dfrac{dP}{de})} \) must be less than one. We depict in Fig. 2 this ratio as a function of the pressure for each quark matter EOS. It is seen that our NJL-type EOSs fulfill both the causality and hydrodynamic stability requirements. At higher pressures, the value of \(v_{s}/c\) is less sensitive to the changes of P. Among these quark models, this ratio in LKW has the most moderate dependence on the variations of pressure. Meanwhile, the minimum value of this ratio is obtained at \( \eta _{_{V}}=0\) for each quark model.

Fig. 2
figure 2

Ratio of the sound speed to the light speed as a function of pressure in deconfined quark matter obeying the interactions RKH (left panel), HK (middle panel), and LKW (right panel) at \(\eta _{_{V}}\)= 0, 0.15, 0.30

Full size image

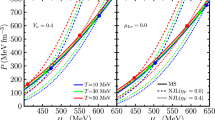
Within the MC, the occurrence of the baryon-quark PT arises from the intersection of the baryonic and quark EOSs in the pressure-baryonic chemical potential (\(P-\mu _{_{B}}\)) plane, according to Fig. 3.

Fig. 3
figure 3

Pressure as a function of baryonic chemical potential for the baryonic interactions SB and MS, accompanied by the quark interactions RKH (left panel), HK (middle panel), and LKW (right panel) at \( \eta _{_{V}} \) = 0, 0.15, 0.30. The crossing points of the baryonic and quark EOSs represent the baryon-quark PT under the MC

Full size image

As can be seen, all cases of the present hybrid EOSs lead to the emergence of the PT. Strengthening the quark vector interactions shifts the intersections to higher pressures and baryonic chemical potentials, while SB with a stiff nuclear symmetry energy meets the lower ones.

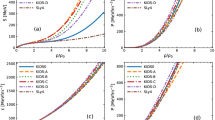
Since the baryonic chemical potential is a key quantity in studying dense stellar matter, we display it in Fig. 4 at various baryonic densities.

Fig. 4
figure 4

Baryonic chemical potential as a function of baryonic density in HNS matter obeying the quark interactions RKH (left panel), HK (middle panel), and LKW (right panel) at \(\eta _{_{V}}\)= 0, 0.04, 0.08, joint to the baryonic interactions SB and MS via the MC. The mixed-phase regions are denoted by the pairs of the solid dots

Full size image

As shown in this figure, the baryonic chemical potential \( \mu _{_{B}} \) rises with the baryon density \( \rho _{_{B}} \) in the pure baryonic and quark phases, while exhibiting a plateau in the mixed phase. The baryonic chemical potential of the mixed phase grows considerably, as \( \eta _{_{V}}\) increases. Meanwhile, the mixed phase related to the SB interaction is formed at higher baryonic chemical potentials.

The nature of the MC requires that the electron chemical potential drops sharply at the baryonic chemical potential of the mixed phase, as seen in Fig. 5. This figure demonstrates that the electron chemical potential in the baryonic interaction SB, reaches considerably larger values. The results indicate that the discrepancy between the electron chemical potential of each phase in the mixed phase region becomes large with rising \( \eta _{_{V}}\). Furthermore, the quark vector interaction accelerates the deleptonization in the pure quark phase due to decreasing the electron chemical potential.

Fig. 5
figure 5

Electron chemical potential as a function of baryonic density in HNS matter obeying from the quark interactions RKH (left panel), HK (middle panel), and LKW (right panel) at \(\eta _{_{V}}\)= 0, 0.04, 0.08, joint to the baryonic interactions SB and MS via the MC. The mixed-phase regions are denoted by the pairs of the solid dots

Full size image
Fig. 6
figure 6

Pressure as a function of baryonic density in HNS matter obeying the quark interactions RKH (left panel), HK (middle panel), and LKW (right panel) at \(\eta _{_{V}}\)= 0, 0.04, 0.08, joint to the baryonic interactions SB and MS via the MC. The mixed-phase regions are denoted by the pairs of the solid dots

Full size image

A striking aspect of the EOS for NS matter is pressure P. Thus, we depict in Fig. 6 the pressure versus the baryon density at the various hybrid EOSs. As can be seen, P increases with \(\rho _{_{B}}\), while being constant in the mixed phase. One indeed realizes that the stiffness of the hybrid EOS relies remarkably on the type of the baryonic EOS and the effects of the quark vector interaction, since SB and larger \( \eta _{_{V}} \) make the hybrid EOS significantly stiffer. In addition, the baryonic EOS has a notable consequence on the width of the mixed-phase rather than the quark EOS. As a consequence, stiffening the quark EOS because of increasing \(\eta _{_{V}}\) delays the appearance of the mixture phase, while it occurs sooner (lower baryonic densities) for the stiffer baryonic EOS SB. To reach a deeper insight into the hybrid EOS, the pressure as a function of the baryonic and electron chemical potentials is depicted in 3D space (see Figs. 7 and 8 for SB and MS, respectively). It can be more clearly seen in these figures that the width of the mixed-phase region is not significantly changed with the quark vector coupling constant. For a given \(\eta _{_{V}}\), the baryonic EOS type has a stronger influence on the mixed-phase properties than the quark EOS.

Fig. 7
figure 7

Pressure as a function of baryonic and electron chemical potentials in HNS matter obeying the quark interactions of RKH (a), HK (b), and LKW (c) at \(\eta _{_{V}}\)= 0, 0.15, 0.30, joint to the baryonic interaction SB via the MC

Full size image
Fig. 8
figure 8

Pressure as a function of baryonic and electron chemical potentials in HNS matter obeying the quark interactions of RKH (a), HK (b), and LKW (c) at \(\eta _{_{V}}\)= 0, 0.15, 0.30, joint to the baryonic interaction MS via the MC

Full size image

Utilizing the EOS of NS matter in a wide baryonic density range, one can calculate the mass of NSs in terms of their radius and center of energy density with the help of the Tolman–Oppenheimer–Volkoff (TOV) equations [63, 64]:

$$\begin{aligned} \frac{\textrm{d}P(r)}{\textrm{d}r}= & {} -\frac{\textrm{G}m(r)e(r)}{r^{2}}\frac{[1+\frac{P(r)}{e(r)c^{2}}][1+\frac{4\pi r^{3}P(r)}{m(r)c^{2}}]}{1-\frac{2Gm(r)}{rc^{2}}}, \end{aligned}$$
(32)
$$\begin{aligned} \frac{\textrm{d}m(r)}{\textrm{d}r}= & {} 4\pi r^{2}e(r), \end{aligned}$$
(33)

where m, e,  and P represent the enclosed mass, energy density, and pressure at the radius r, respectively (G being the gravitational constant). The calculations begin from a central energy density \( e_{c} \) and continue to reach the energy density of iron on the surface signified by the stellar radius R. For the HNS crust, the inner-crust EOS of Negele and Vautherin [65], which relies on the Hartree–Fock approach, is attached to the outer-crust EOS based on the properties of heavy nuclei by Baym et al. [66]. The gravitational mass (in units of the solar mass \( M_{\odot }) \) versus the stellar radius is depicted in Fig. 9. As can be seen, the gravitational mass attains a maximum value, which is indicated by a circle point. Due to the instability against radial oscillations, a stellar configuration with a radius smaller than the one of the maximum mass is ruled out. The more repulsive nature of the baryonic EOS SB could lead to the formation of a HNS with larger values of the gravitational mass, and radius. In addition, the quark vector interaction has a considerable influence on the maximum mass of NSs, so that the maximum mass increases with \(\eta _{_{V}}\), and smaller radii are allowed. Consequently, the maximum mass of a HNS is estimated to be around \( 2M_{\odot } \), complying with the observational range from the mass measurement of heavy pulsars. The stability of a HNS under the MC demands a connected mixed-phase branch for the HNS structure, meaning that the existence of a pure quark core (where the central pressure lies just above the transition pressure \(P^\mathrm{(tr)}\)) is inevitable even if its contribution to the total gravitational mass is negligible. Based on the CSS parameters of PT, the stability condition is given independently of the sound speed in the pure quark phase [55, 56] as

$$\begin{aligned} \bigtriangleup e^\mathrm{(tr)} < \bigtriangleup e_{\rm cr}^\mathrm{(tr)}, \end{aligned}$$
(34)

where

$$\begin{aligned} \bigtriangleup e^\mathrm{(tr)}= & {} e^\mathrm{(tr)}_{Q}-e^\mathrm{(tr)}_{_{B}}, \end{aligned}$$
(35)
$$\begin{aligned} \bigtriangleup e_{\rm cr}^\mathrm{(tr)}= & {} \dfrac{1}{2}e^\mathrm{(tr)}_{_{B}}+ \dfrac{3}{2}P^\mathrm{(tr)}. \end{aligned}$$
(36)

Thus, the mixed-phase energy density range \(\bigtriangleup e^\mathrm{(tr)}\) must be smaller than the critical value \(\bigtriangleup e_{\rm cr}^\mathrm{(tr)}\) to fulfill the stability condition within the MC. The maximum mass properties, associated with the CSS parameters \(e^\mathrm{(tr)}\) and \(\bigtriangleup e_{\rm cr}^\mathrm{(tr)}\), are listed in Table 2 for each hybrid EOS.

Fig. 9
figure 9

Mass-radius diagrams of HNS matter obeying the quark interactions RKH (left panel), HK (middle panel), and LKW (right panel) at \(\eta _{_{V}}\)= 0, 0.04, 0.08, joint to the baryonic interactions SB and MS via the MC. The dots and pluses display the mixed-phase (MP), and maximum mass (\({M^\mathrm{(max)}_{G}}/{M_{\odot }}\)) configurations, respectively. The arrow is used to distinguish the structures comprising the pure baryonic (BP), mixed (MP), and pure quark (QP) phases in the center of the star. The horizontal bands indicate the observational mass constraint from PSR J0740\( + \)6620 [67], and the gravitational mass inferred for the light component of GW190814 [68]. We also show the area of the mass-radius limits deduced from the NICER measurements of PSR J0030\(+\)0451 [69, 70]. The region on the top-left of each panel is excluded by causality [71]

Full size image
Table 2 Characteristics of the maximum mass configuration of a HNS obtained from the baryonic interactions SB and MS, as the quark interactions RKH, HK, and LKW at \(\eta _{_V}\)= 0, 0.15, 0.30 are joint via the MC
Full size table

As realized from this table, the formation of a stable HNS within the MC is not allowed for the hybrid EOS SB-LKW at any \(\eta _{_{V}}\), and the one given by MS-LKW in the absence of the quark vector interaction (their corresponding data are denoted in bold). Therefore, based on our phase-space-based baryonic models, only the quark interaction LKW can destabilize the star under the MC. Meanwhile, the present results cannot confirm the scenario that the light object of GW190814 [68] is a massive HNS.

The tidal deformability of NSs is an important parameter in the gravitational-wave (GW) astronomy of the pre-merger phase of a binary compact object coalescence, while playing a significant role in giving data about the EOS of dense matter. For the first time, the tidal effects have been measured after the LIGO-Virgo collaboration detected the GW170817 signal. The dimensionless tidal deformability (polarizability) \(\Lambda _{_{T}}\), by which the linear response of the quadrupole deformation of a compact star to the external tidal field of its companion is measured, can be determined by the tidal Love number k2 and the star compactness \(C_{_{S}}= M/R\) [72, 73] (\( G=c=1 \)) as

$$\begin{aligned} \Lambda _{_{T}}=\frac{2}{3} k_{2} C_{_{S}}^{-5}, \end{aligned}$$
(37)

with

$$\begin{aligned} k_{2}={} & {} \frac{8 C_{_{S}}^{5}}{5}(1-2 C_{_{S}})^{2}\left[ 2+2 C_{_{S}} \left( h_{_{R}}-1\right) -h_{_{R}}\right] \nonumber \\{} & {} \times \left\{ 2 C_{_{S}}\left[ 6-3 h_{_{R}}+3 C_{_{S}} \left( 5 h_{_{R}}-8\right) \right] \right. \nonumber \\{} & {} +4 C_{_{S}}^{3}\left[ 13-11 h_{_{R}}+C_{_{S}}\left( 3 h_{_{R}}-2\right) +2 C_{_{S}}^{2}\left( 1+h_{_{R}}\right) \right] \nonumber \\{} & {} \left. +3(1-2 C_{_{S}})^{2}\left[ 2-h_{_{R}}+2 C_{_{S}}\left( h_{_{R}}-1\right) \right] \ln (1-2 C_{_{S}})\right\} ^{-1}, \end{aligned}$$

Here, \( h_{_{R}} \) is equal to the function \( h_{_{}}(r) \) at the stellar radius R, calculated simultaneously by solving the following nonlinear first-order differential equation, and the TOV Eqs. (32) and (33) for the boundary condition \( h_{_{}}(0) =2 \) [74]:

$$\begin{aligned} r \frac{\textrm{d} h_{_{}}(r)}{\textrm{d} r}+h_{_{}}(r)^{2}+F_{1}(r) h_{_{}}(r)+r^{2} F_{2}(r)=0, \end{aligned}$$
(38)

where

$$\begin{aligned} F_{1}(r)=\frac{1-4 \pi r^{2}[e(r)-P(r)]}{1-\frac{2 m(r)}{r}}, \end{aligned}$$
(39)

and

$$\begin{aligned} F_{2}(r)=\frac{4 \pi \left[ 5 e(r)+9 P(r)+\frac{e(r)+P(r)}{d p / d e}-\frac{6}{4 \pi r^{2}}\right] }{1-\frac{2 m(r)}{r}} -\frac{4}{r^{4}}\left[ \frac{m(r)+4 \pi r^{3} P(r)}{1-\frac{2 m(r)}{r}}\right] ^{2}. \end{aligned}$$
(40)

In Fig. 10, we depict the dimensionless tidal deformability \(\Lambda _{_{T}}\) in HNSs as a function of the gravitational mass (in units of the solar mass \( M_{\odot } \)).

Fig. 10
figure 10

Tidal deformability of HNSs as a function of gravitational mass (in units of the solar mass \( M_{\odot } \)) in the quark interactions RKH (left panel), HK (middle panel), and LKW (right panel) at \(\eta _{_{V}}\)= 0, 0.15, 0.30, joint to the baryonic interactions SB and MS via the MC. The dots and pluses display the mixed-phase (MP), and maximum mass (\({M^\mathrm{(max)}_{G}}/{M_\odot }\)) configurations, respectively. The arrow is used to distinguish the structures comprising the pure baryonic (BP), mixed (MP), and pure quark (QP) phases in the center of the star. The vertical bar shows the tidal deformability range of a \(1.4M_{\odot }\) NS, obtained by the analysis of the GW170817 signal [75]

Full size image

As indicated in this figure, \(\Lambda _{_{T}}\) decreases drastically with rising the gravitational mass, while its larger values correspond to the SB interaction. It can be seen that stiffening the quark EOS with increasing \(\eta _{_{V}}\) reduces the tidal deformability of the maximum gravitational mass. In addition, stiffening the quark EOS with increasing the vector coupling ratio reduces the tidal deformability of the maximum gravitational mass, as more significantly indicated in SB than in MS (see also Table 2). According to the %90 confidence-level estimate \(70\le \Lambda _{_{T}}\le 580\) for a \(1.4M_{\odot }\) NS [75], which is congruent with the data obtained in MS, our results show that its core is not dense enough to form a HNS.

4 Summary and conclusion

We have used the MC in this study to investigate the baryon-quark PT in the HNS structure. Based on a phase-space approach complying with the Thomas–Fermi approximation, the EOS of baryonic matter has been obtained using the SB interaction, and its density-dependent extension called the MS interaction. Utilizing the standard (local) NJL interactions RKH, HK, and LKW, we have computed the EOS of quark matter. The softer nature of the baryonic EOS MS due to being less repulsive than the one SB, makes it more consistent with heavy-ion flow data. We have shown that the sound speed (in units of the light speed) in the pure quark phase varies more weakly with the pressure, especially for the LKW model, as the pressure increases. The repulsive vector coupling ratio \(\eta _{_V}\) has a strong influence on the stiffness of the quark EOS, and the properties of the baryon-quark mixed phase. With an increase in \(\eta _{_V}\), the pressure and baryonic chemical potential of the PT are shifted to higher values, as the transition density for the onset of the mixed phase is delayed, and the width of the mixed phase is enlarged. According to the CSS parameters extracted from the present hybrid EOSs, a stable \(2M_{\odot }\) HNS can be predicted under the MC. By adopting the MC, a HNS can be destabilized if the quark interaction LKW is used, whereas the LKW and HK interactions always lead to a stable HNS. We found that the hybrid EOSs using the SB interaction provide larger values of the gravitational mass, radius, and tidal deformability for a HNS than those employing the MS interaction. It should be noted that the MS interaction demonstrates better compatibility with the estimated range for the tidal deformability of a \(1.4M_{\odot }\) NS than the SB one. Our finding for the maximum gravitational masses cannot account for the scenario that the light component of GW190814 is a massive HNS. In the future, we aim at extending the present approach for the baryonic and quark EOSs to investigate different aspects of the baryon-quark PT in HNSs.