Dynamics of modulated waves in the spring-block model of earthquake with time delay

Abstract

In geological fault modeling, several fragmented blocks are coupled by springs and the motion between them is not transmitted instantly, but with a delay. The dynamics of geological media is investigated by considering the time delay between blocks’ deformations. Our modelization led to a complex-Landau equation, from which we derived solitary waves induced by the stick–slip process. A solitary wave propagating along the contact surface between two plates becomes stable or unstable as the time delay varies, thus producing states of solitary wave. The modulational instability of the system is performed, showing that the instability of the amplitude increases with the time delay and the nonlinear parameters. Also, the bandwidth of instability varies with the system parameters. It is shown from our results that the time delay decelerates the propagating soliton.

1 Introduction

Mantle convection process is responsible of up and down welling of hot and cold material, respectively, in the Earth’s interior. Lithospheric plates are affected by convectional currents that induced slow motion in order of cm/yr [1]. On Earth, a plate tectonic has three main boundaries: mid-oceanic ridges, subduction zones and transform faults. These plates move with respect to each other due to convection currents within the mantle below the terrestrial crust [2]. The motion along a transform fault is explained by the stick–slip phenomenon in which two phases are distinguished, stress accumulation (corresponding to the stick) and the stress drop (corresponding to the fault slip) [3, 4]. Asperities between the plates may increase stress, leading to strain energy accumulation around the fault surface [5]. Occasionally, when the stress is sufficiently high to break through the asperities, a sudden motion of the plates occurs, accompanied by energy release, causing an earthquake. This energy propagates in the form of a wave at the speed of two to three kilometers per second (2–3 km/s). The size of an earthquake strongly depends on the area over which the rupture occurs and how the fault is ruptured.

During the rupture process, different elastic waves take place in the Earth’s crust and propagate in all directions away from the rupture and with a faster velocity than the rupture propagates. However, the real speed of the waves depends on the elastic properties of the rock materials which constitute the Earth’s crust and also on the nature of the waves. Physically, rock materials are not continuous; they consist of grains, crystals or blocks of different sizes separated from each other by cracks of all possible sizes. Indeed, the earthquake is the onset of some complex behaviors, due to the presence of relevant physical phenomena occurring at the same place for a short time. In this respect, many researches have been devoted to explaining the behavior of earthquakes [6,7,8].

The effect of time delay was previously and implicitly introduced in the friction term [9, 10], and between the neighboring blocks in a one-dimensional chain of blocks with rate-dependent friction law [11]. Kostić et al. [12] also studied the transition between different seismic cycles considering the delayed interaction among the blocks with a rate- and state-dependent friction law. All these works do not study the dynamic of waves in the Burridge and Knopoff model.

The dynamics of solitary waves has been investigated by some authors [8, 13,14,15] based on the 1D spring-slider model proposed by Burridge and Knopoff. None of these works took into account the time delay.

In this paper, we analyze the dynamics of modulation waves considering the delayed interaction among the blocks with a velocity-weakening frictional force and a nonlinear elastic force.

2 Model and equation of motion

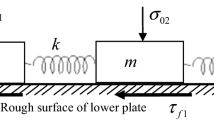
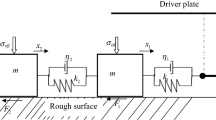
The model under study is depicted in Fig. 1; it displays a preexisting fault broken on one side.

Fig. 1.

1D model of rock block materials moving in a rough. The blocks are connected to a moving loader plate which represents the other side of the fault through spring interactions [7]

It consists of N blocks of rocks materials with mass $m$, connected to each other by the springs of stiffness $k_{c}$(materializing the linear elastic properties of the medium surrounding the fault) with normal length $a$ and a viscous damping (that corresponds to the viscous character of rocks constituting the fault) with damping coefficient $C$. Each block is attached by a leaf spring of stiffness $k_{p}$ to a driver plate.

The blocks rest upon a stationary surface (punt form), which provides a velocity-dependent frictional force that impedes their motion; the viscous damping force (the restraining of vibratory motion of the oscillations of a mechanical system by the dissipation of energy is known as damping force) is proportional to the relative block velocity. Initially, the system is at rest, and the elastic energy accumulated in “horizontal” springs is only due to randomly generated small initial displacements of the blocks from their initial positions. In this paper, we consider a nonlinear stiffness of the elasticity of the rocks. The nonlinear elastic force in the spring blocks with stiffness $k_{0}$ is given by [8, 16,17,18]

$$F_{e} \left( x \right) = - k_{0} \left( {x + \frac{\varepsilon }{{2b^{2} }}x^{3} } \right)$$

(1)

The equation of motion is given by the following expression:

$$\begin{gathered} m\frac{{d^{2} x_{n} }}{{dt^{2} }} = - k_{p} \left( {x_{n} - V_{0} t} \right) - k_{c} \left( {x_{n + 1} - 2x_{n} + x_{n - 1} } \right) - C\left( {\dot{x}_{n + 1} - 2\dot{x}_{n} + \dot{x}_{n - 1} } \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{{k_{p} \varepsilon }}{{2b^{2} }}x_{n}^{3} + \frac{{k_{c} \varepsilon }}{{2b^{2} }}\left[ {\left( {x_{n + 1} - x_{n} } \right)^{3} - \left( {x_{n} - x_{n - 1} } \right)^{3} } \right] - F_{0} \phi \left( {\dot{x}_{n} /V_{c} } \right) \hfill \\ \end{gathered}$$

(2)

in which $F_{0}$ represents the static frictional force in the dry fault ($F_{0}$ is the force which enables the block to resist the motion induced by the tectonic plates in dry conditions),$x_{n} \,\left( {n = 1,\,....,\,N} \right)$ measures the displacement of the block, and $V_{c}$ stands for the characteristic velocity of the friction.

The late 1970s saw an increased interest in stick–slip instabilities present in laboratory rock experiments as a means of understanding earthquake ruptures. Many authors [19, 20] used these experiments to formulate constitutive laws capable of describing the frictional stress when rocks were sheared against each other or over a surface. Fault behavior strongly depends on these constitutive models. Therefore, we use the velocity-weakening frictional force given by [21].

$$\phi \left( x \right) = \frac{{{\text{sign}}\left( x \right)}}{1 + \left| x \right|}.$$

(3)

In our current investigation, we focus on the weak displacements of the block $\left( {i.e.\,\dot{x}_{n} < < V_{c} } \right)$. The function $\phi \left( {\dot{x}_{n} /V_{c} } \right)$ is developed in linear approximation in terms of the Taylor series according to [22] as follows:

$$\phi \left( {\dot{x}/Vc} \right) = 1 - \dot{x}/Vc.$$

(4)

In the continuation of this work, we introduce time delay between the coupled blocks. The effect of the middle set of blocks (with different viscosity properties in comparison to others) is replicated by the delayed interaction between the two blocks [12]. Using the above approximation and introducing the time delay $\tau_{0}$, the equation of motion can now be rewritten as

$$\begin{aligned} & \ddot{x}_{n} = - k_{1} \left( {x_{{n + 1}} \left( {t - \tau _{0} } \right) - 2x_{n} \left( t \right) + x_{{n - 1}} \left( {t - \tau _{0} } \right)} \right) - \eta \left( {\dot{x}_{{n + 1}} \left( {t - \tau _{0} } \right) - 2\dot{x}_{n} \left( t \right) + \dot{x}_{{n - 1}} \left( {t - \tau _{0} } \right)} \right) \\ & \;\;\;\;\;\;\; - k_{2} \left( {x_{n} - V_{0} t} \right)\,\,\, + \beta x_{n}^{3} + \gamma \left[ {\left( {x_{{n + 1}} \left( {t - \tau _{0} } \right) - x_{n} \left( t \right)} \right)^{3} - \left( {x_{n} \left( t \right) - x_{{n - 1}} \left( {t - \tau _{0} } \right)} \right)^{3} } \right] + \alpha \dot{x}_{n} - \frac{{F_{0} }}{m} \\ \end{aligned}$$

(5)

with

$$\begin{aligned} \beta = & \frac{{k_{p} \varepsilon }}{{2mb^{2} }},\gamma = \frac{{k_{c} \varepsilon }}{{2mb^{2} }},k_{1} = \frac{{k_{c} }}{m} \\ k_{2} = & \frac{{k_{p} }}{m},\,\eta = \frac{C}{m},\,\alpha = \frac{{F_{0} }}{{mV_{c} }}. \\ \end{aligned}$$

(6)

The solution $x_{n}$ can be divided into two parts: an oscillating part $u_{n} \,$ and a non-oscillating part $x_{n}^{\left( 0 \right)}$

$$x_{n} = u_{n} + x_{n}^{{(0)}} \,{\text{with}}\,x_{n}^{{(0)}} = a_{n} + b_{n} t$$

(7)

The oscillating part is given by:

$$\begin{gathered} \ddot{u}_{n} = - k_{1} \left( {u_{n + 1} \left( {t - \tau_{0} } \right) - 2u_{n} \left( t \right) + u_{n - 1} \left( {t - \tau_{0} } \right)} \right) - \eta \left( {\dot{u}_{n + 1} \left( {t - \tau_{0} } \right) - 2\dot{u}_{n} \left( t \right) + \dot{u}_{n - 1} \left( {t - \tau_{0} } \right)} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\, - k_{2} u_{n} + \alpha \dot{u}_{n} \, + \gamma \left[ {\left( {u_{n + 1} \left( {t - \tau_{0} } \right) - u_{n} \left( t \right)} \right)^{3} - \left( {u_{n} \left( t \right) - u_{n - 1} \left( {t - \tau_{0} } \right)} \right)^{3} } \right] + \beta u_{n}^{3} \hfill \\ \end{gathered}$$

(8)

Equation (8) represents a delay differential equation (DDE). It is almost impossible to solve this equation analytically; however, near exact solutions can be obtained using perturbation methods. In order to determine the order of the different terms, we introduce the variable

$$u_{n} = \varepsilon \rho_{n} ,$$

(9)

where $\varepsilon < < 1$. In a regime of weakening frictional force between tectonic plates $\alpha$ is considered to be perturbed at the order $\varepsilon^{2}$. In the case of a weakly dissipative medium, we consider the perturbation of the damping coefficient to be $\left( {\eta \leftarrow \eta_{0} + \varepsilon^{2} \eta } \right)$. Equation (8) becomes

$$\begin{gathered} \ddot{\rho }_{n} = - k_{1} \left( {\rho_{n + 1} \left( {t - \tau_{0} } \right) - 2\rho_{n} \left( t \right) + \rho_{n - 1} \left( {t - \tau_{0} } \right)} \right) - \left( {\eta_{0} + \varepsilon^{2} \eta } \right)\left( {\dot{\rho }_{n + 1} \left( {t - \tau_{0} } \right) - 2\dot{\rho }_{n} \left( t \right) + \dot{\rho }_{n - 1} \left( {t - \tau_{0} } \right)} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\, - k_{2} \rho_{n} + \varepsilon^{2} \alpha \dot{\rho }_{n} + \varepsilon^{2} \gamma \left[ {\left( {\rho_{n + 1} \left( {t - \tau_{0} } \right) - \rho_{n} \left( t \right)} \right)^{3} - \left( {\rho_{n} \left( t \right) - \rho_{n - 1} \left( {t - \tau_{0} } \right)} \right)^{3} } \right] + \varepsilon^{2} \beta \rho_{n}^{3} \hfill \\ \end{gathered}$$

(10)

We are looking for a soliton made up of carrier waves modulated by an envelope signal, which are called envelope solitons. This type of soliton appears naturally for most weakly dispersive and nonlinear systems, which are described by a wave equation in the small amplitude limit [23]. Since the interactions between adjacent blocks are assumed weak, it is adequate to use multiple scale expansions in the semi-discrete approximation. Thus, the aim of the following section is to find analytically an envelope soliton of Eq. (10).

We will start by describing the multiple scale method in the semi-discrete approximation and then apply it to our model to obtain a complex Ginzburg–Landau (CGL) equation.

3 Multiple scale expansion in the semi-discrete approximation and oscillatory solutions

3.1 Multiple scale expansion in the semi-discrete approximation

The semi-discrete approximation is a perturbation technique in which the carrier waves are kept discrete while the amplitude is treated in the continuum limit [24]. Applying this method allows one to study the modulation of a plane wave caused by nonlinear effects.

We proceed by making a change of variables according to the new space and time scales $X_{i} = \varepsilon^{i} x$ and $T_{i} = \varepsilon^{i} t,$ respectively. Thus, the solution $u_{n} \left( {x,\,t} \right)$ is found as a perturbation series of functions. We consider here that

$$u_{n} \left( {x,\,t} \right) = \sum\limits_{j = 1}^{\infty } {\varepsilon^{j} \rho_{j} \left( {X_{0} ,\,X_{1} ,\,X2,\,.....,\,T_{0} ,\,T_{1} ,T_{2} } \right)} ,$$

(11)

and the derivative operators $\frac{\partial }{\partial t}\,$ and $\frac{\partial }{\partial x}$ are expanded as

$$\frac{\partial }{\partial x} = \frac{\partial }{{\partial X_{0} }} + \varepsilon \frac{\partial }{{\partial X_{1} }} + \varepsilon^{2} \frac{\partial }{{\partial X_{2} }} + 0\left( {\varepsilon^{3} } \right)$$

(12)

$$\frac{\partial }{\partial t} = \frac{\partial }{{\partial T_{0} }} + \varepsilon \frac{\partial }{{\partial T_{1} }} + \varepsilon^{2} \frac{\partial }{{\partial T_{2} }} + 0\left( {\varepsilon^{3} } \right)$$

(13)

3.2 Oscillatory solutions

In this subsection, our interest is focused on the propagation of modulated waves in the system. To do this, we use the semi-discrete approximation [25] to obtain wavelength envelope solitons. This approach allows us to treat properly the carrier wave with its discrete character and to describe the envelope in the continuum approximation. Modulated wave solutions of Eq. (10) are considered of the form

$$\rho_{n} = \Psi_{n} \left( {x,t} \right)e^{{i\theta_{n} }} + \Psi^{*}_{n} \left( {x,t} \right)e^{{ - i\theta_{n} }}$$

(14)

where $\theta_{n} = qan - \omega t$ is the phase of the soliton. The parameters $q,a\,$ and $\omega$ are the wave number, the distance of neighboring blocks and the optical frequency of the linear approximation of blocks vibrations. The amplitude $\Psi_{n}$ will be considered slowly changing in space and time. Applying now the continuum limit approximation on these amplitudes will yield $\Psi_{n}$ becoming $\Psi \left( {x,t} \right)$. $\Psi_{n \pm 1}$ is obtained at $a^{2}$ by Taylor expansion

$$\Psi_{n \pm 1} = \Psi \pm a\frac{\partial \Psi }{{\partial x}} + \frac{{a^{2} }}{2}\frac{\partial \Psi }{{\partial x^{2} }} + 0\left( {a^{3} } \right)$$

(15)

Introduction of $\rho_{n}$ and its derivatives into Eq. 10 yields a series of equations distinguished by the power of $\varepsilon$.

At the order $\varepsilon^{0}$, one obtains the dispersion relation of linear waves of the system made up of Eq. (17) (see Fig. 2):

$$\omega^{2} + 2i\eta \omega + 2\left( {k_{1} - i\eta \omega } \right)\cos \left( {qa} \right)e^{{i\omega \tau_{0} }} - 2k_{1} - k_{2} = 0$$

(16)

Fig. 2

a Angular frequency. b Three-dimensional representation of the angular frequency. c The evolution of the group velocity. d Three-dimensional representation of the group velocity in terms of wave number $q$, as function of the time delay parameter. Parameters chosen are $k_{1} = k_{2} = 1.0,\,\eta_{0} = 0.6,\,a = 1.0$

Let us consider $\omega \tau_{0} < < 1$. In this approximation, one obtains the angular frequency.

$$\omega = \omega_{r} + i\omega_{i} ,\,\omega_{r} = \omega_{0} \sqrt {1 - \frac{{\gamma_{1}^{2} }}{{4\omega_{0}^{2} }}} ,\,\omega_{i} = - \frac{{\gamma_{1} }}{2},$$

(17)

where

$$\gamma_{1} = \frac{{2\left( {k_{1} \tau_{0} \cos \left( {qa} \right) + 2\eta_{0} \sin^{2} \left( {qa/2} \right)} \right)}}{{1 + 2\eta_{0} \tau_{0} \cos \left( {qa} \right)}},\,\omega_{0}^{2} = \frac{{k_{2} + 4k_{1} \sin^{2} \left( {qa/2} \right)}}{{1 + 2\eta_{0} \tau_{0} \cos \left( {qa} \right)}}.$$

(18)

$\omega_{0}$ is the angular frequency of vibrations of block in the absence of damping, and the parameter $\gamma_{1}$ is the dissipative term due to damping and time delay.

At the order $\varepsilon^{1}$, we obtain the group velocity (see Fig. 3) as.

$$V_{g} = V_{g,r} + iV_{g,i} ,\,V_{g,r} = \frac{{\gamma_{r} \mu_{r} + \gamma_{i} \mu_{i} }}{{\mu_{r}^{2} + \mu_{i}^{2} }},\,V_{g,i} = \frac{{\gamma_{i} \mu_{r} - \gamma_{r} \mu_{i} }}{{\mu_{r}^{2} + \mu_{i}^{2} }},$$

(19)

where

$$\begin{gathered} \mu _{r} = \,2\eta _{0} \left( {1 - e^{{ - \omega _{i} \tau _{0} }} \cos \left( {qa} \right)\cos \left( {\omega _{r} \tau _{0} } \right)} \right),\, \hfill \\ \mu _{i} = \,\omega _{r} - 2\eta _{0} e^{{ - \omega _{i} \tau _{0} }} \cos \left( {qa} \right)\sin \left( {\omega _{r} \tau _{0} } \right), \hfill \\ \end{gathered}$$

(20)

$$\begin{gathered} \gamma _{r} = \,2a\eta _{0} \left( {\omega _{r} \cos \left( {\omega _{r} \tau _{0} } \right) - \omega _{i} \sin \left( {\omega _{r} \tau _{0} } \right)} \right)e^{{ - \omega _{i} \tau _{0} }} , \hfill \\ \gamma _{i} = \,2ak_{1} \sin \left( {qa} \right) + 2a\eta _{0} \left( {\omega _{i} \cos \left( {\omega _{r} \tau _{0} } \right) + \omega _{r} \sin \left( {\omega _{r} \tau _{0} } \right)} \right)e^{{ - \omega _{i} \tau _{0} }} . \hfill \\ \end{gathered}$$

(21)

Fig. 3 

Dissipation coefficients evolution in terms of the wave number $q$ in a 2 D for different values of time delay $\tau_{0}$ and b 3D representations. Parameter chosen are $k_{1} = k_{2} = 1.0,\,\eta_{0} = 0.6,\,$$\eta = 0.01,\,\alpha = 0.5,\,$$\gamma = 0.1,\,\beta = 0.1,\,a = 1.0$

By going into the reference frame moving with the group velocity $V_{g}$ in which waves seem to be stationary, we collect the terms of $\varepsilon^{2}$ and we set

$$y = X_{1} - V_{g} T_{1} ,\,\tau = \varepsilon T_{1} .$$

(22)

By exploiting the transformation (Eq. 22), we obtain the complex Ginzburg–Landau (Eq. 23) that describes the evolution of a packet wave.

$$i\frac{\partial \Psi }{{\partial \tau }} + P\frac{{\partial^{2} \Psi }}{{\partial y^{2} }} + Q\left| \Psi \right|^{2} \Psi + iR\Psi = 0,$$

(23)

with

$$P = P_{r} + iP_{i} ,$$

(24)

$$Q = Q_{r} + iQ_{i} ,\,$$

(25)

$$R = R_{r} + iR_{i} ,\,$$

(26)

$$\,\,P_{r} = \frac{{b_{r} a_{i} - a_{r} b_{i} }}{{a_{r}^{2} + a_{i}^{2} }},\,\,\,$$

(27)

$$P_{i} = \frac{{a_{i} b_{i} + a_{r} b_{r} }}{{a_{r}^{2} + a_{i}^{2} }},\,$$

(28)

$$Q_{r} = \frac{{d_{r} a_{i} - d_{i} a_{r} }}{{a_{r}^{2} + a_{i}^{2} }},$$

(29)

$$Q_{i} = \frac{{d_{r} a_{r} + d_{i} a_{i} }}{{a_{r}^{2} + a_{i}^{2} }},$$

(30)

$$R_{r} = \frac{{c_{r} a_{r} + c_{i} a_{i} }}{{a_{r}^{2} + a_{i}^{2} }},$$

(31)

$$R_{i} = \frac{{c_{i} a_{r} - c_{r} a_{i} }}{{a_{r}^{2} + a_{i}^{2} }},$$

(32)

$$a_{r} = \omega_{i} - 2\eta_{0} \cos \left( {qa} \right)\cos \left( {\omega_{r} \tau_{0} } \right)e^{{ - \omega_{i} \tau_{0} }} ,$$

(33)

$$a_{i} = - \omega_{r} - 2\eta_{0} \cos \left( {qa} \right)\sin \left( {\omega_{r} \tau_{0} } \right)e^{{ - \omega_{i} \tau_{0} }} ,$$

(34)

$$\begin{gathered} b_{r} = V_{g,r}^{2} - V_{g,i}^{2} - 2\eta_{0} a\sin \left( {qa} \right)\left( {V_{g,r} \sin \left( {\omega_{r} \tau_{0} } \right) + V_{g,i} \cos \left( {\omega_{r} \tau_{0} } \right)} \right)e^{{ - \omega_{i} \tau_{0} }} \hfill \\ \,\,\,\,\,\,\, + a^{2} \left[ {\eta_{0} \left( {\omega_{r} \cos \left( {\omega_{r} \tau_{0} } \right) - \omega_{i} \sin \left( {\omega_{r} \tau_{0} } \right)} \right) - k_{1} \cos \left( {\omega_{r} \tau_{0} } \right)} \right]\cos \left( {qa} \right)e^{{ - \omega_{i} \tau_{0} }} , \hfill \\ \end{gathered}$$

(35)

$$\begin{gathered} b_{i} = 2V_{g,r} V_{g,i} + 2a\eta_{0} \sin \left( {qa} \right)\left( {V_{g,r} \cos \left( {\omega_{r} \tau_{0} } \right) - V_{g,i} \sin \left( {\omega_{r} \tau_{0} } \right)} \right)e^{{ - \omega_{i} \tau_{0} }} \hfill \\ \,\,\,\,\,\,\,\, + a^{2} \left[ {\eta_{0} \omega_{i} \left( {\omega_{r} \sin \left( {\omega_{r} \tau_{0} } \right) + \omega_{i} \cos \left( {\omega_{r} \tau_{0} } \right)} \right) - k_{1} \sin \left( {\omega_{r} \tau_{0} } \right)} \right]\cos \left( {qa} \right)e^{{ - \omega_{i} \tau_{0} }} , \hfill \\ \end{gathered}$$

(36)

$$c_{r} = 2\eta \left( {\omega_{r} \cos \left( {qa} \right)\cos \left( {\omega_{r} \tau_{0} } \right)e^{{ - \omega_{i} \tau_{0} }} - \omega_{i} \left( {1 - \cos \left( {qa} \right)\sin \left( {\omega_{r} \tau_{0} } \right)e^{{ - \omega_{i} \tau_{0} }} } \right)} \right) + \alpha \omega_{r} ,$$

(37)

$$c_{i} = 2\eta \left( {\omega_{i} \cos \left( {qa} \right)\sin \left( {\omega_{r} \tau_{0} } \right)e^{{ - \omega_{i} \tau_{0} }} + \omega_{r} \left( {1 - \cos \left( {qa} \right)\cos \left( {\omega_{r} \tau_{0} } \right)e^{{ - \omega_{i} \tau_{0} }} } \right)} \right) + \alpha \omega_{i} ,$$

(38)

$$d_{r} = 3\beta + 12\gamma \sin \left( {qa} \right)\sin \left( {\omega_{r} \tau_{0} } \right)e^{{ - \omega_{i} \tau_{0} }} ,$$

(39)

$$d_{i} = 12\gamma \left( {\cos \left( {\omega_{r} \tau_{0} } \right)e^{{ - \omega_{i} \tau_{0} }} - \cos \left( {qa} \right)\cos \left( {2\omega_{r} \tau_{0} } \right)e^{{ - 2\omega_{i} \tau_{0} }} } \right)\sin \left( {qa} \right),$$

(40)

The variations of the dispersion relation and the group velocity with respect to the wave vector $q$ are represented in Fig. 2. In Fig. 2, we remark that the angular frequency (Fig. 2a, b) and group velocity (Fig. 2c, d) increase with increasing time delay $\tau_{0}$. This clearly shows that when the time delay increases, the seismic wave propagates more quickly in the rock medium. We also note that for nonzero time delay the group velocity (Fig. 2c) is positive. The seismic wave propagates to the $y$ positive direction. In order to show the effect of the time delay parameter, damping coefficient and damping perturbed parameter on the dissipation coefficients, we display the dissipation coefficient versus the wave number on these parameters in Figs. 3, 4, 5.

Fig. 4

Dissipation coefficients evolution in terms of the wave number $q$ in a 2 D for different values of damping $\eta_{0}$ and b 3D representations. Parameters are the same as in Fig. 3, but $\tau_{0} = 0.1$

Fig. 5

Dissipation coefficients as the functions of the wave number $q$ in a 2 D for different values of perturbed damping coefficient $\eta$ and b 3D representations. Parameters are the same as in Fig. 3, but $\tau_{0} = 0.1$

In Fig. 3, we note that the real dissipative coefficient is negative when time delay varies. We also note that the real dissipative coefficient is positive for negative values of perturbation damping coefficient $\eta$ and negative for positive values of $\eta$ (Fig. 5).

4 Modulational instability

Several nonlinear systems like spring block exhibit an instability that leads to a self-induced modulation of an input plane wave with the subsequent generation of localized pulses [26]. In this section, we are looking for conditions under which a plane wave propagating in the spring-block model of the earthquake is stable or unstable to a small perturbation. The instability of the plane wave will generate amplitude-modulated waves. Hence, we are searching for a plane wave in the form (Eq. 41)

$$\Psi \left( {y,\tau } \right) = \Psi_{0} \exp \left[ {i\left( {vy - \Lambda \tau } \right)} \right]e^{ - R\tau } ,$$

(41)

where $\Psi_{0}$ is the complex amplitude, $v$ the wave number and $\Lambda \,$ the wave frequency. Substituting Eq. (41) into Eq. (23), we obtained the nonlinear dispersion relation of the plane wave given by Eq. (42)

$$\begin{gathered} \Lambda = P_{r} \nu^{2} - Q_{r} \left| {\Psi_{0} } \right|^{2} e^{{ - 2R_{r} \tau }} , \hfill \\ P_{i} \nu^{2} - Q_{i} \left| {\Psi_{0} } \right|^{2} e^{{ - 2R_{r} \tau }} = 0, \hfill \\ \end{gathered}$$

(42)

Equation (42) shows that the angular frequency depends on the wave number, the dissipation coefficient and the wave amplitude. To examine the linear stability of the nonlinear plane wave, we look for a solution in the form [24]

$$\Psi \left( {y,\tau } \right) = \left( {\Psi_{0} + B\left( {y,} \right)} \right)\exp \left[ {i\left( {\nu y - \Lambda \tau } \right) + \phi \left( {y,\tau } \right)} \right]e^{ - R\tau } ,$$

(43)

where $B\left( {y,\tau } \right)\,$ is the amplitude perturbation and $\phi \left( {y,\tau } \right)$ the phase perturbation.

Inserting Eq. (42) into Eq. (23), and neglecting the nonlinear terms, a separation of the real part from the imaginary leads to the following two coupled linear differential equations:

$$\begin{gathered} P_{r} \frac{{\partial^{2} B}}{{\partial y^{2} }} - 2P_{i} \nu \frac{\partial B}{{\partial y}} + 2Q_{r} \left| {\Psi_{0} } \right|^{2} e^{{ - 2R_{r} \tau }} B - \left( {\frac{\partial \phi }{{\partial \tau }} + P_{i} \frac{{\partial^{2} \phi }}{{\partial y^{2} }} + 2P_{r} \nu \frac{\partial \phi }{{\partial y}}} \right)\Psi_{0} = 0, \hfill \\ \frac{\partial B}{{\partial \tau }} + P_{i} \frac{{\partial^{2} B}}{{\partial y^{2} }} + 2P_{r} \nu \frac{\partial B}{{\partial y}} + 2Q_{i} \left| {\Psi_{0} } \right|^{2} e^{{ - 2R_{r} \tau }} B + \left( {P_{r} \frac{{\partial^{2} \phi }}{{\partial y^{2} }} - 2P_{i} \nu \frac{\partial \phi }{{\partial y}}} \right)\Psi_{0} = 0, \hfill \\ \end{gathered}$$

(44)

and the solution of Eq. (44) can be taken as

$$B = B_{0} \exp \left[ {i\left( {Ky + \Omega \tau } \right)} \right] + c.c.,$$

(45)

$$\phi = \phi_{0} \exp \left[ {i\left( {Ky + \Omega \tau } \right)} \right] + c.c.,$$

(46)

where $B_{0} \,$ and $\phi_{0}$ are the real constant; $K$ and $\,\Omega$ are the wave number and the angular frequency, respectively, of the perturbation. Insertion of Eqs. (45) and (46) into Eq. (44) results in a linear homogeneous system for $B_{0} \,$ and $\phi_{0}$:

$$\left\{ \begin{gathered} \left( { - P_{r} K^{2} - i2P_{i} K\nu + 2Q_{r} \left| {\Psi_{0} } \right|^{2} e^{{ - 2R_{r} \tau }} } \right)B_{0} + \left( {i\Omega + P_{i} K^{2} - i2P_{r} K\nu } \right)\Psi_{0} \phi_{0} = 0, \hfill \\ \left( { - i\Omega - P_{i} K^{2} + i2P_{r} K\nu + 2Q_{i} \left| {\Psi_{0} } \right|^{2} e^{{ - 2R_{r} \tau }} } \right)B_{0} + \left( { - P_{r} K^{2} - i2P_{i} K\nu } \right)\Psi_{0} \phi_{0} = 0. \hfill \\ \end{gathered} \right.$$

(47)

System (47) has non-trivial solutions if the angular frequency obeys the relation

$$\Omega^{2} - \left( {\kappa_{r} + i\kappa_{i} } \right)\Omega + \rho_{r} + i\rho_{r} = 0$$

(48)

with

$$\begin{gathered} \kappa _{i} = \,4P_{r} K\nu ,\, \hfill \\ \kappa _{r} = \,2\left( {P_{i} K^{2} - Q_{i} \left| {\Psi _{0} } \right|^{2} e^{{ - 2R_{r} \tau }} } \right), \hfill \\ \end{gathered}$$

(49)

$$\begin{gathered} \rho _{r} = \,2P_{i}^{2} K^{2} \nu ^{2} - P_{r}^{2} K^{4} - 2P_{r} Q_{r} \left| {\Psi _{0} } \right|^{2} e^{{ - 2R_{r} \tau }} , \hfill \\ \rho _{i} = \,4P_{i} Q_{r} K\nu \left| {\Psi _{0} } \right|^{2} e^{{ - 2R_{r} \tau }} - 4P_{r} P_{i} K^{3} \nu , \hfill \\ \end{gathered}$$

(50)

The discriminant of Eq. (48) is given by

$$\Delta = \Delta_{r} + i\Delta_{i}$$

(51)

with

$$\begin{gathered} \Delta_{r} = 4\left( {P_{r}^{2} - P_{i}^{2} } \right)K^{4} + 8\left( {P_{r}^{2} - P_{i}^{2} } \right)K^{2} \nu^{2} - 4Q_{i}^{2} \left| {\Psi_{0} } \right|^{4} e^{{ - 4R_{r} \tau }} + 8\left( {P_{r} Q_{r} + P_{i} Q_{i} } \right)K^{2} \left| {\Psi_{0} } \right|^{2} e^{{ - 2R_{r} \tau }} , \hfill \\ \Delta_{i} = 32P_{r} P_{i} K^{3} \nu - 16\left( {P_{r} Q_{i} + P_{i} Q_{r} } \right)K\nu \left| {\Psi_{0} } \right|^{2} e^{{ - 2R_{r} \tau }} , \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \hfill \\ \end{gathered}$$

(52)

The solution of Eq. (48) depends on the sign of the imaginary part of the discriminant.

If $\Delta_{i} > 0$ the solution of Eq. (48) is given by

$$\Omega_{1} = \left( {\kappa_{r} - h_{1} + i\left( {\kappa_{i} - h_{2} } \right)} \right)/2,$$

(53)

$$\Omega_{2} = \left( {\kappa_{r} + h_{1} + i\left( {\kappa_{i} + h_{2} } \right)} \right)/2,$$

(54)

where

$$h_{1} = \sqrt {\left( {\Delta_{r} + \sqrt {\Delta_{r}^{2} + \Delta_{i}^{2} } } \right)/2} ,$$

(55)

$$h_{2} = \sqrt {\left( { - \Delta_{r} + \sqrt {\Delta_{r}^{2} + \Delta_{i}^{2} } } \right)/2} .$$

(56)

If $\Delta_{i} < 0$ the solution of Eq. (55) is given by

$$\Omega_{1} = \left( {\kappa_{r} + h_{1} + i\left( {\kappa_{i} - h_{2} } \right)} \right)/2,$$

(57)

$$\Omega_{2} = \left( {\kappa_{r} - h_{1} + i\left( {\kappa_{i} + h_{2} } \right)} \right)/2.$$

(58)

From Eq. 53, 54, 57 and 58, the angular frequency can be written as $\Omega = \Omega_{0} + i\sigma \,$, where $\Omega_{0}$ being its real part and $\sigma$ its imaginary part, also known as the growth rate of the instability. Thus, the perturbation wave in Eq. (44) and Eq. (45) can be rewritten as

$$B\left( {y,\tau } \right) = B_{0} e^{ - \sigma \tau } e^{{i\left( {ky + \Omega_{0} \tau } \right)}} + c.c.,\,\,\,\,\,\,\,\,\,\,\,\phi \left( {y,\tau } \right) = \phi_{0} e^{ - \sigma \tau } e^{{i\left( {ky + \Omega_{0} \tau } \right)}} + c.c.,$$

(59)

The behavior of the wave propagating in the media is related to the sign of $\sigma$. For $\sigma < 0$, the perturbation amplitude of the wave grows exponentially with time. In this case, the perturbation amplitude will no longer disappear; it will affect continuously the amplitude of earthquake nonlinear waves. The system becomes unstable, leading to earthquake pattern formation through the system and related energy.

For $\sigma > 0$, the small perturbation in the amplitude of the earthquake waves will vanish after short time propagation. The amplitude of the waves will remain constant, showing the stability character of the system.

The modulational instability criterion related to the CGL equation is given by [25, 27]

$$P_{r} Q_{r} + P_{i} Q_{i} > 0.$$

(60)

Equation (60) is a generalization of the Lange and Newell’s [28] modulational instability criterion for physical systems governed the CGL equation.

Figures 6, 7, 8 give the effects of the time delay $\tau_{0}$(Fig. 6), the damping coefficient $\,\eta_{0}$ (Fig. 7) and the nonlinear elastic parameter $\gamma$(Fig. 8) on the product $P_{r} Q_{r} + P_{i} Q_{i}$. The system is stable if this product is negative and unstable if it is positive.

Fig. 6

Schematic representation of the product $P_{r} Q_{r} + P_{i} Q_{i}$ a 2D in terms of the wave number, for different values of the time delay and b 3D as a function of the wave number and the time delay. Parameters chosen are the same as in Fig. 3

Fig. 7

Schematic representation of the product $P_{r} Q_{r} + P_{i} Q_{i}$ a 2D in terms of the wave number, for different values of the damping coefficient and b 3D as a function of the wave number and the damping coefficient. Parameters chosen are the same as in Fig. 4

Fig. 8

Schematic representation of the product $P_{r} Q_{r} + P_{i} Q_{i}$ a 2D in terms of the wave number, for different values of the nonlinear elastic parameter and b 3D as a function of the wave number and the nonlinear elastic parameter. Parameters chosen are the same as in Fig. 4

The local growth rate of the modulational instability or the gain is then given by

$$G\left( K \right) = \min \left( {\left| {{\text{Im}} \left( \Omega \right)} \right|} \right) = \left| {\kappa_{i} - h_{2} } \right|.$$

(61)

The growth rate of the instability is plotted in Figs. 9, 10 and 11. We observe that changes in the time delay (Fig. 9), the nonlinear cubic elastic coefficient (Fig. 10), the damping coefficient (Fig. 11a), the distance of neighboring blocks (Fig. 11b) and the spring stiffness (Fig. 11c, d) affect the modulation gain in the system. We also observed that the maximum value of $G\left( K \right)$ decreases with an increase the parameters $\tau_{0}$ (Fig. 9), $a,\,k_{1} ,k_{2}$ (Fig. 11b–d), and $G\left( K \right)$ increases with an increase $\beta$(Fig. 10) and $\eta_{0}$(Fig. 11a).

Fig. 9

a Gain spectrum in 2D representation versus the wave number of the perturbation wave for different values of time delay, b Three-dimensional representation of the gain as a function of wave number and the nonlinear cubic elastic coefficient $\beta$. Parameters chosen are $k_{1} = k_{2} = 1.0,\,\eta_{0} = 0.6,\,\eta = 0.2,\,\alpha = 0.5,\,\beta = 10.0,\,\gamma = - 0.3,\,a = 0.8,\,\left| {\Psi_{0} } \right| = 1.0,\,\tau = 10^{ - 4}$

Fig. 10

a Gain spectrum in 2D representation versus the wave number of the perturbation wave for different values of $\beta$, b Three-dimensional representation of the gain as a function of wave number and the nonlinear cubic elastic coefficient $\beta$. Parameters chosen are the same as in Fig. 9 but $\tau_{0} = 0.2.$

Fig. 11

Gain spectrum in 2D representation versus the wave number of the perturbation wave for different values of a $\eta_{0}$, b $a$, c $k_{1}$ and d $k_{2}$. Parameters chosen are the same as in Fig. 10

The presence of time delay decreases the amplitude of the perturbation growth rate. This means that the introduction time delay in the spring-block model of earthquake can play the same role as the viscosity of a fault which plays a crucial role in the transmission of a movement along the fault [12]. The cubic elastic coefficient $\beta$, the damping coefficient $\eta_{0}$, the spring’s stiffness $k_{1} ,\,k_{2}$ and the distance of neighboring blocks $a$ affect considerably the bandwidth of modulation instability (MI). From the viewpoint of seismology, these findings indicate a key role in the interaction among different parts of a compound fault in the generation of seismogenic motion. This feature could have significant implications. In an earthquake analogy, the stability of the seismic fault can be controlled through the rock properties which vary from one zone to another.

The gain spectrum is equal to zero at the critical value $K_{{{\text{cri}}}}$ of the wave number. This critical value corresponds to the transition point from instability to stability domain. The system is unstable when $0 < K < K_{{{\text{cri}}}}$ and becomes stable when $K > K_{{{\text{cri}}}}$.

The critical value $K_{{{\text{cri}}}}$ decreases with increasing the parameters $\eta_{0} ,\,a\,$ and $k_{1}$ (see Fig. 11). It increases with increasing the nonlinear coefficient $\beta \,$(see Fig. 10) and the spring stiffness $k_{2}$. The critical value $K_{{{\text{cri}}}}$ remained unchanged when the time delay increases (see Fig. 9). Increasing the critical value of the wave number increases the instability bandwidth $\left[ {0,\,K_{{{\text{cri}}}} } \right]$ (domain in which the imaginary part of the angular frequency is negative). All this shows that the stability of the system strongly depends on the parameters of the system. To appreciate this influence, we draw in the following the parameters diagram of stability. Figure 12 shows the parameters diagram in which the imaginary part of the angular frequency can be negative or positive. This diagram shows that the earthquake wave is unstable for the parameter selected in the red domain and stable in the green domain of the diagram. In the all above, the instability modulational in the spring-block model of earthquake strongly depends on interaction between the blocks, the viscous damping and the nonlinear character of the spring.

Fig.12

Stability/instability diagram in the parameters planes a$\left( {\tau_{0} ,K} \right)\,$, b$\left( {\tau_{0} ,\beta } \right)$, c$\left( {\tau_{0} ,\eta } \right)\,$ d $\left( {\tau_{0} ,\eta_{0} } \right)$ e$\left( {\tau_{0} ,k_{1} } \right)\,$, f $\left( {\tau_{0} ,k_{2} } \right)$ and g $\left( {\tau_{0} ,a} \right)$ with $k_{1} = k_{1} = 1.0,\,\eta_{0} = 0.5,\,\alpha = 0.5,\,a = 0.8,\,\beta = 10,\,,\,\gamma = 0.2,\,$ $\tau = 10^{ - 4} ,\,$ $K = \pi /2$ and $q = \pi /4$. System is stable in the green domain and unstable in the red domain of the diagram

5 Nonlinear solution of the equation of motion

The form of the dissipative envelope soliton solution of Eq. (23) will be given by [29]:

$$\Psi \left( {y,\tau } \right) = \frac{{A_{0} e^{{ - iR_{i} \tau }} e^{\theta } }}{{\left[ {1 + e^{{\theta + \theta^{*} }} } \right]^{1 + i\delta } }},$$

(62)

where $\theta = \left( {\ell_{r} + i\ell_{i} } \right)y - \left( {\lambda_{r} + i\lambda_{i} } \right)\tau$.

Substituting of (Eq. 62) into (Eq. 23), we obtain

$$\begin{gathered} \ell_{r}^{2} = \frac{{3R_{r} \mho }}{{2Q_{i} - \left( {1 + \delta^{2} } \right)\mho P_{i} }},\,\left| {A_{0} } \right|^{2} = \frac{{4\ell_{r}^{2} }}{\mho },\,\ell_{i} = \delta \ell_{r} ,\,\lambda_{r} = 0,\, \hfill \\ \lambda_{i} = \ell_{r}^{2} \left[ {2\delta P_{i} - \left( {1 - \delta^{2} } \right)P_{r} } \right],\,\mho = \frac{{P_{r} Q_{r} + P_{i} Q_{i} }}{{\left( {2 - \delta^{2} } \right)\left| P \right|^{2} }}. \hfill \\ \end{gathered}$$

(63)

$$\begin{gathered} \delta = \mathchar'26\mkern-10mu\lambda \pm \left( {2 + \mathchar'26\mkern-10mu\lambda ^{2} } \right)^{{1/2}} , \hfill \\ \mathchar'26\mkern-10mu\lambda = \frac{{P_{r} Q_{r} + P_{i} Q_{i} }}{{2\left( {P_{r} Q_{i} - P_{i} Q_{r} } \right)}}. \hfill \\ \end{gathered}$$

(64)

The dark form of soliton solution of Eq. (30) will be given by [26]:

$$\Psi \left( {y,\tau } \right) = A_{0} e^{{ - iR_{i} \tau }} e^{{i\left( {Ky - \Omega \tau } \right)}} \frac{{1 - e^{2\ell y} }}{{\left[ {1 + e^{2\ell y} } \right]^{1 + i\delta } }},$$

(65)

and substituting (Eq. 65) into the amplitude equation (Eq. 23), one obtains

$$\begin{gathered} K = \delta \ell ,\,\,\Omega = K^{2} P_{r} - Q_{r} \left| {A_{0} } \right|^{2} ,\,\,\ell^{2} = - R_{r} \mho \left( {Q_{i} + \delta^{2} \mho Pi} \right), \hfill \\ \left| {A_{0} } \right|^{2} = \left( {R_{r} + K^{2} P_{i} } \right)/Q_{i} ,\,\, \hfill \\ \end{gathered}$$

(66)

$$\begin{gathered} \delta = \mathchar'26\mkern-10mu\lambda + \left( {2 + \mathchar'26\mkern-10mu\lambda^{2} } \right)^{1/2} , \hfill \\ \mathchar'26\mkern-10mu\lambda = \frac{{P_{r} Q_{r} + P_{i} Q_{i} }}{{2\left( {P_{r} Q_{i} - P_{i} Q_{r} } \right)}}. \hfill \\ \end{gathered}$$

(67)

The solution of (Eq. 8) is given by using (Eqs.62 and 65), and then inserting the expression

$$u_{n} \left( {x,t} \right) = \varepsilon \Psi \left( {x,t} \right)\exp \left[ {i\left( {qan - \omega t} \right)} \right]$$

(68)

The bright solution and the energy transported by the waves are depicted in Figs. 13 and 14.

Fig. 13

Evolution of the bright soliton with the variation of the time for different values of time delay. The parameters used are $k_{1} = k_{1} = 1.0,\,\eta_{0} = 0.5,\,\alpha = 0.5,\,a = 0.8,\,\beta = 0.5,\,\varepsilon = 0.05,\,\gamma = 0.2$ and $q = 2.5$

Fig. 14

Amplitude soliton $\left| {u_{n} \left( {t,x} \right)} \right|^{2}$ evolution with the variation of the time for different values of time delay. a $\,\tau_{0} = 0.3$ and b $\tau_{0} = 0.6$.The parameters used are $k_{1} = k_{1} = 1.0,\,\eta_{0} = 0.5,\,\alpha = 0.5,\,a = 0.8,\,\beta = 0.5,\,\varepsilon = 0.05,\,\gamma = 0.2$ and $q = 2.5$

These figures show the localized soliton wave having the form of the symmetric envelope soliton. Also, Figs.13 and 14 show that the wave propagation along the fault is affected by time delay. It is obvious from the figures that the time delay decelerates the propagating soliton. The time delay tends to increase the wave amplitude at $t \ne 0.0$.

The evolution of the dark soliton solution is depicted in Figs. 15 and 16. Figure 15 shows that time delay tends to decrease the wave amplitude for fixed time. In Fig. 16, we notice that the magnitude of waves decreases with time delay. This indicates that time delay introduced in our model can contribute to stabilize the fault system. We also observed the increase in the magnitude of the wave in time without time delay introduction.

Fig. 15

Evolution of the dark soliton with the variation of the time for different values of time delay. The parameters used are $k_{1} = k_{1} = 1.0,\,\eta_{0} = 0.05,\,\eta = 0.001,\alpha = 5.0,\,a = 0.4,\,\beta = 0.5,\,\varepsilon = 0.05,\,\gamma = 0.2$ and $q = 2.5$

Fig. 16

Temporal evolution of the dark soliton for different values of time delay. The parameters used are $k_{1} = k_{1} = 1.0,\,\eta_{0} = 0.05,\,\eta = 0.001,\alpha = 5.0,\,a = 0.4,\,\beta = 0.5,\,\varepsilon = 0.05,\,\gamma = 0.2$ and $q = 2.5$

6 Conclusion

The modulational instability of the system was analyzed, and we observed that the magnitude of the modulated waves and the energy generated by the earthquake strongly depend on the time delay, viscous damping coefficient and the nonlinear cubic elastic parameter. We also showed that the time delay decelerates the propagating soliton. In addition, the amplitude of the wave can be influenced by the interaction between the different parts of the fault. Our results showed that the system converges to the stationary state with increasing time delay, indicating its stability. This suggests that the interaction between blocks may cause an oscillation’s death. This oscillation’s death corresponds to the aseismic fault [20]. It also appears from our analyses that the introduction of the time delay may induce transition from an unstable state to a stable one. It is possible that under certain conditions in the earth’s crust or in certain areas, motion along the fault could be suppressed or reduced to aseismic creep. This could have profound implications for earthquake dynamics.

This behavior is most often observed in the lower crust “Plastosphere” where rocks are deformed by flow and also in the fault segments that incorporate the clayey rocks. In these zones, slip is controlled by plastic or viscous yielding [30, 31]. The delay therefore provides under certain condition the effects of viscosity (internal friction) on the propagation of waves in the earth’s crust. From the viewpoint of seismology, these findings indicate a key role of the interaction among different parts of a compound fault in generation of seismogenic motion. The instability bandwidth and the amplitude of the gain spectrum strongly depend on the parameters of the system.