1 Introduction

The article under discussion is intended to give an extension of a known Darcy–Forchheimer flow in porous media with applications in MHD. The new ideas can be mentioned as follows:

  • The introduction of a generalized viscosity law that ends in a p-Laplacian operator.

  • The reformulation of the Darcy-Forchheimer law, with a new independent term, to model the effect of variations in the velocity profile, together with the kinematic conditions close the nanoboundaries induced by the existence of porosity.

The shear stress in a fluid can be described based on the relative motion between fluid layers. Mathematically, and given a velocity scalar function \(v_1\), this can be expressed by a term of the form \(\vert \nabla v_1 \vert ^{p-2}\), where \(p \in \mathbb {R}\). For \(p<2\), the fluid can be considered as non-viscous (for example, superflowing fluids, volatile gases and unsaturated gas flows) For \(p=2\), the flow falls in the category of a Newtonian fluid (typical of air and water flows), while for \(p>2\), the fluid motion is mainly driven by viscosity (porous media flows and oils, for example). Considering the term \(\vert \nabla v_1 \vert ^{p-2}\) to describe the shear stress in a fluid flow, and after making standard operations, the momentum equation is formulated in terms of a p-Laplacian operator.

The use of a p-Laplacian operator in fluid dynamics is not new. It has been used to model filtration in flow of fluids within a porous medium. The works introduced by Smreker, to make further accurate the application of the Darcy’s law, led to a p-Laplacian diffusion (refer to [1, 2]). To support the theoretical analysis introduced by Smreker, Missbach performed important contributions based on experimental works (refer to [3] and the studies referenced therein).

Within a purely mathematical scope, in [4] the authors analyzed the quenching behavior of solution for a p-Laplacian filtration together with different applications. In [5], a similar filtration equation was introduced. In this occasion with a local source to study the existence and blow-up behavior of solutions. Furthermore, in [6], the authors studied a 1-D filtration equation formulated with a free, and physically plausible, parameter. They obtained results about the existence of a boundary layer together with the dependency of such solution and layer with the free parameter. The references mentioned up to now are fully representative of the mathematical techniques employed to study solutions for a p-Laplacian equation, nonetheless we should notice that the literature is vast in this regards (see [7] for an interesting compilation).

In many situations, the researchers have introduced different models supported by the p-Laplacian operator (see the remarkable references [8,9,10]). Bognar [11], considered problems involving fluid mechanics and the p-Laplacian operator. He introduced several methods based on numerical and analytical procedures that are of interest to study nonlinear problems. Diaz and Thelin [12] introduced a turbulent flow in a pipe of porous medium supported by the p-Laplacian operator. They provided different behaviors in the solutions under a weak formulation approach. Douchet [13], provided an analysis about the positive solutions for problems involving discontinuous nonlinearities. Drabek et al. [14], introduced the quasilinear elliptic problem formulated with the p-Laplacian operator and got some existence criteria for global solutions.

Other interesting works can be mentioned dealing with non-Newtonian fluids formulated with the p-Laplacian operator, in particular the studies: [15,16,17]. Additionally, in [18], the authors introduced a general equation to study the Euler fluids. They considered the Benamou–Brenier characterization of Wasserstein-p distances to obtain a generalized constitutive relation, that in turn was based on the Euler–Lagrange equation. The resulting formulation is known as p-Navier–Stokes equation.

The fact of modeling with nonlinear operators is not only linked to the p-Laplacian one. Indeed, in some occasions, a nonlinear diffusion phenomena can be modeled with a porous medium equation constituted by a degenerate diffusivity (see [19, 20] for a wide mathematical treatment). Both, the already cited p-Laplacian and the porous medium equation, are interesting examples of how some mathematical properties, introduced by the mentioned diffusion operators, can permit to model any physical phenomena. Indeed, we may consider the mathematical properties of the p-Laplacian operator to model special kinds of broad diffusion emerging in biology [21,22,23,24,25], as already mentioned in porous flows [26,27,28], glaciology [35] or petroleum extraction [29] .

The equation, motivating our coming analyses, is based on the MHD science that is actually an important area of applications of non-Newtonian fluids. For instance, in [30], the authors provided an interesting mathematical approach to explain the relation between the wave dynamics in a thin film compressible isothermal MHD viscous-plastic fluid and the instabilities. In our case, we will show that the solutions are regular, so that the perturbations introduced will no became unstable (in an asymptotic condition). In addition, in [31], another perturbation approach, named as noisy reduced magnetohydrodynamic (NRMHD) model, was used to predict the turbulent fluctuations in the fluid. Furthermore, in some cases, other physical variables have been considered in MHD fluids. For instance, in [32], the temperature variable is considered to model a heat transfer process in a viscoelastic fluid flowing through a flat plate. There exist other interesting analyses concerning MHD and non-Newtonian fluids, that allow us to remark the vigor of this area of research. Akbar et al. [33] employed an Eyring–Powell MHD fluid to model a two- dimensional flow in a stretching surface. In addition, Bhatti et al. [34] considered, as well, a two-dimensional Erying–Powell MHD fluid, for carrying out the heat transfer analysis by introducing a set of ordinary differential equations.

To introduce the driving equation, firstly consider the known equation of a Darcy–Forchheimer fluid in porous medium and under the MHD scope. The fluid is flowing through the x-axis (then the velocity profile under study varies with the orthogonal spatial variable) and the associated velocity profile under study is considered to be radially symmetric. These hypothesis allow us to consider a velocity vector of the form \({\textbf {V}} = (v_1(y,t), 0, 0),\) so that the equation reads:

$$\begin{aligned} \frac{\partial v_{1}}{\partial t} =-\frac{1}{\rho }\frac{{\mathrm{d}} P}{{\mathrm{d}}x} +\nu \frac{\partial ^{2}v_{1}}{\partial y^{2}} -\left( \frac{\sigma B_{0}^{2}}{\rho }+\frac{\nu }{K}\right) v_{1} -\frac{v_{1}^{2}}{\rho K_{1}}, \end{aligned}$$
(1.1)

where \(\rho \) and \(\nu =\frac{\mu }{\rho }\) refer to the fluid density and kinetic viscosity, respectively, \(\sigma \) is the electrical fluid conductivity, P refers to the fluid pressure distribution in the flowing fluid, K is the permeability (or hydraulic conductivity), \(B_{0}\) is the externally imposed magnetic field that makes the fluid to flow and \(K_{1}\) is the inertial permeability typical in porous medium.

The new model introduced, as an alternative to the last equation, started based on the literature review done by the authors and is supported by the mathematical principles introduced by the p-Laplacian operator (in fact, this operator allows the definition of a finite speed of propagation for compactly supported functions, that can be used to model with accuracy the slow motion of a fluid in porous media). In addition, we introduce a new term, to generalize the well-known Darcy–Forchheimer independent term in (1.1). Such a new term has the form:

$$\begin{aligned} f(v_1) = -\left( \frac{\sigma B_{0}^{2}}{\rho }+\frac{\nu }{K}\right) v_{1}^{b} -\frac{v_{1}^{2}}{\rho K_{1}}, \end{aligned}$$
(1.2)

where \(0<b<1\).

The new term \(v_1^b\) aims at modeling the following idea: Given a set of distributed porous points in the domain, there may be zones where the fluid velocity is almost null to comply with the nanoboundary conditions in the proximity of the porous zones. Under the influence of such nanoboundary, it may be the case that the fluid is perturbed, or simply the velocity changes as a result of a higher external magnetic field applied. Then, the new term \(v_1^b\) can model any fast variation in the velocity profile that can impact the nanoboundary. In addition, the newly introduced p-Laplacian operator exhibits the property of propagating support that, combined with the last mention effect, would lead us to model any possible induced velocity change in the domain characterized by a finite speed (this is important for fluids with p > 2).

As a consequence, the following equation holds:

$$\begin{aligned} \frac{\partial v_{1}}{\partial t} =-\frac{1}{\rho }\frac{{\mathrm{d}}P}{{\mathrm{d}}x} +\nu \frac{\partial }{\partial y}\left( \left( \frac{\partial v_{1}}{\partial y}\right) ^{p-2}\frac{\partial v_{1}}{\partial y}\right) -\left( \frac{\sigma B_{0}^{2}}{\rho }+\frac{\nu }{K}\right) v_{1}^{b} -\frac{v_{1}^{2}}{\rho K_{1}}, \end{aligned}$$
(1.3)

with the non-dimensional variables given by (see [36] and references therein as supporting material):

$$\begin{aligned} v_{1}^{*}= & {} \frac{v_{1}}{v_{0}},\text { } x^{*}=\frac{x}{L}, \text { }y^{*}=\frac{y}{L}, \text { } t^{*}=\frac{v_{0}t}{L}, P^{*}=\frac{P}{\rho v_{0}^{2}}, \, \, R_{e}=\frac{v_{0}L}{\nu },\nonumber \\ M= & {} B_{0}L\sqrt{\frac{\sigma }{\rho \nu }},\,\, A_{1}=\frac{v_{0}^{p-4}}{R_{e}L^{p-2}},\,\,A_{2}=\frac{\nu }{v_{0}K},\,\, A_{3}=\frac{1}{\rho K_{1}}. \end{aligned}$$
(1.4)

The Eq. (1.3) can be rewritten as follows (ignore * for the sake of simplicity):

$$\begin{aligned} \frac{\partial v_{1}}{\partial t} =-\frac{1}{\rho }\frac{{\mathrm{d}}P}{{\mathrm{d}}x} +A_{1} \frac{\partial }{\partial y}\left( \left( \frac{\partial v_{1}}{\partial y}\right) ^{p-2}\frac{\partial v_{1}}{\partial y}\right) -\frac{1}{v_{0}^{1-b}}\left( \frac{M^{2}}{R_{e}}+A_{2}\right) v_{1}^{b} -A_{3}v_{1}^{2}, \end{aligned}$$
(1.5)

where \(y>0,\) \(t>0,\) \(p>1.\)

Making the first differentiation with regards to x,  and integrating, it holds that \(-\frac{1}{\rho }\frac{{\mathrm{d}}P}{{\mathrm{d}}x}=A_{4}.\) Renaming as \(\frac{1}{v_{0}^{1-b}}\left( \frac{M^{2}}{R_{e}}+A_{2}\right) =A_{5}\), the Eq. (1.5) reads

$$\begin{aligned} \frac{\partial v_{1}}{\partial t} =A_{4} +A_{1} \frac{\partial }{\partial y}\left( \left( \frac{\partial v_{1}}{\partial y}\right) ^{p-2}\frac{\partial v_{1}}{\partial y}\right) -A_{5}v_{1}^{b} -A_{3}v_{1}^{2}. \end{aligned}$$
(1.6)

This previous equation constitutes the basis for the coming analyses. We should consider that the equation is formulated with no additional constrains in terms of boundary conditions and geometrical structures. This approach is followed to provide the widest scope and to allow us to provide evidences on new solutions to the involved fluid that can be used in all kind of applications.

Furthermore, we shall consider a bounded and Lebesgue measurable distribution as initial data. This approach is common in fluid flow modeling, so that the results are given under the most general initial data (refer to [3] for additional insights). Essentially, we shall require that the initial distribution is bounded, together with the condition of a finite velocity profile in the sense of the \(L^1\) space.

$$\begin{aligned} v_{1}(y,0)=v_{0}(y)\in L^{\infty }(\mathbb {R})\cap L^{1}(\mathbb {R}). \end{aligned}$$
(1.7)

2 Previous supporting results

The following Propositions 1 and 2 are introduced based on the works in [37, 38] and are reproduced here for convenience.

Proposition 1

Given the basic p-Laplacian equation \(v_{t}=\nabla \cdot \left( \left| \nabla v\right| ^{p-2}\nabla v\right) ,\) in \(\mathbb {R}^d \times (0, T]\), where \(p>1\) with a finite mass of size \(N_{\delta }\) at the origin \(v(y,0)=N_{\delta }\delta (x),\) \(N_{\delta }>0.\) Then; the following solution, in the sense of Barenblatt, holds:

$$\begin{aligned} v(y,t)=t^{-a_{0}}\Big (C_{1}-C_{2}\left| \zeta \right| ^{\frac{p}{p-1}}\Big )_{+}^{\frac{p-1}{p-2}}, \end{aligned}$$
(2.1)

where

$$\begin{aligned} \zeta =y / t^{\frac{a_{0}}{d}},\,\,a_{0}=\Big (p-2+\frac{p}{d}\Big )^{-1},\,\, C_{1}=C_{3}(d,p)N_\delta ^{\beta }, \,\, C_{2}=\Big (\frac{p-2}{p}\Big ) \Big (\frac{a_0}{d}\Big )^{\frac{1}{p-1}}, \,\, \beta =p(p-2)/d(p-1), \end{aligned}$$
(2.2)

and \(C_{3}\) can be obtained based on the mass preserving condition: \(\int v(y,t)dy=N_{\delta .}\)

Proposition 2

Assume that \(v_{0}(y)\in L^{1}(\mathbb {R}^{d}),\) then there exits a time \(T(||v_{0}||_{1})\) and a weak solution for the basic p-Laplacian equation\(v_{t}=\nabla \cdot \left( \left| \nabla v\right| ^{p-2}\nabla v\right) \) in \(0<t\le T(||v_{0}||_{1})\) such that:

$$\begin{aligned} T(||v_{0}||_{1})\le C_{4}(d,p)||v_{0}||_{1}^{-(p-2)}. \end{aligned}$$
(2.3)

Furthermore, if the initial data has compact support, then the following bounds hold for any \(R > 0\):

$$\begin{aligned}&|v(\cdot ,t)|_{1}\le C_{5}(d,p)||v_{0}||_{1}, \end{aligned}$$
(2.4)
$$\begin{aligned}&|v(y,t)|\le C_{6}(d,p)t^{-a_{0}}R^{p(p-2)}||v_{0}||_{1}^{\frac{pa_{0}}{d}},\,\,\,|y|\le R, \end{aligned}$$
(2.5)
$$\begin{aligned}&|\nabla v(y,t)|\le C_{7}(d,p)t^{-\frac{(d+1)a_{0}}{d}}R^{\frac{2}{p-2}}||v_{0}||_{1}^{\frac{2a_{0}}{d}},\,\,\,|y|\le R, \end{aligned}$$
(2.6)

The results, provided in the last propositions, were obtained for \( y \in \mathbb {R}^d\) and they can be made applicable to the one- dimensional case as well. Indeed, the propositions were provided for \(\vert y \vert < R\), that can be similarly obtained, with no formal inconsistency, for \(d = 1\). Furthermore, the constants \(C_3\), \(C_4\) and \(C_5\) are assessed in a ball as per Proposition 2.1 in [37] that can be similarly defined for the case of a one- dimensional spatial variable. Eventually, the results related to the existence and the uniqueness of the solutions are based on assessments in bounded domains (this is balls in \(\mathbb {R}^d\)) that can be made applicable with no formal constrains for the case of \(d=1\).

The following proposition is introduced hereunder to support the regularity analysis to come.

Proposition 3

Consider that a particular flat solution to (1.6) is given by the following expression:

$$\begin{aligned} v_{1} (t)=\frac{1}{A_{3}t}+\frac{\epsilon t^{-b}}{A_{3}^{1+b}(b-2)}+O(\epsilon ^{2}) \end{aligned}$$
(2.7)

where \(A_3\) is a constant defined in (1.4), and \(\epsilon \) is a small parameter that compiles the terms of order two and higher. This solution has been obtained under the assumption of a null pressure gradient at \(y\rightarrow \infty \), i.e., \(A_{4} \sim 0.\)

Proof

For the particular flat solution searching, we take the following time evolution based on (1.6):

$$\begin{aligned} \frac{\partial v_{1}}{\partial t} =-A_{5}v_{1}^{b}-A_{3}v_{1}^{2}, \end{aligned}$$
(2.8)

where \(A_{5}\) is considered as a small parameter. Assuming \(A_{5}=\epsilon \) and using a perturbation technique, the solution of (2.8) is of the form:

$$\begin{aligned} v_{1} (t)=v_{10}+ \epsilon v_{11}+\epsilon ^{2} v_{12}... \end{aligned}$$
(2.9)

After using (2.8), we have

$$\begin{aligned} \frac{\partial }{\partial t}\Big (v_{10}+ \epsilon v_{11}+\epsilon ^{2} v_{12}...\Big ) =-A_{5}\Big (v_{10}+ \epsilon v_{11}+\epsilon ^{2} v_{12}...\Big )^{b}-A_{3}\Big (v_{10}+ \epsilon v_{11}+\epsilon ^{2} v_{12}...\Big )^{2}. \end{aligned}$$
(2.10)

comparing coefficient of \(\epsilon \) and \(\epsilon ^{2},\) we have

$$\begin{aligned} \frac{\partial v_{10}}{\partial t} =-A_{3}v_{10}^{2}, \end{aligned}$$
(2.11)

and

$$\begin{aligned} \frac{\partial v_{11}}{\partial t} =v_{10}v_{10}^{b}-2A_{3}v_{10}v_{11}. \end{aligned}$$
(2.12)

Solving (2.11), we have

$$\begin{aligned} v_{10}=\frac{1}{A_{3}t}. \end{aligned}$$
(2.13)

After using \( v_{10}\) into (2.12), we get

$$\begin{aligned} \frac{\partial v_{11}}{\partial t} +\frac{2}{t}v_{11} =-\frac{t^{-1-b}}{A_{3}^{1+b}}. \end{aligned}$$
(2.14)

The solution of (2.14) is

$$\begin{aligned} v_{11}=\frac{t^{-b}}{A_{3}^{1+b}(b-2)}. \end{aligned}$$
(2.15)

Combining (2.13) and (2.15) with (2.9), the solution of (2.8) is

$$\begin{aligned} v_{1}=\frac{1}{A_{3}t}+\frac{\epsilon t^{-b}}{A_{3}^{1+b}(b-2)} +O(\epsilon )^{2}. \end{aligned}$$
(2.16)

\(\hfill\square \)

3 General discussion about solutions

3.1 On existence and uniqueness of solutions

Theorem 1

Assuming that \(v_{1}(y,t)\ge 0\) is a solution to (1.6) with \(v_{0}\in L^{1}(\mathbb {R})\); then, the following asymptotic convergence holds:

$$\begin{aligned} \lim _{t\rightarrow \infty }\left| v_{1}(y,t)-v(y,t)\right| =0, \end{aligned}$$
(3.1)

uniformly for any \(y \in \mathbb {R}.\)

Proof

Let us consider a smooth test function, \(\phi _7\), satisfying the following regularity condition: \(\phi _{7}\in C^{\infty }([0,T]\times \mathbb {R})\cap L^{\infty }([0,T], W^{1,p}(\mathbb {R}))\). After multiplying the expression (1.6) by \(\phi _{7}\) and making the integration, the following weak formulation holds (see [39] for additional insights):

$$\begin{aligned} \begin{aligned}&\int _{\mathbb {R}}v_{1}(t)\phi _{7}(t) = \int _{\mathbb {R}}v_{1}(0)\phi _{7}(0) \\&\quad +\int _{0}^{t}\int _{\mathbb {R}}\left( v_{1}\frac{\partial \phi _{7}}{\partial t}- A_{1}\left| \frac{\partial v_{1}}{\partial y}\right| ^{p-1}\frac{\partial \phi _{7}}{\partial y}-A_{5}\phi _{7} v_{1}^{b}-A_{3}\phi _{7} v_{1}^{2}+A_{4}\phi _{7}\right) {\mathrm{d}}s. \end{aligned} \end{aligned}$$
(3.2)

The fundamental solution, v,  can be weakly formulated as well

$$\begin{aligned} \int _{\mathbb {R}}v\phi _{7}(t)= \int _{\mathbb {R}}v(0)\phi _{7}(0) +\int _{0}^{t}\int _{\mathbb {R}}\left( v\frac{\partial \phi _{7}}{\partial t}- A_{1}\left| \frac{\partial v}{\partial y}\right| ^{p-1}\frac{\partial \phi _{7}}{\partial y}\right) {\mathrm{d}}s. \end{aligned}$$
(3.3)

Assume a test function of the form

$$\begin{aligned} \phi _{7}(y,t)= \frac{e^{-j_{2}(t)}}{(1+|y|^{2})^{b_{1}}}, \end{aligned}$$
(3.4)

where \(j_{2}(t)\ge 0\) is a Holder continuous function and \(b_{1}>0\) shall be selected for the asymptotic convergence of the involved integrals in the last two weak formulations.

Since v is the fundamental solution, we can make use of Proposition 2 so that the integral in (3.3) can be evaluated as:

$$\begin{aligned} \int _{\mathbb {R}}\left| \frac{\partial v}{\partial y}\right| ^{p-1}\frac{\partial \phi _{7}}{\partial y}{\mathrm{d}}s\le \int _{\mathbb {R}}C_{7}^{p-1}t^{-2a_{0}(p-1)}|y|^{2 +\frac{2}{p-2}}\left\| v_{0}\right\| _{1}^{2a_{0}(p-1)}|-b_{1}| \frac{2|y|e^{-j_{2}(t)}}{(1+|y|^{2})^{b_{1}+1}}. \end{aligned}$$
(3.5)

The convergence in the last integral requires to select \(b_1 \ge b_{2} = \frac{p-1}{2(p-2)}\), then the integral vanishes asymptotically in the test function tail.

Subtracting (3.3) from (3.2) and using the resulting expression in (3.5), we have

$$ \begin{aligned} \int_{\mathbb{R}} {(v_{1} - v)} (t)\phi _{7} (t) & \le \int_{\mathbb{R}} {(v_{1} - v)} (0)\phi _{7} (0) + \int_{0}^{t} {\int_{\mathbb{R}} {(v_{1} - v)} } \frac{{\partial \phi _{7} }}{{\partial t}}{\text{d}}s \\ & \quad - \int_{0}^{t} {\int_{\mathbb{R}} {A_{1} } } \left( {\left| {\frac{{\partial v_{1} }}{{\partial y}}} \right|^{{p - 1}} \frac{{\partial \phi _{7} }}{{\partial y}} - A_{5} \phi _{7} v_{1}^{b} - A_{3} \phi _{7} v_{1}^{2} + A_{4} \phi _{7} } \right){\text{d}}s. \\ \end{aligned} $$
(3.6)

After using Propositions 2 and 3, the following holds:

$$\begin{aligned}&A_{1}\int _{0}^{t}\int _{\mathbb {R}}\left| \frac{\partial v_{1}}{\partial y}\right| ^{p-1}\frac{\partial \phi _{7}}{\partial y}{\mathrm{d}}s\le \int _{0}^{t}\int _{\mathbb {R}}A_{1}\Big (C_{7}^{p-1}t^{-2a_{0}(p-1)}|y|^{2 +\frac{2}{p-2}}\left\| v_{0}\right\| _{1}^{2a_{0}(p-1)}\nonumber \\&\quad +\Big (\frac{1}{A_{3}t}+\frac{\epsilon t^{-b}}{A_{3}^{b+1}(b-2)}+O(\epsilon ^{2})\Big )^{p-1}\Big ) \frac{2|-b_{1}||y|e^{-j_{2}(t)}}{(1+|y|^{2})^{b_{1}+1}}{\mathrm{d}}s \end{aligned}$$
(3.7)

For asymptotic convergence in the involved integrals, we require \(b_{1}\ge b_3 = \frac{p-1}{2(p-2)}.\)

Again, based on Propositions 2 and 3, it holds that

$$\begin{aligned}&\int _{0}^{t}\int _{\mathbb {R}}A_{5}v_{1} \phi _{7}{\mathrm{d}}s\le \int _{0}^{t}\int _{\mathbb {R}}A_{5}\Big (C_{6}t^{-a_{0}}|y|^{ p(p-2)}\left\| v_{0}\right\| ^{pa_{0}}\nonumber \\&\quad +\frac{1}{A_{3}t}+\frac{\epsilon t^{-b}}{A_{3}^{b+1}(b-2)}+O(\epsilon ^{2})\Big ) \frac{e^{-j_{2}(t)}}{(1+|y|^{2})^{b_{1}+1}}{\mathrm{d}}s. \end{aligned}$$
(3.8)

The integral is asymptotically convergent if \(b_{1}\ge b_4 = \frac{p(p-2)}{2}.\)

Using again Proposition 2 and 3, we get that

$$\begin{aligned}\int _{0}^{t}\int _{\mathbb {R}}A_{3}v_{1}^{2} \phi _{7}{\mathrm{d}}s& \le \int _{0}^{t}\int _{\mathbb {R}}A_{3}\Big (C_{6}^{2}t^{-2a_{0}}|y|^{ 2p(p-2)}\left\| v_{0}\right\| ^{2pa_{0}}\nonumber \\&\quad +\left( \frac{1}{A_{3}t}+\frac{\epsilon t^{-b}}{A_{3}^{b+1}(b-2)}+O(\epsilon ^{2})\right) ^{2}\Big ) \frac{e^{-j_{2}(t)}}{(1+|y|^{2})^{b_{1}+1}}{\mathrm{d}}s. \end{aligned}$$
(3.9)

In this case, we shall choose \(b_{1}\ge b_5 = p(p-2).\)

Eventually, the asymptotic convergence of the last term in (3.6) requires to select \(b_1\) such that \(b_{1}\ge b_6 \frac{1}{p-2}.\)

Making an overall compilation of the assessed integrals, any value of \(b_1\) complying with the asymptotic behavior of solutions for (3.6) shall be

$$\begin{aligned} b_{1}\ge \text {max}\left( b_{2}, b_{3}, b_{4}, b_{5}, b_{6}\right) . \end{aligned}$$
(3.10)

Coming again to the expression (3.6) and considering the contraction condition in the space \(L_{1}\) (see [40]):

$$\begin{aligned} \int _{\mathbb {R}}(v_{1}-v)\phi _{7}(t)\le \left\| v_{1}-v\right\| _{1}\left\| \phi _{7}\right\| _{\infty }(t) \le \left\| v_{0}-v_{0}\right\| _{1}\left\| \phi _{7}\right\| _{\infty }(t) +\int _{0}^{t}\epsilon (s)\left\| v_{1}-v\right\| _{1}(s){\mathrm{d}}s,\nonumber \\ \end{aligned}$$
(3.11)

where \(\epsilon (s)=\text {max}_{R}\left\{ \frac{\partial \phi _{7}}{\partial t}\right\} \) and exists given the defined regularity condition in the test function.

Since \(v_{0}(y)\) is a finite mass distribution, i.e., \(\int _R v_{0}=K,\) we can consider a sequence \(\{v_{0,n}\}\) of compactly supported distributions that approximates to \(v_{0}\) with \(0\le v_{0,n}\le v_{0}, \,\, n\in \mathbb {N}.\) Each element in the sequence is finite mass as well, \(\int v_{0,n}=K_{n},\) with \(K_{n}\nearrow K.\)

Assuming now the following scaling (refer to [41] for additional insights):

$$\begin{aligned} T_{k}v_{1}=\frac{1}{k^{a_{0}}}v_{1}\left( \frac{y}{k^{a_{0}}},\frac{t}{k}\right) , \end{aligned}$$
(3.12)

that is introduced as a normalizing scaling to compare any evolution in the sequence departing from each \(\{v_{0,n}\}\). Such evolution sequence of solutions is given by \(\{v_{1,n}\}\), then the following holds:

$$\begin{aligned} \left\| T_{k}(v_{1,n})-T_{k}(v)\right\| _{1}(t)\left\| \phi _{7}\right\| _{\infty }(t) \le \left\| v_{0,n}-v_{0}\right\| _{1}\left\| \phi _{7}\right\| _{\infty }(t) +\int _{0}^{t}\epsilon (s)\left\| v_{1}-v\right\| _{1}(s){\mathrm{d}}s \end{aligned}$$
(3.13)

Consider no the first term on the right-hand side of (3.13), so that the following holds:

$$\begin{aligned} \left\| v_{0,n}-v_{0}\right\| _{1} \le \int v_{0,n}-\int v_{0}=K_{n}-K. \end{aligned}$$
(3.14)

After using the integration over mean values in the last term of (3.13), and using (3.14), we have

$$\begin{aligned} \left( \left\| \phi _{7}\right\| _{\infty }(t)-t\epsilon (\tau )\right) \left\| T_{k}(v_{1,n})-T_{k}(v)\right\| _{1}(t) \le (K_{n}-K)\left\| \phi _{7}\right\| _{\infty }(t). \end{aligned}$$
(3.15)

for an appropriate \(0<\tau <t.\) Making \(n \rightarrow \infty ,\) the convergence of \( \, K_{n}\nearrow K\) and hence \(v_{1,n}\nearrow v_{1}\) hold, leading to:

$$\begin{aligned} \left( \left\| \phi _{7}\right\| _{\infty }(t)-t\epsilon (\tau )\right) \left\| T_{k}(v_{1,n})-T_{k}(v)\right\| _{1}(t) \le 0. \end{aligned}$$
(3.16)

In the asymptotic approach \(1<< k<<t\) then:

$$\begin{aligned} T_{k}(v_{1})=\epsilon (k)v_{1}\left( \frac{y}{k^{a_{0}}},\frac{t}{k}\right) , \,\,\,\,\, T_{k}(v)=\epsilon (k)v\left( \frac{y}{k^{a_{0}}},\frac{t}{k}\right) . \end{aligned}$$
(3.17)

Now, when \(|\epsilon (k)|<<1,\) then (3.17) becomes

$$\begin{aligned} v_{1}(y',t')=v(y',t'), \,\, y'\rightarrow 0,\,\, t'\rightarrow 0, \end{aligned}$$
(3.18)

where \((y',t')\) are the rescaled variables.

Similarly for \(k\rightarrow 0\):

$$\begin{aligned} v_{1}(y'',t'')=v(y'',t''), \,\, y''\rightarrow \infty ,\,\, t''\rightarrow \infty . \end{aligned}$$
(3.19)

Based on the provided arguments, we conclude on the asymptotic convergence of any spatially distributed solution to the fundamental solution. \(\hfill\square \)

Based on the last theorem shown, it is possible to state that given any initial distribution, and the associated solution evolving as per (1.6), the solution behaves asymptotically as the Barenblatt solution given in Proposition 1.

The coming intention is to introduce an analysis about the boundedness of the weak solutions. To this end and previously, it shall be introduced the regularity of the evolution under the weak formulation scope with the test function (3.4). Assume that \(r \gg |y| \gg 1\) and the ball, \(B_{r}\), centered at the origin and with radium r. Consider now the coming problem \(P^{\phi _{7}}\) defined in \([0,T]\times B_{r}\):

$$\begin{aligned} v_{1}\frac{\partial \phi _{7}}{\partial t}- A_{1}\left| \frac{\partial v_{1}}{\partial y}\right| ^{p-1}\frac{\partial \phi _{7}}{\partial y}-A_{3}\phi _{7} v_{1}^{2}+A_{4}\phi _{7}-A_{5}\phi _{7} v_{1}^{b}=0. \end{aligned}$$
(3.20)

Here we consider that the ball \(B_{r}\) has sufficiently smooth boundary \(\partial B_r,\) where the test function satisfies the following null flux condition:

$$\begin{aligned} \nabla \phi _{7}\cdot \pi =0, \end{aligned}$$
(3.21)

where \(\pi \) refers to the unitary normal vector to \(\partial B_r.\) It should be noticed that the initial distribution is bounded, i.e., \(v_{0}(y)\in L^{1}(\mathbb {R})\cap L^{\infty }(\mathbb {R}),\) and the domain \(B_r\) as well. Then, the regularity study of \(P^{\phi _{7}}\) requires us to introduce the following truncatures to control the boundedness of the involved terms:

$$\begin{aligned} v_{1,\vartheta }= \left\{ \begin{array}{cc} v_{1},\,\,\,|v_{1}|< \vartheta \\ \vartheta ,\,\,\,|v_{1}|\ge \vartheta \end{array} \right\} . \end{aligned}$$
(3.22)

Further, the following Lipschitz approximation to the reaction term is introduced as for a generic function g:

$$\begin{aligned} V_{\delta }(g)= \left\{ \begin{array}{cc} \delta ^{b-1}g,\,\,\,0\le g< \delta \\ g^{b},\,\,\,g\ge \delta \end{array} \right\} , \end{aligned}$$
(3.23)

where \(\delta > 0\). Similarly, the following truncatures can be defined for (3.23) leading to:

$$\begin{aligned} V_{\delta ,\vartheta }(g_{\vartheta })= \left\{ \begin{array}{cc} \delta ^{b-1}g_{\vartheta },\,\,\,0\le g_{\vartheta }< \delta \\ g_{\vartheta }^{b},\,\,\,g_{\vartheta }\ge \delta \end{array} \right\} ,\,\, g_{\vartheta }= \left\{ \begin{array}{cc} g,\,\,\,|g|< \vartheta \\ \vartheta ,\,\,\,|g|\ge \vartheta \end{array} \right\} ,\,\, g_{\vartheta }^{b}= \left\{ \begin{array}{cc} g^{b},\,\,\,|g^{b}|< \vartheta ^{\frac{1}{b}}\\ \vartheta ^{\frac{1}{q}},\,\,\,|g^{b}|\ge \vartheta ^{\frac{1}{b}} \end{array} \right\} . \end{aligned}$$
(3.24)

As a consequence, the following truncated problem \(P_{\vartheta }^{\phi _{7}}\) is proposed:

$$\begin{aligned} v_{1,\vartheta }\frac{\partial \phi _{7}}{\partial t}- A_{1}\left| \frac{\partial v_{1,\vartheta }}{\partial y}\right| ^{p-1}\frac{\partial \phi _{7}}{\partial y}-A_{3}\phi _{7} v_{1,\vartheta }^{2}+A_{4}\phi _{7}-A_{5}\phi _{7} V_{\delta ,\vartheta }=0, \end{aligned}$$
(3.25)

where the boundary and initial set of conditions are the same to the previous problem \(P^{\phi _{7}}.\) The solution, \(\phi _{7}(y,t)\), of problem \(P_{\vartheta }^{\phi _{7}}\) does exist and is unique. This can be shown based on available results in the literature (see [37, 41] for some analyses in this regard involving weak derivatives) and the maximum principle for the p-Laplacian operator for positive solutions (see [37, 38]).

Once we have shown that there exists a parabolic evolution of a test function, we shall recall that our objective is to obtain the boundedness of weak solutions. To this end, consider the following theorem:

Theorem 2

Any positive solution \(v_{1}(y,t)\) to the problem (1.6) is bounded in \(t\in [0,\infty )\) and for \(y \in B_{r}\), where \(0<r<\infty .\)

Proof

Consider firstly \(\zeta \in \mathbb {R}^{+}\) so that the following cut off function \((\psi )\) is defined (refer to [42]):

$$\begin{aligned}&\psi _{\zeta }\in C_{0}^{\infty }(\mathbb {R}), \qquad 0\le \psi _{\zeta }\le 1,\nonumber \\&\quad \psi _{\zeta }=1, \quad y\in B_{r-\zeta },\quad \psi _{\zeta }=0, \quad y\in \Big [R-B_{r-\zeta }\Big ] \end{aligned}$$
(3.26)

so that

$$\begin{aligned} \left| \nabla \psi _{\lambda }\right| \le \frac{d_{1}}{\zeta },\quad \left| \Delta \psi _{\lambda }\right| \le \frac{d_{1}}{\zeta ^{2}}. \end{aligned}$$
(3.27)

Multiplying (3.25) by \(\psi _{\zeta }\), the following holds for \((t,y)\in (0,\tau )\times B_{r}\) where \(0<\tau<t<\infty{:}\)

$$\begin{aligned}&\int _{0}^{\tau }\int _{B_{r}}v_{1,\vartheta }\frac{\partial \phi _{7}}{\partial t}\psi _{\zeta }- A_{1}\int _{0}^{\tau }\int _{B_{r}}\left| \frac{\partial v_{1,\vartheta }}{\partial y}\right| ^{p-1}\frac{\partial \phi _{7}}{\partial y}\psi _{\zeta } -A_{5}\int _{0}^{\tau }\int _{B_{r}}\phi _{7}v_{1,\vartheta }^{b}\psi _{\zeta }\nonumber \\&\quad -A_{3}\int _{0}^{\tau }\int _{B_{r}}\phi _{7} v_{1,\vartheta }^{2}\psi _{\zeta } +A_{4}\int _{0}^{\tau }\int _{B_{r}}\phi _{7}\psi _{\zeta }=0, \end{aligned}$$
(3.28)

where \(\phi _{7},\) \(\frac{\partial \phi _{7}}{\partial t}\) and \(\psi _{\zeta }\) are continuous and smooth functions complying with a decaying behavior at infinity. For the boundedness of any solution, we have to show that \(\int _{0}^{\tau }\int _{B_{r}}v_{1,\vartheta }\frac{\partial \phi _{7}}{\partial t}\psi _{\zeta }\) is finite. For this, we use Proposition 2 to show the asymptotic convergence of each of the involved integrals in the last expression together with the test function \(\phi _{7}\) given in (3.4):

$$\begin{aligned} &A_{1}\int _{0}^{t} \int _{B_{r}}\left| \frac{\partial v_{1,\vartheta }}{\partial y}\right| ^{p-1}\frac{\partial \phi _{7}}{\partial y}\psi _{\zeta } \\&\quad \le \int _{0}^{t}\int _{B_{r}}A_{1}\left( C_{7}^{p-1}t^{-2a_{0}(p-1)} r^{\frac{2(p-1)}{p-2}}\left\| v_{0}\right\| _{1}^{2a_{0}(p-1)}\right) \frac{2|-b_{1}|re^{-j_{2}(t)}}{(1+r^{2})^{b_{1}+1}}\psi _{\zeta } \\&\quad \le \int _{0}^{t}\int _{B_{r}}A_{1}\left( C_{7}^{p-1}t^{-2a_{0}(p-1)} r^{\frac{2(p-1)}{p-2}}\left\| v_{0}\right\| _{1}^{2a_{0}(p-1)}\right) \frac{2b_{1}re^{-j_{2}(t)}}{(1+r^{2})^{b_{1}+1}}\frac{b_{1}}{\zeta }\\&\quad \le \int _{0}^{t}\int _{B_{r}}A_{1}\left( C_{7}^{p-1}t^{-2a_{0}(p-1)} r^{\frac{2(p-1)}{p-2}+2b_{1}+2}\left\| v_{0}\right\| _{1}^{2a_{0}(p-1)}\right) 2b_{1}b_{1}e^{-j_{2}(t)}. \end{aligned}$$
(3.29)

The asymptotic convergence in the previous integral requires to consider that \( b_1 \ge b_{7} = \frac{p-1}{2(p-2)}.\)

Similarly:

$$\begin{aligned} \int _{0}^{t}\int _{B_{r}}A_{5}v_{1,\vartheta } \phi _{7}\psi _{\zeta }\le \int _{0}^{t}\int _{B_{r}}A_{5}C_{6}^{b}t^{-a_{0}}r^{ bp(p-2)}\left\| v_{0}\right\| ^{pba_{0}}r^{-2b_{1}} \end{aligned}$$
(3.30)

The integral is asymptotically convergent for \(b_1 \ge b_8 = \frac{pb(p-2)}{2}.\)

$$\begin{aligned} \int _{0}^{t}\int _{B_{r}}A_{3}v_{1,\vartheta }^{2} \phi _{7}\psi _{\zeta }\le \int _{0}^{t}\int _{B_{r}}A_{3}C_{6}^{2}t^{-2a_{0}}r^{ 2p(p-2)}\left\| v_{0}\right\| ^{2pa_{0}}r^{-2b_{1}}. \end{aligned}$$
(3.31)

Again, the integral is asymptotically convergent for \(b_1 \ge b_9 = p(p-2).\) In addition:

$$\begin{aligned} \int _{0}^{t}\int _{B_{r}}A_{4} \phi _{7}\psi _{\zeta }\le \int _{0}^{t}\int _{B_{r}}A_{4}r^{-2b_{1}}. \end{aligned}$$
(3.32)

The integral converges asymptotically if \(b_1 >0.\)

Consequently, for the convergence of (3.28), the following holds:

$$\begin{aligned} b_{1} > \text {max}\left( b_{7}, b_{8}, b_{9}, 0\right) . \end{aligned}$$
(3.33)

Coming back to (3.28), considering the initial condition of a positive solution and taking \(r\rightarrow \infty ,\) we have

$$\begin{aligned} 0<\int _{0}^{\tau }\int _{B_{r}}v_{1,\vartheta }\frac{\partial \phi _{7}}{\partial t}\psi _{\zeta }\le M^+, \end{aligned}$$
(3.34)

where \(M^+\) is the resulting value after compilation of the assessed asymptotically convergent integrals. This implies that any solution \(v_{1,\vartheta }\) is bounded. To recover the original solution, we shall make \(\vartheta \gg 1\) to conclude on the boundedness of any weak solution \(v_{1}(y,t)\) to the problem (1.6). \(\hfill\square \)

The theorem to come shows the uniqueness of solutions to (1.6).

Theorem 3

Assume any initial distribution with a positive mass, together with the pairs \((\tilde{v}_{1,\vartheta },\tilde{V}_{\delta ,\vartheta })\) and \((\bar{v}_{1,\vartheta },\bar{V}_{\delta ,\vartheta })\) formed of maximal and minimal solutions, respectively, for (3.25) in \(B_{r}\times (0,T).\) Then, the maximal and minimal solutions to (3.25) coincides, leading to the existence of asymptotic uniqueness to the problem (1.6).

Proof

Assuming that \(\tilde{v}_{1,\vartheta }\) is the maximal solution of (3.25), such a solution is obtained departing from an initial data of form:

$$\begin{aligned} \tilde{v}_{1,\vartheta }(y,0)=v_{0}(y)+\epsilon , \end{aligned}$$
(3.35)

with \(\epsilon >0\). The minimal solution of (3.25), \(\bar{v}_{1,\vartheta },\) departs from the following initial distribution:

$$\begin{aligned} \bar{v}_{1,\vartheta }(y,0)=v_{0}(y), \end{aligned}$$
(3.36)

where \(\int _{B_{r}} v_0 > 0\). The weak formulations for the maximal and minimal solutions are given by:

$$\begin{aligned}\int _{B_{r}}\tilde{v}_{1,\vartheta }(t)\phi _{7}(t) = &\int _{B_{r}}\tilde{v}_{1,\vartheta }(0)\phi _{7}(0) +\int _{0}^{\tau }\int _{B_{r}}\Big (\tilde{v}_{1,\vartheta }\frac{\partial \phi _{7}}{\partial t}- A_{1}\left| \frac{\partial \tilde{v}_{1,\vartheta }}{\partial y}\right| ^{p-1}\frac{\partial \phi _{7}}{\partial y}\Big )\nonumber \\&\quad -\int _{0}^{\tau }\int _{B_{r}}\Big (A_{3}\phi _{7} \tilde{v}_{1,\vartheta }^{2}+A_{4}\phi _{7} -A_{5}\phi _{7} \tilde{V}_{\delta ,\vartheta }\Big ) \end{aligned}$$
(3.37)
$$\begin{aligned}\int _{B_{r}}\bar{v}_{1,\vartheta }(t)\phi _{7}(t) = &\int _{B_{r}}\bar{v}_{1,\vartheta }(0)\phi _{7}(0) +\int _{0}^{\tau }\int _{B_{r}}\Big (\bar{v}_{1,\vartheta }\frac{\partial \phi _{7}}{\partial t}- A_{1}\left| \frac{\partial \tilde{v}_{1,\vartheta }}{\partial y}\right| ^{p-1}\frac{\partial \phi _{7}}{\partial y}\Big )\nonumber \\&\quad -\int _{0}^{\tau }\int _{B_{r}}\Big (A_{3}\phi _{7} \bar{v}_{1,\vartheta }^{2}+A_{4}\phi _{7} -A_{5}\phi _{7} \bar{V}_{\delta ,\vartheta }\Big ) \end{aligned}$$
(3.38)

As shown in Theorem 1:

$$\begin{aligned} \int _{0}^{\tau }\int _{\mathbb {R}}\left| \frac{\partial \tilde{v}_{1,\vartheta }}{\partial y}\right| ^{p-1}\frac{\partial \phi _{7}}{\partial y}=0, \quad \int _{0}^{\tau }\int _{\mathbb {R}}\left| \frac{\partial \bar{v}_{1,\vartheta }}{\partial y}\right| ^{p-1}\frac{\partial \phi _{7}}{\partial y}=0. \end{aligned}$$
(3.39)

Subtracting (3.38) from (3.37) and taking \(\epsilon \rightarrow 0,\) we have

$$\begin{aligned}&\int _{B_{r}}\Big (\tilde{v}_{1,\vartheta }-\bar{v}_{1,\vartheta }\Big )(t)\phi _{7}(t) \nonumber \\&\quad =\int _{0}^{\tau }\int _{B_{r}}\Big (\big (\tilde{v}_{1,\vartheta }-\bar{v}_{1,\vartheta }\big )\frac{\partial \phi _{7}}{\partial t}-A_{3}\phi _{7} \big (\tilde{v}_{1,\vartheta }^{2}-\bar{v}_{1,\vartheta }^{2}\big ) -A_{5}\phi _{7} \big (\tilde{V}_{\delta ,\vartheta }-\bar{V}_{\delta , \vartheta }\big )\Big )\nonumber \\&\quad \le \int _{0}^{\tau }\int _{B_{r}}\Big (\big (\tilde{v}_{1,\vartheta }-\bar{v}_{1,\vartheta }\big )\frac{\partial \phi _{7}}{\partial t}-A_{3}\phi _{7} \big (\tilde{v}_{1,\vartheta }+\bar{v}_{1,\vartheta }\big ) \big (\tilde{v}_{1,\vartheta }-\bar{v}_{1,\vartheta }\big ) -A_{5}\phi _{7} \big (\tilde{V}_{\delta ,\vartheta }-\bar{V}_{\delta , \vartheta }\big )\Big ). \end{aligned}$$
(3.40)

Since \(\tilde{v}_{1,\vartheta }\) and \(\bar{v}_{1,\vartheta }\) are bounded solutions, in accordance with the results of Theorem 1, we can choose \(A_{6}\) such that \(A_{3}\big (\tilde{v}_{1,\vartheta }+\bar{v}_{1,\vartheta }\big )\Big )\le A_{6}.\) Then, the expression (3.34) becomes:

$$\begin{aligned}&\int _{B_{r}}\Big (\tilde{v}_{1,\vartheta }-\bar{u}_{11}\Big )(t)\phi _{7}(t)\le \int _{0}^{\tau }\int _{B_{r}}\Big (\frac{\partial \phi _{7}}{\partial t}\big (\tilde{v}_{1,\vartheta }-\bar{v}_{1,\vartheta }\big )\nonumber \\&\quad + A_{6}\phi _{7}\big (\tilde{v}_{1,\vartheta }-\bar{v}_{1,\vartheta }\big ) +A_{5}\phi _{7}\big (\tilde{V}_{\delta ,\vartheta }-\bar{V}_{\delta ,\vartheta }\big )\Big ). \end{aligned}$$
(3.41)

As both \(\tilde{V}_{\delta ,\vartheta }\) and \(\bar{V}_{\delta ,\vartheta }\) are Lipschitz:

$$\begin{aligned} \left| \tilde{V}_{\delta ,\vartheta }-\bar{V}_{\delta ,\vartheta }\right| \le \delta ^{b-1}\left| \tilde{v}_{1,\vartheta }-\bar{v}_{1,\vartheta }\right| \end{aligned}$$
(3.42)

After using (3.42) into (3.41), we have

$$\begin{aligned} \int _{B_{r}}\Big (\tilde{v}_{1,\vartheta }-\bar{u}_{11}\Big )(t)\phi _{7}(t)\le \int _{0}^{\tau }\int _{B_{r}}\Big (\frac{\partial \phi _{7}}{\partial t}\big (\tilde{v}_{1,\vartheta }-\bar{v}_{1,\vartheta }\big )+ \big (A_{6}\phi _{7}+A_{5}\phi _{7}\delta ^{b-1}\big )\big (\tilde{v}_{1,\vartheta }-\bar{v}_{1,\vartheta }\big ). \end{aligned}$$
(3.43)

Given the particular form of a test function in (3.4), we can introduce a bounding constant as \( A_7 =\max \left\{ \frac{\partial \phi _7}{\partial t} \right\} < 0 \). Then for a large time, \(\tau \gg 1,\) in (3.43), it holds that:

$$\begin{aligned}&\int _{B_{r}}\Big (\tilde{v}_{1,\vartheta }-\bar{v}_{1,\vartheta }\Big )(t)\phi _{7}(t)\nonumber \\&\quad \le \int _{B_{r}}\Big (A_{7}+ A_{5}\phi _{7}\delta ^{b-1}\Big )t\big (\tilde{v}_{1,\vartheta }-\bar{v}_{1,\vartheta }\big ), \end{aligned}$$
(3.44)

which implies that

$$\begin{aligned} \int _{B_{r}}\Big (\tilde{v}_{1,\vartheta }-\bar{v}_{1,\vartheta }\Big ) \Big (\phi _{7}-A_{5}\delta ^{b-1}t-A_{7}t\Big )\le 0. \end{aligned}$$
(3.45)

Note that

$$\begin{aligned} \tilde{v}_{1,\vartheta }-\bar{v}_{1,\vartheta }\ge 0, \quad \phi _{7}-A_{5}\delta ^{b-1}t-A_{7}t> 0, \end{aligned}$$
(3.46)

where the value of \(A_{7}\) is negative, therefore

$$\begin{aligned} \int _{B_{r}}\Big (\tilde{v}_{1,\vartheta } -\bar{v}_{1,\vartheta }\Big )\Big (\phi _{7}-A_{5}\delta ^{b-1}t-A_{7}t\Big )\ge 0, \end{aligned}$$
(3.47)

which contradict (3.45). Then we shall consider that \(\tilde{v}_{1,\vartheta }-\bar{v}_{1,\vartheta }=0\) which implies that \(\tilde{v}_{1,\vartheta }=\bar{v}_{1,\vartheta },\) leading to the uniqueness of solutions to the problem (3.25). The asymptotic uniqueness of solution to the original problem (1.6) is achieved in the limit with \(\vartheta \rightarrow \infty \) and \(\delta \rightarrow 0^+\). \(\hfill\square \)

As an additional piece of analysis, the uniqueness of the solutions can be proved based on the positivity property of the p-Laplacian operator for positive solutions (see [37]). Indeed, assume again that \(\tilde{v}_{1,\vartheta }\) is a maximal solution with initial data (3.35) and \(\bar{v}_{1,\vartheta }\) is a minimal solution with initial data (3.36), together with a particular form of a test function given by:

$$\begin{aligned} \phi _{7}(y,s)=e^{a_{1}(T-s)}\left( 1+y^{2}\right) ^{-b_{1}}, \end{aligned}$$
(3.48)

where \(a_{1}\) and \(b_{1}\) are finite constants. Differentiate (3.48) with respect to s, 

$$\begin{aligned} \frac{\partial \phi _{7}}{\partial s} =-a_{1}\phi _{7}. \end{aligned}$$
(3.49)

After subtraction of the equations involving the mentioned maximal and minimal solutions, which are expressed in (3.37) and (3.38), the expression (3.40) becomes

$$\begin{aligned}\int _{B_{r}}\Big (\tilde{v}_{1,\vartheta }-\bar{v}_{1,\vartheta }\Big )(t)\phi _{7}(t)\le & \int _{0}^{\tau }\int _{B_{r}}\Big (\big (A_{6}-a_{1}\big )(\tilde{v}_{1,\vartheta }-\bar{v}_{1,\vartheta }\big )(t)\phi _{7}(t) +A_{5}(\tilde{V}_{\delta ,\vartheta }-\bar{V}_{\delta ,\vartheta }\big )(t)\phi _{7}(t)\Big )\nonumber \\&\quad \le \left| A_{6}-a_{1}+A_{5}\delta ^{b-1} \right| \int _{0}^{\tau }\int _{B_{r}}(\tilde{v}_{1,\vartheta }-\bar{v}_{1,\vartheta }\big )(t)\phi _{7}(t). \end{aligned}$$
(3.50)

where we have used the Lipschitz condition (3.42). After differentiating with respect to t,  we have

$$\begin{aligned} 0\le \frac{d}{dt}\int _{B_{r}}\Big (\tilde{v}_{1,\vartheta }-\bar{v}_{1,\vartheta }\Big )(t)\phi _{7}(t) \le \left| A_{6}-a_{1}+A_{5}\delta ^{b-1}\right| \int _{B_{r}}(\tilde{v}_{1,\vartheta }-\bar{v}_{1,\vartheta }\big )(t)\phi _{7}(t). \end{aligned}$$
(3.51)

Now, after application of the Gronwall inequality, we have

$$\begin{aligned} \int _{B_{r}}\Big (\tilde{v}_{1,\vartheta }-\bar{v}_{1,\vartheta }\Big )(t)\phi _{7}(t) \le e^{\left| A_{6}-a_{1}+A_{5}\delta ^{b-1}\right| }\int _{B_{r}}\epsilon \phi _{7}(0). \end{aligned}$$
(3.52)

Taking \(\epsilon \) sufficient small (this is, making the initial conditions (3.35) and (3.36) sufficiently close) in the last expression, the minimal solution \(\bar{v}_{1,\vartheta }\) converges to the maximal solution \(\tilde{v}_{1,\vartheta },\) showing then the asymptotic uniqueness of solutions.

3.2 A comparison principle

The next intention is to show the asymptotic order preservation of solutions. To this end, the following theorem is given:

Theorem 4

Assuming that \(v_{0,1}(y,t)\) and \(v_{0,2}(y,t)\) are different and positive initial distributions complying with the order: \(v_{0,1}(y,t)\ge v_{0,2}(y,t)\), then the resulting solutions, according to these initial conditions, preserve the order property; this is: \(v_{11}(y,t)\ge v_{12}(y,t)\) in \(B_{r}\times (0,T).\)

Proof

Considering the involved truncatures in (3.22), (3.23), (3.24), the already discussed weak formulations and the expression (3.41) for \(r\gg 1\) in \(0<\tau \le T\) the following applies (note that the term \(\thicksim \) refers to a sufficiently close condition for our purposes):

$$\begin{aligned}&\int _{B_{r}}\Big (v_{11,\vartheta }-v_{12,\vartheta }\Big )(t)\phi _{7}(t)\thicksim \int _{B_{r}}\Big (v_{0,1}-v_{0,2}\Big )(0)\phi _{7}(0)\nonumber \\&\quad + \int _{0}^{\tau }\int _{B_{r}}\Big (\frac{\partial \phi _{7}}{\partial t}\big (v_{11,\vartheta }-v_{12,\vartheta }\big )+ A_{6}\phi _{7}\big (v_{11,\vartheta }-v_{12,\vartheta }\big ) -A_{5}\phi _{7}\big (V_{11,\delta ,\vartheta }-V_{12,\delta ,\vartheta }\big )\Big ) \end{aligned}$$
(3.53)

which implies that

$$\begin{aligned} &\int _{B_{r}}\Big (v_{11,\vartheta }-v_{12,\vartheta }\Big )(t)\phi _{7}(t)\\&\quad -\int _{0}^{\tau }\int _{B_{r}}\Big (\frac{\partial \phi _{7}}{\partial t}\big (v_{11,\vartheta }-v_{12,\vartheta }\big )+ A_{6}\phi _{7}\big (v_{11,\vartheta }-v_{12,\vartheta }\big ) -A_{5}\phi _{7}\big (V_{11,\delta ,\vartheta }-V_{12,\delta ,\vartheta }\big )\Big )\\&\quad \thicksim \int _{B_{r}}\Big (v_{0,1}-v_{0,2}\Big )(0)\phi _{7}(0) \ge 0 \end{aligned}$$
(3.54)

From (3.48) \(\frac{\partial \phi _{7}}{\partial t}=-a_{1}\phi _{7}\), and after applying the Gronwall inequality, the expression (3.54) becomes

$$\begin{aligned}&\int _{B_{r}}\Big (v_{11,\vartheta }-v_{12,\vartheta }\Big )(t)\phi _{7}(t)+ \int _{B_{r}}A_{8}\Big ( a_{1}-A_{6}\Big )\big (v_{11,\vartheta }-v_{12,\vartheta }\big )\phi _{7}\nonumber \\&\quad -\int _{B_{r}}A_{9}\Big ( a_{1}-A_{6}\Big )\Big (v_{0,1}-v_{0,2}\Big )(0)\phi _{7}(0)- \int _{B_{r}}A_{10}\big (V_{11,\delta ,\vartheta }-V_{12,\delta \vartheta }\big )\phi _{7}\nonumber \\&\quad + \int _{B_{r}}A_{11}\Big (v_{0,1}-v_{0,2}\Big )(0)\phi _{7}(0) \ge 0. \end{aligned}$$
(3.55)

where \(A_{i}\ge 0,\) \(i=(1,2,3,4)\) refer to the Gronwall’s constants. Asymptotically, for \(|y| \gg 1\), recovering the original solution for \(\delta \rightarrow 0^+,\) \(\vartheta \gg 1\) and using the Lipschitz condition (3.42), we have

$$\begin{aligned} \int _{B_{r}}\Big (1+A_{8}\big (a_{1}-A_{6}\big )-A_{10}\delta ^{b-1}\Big )\Big (v_{11,\vartheta }-v_{12,\vartheta }\Big )(t)\phi _{7}(t)\nonumber \\ \ge \int _{B_{r}}\Big (A_{9}\big (a_{1}-A_{6}\big )-A_{11}\Big )\big (v_{0,1}-v_{0,2}\big )\phi _{7}(0)\ge 0, \end{aligned}$$
(3.56)

where the \(a_{1}\) constant can be selected such that \(1+A_{10}a_{1}>A_{8}A_{6}+A_{10}\delta ^{b-1}\) and \(A_{9}a_{1}>A_{9}A_{6}+A_{11},\) i.e.,

$$\begin{aligned} a_{1}>\max \left[ \frac{A_{8}A_{6}+A_{10}\delta ^{b-1}-1}{A_{10}},\,A_{6}+\frac{A_{11}}{A_{9}}\right] . \end{aligned}$$
(3.57)

In return to (3.56), and considering the positivity of the test function, we get that

$$\begin{aligned} v_{0,1}\ge v_{0,2}\rightarrow v_{11,\vartheta }\ge u_{12,\vartheta }, \end{aligned}$$
(3.58)

as intended to prove. \(\hfill\square \)

4 Profiles of analytical solutions

The objective in this section is to continue the exploration about the behavior of solutions to (1.6) for \(p \ne 2\). To this end, consider that \(A_{4}=0\) for the sake of simplicity and with no impact in the generality of the obtained results, together with the following truncation to the reaction term:

$$\begin{aligned} f_{\phi _{2}}=\text {min}\Big [v_{1}^{b},\,\,\phi _{2}^{b-1}v_{1}\Big ], \,\,\,\phi _{2}>0 \end{aligned}$$
(4.1)

Note that the original reaction term holds for \(\phi _{2}\rightarrow 0^+.\) Based on the truncation introduced, the following problem is proposed:

$$\begin{aligned} \frac{\partial v_{1}}{\partial t} =A_{1} \frac{\partial }{\partial y}\left( \left( \frac{\partial v_{1}}{\partial y}\right) ^{p-2}\frac{\partial v_{1}}{\partial y}\right) -A_{5}f_{\phi _{2}} -A_{3}v_{1}^{2}, \end{aligned}$$
(4.2)

where the reaction term is now a Lipschitz function. The exploration of solutions is performed based on selfsimilar structures of the form:

$$\begin{aligned} v_{1}(y,t)=t^{-\alpha _{0}}g\big (\eta \big ),\,\,\eta =|y|t^{\beta _0}, \end{aligned}$$
(4.3)

where \(g(\eta )\) refers to the selfsimilar and radially symmetric profile.

It should be noted that the assessments to come are given for \(y \in \mathbb {R}^d\), where \(d \ge 1\), to account for a further general analysis, and in the consideration that working in \(\mathbb {R}^d\) provides easier computations.

Substituting (4.3) into (4.2), we have

$$\begin{aligned} -\alpha _{0}t^{-\alpha _{0}-1}g+\beta _{0}\eta t^{-\alpha _{0}-1}g'= A_{1}t^{-\alpha _{0}(p-1)}(p-1)\big (g'\big )^{p-2}g'' +\frac{d-1}{\eta }\big (g'\big )^{p-1} -A_{5}g_{\phi _{2}}+A_{3}t^{-2\alpha _{0}}g^{2}, \end{aligned}$$
(4.4)

where

$$\begin{aligned} f_{\phi _{2}}(g,t)=\text {min}\Big [g^{b},\,\,\phi _{2}^{b-1}t^{-\alpha _{0}(b-1)}g\Big ], \end{aligned}$$
(4.5)

or equivalently:

$$\begin{aligned} f_{\phi _{2}}(g,t)=\text {min}\Big [t^{-\alpha _{0}b}g^{b},\,\,\phi _{2}^{b-1}t^{-\alpha _{0}}g\Big ]. \end{aligned}$$
(4.6)

A value for \(\alpha _0\) can be obtained based on the balance between the time and the spatial derivatives in the expression (4.4), to have:

$$\begin{aligned} \alpha _0 = \frac{1}{p-2}. \end{aligned}$$
(4.7)

Note that both terms defined in (4.5) and (4.6) have the same intersection in \(g=f\phi _{2.}\) For the sake of simplicity, the coming assessments are done with the linear term g in (4.5). In addition and for a sufficiently large time, the following holds:

$$\begin{aligned} f_{\phi _{2}}(g,t)\ge kg, \end{aligned}$$
(4.8)

so that k is selected as \(k=-\alpha _{0}+\beta _{0} d\), for convenience in solving (4.4).

Note that the selfsimilar profile \(g(\eta )\) is a solution to the elliptic problem (4.4) at each selected time (for simplification and without loss of generality consider \(t=1\)), then a solution profile is obtained to the equation:

$$\begin{aligned} -\alpha _{0}g+\beta _{0}\eta g'= A_{1}(p-1)\big (g'\big )^{p-2}g'' +\frac{A_{1}(d-1)}{\eta }\big (g'\big )^{p-1} -A_{5}(-\alpha _{0}+\beta _{0} d)g-A_{3}g^{2}. \end{aligned}$$
(4.9)

Assuming that \(\epsilon =A_{5}(-\alpha _{0}+\beta _{0} d)\) (this is for \(\Vert v_0 \Vert _1 \gg 1\) so as \(A_5 \ll 1\)) is a small and positive parameter, a solution to (4.9) can be analyzed by using a perturbation technique. Then the solution is expressed as:

$$\begin{aligned} g=g_{0}+\epsilon g_{1}+\epsilon ^{2}g_{2}+\cdots \end{aligned}$$
(4.10)

Note that this imposes a condition for \(\beta _0\) given by:

$$\begin{aligned} -\alpha _{0} + \beta _{0} d \ge 0 \, \rightarrow \, \beta _0 \ge \frac{\alpha _0}{d}. \end{aligned}$$
(4.11)

After using (4.10) into (4.9), we have

$$\begin{aligned}&A_{1}(p-1)\big (g_{0}'+\epsilon g_{1}'+\epsilon ^{2}g_{2}'+\cdots \big )^{p-2}\big (g_{0}''+\epsilon g_{1}''+\epsilon ^{2}g_{2}''+\cdots \big )\nonumber \\&\quad +\frac{A_{1}(d-1)}{\eta }\big (g_{0}'+\epsilon g_{1}'+\epsilon ^{2}g_{2}'+\cdots \big )^{p-1}-\beta _{0}\eta \big (g_{0}'+\epsilon g_{1}'+\epsilon ^{2}g_{2}'+\cdots \big )\nonumber \\&\quad -\epsilon \big (g_{0}+\epsilon g_{1}+\epsilon ^{2}g_{2}+\cdots \big )-A_{3}\big (g_{0}+\epsilon g_{1}+\epsilon ^{2}g_{2}+\cdots \big )^{2}=0 \end{aligned}$$
(4.12)

Comparing the coefficient of \(\epsilon ^{0},\) we have

$$\begin{aligned} A_{1}(p-1)\big (g_{0}'\big )^{p-2}g_{0}'' +\frac{A_{1}(d-1)}{\eta }\big (g_{0}'\big )^{p-1}-\beta _{0}\eta g_{0}' -A_{3}\big (g_{0}\big )^{2}=0 \end{aligned}$$
(4.13)

Assuming \(\gamma =A_{3}\) is a small parameter, a solution to (4.13) can be analyzed again by using a perturbation technique, such that

$$\begin{aligned} g_{0}=g_{00}+\gamma g_{01}+\gamma ^{2}g_{02}+\cdots \end{aligned}$$
(4.14)

After using (4.14) into (4.13), we have

$$\begin{aligned}&A_{1}(p-1)\big (g_{00}'+\gamma g_{01}'+\gamma ^{2}g_{02}'+\cdots \big )^{p-2}\big (g_{00}''+\gamma g_{01}''+\gamma ^{2}g_{02}''+\cdots \big )\nonumber \\&\quad +\frac{A_{1}(d-1)}{\eta }\big (g_{00}'+\gamma g_{01}'+\gamma ^{2}g_{02}'+\cdots \big )^{p-1}-\gamma _{0}\eta \big (g_{00}'+\gamma g_{01}'+\gamma ^{2}g_{02}'+\cdots \big ) \nonumber \\&\quad -\gamma \big (g_{00}+\gamma g_{01}+\gamma ^{2}g_{02}+\cdots \big )^{2}=0 \end{aligned}$$
(4.15)

Comparing coefficient of \(\gamma ^{0}\) and \(\gamma ^{1}\), we have

$$\begin{aligned} A_{1}(p-1)\big (g_{00}'\big )^{p-2}g_{00}'' +\frac{A_{1}(d-1)}{\eta }\big (g_{00}'\big )^{p-1}-\beta _{0}\eta g_{00}' =0 \end{aligned}$$
(4.16)

and

$$\begin{aligned}&A_{1}(p-1)\big (g_{00}'\big )^{p-2}g_{01}'' +A_{1}(p-1)(p-2)\big (g_{00}'\big )^{p-1}g_{00}''g_{01}' \nonumber \\&\quad +\frac{A_{1}(d-1)(p-1)}{\eta }\big (g_{00}'\big )^{p-2}g_{01}' -\beta _{0}\eta g_{01}' -\big (g_{00}\big )^{2}=0. \end{aligned}$$
(4.17)

After solving (4.17), we get

$$\begin{aligned} g_{00}=A_{12}\eta ^{\frac{p}{p-2}}, \end{aligned}$$
(4.18)

where \(A_{12}=\frac{\beta _{0}^{\frac{p-1}{p-2}}(p-2)^{\frac{2p-3}{p-2}}}{A_{1}^{\frac{p-1}{p-2}}(dp+2d=p)^{\frac{p-1}{p-2}}},\) using (4.18) into (4.17), we have

$$\begin{aligned} \eta ^{2}g_{01}''+\left( \frac{2A_{1}p^{2}A_{12}^{2}}{(p-2)^{2}} +1 -\frac{\beta _{0}(p-2)^{p-2}}{A_{1}A_{12}^{p-2}p^{p-2}}\right) \eta g_{01}' =\frac{(p-2)^{p-2}\eta ^{\frac{4}{p-2}}}{A_{1}A_{12}^{p-4}p^{p-4}}. \end{aligned}$$
(4.19)

Here for simplicity we assume \(\frac{p+2}{p-2}\sim 1\), because the solution of (4.19) is finally the product of a small parameter \(\gamma \) and does not impact the solution of (4.9). Hence, the approximate solution of (4.19) is

$$\begin{aligned} g_{01}=A_{13}\eta ^{-A_{14}+1} + \frac{(p-2)^{p-2}\eta ^{\frac{4}{p-2}}}{(16+4(A_{14}-1)(p-2))A_{1}A_{12}^{p-4}p^{p-4}}, \end{aligned}$$
(4.20)

where \(A_{14}=\frac{2A_{1}p^{2}A_{12}^{2}}{(p-2)^{2}} +1 -\frac{\beta _{0}(p-2)^{p-2}}{A_{1}A_{12}^{p-2}p^{p-2}}.\) Combining (4.20) and (4.18) with (4.14), we have

$$\begin{aligned}&g_{0}=A_{12}\eta ^{\frac{p}{p-2}}+\gamma \left( A_{13}\eta ^{-A_{14}+1} +\frac{(p-2)^{p-2}\eta ^{\frac{4}{p-2}}}{(16+4(A_{14}-1)(p-2))A_{1}A_{12}^{p-4}p^{p-4}}\right) . \end{aligned}$$
(4.21)

Now comparing the coefficients of \(\epsilon ^{1}\) and then using (4.21) (also here, we neglect the product terms of \(\epsilon \) and \(\gamma ,\) as both are small parameters), we have

$$\begin{aligned} \eta ^{2}g_{1}''+A_{14}\eta g_{01}' =\frac{(p-2)^{p-2}\eta ^{\frac{4}{p-2}}}{A_{1}A_{12}^{p-3}p^{p-4}}. \end{aligned}$$
(4.22)

After solving (4.22), we have

$$\begin{aligned} g_{1}=A_{13}\eta ^{-A_{14}+1} + \frac{(p-2)^{p-2}\eta ^{\frac{4}{p-2}}}{(4+2(A_{14}-1)(p-2))A_{1}A_{12}^{p-3}p^{p-4}}. \end{aligned}$$
(4.23)

Putting the value of \(g_{0}\) and \(g_{1}\) into (4.10) a solution is finally given by the following expression:

$$\begin{aligned} \begin{aligned}&g=A_{12}\eta ^{\frac{p}{p-2}}+\gamma \left( A_{13}\eta ^{-A_{14}+1} + \frac{(p-2)^{p-2}\eta ^{\frac{4}{p-2}}}{(16+4(A_{14}-1)(p-2))A_{1}A_{12}^{p-4}p^{p-4}}\right) \\&\qquad + \epsilon \left( A_{13}\eta ^{-A_{14}+1} + \frac{(p-2)^{p-2}\eta ^{\frac{4}{p-2}}}{(4+2(A_{14}-1)(p-2))A_{1}A_{12}^{p-3}p^{p-4}}\right) +O(\gamma )^{2}+O(\epsilon )^{2}. \end{aligned} \end{aligned}$$
(4.24)

It should be considered that the last solution holds provided the associated constants are determined. This process is strongly influenced by the dedicated applications. Furthermore, particular value for p should be analyzed based on experimental settings that are out of the scope of the presented study. Such a kind of experimental work depends on the considered fluid, the particular geometry and the set of boundary conditions. An example of this approach is given in [1], wherein a power law was obtained as an alternative to the classical Darcy’s law. In this case a value of \(p = 5/3\) was provided.

4.1 Numerical assessment

In this section, we provide numerical solutions to the Eq. (4.4) in order to validate the perturbation approach followed to obtain the solution in (4.24), and that will be referred as \(g_{\mathrm{per}}\) in this section.

The numerical approach introduced is not intended to develop a complete numerical exploration for different values in the involved constant. In the opinion of the authors, the experimental work should provide firstly particular settings for the modeling constant. Then, we have preferred to give certain values to such constants and then provide the required evidences to support the adequacy of the analytical method followed that was based on the introduction of the perturbation parameters. Then, the following set of values has been considered:

$$\begin{aligned} p = \frac{3}{2}; A_1=A_{12} = A_{13} =A_{14} = A_3 = 1; \epsilon = \gamma = 0.001; d = 1; b=0.5. \end{aligned}$$
(4.25)

We remark the following ideas as basic principles to execute the numerical analysis:

  • The numerical routine has been developed in MATLAB and with the help of the function bvp4c. This function has been built based on a Runge–Kutta implicit algorithm with interpolant extensions [43]. The bvp4c requires to introduce the boundary conditions to execute the collocation method at the borders. Consequently, we have introduced the following conditions that preserve the radial symmetry: \(g(-\infty ) = 0\) and \(g(\infty ) = 0\).

  • The effect of the collocation method over the integration domain shall be minimized to avoid mishaps in the solutions interpretations. Then, the domain of integration has been considered as sufficiently large, \((-1000, 1000)\), compared to the region in which we will focus the solution representations.

  • To make the numerical assessment tractable, in what regards with the computational costs, the domain of integration was split in 10000. The accumulated maximum error considered for the simulation was \(10^{-4}\). With such level of error and discretization, the problem was simulated with a desktop computer leading to reasonable lead times of the order of several minutes.

  • We should recall that the solution obtained, under the perturbation technique, was valid provided that \(\Vert v_0 \Vert _1 \gg 1\) to have \(A_5 \ll 1\) (leading to a small \(\epsilon \)-parameter). Then, the initial condition considered was given by the following radially symmetric expression:

    $$\begin{aligned} v_0(\eta ) = C_g \, e^{-\eta ^2}, \end{aligned}$$
    (4.26)

    where \(C_g \gg 1\).

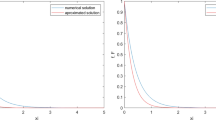
The results are compiled in Figs. 1 and 2. It should be mentioned that both solutions, g as solution to (4.4) and \(g_{\mathrm{per}}\) as the solution in (4.24), are asymptotically convergent for \(\eta \gg 1\). As pointed in the figure’s footprints, the criteria for asymptotic convergence between both solutions is given by a global or accumulated distance of \(\le 10^{-2}\) firstly and \(\le 10^{-3}\) afterward. A minimum value for \(\eta \) has been determined, such that for any value beyond the minimum, the global distance is kept within the mentioned global errors.

Fig. 1
figure 1

Representation of the numerical and analytical solutions. Note that \(g(\eta )\) is the numerical solution to (4.4) while \(g_{\mathrm{per}}\) is a representation of the expression (4.24). For \(\eta > 5.125\), the global, or accumulated distance, between the numerical solution and the analytical one is below \(10^{-2}\). It should be remarked that the decreasing order in the numerical profile is higher compared to the perturbation solution. For this reason the numerical solution is close to zero compared with the perturbation one. Although the decreasing orders are different, the global error is kept within the mentioned level. This leads to consider the adequacy of the perturbation approach under the fluid relaxation condition for \(\eta \gg 1\)

Full size image
Fig. 2
figure 2

Representation of the numerical and analytical solutions. Note that \(g(\eta )\) is the numerical solution to (4.4) while \(g_{\mathrm{per}}\) is a representation of the expression (4.24). For \(\eta > 12.258\), the global, or accumulated distance, between the numerical solution and the analytical one is below \(10^{-3}\)

Full size image

5 Main discussion

The intention, in this section, is to introduce a summary, together with some brief discussions, on the obtained results. Firstly, we should state that the Eq. (1.3), with initial distributions as per (1.7), was not previously reported in the existing literature to our best knowledge. The introduced p-Laplacian operator has a non-regular diffusivity term, leading to the analysis of weak solutions departing from the general initial distribution (1.7). As the problem (1.3) was not previously reported, we started our analysis by the assessments about existence and uniqueness of weak solutions. Previously, Theorem 1 stated the asymptotic convergence of any weak solution to the fundamental one. This is certainly an interesting result in its own right, as it is the basis to ensure the asymptotic regularity of weak solutions to (1.3). Once we successfully showed the regularity of weak solutions, we introduced additional assessments to look for selfsimilar solutions. Actually, and supported by a perturbation approach, we proved that such kind of solutions existed and that an analytical expression held. The numerical assessments allowed us to corroborate the analytical approaches followed. Both solutions, the analytical by perturbation approaches and the numerical one, were shown to be sufficiently close. The global distance between both solutions decreases for increasing values in the selfsimilar variable \(\eta \), which allowed us to validate the asymptotic approach presented.

6 Conclusions

In the present analysis, we provided a generalization of a MHD fluid flow raised in porous media. Such a generalization was introduced based on a nonlinear diffusion (of a p-Laplacian type) and a non-Lipschitz reaction term. To our best knowledge the postulated problem was not previously reported in the literature, being then one piece of contribution to the analysis of non-Newtonian fluids in porous media. The introduced analyses were mainly concerned with showing the behavior of weak solutions to the proposed problem. These contributions can be regarded as the starting points to support other more experimental works (and possibly additional searches of numerical and analytical solutions). Firstly, we developed the analyses related to regularity, boundedness, existence and uniqueness of the solutions. Afterward, we explored analytical solutions based on a radially symmetric selfsimilar profile. Such a profile was obtained analytically making use of a perturbation technique. Eventually, we carried out a numerical validating exercise to determine the adequacy of the perturbation approach followed to get the analytical solution.