Heavy quarks in the early stage of high energy nuclear collisions at RHIC and LHC: Brownian motion versus diffusion in the evolving Glasma

Abstract

We study the transverse momentum, $p_T$, broadening of charm and beauty quarks in the early stage of high energy nuclear collisions. We aim to compare the diffusion in the evolving Glasma fields with that of a standard, Markovian–Brownian motion in a thermalized medium with the same energy density of the Glasma fields. The Brownian motion is studied via Langevin equations with diffusion coefficients computed within perturbative quantum chromodynamics. We find that for small values of the saturation scale, $Q_s$, the average $p_T$ broadening in the two motions is comparable that suggests that the diffusion coefficient in the evolving Glasma fields is in agreement with the perturbative calculations. On the other hand, for large $Q_s$, the $p_T$ broadening in the Langevin motion is smaller than that in the Glasma fields. This difference can be related to the fact that heavy quarks in the latter system experience diffusion in strong, coherent gluon fields that leads to a faster momentum broadening due to memory, or equivalently to a strong correlation in the transverse plane.

1 Introduction

The research of the pre-thermalization phase of the system formed in high-energy collisions at the Relativistic Heavy Ion Collider (RHIC) and at the Large Hadron Collider (LHC), and of its evolution to the Quark–Gluon Plasma (QGP) [1, 2] is a fascinating topic in the field of heavy-ion phenomenology. The high-energy collisions are modeled as those of two sheets of colored glass [3,4,5,6,7,8,9]. According to the effective field theory of color-glass condensate (CGC), the interaction of two colored glasses generates strong longitudinal gluonic fields in the forward light cone. These fields are called the Glasma [10,11,12,13,14,15,16,17,18,19,20]. Glasma is a set of classical fields due to their large intensity, $A_\mu ^a \simeq Q_s/g$, where $Q_s$ is the saturation scale and g is the coupling of quantum chromodynamics (QCD). The time evolution of these gluon fields is described by Classical Yang–Mills (CYM) equations. In this work, we reserve the notation EvGlasma for the evolving Glasma fields and preserve the name Glasma for the initial condition. The duration of the EvGlasma is that of the pre-hydro stage; therefore, typical duration of this stage is of the order of $1~\mathrm {fm/c}$ for AA collisions at the RHIC energy, and approximately 0.3 fm/c for AA collisions at LHC.

Heavy quarks [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48] are produced in the primordial stage of the high-energy nuclear collisions are noble probes of EvGlasma. In fact, their production time is approximately $\tau _{\hbox {form}} \approx 1/(2m)$, where m is the mass of heavy quark. Thus, heavy quarks are produced shortly after the collision and potentially diffuse through the medium, testing in particular the pre-hydrostage of the system.

The diffusion of heavy quarks in the EvGlasma can be different from that in a thermal medium with uncorrelated noise. In fact, in the former case, the heavy quarks diffuse among domains in which the fields are correlated that have transverse area $\approx 1/Q_s^2$, namely the flux tubes or the filaments. The arrangement of the filaments in the transverse plane is random, therefore if heavy quarks are slow enough, they can diffuse within a single filament for a finite amount of time and experience the coherent gluon field. Instead, if the transverse velocity of the heavy quark is large enough, it effectively jumps between uncorrelated filaments and its diffusion is more similar to that in a random medium. A corollary of this qualitative picture is that heavy quarks with larger mass, namely beauty quarks, experience the strong coherent gluonic field mode than the charm quarks. This is confirmed by our calculations, see Section III for details.

It is of a certain interest to compare the motion of heavy colored probes in the EvGlasma, with that in a hot thermalized medium. This is the main subject of our study. From previous studies [49,50,51,52] it is known that the evolution of heavy quarks in the strong gluon fields produced in the early stage of high energy nuclear collisions is even qualitatively different from a standard Brownian motion, due to memory effects that make the diffusion ballistic [53]. In fact, as a result of memory in the gluon fields, the transverse momentum broadening in the evolving Glasma overshoots the one that the heavy quarks would experience in a hot QCD plasma. It is useful to remark that this memory effect in the early stage is important due to the fact that the memory time, $\tau _\mathrm {mem}\approx 0.1$ fm/c is comparable with the lifetime of the early stage, as well as to the fact that thermalization time $\tau _\mathrm {therm}\gg \tau _\mathrm {early}$: the combination of these makes the perfect scenario for observing memory effects, as well as to make the early evolution of heavy quarks resemble a diffusive motion with negligible drag.

In particular, we perform a systematic comparison of the diffusion in the EvGlasma and in a hot medium, computing the transverse momentum, $p_T$, broadening

$$\begin{aligned} \sigma _p = \frac{1}{2} \langle (p_x(t)-p_{0x})^2 + (p_y(t)-p_{0y})^2 \rangle , \end{aligned}$$

(1)

where $p_{0x}$ and $p_{0y}$ are the initial x and y components of the initial transverse momentum. Hence, $p_T^2 = p_x^2 + p_y^2$. In realistic collisions, the geometry of the early stage is that of a longitudinally expanding medium. However, we firstly analyze the diffusion in a static box. The use of the static box is necessary because the estimate and the comparison of the diffusion coefficients of the heavy quarks in the two systems should be done firstly for configurations with a fixed energy density, or equivalently with a fixed temperature. After this scenario is clarified, it is possible to elucubrate on similarities and differences of the diffusion in systems with expansion. Therefore, the use of a static box is far from being academic: it is the natural framework to define the diffusion coefficients. In the EvGlasma case, we find that $\sigma _p\propto t^2$ in the very early stage, while $\sigma _p\propto t$ in the later stage in analogy with the standard Brownian motion. This behavior that was anticipated in [53] leads to a fast increase in the $\sigma _p$, in fact faster than that found within Langevin equation with the pQCD diffusion coefficient.

The main difference between [53] and the present study is that here we adopt the diffusion coefficient computed within pQCD depending on temperature and momentum, while in [53], the diffusion coefficient is a constant extracted from the momentum broadening of heavy quarks in the evolving Glasma. The use of pQCD is justified by the fact that the saturation scale in the problem is quite large, $Q_s=O(1 \mathrm {GeV})$ that in turn leads to a large effective temperature of the medium, $T=O(Q_s)$. The motivation is to analyze the quantitative difference between the motion of the heavy quarks in the intense Glasma fields, and that in a plasma with a perturbative dynamics.

We analyze briefly the role of the longitudinal expansion on $p_T$ broadening in the EvGlasma fields. We show that in this case, $\sigma _p$ tends to saturate at the end of the EvGlasma phase. This late time behavior looks similar to that of the standard Brownian motion and in that context it is understood as the equilibration of the heavy quarks with the medium: however, the reason why $\sigma _p$ saturates in the EvGlasma is not related to the equilibration of the heavy quarks, rather to the dilution of the energy density during the expansion.

The implications of this early stage scenario are far from being purely abstract. As a matter of fact, it has been shown that the diffusion in the evolving Glasma can affect observables, namely the nuclear modification factor, $R_\mathrm {AA}$, the elliptic flow and the momentum broadening parameter of hadrons containing heavy quarks [49, 50, 54].

The plan of the article is as follows. In Section II, we review the formalism of the work. In Section III, we present our results on $\sigma _p$ for the EvGlasma, the thermalized medium and the EvGlasma with longitudinal expansion. Finally, in Section IV, we present our conclusions and discuss possible improvements that will be implemented in future works.

2 Formalism

2.1 Glasma and classical Yang–Mills equations for its evolution

We summarize here the McLerran–Venugopalan (MV) model. According to the effective field theory of color-glass condensate (CGC), the two colliding objects can be described as two thin Lorentz-contracted sheets of a colored glass where fast parton dynamics is frozen by time dilation. These fast partons act as the sources for the slow gluon fields in the saturation regime and thus behave like classical fields.

In the MV model, the sources of the CGC fields are the fast partons which are represented by the randomly distributed static color charge densities in the two colliding nuclei that we label as A and B. The static color charge densities $\rho ^a_{A}$ on the colliding nucleus A are considered as random variables which are normally distributed with zero mean and variance specified by

$$\begin{aligned} \langle \rho ^a_{A}({{\varvec{x}}}_T)\rho ^b_{A}({{\varvec{y}}}_T)\rangle = (g\mu _A)^2 \delta ^{ab} \delta ^{(2)}({{\varvec{x}}}_T - {{\varvec{y}}}_T). \end{aligned}$$

(2)

Here, a and b indicate the adjoint color index. This work is limited to the SU(2) color group, hence $a, b=1,2,3$. $\mu$ is the density of the color charge carriers in the transverse plane; therefore, $g\mu$ denotes the color charge density; $g^2\mu = O(Q_s)$ [55] where $Q_s$ is the saturation momentum.

The static color sources ${\rho }$ generate pure gauge fields outside and on the light cone. They combine in the forward light cone and give the initial boost-invariant Glasma fields. To determine these fields, firstly we solve the Poisson’s equations for the gauge potentials generated by the color charge distribution of the $i^{th}$ nuclei,

$$\begin{aligned} -\partial ^2_{\perp }\Lambda ^{(i)}({{\varvec{x}}}_T) =\rho ^{(i)}({{\varvec{x}}}_T), \end{aligned}$$

(3)

where $i=A, B$. The Wilson lines are calculated as $V^\dagger ({{\varvec{x}}}_T) =e^{-ig\Lambda ^{(A)}({{\varvec{x}}}_T)}$ and $W^\dagger ({{\varvec{x}}}_T) =e^{-ig\Lambda ^{(B)}({{\varvec{x}}}_T)}$ and the gauge fields of the two colliding objects are given as

$$\begin{aligned} \alpha _i^{(A)}= & {} \frac{-i}{g}V\partial _iV^\dagger , \end{aligned}$$

(4)

$$\begin{aligned} \alpha _i^{(B)}= & {} \frac{-i}{g} W\partial _iW^\dagger . \end{aligned}$$

(5)

The solution of the CYM in the forward light cone at initial time, namely the Glasma gauge potential in terms of the gauge fields can be written as:

$$\begin{aligned} A_i = \alpha _i^{(A)} +\alpha _i^{(B)},~~~A_z=0, \end{aligned}$$

(6)

where $i = x, y$. Assuming z to be the direction of the collision, the initial longitudinal Glasma fields are

$$\begin{aligned} E^z= & {} -ig \sum _{i=x,y}\bigg [\alpha ^{(B)}_i, \alpha ^{(A)}_i\bigg ], \end{aligned}$$

(7)

$$\begin{aligned} B^z= & {} -ig \bigg (\bigg [\alpha ^{(B)}_x, \alpha ^{(A)}_y\bigg ]+\bigg [\alpha ^{(A)}_x, \alpha ^{(B)}_y\bigg ]\bigg ), \end{aligned}$$

(8)

while the transverse fields vanish at the initial time.

The evolution of the pre-equilibrium period of the heavy-ion collisions, namely the Glasma fields is described by the classical Yang-Mills (CYM) equations. We look after the QCD evolution of the dense gluonic background fields at the classical level using CYM equations which are nothing just the non-abelian generalization of the well-known Maxwell equations in the empty space. The equations of the motion of the fields and the conjugate momenta, i.e., the CYM equations are

$$\begin{aligned}&\frac{\hbox {d}A^a_i(x)}{\hbox {d}t}= E^a_i(x), \end{aligned}$$

(9)

$$\begin{aligned}&\frac{\hbox {d}E^a_i(x)}{\hbox {d}t}= \partial _jF^a_{ji}(x)+g f^{abc} A^b_j(x)F^c_{ji}(x), \end{aligned}$$

(10)

where $f^{abc} = \varepsilon ^{abc}$ with $\varepsilon ^{123}=+1$ and $F^a_{ij}$ is the magnetic part of the field strength tensor given by

$$\begin{aligned} F^a_{ij}(x) = \partial _i A^a_j(x)- \partial _j A^a_i(x)+ g f^{abc} A^b_i(x)A^c_j(x) \end{aligned}$$

(11)

Here, we have used the standard Einstein summation convention. In this work, we do not include the color current carried by the heavy quarks: this would be necessary to take the energy loss effects into account, but its effect has been studied previously and it has been shown that it does not lead to any substantial effect within the time range in which EvGlasma is physically relevant [53].

2.2 Wong equations for the heavy quarks

Heavy quarks are created in the initial phase of the relativistic heavy-ion collisions in a very short time of 0.1 fm/c. The equations of motion of these colored probes in the EvGlasma are the Wong equations [49,50,51, 54, 56]

$$\begin{aligned}&\frac{\hbox {d}x_i}{\hbox {d}t} = \frac{p_i}{E}, \end{aligned}$$

(12)

$$\begin{aligned}&\frac{\hbox {d}p_i}{\hbox {d}t}=g Q_a F^a_{i\nu }\frac{p^{\nu }}{E}, \end{aligned}$$

(13)

with $i=x,y,z$ and $E=\sqrt{\mathbf{p }^2 + m^2}$ where m is the mass of the heavy quark. These equations are the well-known Hamilton equations of motion for the position and its conjugate momentum. In our setup, the term on the right-hand side of (13) is the force that the EvGlasma fields exert on the heavy quarks. Since the distribution of these fields is almost random in the transverse plane that force can be equated to the random diffusive force in the Langevin equations, see below. For the sake of nomenclature, we call this the Lorentz force, because it is formally the nonabelian version of the force that the quarks would experience in electromagnetic fields.

The third set of equations describes the conservation of the color current, namely

$$\begin{aligned} \frac{\hbox {d}Q_a}{\hbox {d}t} = g \varepsilon ^{abc}A^\mu _b \frac{p_\mu }{E}Q_c, \end{aligned}$$

(14)

where $a=1, 2, \dots ,N_c^2-1$ and $Q_a$ is the charm quarks effective color charge. Here, we initialize this color charge on a $3-$dimensional sphere with radius one; $Q_a Q_a$ corresponds to the total squared color charge which is conserved in the evolution. Differently from previous work, for example [53], in this work, we use the QCD coupling, g, explicitly, to facilitate the comparison with the Langevin evolution with pQCD diffusion coefficients. For each heavy quark, we fix an anti-quark with the same initial position that of the companion quark but opposite momentum, while the color charge is chosen again randomly.

2.3 Brownian motion and Langevin dynamics

The motion of a Brownian particle with mass m is governed by the Langevin equations, namely

$$\begin{aligned}&\frac{\hbox {d}x_i}{\hbox {d}t} = \frac{p_i}{E}, \end{aligned}$$

(15)

$$\begin{aligned}&\frac{\hbox {d}p_i}{\hbox {d}t}= -\gamma p_i + \xi _i (t). \end{aligned}$$

(16)

Here, $\gamma$ is the drag coefficient and ${\varvec{\xi }}$ is the random force. It is assumed that the latter is a Gaussian random variable that satisfies the conditions

$$\begin{aligned} \langle \xi _i(t)\rangle =0 \end{aligned}$$

(17)

and

$$\begin{aligned} \langle \xi _i(t_1) \xi _j(t_2)\rangle = 2\mathcal {D} \delta _{ij} \delta (t_1 - t_2), \end{aligned}$$

(18)

where $\mathcal {D}$ is the diffusion coefficient. The assumption in Eq. (18) is that the motion is a Markovian process, namely that no correlation of the random force at two different times exists.

For what follows, it is useful to consider the momentum broadening, that for a one-dimensional motion reads $\sigma _p = \langle (p- p_0)^2\rangle$; in the case of the Brownian motion, we have [53]

$$\begin{aligned} \sigma _p = p^2_0(e^{-\gamma t}-1)^2 + \frac{\mathcal {D}}{\gamma }(1- e^{-2\gamma t}). \end{aligned}$$

(19)

For times smaller than the equilibration time, $t\ll 1/\gamma$, we find $\sigma _p \approx 2\mathcal {D} t$.

3 Results

In our calculations, we fix the saturation scale, $Q_s$, and the QCD coupling, g. For the latter, we use the one-loop QCD $\alpha _s$ at the scale $Q_s$; then, we compute $g=\sqrt{4\pi \alpha _s}$. Therefore, we have $g=g(Q_s)$. From these two parameters, we fix $g\mu$, to be used in Eq. (2), by virtue of $g\mu \approx Q_s/0.6 g$ [55]. For each set of parameters, we perform $N_\mathrm {events}$ initializations and evolutions up to $t=1$ fm/c, then average physical quantities over all the events. Unless specified differently, all the results correspond to $N_\mathrm {events}=150$, having verified that this is enough to achieve convergence.

Fig. 1

$\sigma _p$ versus proper time for charm quarks, for the initial values $p_T=0.5$ GeV. The calculation corresponds to evolving Glasma fields in a static box

dummy

3.1 Momentum broadening in the static box

In Fig. 1, we plot $\sigma _p$, defined in Eq. (1), for charm quarks versus proper time, for several values of $Q_s$: tuning this parameter results in the change of the energy density, thus of the effective temperature, of the EvGlasma medium in which heavy quarks diffuse. In the lower panel of Fig. 1, we zoom to the very early stage, up to $\tau =0.4$ fm/c that roughly corresponds to the time range in which the EvGlasma is relevant in realistic collisions. Calculations correspond to the initial value $p_T=0.5$ GeV; results for different initializations are similar.

It is interesting that in the very early time, $\sigma _p$ versus time is not linear, differently from the standard Brownian motion, see (19). As analyzed in [53], this difference is due to the correlations of the Lorentz force acting on the charm quarks at different times, namely to the memory of the gluon fields. In [53], the memory argument has been supported by a calculation of the color-electric field in the EvGlasma: a direct calculation of the gauge-invariant correlator of the Lorentz force acting on the heavy quarks confirms this scenario [57]. The memory time, $\tau _\mathrm {mem}$, has been estimated in [53] by means of the decay of the correlator of the electric field in the EvGlasma, and it has been found $\tau _\mathrm {mem}\approx 1/Q_s$. After the initial transient, $\sigma _p$ grows up linearly as in the Brownian motion without a drag [53]. The shift among the two regimes happens on a time scale $t\approx \tau _\mathrm {mem}$.

Fig. 2

$\sigma _p$ versus proper time for beauty quarks. Initial values of $p_T=0.5$ GeV. The calculation corresponds to evolving Glasma fields in a static box

In Fig. 2, we plot $\sigma _p$ for beauty quarks; the results agree qualitatively with those obtained for the charm quarks. The only relevant difference that we have found is that $\sigma _p$ of beauty quarks is slightly larger than that of charms.

Fig. 3

$\sigma _p$ versus time for several values of the heavy quark mass and for $Q_s=3$ GeV

In order to explore this difference in more detail, in Fig. 3, we plot $\sigma _p$ for $Q_s=3$ GeV and for several values of the heavy quark mass; we limit to show results up to 0.4 fm/c since after that time momentum diffusion is already in the linear regime and nothing exciting happens. In the figure, we have put $\tau _\mathrm {form}=0.02$ fm/c for all quarks, that is the initialization time of beauty. We find that increasing the heavy quark mass results in the increase in $\sigma _p$ and in its faster evolution. This can be understood easily: on average, heavy quarks with larger mass and same $p_T$ have smaller transverse velocity, therefore they spend more time within one correlation domain (that is, the same flux tube) of the EvGlasma and are accelerated more efficiently by the gluon field, resulting in $\sigma _p\propto t^2$; then their speed becomes large enough that they can move within uncorrelated domains and experience a Brownian motion, resulting in the linear increase in $\sigma _p$.

Fig. 4

$\sigma _x$ versus time for charm quarks (solid lines) and beauty quarks (dot-dashed lines)

This picture is supported by the spatial diffusion in the transverse plane. In Fig. 4, we plot $\sigma _x$,

$$\begin{aligned} \sigma _x = \frac{1}{2} \left\langle (x(t)-X_{0})^2 + (y(t)-Y_{0})^2 \right\rangle , \end{aligned}$$

(20)

where $X_{0}$ and $Y_{0}$ are the initial transverse plane coordinates of the heavy quark. Besides, the results in Fig. 4 show that the average velocity of beauty quarks is smaller than that of charm quarks, as the formers spread more slowly in the transverse plane. Therefore, beauty quarks spend more time within a correlation domain and get accelerated coherently by the gluon fields.

Fig. 5

Time average of $\sigma _p$ versus $Q_s$ for charm quarks (upper panel) and beauty quarks (lower panel). Average has been computed on the time ranges $t=0.4$ fm/c and $t=1$ fm/c, respectively

In Fig. 5, we plot the time averaged $\sigma _p$ versus $Q_s$,

$$\begin{aligned} \mathrm {Av}\sigma _p = \frac{1}{t}\int _0^t\sigma _p(t^\prime ) \hbox {d}t^\prime . \end{aligned}$$

(21)

This quantity is of some interest because it allows us to compare, on average, the momentum broadening of heavy quarks in the EvGlasma and pQCD-plasma, despite the different time dependence of $\sigma _p$ in the two cases. We have computed the average for $t=0.4$ fm/c (orange diamonds) and $t=1$ fm/c (green squares). In the upper panel, we show the results for the charm quarks, while in the lower panel, we plot those for the beauty quarks. Comparing the results of charm and beauty, again we notice the slightly higher values obtained for the latter.

3.2 Comparison with the Langevin dynamics

Next, we turn to the comparison of momentum diffusion in the EvGlasma with those of a standard, collisional Langevin dynamics. We prepare a bulk of thermalized massless gluons with the same energy density, $\varepsilon$, of the EvGlasma, putting

$$\begin{aligned} \varepsilon = 2(N_c^2-1)\int \frac{d^3p}{(2\pi )^3} \frac{p}{e^{\beta p}-1} =\frac{(N_c^2-1)\pi ^2 T^4}{15}, \end{aligned}$$

(22)

where $T=1/\beta$ is the temperature of the gluon system. We use (22) to compute T for a given $\varepsilon$. Then, we run simulations of the Langevin equation with the pQCD diffusion coefficient computed at the temperature T with the coupling $g=g(Q_s)$ used for the EvGlasma calculation. We show for completeness the T versus $Q_s$ in Appendix A. As expected, we find $T=O(Q_s)$.

In Langevin Eq. (16) and in the thermal noise average (18), we use the kinetic coefficients of $c \ell \rightarrow c \ell$ and $b \ell \rightarrow b \ell$, where $\ell$ denotes a massless gluon in the thermal medium. The basic equations for the diffusion coefficient are well-known and can be found in the literature, see for example [58, 59]. Here, it is enough to quote the expression of the squared invariant scattering amplitude; for example, for the $c \ell \rightarrow c \ell$ scattering, this is given by

$$\begin{aligned} |{\mathcal {M}}_{c\ell \rightarrow c\ell }|^2= & {} {\pi ^2 \alpha _s^2} \bigg [\frac{32(s-m^2)(m^2-u)}{(t-m_D^2)^2} \nonumber \\&+\frac{64}{9}\frac{(s-m^2)(m^2-u)+2M^2(s+m^2)}{(s-m^2)^2} \nonumber \\&+\frac{64}{9}\frac{(s-m^2)(m^2-u)+2m^2(m^2+u)}{(m^2-u)^2}\nonumber \\&+ \frac{16}{9}\frac{m^2(4m^2-t)}{(s-m^2)(m^2-4)} \nonumber \\&+16\frac{(s-m^2)(m^2-u)+m^2(s-u)}{(t-m_D^2)(s-m^2)}\nonumber \\&-16\frac{(s-m^2)(m^2-u)-m^2(s-u)}{(t-m_D^2)(m^2-u)}\bigg ], \end{aligned}$$

(23)

where s, t and u denote the standard Mandelstam variables and m is the mass of the charm quark. A similar expression holds for the beauty. $m_D$ is the Debye mass that we assume to be

$$\begin{aligned} m_D = g T. \end{aligned}$$

(24)

Fig. 6

pQCD diffusion coefficient versus momentum, for three temperatures, used in the Langevin equation

We aim to compare the diffusion within the Langevin dynamics with that in the EvGlasma with the same energy density. To this end, for each EvGlasma calculation with a $Q_s$, we compute the temperature of the thermalized medium by means of (22). This temperature enters in the Debye mass (24) and in the distribution functions of the thermalized gluon medium. Moreover, we use the same $\alpha _s=\alpha _s(Q_s)$ in both the Langevin and the EvGlasma calculations: this enters both as an overall factor in $|{\mathcal {M}}_{c\ell \rightarrow c\ell }|^2$ and in the Debye mass. For completeness, in Fig. 6, we plot the diffusion coefficient that we use in the Langevin equation; we show D versus momentum for three values of temperature that are of interest in this study.

Fig. 7

$\sigma _p$ versus time for EvGlasma and pQCD Langevin dynamics. The $Q_s$ in the legend for each Langevin calculation reminds that the calculation has been performed on the top of a gluon bulk with the energy density of the EvGlasma with that $Q_s$

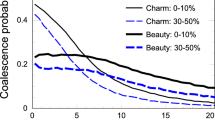
In Fig. 7, we plot $\sigma _p$ versus time for EvGlasma and pQCD Langevin dynamics; results for both charm and beauty quarks are shown. In the legend, the $Q_s$ for the Langevin calculations is a reminder that the calculation has been performed on the top of a gluon bulk with the energy density of the EvGlasma with that $Q_s$. In Fig. 8, we plot the time averaged $\sigma _p$ at $t=1$ fm/c and $t=0.4$ fm/c for both EvGlasma and Langevin cases.

Fig. 8

Time average of $\sigma _p$ at $t=1$ fm/c (upper panel) and $t=0.4$ fm/c (lower panel) versus $Q_s$ for EvGlasma and pQCD Langevin dynamics. Calculations correspond to the static box geometry

The Langevin results in Figs. 7 and 8 are quite interesting. Firstly, we notice that $\sigma _p$ versus time is qualitatively different from that of the EvGlasma because in the former there is no memory, therefore $\sigma _p\propto t$ in the time range considered (drag would make the growth of $\sigma _p$ slower for times of the order of the thermalization time of the heavy quarks).

However, looking in particular in Fig. 8, we note that for small $Q_s$, namely when the fields of the EvGlasma are not intense, the average $\sigma _p$ in the two calculations is comparable. This is due to the fact that for small $Q_s$ the energy density is small so the EvGlasma is closer to a dilute gluon system and momentum diffusion is similar to that of a collisional dynamics. For large $Q_s$, the discrepancy between the two systems becomes substantial, and it is due to the fact that heavy quarks in the EvGlasma experience strong coherent gluon fields while the dynamics remains collisional in the Langevin case. Therefore, one way to read Fig. 8 is that on average, the diffusion coefficient of EvGlasma and pQCD are similar for small $Q_s$, in the sense that on the same time scale, the momentum spreading is comparable in the two cases.

One interesting point in Fig. 8 is that in the Langevin case, $\sigma _p$ decreases with the quark mass, while the opposite behavior is found for the EvGlasma. This qualitative difference can be understood easily. In the pQCD Langevin, the scattering rate of the heavy quarks with the thermal bath decreases with the mass, because the velocity of the quarks themselves decreases with the mass and the scattering rate is proportional to the cross section times the velocity. On the other hand, in the EvGlasma case, the larger mass of the quark implies a smaller velocity in the transverse plane, hence a larger time spent within a flux tube where the gluon field is coherent; therefore, beauty quarks experience the nonlinear growth $\sigma _p\propto t^2$ for a longer time than charm quarks do, eventually leading to larger $\sigma _p$.

3.3 Momentum broadening for the system with the longitudinal expansion

In this subsection, we report on the momentum broadening of charm quarks obtained in a gluon system subject to a boost-invariant longitudinal expansion, and we compare it with that of the gluon system in a static box. Again, we show some results up to $\tau =1$ fm/c for illustrative purposes only, keeping in mind that in realistic collisions at the LHC the expanding EvGlasma is relevant up to $\tau \approx 0.4$ fm/c.

In the case of the longitudinally expanding medium it is convenient to shift from (t, z) to $(\tau ,\eta )$ coordinates, to take advantage of the boost invariance of the EvGlasma fields. In this case, the initial longitudinal, $\eta -$components of the fields are given by

$$\begin{aligned} E^\eta= & {} -ig \sum _{i=x,y} \Big [\alpha ^{(B)}_i, \alpha ^{(A)}_i\Big ], \end{aligned}$$

(25)

$$\begin{aligned} B^\eta= & {} -ig \Big (\Big [\alpha ^{(B)}_x, \alpha ^{(A)}_y\Big ]+\Big [\alpha ^{(A)}_x, \alpha ^{(B)}_y\Big ]\Big ), \end{aligned}$$

(26)

while the transverse components vanish; the $\alpha _i$ fields are defined as in (4) and (5). The CYM equations read

$$\begin{aligned} E^{i}= & {} \tau \partial _{\tau } A_{i}, \end{aligned}$$

(27)

$$\begin{aligned} E^{\eta }= & {} \frac{1}{\tau } \partial _{\tau } A_{\eta }, \end{aligned}$$

(28)

and

$$\begin{aligned} \partial _{\tau } E^{i}= & {} \frac{1}{\tau } D_{\eta } F_{\eta i}+\tau D_{j} F_{j i}, \end{aligned}$$

(29)

$$\begin{aligned} \partial _{\tau } E^{\eta }= & {} \frac{1}{\tau } D_{j} F_{j \eta }. \end{aligned}$$

(30)

Finally, the energy density is given by

$$\begin{aligned} \varepsilon = \mathrm {Tr}\left[ \frac{1}{\tau ^2}E^i E^i + E^\eta E^\eta +\frac{1}{\tau ^2} B^i B^i + B^\eta B^\eta \right] . \end{aligned}$$

(31)

Fig. 9

Energy density, $\varepsilon$, versus proper time for the static (solid green) and the longitudinally expanding (dot-dashed blue) boxes. Calculations correspond to $Q_s=2$ GeV. Dashed black line guides the eyes on the free streaming $\tau ^{-1}$ behavior of $\varepsilon$, that occurs for $Q_s t\approx 1$ namely for $t\approx 0.1$ fm/c

In Fig. 9, we plot, for the sake of reference, the energy density versus the proper time for $Q_s=2$ GeV, in the cases of a static box and a longitudinally expanding medium. Obviously, $\varepsilon$ stays constant in the case of the static box, while it decays with the free streaming behavior $\varepsilon \propto \tau ^{-1}$ after a short transient in the case of the expanding system. The transition from the initial state to the free streaming solution happens around $Q_s t\approx 1$.

Fig. 10

$\sigma _p$ versus proper time for charm quarks. Values of $Q_s$ used in the calculations are shown in the legend. In the upper panel, we perform calculations up to $\tau =1$ fm/c, while in the lower panel, we zoom in the range up to $\tau =0.4$ fm/c

In Fig. 10, we plot $\sigma _p$ of charm quarks, computed for a system subject to a boost-invariant longitudinal expansion, and we compare it with that obtained for a static box. The longitudinal expansion mimics better the initial stage of the high energy nuclear collisions. In the lower panel of Fig. 10, we offer a zoom of the upper panel for very early time, up to $\tau \approx 0.4$ fm/c, which corresponds to the effective time range in which our calculation is phenomenologically interesting.

Fig. 11

Time average of $\sigma _p$ for charm quarks, in the case of the longitudinally expanding box

For the sake of completeness, in Fig. 11, we plot the time average of $\sigma _p$ for charm quarks, in the case of the longitudinally expanding box; results for beauty are similar. In comparison with the results of the static box, see Fig. 8, we note that the expansion lowers the average $\sigma _p$ of a factor of about 2–5: this is expected due to the dilution of the energy density for the expansion. However, as shown already in [51], this is enough to tilt the spectrum of the heavy quarks, see also [50]. A systematic study of the potential effects on the observables will be the subject of a future study.

4 Conclusions

We have analyzed in some detail the diffusion of heavy quarks, charm and beauty, in the strong gluon fields that are produced in the early stage of relativistic heavy ion collisions. The dynamics of the fields is described by the classical Yang–Mills equations with the Glasma initialization, while heavy quarks are evolved via the relativistic kinetic Wong equations in the probe approximation. The evolving gluon fields have been baptized as the EvGlasma, where Ev stands for evolving.

We have studied the transverse momentum broadening, $\sigma _p$, as well as the diffusion in the transverse coordinate plane, $\sigma _x$, for both c and b. We have found that differently from the standard Brownian motion, $\sigma _p\propto t^2$ in the very early stage, while the linear behavior $\sigma _p\propto t$ is achieved in the later stage. The early stage behavior is related to the memory in the Lorentz force acting on the heavy quarks; the linear increase in $\sigma _p$ with time in the later stage is interpreted by noticing that heavy quarks get enough transverse velocity by the color fields, so on average they can jump from one flux tube to another; since the tubes are placed randomly in the transverse plane, fast heavy quarks experience, on average, a diffusion in a random medium like particles in the standard Brownian motion without a drag force, hence $\sigma _p\propto t$.

We have found that momentum diffusion in the EvGlasma is enhanced by the quark mass; we understand this by noticing that that the larger the mass, the slower the heavy quark is, therefore a large mass quark spends more time within a single flux tube than a light quark, and experiences the nonlinear growth of $\sigma _p$ resulting in a larger averaged $\sigma _p$. This interpretation is supported by the coordinate diffusion that instead is suppressed by the quark mass confirming that the large mass quarks diffuse into small regions of the transverse plane.

We have then compared the diffusion in the EvGlasma with that of a standard Langevin dynamics: the kinetic coefficients in the latter case have been computed within pQCD at finite temperature. To this end, we have prepared a bath of thermalized, massless gluons with energy density, $\varepsilon$, equal to that of the EvGlasma for a given value of $Q_s$. From $\varepsilon$, we have extracted the temperature, T, that we have used to compute the screened cross sections in the thermal medium. The strong coupling used in the Langevin calculations is the same that we have used for the EvGlasma, $g=g(Q_s)$.

We have found that for small $Q_s$, the average $\sigma _p$ in the two systems is fairly the same. This can be interpreted by noticing that for small $Q_s$ the EvGlasma is made of diluted gluon fields, thus the dynamics of the heavy quarks is expected to be similar to a collisional one. This result also shows that the diffusion coefficient of heavy quarks in the EvGlasma is in agreement with that of pQCD, in the case of small energy density.

On the other hand, quantitative differences appear for large $Q_s$: in this case, the dynamics of the heavy quarks in the EvGlasma cannot be reduced to a collisional one because the gluon fields are too intense. In particular, the Langevin dynamics with pQCD coefficients underestimates the $\sigma _p$, meaning that one would need to input a larger diffusion coefficient in the Langevin equations to reproduce the $\sigma _p$ in the EvGlasma. As a result, one cannot use the Langevin equations with pQCD coefficients to analyze the diffusion in intense EvGlasma and the relativistic kinetic equations coupled to the evolving gluon fields have to be considered.

Another interesting result, shown in Fig. 8, is that beauty quarks are more affected by the evolution in the EvGlasma: this is understood because beauty quarks are slower, then they spend more time within a single filament and experience more the coherent gluonic fields that lead to $\sigma _p\propto t^2$.

We have also studied the effect of the longitudinal expansion on the transverse momentum broadening. For this, we have limited to a few representative values of $Q_s$ and to the charm quarks, since results for different $Q_s$ and beauty quarks are similar. We have found that in this case, $\sigma _p$ tends to saturate while for the static box it increases indefinitely. We can explain this easily in terms of the dilution of the energy density due to the expansion, that implies that the average magnitude of the color fields, thus of the force acting on the heavy quarks, becomes smaller and the EvGlasma diffuses $p_T$ less efficiently.

In the future, we would like to study in a more systematic way the impact of the momentum broadening in the early stage on some observables: among these, collective flows and two-particle correlations are of a certain interest, both in pA and in AA collisions.

We could improve our calculations in several ways. Firstly, the drag force could be introduced by adding the color current carried by c and b in the Yang–Mills equations. This force would slow down the evolution of $\sigma _p$ with time; however, as shown in [53], the equilibration time of heavy quarks in th EvGlasma is of the order of $\tau _\mathrm {equil}\approx 10$ fm/c at least, and any effect of the drag would become evident only for $t\approx \tau _\mathrm {equil}$. Therefore, this would not affect the early evolution in a substantial way; however, its inclusion is possible, and we plan to add it in our future works. Another improvement will be the formulation with three colors. Finally, we aim to prepare realistic initializations that include initial state fluctuations, the correct geometrical shape of the initial state and the small-x evolution of the initial color charges. We plan to add all these things in future works.

Appendix A: Temperature

Fig. 12

Temperature of a massless gluon system versus $Q_s$ obtained by means of Eq. (22), where $\varepsilon$ is the energy density of Glasma corresponding to the specified value of $Q_s$

In Fig. 12, we plot, for completeness, the temperature of a massless gluon system versus $Q_s$ obtained by means of Eq. (22), where $\varepsilon$ is the energy density of Glasma corresponding to the specified value of $Q_s$. This is the temperature that we use to compute the diffusion coefficient in pQCD that we have used in the Langevin equation in Sect. 3.2.