1 Introduction

Recent observation of evidence of astrophysical black holes, such as images of supermassive black hole [1,2,3,4,5,6], X-ray flare due to the orbital motion of matter near a supermassive black hole [7,8,9] and other type of stellar X-ray sources, provide new motivations for studying the dynamical motion of test particles and massless photons in the framework of general relativity and theories of gravity. The neutral particles motion is governed by geodesic equations and directly examines the geodesic structure of spacetime. However, charged test particles can experience not only gravitational, but also an electromagnetic field, and, accordingly can provide information about the electromagnetic properties of black holes being responsible for their rich observational phenomenology in high energy electromagnetic radiation.

It is also widely believed that high-energy cosmic rays are produced due to relativistic charged particle in the presence of the external electromagnetic field in the vicinity of the black hole [10,11,12,13,14,15]. The high-energy acceleration of ionized particles by electric Penrose process has been discussed in [16]. The producing high energy caused by the collisions of two particles in the vicinity of the regular black holes has been studied in Refs. [17,18,19,20]. The quasi-periodic oscillations (QPOs) occurred in the inner parts of the accretion disks around the black holes have been extensively explored in Refs. [21,22,23,24,25]. The detailed description of the oscillation models in the accretion disk is presented in the review paper [26].

In Refs. [27, 28], the significance of the electric and magnetic charges of the astrophysical black hole has been discussed. The detailed analyses of neutral particles motion [29], dynamics of charged particles [30,31,32,33,34] in Reissner–Nordström spacetime has been studied. In the Ref. [35], the dynamics of electrically and magnetically charged test particles in the Reissner–Nordström spacetime has been investigated. The capture cross-section of massless and massive particles by the charged black hole has been investigated in [36]. Charged particle motion around string charged black hole has been discussed in [37]. The innermost stable circular orbits of charged spinning test particles have been analyzed in [38]. The analytical and numerical analysis of the quasi-normal modes and relaxation rate of wave in the spacetime of the charged black hole has been discussed in [39,40,41,42,43,44]. In Ref. [45], the effect of charged particles acceleration by the black holes in Reissner–Nordström spacetime has been studied. The acceleration of charged particles from the polar cap of the magnetized neutron star has been studied in [46,47,48]. The dynamics and stable orbital motion circular of the test particle around tidal charged black hole has been studied in [49, 50].

It is well-known that spherically symmetric, charged gravitational body with the mass M and charge Q can be described by the Reissner–Nordström spacetime [51]:

$$\begin{aligned} -g_\mathrm{tt}=g_\mathrm{rr}^{-1}=1-\frac{2GM}{c^2r}+\frac{GQ^2}{c^4r^2}\ ,\qquad g_{\theta \theta }=r^2\ , \qquad g_{\theta \theta }=r^2 \sin ^2\theta \ . \end{aligned}$$
(1)

where \(G=6.674 30(15)\times 10^{-8}\mathrm{cm^3 g^{-1}s^{-1}}\) is the Newtonian gravitational constant, and \(c=2.99 792 458\times 10^{10}\mathrm{cm\, s^{-1}}\) is the speed of light (see, for example [52]). However, throughout the paper, we use a spacelike signature \((-,+,+,+)\) and a geometrized units with \(G=c=1\), while in the estimation of observational quantities we restore the gravitational constant and speed of light. It is worth noting that Q can be either the electric charge (\(Q=Q_\mathrm{e}\)) or magnetic charge (\(Q=Q_\mathrm{m}\)) of the black hole, and associated electromagnetic vector potential can be expressed as

$$\begin{aligned} A_\alpha =\left( -\frac{Q_e}{r},0,0,0\right) ,\qquad A_\alpha =\left( 0,0,0,-Q_m\cos \theta \right) \ , \end{aligned}$$
(2)

with the following components of the electromagnetic fields \(E_{{\hat{r}}}=Q_e/r^2\) and \(B_{{\hat{r}}}=Q_m/r^2\), respectively.

Note that both solutions for vector potential in (2) together with the spacetime metric (1) satisfy the Einstein-Maxwell field equations. In the literature, it is claimed by several authors that the black hole can be dyonically charged, which means that it possesses both electric and magnetic charges, simultaneously with a total charge \(Q=\sqrt{Q_e^2+Q_m^2}\). In this case, the components of the associated vector potential will be given by the superposition of solutions in (2) (See, for example: [35]). However, according to Refs. [53, 54], the electric and magnetic charges of the black hole can be imposed simultaneously.

From the astrophysical point of view, it is interesting to estimate the charge of the black hole. The maximal charge of the Reissner–Nordström black hole can be estimated from the fact of existence of the black hole horizon, as \(Q_{\mathrm{max}}=\sqrt{G}M\), more precisely, one can get

$$\begin{aligned} Q_{\mathrm{max}}\simeq 5.13843\times 10^{29} \left( \frac{M}{M_\odot }\right) \mathrm{statC}\ , \end{aligned}$$
(3)

which is huge charge in nature. However, the maximal specific charge for Reissner–Nordström black hole can be estimated as \(Q_{\mathrm{max}}/M\simeq 2.58342\times 10^{-4}\mathrm{statC/g}\). On the other hand, it is well-known that the specific charge of the electron is \(e/m_e\simeq 5.27281\times 10^{17}\mathrm{statC/g}\) (see, for example [52]), and it can be easily found that

$$\begin{aligned} \frac{e}{m_e}>>\frac{Q_{\mathrm{max}}}{M}\ , \end{aligned}$$
(4)

where \(m_e\), e are the mass and charge of electron, respectively.

Here we plan to study charged test particle motion around spherically symmetric, electrically (ECBH) and magnetically (MCBH) charged black holes. In order to compare the effect of the gravitational and electromagnetic fields one can consider the ratio of the Coulomb potential and the rest energy of particle as \(-qQ/(rmc^2)\), which can be easily estimated as

$$\begin{aligned} \frac{qQ}{mc^2r}\le \frac{qQ_\mathrm{max}}{mc^2r}\simeq 2\times 10^{21}\left( \frac{q}{e}\right) \left( \frac{m_e}{m}\right) \left( \frac{1}{\bar{r}}\right) \ , \end{aligned}$$
(5)

where \(\bar{r}=r/(GM/c^2)\) is the normalized radial coordinate. One can see here that electromagnetic interaction dominates for charged particle which means that the small value of the black hole charge is enough to accelerate charged particles.

In the present paper, we investigate charged particle dynamics in the vicinity of the charged black hole. We explicitly show the difference between ECBH and MCBH by studying the circular motion of a charged particle around a charged black hole. (1) studying the ISCO position of charged particle around charged black hole which is widely believed to be a candidate for an inner edge of the accretion disk surrounding an astrophysical black hole. (2) the fundamental frequencies, namely, Keplerian, Larmor and epicyclic frequencies, which are good candidate to explore quasi-periodic oscillation QPO in the accretion disk around X-ray sources. (3) the synchrotron radiation from charged particle orbiting around the charged black hole.

The paper has been organized as follows: In Sect. 2, we provide basic necessary equations related to charged particle motion in the spacetime of the charged black hole. In Sect. 3, we investigate the general description to derive the fundamental frequencies for charged particles orbiting around static black hole described by an arbitrary spacetime with given stationary, axially-symmetric metric coefficients, and electromagnetic fields. Later on, we apply results obtained for Reissner–Nordsröm spacetime in order to derive the difference between properties of ECBH and MCBH. In next Sect. 4, we overview basic equations in curved spacetime to determine the intensity of relativistic charged particle accelerated by the black hole, as well as ECBH and MCBH. Then we compare the results obtained for these two different black holes. Finally, in Sect. 5, we summarize the main results and give a future outlook related to this work.

2 Basic equations

In this section, we investigate charged particle dynamics in the vicinity of the ECBH and MCBH separately. We study the dynamical motion of charged particle around a charged black hole. The Lagrangian for a charged particle with mass of m and charge q can be expressed as

$$\begin{aligned} {{\mathscr {L}}}=\frac{1}{2}mg_{\alpha \beta }U^\alpha U^\beta +q U^\alpha A_\alpha \ , \end{aligned}$$
(6)

and the dynamical motion of charged particle is governed by the following equation

$$\begin{aligned} \frac{dU^\alpha }{d\lambda }+{\varGamma }_{\mu \nu }^\alpha U^\mu U^\nu =\frac{q}{m} F^\alpha _{\,\,\beta }U^\beta \ , \end{aligned}$$
(7)

where \(U^\alpha =dx^\alpha /d\lambda \) is the four-velocity of particle normalized as \(g_{\alpha \beta }U^\alpha U^\beta =-1\), \(\lambda \) is an affine parameter, \(F_{\alpha \beta }=A_{\beta ,\alpha }-A_{\alpha ,\beta }\) is the electromagnetic field tensor and \({\varGamma }_{\mu \nu }^\alpha \) are the Christoffel symbols. Notice that Eq. (7) is valid for charged particle motion around both ECBH and MCBH, respectively. However, difference arises due to the canonical four-momentum of charged particle defined as \(P_\alpha =mU_\alpha +qA_\alpha \). Taking into account the definitions of the four-potential in (2), the conserved quantities, namely, specific energy \({{\mathcal {E}}}\), and specific angular momentum \({{\mathcal {L}}}\) of charged particle, measured at the infinity, around ECBH can be found as

$$\begin{aligned} g_{tt}U^t+\frac{q}{m}A_t=-{{\mathcal {E}}}\ , \qquad g_{\phi \phi }U^\phi ={{\mathcal {L}}}\ , \end{aligned}$$
(8)

while around MCBH, they have the form

$$\begin{aligned} g_{tt} U^t=-{{\mathcal {E}}}\ , \qquad g_{\phi \phi }U^\phi +\frac{q}{m}A_\phi ={{\mathcal {L}}}\ . \end{aligned}$$
(9)

As we can see from Eqs. (8) and (9) that the specific energy of charged particle in the vicinity of ECBH is shifted by \(-(q/m)A_t\), and its angular momentum does not change, while in the vicinity of MCBH the specific energy does not change, and the angular momentum is shifted by \((q/m)A_\phi \), respectively.

Hereafter, using normalization of the four-velocity, taking into account the expressions (8) and (9), one can obtain

$$\begin{aligned} g_{rr}(U^r)^2+g_{\theta \theta }(U^\theta )^2+V(r,\theta )=0\ , \end{aligned}$$
(10)

where the function \(V(r,\theta )\) is defined as

$$\begin{aligned} V(r,\theta )= 1+\frac{1}{g_{tt}}{{\mathcal {E}}}^2+\frac{1}{g_{\phi \phi }}\left( {{\mathcal {L}}}-\frac{q}{m}A_\phi \right) ^2. \end{aligned}$$
(11)

On the other hand, using the normalization of four-velocity and hereafter introducing the spatial components of three-velocity of test particle measured by local observer

$$\begin{aligned} v_{{\hat{r}}}=\frac{\mathrm{d}r}{\mathrm{d}t}\sqrt{-\frac{g_\mathrm{rr}}{g_\mathrm{tt}}}\ ,\qquad v_{{\hat{r}}}=\frac{\mathrm{d}\theta }{\mathrm{d}t}\sqrt{-\frac{g_{\theta \theta }}{g_\mathrm{tt}}}\ ,\qquad v_{{\hat{r}}}=\frac{\mathrm{d}\phi }{\mathrm{d}t}\sqrt{-\frac{g_{\phi \phi }}{g_\mathrm{tt}}}\ , \end{aligned}$$
(12)

with \(v^2=v_{{\hat{r}}}^2+v_{{\hat{\theta }}}^2+v_{{\hat{\phi }}}^2\), one can obtain the classical expression for the energy of charged test particle, in the presence of the external electromagnetic fields, in curved spacetime as

$$\begin{aligned} {{\mathcal {E}}}=\sqrt{\frac{-g_{tt}}{1-v^2}}-\frac{q}{m}A_t\ . \end{aligned}$$
(13)

2.1 Innermost stable circular orbit (ISCO)

It is important to compute the radius of the stable circular orbit for charged particles, so-called innermost stable circular orbit (ISCO), orbiting around ECBH and MCBH. In order to find ISCO radius for charged test particle, one can explore the following conditions:

$$\begin{aligned} V(r,\theta )=0,\qquad \partial _r V(r,\theta )=\partial _\theta V(r,\theta )=0, \qquad \partial _r^2 V(r,\theta )\ge 0, \qquad \partial _\theta ^2 V(r,\theta )\ge 0. \end{aligned}$$
(14)

Here the first condition in Eq. (14) provides the particle motion to be in the circular orbit i.e. \(U^r=U^\theta =0\), which can be easily derived from Eq. (10), while the first-order derivatives with respect to coordinates (\(r,\theta \)) represent the stationary point of the function \(V(r,\theta )\), and finally, the last two conditions in (14) correspond to the minimum of the function \(V(r,\theta )\), which allows to write equation for ISCO radius of charged test particle. Here we will discuss the different aspects of the properties of ECBH and MCBH. The function \(V(r,\theta )\) explains the behavior of charged particles in the vicinity of ECBH and MCBH, where they are influenced by the gravitational and electromagnetic forces, simultaneously.

Now we are in a position to determine the ISCO radius for charged particles orbiting around ECBH and MCBH. For simplicity, we assume that the contribution of the black hole’s charge on background spacetime is comparatively small, however, the electromagnetic interaction between the black hole and charged particle is very important. For simplicity, one can simply ignore the effect of the electromagnetic contribution on the background spacetime \(Q^2\rightarrow 0\). In this section, the whole analysis will be done by using the dimensionless charge coupling parameters which are given by, \(\sigma _e=qQ_e/(\sqrt{G}mM)\) and \(\sigma _m=qQ_m/(\sqrt{G}mM)\), or

$$\begin{aligned} \sigma _{e,m}< 2\times 10^{21} \left( \frac{q}{e}\right) \left( \frac{m_e}{m}\right) \ . \end{aligned}$$
(15)

The charged particle motion around ECBH (i.e., \(\sigma _e\ne 0\), \(\sigma _m=0\)) is quite well-known task and been studied by many authors (see, for example: [32, 33, 35]). Nevertheless, we produce all results in order to show the difference between ECBH and MCBH through particle dynamics. The ISCO radius for charged particle around MCBH is rather simple than that obtained in ECBH. Using the conditions (14), we find that the ISCO radius and the energy of the charged particle at ISCO will be the same as for a neutral particle, as shown in Ref. [29], however, the critical angular momentum takes a form \({{\mathcal {L}}}_0=\sqrt{\sigma _m^2+12}\). Another interesting result is that the position of a charged particle rotating around MCBH is displaced from the equatorial plane with angle \(\theta _0=\tan ^{-1}\left( 2\sqrt{3}/\sigma _m\right) \), depending on the coupling parameter \(\sigma _m\), which concludes that the charge separation will happen around MCBH. Figure  1 shows the ISCO position for charged particles orbiting around ECBH and MCBH.

Fig. 1
figure 1

Dependence of the ISCO radius for charged particle orbiting around ECBH and MCBH from the various values of coupling parameters \(\sigma _e=qQ_e/(mM)\) and \(\sigma _m=qQ_m/(mM)\) in the range between \((-5,1)\) assuming that both coupling parameters are in the same scale. (Left panel) The ISCO radius for charged particle is function of the coupling parameters. (Right panel) The off-equatorial position of the ISCO is the function of the coupling parameters

Full size image

In order to better understand charged particle motion in the vicinity of the charged black hole, we produce the trajectory of charged particles around the MCBH illustrated in Fig. 2. This consideration has been studied in the Refs. [55,56,57,58]. We set the constants of motion, which are the specific energy and specific angular momentum, and the initial position of the particle (\(r_0, \theta _0\)). One can observe that in (x, y) plane there is no difference between trajectories of positively and negatively charged particles around the MCBH. In opposite, in (x, z) plane, one can observe the charge separation symmetrically to the equatorial plane in vertical directions, which is shown in central panel of Fig. 2. In the last panel the same plot is illustrated in (\(x-y-z\)) plane.

Fig. 2
figure 2

The trajectories of charged particles in the vicinity of the MCBH in the different horizontal and vertical planes. The trajectories of charged test particle in the \((x-y)\) plane in the left, in the \((x-z)\) plane in the right panel are illustrated

Full size image

The energy efficiency of the particle can be determined as \(\eta =1-{{\mathcal {E}}}_0\), where \({{\mathcal {E}}}_0\) is the specific energy of a particle at the ISCO. This value of the energy efficiency for a neutral particle in Schwarzschild space is about \(\sim 5.7\%\), while for a maximally charged black hole it is \(\sim 8.9\%\). It can reach up to \(\sim 70\%\) for a charged particle orbiting around ECBH, while around MCBH it is independent of coupling parameter \(\sigma _m\) and will be the same as for neutral particle.

In Table 1, the detailed numerical calculations of the ISCO parameters such as radius, location, orbital velocity, specific energy, specific angular momentum, and energy efficiency of charged particles are listed. It can be easily seen from Table 1 that the ISCO radius for a charged particle around MCBH is the same as for a neutral particle, while around ECBH it is always larger for positively and negatively charged particles. Interestingly, one can see that the location of charged particles around ECBH is in the equatorial plane, however, around MCBH it is displaced from the equatorial plane, which concludes that charged separation can be observed near the equatorial plane depending on the coupling parameter \(\sigma _m\). One can see that the orbital velocity of a charged particle around MCBH is half the speed of light, however, around ECBH it can reach the values between zero and the speed of light.

Table 1 The critical values of radius, angle, specific energy, specific angular momentum, energy efficiency and orbital velocity of charged particle at the innermost stable circular orbit (ISCO) around ECBH and MCBH are listed. For simplicity, we assume that the square of the black hole charge is negligible \(Q^2\rightarrow 0\)
Full size table

3 Fundamental frequency of charged particle

It is interesting to consider the periodic motion of charged particles orbiting around the black hole which allows determining the fundamental frequencies such as Keplerian and Larmor frequencies. The most simple way of deriving the expressions for the frequencies is to consider motion in the stable circular orbit with, \(U^\alpha =(U^t,0,0,U^\phi )\), which allows to write

$$\begin{aligned} U^t=\frac{1}{\sqrt{-g_\mathrm{tt}-{\varOmega }^2g_{\phi \phi }}}\ , \end{aligned}$$
(16)

where \({\varOmega }=d\phi /dt\) is the angular velocity of the orbital motion measured by a distant observer. Using the expression (16), the expressions for the conservative quantities in the spacetime of ECBH are rewritten as

$$\begin{aligned} {{\mathcal {E}}}=-\frac{g_\mathrm{tt}}{\sqrt{-g_\mathrm{tt}-{\varOmega }^2g_{\phi \phi }}}-\frac{q}{m}A_t\ , \qquad {{\mathcal {L}}}=\frac{{\varOmega } g_{\phi \phi }}{\sqrt{-g_{tt}-{\varOmega }^2g_{\phi \phi }}}\ , \end{aligned}$$

while in the spacetime of MCBH, they take the form:

$$\begin{aligned} {{\mathcal {E}}}=-\frac{g_{tt}}{\sqrt{-g_{tt}-{\varOmega }^2g_{\phi \phi }}}\ , \qquad {{\mathcal {L}}}=\frac{{\varOmega } g_{\phi \phi }}{\sqrt{-g_{tt}-{\varOmega }^2g_{\phi \phi }}}+\frac{q}{m}A_\phi \ . \end{aligned}$$
(17)

We determine the orbital velocity of charged particle around black hole. The expression for the orbital velocity of particle measured by a local observer in curved spacetime is defined as [32, 59]

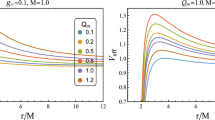
$$\begin{aligned} v={\varOmega }\sqrt{-\frac{g_{\phi \phi }}{g_{tt}}}\ . \end{aligned}$$
(18)

In order to evaluate the orbital linear velocity of the neutral particles orbiting around a charged black hole, we first calculate it at the different radii as illustrated in Fig. 3. One can easily see from Fig. 3 that the neutral particle rounds with half of the speed of light, \(v_0=0.5\), at the ISCO position around the Schwarzschild black hole, while it can orbit rapidly around charged black hole depending on the value of the charge parameter. For extreme Reissner–Nordström black hole, the orbital velocity can reach up to \(v_0=1/\sqrt{3}\). We have also calculated the orbital linear velocity of the neutral particle at the marginally bound orbit (MBO), it is about \(v_0=1/\sqrt{2}\) with respect to that around Schwarzschild black hole. The value of the orbital velocity of the neutral particle at the stable orbit around the extreme black hole is about \(v_0=c\). Similarly, the orbital velocity of charged particles orbiting around the charged black hole can be derived. The numerical values of the orbital velocities of charged particles at the ISCO position around ECBH and MCBH are listed in the top and bottom panels of Table 1, respectively.

Fig. 3
figure 3

Dependence of orbital velocity of particle from blackhole’s charge in positions with different radii

Full size image

3.1 Keplerean and Larmor frequencies

Now we focus on the derivation of the expression for the orbital angular frequencies, such as Keplerian and Larmor frequencies of the charged particles orbiting around the black hole. To do this, we assume motion of particles in circular orbit with \(U^\alpha =U^t(1,0,0,{\varOmega })\). In this case, according to (7), equations for radial and vertical motion for charged particles around ECBH can be written as

$$\begin{aligned} g_{tt,r}+{\varOmega }^2g_{\phi \phi ,r}=-\frac{2q}{m}\frac{F_{rt}}{U^t},\quad {\varOmega } g_{\phi \phi ,\theta }=0, \end{aligned}$$
(19)

and around MCBH it takes a form:

$$\begin{aligned} g_{tt,r}+{\varOmega }_G^2g_{\phi \phi ,r}=0,\quad {\varOmega }_{\mathrm{L}} g_{\phi \phi ,\theta }=-\frac{2q}{m}\frac{F_{\theta \phi }}{U^t}. \end{aligned}$$
(20)

Note that the physical meaning of the quantity \({\varOmega }\) in equations (19) is the angular velocity of a charged particle orbiting around ECBH, while \({\varOmega }_G\) and \({\varOmega }_L\) in Eq. (20) are the angular velocity of charged particle around MCBH due the gravitational and electromagnetic fields, respectively. However \({\varOmega }\) and \({\varOmega }_G\) have the same meaning for a neutral particles i.e., when \(q=0\). In this case, the solution of the first Eqs. in (19) and (20) becomes, \({\varOmega }_K=\sqrt{-g_{tt,r}/g_{\phi \phi ,r}}\) at \(\theta =\pi /2\), which represents Keplerian frequency for neutral particle, while the solution of the second equation will vanish. The solution of Eq. (19) is responsible for the angular velocity of charged particle. Hereafter we eliminate \(U^t\) by inserting the expression (18) into (19), and after performing simple algebraic manipulations the angular velocity for charged particle orbiting around the ECBH can be found as

$$\begin{aligned} {\varOmega }_{\mathrm{ECBH}}^2={\varOmega }_K^2-\frac{g_{\phi \phi }}{2}\left( \frac{2qF_{rt}}{mg_{\phi \phi ,r}}\right) ^2\pm \frac{2qF_{rt}}{mg_{\phi \phi ,r}}\sqrt{-g_{tt}-{\varOmega }_K^2g_{\phi \phi }+\frac{g_{\phi \phi }^2}{4}\left( \frac{2qF_{rt}}{mg_{\phi \phi ,r}}\right) ^2}\ . \end{aligned}$$
(21)

On the other hand, the same problem can be easily considered for charged particle around the MCBH. However, one needs to be careful because the angular velocity of charged particle is caused due to the gravitational and magnetic field effects. One needs to take the effects simultaneously and find the angular velocity \({\varOmega }_{\mathrm{MCBH}}\) for charged particle. The solution of the first Eq. (20) gives the angular velocity of charged particle due to pure gravitational field \({\varOmega }_G\) while the second one represents the Larmor frequency \({\varOmega }_L\) due to the external monopole magnetic field. One can get \({\varOmega }_{\mathrm{MCBH}}={\varOmega }_G+{\varOmega }_L\) for the explicit expressions for angular frequency of charged particle orbiting around MCBH. Replacing \({\varOmega }\) in Eq. (16) with \({\varOmega }_{\mathrm{MCBH}}\) and combining it with Eq. (20) one can find \({\varOmega }_G\) and \({\varOmega }_L\). Indeed, in this case, one can solve three equations for three unknown quantities. The solution of the first Eq. (20) is simple and can be found as \({\varOmega }_G=\sqrt{-g_{tt,r}/g_{\phi \phi ,r}}\). The Larmor frequency \({\varOmega }_L\) satisfies the following equation:

$$\begin{aligned} {\varOmega }_L^2\left( 1+\delta \right) +2{\varOmega }_G{\varOmega }_L+{\varOmega }_G^2+\frac{g_{tt}}{g_{\phi \phi }}=0\ , \end{aligned}$$
(22)

where

$$\begin{aligned} \delta =\frac{2}{g_{\phi \phi }}\left( \frac{mg_{\phi \phi ,\theta }}{2qF_{\theta \phi }}\right) ^2\ . \end{aligned}$$

Finally, the angular velocity of charged particle orbiting around MCBH can be expressed as

$$\begin{aligned} {\varOmega }_{\mathrm{MCBH}}=\frac{1}{1+\delta }\left[ \delta {\varOmega }_G+\sqrt{-\delta {\varOmega }_G^2-(1+\delta )\frac{g_{tt}}{g_{\phi \phi }}}\right] \ . \end{aligned}$$
(23)

Indeed, for neutral particle i.e. \(q=0\), \({\varOmega }_{\mathrm{MCBH}}\) simply reduces to Keplerian frequency, which can be easily verified by considering the following limit:

$$\begin{aligned} \lim _{\sigma _m\rightarrow 0}{\varOmega }_{\mathrm{MCBH}}=\lim _{\delta \rightarrow \infty }{\varOmega }_{\mathrm{MCBH}}={\varOmega }_G={\varOmega }_{K}, \end{aligned}$$
(24)

at the equatorial plane \(\theta =\pi /2\).

3.2 The epicyclic frequencies

It is also interesting to derive the expressions for the epicyclic frequencies (\({\varOmega }_r, {\varOmega }_\theta \)) produced by the oscillatory motion of charged particles (hot spots) along the radial and vertical directions located at the stable circular orbits around the black hole. Our main interest is in study of the quasi-periodic oscillations (QPOs) of charged particles in the vicinity of the black hole. The QPO is quite well-known observational feature of the accretion disk around the black hole. One of the simple models of explanation of the QPO origin is described by harmonical oscillatory test particles motion [60, 61]. In order to find the epicyclic frequencies, one may expand the function \(V(r,\theta )\) around stationary points (\(r_0,\theta _0\)) in the form:

$$\begin{aligned} V(r,\theta )= & {} V(r_0,\theta _0)+\partial _r V(r,\theta )\delta _r +\partial _\theta V(r,\theta )\delta _\theta +\frac{1}{2}\partial _r^2V(r,\theta )\delta _r^2+\frac{1}{2}\partial _\theta ^2V(r,\theta )\delta _\theta ^2+\partial _r\partial _\theta V(r,\theta )\delta _r\delta _\theta +{{\mathcal {O}}}\left( \delta r^3,\delta \theta ^3\right) \nonumber \\\simeq & {} \frac{1}{2}\delta _r^2\,\partial _r^2V(r,\theta )+\frac{1}{2}\delta _\theta ^2\,\partial _\theta ^2V(r,\theta )\ , \end{aligned}$$
(25)

which is analog of the harmonic oscillator problem. Here we have used the conditions represented in (14). Now, inserting the expression (11) into (10), and using the expression (25) one can obtain equation of harmonic oscillatory motion for charged particles along the stationary orbit (\(r_0, \theta _0\)), for the displacement \(\delta _r=r-r_0\), \(\delta _\theta =\theta -\theta _0\) in the form: \(\ddot{\delta _r}+{\varOmega }_{\mathrm{r}}^2\delta _r=0\) and \(\ddot{\delta _\theta }+{\varOmega }_{\mathrm{\theta }}^2\delta _\theta =0\), where double dots indicate derivative with respect to time and the epicyclic frequencies are determined as

$$\begin{aligned} \left( {\varOmega }_r^2,{\varOmega }_\theta ^2\right) =\frac{1}{2(U^t)^2}\left( \frac{1}{g_{rr}}\partial _r^2V(r,\theta ),\frac{1}{g_{\theta \theta }}\partial _\theta ^2V(r,\theta )\right) \ . \end{aligned}$$
(26)

Finally, using Eqs. (17) and (25), the explicit form of the epicyclic frequencies (\({\varOmega }_r, {\varOmega }_\theta \)) of charged particle orbiting around ECBH can be expressed as

$$\begin{aligned} g_{ii}{\varOmega }_i^2=\frac{(g_{tt,i})^2}{g_{tt}}-\frac{1}{2}g_{tt,ii}+{\varOmega } ^2\left( \frac{(g_{\phi \phi ,i})^2}{g_{\phi \phi }}-\frac{1}{2}g_{\phi \phi ,ii}\right) -\frac{q}{m} \frac{1}{U^t}\left( A_{t,ii}-2A_{t,i}\frac{g_{tt,i}}{g_{tt}}\right) -\left( \frac{q}{m}\right) ^2 \frac{1}{(U^t)^2}\frac{A_{t,i}^2}{g_{tt}}\ , \end{aligned}$$
(27)

while around MCBH, they take the form:

$$\begin{aligned} g_{ii}{\varOmega }_i^2=\frac{(g_{tt,i})^2}{g_{tt}}-\frac{1}{2}g_{tt,ii}+{\varOmega } ^2\left( \frac{(g_{\phi \phi ,i})^2}{g_{\phi \phi }}-\frac{1}{2}g_{\phi \phi ,ii}\right) -\frac{q}{m} \frac{{\varOmega }}{U^t}\left( A_{\phi ,ii}-2A_{\phi ,i}\frac{g_{\phi \phi ,i}}{g_{\phi \phi }}\right) -\left( \frac{q}{m}\right) ^2\frac{1}{(U^t)^2}\frac{A_{\phi ,i}^2}{g_{\phi \phi }}\ , \end{aligned}$$
(28)

where \(i=(r,\theta )\). From Eqs. (27) and (28), one can see that the radial and vertical frequencies (\({\varOmega }_r, {\varOmega }_\theta \)) depend on the background geometry, the external electromagnetic field, and also parameters of the test particle. Once background spacetime geometry and external magnetic field are given,one can immediately determine \({\varOmega }_r\) and \({\varOmega }_\theta \), however, keep in mind that they still depend on Keplerian frequency, which is the most important quantity in the calculation of the fundamental frequencies.

4 Radiation intensity of accelerated charged particle

Accretion of surrounding matter onto a super massive and stellar mass black holes is strongly believed and justified to produce the high energy relativistic particles in the vicinity of the active galactic nuclei (AGN) and stellar low mass X-ray binary sources. The detailed mechanisms of the production of energy in such high energetic sources are still need to be clarified. However, it is widely believed that the magnetic field in rotating black hole environment plays an important role to produce the high energetic relativistic particles (See for example, [13, 14, 16]). Now question arises how the charge of black hole is important to produce energy extraction from the black hole. It is well-known that relativistic charged particle accelerated, in particular, by an external electromagnetic field emits electromagnetic radiation. One of the simplest examples of such radiation processes is known as synchrotron radiation of an accelerated charged particle, which is formed as a relativistic form of the cyclotron radiation. For example synchrotron radiation from charged particle near the magnetized Schwarzschild black hole has been studied in [62]. Here we concentrate on study of the electromagnetic radiation from the accelerated charged particle orbiting the charged black hole. The radiation spectrum of the relativistically moving charged particle in strongly curved spacetime can be expressed as [63]

$$\begin{aligned} I=\frac{2q^2}{3}w_\alpha w^\alpha , \end{aligned}$$
(29)

where \(w^\alpha \) is the four-acceleration of particle in a curved spacetime, defined as \(w^\alpha =U^\beta \nabla _\beta U^\alpha \), on the other hand, taking into account non-geodesic equation (7), one can write

$$\begin{aligned} w^\alpha =\frac{q}{m}F^\alpha _{\,\,\,\beta }U^\beta \ ,\qquad w_\alpha U^\alpha \equiv 0. \end{aligned}$$
(30)

As one can see from Eq. (30) that four-acceleration of particle is an orthogonal to its four-velocity. Finally, taking into account all above-mentioned, one can write expression for the electromagnetic radiation spectrum as

$$\begin{aligned} I=\frac{2q^4}{3m^2}F_{\alpha \gamma }F^{\gamma \beta }U^\alpha U_\beta \ . \end{aligned}$$
(31)

For simplicity, we consider the motion of charged particle in the stable circular orbit with \(U^\alpha =U^t(1,0,0,{\varOmega })\) to see the behavior of the radiation spectrum. Since the velocity and acceleration of particle are orthogonal to each other, i.e., \(w_\alpha U^\alpha \equiv 0\), we can immediately express the four-acceleration of particle in the form, \(w^\alpha =(0,w^r,w^\theta ,0)\), where the components of the acceleration of charged particle around ECBH can be found as

$$\begin{aligned} w_r=\frac{qF_{rt}}{m\sqrt{-g_{tt}-{\varOmega }^2g_{\phi \phi }}}\ ,\qquad w_\theta =0\ , \end{aligned}$$
(32)

while around MCBH, they are defined as

$$\begin{aligned} w_r=0, \qquad w_\theta =\frac{q{\varOmega } F_{\theta \phi }}{m\sqrt{-g_{tt}-{\varOmega }^2g_{\phi \phi }}}\ . \end{aligned}$$
(33)

Finally, the expressions for the intensity of electromagnetic radiation (29) of the radiating accelerated charged particle orbiting around ECBH and MCBH are

$$\begin{aligned} I_{\mathrm{ECBH}}= & {} \frac{2q^4}{3m^2}\left( \frac{1}{-g_{tt}-{\varOmega }^2g_{\phi \phi }}g^{rr}F_{rt}^2\right) _{\mathrm{ECBH}}\ , \end{aligned}$$
(34)
$$\begin{aligned} I_{\mathrm{MCBH}}= & {} \frac{2q^4}{3m^2}\left( \frac{{\varOmega }^2}{-g_{tt}-{\varOmega }^2g_{\phi \phi }}g^{\theta \theta }F_{\theta \phi }^2\right) _{\mathrm{MCBH}}\ , \end{aligned}$$
(35)

which can be estimated as

$$\begin{aligned}&I_{\mathrm{ECBH}}\simeq 1.3\times 10^{24}\left( \frac{q}{e}\right) ^4\left( \frac{m_e}{m}\right) ^{2}\left( \frac{M_\odot }{M}\right) ^{2}\left( \frac{f}{f-{\varOmega }^2r^2}\right) _{\mathrm{ECBH}}\ , \end{aligned}$$
(36)
$$\begin{aligned}&I_{\mathrm{MCBH}}\simeq 1.3\times 10^{24}\left( \frac{q}{e}\right) ^4\left( \frac{m_e}{m}\right) ^{2}\left( \frac{M_\odot }{M}\right) ^{2}\left( \frac{{\varOmega }^2r^2}{f-{\varOmega }^2r^2}\right) _{\mathrm{MCBH}}\ , \end{aligned}$$
(37)

for maximally charged black hole with \(Q_{\mathrm{max}}=\sqrt{G}M\). The ratio of the intensities of charged particle at the ISCO position around MCBH and ECBH is \(I_{\mathrm{MCBH}}/I_{\mathrm{ECBH}}\simeq 1.41(Q_m/Q_e)^2\), while for the identical electric and magnetic charges this ratio reduces to \(I_{\mathrm{MCBH}}/I_{\mathrm{ECBH}}\simeq 1.41\).

Similarly, one can also explore more realistic situation when the charged particle falling into black hole with the four-velocity, \(U^\alpha =U^t(1,u,0,\omega )\), where \(u=\mathrm{d}r/\mathrm{d}t\) is radial velocity and \(\omega =\mathrm{d}\phi /\mathrm{d}t\) is angular velocity of the particle. In this case, the four-acceleration of charged particle falling onto ECBH can be introduced as \(w^\alpha =(w^t,w^r,0,0)\), where \(w_t=(q/m)F_{tr}U^r\) and \(w_r=(q/m)F_{rt}U^t\), which satisfies the orthogonality condition \(w_\alpha U^\alpha =0\). On the other hand, the four-acceleration of charged particle falling into MCBH can be written as \(w^\alpha =(0,0,w^\theta ,0)\). Finally, the intensity of electromagnetic radiation from relativistic charged particle can be expressed as

$$\begin{aligned} I_{\mathrm{ECBH}}= & {} -\frac{2q^4}{3m^2}\left( \frac{u^2g^{tt}+g^{rr}}{g_{tt}+u^2g_{rr}+\omega ^2g_{\phi \phi }}\right) F_{\theta \phi }^2\ , \end{aligned}$$
(38)
$$\begin{aligned} I_{\mathrm{MCBH}}= & {} -\frac{2q^4}{3m^2}\left( \frac{\omega ^2g^{\theta \theta }}{g_{tt}+u^2g_{rr}+\omega ^2g_{\phi \phi }}\right) F_{\theta \phi }^2\ , \end{aligned}$$
(39)

which concludes that charged particles accreting onto ECBH and MCBH with radial and angular velocities \(u_r\) and \(\omega \), emit the electromagnetic radiation. Now using the three-velocity (12) and replacing the electromagnetic tensor as \(F_{rt}=Q_e/r^2\) and \(F_{\theta \phi }=Q_m\sin \theta \) above expression can be expressed as

$$\begin{aligned} I_{\mathrm{ECBH}}=\frac{2q^4Q_e^2}{3m^2r^4}\left( \frac{1-v_{{\hat{r}}}^2}{1-v^2}\right) \ ,\qquad I_{\mathrm{MCBH}}=\frac{2q^4Q_m^2}{3m^2r^4}\left( \frac{v_{{\hat{\phi }}}^2}{1-v^2}\right) \ ,\qquad \quad v^2=v_{{\hat{r}}}^2+v_{{\hat{\phi }}}^2\ . \end{aligned}$$
(40)

5 Conclusions and future outline

In this research note, we investigate the charged particle motion around ECBH and MCBH. We perform analyses on the effects of the charge coupling parameter on the ISCO parameters, namely, the specific energy, specific angular momentum, the critical angle, and the innermost radius, respectively. Our numerical calculations show that the ISCO position for charged particle around ECBH at the equatorial plane gets always larger than that obtained for neutral particle, depending on the charge parameter \(\sigma _e\), while around MCBH the ISCO position can be derived analytically, and it will be the same as for neutral particle, however it is displaced from the equatorial plane by angle \(\theta _0=\tan ^{-1}(2\sqrt{3}/\sigma _m)\) depending on the coupling parameter \(\sigma _m\). It concludes that one can distinguish charge separation in accreting matter around MCBH.

According to the standard way of deriving the fundamental frequencies, such as Keplerian and Larmor frequencies, for charged particles around the charged black hole they have been explicitly derived. We show that Keplerian frequency of charged particle can be either greater or less than that is obtained in the Schwarzschild spacetime depending on the sign of the coupling parameter.

Finally, it has been investigated the synchrotron radiation caused by acceleration of charged particle in the vicinity of the charged black hole. The explicit expressions for the intensity of the radiating charged relativistic particle around ECBH and MCBH due to acceleration by electromagnetic (Coulomb and Lorentz) have been derived. Numerical calculations show that the radiation intensity of accelerated charged particle around MCBH is always greater than the radiation intensity around ECBH. Another important result shows that radially falling charged particles onto ECBH and MCBH, with arbitrary radial and angular velocities (\(u,\omega \)), produce synchrotron radiation with intensity proportional to \(I\sim (2q^4Q^2)/(3m^2r^4)\) with the different factors. These facts also show various distinguishable features of the electric and magnetic charge of a black hole.

It would also be interesting to study charged particle acceleration around rotating electrically charge (Kerr-Newman) black hole and magnetized black hole, as well as the effects of rotation of the black hole and external magnetic field on synchrotron radiation from accelerated charged particle.