1 Introduction

Dengue fever (DF) is the most widely spread vector-borne viral infection in the world [1, 2]. Usually, the disease occurs in tropical and subtropical regions and is predominant in more than 100 countries [3, 4] in Africa, Asia, the Eastern Mediterranean and the Americas [3]. It has become the major cause of deaths and hospitalizations by dengue haemorrhagic fever (DHF) and dengue shock syndrome (DSS) [5]. DHF is a main cause of morbidity and death among children in South-East Asia [1, 5]. Annually, about 50 million people are affected worldwide, particularly in urban and semi-urban areas [1, 5]. According to the World Health Organization, about \(40\%\) of the world’s population is at the risk of dengue infection [6].

DF is transmitted via bites by infected female Aedes aegypti and Aedes albopictus mosquitoes. The disease is caused by four serologically distinct viruses identified as DEN-1-DEN-4 [4, 7, 8]. Recovery from an infection by one virus serotype confers lifelong immunity to the strain, and temporary cross-immunity to the rest. However, it increases the susceptibility of the recovered person to the other three serotypes [4].

Presently, there is no perfect vaccine for dengue, although a number of vaccines are under way. The live attenuated tetravalent Dengvaxia (CYD-TDV) was licensed in 2015 [9], but the efficacy of the vaccine is yet to be properly established. Hence, dengue control measures still rely on the strategies that focus on the reduction of vector population and host–vector contacts. These include applying larvicide to mosquito breeding sites, open space spraying of insecticide, destroying artificial mosquito breeding sites, and individual protection against mosquito bites [3, 9, 10].

Over the last few years, a number of factors have contributed to the significant increase in the incidence of dengue globally. These factors include human movement, vertical transmission and changes in local weather and habitat conditions [11]. Taghikhani and Gumel [11] reported that vertical (transovarial) transmission in vector population has marginal impact on the dynamics of dengue. Also, human movement is known to be one of the major factors responsible for the re-emergence of infectious diseases [4, 12]. It contributes to the expansion of the geographic range of the diseases [4].

A mathematical modelling approach is one of the tools that are helpful in studying the dynamical behaviour and developing some useful strategies for possible control and eradication of infectious diseases. In many previous works [13,14,15,16,17,18,19,20,21], several nonlinear mathematical models have been developed to study the transmission dynamics and control of vector-borne diseases, particularly dengue in a homogeneous environment. Alade et al. [22] studied a nonlinear mathematical model with multi-target cells to describe the within-host transmission dynamics of viral infections. In a similar study [23], global asymptotic behaviour of generalized within-host Chikungunya virus models around the steady states was investigated. Furthermore, several studies have been conducted based on the use of autonomous mathematical model to facilitate the understanding of the transmission dynamics of vector-borne diseases involving human movement in a patchy environment [4, 7, 24,25,26,27,28,29,30,31] and non-autonomous model to gain epidemiological insights into the optimal strategy needed to minimize the spread of the diseases in a coupling environments at minimum costs [10, 32,33,34]. There are two approaches for modelling the effect of dispersal, namely metapopulation (Eulerian approach) and Lagrangian approach [7, 35]. The two concepts have been applied to explore the role of human movement in the context of dengue. For instance, [4] developed a multi-patch dengue model by using the Eulerian approach to investigate the roles of human movement and temperature on the dynamics of dengue disease transmission in a patchy environment. The model follows the SEIR (susceptible–exposed–infectious–recovered) and SIR (susceptible–infectious–recovered) structures for human and mosquito populations, respectively. Moreover, [24] constructed a two-patch SIR + SI model to study the transmission dynamics of dengue in two interconnected patches with coexistence of two virus serotypes. In [7], a two-patch SEIR+SEI dengue model, using the Lagrangian approach, is developed to investigate the impact of host mobility on dengue disease spread in two connected patches.

In Bock and Jayathunga [10], a multi-patch dengue model was based on the SIR+SI structure to examine the optimal strategy for controlling the transmission and spread of dengue in n-connected patches using patch-specific personal protection control measure. The control model was analysed using optimal control theory. In similar studies [32, 34], a two-patch SEIR+SEI model was used to estimate the impact of patch-specific optimal personal protection control on the dynamics of dengue disease transmission in the populations of the connected patches. More recently, Kim et al. [33] developed a two-patch dengue model with temperature-dependent parameters, in which patch 1 is assumed to be a park area where mosquitoes prevail, while patch 2 is considered as a residential area where people live. The model was used to assess the impacts of inter-patch travel blockage, vector control and virus transmission control on the dynamics of dengue spread in the two connected patches. The study suggested that the combination of the three control measures is the most effective. Later, the authors extended the model to a non-autonomous system incorporating two time-dependent control strategies, namely preventive measure and adult mosquito reduction effort, to describe the transmission dynamics and optimal control of dengue influenced by climate change in two coupling patches. The authors explicitly proved the existence result for the optimal control couple, which minimizes dengue infections and implementation costs in the two patches using optimal control theory.

However, despite the fact that the efficacy of combined effort of aquatic stage mosquitoes control (either ecological control, chemical control or both) with other dengue control interventions such as preventive measure, case management (including detection, diagnosis and treatment) and insecticide control of adult mosquito population has been demonstrated in several studies on single-patch dengue models [14, 18, 19], none of the previous studies on multi-patch dengue model (to the best of our knowledge) have evaluated the impact of integrated dengue control strategy involving the aquatic stage mosquito control on the spread of dengue in interconnected patches. To fill this gap, our interest in this work is to propose and analyse a two-patch model that is more adapted to the reality of dengue disease which does not only capture both the aquatic (immature) and adult stage (female) mosquitoes, but also incorporates three patch-specific control parameters representing human personal protection, larvicide and adulticide controls in order to investigate the impacts of host migration and different strategies for implementing the combined efforts of the three control interventions on dengue disease transmission dynamics in two interconnected patches. In order to examine the effect of vertical transmission, the model also incorporates the vertical transmission in the vector population.

The rest of this paper is organized as follows: In Sect. 2, a two-patch dengue model is designed. Also, the qualitative analysis of the basic properties of solutions the model and its global asymptotic behaviour around the disease-free equilibrium are discussed in Sect. 3. In Sect. 4, numerical simulation of the model is carried out. Section 5 presents the simulated results of the two-patch model with their discussions. This is followed up by a concluding remark in Sect. 6.

2 Formulation of model

Considering the single-patch dengue model proposed and studied in a previous work [16] and the multi-patch models presented in [4, 28, 30, 36], we formulate a mathematical model capturing the effect of human migration between two patches. The patches are considered to be an urban centre (large city) and a satellite city. The model also incorporates vertical transmission in the vector population. The total human population in the urban centre (city 1) and satellite city (city 2), denoted as \(N_{h1}(t)\) and \(N_{h2}(t)\), respectively, are stratified into four mutually exclusive epidemiological states: \(S_{hi}(t)\)—susceptible individuals who can contract the disease at time t, \(E_{hi}(t)\)—exposed individuals at time t, \(I_{hi}(t)\)—infectious individuals at time t and \(R_{hi}(t)-\)—recovered individuals at time t, for \(i=1,2\). Furthermore, in each city, the aquatic phase mosquito subpopulation (including the egg, larva and pupa stages) at any time t is described by an epidemiological state \(A_{vi}(t)\), while the total adult (female) mosquito subpopulation, denoted as \(N_{vi}(t)\), is stratified into susceptible mosquitoes at time t (\(S_{vi}(t)\)), exposed mosquitoes at time t (\(E_{vi}(t))\) and infectious mosquitoes at time t (\(I_{vi}(t))\). Thus, the total human and adult mosquito populations in each city are given as:

$$\begin{aligned} N_{hi}(t)=S_{hi}(t)+E_{hi}(t)+I_{hi}(t)+R_{hi}(t) \end{aligned}$$
(1)

and

$$\begin{aligned} N_{vi}(t)=S_{vi}(t)+E_{vi}(t)+I_{vi}(t), \end{aligned}$$
(2)

where \(i=1,2\). Then, the total human and mosquito populations after the coupling of the two cities are obtained from Eqs. (1) and (2) as

$$\begin{aligned} N_h(t)&=\sum _{i=1}^2N_{hi}(t)=\sum _{i=1}^2\left( S_{hi}(t)+E_{hi}(t)+I_{hi}(t)+R_{hi}(t)\right) \end{aligned}$$
(3)

and

$$\begin{aligned} N_v(t)&=\sum _{i=1}^2N_{vi}(t)=\sum _{i=1}^2\left( S_{vi}(t)+E_{vi}(t)+I_{vi}(t)\right) . \end{aligned}$$
(4)

We let \(m_{1}\) and \(m_{2}\) be the respective migration rates of individuals from city 1 to city 2 and from city 2 to city 1 with the assumption that the symptomatic infectious individuals in both cities (those who are in class \(I_{hi}\)) do not migrate as a result of dengue-induced weakness. Also, it is assumed that the migration of mosquitoes between patches is negligible since Aedes mosquitoes have short distance travel coverage over their lifetime [7]. Consequently, mosquito’s dispersal is neglected in the formulation of our model.

Since the urban centre is much larger than the satellite city, there is difference in the nature of contacts in the cities. We then make similar assumptions in [29], that a standard (or proportional) form of incidence term is appropriate for larger communities, while a bilinear mass-action incidence function better fits smaller communities. On the one hand, it is quite conceivable that people in the smaller community can easily meet each other, which is better described by a bilinear mass-action incidence function. On the other hand, there are numerous main shopping areas, several neighbourhoods and so on in a large urban centre. Many people in the urban centre spend their days in a small number of neighbourhoods, and they rarely or do not even visit others. A proportional form of incidence term is appropriate to describe this situation. So, the incidence rates for human and mosquito populations in city 1 are modelled as: \(b_{v1}\beta _{h1}\frac{I_{v1}}{N_{h1}}S_{h1}\) and \(b_{v1}\beta _{v1}\frac{I_{h1}}{N_{h1}}S_{h1}\), respectively, while for those of city 2 are formulated as \(b_{v2}\beta _{h2}I_{v2}S_{h2}\) and \(b_{v2}\beta _{v2}I_{h2}S_{v2}\), where \(b_{vi}\) is the mosquitoes biting rate, and \(\beta _{vi}\) and \(\beta _{hi}\) denote the transmission probability in humans and mosquitoes, respectively, in city i (\(i=1,2\)). This is unlike in the previous study [36], where the incidence rates for human and mosquito populations of the two connected patches were formulated under a standard (proportional) form of incidence terms.

Further, the effect of the implemented proportions of human personal protection, larvicide and adulticide control interventions in city i (\(i=1,2\)) is accounted for by three patch-specific control parameters, namely \(c_{P_i}\), \(c_{L_i}\) and \(c_{A_i}\), respectively. The control \(c_{P_i}\) is introduced in order to reduce the vector–human contacts in city i, thereby reducing the effective contact rate in city i by a factor \((1-c_{P_i})\). Thus, the human and mosquito incidence rates of city 1 and city 2 are modified as:

$$\begin{aligned} (1-c_{P_1})b_{v1}\beta _{h1}\frac{I_{v1}}{N_{h1}}S_{h1}, \quad (1-c_{P_1})b_{v1}\beta _{v1}\frac{I_{h1}}{N_{h1}}S_{h1}, \qquad \text{(for } \text{ city } \text{1) } \end{aligned}$$

and

$$\begin{aligned} (1-c_{P_2})b_{v2}\beta _{hi}I_{v2}S_{h2}, \quad (1-c_{P_2})b_{v2}\beta _{v2}I_{h2}S_{v2} \qquad \text{(for } \text{ city } \text{2) }, \end{aligned}$$

where \(c_{P_i}\in [0,1]\) is the control parameter for personal protection in city i (\(i=1,2\)). Vector larvae can be effectively controlled through larvicide treatment and mechanical control, which is related to public enlightenment on removal of still water from domestic recipients and elimination of possible mosquito breeding sites. Here, larvicide treatment is considered so that control \(c_{L_i}\) is incorporated. It primarily focuses on the use of appropriate chemicals such as Bacillus thuringiensis israelensis (Bti) insecticide to outdoor mosquito breeding sites in order to reduce the number of immature mosquitoes living in water. Hence, the natural mortality rate of aquatic mosquitoes of city i, represented by \(\mu _{ai}\), is increased as \(\mu _{ai}+c_{L_i}\), where \(c_{L_i}\in [0,1]\) is the level of larviciding in city i. Also, the natural mortality rate of adult mosquitoes of city i, denoted by \(\mu _{vi}\), is increased by \(c_{A_i}\) so that the mortality rate of mosquitoes in city i becomes \(\mu _{vi}+c_{A_i}\), where \(c_{A_i}\in [0,1]\) is the proportion of open spray of insecticide (adulticide) control administration in city i.

Hence, the model governing the dynamics of dengue population in the urban centre (city 1) is given as in Eq. (5) as

$$\begin{aligned} \frac{\hbox {d}S_{h1}}{\hbox {d}t}&=Q_{h1}-\frac{(1-c_{P_1})b_{v1}\beta _{h1}I_{v1}S_{h1}}{N_{h1}}+m_{2}S_{h2}-m_{1}S_{h1}-\mu _{h}S_{h1}, \end{aligned}$$
(5a)
$$\begin{aligned} \frac{\hbox {d}E_{h1}}{\hbox {d}t}&=\frac{(1-c_{P_1})b_{v1}\beta _{h1}I_{v1}S_{h1}}{N_{h1}}+m_{2}E_{h2}-m_{1}E_{h1}-(\gamma _{h1}+\mu _{h})E_{h1}, \end{aligned}$$
(5b)
$$\begin{aligned} \frac{\hbox {d}I_{h1}}{\hbox {d}t}&=\gamma _{h1}E_{h1}-(\theta _{h1}+\mu _{h})I_{h1}, \end{aligned}$$
(5c)
$$\begin{aligned} \frac{\hbox {d}R_{h1}}{\hbox {d}t}&=\theta _{h1}I_{h1}+m_{2}R_{h 2}-m_{1}R_{h1}-\mu _{h}R_{h1}, \end{aligned}$$
(5d)
$$\begin{aligned} \frac{\hbox {d}A_{v1}}{\hbox {d}t}&=\mu _{e1}\left( 1-\frac{A_{v1}}{K_{L1}}\right) (S_{v1}+E_{v1}+(1-\tau )I_{v1})-(\gamma _{a1}+\mu _{a1}+c_{L_1})A_{v1}, \end{aligned}$$
(5e)
$$\begin{aligned} \frac{\hbox {d}S_{v1}}{\hbox {d}t}&=\gamma _{a1}A_{v1}-\frac{(1-c_{P_1})b_{v1}\beta _{v1}I_{h1}S_{v1}}{N_{h1}}-(\mu _{v}+c_{A_1})S_{v1}, \end{aligned}$$
(5f)
$$\begin{aligned} \frac{\hbox {d}E_{v1}}{\hbox {d}t}&=\frac{(1-c_{P_1})b_{v1}\beta _{v1}I_{h1}S_{v1}}{N_{h1}}-(\gamma _{v1}+\mu _{v}+c_{A_1})E_{v1}, \end{aligned}$$
(5g)
$$\begin{aligned} \frac{\hbox {d}I_{v1}}{\hbox {d}t}&=\gamma _{v1}E_{v1}-(\mu _{v}+c_{A_1})I_{v1}. \end{aligned}$$
(5h)

Similarly, the dynamics of dengue population in the satellite city (city 2) is described as:

$$\begin{aligned} \frac{\hbox {d}S_{h2}}{\hbox {d}t}&=Q_{h2}-(1-c_{P_2})b_{v2}\beta _{h2}I_{v2}S_{h2}+m_{1}S_{h1}-m_{2}S_{h2}-\mu _{h}S_{h2}, \end{aligned}$$
(5i)
$$\begin{aligned} \frac{\hbox {d}E_{h2}}{\hbox {d}t}&=(1-c_{P_2})b_{v2}\beta _{h2}I_{v2}S_{h2}+m_{1}E_{h1}-m_{2}E_{h2}-(\gamma _{h2}+\mu _{h})E_{h2}, \end{aligned}$$
(5j)
$$\begin{aligned} \frac{\hbox {d}I_{h2}}{\hbox {d}t}&=\gamma _{h2}E_{h2}-(\theta _{h2}+\mu _{h})I_{h2}, \end{aligned}$$
(5k)
$$\begin{aligned} \frac{\hbox {d}R_{h2}}{\hbox {d}t}&=\theta _{h2}I_{h2}+m_{1}R_{h 1}-m_{2}R_{h2}-\mu _{h}R_{h2}, \end{aligned}$$
(5l)
$$\begin{aligned} \frac{\hbox {d}A_{v2}}{\hbox {d}t}&=\mu _{e2}\left( 1-\frac{A_{v2}}{K_{L2}}\right) (S_{v2}+E_{v2}+(1-\tau )I_{v2})-(\gamma _{a2}+\mu _{a2}+c_{L_2})A_{v2}, \end{aligned}$$
(5m)
$$\begin{aligned} \frac{\hbox {d}S_{v2}}{\hbox {d}t}&=\gamma _{a2}A_{v2}-(1-c_{P_2})b_{v2}\beta _{v2}I_{h2}S_{v2}-(\mu _{v}+c_{A_2})S_{v2}, \end{aligned}$$
(5n)
$$\begin{aligned} \frac{\hbox {d}E_{v2}}{\hbox {d}t}&=(1-c_{P_2})b_{v2}\beta _{v2}I_{h2}S_{v2}-(\gamma _{v2}+\mu _{v}+c_{A_2})E_{v2}, \end{aligned}$$
(5o)
$$\begin{aligned} \frac{\hbox {d}I_{v2}}{\hbox {d}t}&=\gamma _{v2}E_{v2}-(\mu _{v}+c_{A_2})I_{v2}, \end{aligned}$$
(5p)

subject to the initial conditions (ICs) expressed by Eq. (6) as

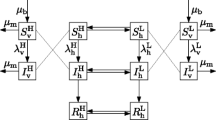
$$\begin{aligned} \begin{aligned} S_{hi}(0)&>0, \ E_{hi}(0),I_{hi}(0),R_{hi}(0)\ge 0, \ \sum _{i=1}^2E_{hi}(0)+I_{hi}(0)>0,\\ A_{vi}(0)&>0, \ S_{vi}(0)>0, \ E_{vi}(0),I_{vi}(0)\ge 0, \ \sum _{i=1}^2E_{vi}(0)+I_{vi}(0)>0, \end{aligned} \end{aligned}$$
(6)

where \(i=1,2\). Figure 1 presents the schematic diagram showing the population dynamics of dengue in two connected patches. Table 1 provides the definitions of parameters of the two-patch dengue model (5).

Fig. 1
figure 1

Schematic diagram of the two-patch dengue model (5), where \(\lambda _{h1}=\frac{(1-c_{P_1})b_{v1}\beta _{h1}I_{v1}}{N_{h1}}\), \(\lambda _{v1}=\frac{(1-c_{P_1})b_{v1}\beta _{v1}I_{h1}}{N_{h1}}\), \(\lambda _{h2}=(1-c_{P_2})b_{v2}\beta _{h2}I_{v2}\), and \(\lambda _{v2}=(1-c_{P_2})b_{v2}\beta _{v2}I_{h2}\)

Full size image
Table 1 Description of the used parameters for the two-patch dengue model, Eq. (5)
Full size table

3 Analysis of the model

3.1 Positivity of solutions

Lemma 1

Let the initial conditions of model (5) be \(S_{hi}\ge 0\), \(E_{hi}\ge 0\), \(I_{hi}\ge 0\), \(R_{hi}\ge 0\), \(A_{vi}\ge 0\), \(S_{vi}\ge 0\), \(E_{vi}\ge 0\) and \(I_{vi}\ge 0\) for \(i=1,2\). Then, the solutions of the two-patch dengue model (5) are non-negative for all \(t>0\).

Proof

Let \(t_1=\sup \left\{ t>0:S_{hi}>0, E_{hi}>0, I_{hi}>0, R_{hi}>0, A_{vi}>0, S_{vi}>0, E_{vi}>0, I_{vi}>0\in [0,t], \ i=1,2\right\} \). Thus, \(t_1>0\). It follows from (5a) that

$$\begin{aligned} \frac{\hbox {d}S_{h1}}{\hbox {d}t}=Q_{h1}+m_{2}S_{h2}-\lambda _{h1}(t)S_{h1}-m_{1}S_{h1}-\mu _{h}S_{h1}, \quad \text{ where } \ \lambda _{h1}(t)=\frac{(1-c_{P_1})b_{v1}\beta _{h1}I_{v1}}{N_{h1}}. \end{aligned}$$
(7)

Using integrating factor method, Eq. (7) can be written as:

$$\begin{aligned}&\frac{\hbox {d}}{\hbox {d}t}\left\{ S_{h1}(t)\exp \left\{ m_1t+\mu _ht+\int _0^{t}\lambda _{h1}(s)\hbox {d}s\right\} \right\} \\&\quad =(Q_{h1}+m_2S_{h2})\exp \left\{ m_1t+\mu _ht+\int _0^t\lambda _{h1}(s)\hbox {d}s\right\} . \end{aligned}$$

Hence,

$$\begin{aligned}&S_{h1}(t_1)\exp \left\{ m_1t_1+\mu _ht_1+\int _0^{t_1}\lambda _{h1}(s)\hbox {d}s\right\} -S_{h1}(0)\\&\quad =\int _0^{t_1}(Q_{h1}+m_2S_{h2}(u))\exp \left\{ m_1u+\mu _hu+\int _0^u\lambda _{h1}(s)\hbox {d}s\right\} \hbox {d}u, \end{aligned}$$

implying that

$$\begin{aligned} S_{h_1}(t_1)&=S_{h1}(0)\exp \left\{ -m_1t_1-\mu _ht_1-\int _0^{t_1}\lambda _{h1}(s)\hbox {d}s\right\} +\exp \left\{ -m_1t_1-\mu _ht_1-\int _0^{t_1}\lambda _{h1}(s)\hbox {d}s\right\} \\&\quad \int _0^{t_1}(Q_{h1}+m_2S_{h2}(u))\times \exp \left\{ m_1u+\mu _hu+\int _0^{u}\lambda _{h1}(s)\hbox {d}s\right\} \hbox {d}u\\&>0. \end{aligned}$$

In the same approach, it is easy to show that all the other state variables (\(S_{h2}\), \(E_{hi}\), \(I_{hi}\), \(R_{hi}\), \(A_{vi}\), \(S_{vi}\), \(E_{vi}\) and \(I_{vi}\), where \(i=1,2\)) are non-negative for all \(t>0\). \(\square \)

3.2 Region of positive invariant

In order to show that the two-patch dengue model, Eq. (5), is biologically well posed, then the dynamics of the system, Eq. (5), is studied in the feasible region, \(\Omega \), presented in Lemma 2.

Lemma 2

The closed set

$$\begin{aligned} \begin{aligned} \Omega&=\left\{ \left( S_{h1},E_{h1},I_{h1},R_{h1},A_{v1},S_{v1},E_{v1},I_{v1},S_{h2},E_{h2},I_{h2},R_{h2},A_{v2},S_{v2},E_{v2},I_{v2}\right) \in \mathbb {R}_+^{16}:\right. \\&\quad \left. N_h\le \frac{Q_{h1}+Q_{h2}}{\mu _h}, A_{v1}\le K_{L1}, A_{v2}\le K_{L2}, N_v\le \frac{\gamma _{a1}K_{L1}+\gamma _{a2}K_{L2}}{\mu _v}\right\} \end{aligned}\nonumber \\ \end{aligned}$$
(8)

is positively invariant for the two-patch dengue model (5).

Proof

Let \(N_h(t)\) be the total human population of the coupled cities 1 and 2 as defined in Eq. (3). Also, let \(N_v(t)\) accounts for the total mosquito population in the connected cities as given in Eq. (4). Then, it follows from adding the dynamics of host population in model (5) that

$$\begin{aligned} \frac{\hbox {d}N_h(t)}{\hbox {d}t}=Q_{h1}+Q_{h2}-\mu _hN_{h}, \end{aligned}$$

where the rates of human death in both cities are assumed to be equal (i.e. \(\mu _{h1}=\mu _{h2}=\mu _h\)) for simplicity. Unless otherwise stated, this assumption is retained throughout the remainder of this paper. So,

$$\begin{aligned} 0\le N_h(t)\le \frac{Q_{h1}+Q_{h2}}{\mu _h}+\left( N_h(0)-\frac{Q_{h1}+Q_{h2}}{\mu _h}\right) \hbox {e}^{-\mu _ht}. \end{aligned}$$

Thus, \(0\le N_h(t)\le \frac{Q_{h1}+Q_{h2}}{\mu _h}\) as \(t\rightarrow \infty \).Again, adding Eqs. (5f)–(5h) and Eqs. (5n)–(5p) related to vector dynamics yields

$$\begin{aligned} \frac{\hbox {d}N_v(t)}{\hbox {d}t}=\gamma _{a1}A_{v1}+\gamma _{a2}A_{v2}-\mu _vN_v-c_AN_v\le \gamma _{a1}A_{v1}+\gamma _{a2}A_{v2}-\mu _vN_v, \end{aligned}$$

where it is assumed that the natural mortality rates of mosquitoes in both cities are equal (i.e. \(\mu _{v1}=\mu _{v2}=\mu _v\)) and \(c_{A_1}=c_{A_2}=c_A\). So,

$$\begin{aligned} 0\le N_v(t)\le \frac{\gamma _{a1}A_{v1}+\gamma _{a2}A_{v2}}{\mu _v}+\left( N_v(0)-\frac{\gamma _{a1}A_{v1}+\gamma _{a2}A_{v2}}{\mu _v}\right) \hbox {e}^{-\mu _vt}. \end{aligned}$$

Consequently, \(0\le N_v(t)\le \frac{\gamma _{a1}K_{L1}+\gamma _{a2}K_{L2}}{\mu _v}\) as \(t\rightarrow \infty \) since \(A_{vi}\le K_{Li}, \ i=1,2\). Hence, all the solutions of model (5) converge towards the closed set \(\Omega \) given in (8). \(\square \)

Lemma 2 suggests that model (5) has solutions that are all non-negative and bounded. Therefore, model (5) is well-posed mathematically and biologically.

3.3 Equilibrium points, reproductive number and stability analysis

Proposition 1

Let \(\mathcal N_i=\frac{\mu _{ei}\gamma _{ai}}{(\mu _{v}+c_{A_i})(\gamma _{ai}+\mu _{ai}+c_{L_i})}\), for \(i=1,2\). Then, the two-patch dengue model (5) admits at most two disease-free equilibrium (DFE) points stated as follows:

  1. 1.

    If \({\mathcal {N}}_i\le 1\), then there is a trivial equilibrium (TE) (i.e. a mosquito and dengue-free equilibrium) given by

    $$\begin{aligned} \mathcal E_1=\left( S_{h1}^*,0,0,0,0,0,0,0,S_{h2}^*,0,0,0,0,0,0,0\right) , \end{aligned}$$
    (9)
  2. 2.

    If \({\mathcal {N}}_{i}>1\), then there exists a non-trivial biologically realistic DFE (BRDFE), which is a mosquito-present and dengue-free equilibrium, given by

    $$\begin{aligned} \mathcal E_2=\left( S_{h1}^*,0,0,0,A_{v1}^*,S_{v1}^*,0,0,S_{h2}^*,0,0,0,A_{v2}^*,S_{v2}^*,0,0\right) , \end{aligned}$$
    (10)

    with the components given as

    $$\begin{aligned} \begin{aligned} S_{h1}^*&=\frac{Q_{h1}(m_2+\mu _{h})+Q_{h2}m_2}{\mu _{h}(\mu _{h}+m_{1}+m_{2})},\quad S_{h2}^*=\frac{Q_{h1}m_1+Q_{h2}(m_1+\mu _{h})}{\mu _{h}(\mu _{h}+m_{1}+m_{2})},\\ A_{vi}^*&=\left( 1-\frac{1}{{\mathcal {N}}_i}\right) K_{L_i},\ S_{vi}^*=\frac{\gamma _{ai}}{(\mu _{v}+c_{A_i})}\left( 1-\frac{1}{\mathcal N_i}\right) K_{L_i}, \\ \mathcal N_i&=\frac{\mu _{ei}\gamma _{ai}}{(\mu _{v}+c_{A_i})(\gamma _{ai}+\mu _{ai}+c_{L_i})}, \ (i=1,2). \end{aligned} \end{aligned}$$

Proof

Details of the proof can be found in “Appendix A”. \(\square \)

The TE (\({\mathcal {E}}_1\)) and the BRDFE (\({\mathcal {E}}_2\)) given in Eqs. (9) and (10), respectively, represent the steady-state solutions of the two-patch dengue model, Eq. (5), when there is no disease in the population and no mosquito, and when there exists no disease in the population with the coexistence of humans and mosquitoes. However, it is more realistic that humans and mosquitoes may coexist without dengue disease in the community. Hence, the local asymptotic behaviour of the model is later investigated at BRDFE, \({\mathcal {E}}_2\). In Proposition 1, it is established that the threshold \({\mathcal {N}}_i\) (\(i=1,2\)), which is the effective offspring of the mosquito population in patch i, regulates the existence of mosquitoes in the coupling patches.

It is necessary to derive the effective (or control) reproductive number, denoted as \({\mathcal {R}}_T\), of the two-patch dengue model (5). The dimensionless threshold can be used to forecast the potential of dengue disease either to invade or eradicate from a completely susceptible population. Next, we present \({\mathcal {R}}_T\) associated with the two-patch dengue model (5). The result is summarized in Proposition 2.

Proposition 2

If \({\mathcal {N}}_i\) is as defined in Proposition 1 and satisfies the inequality \({\mathcal {N}}_i>1\) (for \(i=1,2\)), then the control reproductive number related to the two-patch dengue model (5) is given as:

$$\begin{aligned} {\mathcal {R}}_T^2={\frac{1}{2}a_1\left( \mathcal R_{T,1}^2+\mathcal R_{T,2}^2\right) +\frac{1}{2}\sqrt{a_1^2\left( \mathcal R_{T,1}^2+{\mathcal {R}}_{T,2}^2\right) ^2-4a_2{\mathcal {R}}_{T,1}^2\mathcal R_{T,2}^2}}, \end{aligned}$$
(11)

where

$$\begin{aligned} {\mathcal {R}}_{T,1}&=\sqrt{\frac{(1-c_{P_1})b_{v1}^2\beta _{h1}\beta _{v1}\gamma _{h1}\gamma _{v1}}{(m_1+\gamma _{h1}+\mu _{h})(\theta _{h1}+\mu _{h})(\mu _{v}+c_{A_1})(\gamma _{v1}+\mu _{v}+c_{A_1})}\frac{S_{h1}^*}{N_{h1}^*}\frac{S_{v1}^*}{N_{h1}^*}},\\ R_{T,2}&=\sqrt{\frac{(1-c_{P_2})b_{v2}^2\beta _{h2}\beta _{v2}\gamma _{h2}\gamma _{v2}}{(m_2+\gamma _{h2}+\mu _{h})(\theta _{h2}+\mu _{h})(\mu _{v}+c_{A_2})(\gamma _{v2}+\mu _{v}+c_{A_2})}S_{h2}^*S_{v2}^*}, \end{aligned}$$
(12)
$$\begin{aligned} a_1&=\frac{b_1b_2}{b_1b_2-m_1m_2},\quad a_2=\frac{b_1c_1b_2c_2}{(\gamma _{h1}\mu _h+\gamma _{h1}\theta _{h2}+c_2\mu _h)(m_2\gamma _{h1}+b_3\mu _h+b_3\gamma _{h2}+b_2\mu _h)},\nonumber \\ b_1&=m_1+\gamma _{h1}+\mu _{h},\quad b_2=m_2+\gamma _{h2}+\mu _{h},\quad b_3=m_1+\gamma _{h1},\nonumber \\ c_1&=\theta _{h1}+\mu _{h},\quad c_2=\theta _{h2}+\mu _{h},\nonumber \end{aligned}$$
(13)

and the components of the BRDFE, \({\mathcal {E}}_2\), are as given in Proposition 1.

Proof

See “Appendix B” for the proof in detail. \(\square \)

By Theorem 2 in [37], the local asymptotic stability of the BRDFE, \({\mathcal {E}}_2\), in the region \(\Omega \) is established by the following result in Lemma 3.

Lemma 3

The BRDFE, \({\mathcal {E}}_2\), of the two-patch dengue model, Eq. (5), is locally asymptotically stable (LAS) whenever \({\mathcal {R}}_T<1\), and unstable whenever \({\mathcal {R}}_T>1\).

Remark 1

The expression \({\mathcal {R}}_T\) in Eq. (11) represents the effective reproductive number for the coupled two patches, while \({\mathcal {R}}_{T,1}\) and \({\mathcal {R}}_{T,2}\) given in Eqs. (12) and (13) are the effective reproductive numbers related to patches 1 and 2, respectively, in the presence of human movement between the patches.

Remark 2

The basic reproductive number (denoted as \({\mathcal {R}}_0\)) of model (5), which corresponds to the scenario when no control interventions are implemented in both patches, can be obtained by setting the control parameters \(c_{P_i}=c_{L_i}=C_{A_i}=0\) (for \(i=1,2\)). Thus, \({\mathcal {R}}_0\) is obtained from the expression \({\mathcal {R}}_T\) in (11) as

$$\begin{aligned} {\mathcal {R}}_0= & {} {\mathcal {R}}_T|_{c_{P_i}=c_{L_i}=c_{A_i}=0 \ (i=1,2)}\nonumber \\= & {} \sqrt{\frac{1}{2}a_1\left( {\mathcal {R}}_{0,1}^2+\mathcal R_{0,2}^2\right) +\frac{1}{2}\sqrt{a_1^2\left( \mathcal R_{0,1}^2+{\mathcal {R}}_{0,2}^2\right) ^2-4a_2{\mathcal {R}}_{0,1}^2\mathcal R_{0,2}^2}}, \end{aligned}$$
(14)

where

$$\begin{aligned} {\mathcal {R}}_{0,1}&=\sqrt{\frac{b_{v1}^2\beta _{h1}\beta _{v1}\gamma _{h1}\gamma _{v1}}{(m_1+\gamma _{h1}+\mu _{h})(\theta _{h1}+\mu _{h})\mu _{v}(\gamma _{v1}+\mu _{v})}\frac{S_{h1}^*}{N_{h1}^*}\frac{S_{v1}^*}{N_{h1}^*}},\\ {\mathcal {R}}_{0,2}&=\sqrt{\frac{b_{v2}^2\beta _{h2}\beta _{v2}\gamma _{h2}\gamma _{v2}}{(m_2+\gamma _{h2}+\mu _{h})(\theta _{h2}+\mu _{h})\mu _{v}(\gamma _{v2}+\mu _{v})}S_{h2}^*S_{v2}^*}, \end{aligned}$$
(15)
$$\begin{aligned} a_1&=\frac{b_1b_2}{b_1b_2-m_1m_2},\quad a_2=\frac{b_1c_1b_2c_2}{(\gamma _{h1}\mu _h+\gamma _{h1}\theta _{h2}+c_2\mu _h)(m_2\gamma _{h1}+b_3\mu _h+b_3\gamma _{h2}+b_2\mu _h)},\nonumber \\ b_1&=m_1+\gamma _{h1}+\mu _{h},\quad b_2=m_2+\gamma _{h2}+\mu _{h},\quad b_3=m_1+\gamma _{h1},\nonumber \\ c_1&=\theta _{h1}+\mu _{h},\quad c_2=\theta _{h2}+\mu _{h},\nonumber \end{aligned}$$
(16)

with \(\mathcal M_i=\frac{\mu _{ei}\gamma _{ai}}{\mu _{v}(\gamma _{ai}+\mu _{ai})}\), \(S_{vi}^*=\frac{\gamma _{ai}}{\mu _v}\left( 1-\frac{1}{\mathcal M_i}\right) K_{Li}\) and \(S_{hi}^*\) is as given in the components of \({\mathcal {E}}_2\) in Eq. (10).

3.4 Global asymptotic stability of the biologically realistic disease-free equilibrium, \({\mathcal {E}}_2\)

Following [38], we examine the global asymptotic stability of the system, Eq. (5). Suppose \(Z=\left( S_{h1},R_{h1},A_{v1},S_{v1},S_{h2},R_{h2},A_{v2},S_{v2}\right) \) and \(I=\left( E_{h1},I_{h1},E_{v1},I_{v1},E_{h2},I_{h2},E_{v2},I_{v2}\right) \), and group the dynamical system, Eq. (5), into subsystems presented by Eq. (17) as

$$\begin{aligned} \frac{\hbox {d}Z}{\hbox {d}t}&=F(Z,0), \end{aligned}$$
(17a)
$$\begin{aligned} \frac{\hbox {d}I}{\hbox {d}t}&=G(Z,I), \ G(Z,I)=0, \end{aligned}$$
(17b)

where F(Z, 0) is the right-hand side of \(\frac{\hbox {d}S_{h1}}{\hbox {d}t}\), \(\frac{\hbox {d}R_{h1}}{\hbox {d}t}\), \(\frac{\hbox {d}A_{v1}}{\hbox {d}t}\), \(\frac{\hbox {d}S_{v1}}{\hbox {d}t}\), \(\frac{\hbox {d}S_{h2}}{\hbox {d}t}\), \(\frac{\hbox {d}R_{h2}}{\hbox {d}t}\), \(\frac{\hbox {d}A_{v2}}{\hbox {d}t}\), \(\frac{\hbox {d}S_{v2}}{\hbox {d}t}\) with \(E_{h1}=I_{h1}=E_{v1}=I_{v1}=E_{h2}=I_{h2}=E_{v2}=I_{v2}=0\) and G(Z, I) is the right-hand side of \(\frac{\hbox {d}E_{h1}}{\hbox {d}t}\), \(\frac{\hbox {d}I_{h1}}{\hbox {d}t}\), \(\frac{\hbox {d}E_{v1}}{\hbox {d}t}\), \(\frac{\hbox {d}I_{v1}}{\hbox {d}t}\), \(\frac{\hbox {d}E_{h2}}{\hbox {d}t}\), \(\frac{\hbox {d}I_{h2}}{\hbox {d}t}\), \(\frac{\hbox {d}E_{v2}}{\hbox {d}t}\), \(\frac{\hbox {d}I_{v2}}{\hbox {d}t}\). Suppose further that G(Z, I) satisfies the following two conditions expressed by Eq. (18) as

$$\begin{aligned} \begin{aligned} \text{ C1: } G(Z,0)&=0, \ \text{ and }\\ \text{ C2: } G(Z,I)&=D_IG(Z^*,0)I-{\hat{G}}(Z,I), \ {{\hat{G}}}(Z,I)\ge 0, (Z,I)\in \Omega , \end{aligned} \end{aligned}$$
(18)

where

$$\begin{aligned} (Z^*,0)=\mathcal E_2=\left( S_{h1}^*,0,A_{v1}^*,S_{v1}^*,S_{h2}^*,0,A_{v2}^*,S_{v2}^*\right) , \end{aligned}$$

with

$$\begin{aligned} \begin{aligned} S_{h1}^*&=\frac{Q_{h1}(m_2+\mu _{h})+Q_{h2}m_2}{\mu _{h}(\mu _{h}+m_1+m_2)},\quad S_{h2}^*=\frac{Q_{h2}(m_1+\mu _{h})+Q_{h1}m_1}{\mu _{h}(\mu _{h}+m_1+m_2)},\\ A_{vi}^*&=\left( 1-\frac{1}{{\mathcal {N}}_i}\right) K_{L_i},\ S_{vi}^*=\frac{\gamma _{ai}}{(\mu _{v}+c_{A_i})}\left( 1-\frac{1}{{\mathcal {N}}_i}\right) K_{L_i},\\ \mathcal N_i&=\frac{\mu _{ei}\gamma _{ai}}{(\mu _{v}+c_{A_i})(\gamma _{ai}+\mu _{ai}+c_{L_i})}, \ (\text{ for }\ i=1,2) \end{aligned} \end{aligned}$$

\(D_IG(Z^*,0)\), a M-matrix having non-negative off-diagonals, is the Jacobian of G(Z, I) derived with respect to \(\left( E_{h1},I_{h1},E_{v1},I_{v1},E_{h2},I_{h2},E_{v2},I_{v2}\right) \) and evaluated at \(\left( Z^*,0\right) \), and \(\Omega \) is the region where the two-patch dengue model, Eq. (5), biologically makes sense. If the reduced systems, Eqs. (17a)–(17b), satisfy the two conditions in Eq. (18), then the global asymptotic stability of the BRDFE, \({\mathcal {E}}_2\), is summarized in the following result.

Theorem 1

The BRDFE, \({\mathcal {E}}_2\), of the two-patch dengue model (5) is globally asymptotically stable (GAS) in \(\Omega \) whenever \({\mathcal {R}}_T<1\). Otherwise, it is unstable.

Proof

Note from the two-patch dengue model, Eq. (5), that

$$\begin{aligned} F(Z,0)=\left( \begin{array}{c} Q_{h1}+m_2S_{h2}-(m_1+\mu _{h})S_{h1}\\ m_2R_{h2}-(m_1+\mu _{h})R_{h1}\\ \mu _{e1}\left( 1-\frac{A_{v1}}{K_{L1}}\right) S_{v1}-(\gamma _{a1}+\mu _{a1}+c_{L_1})A_{v1}\\ \gamma _{a1}A_{v1}-(\mu _{v}+c_{A_1})S_{v1}\\ Q_{h2}+m_1S_{h1}-(m_2+\mu _{h})S_{h2}\\ m_1R_{h1}-(m_2+\mu _{h})R_{h2}\\ \mu _{e2}\left( 1-\frac{A_{v2}}{K_{L2}}\right) S_{v2}-(\gamma _{a2}+\mu _{a2}+c_{L_2})A_{v2}\\ \gamma _{a2}A_{v2}-(\mu _{v}+c_{A_2})S_{v2} \end{array} \right) \end{aligned}$$

and

$$\begin{aligned} D_IG(Z^*,0)=\left( \begin{array}{cccccccc} -\kappa _1 &{} 0 &{} 0 &{} \kappa _9 &{} m_2 &{} 0 &{} 0 &{} 0\\ \gamma _{h1} &{} -\kappa _2 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} \kappa _{10} &{} -\kappa _3 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} \gamma _{v1} &{} -\kappa _4 &{} 0 &{} 0 &{} 0 &{} 0\\ m_1 &{} 0 &{} 0 &{} 0 &{} -\kappa _5 &{} 0 &{} 0 &{} \kappa _{11}\\ 0 &{} 0 &{} 0 &{} 0 &{} \gamma _{h2} &{} -\kappa _6 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \kappa _{12} &{} -\kappa _7 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \gamma _{v2} &{} -\kappa _8 \end{array} \right) \end{aligned}$$

with \(\kappa _1=\left( m_1+\gamma _{h1}+\mu _{h}\right) \), \(\kappa _2=\left( theta_{h1}+\mu _{h}\right) \), \(\kappa _3=(\gamma _{v1}+\mu _{v}+c_{A_1})\), \(\kappa _4=(\mu _{v}+c_{A_1})\), \(\kappa _5=\left( m_2+\gamma _{h2}+\mu _{h}\right) \), \(\kappa _6=\left( \theta _{h2}+\mu _{h}\right) \), \(\kappa _7=(\gamma _{v2}+\mu _{v}+c_{A_2})\), \(\kappa _8=(\mu _{v}+c_{A_2})\), \(\kappa _9=(1-c_{P_1})b_{v1}\beta _{h1}\frac{S_{h1}^*}{N_{h1}^*}\), \(\kappa _{10}=(1-c_{P_1})b_{v1}\beta _{v1}\frac{S_{v1}^*}{N_{h1}^*}\), \(\kappa _{11}=(1-c_{P_2})b_{v2}\beta _{h2}S_{h2}^*\), and \(\kappa _{12}=(1-c_{P_2})b_{v2}\beta _{v2}S_{v2}^*\).

Using the relation of condition C2 in Eq. (18), we have

$$\begin{aligned} {\hat{G}}(Z,I)=\left( \begin{array}{c}{\hat{G}}_1(Z,I)\\ {{\hat{G}}}_2(Z,I)\\ {\hat{G}}_3(Z,I)\\ {\hat{G}}_4(Z,I)\\ {\hat{G}}_5(Z,I)\\ {{\hat{G}}}_6(Z,I)\\ {\hat{G}}_7(Z,I)\\ {\hat{G}}_8(Z,I)\end{array}\right) = \left( \begin{array}{c} (1-c_{P_1})b_{v1}\beta _{h1}\frac{S_{h1}^*}{N_{h1}^*}I_{v1}\left( 1-\frac{S_{h1}}{N_{h1}}\frac{N_{h1}^*}{S_{h1}^*}\right) \\ 0\\ (1-c_{P_1})b_{v1}\beta _{v1}\frac{S_{v1}^*}{N_{h1}^*}I_{h1}\left( 1-\frac{S_{v1}}{N_{h1}}\frac{N_{h1}^*}{S_{v1}^*}\right) \\ 0\\ (1-c_{P_2})b_{v2}\beta _{h2}S_{h2}^*I_{v2}\left( 1-\frac{S_{h2}}{S_{h2}^*}\right) \\ 0\\ (1-c_{P_2})b_{v2}\beta _{v2}S_{v2}^*I_{h2}\left( 1-\frac{S_{v2}}{S_{v2}^*}\right) \\ 0 \end{array} \right) . \end{aligned}$$
(19)

Since \( S_{h1}^*=\frac{Q_{h1}(m_2+\mu _{h})+Q_{h2}m_2}{\mu _{h}(\mu _{h}+m_1+m_2)}\), \(S_{h2}^*=\frac{Q_{h2}(m_1+\mu _{h})+Q_{h1}m_1}{\mu _{h}(\mu _{h}+m_1+m_2)}\), \(N_{h1}^*=S_{h1}^*\), \(S_{vi}^*=\frac{\gamma _{ai}}{(\mu _{v}+c_{A_i})}\left( 1-\frac{1}{\mathcal N_i}\right) K_{L_i}\),\(\mathcal N_i=\frac{\mu _{ei}\gamma _{ai}}{(\mu _{v}+c_{A_i})(\gamma _{ai}+\mu _{ai}+c_{L_i})}\) (for \(i=1,2\)), and we have that \(S_{h1}\le N_{h1}\), \(S_{v1}\le N_{v1}\), \(S_{h2}\le N_{h2}\), \(S_{v2}\le N_{v2}\) in \(\Omega \), then the inequalities \(\left( 1-\frac{S_{h1}}{N_{h1}}\frac{N_{h1}^*}{S_{h1}^*}\right) >0\), \(\left( 1-\frac{S_{v1}}{N_{h1}}\frac{N_{h1}^*}{S_{v1}^*}\right) >0\), \(\left( 1-\frac{S_{h2}}{S_{h2}^*}\right) >0\), and \(\left( 1-\frac{S_{v2}}{S_{v2}^*}\right) >0\) in Eq. (19) must be satisfied if the human and mosquito populations are at the equilibrium state. Thus, \({\hat{G}}(Z,I)\ge 0\). Also, the BRDFE \(Z^*=\left( S_{h1}^*,0,A_{v1}^*,S_{v1}^*,S_{h2}^*,0,A_{v2}^*,S_{v2}^*\right) \) is clearly a GAS equilibrium point of the reduced system, Eq. (18). Consequently, we have from Theorem 1 that the BRDFE, \({\mathcal {E}}_2=\left( Z^*,0\right) \), is GAS. Hence, the proof. \(\square \)

The epidemiological indication of Theorem 1 is that dengue disease will die out in the community whenever \({\mathcal {R}}_T<1\) regardless of the initial sizes of infectious human and mosquito subpopulations in the interacting human and mosquito populations of the two patches.

In what follows, we carry out numerical experimentations on the proposed two-patch dengue model, Eq. (5), to illustrate the role of human movements on the transmission dynamics of dengue between two patches. The impacts of patch-specific controls \(c_{P_i}\), \(c_{L_i}\) and \(c_{A_i}\) (\(i=1,2\)) on putting the sizes of subpopulations of infectious individual and mosquito in a patchy environment near the BRDFE, \({\mathcal {E}}_2\), are also explored.

4 Numerical simulations

In this section, we carry out the numerical simulations on the dengue model, Eq. (5), in order to predict the impacts of host mobility on the dynamics of dengue disease transmission in two connected patches. Further, the model is simulated to investigate an effective strategy for applying controls \(c_{P_i}\), \(c_{A_i}\) and \(c_{L_i}\) (for \(i=1,2\)) in curtailing the disease transmission in two interconnected patches. The simulations are in two folds. In the first part, we examine the effects of unidirectional and bidirectional human movements on the dynamics of dengue disease transmission across two connected patches in the absence of any control interventions. The simulations of different strategies for the implementation of combined control in two connected patches for the cases of unidirectional and bidirectional host mobilities are discussed in the second part.

We consider patch as city and assume the following initial data values for the human and mosquito populations of city 1: \(N_{h1}(0)=663617\), \(E_{h1}(0)=2500\), \(I_{h1}(0)=150\), \(R_{h1}(0)=0\), \(S_{h1}(0)=N_{h1}(0)-E_{h1}(0)-I_{h1}(0)-R_{h1}(0)\), \(A_{v1}(0)=3\times N_{h1}(0)\), \(E_{v1}(0)=10{,}000\), \(I_{v1}(0)=100\), so that \(S_{v1}(0)=3\times N_{h1}(0)-E_{v1}(0)-I_{v1}(0)\). Also, the initial conditions for the ODEs describing the host–vector interactions for dengue disease transmission in city 2 are taken as: \(N_{h2}(0)=9834\), \(E_{h2}(0)=1500\), \(I_{h2}(0)=50\), \(R_{h2}(0)=0\), \(A_{v2}(0)=3\times N_{h2}(0)\), \(E_{v2}(0)=1000\), \(I_{v2}(0)=100\), so that \(S_{v2}(0)=3\times N_{h2}(0)-E_{v2}(0)-I_{v2}(0)\). The parameter values of the models used to study the disease outbreak in the two cities are obtained from the literature [7, 39, 40] as follows: \(b_{v1}\beta _{h1}=0.375\) day\(^{-1}\), \(b_{v1}\beta _{v1}=0.375\) day\(^{-1}\), \(\frac{1}{\mu _{h}}=60\times 365\) days, \(\gamma _{h1}=0.25\) day\(^{-1}\), \(\theta _{h1}=\frac{1}{3}\) day\(^{-1}\), \(\gamma _{v1}=\frac{1}{11}\) day\(^{-1}\), \(\frac{1}{\mu _{v}}=11\) days, \(\mu _{e1}=6\) day\(^{-1}\), \(\frac{1}{\mu _{a1}}=4\) days, \(\gamma _{a1}=0.08\) day\(^{-1}\), \(b_{v2}\beta _{h2}=0.000025\) day\(^{-1}\), \(b_{v2}\beta _{v2}=0.000025\) day\(^{-1}\), \(\frac{1}{\mu _{h2}}=60\times 365\) days, \(\gamma _{h2}=0.25\) day\(^{-1}\), \(\theta _{h2}=\frac{1}{3}\) day\(^{-1}\), \(\gamma _{v2}=\frac{1}{11}\) day\(^{-1}\), \(\mu _{e2}=6\) day\(^{-1}\), \({\mu _{a2}}=0.2363\) day\(^{-1}\), \(\gamma _{a2}=0.08\) day\(^{-1}\). We take data for the rates of migration \(m_1\) and \(m_2\) as \(m_1=m_2=0.1\), implying that about \(10\%\) of susceptible, exposed and recovered individuals leave each city per day. In addition, the patch-specific control parameters \(c_{P_i}\), \(c_{L_i}\), and \(c_{A_i}\) (for \(i=1,2\)) are considered as bounded variable parameters (i.e. \(c_{P_i}, c_{L_i}, c_{A_i}\in [0,1]\)). Notably, the initial data and parameter values are chosen for the numerical illustrations of dengue transmission and spread between the connected urban centre (city 1) and satellite city (city 2) where the disease is endemic in both.

5 Results and discussion

5.1 Effect of vertical transmission in mosquito population on the spread of dengue

Figure 2 shows that, with increasing proportion of infected eggs of mosquitoes, the size of infected mosquito subpopulation significantly increases. This suggests that vertical transmission in the mosquito population significantly affects the number of infected mosquitoes. This result is in agreement with the results reported in [11].

Fig. 2
figure 2

Dynamics of infectious mosquitoes of cities 1 and 2 for uncoupled system (5)

Full size image

5.2 Effect of human travel on dengue disease spread between two connected cities

Setting human migration rates \(m_1\) and \(m_2\) to zero in Eqs. (15) and (16), respectively, the basic reproductive numbers of the isolated city 1 (denoted as \({\mathcal {R}}_{0,1}\)) and that of city 2 (represented by \({\mathcal {R}}_{0,2}\)) for this outbreak are approximately \({\mathcal {R}}_{0,1}=2.396\) and \(\mathcal R_{0,2}=1.573\) when no control intervention is administered in either city. These results epidemiologically imply that dengue disease is present in the two cities. Also, the basic reproductive number for the complete system (5) using the expression for \({\mathcal {R}}_0\) in Eq. (14) when no control interventions are implemented in both cities (that is, \(c_{P_i}=c_{L_i}=c_{A_i}=0\)) with the presence of bidirectional host mobility between the patches, is obtained as \({\mathcal {R}}_0=1.891\). Hence, the disease persists in the two cities as the inequality \({\mathcal {R}}_0^2<1\), which guarantees the stability of BRDFE, \({\mathcal {E}}_2\), is violated as illustrated in Fig. 5 as well as Figs. 12, 13 and 14 when there is no control implementation in both cities. The estimated value \(\mathcal R_0=1.891\) suggests that bidirectional host migration from high dengue-endemic city 1 to low dengue-endemic city 2 and vice versa leads to a decrease and an increase in dengue prevalence in city 1 and city 2, respectively, which consequently result into a reduction and an increment in \({\mathcal {R}}_{0,1}\) and \({\mathcal {R}}_{0,2}\) values, respectively, as \({\mathcal {R}}_{0,1}=2.396>\mathcal R_0=1.891>{\mathcal {R}}_{0,2}=1.573\). This is justified in Fig. 5 as the numbers of infectious individuals and mosquitoes decrease in city 1 and increase in city 2. The effect of human travels on spatial dissemination of dengue disease is graphically demonstrated in Figs. 3, 4 and 5.

Figure 3 illustrates the effects of human unidirectional migration from city 1 to city 2 on the dynamics of infectious human and mosquito subpopulations of the two cities in the absence of any control intervention. It is shown that the subpopulations of infectious human and mosquito of city 1 with human movement decrease more rapidly to zero than the subpopulations without human travel (see Fig. 3a, b). Also, Fig. 3c, d depicts that the numbers of infectious individuals and mosquitoes of city 2 are increased with human movement when compared with the case of no movement. Thus, the unidirectional host migration from city 1 to city 2 can greatly impact the disease burden of the two connected cities. As the population size of city 1 (urban centre and high-dengue endemic) decreases, the number of dengue infections decreases in both the human and mosquito population of the city, while the number of dengue infections increases in city 2 (satellite city and low dengue-endemic) as the population size of the city increases. Our result is in agreement with the results in [4], where the authors used a two-patch nonlinear mathematical model with temperature-dependent parameters to analyse the effect of human travel on dengue disease transmission between two connected patches without any consideration for the aquatic phase mosquito.

Fig. 3
figure 3

Dynamics of infectious individuals and mosquitoes of cities 1 and 2 with unidirectional host mobility from city 1 to city 2 in the absence of any control measure

Full size image
Fig. 4
figure 4

Dynamics of infectious individuals and mosquitoes of cities 1 and 2 with unidirectional host mobility from city 2 to city 1 in the absence of any control measure

Full size image

The impact of unidirectional human movement from city 2 to city 1 on the dynamics of the sub-populations of infectious human and mosquito of cities 1 and 2 when there is no control intervention implementation in both cities is shown in Fig. 4. It can be seen from Fig. 4a, b, respectively, that the numbers of infectious individuals and mosquitoes of city 1 first increased with human movement until the epidemic peaks before dropping below the sizes of the sub-populations of infectious human and mosquito with no movement throughout the remaining simulation period. In city 2, the disease prevalence is considerably decreased in both the human and mosquito populations as shown in Fig. 4c, d, respectively. These results are in agreement with those reported earlier in [4]. Unlike the previous case when human movement from city 2 is restricted in city 1 where the dengue prevalence considerably increases with human movement in city 2, the disease prevalence slightly increased in city 1 and significantly reduced in city 2 when human movement from city 1 is restricted in city 2. This implies that the blockage of human travel from city 1 (high dengue-endemic and population density city) to city 2 (low dengue-endemic city) may be helpful in reducing dengue disease transmission. This result is in line with the results obtained in [33], where the authors used a two-patch model describing the transmission dynamics between the coupled park area where mosquitoes prevail (patch 1) and residential area where people live (patch 2) to investigate the effect of short-term and long-term blockage between the two patches. The study revealed that long-term blockage of the park area is effective to curtail the transmission dynamics of dengue.

Fig. 5
figure 5

Dynamics of infectious individuals and mosquitoes of cities 1 and 2 with bidirectional host mobility between the cities in the absence of any control measure

Full size image

Figure 5 presents the effects of bidirectional host movement between city 1 and city 2 on the dynamics of the subpopulations of infectious individual and mosquito in the absence of any control measures. Figure 5a–c shows that there are two epidemic peaks, one corresponding to the presence of human migration between the connected cities while the other associates with the case of no migration. It is observed that the disease epidemic peak earlier at a considerably reduced value in city 1, while the epidemic is slightly delayed to peak at increased value in city 2 (as shown in Fig. 5c, d, respectively). The results indicate that bidirectional host migration between a high endemic city and a low endemic city may cause the two cities to become low and high dengue prevalent, respectively. These results agree with the results obtained in other studies on dengue [4].

5.3 Effect of patch-specific personal protection, larvicide and adulticide controls on dengue disease transmission dynamics in a patchy environment

The implementation of patch-specific control parameters \(c_{P_i}\), \(c_{L_i}\) and \(c_{A_i}\) (for \(i=1,2\)) affects the dynamics of the two-patch dengue model, Eq. (5), and the associated basic reproductive number defined by Eq. (11). For instance, fixing all the control parameters \(c_{P_i}\), \(c_{L_i}\) and \(c_{A_i}\) (where \(i=1,2\)) at 0.1, the \({\mathcal {R}}_0\) value for the system, Eq. (5), in the case of bidirectional human movement reduces to \({\mathcal {R}}_0=0.461\). Hence, the choice of these controls may help to diminish the number of infectious individuals and mosquitoes in both cities near zero and consequently leads to the stability of BRDFE, \({\mathcal {E}}_2\), as the inequality \({\mathcal {R}}_0^2<1\) is satisfied. The effects of combined efforts of patch-specific personal protection, larvicide and adulticide controls under various scenarios on the transmission dynamics of dengue disease with human movement are represented by Figs. 6, 7, 8, 9, 10, 11, 12, 13 and 14.

Figure 6 illustrates the impacts of the application of combined control only in city 1 on the dynamics of the numbers of infectious humans and mosquitoes of city 1 and city 2 with unidirectional human movement from city 1 to city 2. It can be observed in Fig. 6a, b that the application of \(50\%\) of combined control causes the populations of infectious human and mosquito of city 1 to remain at zero from 25th day and 15th day till the end of the intervention period, respectively. However, this control strategy is insignificant to decrease the number of infectious individuals and mosquitoes of city 2 over the intervention period (see Fig. 6c, d).

Fig. 6
figure 6

Dynamics of infectious individuals and mosquitoes of cities 1 and 2 with unidirectional host mobility from city 1 to city 2 at different levels of implementation of combined control in city 1 (i.e. \(c_{P_1}=c_{L_1}=c_{A_1}=0,0.25,0.50\))

Full size image
Fig. 7
figure 7

Dynamics of infectious individuals and mosquitoes of cities 1 and 2 with unidirectional host mobility from city 1 to city 2 at different levels of combined control implementation in city 2 (i.e. \(c_{P_2}=c_{L_2}=c_{A_2}=0,0.25,0.50\))

Full size image

The effects of the application of combined control only in city 2 on the dynamics of the subpopulations of infectious individual and mosquito of city 1 and city 2 when there is unidirectional host mobility from city 1 to city 2 is represented in Fig. 7. Figure 7d shows a high impact of applying about \(50\%\) of combined control on the dynamics of the numbers of infectious mosquitoes of city 2. However, this control intervention strategy has no significant impact on the dynamics of the subpopulations of infectious individual and mosquito of city 1 (as shown in Fig. 7a, b, respectively) as well as the number of infectious humans in city 2 (as shown in Fig. 7c). These results suggest that implementing control interventions only in a less dengue-endemic city when only human migration from high dengue-endemic city to less dengue-endemic city is possible is not effective, implying that human migration reduces the efficacy of the implemented control interventions in the less dengue-endemic city.

Fig. 8
figure 8

Dynamics of infectious individuals and mosquitoes of cities 1 and 2 with unidirectional host mobility from city 1 to city 2 at different levels of simultaneous implementation of combined control in cities 1 and 2 (i.e. \(\text{ control }=0,0.25,0.50\))

Full size image

Figure 8 shows the impacts of combined control applied simultaneously in city 1 and city 2 on the dynamics of the numbers of infectious individuals and mosquitoes in the presence of the host mobility between the two cities. The numbers of infectious humans and mosquitoes in city 1 drastically reduce to zero using about \(50\%\) each of control interventions as seen in Fig. 8a, b. By implementing the control interventions, the number of infectious mosquitoes in city 2 is sufficiently diminished to zero after 20th day from the commencement of the interventions, whereas the number of infectious individuals in city 2 does not reduce using this control efforts (as shown in Fig. 8c).

Hence, the simulated results reveal that, in the presence of unidirectional human movement from city 1 to city 2, the application of combined efforts of the three control interventions is sufficient to diminish the number of infections in the population of city 1 to zero when the city is a control-target, while there is also a significant impact of the implemented control, particularly on the infected mosquito subpopulation, when city 2 becomes the only control-target city. In [10, 34], the simulated results of the effect of patch-specific optimal personal protection control on the dynamics of the infectious individual and mosquito subpopulations with unidirectional human movement between patches reveal that the separate use of the control simultaneously implemented in the connected patches is not enough to diminish the numbers of infectious humans and mosquitoes of both patches to zero. Hence, our results indicate the efficacy of the application of combined efforts of different control measures over a single intervention. In Kim et al. [33], the authors also demonstrated the efficacy of joint application of transmission control (preventive measure), vector (adulticide) control and travel blockage control over their separate use as a fight against dengue in two connected patches.

Furthermore, Fig. 9 presents the dynamics of the infectious individual and mosquito subpopulations of city 1 and city 2 under the influence of various levels of combined control efforts applied only in city 1 and unidirectional host mobility from city 2 to city 1. As shown in Fig. 9a, b, the size of subpopulations of infectious human and mosquito of city 1 drastically reduces to zero by applying about \(50\%\) of combined control effort. However, the control strategy has no significant impact on the dynamics of the numbers of infectious individuals and mosquitoes of city 2 as depicted in Fig. 9c, d, respectively.

Fig. 9
figure 9

Dynamics of infectious individuals and mosquitoes of cities 1 and 2 with unidirectional host mobility from city 2 to city 1 at different levels of combined control implementation only in city 1 (i.e. \(c_{P_1}=c_{L_1}=c_{A_1}=0,0.25,0.50\))

Full size image
Fig. 10
figure 10

Dynamics of infectious individuals and mosquitoes of cities 1 and 2 with unidirectional host mobility from city 2 to city 1 at different levels of combined control implementation only in city 2 (i.e. \(c_{P_2}=c_{L_2}=c_{A_2}=0,0.25,0.50\))

Full size image

In Fig. 10, the impacts of applying combined control at various levels only in city 2 on the dynamics of infectious humans and mosquitoes when there is unidirectional host mobility from city 2 to city 1 are illustrated. Using about \(50\%\) of combined control sharply reduces the number of infectious mosquitoes in city 2 to zero and remain there from the 20th day till the end of the control intervention as shown in Fig. 10d. However, Fig. 10a–c reveals that the effect of unidirectional movement drastically reduces the efficacious of this control strategy to the extent of not having any impact on the infected human and mosquito subpopulations.

Fig. 11
figure 11

Dynamics of infectious individuals and mosquitoes of cities 1 and 2 with unidirectional host mobility from city 2 to city 1 at different levels of simultaneous application of combined control in cities 1 and 2 (i.e. \(\text{ control }=0,0.25,0.50\))

Full size image

Figure 11 presents the effects of simultaneous application of combined control efforts at different levels in city 1 and city 2 on the dynamics of the subpopulations of infectious human and mosquito with bidirectional human movement between the cities. It can be observed that this control strategy is sufficient to diminish the numbers of infectious individuals and mosquitoes of city 1 to zero at about \(50\%\) level of the control application in the two interconnected cities (see Fig. 11a, b). Also, the subpopulation of infectious mosquito with control decreases rapidly to zero when compared with the case of no intervention; however, there is no significant impact of using the control efforts on the number of infectious individuals in city 2 (as illustrated in Fig. 11c).

Also, Fig. 12 illustrates the impacts of combined control applied at various levels only in city 1 on the dynamics of the subpopulations of infectious individual and mosquito in city 1 and city 2 when there is bidirectional human movement between the cities. The use of about \(50\%\) level of combined control significantly reduces the number of infectious individuals and mosquitoes more rapidly to zero when compared with the case of no control administration in city 1 as shown in Fig. 12a, b. In addition, the implementation of the control increases dengue disease burden in human population from 25th day to 70th day with no significant impact on the number of infectious mosquitoes in city 2 (see Fig. 12c, d). Hence, the strategy is not enough to decrease both the subpopulations of infectious individual and mosquito of city 1 and city 2 to zero.

Fig. 12
figure 12

Dynamics of infectious individuals and mosquitoes of cities 1 and 2 with bidirectional host mobility between the cities at different levels of combined control implementation only in city 1 (i.e. \(c_{P_1}=c_{L_1}=c_{A_1}=0,0.25,0.50\))

Full size image
Fig. 13
figure 13

Dynamics of infectious individuals and mosquitoes of cities 1 and 2 with bidirectional host mobility between the cities at different levels of combined control implementation in city 2 (i.e. \(c_{P_2}=c_{L_2}=c_{A_2}=0,0.25,0.50\))

Full size image

Figure 13 demonstrates the effects of different levels of the application of combined control only in city 2 on the dynamics of the numbers of infectious individuals and mosquitoes of city 1 and city 2 in the presence of bidirectional host mobility between the two connected cities. It is observed that the dynamical behaviours of the infected human and mosquito subpopulations in both cities are similar to those presented in Fig. 10. Hence, discussions of the results obtained under this control implementation are similar to those given for the results in Fig. 10.

Fig. 14
figure 14

Dynamics of infectious individuals and mosquitoes of cities 1 and 2 with bidirectional host mobility between the cities at different levels of simultaneous implementation of combined control in cities 1 and 2 (i.e. \(\text{ control }=0,0.25,0.50\))

Full size image

Figure 14 illustrates the effects of combined control administered simultaneously at different levels in city 1 and city 2 on the dynamics of the subpopulations of infectious human and mosquito of cities 1 and 2 in the presence of bidirectional human movement between the two cities. Figure 14a, b shows that the simultaneous application of about \(50\%\) of combined control in city 1 and city 2 decreases the size of infected human and mosquito subpopulations more rapidly than when the control efforts are not implemented. Furthermore, Fig. 14d reveals that the use of about \(50\%\) of combined control simultaneously in city 1 and city 2 diminishes the number of infectious mosquitoes in city 2 to zero between 20th day and 120th day from the commencement of the control intervention program; however, the number of infected individuals with control in city 2 increases between the 25th day and 80th day counting from the beginning of control implementation period (as shown in Fig. 14c). Lee and Castillo-Chavez [34], in their study on the optimal control strategies for dengue disease transmission dynamics in a patchy environment, estimated the effect of patch-specific optimal personal protection control simultaneously implemented in the two connected patches through bidirectional human movement. The results of their numerical simulations show that the control strategy is not sufficient to reduce the number of infectious individuals of both patches to zero. In a similar study, Bock and Jayathunga [10] applied optimal control theory to derive the optimal personal protection control needed for an effective control of dengue disease spread in a patchy environment. The numerical results obtained revealed that the use of only personal protection is not enough to reduce the size of infected subpopulation in the community to zero. Therefore, our results show that the administration of combined efforts of several control strategies is more efficacious than their separate use in controlling dengue disease spread within the populations of two connected patches (or cities).

6 Conclusions

This paper has presented and analysed a two-patch model, which captures both the aquatic phase and adult mosquitoes, effect of human movement and vertical transmission in vector population, for dengue disease transmission dynamics. The model incorporates three patch-specific control parameters accounting for human personal protection, larvicide and adulticide. The two-patch model has provided a new framework for assessing the role of human movement, vertical transmission in vector population, as well as gaining insights into the impacts of combined efforts of patch-specific three control measures (i.e. personal protection, larvicide and adulticide) on the transmission dynamics of dengue disease between two interconnected high dengue-endemic city 1 (large urban centre) and low dengue-endemic city 2 (satellite city). The results observed from our analyses and simulations of the model are as follows:

  1. i.

    The two-patch model admits two disease-free equilibria, namely the TE and the BRDFE.

  2. ii.

    The BRDFE point \({\mathcal {E}}_2\), associated with the model, is LAS if \({\mathcal {R}}_T<1\), and unstable otherwise.

  3. iii.

    It is shown that the BRDFE point \({\mathcal {E}}_2\) of the two-patch dengue model is GAS whenever \({\mathcal {R}}_T<1\), and unstable otherwise. The epidemiological insight from this result is that dengue disease will eventually die out from the population in both cities whenever the threshold quantity \({\mathcal {R}}_T\) is below unity.

  4. iv.

    Without any control implementation, the basic reproductive number for dengue outbreaks in isolated city 1 and city 2 is approximately \({\mathcal {R}}_{0,1}=2.396\) and \({\mathcal {R}}_{0,2}=1.573\), respectively, and the basic reproductive number of the two-patch model in the absence of any control is approximately \({\mathcal {R}}_0=1.891\).

  5. v.

    Assessing the role of vertical transmission in vector population, the simulated results reveal that vertical transmission has significant influence on the disease dynamic, particularly in city 2.

  6. vi.

    In the case of no control, it is observed that with the presence of human movements (either unidirectional or bidirectional movements) between the large urban centre (city 1) and satellite city (city 2), the prevalence of dengue disease decreases as the subpopulation sizes increase. This indicates that the higher the population density of a dengue-endemic city, the higher the transmission rate of dengue, and vice versa.

  7. viii.

    When the efforts of combined control can only be implemented in one city due to limited resources, it is more effective to control the high dengue-endemic city 1 in the case of unidirectional human movement between the two connected cities. Also, controlling city 1 gives a better reduction in dengue prevalence in the presence of bidirectional human movement between cities 1 and 2.

  8. ix.

    In both cases of unidirectional and bidirectional human movements between the connected cities 1 and 2, applying the combined control in city 1 and city 2 simultaneously is found to be most effective in eliminating dengue disease from human and mosquito populations in the two cities. However, the level of implemented combined control effort should be increased in both city 1 and city 2 as the population size of city 1 increases in order to achieve a dengue-free population in the two cities.

In this study, we considered the effect of combined efforts of bounded patch-specific control parameters \(0\le c_{P_i}\le 1\), \(0\le c_{L_i}\le 1\) and \(0\le c_{A_i}\le 1\) (for \(i=1,2\)) separately and simultaneously administered in two connected patches on dengue disease transmission dynamics. However, the implementation of the strategies may be too expensive to apply. Therefore, in future work, we intend to obtain the optimal control functions \(c_{P_i}(t)\), \(c_{L_i}(t)\) and \(c_{A_i}(t)\) that optimally curtail the spread of dengue in two connected patches using optimal control theory.