Forced vibration analyses of FGP shallow shells with variable curvature

Abstract

The functionally graded porous material is an emerging material that is able to reduce structural weight and keeps the superiority of mechanical property of the structure. Therefore, this work is devoted to the investigation of the dynamic behavior for the functionally graded porous (FGP) shallow shells with variable curvature under forced vibrations. First, the analysis method is derived based on the first-order shear deformation theory, the virtual spring technology, the multi-segment partition technique, the third kind of Chebyshev polynomials, the semi-analysis Rayleigh–Ritz approach, and the Newmark-Beta method. Afterwards, the frequency parameters, modal shapes, and vibration responses are systematically calculated via the present model. Besides, the convergency and correctness of the present model are verified, respectively. With the verified model, the forced vibration behaviors of the FGP shallow shells with different parameters, such as porosity distribution types, porosity ratios, boundary condition types, geometry parameters, and load types, are investigated in detail.

1 Introduction

The shallow shell structure is widely employed in aeronautics, aircraft engineering, ship engineering, petrochemical container, and other application fields due to its high specific stiffness, excellent fatigue characteristics and good corrosion resistance [1,2,3,4,5]. However, the structures are always exposed to a complex working environment. It is inevitable to generate various failure modes [6,7,8]. Therefore, it is meaningful to improve the mechanical characteristics and dynamic behaviors of the structure. The functionally graded porous (FGP) design is an emerging strengthening technique and has been widely employed in industry fields due to its excellent energy absorption, high-temperature resistance, and electrical conductivity [9,10,11]. Therefore, the dynamic behaviors of the FGP shallow shells are investigated in this work.

At present, the modeling method of the FGP structure has been widely investigated [12]. In light of the Timoshenko beam theory, Chen et al. [13] constructed a FGP beam model and studied the elastic buckling and static bending behaviors of the beam. Chen et al. [14] studied the free and forced vibration behaviors of the FGP beam with non-uniform porosity distribution. Wang et al. [15] built a FGP cylindrical shell model with different sets of immovable boundary conditions and investigated the free vibration characteristics of the shell. Shi et al. [16] focused on the free vibration analysis of the FGP shallow shell by adopting the improved Fourier series method. Li et al. [17] studied the nonlinear vibration and the dynamic buckling of the FGP graphene platelet reinforced sandwich plate resting on Winkler–Pasternak elastic foundation. Based on the modified Fourier series, Zhao et al. [18] mainly investigated the free vibration characteristics of the FGP double curve shallow shells. Chan et al. [12] studied the nonlinear dynamic response and free vibration of the FGP truncated conical panel with piezoelectric actuators in thermal environment. Based on the general third-order shear deformation plate theory and the modified couple stress theory, a nonlinear finite element model for FGP micro-plates was built by Genao et al. [19]. As mentioned above, few investigations can be found on the dynamic behaviors of the FGP shallow shells under forced vibration. However, the forced vibration was able to reflect the structural inherent characteristics, vibration suppression capacity [20,21,22], etc. Therefore, the dynamic characteristics analyses of the FGP shallow shells with variable curvature under forced vibration are conducted in this work.

Furthermore, the boundary condition shows a stronger impact on the dynamic characteristics of structures [23,24,25,26,27,28], and the influence of the boundary conditions on structures has been widely investigated. Hajianmaleki et al. [29] studied the static and vibration behaviors of the thick, general laminated deep curved beams with different boundary conditions by adopting the first-order shear deformation theory. Li et al. [30] calculated the natural frequencies, mode shapes, and buckling loads of the laminated composite beams with general boundary conditions. Song et al. [31] studied the free vibration characteristics of the symmetrically laminated composite cylindrical shells with arbitrary boundary conditions. Wang et al. [32] proposed a unified solution for the orthotropic circular, annular and sector plates and studied the free in-plane vibration of the structures with general boundary conditions. Based on the first-order shear deformation theory, Wang et al. [5] investigated the free vibration characteristics of the FG carbon nanotube-reinforced composite shallow shells with arbitrary boundary conditions. Chen et al. [33] studied the thermo-elastic vibration of FGM beams with general boundary conditions. Kim et al. [34] constructed an analysis model to investigate the vibration characteristics of the cracked laminated composite beam of uniform rectangular cross section with arbitrary boundary conditions. Li et al. [35] investigated the nonlinear vibration characteristics of the thin-walled cylindrical shell with point-supported condition. As mentioned above, the nonclassical boundary conditions have attracted a lot of interest. Therefore, the general boundary conditions are considered to thoroughly study its effect on the dynamic behaviors of the FGP shallow shell structures with variable curvature under forced vibration.

Motivated by the above analysis, it is of significance to investigate the effect of the porous design and the general boundary conditions on the shallow shells with variable curvature under forced vibration. Therefore, a unified formulation for forced vibration analysis of the FGP shallow shell with variable curvature is employed. The main contribution of this work is summarized as: (1) The admissible displacement function employs the third kind of Chebyshev polynomials, which simplifies the programming for the dynamic analysis of the FGP shallow shell to some extent; (2) The dynamic characteristics of the FGP shallow shell under forced vibration are systematically studied. Furthermore, this work is divided into three parts: The theoretical model is constructed first in Sect. 2. Then, numerical results of the FGP shallow shell structures under the free vibration and the forced vibration are shown in Sect. 3, such as the convergency verification, the numerical validation, and the parametric analysis. Finally, conclusions of this work are given in Sect. 4.

2 Theoretical formulation

2.1 Modeling of FGP shallow shells with variable curvature

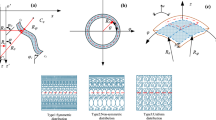
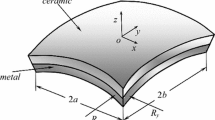
The FGP shallow shell models with variable curvature are constructed at spherical coordinate system o-xyz, as shown in Fig. 1. The symbols R_x and R_y stand for the principal radius of curvature along x and y directions; a, b and h denote the length, width, and thickness of the structures. Furthermore, Fig. 2 shows that the shallow shell is able to be transformed into various shapes by adjusting the two radii of curvature, such as plate (R_x = R_y = $\infty$), spherical shell (R_x = R_y = R), cylindrical shell (R_x = $\infty$, R_y =  R) and hyperbolic paraboloidal shell (R_x = $-$ R_y =  R).

Fig. 1

Structure modeling of the FGP shallow shell with general boundary conditions

Fig. 2

Schematic diagram of the FGP shallow shell with various curvature

2.2 Material parameters of the FGP

Three types of porous distributions are considered in this work [14, 18, 36], including the symmetric distribution T-1, non-symmetric distribution T-2, and uniform distribution T-3. The material parameters of the FGP shallow shell along the z-axis are nonlinear since the porous distribution is nonlinear. Therefore, the Young’s modulus E(z), shear modulus G(z), and mass density ρ(z) of the FGP shallow shell are expressed as follows

$$ E(z) = E_{{1}} {\kern 1pt} \lambda (z) $$

(1a)

$$ G(z) = G_{1} \lambda (z) $$

(1b)

$$ \rho (z) = \rho_{1} \eta (z) $$

(1c)

where E₁ denotes the maximum values of Young’s modulus along the z-axis; G₁ expresses the maximum values of shear modulus along the z-axis; ρ₁ is the maximum values of mass density along the z-axis; λ(z) and η(z) are the porous distribution function, which can be defined as

$$ \lambda (z) = \left\{ {\begin{array}{*{20}l} {\left[ {1 - e_{0} \cos \left( {\frac{{\pi z}}{h}} \right)} \right]} \hfill & {{\text{Type}}{\mkern 1mu} 1} \hfill \\ {\left[ {1 - e_{0} \cos \left( {\frac{{\pi z}}{{2h}} + \frac{\pi }{4}} \right)} \right]{\text{ }}} \hfill & {{\text{Type}}{\mkern 1mu} 2} \hfill \\ {\left[ {1 - e_{0} \alpha } \right]{\text{ }}} \hfill & {{\text{Type}}{\mkern 1mu} 3} \hfill \\ \end{array} } \right.$$

(2a)

$$ \eta (z) = = \left\{ {\begin{array}{*{20}l} {\left[ {1 - e_{m} \cos \left( {\frac{{\pi z}}{h}} \right)} \right]} \hfill & {{\text{Type}}\,1} \hfill \\ {\left[ {1 - e_{m} \cos \left( {\frac{{\pi z}}{{2h}} + \frac{\pi }{4}} \right)} \right]} \hfill & {{\text{Type}}\,{\text{2}}} \hfill \\ {\left[ {1 - e_{0} \alpha } \right]} \hfill & {{\text{Type}}\,{\text{3}}} \hfill \\ \end{array} } \right.$$

(2b)

where α is the coefficient of uniform porosity distribution; e₀ and e_m are the porosity coefficient, respectively, which can be given as

$$ e_{0} = 1 - \frac{{E_{2} }}{{E_{1} }} = 1 - \frac{{G_{2} }}{{G_{1} }},{\kern 1pt} {\kern 1pt} 0 \le e_{0} \le 1 $$

(3a)

$$ e_{m} = 1 - \frac{{\rho_{2} }}{{\rho_{1} }},{\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \le e_{m} \le 1 $$

(3b)

where E₂, G₂, ρ₂ denote the minimum values of Young’s modulus, shear modulus, and mass density along the z-axis, respectively.

Based on the open-cell metal foam theory [37], the porosity coefficient e₀, the mass coefficient e_m, and the coefficient of uniform porosity distribution α can be calculated by the following equation

$$ e_{m} = 1 - \sqrt {1 - e_{0} } $$

(4a)

$$ \alpha = \frac{1}{{e_{0} }} - \frac{1}{{e_{0} }}\left( {\frac{2}{\pi }\sqrt {1 - e_{0} } - \frac{2}{\pi } + 1} \right)^{2} $$

(4b)

2.3 Kinematic relations and energy expression

Based on the first-shear deformation theory, the displacement fields (U, V, W) of the shallow shells on the (i, j)th are given as [38]

$$ U^{i,j} (x,y,z,t) = u_{0}^{i,j} (x,y,t) + z\phi_{x}^{i,j} (x,y,t) $$

(5a)

$$ V^{i,j} (x,y,z,t) = v_{0}^{i,j} (x,y,t) + z\phi_{y}^{i,j} (x,y,t) $$

(5b)

$$ W^{i,j} (x,y,z,t) = w_{0}^{i,j} (x,y,t) $$

(5c)

where ${u}_{0}^{i,j}$, ${v}_{0}^{i,j}$ v0i,j and ${w}_{0}^{i,j}$ w0i,j are the middle surface displacements of the FGP shallow shells along x, y and z directions; ϕxi,j ${\phi }_{x}^{i,j}$ and ${\phi }_{y}^{i,j}$ express the rotation about x and y directions; t denotes the time variable. The superscripts ‘i’ and ‘j’ represent the segment number. In addition, the strains in the cross section can be given as

$$ \varepsilon_{x}^{i,j} = \varepsilon_{x}^{0,i,j} + z\chi_{x}^{i,j} ,\varepsilon_{y} = \varepsilon_{y}^{0,i,j} + z\chi_{y}^{i,j} $$

(6a)

$$ \gamma_{xy}^{i,j} = \gamma_{xy}^{0,i,j} + z\chi_{xy}^{i,j} ,\gamma_{xz}^{i,j} = \gamma_{xz}^{0,i,j} ,\gamma_{yz}^{i,j} = \gamma_{yz}^{0,i,j} $$

(6b)

where ${\varepsilon }_{x}^{0,i,j}$ and ${\varepsilon }_{y}^{0,i,j}$ represent the normal strains, and ${\gamma }_{xy}^{0,i,j}$ is the shear strains; ${\gamma }_{xz}^{0,i,j}$ and ${\gamma }_{yz}^{0,i,j}$ denote the transverse shear strains of the middle surface; ${\chi }_{x}^{i,j}$ and ${\chi }_{y}^{i,j}$ express the curvature changes along x and y directions, and ${\chi }_{xy}^{i,j}$ stands for the twist change. Moreover, the above strains of the middle surface can be substituted by the displacement field as follows

$$ \varepsilon_{x}^{0,i,j} = \frac{{\partial u_{0} }}{\partial x} + \frac{{w_{0} }}{{R_{x} }},\varepsilon_{y}^{0,i,j} = \frac{{\partial v_{0} }}{\partial y} + \frac{{w_{0} }}{{R_{y} }} $$

(7a)

$$ \chi_{x}^{i,j} = \frac{{\partial \phi_{x} }}{\partial x},\chi_{y}^{i,j} = \frac{{\partial \phi_{y} }}{\partial y},\chi_{xy}^{i,j} = \frac{{\partial \phi_{y} }}{\partial x} + \frac{{\partial \phi_{x} }}{\partial y} $$

(7b)

$$ \gamma_{xz}^{0,i,j} = \frac{{\partial w_{0} }}{\partial x} - \frac{{u_{0} }}{{R_{x} }} + \phi_{x} ,\gamma_{yz}^{0,i,j} = \frac{{\partial w_{0} }}{\partial y} - \frac{{v_{0} }}{{R_{y} }} + \phi_{y} ,\gamma_{xy}^{0,i,j} = \frac{{\partial v_{0} }}{\partial x} - \frac{{\partial u_{0} }}{\partial y} $$

(7c)

Based on general Hooke’s law, the stresses of the structure can be expressed with the following equation

$$ \left\{ \begin{gathered} \sigma_{rr} \hfill \\ \sigma_{\theta \theta } \hfill \\ \tau_{r\theta } \hfill \\ \tau_{rz} \hfill \\ \tau_{\theta z} \hfill \\ \end{gathered} \right\} = \left[ {\begin{array}{*{20}l} {Q_{11} (z)} & {Q_{12} (z)} & {} & {} \\ {Q_{12} (z)} & {Q_{11} (z)} & {} & {} \\ {} & {} & {Q_{66} (z)} & {} \\ \begin{gathered} \hfill \\ \hfill \\ \end{gathered} & \begin{gathered} \hfill \\ \hfill \\ \end{gathered} & \begin{gathered} \hfill \\ \hfill \\ \end{gathered} & \begin{gathered} Q_{66} (z) \hfill \\ \hfill \\ \end{gathered} \\ \end{array} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}l} {} \\ {} \\ {} \\ \begin{gathered} \hfill \\ Q_{66} (z) \hfill \\ \end{gathered} \\ \end{array} } \right]\left\{ \begin{gathered} \varepsilon_{rr} \hfill \\ \varepsilon_{\theta \theta } \hfill \\ \gamma_{r\theta } \hfill \\ \gamma_{rz} \hfill \\ \gamma_{\theta z} \hfill \\ \end{gathered} \right\} $$

(8)

in which

$$ Q_{11} (z) = \frac{E(z)}{{1 - v(z)^{2} }},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} Q_{12} (z) = \frac{v(z)E(z)}{{1 - v(z)^{2} }},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} Q_{66} (z) = \frac{E(z)}{{2\left( {1 + v(z)} \right)}} $$

(9)

By integrating the normal and shear stresses over the cross section of the FGP shallow shells, the stress–strain relationship of Eq. (8) on the (i, j)th segment can be transformed as

$$ \left[ {\begin{array}{*{20}l} {N_{rr}^{i,j} } \\ {N_{\theta \theta }^{i,j} } \\ {N_{r\theta }^{i,j} } \\ {M_{rr}^{i,j} } \\ {M_{\theta \theta }^{i,j} } \\ \begin{gathered} M_{r\theta }^{i,j} \hfill \\ {\kern 1pt} {\kern 1pt} Q_{rr}^{i,j} \hfill \\ {\kern 1pt} {\kern 1pt} Q_{\theta \theta }^{i,j} \hfill \\ \end{gathered} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {A_{11} } & {A_{12} } & 0 & {B_{11} } & {B_{12} } & 0 \\ {A_{12} } & {A_{11} } & 0 & {B_{12} } & {B_{11} } & 0 \\ 0 & 0 & {A_{66} } & 0 & 0 & {B_{66} } \\ {B_{11} } & {B_{12} } & 0 & {D_{11} } & {D_{12} } & 0 \\ {B_{12} } & {B_{11} } & 0 & {D_{12} } & {D_{11} } & 0 \\ \begin{gathered} 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{gathered} & \begin{gathered} 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{gathered} & \begin{gathered} B_{66} \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{gathered} & \begin{gathered} 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{gathered} & \begin{gathered} 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{gathered} & \begin{gathered} D_{66} \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{gathered} \\ \end{array} {\kern 1pt} \begin{array}{*{20}l} 0 \\ 0 \\ 0 \\ \begin{gathered} 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ \kappa A_{66} \hfill \\ 0 \hfill \\ \end{gathered} \\ \end{array} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}l} 0 \\ 0 \\ 0 \\ \begin{gathered} 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ \kappa A_{66} \hfill \\ \end{gathered} \\ \end{array} } \right]\left[ \begin{gathered} \varepsilon_{rr}^{0,i,j} \hfill \\ \varepsilon_{\theta \theta }^{0,i,j} \hfill \\ \gamma_{r\theta }^{0,i,j} \hfill \\ \chi_{rr}^{i,j} \hfill \\ \chi_{\theta \theta }^{i,j} \hfill \\ \chi_{r\theta }^{i,j} \hfill \\ \gamma_{rz}^{0,i,j} \hfill \\ \gamma_{\theta z}^{0,i,j} \hfill \\ \end{gathered} \right] $$

(10)

in which $\kappa$ stands for the shear correction factor; ${A}_{ij}$, ${B}_{ij}$ and ${D}_{ij}$ (i, j = 1, 2 and 6) denote the extensional stiffness coefficients, coupling stiffness coefficients and the bending stiffness coefficients, respectively. Besides, the stiffness coefficients can be calculated as

$$ \left( {A_{ij}^{{}} ,B_{ij}^{{}} ,D_{ij}^{{}} } \right) = \int_{ - h/2}^{h/2} {Q_{ij}^{{}} (1,z,z^{2} )dz} $$

(11)

The energy of the structure can be divided into strain energy and kinetic energy. The kinetic energy ${T}^{i,j}$ on the (i, j)th segment is expressed as

$$ T^{i,j} = \frac{1}{2}\iiint\limits_{V} {\left\{ {\left( {\frac{{\partial U^{i,j} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial V^{i,j} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial W^{i,j} }}{\partial t}} \right)^{2} } \right\}dV} $$

(12)

Substituting Eqs. (5a-c) into Eq. (12), the kinetic energy can be further expressed as

$$\begin{aligned} T^{i,j} = \frac{1}{2}\int_{{y_{i} }}^{{y_{i + 1} }} \int_{{x_{i} }}^{{x_{i + 1} }} \left\{ \begin{gathered} I_{0} \left( {\left( {\frac{{\partial u_{0}^{i,j} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial v_{0}^{i,j} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial w_{0}^{i,j} }}{\partial t}} \right)^{2} } \right)\\ + 2I_{1} \left( {\left( {\frac{{\partial u_{0}^{i,j} }}{\partial t}} \right)\left( {\frac{{\partial \phi_{x}^{i,j} }}{\partial t}} \right) + \left( {\frac{{\partial v_{0}^{i,j} }}{\partial t}} \right)\left( {\frac{{\partial \phi_{y}^{i,j} }}{\partial t}} \right)} \right) \hfill \\ + I_{2} \left( \left( {\frac{{\partial \phi_{x}^{i,j} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial \phi_{y}^{i,j} }}{\partial t}} \right)^{2} \right) \hfill \\ \end{gathered} \right\}dxdy \end{aligned} $$

(13)

where

$$ \left( {I_{0} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} I_{1} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} I_{2} } \right) = \int_{ - h/2}^{h/2} {\rho (z)\left( {1,{\kern 1pt} {\kern 1pt} {\kern 1pt} z,{\kern 1pt} {\kern 1pt} {\kern 1pt} z^{2} } \right)dz} $$

(14)

in which ${I}_{0}$, ${I}_{1}$ and ${I}_{2}$ denote the inertial terms.

Besides, the strain energy ${\text{U}}_{\text{s}}^{\text{ i, j}}$ on the (i, j)th of the FGP shallow shells is denoted as

$$ U_{s}^{i,j} = \frac{1}{2}\int_{{y_{i} }}^{{y_{i + 1} }} {\int_{{x_{i} }}^{{x_{i + 1} }} {\left\{ \begin{gathered} N_{x}^{i,j} \varepsilon_{x}^{0,i,j} + N_{y}^{i,j} \varepsilon_{y}^{0,i,j} + N_{xy}^{i,j} \gamma_{xy}^{0,i,j} + M_{x}^{i,j} \chi_{x}^{i,j} + \hfill \\ M_{y}^{i,j} \chi_{y}^{i,j} + M_{xy}^{i,j} \chi_{xy}^{i,j} + Q_{x}^{i,j} \gamma_{xz}^{0,i,j} + Q_{y}^{i,j} \gamma_{yz}^{0,i,j} \hfill \\ \end{gathered} \right\}dxdy} } $$

(15)

The virtual spring technique is adopted in this work to simulate the general boundary conditions. Those virtual springs are composed of three groups of linear springs (i.e., ${k}_{u}$, ${k}_{v}$, ${k}_{w}$) and two groups of turning springs (i.e., ${k}_{x}$, ${k}_{y}$). The potential energy of boundary springs U_b has the following form

$$ U_{b} = \frac{1}{2}\int_{{y_{i} }}^{{y_{i + 1} }} {\left( {\sum\limits_{{}} {K_{{x_{0} }}^{\varpi } \vartheta^{2} } + \sum\limits_{{}} {K_{{x_{1} }}^{\varpi } \vartheta^{2} } } \right)dy} + \frac{1}{2}\int_{{x_{0} }}^{{x_{1} }} {\left( {\sum\limits_{{}} {K_{{y_{0} }}^{\varpi } \vartheta^{2} } + \sum\limits_{{}} {K_{{y_{1} }}^{\varpi } \vartheta^{2} } } \right)dx} $$

(16)

where ${K}_{{x}_{0}}^{\varpi }$, ${K}_{{x}_{1}}^{\varpi }$ ${K}_{{y}_{0}}^{\varpi }$, ${K}_{{y}_{1}}^{\varpi }$ ($\varpi =u, v, w, x, y$) are the stiffness parameters of five sets of degrees of freedom at ${x}_{0}$, ${x}_{1}$, ${y}_{0}$ and ${y}_{1}$ boundaries, respectively; the symbol $\vartheta$ stands for the five groups of relative displacement ($u, v, w, x, y$).

Moreover, the continuity of each segment can be satisfied based on the virtual spring technique, and the potential energy of convective springs ${U}_{c}^{i,j}$ in each segment is denoted as

$$ U_{c}^{i,j} = \frac{1}{2}\int_{{x_{i} }}^{{x_{i + 1} }} {\sum\nolimits_{{}} {K^{\varpi } (\vartheta^{i,j} - \vartheta^{i,j + 1} )} } {\kern 1pt}^{2} {\kern 1pt} dx + \frac{1}{2}\int_{{y_{i} }}^{{y_{i + 1} }} {\sum\nolimits_{t} {K^{\varpi } (\vartheta^{i,j} - \vartheta^{i + 1,j} )} } {\kern 1pt} {\kern 1pt}^{2} dy $$

(17)

where ${K}^{\varpi }$ ($\varpi =u, v, w, x, y$) are the stiffness parameters of the convective spring.

To study the dynamic behaviors of the FGP structures under forced vibration, the integral form of the work done caused by the external force can be given as

$$ W{ = }\frac{1}{2}\iiint_{V} {\left( {f_{u} u{ + }f_{v} v{ + }f_{w} w{ + }m_{\phi x} \phi_{x} { + }m_{\phi y} \phi_{y} } \right)dV} $$

(18)

where $f_{J} (J = u,v,w)$ depicts the translational forces, and $m_{J} (J = x,y)$ represents the moments.

2.4 Admissible displacement function and solution process

To solve the dynamic equation, the admissible displacement function should be confirmed first. According to the convergency and continuity, the third kind of Chebyshev polynomials is adopted to simulate the unknown displacement functions [39]. Referring to [40,41,42,43,44], the third kind of Chebyshev polynomials is generated from the range of $\varphi \epsilon [-1, 1]$ with following recurrence formulations as

$$ P_{0}^{{}} (\varphi ) = 1 $$

(19a)

$$ P_{1}^{{}} (\varphi ) = \varphi - {1} $$

(19b)

$$ P_{k}^{{}} (\varphi ) = \varphi (2 - \frac{{1}}{k}){\kern 1pt} {\kern 1pt} {\kern 1pt} P_{k - 1}^{{}} (\varphi ) - \frac{{{\kern 1pt} (2k - {1})({2}k - {3})}}{k(2k - 2)}P_{k - 2}^{{}} (\varphi ) $$

(19c)

where $k=2, 3, \dots , N$.

Besides, the displacement expressions of the structures can be assumed as follows

$$ u = \sum\limits_{n = 0}^{N} {\sum\limits_{m = 0}^{M} {U_{mn}^{i,j} P_{m}^{{}} (x)P_{n}^{{}} (y)e^{i\omega t} } } $$

(20a)

$$ v = \sum\limits_{n = 0}^{N} {\sum\limits_{m = 0}^{M} {V_{mn}^{i,j} P_{m}^{{}} (x)P_{n}^{{}} (y)e^{i\omega t} } } $$

(20b)

$$ w = \sum\limits_{n = 0}^{N} {\sum\limits_{m = 0}^{M} {W_{mn}^{i,j} P_{m}^{{}} (x)P_{n}^{{}} (y)e^{i\omega t} } } $$

(20c)

$$ \phi_{x} = \sum\limits_{n = 0}^{N} {\sum\limits_{m = 0}^{M} {\varsigma_{mn}^{i,j} P_{m}^{{}} (x)P_{n}^{{}} (y)e^{i\omega t} } } $$

(20d)

$$ \phi_{y} = \sum\limits_{n = 0}^{N} {\sum\limits_{m = 0}^{M} {\xi_{mn}^{i,j} P_{m}^{{}} (x)P_{n}^{{}} (y)e^{i\omega t} } } $$

(20e)

where ${U}_{mn}^{i,j}$, ${V}_{mn}^{i,j}$, ${W}_{mn}^{i,j}$, ${\varsigma }_{mn}^{i,j}$, and ${\xi }_{mn}^{i,j}$ are the unknown vibration amplitude parameters of the assumed displacement function; subscript ‘m’ and ‘n’ stand for the Chebyshev polynomials of degree along $x$ and $y$ directions, respectively; $\omega$ denotes the natural circular frequency; $t$ stands for the time variable; $M$ and $N$ are the defined truncated number.

Furthermore, the Lagrange equations L with the ideal constraint can be obtained as

$$ L = U_{s} + U_{b} + U_{c} - T - W $$

(21)

Based on the minimum strain energy principle, the Lagrange equations can be transformed as the following equation

$$ \frac{\partial L}{{\partial \wp }} = 0 \left( {\wp = U_{mn} ,V_{mn} ,W_{mn} ,\varsigma_{mn} ,\xi_{mn} } \right) $$

(22)

Substituting Eqs. (13, 15–17) into Eq. (22), the expression can be transformed to matrix form as

$$ (K - \omega^{2} M)q = F $$

(23)

where $\mathbf{K}$ expresses the stiffness matrix of the FGP shallow shells; $\mathbf{M}$ stands for the mass matrix of the structures, respectively; $\mathbf{F}$ denotes the external force vector; ${\varvec{q}}$ stands for the generalized solution vector.

As for the free vibration, the generalized eigenvalues and the generalized column vectors are solved by the following equation as

$$ (K - \omega^{2} M)q = 0 $$

(24)

Therefore, the dynamic vibration solution, such as frequency parameters, vibration responses, and mode shapes of the FGP shallow shells, can be achieved.

Besides, as for the forced vibration, four types of load time domain curves are considered, as shown in Fig. 3, including the rectangular pulse, triangular pulse, half-sine pulse, and exponential pulse. The four types of shock wave pulses can be defined by the mathematical expression as follows

$$ {\text{Rectangular}}\,{\text{pulse: }}f\left( t \right) = \left\{ {\begin{array}{*{20}l} {f_{t} } &\quad {0 \le t \le \tau } \\ 0 &\quad {t > \tau } \\ \end{array} } \right. $$

(25a)

$$ {\text{Triangular\, pulse:}} f\left( t \right) = \left\{ {\begin{array}{*{20}l} {\frac{2t}{\tau }f_{t} } &\quad {0 \le t \le \frac{\tau }{2}} \\ {f_{t} - \frac{2}{\tau }\left( {t - \frac{\tau }{2}} \right)f_{t} } &\quad {\frac{\tau }{2} \le t \le \tau } \\ 0 &\quad {t > \tau } \\ \end{array} } \right. $$

(25b)

$$ {\text{Half-sine}}\,{\text{pulse:}}f\left( t \right) = \left\{ {\begin{array}{*{20}l} {f_{t} \sin \left( {\frac{\pi t}{\tau }} \right)} &\quad {0 \le t \le \tau } \\ 0 &\quad {t > \tau } \\ \end{array} } \right. $$

(25c)

$$ {\text{Exponential}}\,{\text{pulse:}}\,f\left( t \right) = \left\{ {\begin{array}{*{20}l} {f_{t} e^{ - \xi t} } &\quad {0 \le t \le \tau } \\ 0 &\quad {t > \tau } \\ \end{array} } \right. $$

(25d)

Fig. 3

The sketch of load time domain curve: a Rectangular pulse; b Triangular pulse; c Half-sine pulse; d Exponential pulse

where $t$ donates the time variable, $\tau$ stands for the pulse width, ${f}_{t}$ denotes the load amplitude. Furthermore, the structural dynamic equilibrium equation can be expressed as

$$ M\ddot{u} + C\dot{u} + Ku = F $$

(26)

where $\ddot{{\varvec{u}}}$ expresses the acceleration vector; $\dot{{\varvec{u}}}$ stands for the velocity vector; ${\varvec{u}}$ is the displacement vector; $\mathbf{C}$ represents the damping matrix, which can be defined by$C={\gamma }_{1}M+{\gamma }_{2}K$, where ${\gamma }_{1}$ and ${\gamma }_{2}$ are the Rayleigh damping coefficients, $\gamma_{1} = 2\left( {\frac{{\zeta_{2} }}{{\omega_{2}^{3} }} - \frac{{\zeta_{1} }}{{\omega_{1}^{3} }}} \right)/\left( {\frac{1}{{\omega_{2}^{2} }} - \frac{1}{{\omega_{1}^{2} }}} \right)$ and $\gamma_{2} = 4\left( {\frac{{\zeta_{2} - \zeta_{1} }}{{\omega_{2}^{2} - \omega_{1}^{2} }}} \right)$, where $\zeta_{1} , \, \zeta_{2}$ are the attenuation coefficients [45].

In light of the Newmark-Beta method [46], the transient response of the FGP shallow shells can be calculated as follows

$$ \dot{u}_{t + \Delta t} = \dot{u}_{t} + \left[ {(1 - \delta )\ddot{u}_{t} + \delta \ddot{u}_{t + \Delta t} } \right]\Delta t $$

(27a)

$$ u_{t + \Delta t} = u_{t} + \dot{u}_{t} \Delta t + \left[ {\left( {\frac{1}{2} - \alpha } \right)\ddot{u}_{t} + \alpha \ddot{u}_{t + \Delta t} } \right]\Delta t^{2} $$

(27b)

where α and δ are set as 1/4 and 1/2, respectively.

3 Analysis and discussion

In Sect. 2, the unified formulation for forced vibration of the FGP shallow shells with variable curvature and general boundary conditions is derived. Afterwards, the parametric analysis can be further conducted in Sect. 3, and it is divided into three parts as: (1) The convergency investigation of the numerical results is conducted; (2) the dynamic characteristics of the structure under free vibration are investigated; (3) the dynamic behaviors analysis of the structure under forced vibration is conducted, including steady-state response and transient-state response. In the following investigation, the dimensionless frequency parameters $\Omega { = }\omega h\sqrt {{{\rho_{1} } \mathord{\left/ {\vphantom {{\rho_{1} } {E_{1} }}} \right. \kern-\nulldelimiterspace} {E_{1} }}}$ are adopted to express the natural frequency of the structures uniformly. Unless otherwise stated, the material parameters of the FGP shallow shells are uniformly set as: ρ₁ = 2702 kg/m³, E₁ = 70GPa, v = 0.3. Besides, the boundary spring stiffness under different boundary conditions is set as follows

$$ {\text{Clamped}}\,{\text{case}}\,\left(C\right){:}\,K^{u} = K^{v} = K^{w} = K^{x} = K^{y} = 10^{14} $$

$$ {\text{Free}}\,{\text{case}}\,\left(F\right){:}\,K^{u} = K^{v} = K^{w} = K^{x} = K^{y} = 0 $$

$$ {\text{Simply - support}}\,{\text{case}}\,\left(S\right){:}\,K^{u} = K^{x} = 0,K^{v} = K^{w} = K^{y} = 10^{14} $$

$$ {\text{Elastic}}\,{\text{constraint}}\,1\,\left({E1}\right){:}\,K^{u} = K^{v} = 10^{8} ,K^{w} = K^{x} = K^{y} = 10^{14} $$

$$ {\text{Elastic}}\,{\text{constraint}}\,2\,\left({E2}\right){:}\,K^{u} = K^{v} = K^{x} = K^{y} = 10^{14} ,K^{w} = 10^{8} $$

$$ {\text{Elastic}}\,{\text{constraint}}\,3\,\left({E3}\right){:}\,K^{u} = K^{v} = K^{w} = 10^{14} ,K^{x} = K^{y} = 10^{8} $$

$$ {\text{Elastic}}\,{\text{constraint}}\,4\,\left({E4}\right){:}\,K^{u} = K^{v} = K^{w} = K^{x} = K^{y} = 10^{8} $$

3.1 Convergency study

According to Ref. [39], the convergency of the final numerical results can be easily affected by various influence factors, such as the convective spring stiffness values, plate segments, and boundary spring stiffness values. Therefore, the convergency study is conducted via the mentioned three parts.

As shown in Table 1, the effect of the convective stiffness on the convergency of the first four frequency parameters is investigated. The geometrical and material parameters are defined as: a = b = 1 m, e₀ = 0.2; as for FGP plate, the radii of the structure are set as R_x = ∞, R_y = ∞; for FGP cylindrical shell, the radii of the structure are set as R_x = ∞, R_y = 2 m; as for FGP spherical shell, the radii of the structure are set as R_x = 2 m, R_y = 2 m; as for FGP hyperbolic paraboloidal shell, the radii of the structure are set as R_x = 2 m, R_y=$-$ 2 m. It can be observed that the first four frequency parameters show great convergency after the convective stiffness arrives 10¹² regardless of the type of structure. Therefore, to ensure the convergency, the stiffness value of the convective spring is set as 10¹⁴. Furthermore, Table 2 shows the effect of the number of plate segment numbers on the convergency of the first seven frequency parameters. The preset parameters are the same with that in Table 1. Through the comparison, the first seven frequency parameters show good consistency after the number of plate segments is set as 2 $\times$ 2. Specially, the calculated time of the present model from MATLAB software is sharply increased with the growth of the number of plate segments. Therefore, to improve the computational efficiency and the accuracy of numerical results, the number of plate segments is set as 2 $\times$ 2 in the following investigation.

Table 1 The effect of the convective stiffness on the convergency of the first four frequency parameters. (a = b = 1 m, h = 0.1 m, e₀ = 0.2, boundary condition: CCCC)

Table 2 The effect of the number of plate segments on the convergency of the first seven frequency parameters. (a = b = 1 m, h = 0.1 m, e₀ = 0.2, boundary condition: CCCC)

Finally, Fig. 4 shows the effect of the boundary spring stiffness on the convergency of frequency parameters, and the preset parameters are set as: a = 1 m, b = 1 m, h = 0.1 m, e₀ = 0.5. It is assumed that every curve represents the stiffness change along the single degree of freedom (DOF), and the boundary stiffnesses along the other DOFs are set as 10¹⁴. It can be concluded that the frequency parameters have great convergency when the stiffness value of the boundary spring is up to 10¹¹ regardless of the type of structure. Therefore, in this work, the clamped boundary is defined as 10¹⁴.

Fig. 4

The effect of the boundary spring stiffness on the convergency of frequency parameters

3.2 Free vibration of the FGP annular and circular sector plates

In light of the verification of the convergency study for the present model, the dynamic analysis under free vibration is able to be further carried out. This subsection is divided into two parts, including correction verification and parameter analysis.

The first frequency parameters of the FGP plate with various boundary conditions, material, and geometrical parameters are compared with the open literature [47], as shown in Table 3. The preset parameters are the same with that of the literature. It can be concluded that the first frequency parameters obtained from the present model and Ref. [47] show good agreement, which verifies the correctness of the FGP plate under different boundary conditions. Furthermore, Table 4 shows the comparison of the first frequency parameters of the FGP cylindrical and spherical shells with various boundary conditions and geometrical parameters, and the material and geometrical parameters are the same with that in Ref. [47]. From the comparison, it can be observed from Table 4 that the first frequency parameters of the FGP cylindrical and spherical shells with various boundary conditions and geometrical parameters have good consistency, which means that the correctness of the constructed FGP cylindrical and spherical shell models is verified. Finally, Table 5 shows the comparison of the first six frequency parameters of the FGP hyperbolic paraboloidal shell with various boundary conditions, and the preset parameters are the same with that in Ref. [18]. It can be found that the numerical results obtained from the present model and Ref. [18] show little difference. Therefore, the correctness of the FGP hyperbolic paraboloidal shell is also verified. As mentioned above, the four types of shallow shells are verified via the comparison between the calculated results obtained from the present model and the open literature. Therefore, the parameter analysis can be conducted in the following investigation.

Table 3 Comparison of the first frequency parameters of the FGP plate with various boundary conditions, materials, and geometrical parameters

Table 4 Comparison of the first frequency parameters of the FGP cylindrical and spherical shells with various boundary conditions and geometrical parameters

Table 5 Comparison of the first six frequency parameters of the FGP hyperbolic paraboloidal shell with various boundary conditions

Table 6 shows the frequencies of the Type1 FGP shallow shells with different boundary conditions, and the preset parameters are the same with that in Table 1. It can be concluded that the boundary condition has a strong effect on the dynamic behavior of the structure regardless of the type of the shallow shell. Specially, the frequency parameters of the structure with elastic boundary conditions are weakened as compared with the structure with classical boundary conditions, which can be attributed to the weakening effect on the stiffness of the structure caused by the elastic boundary conditions. Therefore, the dynamic characteristics of the shallow shells can be improved by changing the principal radius of curvature. To further investigate the effect of material and geometrical parameters on various types of shallow shells, Tables 7, 8, and 9 show the first natural frequencies of the FGP shallow shells with respect to different ratios of thickness to length, porous distributions, and porosities, and the preset parameters are set as a = b = 1, R_x = 3, R_y = 3. A common nature can be summarized as follows: (1) The frequencies of the FGP shallow shells gradually go up with the growth of the ratio of thickness to length, which means that the increasing ratio of thickness to length enhances the stiffness of the structure. (2) With the going up of the thickness, the Type1 FGP shallow shells show different change trends as compared with other types of porous distributions, that is, the first natural frequency goes down first and then goes up with the growth of the porosities, which can be inferred that when the porosity increases to a certain threshold, the increasing porosity not only decreases the mass of the structure but also enhances the stiffness of the structure. Therefore, the Type1 functionally graded porous distribution shows excellent mechanical capacity. (3) With the comparison of three types of FGP distributions, the frequencies of Type1 shallow shells show the maximum. Therefore, the FGP design is able to improve the dynamic behavior of the structure.

Table 6 The first six of the Type1 FGP shallow shells with respect to different boundary conditions. (a = b = 1 m, h = 0.1 m, e₀ = 0.2)

Table 7 The first natural frequencies of the FGP shallow spherical shell with respect to different ratios of thickness to length, porous distributions, and porosities. (a = b = 1 m, R_x = 3 m, R_y = 3 m, Boundary condition CSSF)

Table 8 The first natural frequencies of the FGP shallow cylindrical shell with respect to different ratios of thickness to length, porous distributions, and porosities (a = b = 1 m, R_x = 3 m, R_y = Boundary condition CSSF)

Table 9 The first natural frequencies of the FGP shallow hyperbolic paraboloidal shell with respect to different ratios of thickness to length, porous distributions, and porosities. (a = b = 1 m, R_x = 3 m, R_y = 3 m, Boundary condition CSSF)

Furthermore, to further understand the dynamic performance of the four types of shallow shells, Figs. 5 and 6 show the first three mode shapes of the Type2 FGP shallow shell with general boundary conditions.

Fig. 5

The first three mode shapes of the Type2 FGP shallow shell with CSCS boundary condition

Fig. 6

The first three mode shapes of the Type2 FGP shallow shell with E2E2E2E2 boundary condition

3.3 Forced vibration of the FGP annular and circular sector plates

In this work, the forced vibration characteristics of the shallow structures are investigated from two aspects, including steady-state response and transient-state response. Steady-state response expresses the output state of the system as time goes to infinity. Transient-state response stands for the change process of system output from an initial state to a stable state under the action of typical signal input.

3.3.1 Steady-state response

First, the correctness of the present model should be examined. As shown in Fig. 7, the steady-state response of Type1 FGP spherical shell with CCCC boundary condition obtained from the present model and the ABAQUS is compared, and the material and geometric parameters are set as: a = 1 m, b = 1 m, h = 0.1 m, R_x = 2 m, R_y = 2 m, e₀ = 0.5; load position is located on (0.5, 0.5); observation points are set as (0.7, 0.5) and (0.9, 0.5); frequency range is set as 500–4000 Hz. It can be easily found that the numerical results show good consistency, which means that the correctness of the present model is verified. Specially, the little difference may attribute to the simplification of the present model. It is meaningful to mention that the simplified approach is able to reduce the calculation burden, and then the complex calculation task can be achieved with less time.

Fig. 7

Comparison of the steady-state response of the Type 1 FGP spherical shell with CCCC boundary condition. (a = 1 m, b = 1 m, h = 0.1 m, R_x = 2 m, R_y = 2 m, e₀ = 0.5, Load position: (0.5, 0.5), f = 500–4000 Hz, Δf = 2 Hz)

Figure 8 shows the effect of the boundary stiffness coefficients on the steady-state of Type 2 FGP shallow shell, and the preset parameters are the same with that in Fig. 7. It can be seen that the boundary stiffnesses along u, v and x directions cannot easily affect the stability of the steady-state response of the structure. On the contrary, the boundary stiffnesses along w and y directions show a strong influence on the steady-state response of the structure. Moreover, the number of resonance peaks decreases with the growth of the boundary spring stiffness. It means that the steady-state response of the structure can be improved by changing the boundary stiffness. Besides, to investigate the effect of geometric parameters on the steady-state response, Fig. 9 shows the effect of the ratio of thickness to radius R_x on the steady-state response of the FGP shallow shell with SSSS boundary condition, and the preset parameters are the same with Fig. 7. It can be concluded as follows: (1) The increasing ratio of thickness to radius enhances the stiffness of the structure, which can be inferred from that the steady-state curve moves to the right with the growth of the ratio of thickness to radius. Moreover, the displacement under the resonance state gradually goes down with the growth of the ratio of thickness to radius, which means that the vibration suppression capacity of the structure is improved to some extent. (2) Under the condition of the small ratio of thickness to radius, the curvature of the shallow shell cannot easily affect the stability of the steady-state response. It is implied that the larger ratio of thickness to radius has more sensitive to the type of the shallow shell. From Fig. 9, the influence of FGP distribution type on the steady-state response is not apparent. Therefore, for further investigating the effect of different FGP distributions, Fig. 10 shows the effect of porosity ratio on the steady-state response of the FGP shallow shell with SSSS boundary condition. The preset parameters are the same with that in Fig. 7. It can be easily seen that the Type1 FGP shallow shells show good stability with the change of porosity as compared with the other two types of FGP shallow shells. Specially, the improvement of the Type1 porous distribution on dynamic characteristics of the shallow shell is further verified via the steady-state response, that is, the steady-state curve moves right when the porosity arrives at a threshold value.

Fig. 8

The effect of the boundary stiffness coefficient on the steady-state responses of the Type 2 FGP shallow shell. (Load position: (0.5, 0.5), Observation location (0.7, 0.5), f = 500–4000 Hz, Δf = 2 Hz)

Fig. 9

The effect of the ratio of thickness to radius R_x on the steady-state response of the FGP shallow shells with SSSS boundary condition

Fig. 10

The effect of the porosity ratio on the steady-state response of FGP shallow shell with SSSS boundary condition

3.3.2 Transient-state response

To ensure the correctness of the transient-state response of the present model, Fig. 11 shows the calculated results of the transient-state response of the Type1 FGP spherical shell with CCCC boundary condition obtained from the present model and the ABAQUS, and the preset parameters are set as: a = 1 m, b = 1 m, h = 0.1 m, R_x = 2 m, R_y = 2 m, e₀ = 0.5; load position is located on (0.5, 0.5); pulse width is defined as 10 ms. It can be easily concluded that the results obtained from the present model have good agreement with those obtained from the ABAQUS. Therefore, the correctness of the present model under transient-state response is examined, and then the parameter analysis can be further investigated.

Fig. 11

Comparison of the transient-state response of the Type 1 FGP spherical shell with CCCC boundary condition. (a = 1 m, b = 1 m, h = 0.1 m, R_x = 2 m, R_y = 2 m, e₀ = 0.5, Load position: (0.5, 0.5), t = τ = 10 ms, Δt = 0.01 ms)

As shown in Fig. 12, the effect of the ratio of thickness to radius R_x on the transient-state of the FGP shallow shell with SSSS boundary condition is studied, and the preset parameters are set as: a = 1 m, b = 1 m, e₀ = 0.2; Load position is located on (0.5, 0.5); Observation location is set as (0.7, 0.5). It can be concluded that the ratio of thickness to radius has a strong effect on the transient-state response. With the increase of the ratio of thickness to radius, the displacement of the structures is significantly decreased, which means that the increasing thickness can greatly improve the vibration suppression capacity of the structure under the transient-state response. Besides, with the comparison of the four types of shallow shells, the spherical shallow shell shows great vibration suppression capacity. To investigate the influence of porous distribution, Fig. 13 shows the effect of porosity rations on the transient-state response of the FGP shallow shell with CSCS boundary conditions, and the preset parameters are the same with that in Fig. 12. Compared with Fig. 9, the Type1 FGP distribution also shows the stability on the transient response. Therefore, the Type1 can improve the stability of the dynamic characteristics of the structure to some extent.

Fig. 12

The effect of the ratio of thickness to radius R_x on the trainset-state response of the FGP shallows shell with SSSS boundary condition

Fig. 13

The effect of the porosity ratio on the transient-state response of the FGP shallow shell with CSCS boundary condition

In addition, Fig. 14 shows the effect of load types on the transient-state response of the FGP shallow shell with E2E2E2E2 boundary condition, and the preset parameters are the same with that in Fig. 12. It can be found that the displacement of the FGP shallow shells under transient-state response can be obviously changed via the load types, which means that the load types have a strong influence on the transient-state response of the structure. Specially, the types of triangular and half-sine show a great effect on vibration suppression regardless of the structure type. Therefore, the transient-state response can be further adjusted via the load type.

Fig. 14

The effect of the load types on the transient-state response of the FGP shallow shell with E2E2E2E2 boundary condition

4 Conclusions

A unified formulation for the functionally graded porous shallow shells with variable curvature under forced vibration was proposed in this work. The effect of various geometric parameters, material parameters, boundary conditions, and load types was discussed. Some conclusions can be drawn as follows:

• (1) The geometric parameters have a strong effect on the forced vibration behaviors of the FGP shallow shells. That is, the increasing ratio of thickness to radius enhances the stiffness of the structure, and thus the vibration suppression capacity of the structures is enhanced. Specially, the stability of the steady-state response of the structures cannot be easily affected by the type of shallow shell under the condition of the small ratio of thickness to radius.

• (2) The porous design shows a great improvement on the dynamic characteristics of the shallow shells. Specially, Type1 FGP distribution shows significant stability on the steady-state response and the transient-state response with the increase of the porosity e₀. Therefore, the Type1 FGP distribution has great potential to further improve the forced vibration performance of the shallow shells.

• (3) The boundary conditions and the load types have a greater effect on the forced vibration behaviors of the FGP shallow shells. For example, the stiffnesses of the structures and displacement under forced vibration have a close relationship with the boundary stiffness value. The displacement of the transient-state response can be changed via the load type. Therefore, the forced behaviors can be adjusted by changing the types of boundary conditions or load types.