Frequency control of cross-ply magnetostrictive viscoelastic plates resting on Kerr-type elastic medium

Abstract

In the present study, a higher-order shear deformation plate theory with hyperbolic shape function is used to analyze vibration suppression of a novel design of a cross-ply composite plate that contains a homogenous core and viscoelastic faces and is embedded in three-parameter Kerr’s foundation. Two magnetostrictive actuating layers and simple velocity feedback control are employed for vibration control of the sandwich plate. Kelvin–Voigt viscoelastic relation is utilized to model faces of the viscoelastic material. The system of the governing equations is formulated utilizing Hamilton’s principle and using Navier’s approach to solve the system analytically. Comprehensive parametric studies are carried out to assess influences of the magnitude of the feedback control gain, magnetostrictive layer location, thickness ratio, aspect ratio, viscoelastic layer thickness-to-core thickness ratio, magnetostrictive layer thickness-to-core thickness ratio, half wave numbers, orientations of the viscoelastic layer’s fiber, and foundation on the vibration suppression characteristics of plates. The present results show that the combination of the passive and active strategies for vibration damping of the structures can develop control systems of the structural applications excellently. Further, the use of the Kerr-type foundation model can improve the vibration suppression characteristics.

1 Introduction

The motion of electrons of ferromagnetic materials generates a magnetostrictive effect where this property represents an inherent property of these materials. In the structure of the atom, the electron revolution about the nucleus generates an orbital magnetic moment, whereas the spinning of the electron about its axis generates a spin magnetic moment. The atomic magnetic moment occurs as a result of the superposition of spin and orbital magnetic moment. Due to the spontaneous magnetization, orientations of all the atomic magnetic moments are the same in the magnetic domain which can be defined as a small region that contains 109–1015 atoms.

On the macroscopic scale, ferromagnetic material exhibits magnetism whenever it is exposed to an external magnetic field. Scientists utilize this attractive property for designing new structures or for controlling the disruptive behavior of the systems and noise control in the heavy application structures in several engineering applications. The magnetostrictive materials are utilized for constructing the intelligent composite structural applications in various fields, such as infrastructure, aerospace, aircraft, automotive, armor and energy, marine, and biomedical industries, that can perform both actuation and sensing functions. Goodfriend et al. [1] examined Terfenol-D magnetostrictive material properties for controlling the active vibration of the system. Anjanappa and Bi [2, 3] studied a model for designing the Terfenol-D actuator and discussed the magnetostrictive mini-actuators feasibility for controlling active vibration of the structural systems. Several researchers have focused on the active vibration control of different structures employing layers of magnetostrictive material such as [4,5,6,7,8,9,10,11,12,13,14,15,16,17]. The vibration of the structures can be isolated by employing the controlled magnetostrictive extensions as mentioned in a study presented by Hiller et al. [4]. Reddy and Barbosa [5] utilized magnetostrictive material layers and direct feedback gain to control the linear frequencies damping of laminated composite beams. Using first-order shear deformation theory, Pradhan et al. and Pradhan [7] analyzed the vibration response of laminated composite plates and shells, respectively, with magnetostrictive actuators. Zhang et al. [8] studied the nonlinear dynamic response of cantilever magnetostrictive laminated composite plate. Subramanian [9] analyzed the model of a magnetostrictive laminated composite sandwich beam by employing a higher-order shear deformation with a constant in-plane rotation tensor through the thickness. Kumar et al. [10, 11] analyzed the vibration response of the magnetostrictive aluminum sandwich beams/plates under different boundary conditions and coil configurations. The thickness of the magnetostrictive actuating layer, the smart layer location, and the feedback gain control are the main elements that play important role in the vibration damping process based on the previous study’s results. Zhou and Zhou [12] discussed the nonlinear frequency behavior of magnetostrictive laminated composite sandwich beams exposed to the control magnetic field. Murty et al. [13] used one magnetostrictive layer to control the vibration damping of flexible beams for three different lamination schemes. Suman et al. [14] studied the bending response of laminated composite plates with/without magnetostrictive layers numerically. Reddy [15] presented a detailed theoretical formulation for vibration control of simply supported laminated composite plate with integrated sensor and actuator under both electrical and mechanical loads based on the classical theory and shear deformation plate theories. Koconis et al. [16] used the Ritz method to solve the dynamic system of fiber-reinforced composite beam/plate/shell containing piezoelectric actuating layers. Lee et al. [17] discussed the effect of the mechanical loading and thickness effect of the smart layer on the vibration damping rate of the smart laminate. Bhattacharya et al. [18] used a strategy that depends on combining passive (layers of ferromagnetic) and active (magnetostrictive material) suppression for controlling vibration of the structures. Furthermore, Zenkour and El-Shahrany [19] carried out several theoretical studies on vibration control of symmetric/asymmetric laminated composite beams with four magnetostrictive actuating layers. Also, they presented a study to discuss the free vibration of a magnetostrictive laminated composite plate embedded in Pasternak’s foundation using a higher-order shear deformation theory with exponential shape function [20]. Then, they employed various shear deformation theories involving transverse shear and normal deformation impacts [21]. In the absence/presence of the feedback control gain influence, Zenkour and El-Shahrany [22] studied the effect of viscoelastic foundations on the vibration of a laminated composite beam containing magnetostrictive material layers. The previous results illustrated that there are some important parametric elements such as many magnetostrictive layers, magnetostrictive layer thickness, feedback control gain value, foundation type, and magnetostrictive layer location that play a significant role in the improvement of the vibration damping characteristics. In addition, Zenkour and El-Shahrany [23] investigated the hygrothermal environment impact on the vibration suppression of a magnetostrictive laminated composite plate lying on Pasternak’s foundation. Shankar et al. [24] studied combined effects of the delamination and hygrothermal loading on the vibration of the delaminated composite plates with active fiber composite actuator and sensor in top and bottom of the laminate based on the first-order shear deformation theory. Results of their study showed that increment of the voltage applied to the actuators layer leads to enhancing the stiffness of the structures.

The viscoelastic materials are used for passive damping of the structural applications vibration due to having a characteristic property of these materials which is dissipating the energy under transient deformations. Many researchers have focused on methods for solving viscoelastic problems in structural applications. Zenkour et al. [25] utilized effective moduli and Ilyushin’s approximation methods to solve the bending problem of an inhomogeneous viscoelastic composite plate supports by Pasternak’s foundation using a higher-order shear deformation plate theory with sinusoidal shape function. Zenkour et al. [26] also studied the bending behavior of a sandwich beam with viscoelastic functionally graded faces and elastic core, embedding in Pasternak’s foundation. Alimirzaei et al. [27] used a higher-order shear deformation plate theory with sinusoidal shape function for studying the wave propagation in a thick viscoelastic composite plate supports by visco-Pasternak’s foundation. Zenkour et al. [28] used quasi-3D transverse shear deformation theory for analyzing the mechanical behavior of laminated composite beams lying on an elastic foundation. Allam and Zenkour [29] presented a bending analysis of a clamped fiber-reinforced viscoelastic beam with quadratic thickness variation. Zenkour [30] analyzed the combined influences of the nonuniform thermal loads and transverse shear deformations on the bending behavior of fiber-reinforced viscoelastic composite plates. Zenkour and Sobhy [31] presented vibration analysis of a smart viscoelastic nanoplate resting on a viscoelastic foundation, subjected to hygrothermal environmental conditions, and utilizing a two-variable shear deformation plate theory with sinusoidal shape function. Sofiyev [32] studied combined effects of the elastic foundation and periodic axial load depending on the time, on linear parametric instability of the viscoelastic inhomogeneous truncated conical shell employing first-order shear deformation theory. In the hygrothermal environment, Zenkour and El-Shahrany [33] analyzed the free vibration of a magnetostrictive laminated composite plate with a core of the viscoelastic material lying on elastic foundations. Zenkour and El-Shahrany [34] studied combined impacts of the transverse shear and normal deformations and elastic foundation on the vibrational behavior of a magnetostrictive laminated composite plate with top and bottom of the viscoelastic material using a higher-order shear deformation theory with sinusoidal shape function. In the two studies, the results indicate that damping time, deflection, and frequencies of the plates decrease by increasing the viscoelastic structural damping value.

Foundations are important members for damping or reducing the vibration/oscillation of structural systems such as high-speed transportation systems, railway tracks, solid propellant rocket motors, or rocket-sled technology. Winkler’s model has substantially utilized one parameter elastic foundation, has closed-spaced linear springs but dealing the normal loads only. Pasternak [35] developed Winkler’s model by introducing a shear layer to deal with the shear loadings. Various models rested on Winkler-Pasternak’s foundation have been presented in the literature even at the nanostructure applications, for example, Civalek et al.[36] and Allahyari et al. [37]. Due to the concentrated line reactions occurrence along the free edges of the structures in the Pasternak’s foundation, Kerr [38, 39] added an extra layer of spring set above the shear layer to develop the Pasternak-type foundation to avoid this influence. Barati and Zenkour [40] analyzed the size-dependent forced vibration of functionally graded nanobeam embedded in Kerr foundations subjecting to uniformly dynamic loadings, hygrothermal load, and lateral concentrated based on a higher-order refined beam theory. Further, Barati [41] discussed the hygrothermal-elastic dynamic response of inhomogeneous porous nanobeam resting on Kerr’s foundations and subjecting to concentrated and distributed loadings. Shahsavari et al. [42] used a new quasi-3D hyperbolic theory and Galerkin method to analyze the free vibration of porous functionally graded plate supporting by Winkler/Pasternak/Kerr’s elastic foundation. In addition, Shahsavari et al. [43] presented a new size-dependent quasi-3D shear deformation theory to study the hygrothermal effect on the shear buckling of a porous functionally graded nanoplate supported by Kerr’s foundations. Recently, Zenkour and El-Shahrany [44] have discussed vibration analysis of the viscoelastic fiber-reinforced magnetostrictive sandwich plate on viscoelastic foundations using higher-order deformation theory with sinusoidal shape function. Moreover, Zenkour and El-Shahrany [45] analyzed hygrothermal loading influence on the forced vibration behavior of viscoelastic smart laminated composite plates supporting by the viscoelastic foundation.

The previous literature refers to that there is no work covering the vibrational behavior analysis of visco-magnetoelastic sandwich structures embedded in Kerr-type foundations. Hence, the current study will present a new model for the design of a visco-magnetoelastic plate in Kerr’s foundation and their vibration damping characteristics will be analyzed. According to the higher shear deformation plate theory with hyperbolic shape function, Hamilton’s principle, and Kelvin–Voigt viscoelastic relation, the equations of motion for the proposed model will be derived and the impact of important parameters on solutions behavior of the dynamic system will be studied and discussed in detail.

2 Theory and formulation of the problem

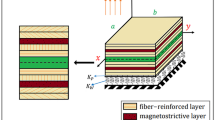
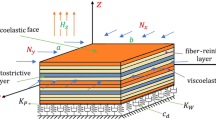
Consider a rectangular cross-ply multilayered viscoelastic magnetostrictive composite sandwich plate with length $a$, width $b$, total thickness $h,$ and $k$ layers, as appeared in Fig. 1. The sandwich plate is composed of viscoelastic faces, homogeneous core, two magnetostrictive materials in [$\left( m \right)$ th, ($k$-$m$ + 1)th] layers, fiber-reinforced material in $k - 6$ remaining layers. The visco-magnetoelastic plate rests on three-parameter foundations, in which containing two independent upper and lower sets of springs and a shear layer connects these two sets. So, the interaction between the surrounding elastic medium is simulated by Kerr’s foundations model and the structure as:

$$ E_{{{\text{Kerr}}}} = \left[ {\frac{{K_{l} K_{u} }}{{K_{l} + K_{u} }} - \frac{{K_{P} K_{u} }}{{K_{l} + K_{u} }}\left( {\frac{{\partial^{2} }}{{\partial x^{2} }} + \frac{{\partial^{2} }}{{\partial y^{2} }}} \right)} \right]w_{0} , $$

(1)

Fig. 1

Schematic diagram of the structure

where $K_{P}$, $K_{u}$, $K_{l}$, and $w_{0}$ are the stiffness of shear layer, upper spring, lower spring, and transverse displacement, respectively.

For viscoelastic faces, Young’s modulus $E_{{{\text{viscoelastic}}}}$, and the shear modulus $G_{{{\text{viscoelastic}}}}$ depending on the Kelvin–Voigt model can be expressed as follows (Jalaeia and Civalek [46]):

$$ { }E_{{{\text{viscoelastic}}}} = E\left( {1 + {\text{g}}\frac{\partial }{\partial t}} \right),{\quad}G_{{{\text{viscoelastic}}}} = G\left( {1 + {\text{g}}\frac{\partial }{\partial t}} \right), $$

(2)

in which $\mathrm{g}$ is the viscoelastic structural damping coefficient.

According to the hyperbolic shear deformation plate theory, the displacement fields can be described as

$$ \begin{array}{*{20}c} {u\left( {x,y,z,t} \right) = { } - z\frac{{\partial w_{0} }}{\partial x} + f\left( z \right)\varphi_{x} \left( {x,y,t} \right),} \\ {v\left( {x,y,z,t} \right) = - z\frac{{\partial w_{0} }}{\partial y} + f\left( z \right)\varphi_{y} \left( {x,y,t} \right),} \\ {w\left( {x,y,z,t} \right) = w_{0} \left( {x,y,t} \right),} \\ \end{array} $$

(3)

$$ f\left( z \right) = h\sinh \left( \frac{z}{h} \right) - \frac{{4z^{3} }}{{3h^{2} }}\cosh \left( \frac{1}{2} \right),{\quad}g\left( z \right) = f^{\prime}\left( z \right). $$

(4)

The unknown function $w_{0}$ is the transverse displacement of $x$, $y$, and $t$ at a point on the plane $z = 0$. The functions $\varphi_{x}$ and $\varphi_{y}$ are rotations of normal to the midplane about the $y$-axes and $x$-axes. Moreover, $f\left( z \right)$ presents the representative shape function which describes the transverse shear stress or strain distribution along with the thickness of the plate.

The nonzero linear strain–displacement fields can be expressed as

$$ \left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ { \gamma_{xy} } \\ \end{array} } \right\} = z\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx}^{\left( 1 \right)} } \\ {\varepsilon_{yy}^{\left( 1 \right)} } \\ {\gamma_{xy}^{\left( 1 \right)} } \\ \end{array} } \right\} + f\left( z \right)\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx}^{e} ,} \\ {\varepsilon_{yy}^{e} ,} \\ {\gamma_{xy}^{e} ,} \\ \end{array} } \right\}, \left\{ {\begin{array}{*{20}c} {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right\} = g\left( z \right)\left\{ {\begin{array}{*{20}c} {\gamma_{xz}^{g} } \\ {\gamma_{yz}^{g} } \\ \end{array} } \right\}, $$

(5)

where

$$ { }\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx}^{\left( 1 \right)} } \\ {\varepsilon_{yy}^{\left( 1 \right)} } \\ {\gamma_{xy}^{\left( 1 \right)} } \\ \end{array} } \right\} = - \left\{ {\begin{array}{*{20}c} {\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}} \\ {\frac{{\partial^{2} w_{0} }}{{\partial y^{2} }}} \\ {2\frac{{\partial^{2} w_{0} }}{\partial x\partial y}} \\ \end{array} } \right\},\;\;\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx}^{e} } \\ {\varepsilon_{yy}^{e} } \\ {\gamma_{xy}^{e} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\frac{{\partial \varphi_{x} }}{\partial x}} \\ {\frac{{\partial \varphi_{y} }}{\partial y}} \\ {\frac{{\partial \varphi_{x} }}{\partial y} + \frac{{\partial \varphi_{y} }}{\partial x}} \\ \end{array} } \right\},\;\;\left\{ {\begin{array}{*{20}c} {\gamma_{xz}^{g} } \\ {\gamma_{yz}^{g} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\varphi_{x} } \\ {\varphi_{y} } \\ \end{array} } \right\}. $$

(6)

For the rth fiber-reinforced layer, the nonzero linear stress–strain fields can be expressed as

$${\left\{ {\begin{array}{*{20}{c}} {{\sigma _{xx}}}\\ {{\sigma _{yy}}}\\ {{\sigma _{yz}}}\\ {{\sigma _{xz}}}\\ {{\sigma _{xy}}} \end{array}} \right\}^{(r)}} = {\left[ {\begin{array}{*{20}{c}} {{{\bar Q}_{11}}}&\quad {{{\bar Q}_{12}}}&\quad 0&\quad 0&\quad 0\\ {{{\bar Q}_{21}}}&\quad {{{\bar Q}_{22}}}&\quad 0&\quad 0&\quad 0\\ 0&\quad 0&\quad {{{\bar Q}_{44}}}&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad {{{\bar Q}_{55}}}&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad {{{\bar Q}_{66}}} \end{array}} \right]^{(r)}}{\left\{ {\begin{array}{*{20}{c}} {{\varepsilon _{xx}}}\\ {{\varepsilon _{yy}}}\\ {{\gamma _{yz}}}\\ {{\gamma _{xz}}}\\ {{\gamma _{xy}}} \end{array}} \right\}^{(r)}}.$$

(7)

For the viscoelastic faces and the magnetostrictive layer, the nonzero linear stress–strain fields can be given as

$${\left\{ {\begin{array}{*{20}{c}} {{\sigma _{xx}}}\\ {{\sigma _{yy}}}\\ {{\sigma _{yz}}}\\ {{\sigma _{xz}}}\\ {{\sigma _{xy}}} \end{array}} \right\}^{(\text{face})}} = \left( {1 + {\rm{g}}\frac{\partial }{{\partial t}}} \right){\left[ {\begin{array}{*{20}{c}} {{{\bar Q}_{11}}}&\quad {{{\bar Q}_{12}}}&\quad 0&\quad 0&\quad 0\\ {{{\bar Q}_{21}}}&\quad {{{\bar Q}_{22}}}&\quad 0&\quad 0&\quad 0\\ 0&\quad 0&\quad {{{\bar Q}_{44}}}&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad {{{\bar Q}_{55}}}&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad {{{\bar Q}_{66}}} \end{array}} \right]^{(\text{face})}}{\left\{ {\begin{array}{*{20}{c}} {{\varepsilon _{xx}}}\\ {{\varepsilon _{yy}}}\\ {{\gamma _{yz}}}\\ {{\gamma _{xz}}}\\ {{\gamma _{xy}}} \end{array}} \right\}^{(\text{face})}},$$

(8)

$${\left\{ {\begin{array}{*{20}{c}} {{\sigma _{xx}}}\\ {{\sigma _{yy}}}\\ {{\sigma _{yz}}}\\ {{\sigma _{xz}}}\\ {{\sigma _{xy}}} \end{array}} \right\}^{(m)}} = {\left[ {\begin{array}{*{20}{c}} {{{\bar Q}_{11}}}&\quad {{{\bar Q}_{12}}}&\quad 0&\quad 0&\quad 0\\ {{{\bar Q}_{21}}}&\quad {{{\bar Q}_{22}}}&\quad 0&\quad 0&\quad 0\\ 0&\quad 0&\quad {{{\bar Q}_{44}}}&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad {{{\bar Q}_{55}}}&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad {{{\bar Q}_{66}}} \end{array}} \right]^{(m)}}{\left\{ {\begin{array}{*{20}{c}} {{\varepsilon _{xx}}}\\ {{\varepsilon _{yy}}}\\ {{\gamma _{yz}}}\\ {{\gamma _{xz}}}\\ {{\gamma _{xy}}} \end{array}} \right\}^{(m)}} - {\left\{ {\begin{array}{*{20}{c}} {{{\bar q}_{31}}}\\ {{{\bar q}_{32}}}\\ 0\\ 0\\ {{{\bar q}_{36}}} \end{array}} \right\}^{(m)}}{H_z},$$

(9)

$$ \overline{q}^{\left( m \right)} = \overline{Q}^{\left( m \right)} d^{\left( m \right)}, {\quad}Q^{\left( m \right)} = E^{\left( m \right)} = \frac{1}{{S^{\left( m \right)} }}, $$

(10)

in which $\overline{Q}_{ij}^{\left( r \right)}$ are the transformed elastic constants which are expanded in Appendix 1. Furthermore, the coefficients $d^{\left( m \right)}$, $E^{\left( m \right)}$, and $S^{\left( m \right)}$ are the magneto-mechanical coupling coefficient, magnetostrictive layer modulus, and $m$ th magnetostrictive layer compliance. In addition, the relation between the magnetic field intensity $H_{z}$ and the coil current $I\left( {x,y,t} \right)$ can be defined as

$$ H_{z} \left( {x,y,t} \right) = k_{c} I\left( {x,y,t} \right) = k_{c} c\left( t \right)\frac{{\partial w_{0} }}{\partial t}, $$

(11)

in which $c\left(t\right)$ and ${k}_{c}$ are the control gain and the coil constant.

For the homogeneous core, the nonzero linear stress–strain fields can be given as

$$ \left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\begin{array}{*{20}c} {\sigma_{zz} } \\ {\sigma_{yz} } \\ {\begin{array}{*{20}c} {\sigma_{xz} } \\ {\sigma_{xy} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right\}^{{\left( {{\text{core}}} \right)}} = \left[ {\begin{array}{*{20}c} {{\text{Q}}_{11} } & {{\text{Q}}_{12} } & {{\text{Q}}_{13} } \\ {{\text{Q}}_{21} } & {{\text{Q}}_{22} } & {{\text{Q}}_{23} } \\ {\begin{array}{*{20}c} {{\text{Q}}_{31} } \\ 0 \\ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {{\text{Q}}_{32} } \\ 0 \\ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {{\text{Q}}_{33} } \\ 0 \\ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ \end{array} } \\ \end{array} { }\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ {\begin{array}{*{20}c} 0 \\ {{\text{Q}}_{44} } \\ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ 0 \\ {\begin{array}{*{20}c} {{\text{Q}}_{55} } \\ 0 \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ 0 \\ {\begin{array}{*{20}c} 0 \\ {{\text{Q}}_{66} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]^{{\left( {{\text{core}}} \right)}} \left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\begin{array}{*{20}c} {\varepsilon_{zz} } \\ {\gamma_{yz} } \\ {\begin{array}{*{20}c} {\gamma_{xz} } \\ {\gamma_{xy} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right\}^{{\left( {{\text{core}}} \right)}} . $$

(12)

3 Governing dynamic system

The governing system of the visco-magnetoelastic plate can be derived using Hamilton’s energy principle

$$ \delta \mathop \int \nolimits_{0}^{t} \left( {U + V - K} \right){\text{d}}t = 0, $$

(13)

in which $\delta U$, $\delta V$, and $\delta K$ are the variation of the strain energy, work done by applied forces and kinetic energy, which can be given as

$$ \begin{aligned} { }\delta U &= \mathop \int \nolimits_{0}^{a} \mathop \int \nolimits_{0}^{b} \mathop \int \nolimits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \Big[\left. {\sigma_{xx} \left( {z\delta \varepsilon_{xx}^{\left( 1 \right)} + f\left( z \right)\delta \varepsilon_{xx}^{e} } \right) + \sigma_{yy} \left( {z\delta \varepsilon_{yy}^{\left( 1 \right)} + f\left( z \right)\delta \varepsilon_{yy}^{e} } \right)} \right. \hfill \\&\, \quad \left. { + g\left( z \right)\left( {\sigma_{xz} \delta \gamma_{xz}^{g} + \sigma_{yz} \delta \gamma_{yz}^{g} } \right) + \sigma _{xy} \left( {z\delta \gamma_{xy}^{\left( 1 \right)} + f\left( z \right)\delta \gamma_{xy}^{e} } \right)} \right.\Big]{\text{d}}z{\text{d}}x{\text{d}}y, \hfill \\ \end{aligned} $$

(14)

$$ \delta V = - \mathop \int \nolimits_{0}^{a} \mathop \int \nolimits_{0}^{b} \left( {q - E_{{{\text{Kerr}}}} } \right)\delta w_{0} {\text{d}}y{\text{d}}x, $$

(15)

$$ \begin{aligned} \delta K & = \mathop \int \nolimits_{0}^{a} \mathop \int \nolimits_{0}^{b} \mathop \int \nolimits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \rho \left[ {\left( { - z\frac{{\partial \dot{w}_{0} }}{\partial x} + f\left( z \right)\dot{\varphi }_{x} } \right)\left( { - z\frac{{\partial \delta \dot{w}_{0} }}{\partial x} + f\left( z \right)\delta \dot{\varphi }_{x} } \right)} \right. \hfill \\ & \, \quad \left. { + \left( { - z\frac{{\partial \dot{w}_{0} }}{\partial y} + f\left( z \right)\dot{\varphi }_{y} } \right)\left( { - z\frac{{\partial \delta \dot{w}_{0} }}{\partial y} + f\left( z \right)\delta \dot{\varphi }_{y} } \right) + \dot{w}_{0} \delta \dot{w}_{0} } \right]{\text{d}}z{\text{d}}x{\text{d}}y, \hfill \\ \end{aligned} $$

(16)

in which $q$ is the transverse distributed load. By employing the previous equations into Eqs. (13)–(16), and the integral by parts is applied, for arriving at the next expression

$$ \begin{aligned} 0 &= \mathop \int \nolimits_{0}^{T} \mathop \int \nolimits_{0}^{a} \mathop \int \nolimits_{0}^{b} \left\{ {\left[ { - \frac{{\partial^{2} M_{xx} }}{{\partial x^{2} }} - 2\frac{{\partial^{2} M_{xy} }}{\partial x\partial y} - \frac{{\partial^{2} M_{yy} }}{{\partial y^{2} }} - q + E_{{{\text{Kerr}}}} } \right.{ }} \right.{ } \hfill \\ &\quad \left. { - I_{2} \left( {\frac{{\partial^{2} \ddot{w}_{0} }}{{\partial x^{2} }} + \frac{{\partial^{2} \ddot{w}_{0} }}{{\partial y^{2} }}} \right) + I_{e} \left( {\frac{{\partial \ddot{\varphi }_{x} { }}}{\partial x} + \frac{{\partial \ddot{\varphi }_{y} }}{\partial y}} \right) + I_{0} \ddot{w}_{0} } \right]\delta w_{0} \hfill \\ &\quad + \left( {Q_{gx} - \frac{{\partial S_{xx} }}{\partial x} - \frac{{\partial S_{xy} }}{\partial y} - I_{e} \frac{{\partial \ddot{w}_{0} }}{\partial x} + I_{e}^{2} \ddot{\varphi }_{x} } \right)\delta \varphi_{x} \hfill \\ & \quad + \left. {\left( {Q_{gy} - \frac{{\partial S_{xy} }}{\partial x} - \frac{{\partial S_{yy} }}{\partial y} - I_{e} \frac{{\partial \ddot{w}_{0} }}{\partial y} + I_{e}^{2} \ddot{\varphi }_{y} } \right)\delta \varphi_{y} } \right\}{\text{d}}x{\text{d}}y \hfill \\& \quad + \mathop {\oint }\nolimits_{\Gamma} \left\{ {\left[ {\left( {\frac{{\partial M_{xx} }}{\partial x} + \frac{{\partial M_{xy} }}{\partial y} + I_{2} \frac{{\partial \ddot{w}_{0} }}{\partial x} - I_{e} \ddot{\varphi }_{x} } \right)n_{x} + \left( {\frac{{\partial M_{xy} }}{\partial x} + \frac{{\partial M_{yy} }}{\partial y} + I_{2} \frac{{\partial \ddot{w}_{0} }}{\partial y} - I_{e} \ddot{\varphi }_{y} } \right)n_{y} } \right]\delta w_{0} } \right. \hfill \\ & \quad- \left( {M_{xx} n_{x} + M_{xy} n_{y} } \right)\frac{{\partial \delta w_{0} }}{\partial x} - \left( {M_{xy} n_{x} + M_{yy} n_{y} } \right)\frac{{\partial \delta w_{0} }}{\partial y} + \left( {S_{xx} n_{x} + S_{xy} n_{y} } \right)\delta \varphi_{x} \hfill \\ &\quad \left. {\left. { + \left( {S_{xy} n_{x} + S_{yy} n_{y} } \right)\delta \varphi_{y} } \right\}{\text{d}}s} \right\}{\text{d}}t, \hfill \\ \end{aligned} $$

(17)

where $\Gamma$ is the boundary, whereas ($M_{i}$, $S_{i}$, $Q_{gs}$) and ($I_{0}$, $I_{2}$, $I_{e}$ and $I_{e}^{2}$) denote the force and moment resultants and the mass inertias, respectively, which can be defined as

$$ \begin{aligned} \left. {\left\{ {\begin{array}{*{20}c} {M_{i} } \\ {S_{i} } \\ \end{array} } \right.} \right\} & = \mathop \sum \nolimits_{r = 1}^{k} \mathop \int \nolimits_{{z_{r} }}^{{z_{r + 1} }} \sigma_{{i{ }}} \left. {\left\{ {\begin{array}{*{20}c} z \\ {f\left( z \right)} \\ \end{array} } \right.} \right\}{\text{d}}z = \left( {1 + {\text{g}}\left. {\frac{\partial }{\partial t}} \right|_{{r = {\text{face}}}} } \right)\left( {\left[ {\begin{array}{*{20}c} {\left[ {\text{D}} \right]} & {\left[ {E^{1} } \right]} \\ {\left[ {E^{1} } \right]} & {\left[ {E^{3} } \right]} \\ \end{array} } \right]\left. {\left\{ {\begin{array}{*{20}c} {\varepsilon^{\left( 1 \right)} } \\ {\varepsilon^{e} } \\ \end{array} } \right.} \right\}} \right) \hfill \\& \quad- \left. {\left\{ {\begin{array}{*{20}c} {M_{i}^{m} } \\ {S_{i}^{m} } \\ \end{array} } \right.} \right\}, i = xx,yy,{ }xy, \hfill \\ Q_{gs}& = \mathop \int \nolimits_{A}^{ } \sigma_{{sz{ }}} g\left( z \right){\text{d}}z = \left( {1 + {\text{g}}\left. {\frac{\partial }{\partial t}} \right|_{{r = {\text{face}}}} } \right)E_{ii}^{3} {\upgamma }_{sz}^{g} ,{ }s = x,y,{\quad}i = 4,5, \hfill \\ \end{aligned} $$

(18)

in which

$$ \begin{aligned} \left\{ {M_{i}^{m} , S_{i}^{m} } \right\} &= k_{c} c\left( t \right)\mathop \sum \nolimits_{r} \mathop \int \nolimits_{{z_{r} }}^{{z_{r + 1} }} \overline{q}_{3i} \left\{ {z,f\left( z \right)} \right\}\frac{{\partial w_{0} }}{\partial t}{\text{d}}z = \left\{ {\beta_{3i} , \gamma_{3i} } \right\}\frac{{\partial w_{0} }}{\partial t}, \hfill \\ & \quad i = 1, 2, 6, r = m,{ }k - m + 1, \hfill \\ \left\{ {D_{ij} ,E_{ij}^{1} ,E_{ij}^{3} } \right\} &= \mathop \sum \nolimits_{r = 1}^{k} \mathop \int \nolimits_{{z_{r} }}^{{z_{r + 1} }} \overline{Q}_{ij}^{\left( r \right)} \left\{ {z^{2} ,zf\left( z \right),\left[ {f\left( z \right)} \right]^{2} } \right\}{\text{d}}z,{\quad}i, j = 1,2,6, \hfill \\ E_{ii}^{3} &= \mathop \sum \nolimits_{r = 1}^{k} \mathop \int \nolimits_{{z_{r} }}^{{z_{r + 1} }} \overline{Q}_{ii}^{\left( r \right)} \left[ {g\left( z \right)} \right]^{2} {\text{d}}z, \quad i = 4,5, \hfill \\ \end{aligned} $$

(19)

$$ \left\{ {I_{0} ,I_{2} ,I_{e} ,I_{e}^{2} } \right\} = \mathop \sum \nolimits_{r = 1}^{k} \mathop \int \nolimits_{{z_{r} }}^{{z_{r + 1} { }}} \rho \left\{ {1,z^{2} ,zf\left( z \right),\left[ {f\left( z \right)} \right]^{2} } \right\}{\text{d}}z,{ } $$

(20)

in which $\rho$ is the mass density for each layer of the plate.

Motion equations of the visco-magnetoelastic plate resting on Kerr’s foundation are presented as

$$ \begin{aligned} & \delta w_{0} :{ }\frac{{\partial^{2} M_{xx} }}{{\partial x^{2} }} + 2\frac{{\partial^{2} M_{xy} }}{\partial x\partial y} + \frac{{\partial^{2} M_{yy} }}{{\partial y^{2} }} + q - E_{{{\text{Kerr}}}} \hfill \\ & \quad+ I_{2} \left( {\frac{{\partial^{2} \ddot{w}_{0} }}{{\partial x^{2} }} + \frac{{\partial^{2} \ddot{w}_{0} }}{{\partial y^{2} }}} \right) - I_{e} \left( {\frac{{\partial \ddot{\varphi }_{x} }}{\partial x} + \frac{{\partial \ddot{\varphi }_{y} }}{\partial y}} \right) - I_{0} \ddot{w}_{0} = 0, \hfill \\ \end{aligned} $$

(21)

$$ \delta \varphi_{x} : \frac{{\partial S_{xx} }}{\partial x} + \frac{{\partial S_{xy} }}{\partial y} - Q_{gx} + I_{e} \frac{{\partial \ddot{w}_{0} }}{\partial x} - I_{e}^{2} \ddot{\varphi }_{x} = 0, $$

(22)

$$ \delta \varphi_{y} : \frac{{\partial S_{xy} }}{\partial x} + \frac{{\partial S_{yy} }}{\partial y} - Q_{gy} + I_{e} \frac{{\partial \mathop w\nolimits_{0} }}{\partial y} - I_{e}^{2} \mathop \varphi \nolimits_{y} = 0. $$

(23)

In terms of the displacements field, dynamic equations of the visco-magnetoelastic plate can be rewritten as

$$ \left[ P \right]\left\{ {w_{0} ,\varphi_{x} ,\varphi_{y} } \right\} = \left\{ F \right\}, $$

(24)

in which

$$ \begin{aligned} P_{11} &= \left( {1 + \left. {{\text{g}}\frac{\partial }{\partial t}} \right|_{{r = {\text{face}}}} } \right)\left[ { {D_{11} \frac{{\partial^{4} }}{{\partial x^{4} }} + D_{22} \frac{{\partial^{4} }}{{\partial y^{4} }} + 2\left( {D_{12} + 2D_{66} } \right)\frac{{\partial^{4} }}{{\partial x^{2} \partial y^{2} }}} } \right] \hfill \\ & \quad - \left( {\frac{{K_{P} K_{u} }}{{K_{l} + K_{u} }} + I_{2} \frac{{\partial^{2} }}{{\partial t^{2} }} - \beta_{31} \frac{\partial }{\partial t}} \right)\frac{{\partial^{2} }}{{\partial x^{2} }} - \left( {\frac{{K_{P} K_{u} }}{{K_{l} + K_{u} }} + I_{2} \frac{{\partial^{2} }}{{\partial t^{2} }} - \beta_{32} \frac{\partial }{\partial t}} \right)\frac{{\partial^{2} }}{{\partial y^{2} }} + I_{0} \frac{{\partial^{2} }}{{\partial t^{2} }} + \frac{{K_{l} K_{u} }}{{K_{l} + K_{u} }}, \hfill \\ P_{12}& = - \left( {1 + \left. {{\text{g}}\frac{\partial }{\partial t}} \right|_{{r = {\text{face}}}} } \right)\left[ {E_{11}^{1} \frac{{\partial^{3} }}{{\partial x^{3} }} + \left( {E_{21}^{1} + 2E_{66}^{1} } \right)\frac{{\partial^{3} }}{{\partial x\partial y^{2} }}} \right] + I_{e} \frac{{\partial^{3} }}{{\partial t^{2} \partial x}}, \hfill \\ P_{13}& = - \left( {1 + \left. {{\text{g}}\frac{\partial }{\partial t}} \right|_{{r = {\text{face}}}} } \right)\left[ {E_{22}^{1} \frac{{\partial^{3} }}{{\partial y^{3} }} - \left( {E_{12}^{1} + 2E_{66}^{1} } \right)\frac{{\partial^{3} }}{{\partial x^{2} \partial y}}} \right] + I_{e} \frac{{\partial^{3} }}{{\partial t^{2} \partial y}}, \hfill \\ P_{21} & = - P_{12} + \gamma_{31} \frac{{\partial^{2} }}{\partial x\partial t},{ }P_{22} = - \left( {1 + \left. {{\text{g}}\frac{\partial }{\partial t}} \right|_{{r = {\text{face}}}} } \right)\left( {E_{11}^{3} \frac{{\partial^{2} }}{{\partial x^{2} }} + E_{66}^{3} \frac{{\partial^{2} }}{{\partial y^{2} }} - E_{55}^{3} } \right) + I_{e}^{2} \frac{{\partial^{2} }}{{\partial t^{2} }}, \hfill \\ P_{23} &= P_{32} = - \left( {1 + \left. {{\text{g}}\frac{\partial }{\partial t}} \right|_{{r = {\text{face}}}} } \right)\left( {E_{12}^{3} + E_{66}^{3} } \right)\frac{{\partial^{2} }}{\partial x\partial y}, \hfill \\ P_{31} &= - P_{13} + \gamma_{32} \frac{{\partial^{2} }}{\partial y\partial t}, \hfill \\ P_{33} &= - \left( {1 + \left. {{\text{g}}\frac{\partial }{\partial t}} \right|_{{r = {\text{face}}}} } \right)\left( {E_{66}^{3} \frac{{\partial^{2} }}{{\partial x^{2} }} + E_{22}^{3} \frac{{\partial^{2} }}{{\partial y^{2} }} - E_{44}^{3} } \right) + I_{e}^{2} \frac{{\partial^{2} }}{{\partial t^{2} }}, \hfill \\ F_{1} &= - q,{\quad}F_{2} = 0, \quad F_{3} = 0. \hfill \\ \end{aligned} $$

(25)

4 Solution method

Firstly, consider $\left\{ {F_{i} } \right\} = 0$ in Eq. (24) for controlling the vibration. To solve the governing equations of the simply supported visco-magnetoelastic plate on the proposed hyperbolic theory, Navier’s solution procedure is utilized. In addition, considering the boundary conditions for a simply supported plate and the next initial conditions to arrive at the final form of solution

$$ \begin{array}{*{20}c} {w = \varphi_{y} = M_{xx} = P_{xx} = S_{xx} = 0 \quad {\text{at}} \quad x = 0,a,} \\ {w = \varphi_{x} = M_{yy} = P_{yy} = S_{yy} = 0 \quad {\text{at}} \quad y = 0,b,} \\ \end{array} $$

(26)

$$ \begin{array}{*{20}c} {w_{0} \left( {x,y,0} \right) = 0,{ }\dot{w}_{0} \left( {x,y,0} \right) = 1,} \\ {\varphi_{x} \left( {x,y,0} \right) = \dot{\varphi }_{x} \left( {x,y,0} \right) = \varphi_{y} \left( {x,y,0} \right) = \dot{\varphi }_{y} \left( {x,y,0} \right) = 0.} \\ \end{array} $$

(27)

The generalized displacement fields which satisfy the applied boundary conditions can be assumed as

$$\begin{array}{l} {w_0}\left( {x,y,t} \right) = \mathop \sum \nolimits_{n = 1}^\infty \mathop \sum \nolimits_{m = 1}^\infty {W_0}_{nm}\sin \frac{{n\pi x}}{a}\sin \frac{{m\pi y}}{b}{{\rm{e}}^{{\lambda _{nm}}t}},\\ {\varphi _x}\left( {x,y,\;t} \right) = \mathop \sum \nolimits_{n = 1}^\infty \mathop \sum \nolimits_{m = 1}^\infty {X_{nm}}\cos \frac{{n\pi x}}{a}\sin \frac{{m\pi y}}{b}{{\rm{e}}^{{\lambda _{nm}}t}},\\ {\varphi _y}\left( {x,y,\;t} \right) = \mathop \sum \nolimits_{n = 1}^\infty \mathop \sum \nolimits_{m = 1}^\infty {Y_{nm}}\sin \frac{{n\pi x}}{a}\cos \frac{{m\pi y}}{b}{{\rm{e}}^{{\lambda _{nm}}t}}, \end{array}$$

(28)

in which subscript $n$ and $m$ denote the half wave numbers (mode numbers), whereas ($W_{nm}^{0}$, $X_{nm}^{0}$, $Y_{nm}^{0}$) and $\lambda_{nm}$ are the unknown Fourier coefficients and the eigenfrequencies. The system can be written as

$$ \left[ {\overline{S}_{ij} } \right]\left\{ {\Re } \right\}^{t} = 0,{\quad}{\Re } = \left\{ {W_{nm}^{0} ,X_{nm}^{0} ,Y_{nm}^{0} } \right\}, \quad i,j = 1,{ }2,{ }3.{ } $$

(29)

For a solving system of the equations in Eq. (29), the next determinant is solved

$$ \left| {\left. {\begin{array}{*{20}c} {\overline{S}_{11} } &\quad {\overline{S}_{12} } &\quad {\overline{S}_{13} } \\ {\overline{S}_{21} } &\quad {\overline{S}_{22} } &\quad {\overline{S}_{23} } \\ {\overline{S}_{31} } &\quad {\overline{S}_{32} } &\quad {\overline{S}_{33} } \\ \end{array} } \right|} \right. = 0, $$

(30)

$$ \overline{S}_{ij} = \hat{S}_{ij} + \lambda_{nm} \hat{M}_{ij} + \lambda_{nm}^{2} \hat{C}_{ij} , \quad i,j = 1,{ }2,{ }3.{ } $$

(31)

in which $\hat{S}_{ij}$, $\hat{M}_{ij}$ and $\hat{C}_{ij}$ can be expanded in Appendix 2. Also, the eigenfrequencies can be expressed as follows:

$$ \lambda_{nm} = - \alpha_{nm} \pm i\omega_{nm} , \quad i = \sqrt { - 1} , $$

(32)

in which $\alpha_{nm}$ and $\omega_{nm}$ indicate, respectively, the damping coefficients and the damped natural frequency coefficients. Finally, the deflection of the dynamic system for the visco-magnetoelastic plate and the magnetic field intensity can be obtained as

$${w_0}{\left( {x,y,t} \right)} = \frac{1}{{{\omega _{nm}}}}{{\rm{e}}^{ - {\alpha _{nm}}t}}\sin {\omega _{nm}}t\sin \frac{{n\pi x}}{a}\sin \frac{{m\pi y}}{b},$$

(33)

$$ H_{z} \left( {x,y,{ }t} \right) = \frac{{k_{c} c\left( t \right)}}{{\omega_{nm} }}\frac{\partial }{\partial t}\left[ {{\text{e}}^{{ - \alpha_{nm} t}} \sin \omega_{nm} t\sin \frac{n\pi x}{a}\sin \frac{m\pi y}{b}} \right]. $$

(34)

5 Simulation results and discussion

A theoretical study and numerical results of eigenfrequencies and deflection for a new model for the cross-ply multilayered magnetostrictive composite plate with viscoelastic faces and homogeneous core, supported by Kerr’s foundation, are presented and discussed in the current section. The plate with the lamination scheme $\left[ {0^{{{\text{core}}}} /m/90/0/90/{\text{core}}} \right]_{s}$ and the following data: $h/a = 0.06$, $a/b = 1$, $K_{l} = K_{u} = K_{P} = 10^{6}$, $\left( {n,m} \right) = \left( {1,1} \right)$, $k_{c} c\left( t \right) = 10^{4}$, and ${\text{g}} = 10^{ - 4}$ are considered for carrying out the numerical results of the study. The used materials properties are written in Table 1, while the homogeneous material properties are: $E_{\text{core}} = 380 {\text{GPa}}$, $\rho_{\text{core}} = 3800 {\text{kg}}/{\text{m}}^{3}$, and $\nu = 0.3$. Comprehensive parametric examples are presented using a higher-order shear deformation with hyperbolic shape function to estimate effects of the velocity feedback gain, magnetostrictive layers positions, thickness ratio, aspect ratio, viscoelastic layer thickness-to-core thickness ratio, magnetostrictive layer thickness-to-core thickness ratio, half wave numbers, orientations of the viscoelastic layer’s fiber, lower and upper spring stiffnesses and shear layer stiffness on the vibration damping characteristics of the structure. The used higher-order shear theory computes the hyperbolic distribution of transverse shear deformation through the thickness of the plate; the present theory is more accurate than the classical theory, or the first-order shear theory that accounts for constant states of the transverse shear deformation or the third-order shear theory which calculates a parabolic transverse shear deformation distribution only. The behavior of the fundamental eigenfrequency values with the change in the geometric parameters (the thickness-to-side ratio and the aspect ratio) and feedback gain control value is illustrated in Table 2. It is clear that the eigenfrequency value of the sandwich plate studied is significantly influenced by the geometric parameters and magnitude of the feedback gain control. In fact, the damping coefficient increases smoothly and the frequency decreases slightly by the increase of the feedback gain control, whereas both the damping and the frequency values rise with increasing the geometric parameters (thickness ratio or aspect ratio) highly. For different values of the thickness ratio, Fig. 2 shows the first linear frequency with the change of the shear layer stiffness. A notable increase in the frequency of the plate is observed as increasing the thickness ratio and the shear layer stiffness constant. In addition, the effect of the geometric parameters and feedback gain control on the deflection of the plate is plotted in Figs. 3, 4, and 5. It is seen from Fig. 3 that in absence of the feedback gain control element, deflection of the plate reduces with time due to the presence of the viscoelastic structural damping effect in the viscoelastic faces of the structure. The figure also indicates that the active damping process improves whenever the velocity feedback gain increases where the deflection reduces and the damping time decreases. Moreover, it is seen from Figs. 4 and 5 that there is a decrease in deflection of the plate due to increasing the geometric parameters: the thickness ratio and aspect ratio, respectively.

Table 1 The properties of used materials in the study

Table 2 Effect of the thickness-to-side ratio $h/a$ and the aspect ratio $a/b$ on the eigenfrequency coefficients of $- \alpha_{11} \pm \omega_{11}$ (rad ${\text{s}}^{ - 1}$) for various values of the feedback control gain

Fig. 2

The behavior of the fundamental frequency with the variation of stiffness of the shear layer for different values of the thickness ratio

Fig. 3

Effect of the feedback control gain on the central displacement of the plate

Fig. 4

The behavior of the central displacement of the plate with the change of damping time for various thickness ratios

Fig. 5

The behavior of the central displacement of the plate with the change of damping time for various aspect ratios

The behavior of the first linear frequency for different values of the linear and shear layers of Kerr foundation ($K_{l}$, $K_{u}$ and $K_{P}$) is displayed in Table 3. It is shown that an increment in the stiffness of the spring results in an increase of the frequencies significantly and a decrease of the damping coefficient insignificantly. Effect of the lower spring, upper spring, and shear layer stiffness on the first linear frequency versus the thickness ratio is plotted in Figs. 6, 7, and 8, respectively. It is seen that the frequencies increase with increasing the values of Kerr foundation constants and this effect reduces as the thickness ratio increases where the difference between curves decreases with increasing the thickness ratio. Also, the effect of the shear layer stiffness on the fundamental frequency with change in the thickness ratio is more than the effect of the upper and lower spring stiffnesses. Furthermore, the effect of the stiffness of the upper springs or the lower springs on the fundamental frequency is unequal as the thickness ratio changes, but the variation is very insignificant, for more illustration see Table 3 and compare the reciprocal effect for $K_{u}$ and $K_{l}$ for $h/a = 0.06$. Figure 9 depicts the behavior of the central displacement of the plate for different values of the shear layer stiffness versus time.

Table 3 Eigen frequency coefficients $- \alpha_{11} \pm \omega_{11}$ (rad ${ }s^{ - 1}$) for different values of the foundation coefficients

Fig. 6

Effect of the lower spring stiffness on the fundamental frequency with change in the thickness ratio, $K_{u} = 10^{9}$

Fig. 7

Effect of the upper spring stiffness on the fundamental frequency with change in the thickness ratio, $K_{l} = 10^{9}$

Fig. 8

Effect of the shear layer stiffness on the fundamental frequency with change in the thickness ratio

Fig. 9

The central displacement of the plate for different values of the shear layer stiffness

The time of the vibration suppression reduces obviously, and the deflection of plate decreases due to increasing the shear layer stiffness. In fact, the models become more rigid due to increasing the springs stiffness and the shear layer stiffness and the shear layer stiffness is more efficient than the upper and lower spring stiffnesses.

The viscoelastic layer magnetostrictive layer and core thickness can be denoted by $h_{v}$,$h_{m}$ and $h_{c}$, respectively. The behavior of eigenfrequency values for viscoelastic layer thickness-to-core thickness ratio $h_{vc} = h_{v} /h_{c}$, magnetostrictive layer thickness-to-core thickness ratio $h_{mc} = h_{m} /h_{c}$ and three values of the viscoelastic structural damping value is illustrated in Table 4. It is observed that increase of the viscoelastic layer thickness-to-core thickness ratio leads to increasing the damping coefficient and damped natural frequencies. Figure 10 describes the behavior of the first linear frequency with change in the shear layer stiffness for different values of $h_{vc}$ parameter. It is noted that with the increasing value of the $h_{vc}$ parameter, the frequencies increase highly, and this influence increases as the shear layer stiffness value rises. It is further observed from the table the damping coefficient increases, while the frequencies decrease as the $h_{mc}$ parameter increases. In addition, the influence of the magnetostrictive layer thickness-to-core thickness ratio on the first linear frequency with the change of the shear layer stiffness is plotted in Fig. 11. With a variation of the shear layer stiffness, the frequencies reduce for all the values studied of ${h}_{mc}$ parameter. Effect of ${h}_{vc}$ and ${h}_{mc}$ on the central displacement of the plate with the change of the time is shown in Figs. 12 and 13, respectively. The two parameters have the same effect on the deflection of the plate where with increasing ${h}_{vc}$ or/and ${h}_{mc}$, the deflection and damping time reduce. Furthermore, the impact of the viscoelastic structural damping on the damping coefficient and the damped natural frequencies is also deduced from the results in Table 4 and Fig. 14. It is noted that there are an increment in the damping coefficient and a decrement in the frequencies with increasing the viscoelastic structural damping value. It is also seen from the figure that the variation between the frequency curves increases as the thickness ratio increases. Figure 15 shows the deflection reduces significantly with decreasing the damping time whenever the viscoelastic structural damping value increases.

Table 4 Effect of the viscoelastic layer thickness-to-core thickness ratio ${h}_{vc}$ and magnetostrictive layer thickness-to-core thickness ratio ${h}_{mc}$ on the damping and frequency parameters $-{\alpha }_{11}\pm {\omega }_{11}$ (rad ${\mathrm{s}}^{-1}$) for various values of the viscoelastic structural damping

Fig. 10

Effect of the viscoelastic layer thickness-to-core thickness layer ratio on the fundamental frequency

Fig. 11

Effect of the magnetostrictive layer thickness-to-core thickness ratio on the fundamental frequency, $h_{vc} = 1.5$

Fig. 12

The central displacement of the plate for various viscoelastic layer thickness-to-core thickness layer ratios

Fig. 13

The central displacement of the plate for various magnetostrictive layer thickness-to-core thickness ratios, $h_{vc} = 1.5$

Fig. 14

Effect of the viscoelastic structural damping on the fundamental frequency of the plate

Fig. 15

Effect of the viscoelastic structural damping on the central displacement of the plate

Effect of orientations of the fiber in the viscoelastic layers for the plate $\left[ {\theta^{{{\text{face}}}} /m/90/0/90/{\text{core}}} \right]_{s}$ on the eigenfrequency values for the first three mode numbers is displayed in Table 5. It is clear that the damping coefficient and the damped natural frequencies are significantly influenced by orientations of the fiber in the viscoelastic layer. It is clear that the lowest and highest frequencies occur in $\theta = 30$ and $45$ orientations of the viscoelastic layer’s fiber cases, respectively, as shown in Fig. 16. Accordingly, $\theta = 30$ and $45$ orientations of the viscoelastic layer’s fiber cases have the lowest and highest flexural rigidity, respectively, and have the longest suppression time and shortest suppression time, respectively, as appeared in Fig. 17. The effect of the variation of mode shapes on values of the eigenfrequencies and the deflection is also deduced from the table, as shown in Fig. 18. It is noted that the damping coefficient and damped natural frequency values increase and the deflection reduces with decreasing the damping time greatly whenever the value of mode numbers rises.

Table 5 Effect of the half wavenumbers on the damping and frequency parameters $- \alpha_{nm} \pm \omega_{nm}$ (rad ${\text{s}}^{ - 1}$) for various orientations of the fiber in the viscoelastic layers for the plate $\left[ {\theta^{{{\text{face}}}} /m/90/0/90/{\text{core}}} \right]_{s}$

Fig. 16

The behavior of the fundamental frequency with change in the thickness ratio for various orientations of the fiber in the viscoelastic layers in the plate $\left[ {\theta^{{{\text{face}}}} /m/90/0/90/{\text{core}}} \right]_{s}$, $K_{P} = 5 \times 10^{6}$

Fig. 17

Controlled motion of the plate $\left[ {\theta^{{{\text{face}}}} /m/90/0/90/{\text{core}}} \right]_{s}$.at the midpoint for various orientations of the fiber in the viscoelastic layers

Fig. 18

Controlled motion of the plate at the midpoint for various half wave numbers

Another important point in vibration suppression of the structure is the effect of the location of the magnetostrictive layer on the deflection damping process. Table 6 displays the influence of this factor on the eigenfrequencies, maximum deflection, and damping time. It is seen that the damping coefficient increases and the frequencies decrease whenever the magnetostrictive layers move toward viscoelastic faces and away from the core of the plate. Figure 19 shows the impact of the location of the magnetostrictive layer on the behavior of the first linear frequencies with the change of the thickness ratio. It is worth noting that the smart layers must be located under the viscoelastic layers and not vice versa, to improve the vibration damping characteristics. In addition, the amplitude of the deflection and interval of the suppression time decrease with moving the smart layer away from the plate core as seen in Fig. 20.

Table 6 The eigenfrequencies, maximum deflection, and damping time for various locations of magnetostrictive layers

Fig. 19

Effect of the location of the magnetostrictive layer on the fundamental frequency

Fig. 20

The central displacement of the plate for various laminations

6 Conclusions

A vibration investigation of a fiber-reinforced sandwich plate with a homogenous core is carried out in this article. The studied simply supported plate has viscoelastic feces, contains two actuated magnetostrictive layers, and rests on Kerr’s foundation. The dynamic system described in the model is derived employing Hamilton’s principle and Kelvin–Voigt relation. Influences of important parameters on Navier’s solution type of system are studied in detail. The comprehensive results of the study reveal that:

• For low-stiffness elastic foundations, the visco-magnetoelastic plate has small natural frequencies and low stiffness, which implies that the plate takes a long interval of time to the vibration suppression.

• For high-stiffness elastic foundations, the visco-magnetoelastic plate has the largest natural frequencies and smallest deflection with the shortest damping time, which implies that the plate achieves the highest stiffness in this case.

• The extra springs layer of Kerr’s foundations and the shear layer of Pasternak’s foundation play strong roles in the vibration frequency behavior of the visco-magnetoelastic plate. The shear layer stiffness is more efficient than the extra springs layer for vibration damping of the plate. However, the study proves the superiority of the three-parameter Kerr’s model compared to Pasternak-type or Winkler-type models to improve the vibration suppression characteristics of the structures.

• Frequencies of the visco-magnetoelastic plate are very sensitive to the mode shapes and the viscoelastic layer, magnetostrictive layer, and core thickness.

• The study findings emphasize that the viscoelastic layer, magnetostrictive layer, and core thickness, magnetostrictive layer location, orientations of the fiber in viscoelastic layers, velocity feedback gain have significant roles in the vibration control process of the visco-magnetoelastic structures.

• A notable increment in frequencies and decrement in deflection of the visco-magnetoelastic plate as a result of increasing the geometric parameters.

• A notable decrement in the damping time and deflection of the visco-magnetoelastic plate due to increasing the viscoelastic structural damping.

Appendices

Appendix 1

The coefficients $\overline{Q}_{ij}^{\left( r \right)}$ and $\overline{q}_{ij}$ that appeared in Eqs. (7)–(9) are expanded as

$$ \overline{Q}_{11}^{\left( r \right)} = Q_{11}^{\left( r \right)} \cos^{4} \theta^{\left( r \right)} + 2\left( {Q_{12}^{\left( r \right)} + 2Q_{66}^{\left( r \right)} } \right)\cos^{2} \theta^{\left( r \right)} \sin^{2} \theta^{\left( r \right)} + Q_{22}^{\left( r \right)} \sin^{4} \theta^{\left( r \right)} , $$

$$ \overline{Q}_{12}^{\left( r \right)} = \left( {Q_{11}^{\left( r \right)} + Q_{22}^{\left( r \right)} - 4Q_{66}^{\left( r \right)} } \right)\cos^{2} \theta^{\left( r \right)} \sin^{2} \theta^{\left( r \right)} + Q_{12}^{\left( r \right)} \left( {\sin^{4} \theta^{\left( r \right)} + \cos^{4} \theta^{\left( r \right)} } \right), $$

$$ \overline{Q}_{22}^{\left( r \right)} = Q_{11}^{\left( r \right)} \sin^{4} \theta^{\left( r \right)} + 2\left( {Q_{12}^{\left( r \right)} + 2Q_{66}^{\left( r \right)} } \right)\cos^{2} \theta^{\left( r \right)} \sin^{2} \theta^{\left( r \right)} + Q_{22}^{\left( r \right)} \cos^{4} \theta^{\left( r \right)} , $$

$$ \overline{Q}_{44}^{\left( r \right)} = Q_{44}^{\left( r \right)} \cos^{2} \theta^{\left( r \right)} + Q_{55}^{\left( r \right)} \sin^{2} \theta^{\left( r \right)} , $$

$$ \overline{Q}_{55}^{\left( r \right)} = Q_{55}^{\left( r \right)} \cos^{2} \theta^{\left( r \right)} + Q_{44}^{\left( r \right)} \sin^{2} \theta^{\left( r \right)} , $$

$$ \overline{Q}_{66}^{\left( r \right)} = \left( {Q_{11}^{\left( r \right)} + Q_{22}^{\left( r \right)} - 2Q_{12}^{\left( r \right)} - 2Q_{66}^{\left( r \right)} } \right)\sin^{2} \theta^{\left( r \right)} \cos^{2} \theta^{\left( r \right)} + Q_{66}^{\left( r \right)} \left( {\sin^{4} \theta^{\left( r \right)} + \cos^{4} \theta^{\left( r \right)} } \right), $$

$$ Q_{11}^{\left( r \right)} = \frac{{E_{1} \left( {1 - {\upnu }_{23}^{\left( r \right)} {\upnu }_{32}^{\left( r \right)} } \right)}}{\Delta },{\quad}Q_{12}^{\left( r \right)} = \frac{{E_{1} \left( {{\upnu }_{21}^{\left( r \right)} + {\upnu }_{31}^{\left( r \right)} {\upnu }_{23}^{\left( r \right)} } \right)}}{\Delta }, \quad Q_{22}^{\left( r \right)} = \frac{{E_{2} \left( {1 - {\upnu }_{13}^{\left( r \right)} {\upnu }_{31}^{\left( r \right)} } \right)}}{\Delta }, $$

$$ Q_{44}^{\left( r \right)} = G_{23}^{\left( r \right)} ,{\quad}Q_{55}^{\left( r \right)} = G_{13}^{\left( r \right)} ,{\quad}Q_{66}^{\left( r \right)} = G_{12}^{\left( r \right)} , $$

$$\Delta = 1 - {{\nu }}_{21}^{\left( r \right)}{\rm{\nu }}_{12}^{\left( r \right)} - {{\nu }}_{23}^{\left( r \right)}{\nu }_{32}^{\left( r \right)} - {{\nu }}_{13}^{\left( r \right)}{\rm{\nu }}_{31}^{\left( r \right)}- 2{\rm{\nu }}_{21}^{\left( r \right)}{\nu}_{13}^{\left( r \right)}{{\nu }}_{32}^{\left( r \right)},$$

$${\nu}_{21}^{\left( r \right)} = \frac{{{\nu}_{12}^{\left( r \right)}E_{22}^{\left( r \right)}}}{{E_1^{\left( r \right)}}}, \quad {\nu}_{31}^{\left( r \right)} = \frac{{{\nu }_{13}^{\left( r \right)}E_3^{\left( r \right)}}}{{E_1^{\left( r \right)}}},\quad {\nu }_{32}^{\left( r \right)} = \frac{{{\nu }_{23}^{\left( r \right)}E_3^{\left( r \right)}}}{{E_2^{\left( r \right)}}},$$

$$ \overline{q}_{31} = q_{31} \cos^{2} \theta + q_{32} \sin^{2} \theta , \quad \overline{q}_{32} = q_{32} \cos^{2} \theta + q_{31} \sin^{2} \theta , $$

$$ \overline{q}_{14} = \left( {q_{15} - q_{24} } \right)\sin \theta \cos \theta , \quad \overline{q}_{24} = q_{24} \cos^{2} \theta + q_{15} \sin^{2} \theta , $$

$$ \overline{q}_{15} = q_{15} \cos^{2} \theta + q_{24} \sin^{2} \theta , \quad \overline{q}_{25} = \left( {q_{15} - q_{24} } \right)\sin \theta \cos \theta , $$

$$ \overline{q}_{36} = \left( {q_{31} - q_{32} } \right)\sin \theta \cos \theta , $$

where ${E}_{i}$, ${v}_{ij}$ and ${G}_{ij}$ refer to Young’s moduli, Poisson’s ratios, and shear moduli, respectively. The coefficients ${q}_{ij}$ denote the magnetostrictive modules.

Appendix 2

The coefficients $\hat{S}_{ij}$, $\hat{M}_{ij}$ and $\hat{C}_{ij}$ ($i = 1, 2, 3$) that appeared in Eq. (31) are expanded as the following:

$$\begin{aligned} \hat{S}_{11} &= \left( {1 + \left. {{\text{g}}\frac{\partial }{\partial t}} \right|_{{r = {\text{face}}}} } \right)\left[ {D_{11} \left( {\frac{n\pi }{a}} \right)^{4} + D_{22} \left( {\frac{m\pi }{b}} \right)^{4} + \left( {2D_{12} + 4D_{66} } \right)\left( {\frac{n\pi }{a}} \right)^{2} \left( {\frac{m\pi }{b}} \right)^{2} } \right]\\ & \quad+ \frac{{K_{P} K_{u} }}{{K_{l} + K_{u} }}\left( {\frac{n\pi }{a}} \right)^{2} + \frac{{K_{P} K_{u} }}{{K_{l} + K_{u} }}\left( {\frac{m\pi }{b}} \right)^{2} + \frac{{K_{l} K_{u} }}{{K_{l} + K_{u} }},\end{aligned}$$

$$ \hat{S}_{12} = - \left( {1 + \left. {{\text{g}}\frac{\partial }{\partial t}} \right|_{{r = {\text{face}}}} } \right)\left[ {E_{11}^{1} \left( {\frac{n\pi }{a}} \right)^{3} + \left( {E_{21}^{1} + 2E_{66}^{1} } \right)\frac{n\pi }{a}\left( {\frac{m\pi }{b}} \right)^{2} } \right], $$

$$ \hat{S}_{13} = - \left( {1 + \left. {{\text{g}}\frac{\partial }{\partial t}} \right|_{{r = {\text{face}}}} } \right)\left[ {E_{22}^{1} \left( {\frac{m\pi }{b}} \right)^{3} + \left( {E_{12}^{1} + 2E_{66}^{1} } \right)\left( {\frac{n\pi }{a}} \right)^{2} \frac{m\pi }{b}} \right], $$

$$ \hat{S}_{22} = \left( {1 + \left. {{\text{g}}\frac{\partial }{\partial t}} \right|_{{r = {\text{face}}}} } \right)\left[ {E_{11}^{3} \left( {\frac{n\pi }{a}} \right)^{2} + E_{66}^{3} \left( {\frac{m\pi }{b}} \right)^{2} + E_{55}^{3} } \right], $$

$$ \hat{S}_{23} = \hat{S}_{23} = \left( {1 + \left. {{\text{g}}\frac{\partial }{\partial t}} \right|_{{r = {\text{face}}}} } \right)\left[ {\left( {E_{12}^{3} + E_{66}^{3} } \right)\frac{n\pi }{a}\frac{m\pi }{b}} \right], $$

$$ \hat{S}_{33} = \left( {1 + \left. {{\text{g}}\frac{\partial }{\partial t}} \right|_{{r = {\text{face}}}} } \right)\left[ {E_{66}^{2} \left( {\frac{n\pi }{a}} \right)^{2} + E_{22}^{3} \left( {\frac{m\pi }{b}} \right)^{2} + E_{44}^{3} } \right], $$

$$ \hat{M}_{11} = - \beta_{31} \left( {\frac{n\pi }{a}} \right)^{2} - \beta_{32} \left( {\frac{m\pi }{b}} \right)^{2} ,\quad \hat{M}_{21} = \gamma_{31} \frac{n\pi }{a},\quad \hat{M}_{31} = \gamma_{32} \frac{m\pi }{b}, $$

$$ \hat{M}_{12} = \hat{M}_{13} = \hat{M}_{22} = \hat{M}_{23} = \hat{M}_{32} = \hat{M}_{33} = 0, $$

$$ \hat{C}_{11} = I_{2} \left[ {\left( {\frac{n\pi }{a}} \right)^{2} + \left( {\frac{m\pi }{b}} \right)^{2} } \right] + I_{0} ,{\quad}\hat{C}_{12} = - I_{e} \frac{n\pi }{a},{\quad}\hat{C}_{13} = - I_{e} \frac{m\pi }{b}, $$

$$ \hat{C}_{22} = I_{e}^{2} ,\quad \hat{C}_{23} = 0,{\quad}\hat{C}_{33} = I_{e}^{2} . $$