1 Introduction

Nowadays, it can be heard that renewable energy such as solar and wind must be taken into account instead of conventional fossil and nuclear energy in order to save the world from pollution and irrevocable damages. To use solar energy, we must be able to convert this energy into other forms that can be used in everyday life with the help of a suitable tool [1, 2]. Photovoltaic (PV) solar systems are a good tool to catch solar energy for electrical energy transformation. Solar cells can be produced with different technologies and some of these technologies, such as silicon cells, have matured and are widely used [3, 4]. Increasing the efficiency and reliability of these technologies is one of the concerns of scientists. Understanding the processes related to power absorption and conversion in these cells and accurate modeling can play an effective role in their proper prediction and design. Building a reliable model of a solar module is one of the most important issues that researchers in photovoltaic systems are looking for [5,6,7]. This model will be especially important when studying the characteristics of the photovoltaic system.

Predicting the output power of the system and creating a system that can extract the maximum power, such as tracking the maximum power point, are features that photovoltaic system modeling can help a lot [8]. A key issue in modeling photovoltaic modules is the nonlinear relationship between current and output voltage, especially when solar arrays are affected by rapidly changing weather conditions and shading [9, 10]. The main problem in modeling is to identify the optimal values of the parameters by which the model best fits the experimental data [8]. Also, to better understand the characteristics, evaluating the optimization performance of a solar cell system, a precise mathematical model has a significant role for researchers. Different models have been used to show the behavior of the system in different operating conditions. These models range from simple hypotheses to models with complex physical variables [11, 12]. The precision of these models is intent by the model parameters, because some of the necessary information for optimization is not announced in the data sheet provided by the factory. For this reason, it is necessary to obtain these parameters, which may be turned into an optimization problem with a specific objective function [13].

In recent decades, several methods have been used to determine the optimal values in solar cell models, which can be divided into conventional and heuristic algorithms [14, 15]. Conventional methods require coherence and derivability to be practical, involve heavy computations, and converge to local and local solutions instead of global solutions [16]. The nonlinearity of the curve (I–V) makes conventional optimization techniques incapable of effectively solving parameter recognition problems [17]. To address this issue, heuristic optimization algorithms such as genetic algorithm, PSO algorithm, etc., have been used to identify the parameters [18, 19]. Although these algorithms have better results than traditional algorithms, they have some limitations, the most important of which are their entrapment in local optimal points and early convergence to these points.

So far, several models have been introduced for solar cells, the most important of which are single-diode model (SDM), double-diode model (DDM), and three-diode model (TDM) [20, 22]. Various algorithms have been posed to estimate the parameters of these models, and many articles in this field have been published with appropriate results, but improving the performance of algorithms and providing an algorithm with better convergence is still a topic of interest for researchers in this field. In this regard, different kinds of optimization algorithms can be found in literature such as genetic algorithms [18], sunflower optimization algorithm [23], flexible particle swarm optimization algorithm [24], coyote optimization algorithm [25], PG JAYA algorithm [26], lozi map [13], flower pollination algorithm [27], artificial bee swarm optimization(ABSO) [28], generalized oppositional teaching–learning based optimization(GOTLBO) [29], whale optimization algorithm [30], chaotic whale optimization [31], and so on [32,33,34].

One of the newest methods introduced is the whale optimization algorithm (WOA) presented by [30]. WOA imitates the behavior of humpback whales. These whales detect the position of the prey and then surround them. The WOA algorithm first finds the best search agent by producing whales and randomly distributing them in the search space. After that, other search agents try to update their positions according to the best acheivemnet. This algorithm has been given a lot of attention in optimization issues, including solar cells and fuel cells parameters extraction and parameters estimation of DC motors [35], designing photonic crystal filter [36], neural networks, and computing [37, 38], maximum power point tracking [39,40,41], terminal voltage control [42], economic prediction [43, 44], and other world problems [45,46,47]. Although WOA has performed better than previous algorithms in solving complex nonlinear problems and multi-model objective function value, it still has difficulty finding optimal solutions. In the algorithm presented in [31], the main idea is the use of irregular maps to calculate and automatically attune the internal parameters of the algorithm. This solution is very useful in complicated problems because; during the iteration process, this scheme enhances the ability of internal parameters to explore for the best solution, which increases the efficiency of the algorithm. Although the CWOA algorithm tries to unravel the problem of getting stuck in the local minimum, there is still the problem that points that are far from the optimal points are ignored from the optimization cycle, which can decline the search capability of the algorithm in complicated optimization problems. In this regard, a modified version of WOA called a springy whale optimization algorithm (SWOA) is presented as a modified optimization algorithm to extract the parameters of PV cell and module models in this study. To ameliorate the performance of the algorithm, some changes have been made in the movement of the whales. A removal phase has been added to apply changes to the whale algorithm. In the first step of each phase, a predetermined number of the worst whales are always removed and new whales are replaced in the new search space. Making these modification to the algorithm reduces the likelihood of being trapped in local minimums and elevates the rapidity of detecting optimal solutions. Furthermore, by removing points that are far from the optimal parameters, we can enhance the search capability of the proposed algorithm. To assess the sufficiency of the proposed algorithm, the performance of this algorithm is tested in different scenarios derived from laboratory information.

The continuation of this article as follows. Section 2 presents the mathematical relationships governing cell models and PV modules. Section 3 hands out the general concepts of the WOA algorithm. The principle idea about SWOA is given in detail in Sect. 4. Section 5 renders some simulation results regarding the experimental data set. Finally, Sect. 6 is devoted to the conclusion.

2 Photovoltaic modeling and problem formulation

Several models of solar cells have been proposed so far that take into account the physical losses of the solar cell, the most important of which are the SDM, DDM, and TDM. The SDM only takes into account losses caused by internal resistors, connections, and connecting lines between each solar cell and the module, so it does not have good accuracy. However, in the more complex models mentioned, in addition to internal losses and connections, losses such as leakage circuiting current and grain boundary are also considered. For this reason, the DDM and TDM are more accurate than SDM. In the following, we will examine the mathematical relationships governing the models and present the formulation of the problem.

2.1 Photovoltaic cell model

2.1.1 Single-diode model (SDM)

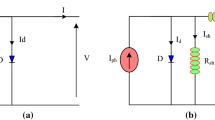
The SDM includes a current source, a diode that produces the distributed current component, and resistors RS and RSh which are responsible for losses caused by internal resistors, connections, and other connecting lines between each solar cell and the module, respectively [20]. The typical model of a single-diode solar cell is demonstrated in Fig. 1, where the output current (IL) from the solar cell is the current produced by the current generator (Iph) minus the currents flowing through the diode Id1 and the shunt resistor (Ish), respectively.

Fig. 1
figure 1

Equivalent circuit of the single-diode model

Full size image

In many articles, this model is referred to as the five-parameter model, because in this model, five parameters exist and can be represented by the vector θ as follows:

$$ \theta = \left[ {\begin{array}{*{20}c} {I_{{{\text{ph}}}} } & {\begin{array}{*{20}c} {R_{s} } & {R_{{{\text{sh}}}} } & {I_{{{\text{SD}}}} } \\ \end{array} } & n \\ \end{array} } \right] $$
(1)

The equations of the practical model of a single diode are as follows:

$$ I_{L} = I_{{{\text{ph}}}} - I_{D} - I_{{{\text{sh}}}} $$
(2)

The diode current ID is expressed by the Shockley equation as:

$$ \begin{aligned} I_{D} = & I_{{{\text{SD}}}} \left[ {\exp \left( {\frac{{\left( {V_{L} + I_{L} R_{s} } \right)}}{{nV_{T} }}} \right) - 1} \right] \\ V_{T} = & \frac{{{\text{KT}}}}{q} \\ \end{aligned} $$
(3)

Furthermore, Ish is calculated from the following equation:

$$ I_{{{\text{sh}}}} = \frac{{V_{L} + I_{L} R_{s} }}{{R_{{{\text{sh}}}} }} $$
(4)

By combining Eqs. (1)–(4), the output current of the diode is obtained as follows:

$$ I_{L} = I_{{{\text{ph}}}} - I_{{{\text{SD}}}} \left[ {\exp \left( {\frac{{q\left( {V_{L} + I_{L} R_{s} } \right)}}{{n{\text{KT}}}}} \right) - 1} \right] - \frac{{V_{L} + I_{L} R_{s} }}{{R_{{{\text{sh}}}} }} $$
(5)

where ISD is the reverse saturation current of the diode, VT is thermal voltage equivalent, K is the Boltzmann’s constant (q is the electronic charge, n is the diode ideality factor, and T is the absolute temperature of the p–n junction in Kelvin, Rsh is the shunt resistance, and RS is the series resistance.

2.1.2 Double-diode model (DDM)

This model consists of a current source, series, and parallel resistors as well as two diodes. Figure 2 shows a DDM of a solar cell. In this model, another diode is added to the SDM, which is placed parallel to the SDM to transmit losses due to carrier recombination in the depletion layer and surface recombination which is defined by Id2 [21]. The current of the first diode (Id1) represents the current component, which is similar to the current Id1 in the single-diode model.

Fig. 2
figure 2

Equivalent circuit of the double-diode model

Full size image

Because another diode is attached to the model, the number of parameters will also change, and in this model, seven parameters will be identified and optimized, which are given as vectors in Eq. (6). Hence, we will encounter more challenging optimization problems.

$$ \theta = \left[\kern-2.5pt {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {I_{{{\text{ph}}}} } & {R_{s} } & {R_{{{\text{sh}}}} } \\ \end{array} } & {I_{{{\text{SD}}1}} } & {I_{{{\text{SD}}2}} } \\ \end{array} } & {\begin{array}{*{20}c} {n_{1} } & {n_{2} } \\ \end{array} } \\ \end{array} } \kern-2.5pt\right] $$
(6)

Using KCL law, the total output current for a solar cell will be calculated from Eq. (7):

$$ I_{L} = I_{{{\text{ph}}}} - I_{D1} - I_{D2} - I_{{{\text{sh}}}} $$
(7)

Thus, the output current may be redefined as:

$$\begin{aligned} I_{L} = I_{{{\text{ph}}}} - I_{{{\text{SD}}1}} \left[ {\exp \left( {\frac{{q\left( {V_{L} + I_{L} R_{s} } \right)}}{{n_{1} {\text{kT}}}}} \right) - 1} \right] - I_{{{\text{SD}}2}} \left[ {\exp \left( {\frac{{q\left( {V_{L} + I_{L} R_{s} } \right)}}{{n_{2} {\text{kT}}}}} \right) - 1} \right] \\ \quad - \frac{{V_{L} + I_{L} R_{s} }}{{R_{{{\text{sh}}}} }} \end{aligned} $$
(8)

2.1.3 Three-diode model (TDM)

Another model presented in [22] is the TDM, which takes into account more losses in comparison with two previous models of solar cells. According to Fig. 3, this model consists of a current source, three diodes, and two resistors. Like DDM, two diodes are included in the model due to losses of recombination and connections, and a third diode due to losses due to recombination defect regions and grain boundary.

Fig. 3
figure 3

Equivalent circuit of the three-diode model

Full size image

This model contains nine parameters that have to be identified. They can be combined in the following vector:

$$ \theta = \left[ {\begin{array}{*{20}l} {I_{{{\text{ph}}}} } \hfill & {R_{s} } \hfill & {R_{{{\text{sh}}}} } \hfill & {I_{{{\text{SD}}1}} } \hfill & {I_{{{\text{SD}}2}} } \hfill & {I_{{{\text{SD}}3}} } \hfill & {n_{1} } \hfill & {n_{2} } \hfill & {n_{3} } \hfill \\ \end{array} } \right] $$
(9)

Using KCL law, the total output current for a solar cell will be calculated from Eq. (10):

$$ I_{L} = I_{{{\text{ph}}}} - I_{D1} - I_{D2} - I_{D3} - I_{{{\text{sh}}}} . $$
(10)

Thus, the output current may be redefined as:

$$ \begin{aligned} I_{L} = & I_{{{\text{ph}}}} - I_{{{\text{SD}}1}} \left[ {\exp \left( {\frac{{q\left( {V_{L} + I_{L} R_{s} } \right)}}{{n_{1} {\text{kT}}}}} \right) - 1} \right] - I_{{{\text{SD}}2}} \left[ {\exp \left( {\frac{{q\left( {V_{L} + I_{L} R_{s} } \right)}}{{n_{2} {\text{kT}}}}} \right) - 1} \right] \\ & \; - I_{{{\text{SD}}3}} \left[ {\exp \left( {\frac{{q\left( {V_{L} + I_{L} R_{s} } \right)}}{{n_{3} {\text{kT}}}}} \right) - 1} \right] - \frac{{V_{L} + I_{L} R_{s} }}{{R_{{{\text{sh}}}} }} \\ \end{aligned} $$
(11)

It should also be noted that analytical modeling of the three-diode model is difficult due to a large number of parameters (nine parameters) and the small number of nonlinear equations.

2.2 Module model

In PV systems, the smallest unit includes several cells connected in series or in parallel to produce more power and output current. This set of cells is known as a module. Figure 4 shows a module.

Fig. 4
figure 4

Equivalent circuit of solar PV module model

Full size image

As we know, the current of each cell is the same, and the output current of each of them is equal to IL; as a result, the output current ratio of the module can be written as Eq. (12). NS is the number of solar cells in series, and NP is the number of solar cells in parallel. It is obvious that five unknown parameters (Iph, ISD, Rs, Rsh, n) need to be identified.

$$ I_{L} = N_{P} \cdot I_{{{\text{ph}}}} - N_{P} \cdot I_{{{\text{SD}}}} \left[ {\exp \left( {\frac{{q\left( {{\raise0.7ex\hbox{${V_{L} }$} \!\mathord{\left/ {\vphantom {{V_{L} } {N_{S} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${N_{S} }$}} + {\raise0.7ex\hbox{${I_{L} \cdot R_{s} }$} \!\mathord{\left/ {\vphantom {{I_{L} \cdot R_{s} } {N_{P} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${N_{P} }$}}} \right)}}{{n{\text{KT}}}}} \right) - 1} \right] - \frac{{{\raise0.7ex\hbox{${N_{P} \cdot V_{L} }$} \!\mathord{\left/ {\vphantom {{N_{P} \cdot V_{L} } {N_{S} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${N_{S} }$}} + I_{L} \cdot R_{s} }}{{R_{{{\text{sh}}}} }} $$
(12)

2.3 Objective function

The objective is to estimate the parameter values of the PV models in such a way that the values obtained from the model are as closest as possible to the measured data. For this, objective functions to be minimized for SDM, DDM and TDM are defined from (13) to (15), respectively:

$$ \left\{ \begin{gathered} f_{k} \left( {V_{L} ,I_{L} ,\theta } \right) = I_{{{\text{ph}}}} - I_{{{\text{SD}}}} \left[ {\exp \left( {\frac{{q\left( {V_{L} + I_{L} R_{s} } \right)}}{{n{\text{KT}}}}} \right) - 1} \right] - \frac{{V_{L} + I_{L} R_{s} }}{{R_{{{\text{sh}}}} }} - I_{L} \hfill \\ \theta = \left[ {\begin{array}{*{20}c} {I_{{{\text{ph}}}} } & {\begin{array}{*{20}c} {R_{s} } & {R_{{{\text{sh}}}} } & {I_{{{\text{SD}}}} } \\ \end{array} } & n \\ \end{array} } \right] \hfill \\ \end{gathered} \right. $$
(13)
$$ \left\{ \begin{gathered} f_{k} \left( {V_{L} ,I_{L} ,\theta } \right) = I_{L} = I_{{{\text{ph}}}} - I_{{{\text{SD}}1}} \left[ {\exp \left( {\frac{{q\left( {V_{L} + I_{L} R_{s} } \right)}}{{n_{1} {\text{kT}}}}} \right) - 1} \right] \hfill \\ - I_{{{\text{SD}}2}} \left[ {\exp \left( {\frac{{q\left( {V_{L} + I_{L} R_{s} } \right)}}{{n_{2} {\text{kT}}}}} \right) - 1} \right] - \frac{{V_{L} + I_{L} R_{s} }}{{R_{{{\text{sh}}}} }} \hfill \\ \theta = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {I_{{{\text{ph}}}} } & {R_{s} } & {R_{{{\text{sh}}}} } \\ \end{array} } & {I_{{{\text{SD}}1}} } & {I_{{{\text{SD}}2}} } \\ \end{array} } & {\begin{array}{*{20}c} {n_{1} } & {n_{2} } \\ \end{array} } \\ \end{array} } \right] \hfill \\ \end{gathered} \right. $$
(14)
$$ \left\{ {\begin{array}{*{20}l} {f_{k} \left( {V_{L} ,I_{L} ,\theta } \right) = I_{L} = I_{{{\text{ph}}}} - I_{{{\text{SD}}1}} \left[ {\exp \left( {\frac{{q\left( {V_{L} + I_{L} R_{s} } \right)}}{{n_{1} {\text{kT}}}}} \right) - 1} \right] - I_{{{\text{SD}}2}} \left[ {\exp \left( {\frac{{q\left( {V_{L} + I_{L} R_{s} } \right)}}{{n_{2} {\text{kT}}}}} \right) - 1} \right]} \hfill \\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - I_{{{\text{SD}}3}} \left[ {\exp \left( {\frac{{q\left( {V_{L} + I_{L} R_{s} } \right)}}{{n_{3} {\text{kT}}}}} \right) - 1} \right] - \frac{{V_{L} + I_{L} R_{s} }}{{R_{{{\text{sh}}}} }}} \hfill \\ {\theta = \left[ {\begin{array}{*{20}l} {I_{{{\text{ph}}}} } \hfill & {R_{s} } \hfill & {R_{{{\text{sh}}}} } \hfill & {I_{{{\text{SD}}1}} } \hfill & {I_{{{\text{SD}}2}} } \hfill & {I_{{{\text{SD}}3}} } \hfill & {n_{1} } \hfill & {n_{2} } \hfill & {n_{3} } \hfill \\ \end{array} } \right]} \hfill \\ \end{array} } \right. $$
(15)

Then, as shown in Eq. (16) [11, 48], by minimizing, the calculated root mean square error (RMSE) is considered as the ultimate goal.

Consequently, parameter can be extracted by minimizing the objective function by seeking for the answer vector θ within the limited area of practical parameters.

$$ {\text{RSME}}\left( \theta \right) = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^{N} {f_{k} \left( {V_{L} ,I_{L} ,\theta } \right)^{2} } } $$
(16)

where N shows the number of experimental data, θ is the decision variable, VL, and IL are the measured voltage and current.

3 Data

Whales are extremely intelligent and emotional animals. The spindle-shaped cells that exist in certain areas of their brain have developed traits such as the ability to think, learn, judge, and social behaviors. Whales can hunt their prey individually and in groups. Some species can live with their families all their lives. One of the largest toothless whales is called the humpback whale. The most fascinating factor about humpback whales is how they hunt [30].

The whale optimization algorithm simulates the behavior of humpback whales. These whales detect the position of the prey and then surround them. The WOA algorithm finds the best search agent after producing whales and randomly distributing them in the search space. After that, other search agents try to update their positions according to the best search agent. This behavior can be represented by the following equations [30]:

$$ \vec{D} = \left| {\vec{C} \cdot \vec{X}^{*} (t) - \vec{X}(t)} \right| $$
(17)
$$ \vec{X}(t + 1) = \vec{X}^{*} (t) - \vec{A} \cdot \vec{D} $$
(18)

where t is the current iteration, \(\vec{A}\) and \(\vec{C}\) is the coefficient vectors, \(\vec{X}^{*} (t)\), the location vector represents the best answer ever obtained, \(\vec{X}(t)\) is the vector of place, | | is the absolute value, and · represents the multiplication of element by element multiplication. It is important to note that if there is a better answer in each iteration, \(\vec{X}^{*} (t)\) then should be updated.

The vectors \(\vec{A}\) and \(\vec{C}\) are obtained using the following formulas:

$$ \vec{A} = 2\vec{a} \cdot \vec{r} - \vec{a} $$
(19)
$$ \vec{C} = 2 \cdot \vec{r} $$
(20)

where \(\vec{a}\) represents a linear decrease from 2 to zero during the iterations (both in the exploration and the exploitation phases) and \(\vec{r}\) represents a random vector in the interval [0,1]. By setting the random values of \(\vec{A}\) in the interval [−1, 1], we can define the new location of the search agent anywhere between the initial position of the agent and the position of the best current agent.

Equation (18) will allow each search agent to update its position in the neighborhood of the current best answer and simulate looping around the prey.

Humpback whales, in addition to the looping strategy around the prey, can also have a spiral motion towards it. This motion can be simulated with the following formula [30]:

$$ \begin{aligned} \vec{X}(t + 1) = & \vec{D}^{ \circ } \cdot e^{bl} \cdot \cos (2\pi l) + \vec{X}^{*} (t) \\ \vec{D}^{ \circ } = & \left| {\vec{X}^{*} (t) - \vec{X}(t)} \right| \\ \end{aligned} $$
(21)

where \(\vec{D}^{ \circ } = \left| {\vec{X}^{*} (t) - \vec{X}(t)} \right|\) and indicates the distance of the ith wale to the prey (best solution obtained so far), b represents a constant that will denote the shape of a logarithmic helix, and l represents a random number in the interval [−1,1].

Note that the humpback whales move around the prey simultaneously, both in the form of a contractile circle and along a spiral path. To model this simultaneous behavior, we assume that there is a 50% probability that the contractile loop mechanism or spiral model can be used to improve the position of the whales during optimization. The mathematical model is as follows:

$$ \vec{X}(t + 1) = \left\{ {\begin{array}{*{20}l} {\vec{X}^{*} (t) - \vec{A} \cdot \vec{D}} \hfill & {{\text{if}}\;p \ge 0.5} \hfill \\ {\vec{D}^{ \circ } \cdot e^{bl} \cdot \cos (2\pi l) + \vec{X}^{*} (t)} \hfill & {{\text{if}}\;p \ge 0.5} \hfill \\ \end{array} } \right. $$
(22)

where p represents a random number in the interval [0,1].

In addition to the bubble net method, humpback whales randomly search for prey. They search randomly, based on each other's position. In order to create a new paradigm in optimization policy, the random value is taken into account for \(\vec{A}\) (higher than 1 and lower than −1) to follow a new position in the search area. This mechanism allows the WOA algorithm to perform a global search. The mathematical model of this work will be as follows [30]:

$$ \begin{aligned} \vec{D} = & \left| {\vec{C} \cdot \vec{X}_{{{\text{rand}}}} - \vec{X}(t)} \right| \\ \vec{X}(t + 1) = & \vec{X}_{{{\text{rand}}}} - \vec{A} \cdot \vec{D} \\ \end{aligned} $$
(23)

where \(\vec{X}_{{{\text{rand}}}}\) represents a random location vector (a random whale) selected from the current population.

4 Springy whale algorithm (SWOA)

Although the whale algorithm has a high rate of convergence, it is stuck in local minima and thus in some cases does not converge to the global minimum. This problem manifests itself better when the amount of unknown parameters to identify is large. In the proposed scheme, changes have been made in the process of moving the whales towards the desired answer so as to improve the performance of the algorithm. A removal phase has been added to the classic whale algorithm to apply the changes. Toward the start of each stage, a certain number of the worst whales will be removed and substituted by new whales in the new search space. Making new early populations allows whales to acquire new ways to get the best response. Regarding this amendment, the probability of being trapped in local minima decreases, and the rapidity of detecting optimal solutions increases.

Preliminary, Elimination Period (ep) (this parameter is added to the classical algorithm and is defined based on the number of iterations) and elimination percent (et) (this parameter is added to the classical algorithm and is determined based on the initial population percentage) are set.

(Th) represents the percentage of the maximum or minimum of the search space. For instance, let us define Th = 95 and the initial search space for the parameters is in the interval [−1, 1]. In each elimination phase, the value of each parameter in the particle is checked, and if it is greater than 95% of the absolute value of the search space, then one unit adds to the search space of that parameter.

The implementation steps of the improved whale algorithm are shown in Fig. 5. The changes applied to the classical algorithm by the blue blocks are shown in this figure.

Fig. 5
figure 5

Flowchart of the SWOA algorithm

Full size image

A prospect of the usage of this method of identifying the unknown parameters of the solar cell system is given in Fig. 6. According to Fig. 6, after repeating the algorithm, each time, the error between the measured current and the extracted current is determined, and by placing this value in Eq. (16), the RMSE will be calculated. The purpose of modifying the classical whale algorithm and to introduce the SWOA algorithm was to minimize the RMSE value.

Fig. 6
figure 6

Overview for parameters estimation of PV Cell models using SWOA

Full size image

5 Experimental results and discussions

In this section, to evaluate the performance of the proposed algorithm, we identify the parameters of the solar cell model and the PV module using the SDM, the DDM, the TDM, and the module model. Voltage–current experimental data from [24, 26] have been chosen as criterion used to test and contrast different methods. These data relate to a commercial silicon solar cell (French RTC Company) with a diameter of 57 mm, at a temperature of 33 ℃ and 1 sun (1000 w⁄m2) and a commercial solar module called Photowatt-PWP201 with 36 polycrystalline cell series at a temperature of 45 ℃ and 1 sun (1000 w⁄m2). Then, the parameters of three types of widely used modules called polycrystalline (SW255), multi-crystalline (KC200GT), and monocrystalline (SM55) have been identified under different radiation and temperature conditions. Then, to test the accuracy of the parameters identified in standard radiation and temperature (\(T_{{{\text{STC}}}} = 25^{ \circ } {\text{C}}, G_{{{\text{STC}}}} = 1000w/m^{2}\)), the behavior of the relevant module was investigated in different radiation and temperature. As a result, it was observed that its behavior with the appropriate error is similar to the diagrams in the module datasheet [9, 49]. Also, the simulation results will be associated with comparing SWOA and some algorithms mentioned in the previous section. These tests were performed in MATLAB 2016b.

To ensure that the exploration space for each problem is identical, the domains correlated with each parameter are maintained as used in the previous literature. Table 1 demonstrates the limited areas for each parameter of the PV cell model and module [26].

Table 1 Parameters ranges of RTC France PV cell and PV module [26]
Full size table

In this paper, for a broader comparison, the algorithms used in each section are different. With the exception of the number of iterations and the number of populations, which are estimated at 5,000 and 30, respectively, the other parameters of the algorithm are set based on the main reference.

5.1 Parameters of RTC France solar cell

In Table 2, the results for estimating the 5 parameters for the SDM are given by SWOA and 10 other algorithms called whale optimization algorithm (WOA) [30], chaotic whale optimization algorithm (CWOA) [31], performance-guided JAYA(PGJAYA) [26], flexible particle swarm optimization (FPSO) [24], improved JAYA (IJAYA) [16], bird mating optimizer (BMO) [24], generalized oppositional teaching learning based optimization (GOTLBO) [29], artificial bee swarm optimization (ABSO) [28], genetic algorithm (GA) [18], and particle swarm optimization algorithm (PSO) [19].

Table 2 Precise results for SDM of RTC France
Full size table

Since no previous data are available for the accurate values of the parameters, the RMSE value is choosing as an index to demonstrate the precision of the parameter estimation. In this comparison, CWOA, FPSO, and PGJAYA methods were able to reach the lowest RMSE value like the SWOA method, and the GA method was able to reach the maximum value.

Tables 3 and 4 show the results for estimating seven parameters for the DDM and nine parameters for the TDM by SWOA and 10 other algorithms, respectively. As can be seen in Tables 3 and 4, the proposed algorithm was able to achieve a better RMSE than other algorithms. It can also be seen that the SWOA algorithm has achieved a lower RMSE value for the TDM than for the other two models. By looking closely at these results, two conclusions can be drawn: First, the TDM is a more accurate model for showing the performance of the RTC FRANCE cell, because in this model, most methods achieved a better RMSE than in the other two models, and second, the SWOA algorithm has a better ability to identify models with more unknown parameters, because it can get a better answer than other algorithms. However, as the number of unknown parameters increased, the rest of the algorithms performed worse, reaching very close RMSE values to the DDM. It should be noted that the best results for all algorithms in TDM were included in the table after 30 runs and were not taken from published results.

Table 3 Precise results for DDM of RTC France
Full size table
Table 4 Precise results for TDM of RTC France
Full size table

Since all meta-heuristic methods start with random points, for a fair comparison, it is necessary to run each method several times and then examine the results. Table 5 demonstrates the results of the studied algorithms during 30 runs. In the first part of this table, which is related to the SDM, it can be seen that most of the methods showed good stability and resistance. But when we increase the number of unknown parameters and move on to the TDM, the algorithms face a difficult challenge. This challenge has led to articles that offer new methods for identifying a cell or solar module parameters. As can be seen from Table 5, SWOA in all three models was able to show considerable stability compared to other algorithms. Also, note that the performance of the CWOA algorithm is also good compared to other algorithms.

Table 5 Comparison between RMSE values of SDM, DDM, TDM of RTC France obtained by different evolutionary methods after 30 runs
Full size table

Table 6 provides information on the estimated current by the SWOA algorithm and the relative error of all three models studied in this paper. To ensure the accuracy of the estimated parameters, it is sufficient to consider the relative error of the current obtained from Eq. (24). As you can see, given that the relative error value is very small, it can be concluded that the parameters have been extracted correctly and the SWOA method was able to estimate the SDM, DDM, and TDM output current well.

$$ R_{{{\text{err}}}} = \frac{{I_{L} - I_{te} }}{{I_{te} }} $$
(24)
Table 6 Relative error for each measurement
Full size table

Another factor that should be in a good way is the speed of getting the best answer. To show the convergence speed of the proposed algorithm, the cost function convergence process (RMSE) for SDM, DDM, and TDM is shown in Figs. 7, 8, and 9, respectively. To ensure that the SWOA has a high convergence rate, it was compared with all the algorithms in Table 5. As shown in Figs. 7, 8, and 9, the SWOA convergence rate is higher than other algorithms.

Fig. 7
figure 7

RMSE evolution of the algorithms for the SD model of RTC France

Full size image
Fig. 8
figure 8

RMSE evolution of the algorithms for the DD model of RTC France

Full size image
Fig. 9
figure 9

RMSE evolution of the algorithms for the TD model of RTC France

Full size image

5.2 Parameters identification of Photowatt-PWP201 PV module

In Table 7, the results for estimating 5 parameters for the SDM are given by SWOA and 9 other algorithms including WOA [30], CWOA [31], PGJAYA [26], JAYA [51], STLBO [8], TLABC [32], CLPSO [33], BLPSO [34], DE/BBO [52].

Table 7 Detailed results for SDM of PWP201
Full size table

In this comparison, STLBO and TLABC methods were able to reach the lowest RMSE value like the SWOA method and WOA and CWOA methods reached the highest value. Note that these two methods performed relatively well in identifying the parameters of the RT. FRANCE system.

Tables 8 and 9 show the results for estimating seven parameters for the DDM and nine parameters for the TDM model by the SWOA and nine other algorithms, respectively. According to Table 8, the SWOA method obtained the lowest RMSE value compared to other methods.

Table 8 Detailed results for DDM of PWP201
Full size table
Table 9 Detailed results for TDM of PWP201
Full size table

Though the RMSE values acquired in the two WOA and SWOA algorithms in DDM are adjacent to each other, and even WOA achieves better results, when we challenge the algorithms and increase the number of parameters from 7 to 9 (TDM), we see that SWOA algorithm showed excellent performance compared to other algorithms and WOA, along with other algorithms, has achieved even worse results than the DDM. However, the TDM is a more accurate model than the DDM. Examining Tables 7, 8, and 9, it is discernible that the SWOA algorithm has reached a lower RMSE value than the SDM and DDM. It should also be noted that the best results for all algorithms in the TDM were included in Table 9 after 30 runs and were not taken from another article.

Table 10 shows the results of the studied algorithms during 30 runs. In the first part of this table, which is related to the SDM, it can be seen that most of the methods showed good stability and resistance. It is very important to note that in practice, an algorithm is efficient that, in addition to quickly finding the optimal point, also has good stability. As you can see from Table 10, this algorithm did not show good stability, while SWOA showed very good stability.

Table 10 Comparison between RMSE values of SDM, DDM, TDM of PWP201 obtained by different evolutionary methods after 30 runs
Full size table

When we add to the number of unknown parameters and move on to the TDM, we are facing algorithms with a difficult challenge. But as can be seen from the table, SWOA in all three models was capable of demonstrating excellent stability compared to other algorithms and once again was able to succeed in this challenge. This success is due to SWOA's high ability to search globally. It should also be noted that the CWOA method showed good stability in the TDM but could not reach the minimum RMSE value, which shows the weakness of this algorithm in global search.

Table 11 is set up to ensure the accuracy of the parameters estimated by the SWOA. As you can see, the relative error value is very low, which points the exactitude of the identified parameters, and the SWOA method was able to estimate well the output current of the single-diode model, DDM, and TDM. Also, in this table, it can be seen that SWOA has reached a lower RMSE value with the TDM than the other two models. To prove it, it is sufficient to calculate the total value of the relative errors of each model separately and compare them with each other. It can be seen that the result of this sum in the model of TDM is less than the DDM and a SDM.

Table 11 Relative error for each measurement
Full size table

To show the convergence speed of the proposed algorithm, the cost function convergence process (RMSE) for single-diode, double-diode, and three-diode PWP201 models is shown in Figs. 10, 11, and 12, respectively. To ensure that the SWOA has a high convergence rate, it was compared with all the algorithms in Table 10. As can be seen from these figures, the SWOA convergence rate is higher than other algorithms.

Fig. 10
figure 10

RMSE evolution of the algorithms for the SD model of PWP201

Full size image
Fig. 11
figure 11

RMSE evolution of the algorithms for the DD model of PWP201

Full size image
Fig. 12
figure 12

RMSE evolution of the algorithms for the TD model of PWP201

Full size image

5.3 Experimental test

In this section, the effect of temperature and radiation changes on voltage-current curves is investigated. In this regard, three different types of PV modules, called monocrystalline (SM55) module [54], multi-crystalline (KC200GT) module [55], and polycrystalline (SW255) module [49], have been taken into account. The experimental data of these solar modules, under STC, have been taken directly from the manufacturer’s datasheet, which is summarized in Table 12.

Table 12 STC specifications for the three modules used in the experiments
Full size table

PV current is a function of temperature and radiation that can be written as Eq. (25):

$$ I_{{{\text{ph}}}} = (I_{{{\text{ph}}\_{\text{STC}}}} + K_{i} \Delta T)\frac{G}{{G_{{{\text{STC}}}} }} $$
(25)

wherein \(I_{{{\text{ph}}\_{\text{STC}}}}\) is the light generated current at STC, \(\Delta T = T - T_{{{\text{STC}}}}\) (\(T_{{{\text{STC}}}} = 25^{ \circ } {\text{C}}\)), G is the surface irradiance of the cell, and GSTC (1000w/m2) is the irradiance at STC. The constant Ki is the short-circuit current coefficient, normally provided by the manufacturer. The following equation can be used to describe the saturation flow with respect to temperature change [55].

$$ I_{{{\text{SD}}}} = \frac{{(I_{{{\text{SC}}\_{\text{STC}}}} + K_{i} \Delta T)}}{{\exp [q(V_{{{\text{OC}}\_{\text{STC}}}} + K_{v} \Delta T)/n{\text{kTN}}] - 1}} $$
(26)

Kv k is coefficient of open-circuit voltage, the value of which is declared by the manufacturer.

From the values presented in the datasheet, the parameters of the selected PV modules are determined using the WHHO algorithm in MATLAB m_script. The results obtained for the three investigated modules are given in Table 13. This table shows that the RMSE value of the proposed method is very small for all the three modules.

Table 13 Identified parameters with the SWOA algorithm at STC
Full size table

The current–voltage and power–voltage curves of the SM55 module are shown in Fig. 13 for different amounts of radiation at a constant temperature T = 25 °C. Figure 14 shows the specifications of the SM55 module for different temperature values at a constant radiation sun = 1000w/m2.

Fig. 13
figure 13

Comparison between the proposed method and the manufacturer Data of the SM55 module for different irradiances, T = 25 °C, a I-V curve, b P–V curve

Full size image
Fig. 14
figure 14

Comparison between the proposed method and the manufacturer Data of the SM55 module for different temperatures, \({\text{G}} = 1000 \, w/m^{2}\), a I–V curve, b P–V curve

Full size image

The I–V and P–V curves of the KC 200GT module are shown in Fig. 15 for various values of irradiance and at T = 25 °C. Figure 16 presents the I–V and the P–V characteristics of this module for different values of temperature and at an irradiance of sun = 1000w/m2.

Fig. 15
figure 15

Comparison between the proposed method and the manufacturer Data of the KC 200GT module for different irradiances, T = 25 °C, a I-V curve, b P–V curve

Full size image
Fig. 16
figure 16

Comparison between the proposed method and the manufacturer Data of the KC 200GT module for different temperatures,\({\text{G}} = 1000 \, w/m^{2}\), a I–V curve, b P–V curve

Full size image

Figure 17 describes I–V and P–V characteristics of the SW255 for ranging of irradiance from 200w/m2 to 1000w/m2 and at T = 25 °C. The I–V curve for different temperatures are not provided in the data sheet issued by the factory.

Fig. 17
figure 17

Comparison between the proposed method and the manufacturer Data of the SW255 module for different irradiances, T = 25 °C, a I–V curve, b P–V curve

Full size image

5.4 The effects of the temperature and irradiance on the module parameters

In Table 14, the results for estimating the 5 parameters for the SDM are given by SWOA for the widely used SM55, KC200GT, and SW255 modules. Model inputs are radiation, temperature, series resistance, parallel resistance. The voltage–current (V–I) characteristic of photovoltaic cells depends on two factors: temperature and radiation. With decreasing temperature and increasing radiation, the output power increases, and with increasing temperature and decreasing the output power decreases. Radiation and temperature are directly and inversely related to the output power, respectively. Tables 14 and 15 show that the estimated parameters \(I_{ph} (A)\) and \(I_{sd1} (\mu A)\) change with changing temperature or radiation conditions, but the variables \(R_{s} (\Omega )\), \(R_{sh} (\Omega )\) and \(n_{1}\) change under different conditions and remain almost constant. From a physical point of view, the parameter \(I_{ph}\) is photo-current and with increasing radiation level, its value increases, which is observable in Table 14. The parameter \(I_{sd1}\) is the reverse saturation current of the diode and its value relies on the temperature. As the temperature gains, the quantity of photons absorbed increases and, as a result, their amount increases. This circumstance is certified by the results presented in Table 15 [26, 50].

Table 14 Estimated optimal parameters by SWOA for three types of PV modules at different irradiance and temperature of 25 °C
Full size table
Table 15 Optimal estimated parameters by WHHO for three modules at different temperature and constant irradiance of 1000 W/m2
Full size table

Besides, it can be found that the resistance value of the \(R_{s}\) series for monocrystalline and multi-crystalline is less than 0.4.

With respect to the ideal factor of diode \(n_{1}\), its value is almost fixed for a specific model under dissimilar circumstances, but its value is distinguished for different types of PV models [26]. It should be noted that the extracted results are close to the results of other methods [19, 24, 29].

6 Conclusion

In this study, a novel improved optimization algorithm called springy whale optimization algorithm (SWOA) is proposed. SWOA has several advantages such as enhancing the performance, high convergence speed, global search capability, and high robustness over WOA. So as to look over the efficiency of SWOA, this algorithm is employed to estimate the parameters of SDM, DDM, TDM and also photovoltaic (PV) modules; the simulation results prove the supremacy of the presented algorithm. Moreover, the effectiveness of SWOA algorithm in the practical application has been assessed using commercial modules, including polycrystalline (SW255), multi-crystalline (KC200GT), and monocrystalline (SM55). This evaluation is accomplished for different operating conditions under different irradiance and temperature conditions, which yield changes in the parameters of the PV model. Finally, the results obtained from various experimental tests confirming the high performance and robustness of the proposed algorithm.